Abstract
For \(n\ge 3\) and \(1<p<\infty \), we prove an \(L^p\)-version of the generalized trace-free Korn-type inequality for incompatible, p-integrable tensor fields \(P:\Omega \rightarrow \mathbb {R}^{n\times n}\) having p-integrable generalized \({\text {Curl}}_{n}\) and generalized vanishing tangential trace \(P\,\tau _l=0\) on \(\partial \Omega \), denoting by \(\{\tau _l\}_{l=1,\ldots , n-1}\) a moving tangent frame on \(\partial \Omega \). More precisely, there exists a constant \(c=c(n,p,\Omega )\) such that
where the generalized \({\text {Curl}}_{n}\) is given by \(({\text {Curl}}_{n} P)_{ijk} :=\partial _i P_{kj}-\partial _j P_{ki}\) and  denotes the deviatoric (trace-free) part of the square matrix X. The improvement towards the three-dimensional case comes from a novel matrix representation of the generalized cross product.
denotes the deviatoric (trace-free) part of the square matrix X. The improvement towards the three-dimensional case comes from a novel matrix representation of the generalized cross product.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The estimate
for
\(n\ge 2\) and \(p\in (1,\infty )\) where  denotes the deviatoric (trace-free) part of the square matrix X and its (compatible) generalizations of (1.1) are well known, cf. [3, 4, 14, 16, 17]. In [9] another generalization to the (incompatible) case
denotes the deviatoric (trace-free) part of the square matrix X and its (compatible) generalizations of (1.1) are well known, cf. [3, 4, 14, 16, 17]. In [9] another generalization to the (incompatible) case
has been given. The main objective of the present paper is to extend (1.2) to the trace-free case for \(n\ge 3\) dimensions. Such a result was expected, cf. [9, Rem. 3.11], and was already proven to hold true for
\(p=2\), cf. [1]. However, the latter used a Helmholtz decomposition and a Maxwell estimate and is not amenable to the
\(L^p\)-case. On the contrary, the argumentation scheme using the Lions lemma resp. Nečas estimate, known from classical Korn inequalities, turned out to be also fruitful in the case of Korn inequalities for incompatible tensor fields, cf. [8,9,10,11] and also [5]. The secret of success is then to determine a linear combination of certain partial derivatives. One such expression in [9] was
 denoting by L a constant coefficients linear operator, for a skew-symmetric matrix field A and scalar field
\(\zeta \). Here, we catch up with a corresponding linear expression in all dimensions
\(n\ge 3\). For that purpose, a careful investigation of the generalized cross product, especially a corresponding matrix representation, will be given. Indeed, it is this matrix representation which allows us to obtain suitable relations which are not easily visible in index notations. Korn’s inequalities in higher dimensions for matrix-valued fields whose incompatibility is a bounded measure and corresponding rigidity estimates were obtained in the recent papers [2, 7], however, without boundary conditions. More precisely, Conti and Garroni [2] obtained as a consequence of a Hodge decomposition with critical integrability due to Bourgain and Brezis for
\(P\in L^1 (\Omega ,\mathbb {R}^{n\times n})\) with
\({\text {Curl}}_{n} P\in \L ^1(\Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\) the sharp geometric rigidity estimate
denoting by L a constant coefficients linear operator, for a skew-symmetric matrix field A and scalar field
\(\zeta \). Here, we catch up with a corresponding linear expression in all dimensions
\(n\ge 3\). For that purpose, a careful investigation of the generalized cross product, especially a corresponding matrix representation, will be given. Indeed, it is this matrix representation which allows us to obtain suitable relations which are not easily visible in index notations. Korn’s inequalities in higher dimensions for matrix-valued fields whose incompatibility is a bounded measure and corresponding rigidity estimates were obtained in the recent papers [2, 7], however, without boundary conditions. More precisely, Conti and Garroni [2] obtained as a consequence of a Hodge decomposition with critical integrability due to Bourgain and Brezis for
\(P\in L^1 (\Omega ,\mathbb {R}^{n\times n})\) with
\({\text {Curl}}_{n} P\in \L ^1(\Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\) the sharp geometric rigidity estimate
with a constant \(c=c(n,\Omega )\), the Sobolev-conjugate exponent \(1^*:=\frac{n}{n-1}\), and where the generalized \({\text {Curl}}_{n}\) is seen without a matrix representation as \(({\text {Curl}}_{n} P)_{ijk} :=\partial _i P_{kj}-\partial _j P_{ki}\). Replacing the geometric rigidity by Korn’s inequality, they deduced from (1.3) furthermore
These estimates remain true for \({\text {Curl}}_{n} P\) being a Radon measure. In that case, the \(L^1\)-norm of \({\text {Curl}}_{n} P\) has to be substituted by the total variation of the measure \({\text {Curl}}_{n} P\), cf. [2]. Lauteri and Luckhaus [7] obtained the rigidity estimate (1.3) in the Lorentz space \(L^{1^*,\infty }\). In [10] we have already established the corresponding results in the \(L^p\)-setting. Here, we focus on the trace-free case showing that the symmetric part can even be replaced by the symmetric deviatoric part.
2 Preliminaries and auxiliary results
By \(.\otimes .\) we denote the dyadic product and by \(\big \langle .,.\big \rangle \) the scalar product, \(\mathfrak {so}(n):=\{A\in \mathbb {R}^{n\times n}\mid A^T = -A\}\) is the Lie-algebra of skew-symmetric matrices and \({\text {Sym}}(n):=\{X\in \mathbb {R}^{n\times n}\mid X^T=X\}\).
Recall that usually the higher-dimensional generalization of the \({\text {curl}}\) is an operation \({\text {curl}}_{n}:\mathscr {D}'(\Omega ,\mathbb {R}^n) \rightarrow \mathscr {D}'(\Omega ,\mathbb {R}^{\frac{n(n-1)}{2}})\) given by
Thus, in order to express this operation using the Hamiltonian formalism as a generalized cross product with \(\nabla \), we focus on the following bijection \(\mathfrak {a}_n: \mathfrak {so}(n)\rightarrow \mathbb {R}^{\frac{n(n-1)}{2}}\) given by
as well as its inverse \(\mathfrak {A}_n:\mathbb {R}^{\frac{n(n-1)}{2}}\rightarrow \mathfrak {so}(n)\), so that
and in coordinates it looks like
Moreover, we will make use of the following notations
and

2.1 A generalized cross product
Regarding our goal to express \({\text {curl}}_{n}\) by the Hamiltonian formalism, we apply the following generalization of the cross product for \(n\ge 2\) acting as \(\times _{n}:\mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}^{\frac{n(n-1)}{2}}\) by
Since for a fixed
\(a\in \mathbb {R}^n\) the operation
\(a\times _{n}.\) is linear, in the second component there exists a unique matrix denoted by
 such that
such that

The matrices
 can be characterized inductively, and for
\(a=(\overline{a},a_n)^T\) the matrix
can be characterized inductively, and for
\(a=(\overline{a},a_n)^T\) the matrix
 has the form
has the form

so,

Remark 2.1
There are many possible identifications of skew-symmetric matrices with vectors. However, it is this matrix representation
 of the generalized cross product
\(\times _{n}\) which allows us to establish the main identities needed for Lemma 2.9. Indeed, they were not easily visible to us before in index notations. Moreover, with this matrix representation in hand, the discussion of the boundary condition (see Observation 2.7) as well as the partial integration formula (2.56) is more transparent.
of the generalized cross product
\(\times _{n}\) which allows us to establish the main identities needed for Lemma 2.9. Indeed, they were not easily visible to us before in index notations. Moreover, with this matrix representation in hand, the discussion of the boundary condition (see Observation 2.7) as well as the partial integration formula (2.56) is more transparent.
Remark 2.2
The entries of the generalized cross product \(a\times _3 b\), with \(a,b\in \mathbb {R}^3\), are permutations (with a sign) of the entries of the classical cross product \(a\times b\). Recall that also the operation \(a\times .\) can be identified with a multiplication with the skew-symmetric matrix
which differs from the expression  and from \(\mathfrak {A}_3(a)\) which reads
and from \(\mathfrak {A}_3(a)\) which reads
Moreover, we have

this allows us to define a generalized cross product of a vector \(b\in \mathbb {R}^n\) and a matrix \(P\in \mathbb {R}^{n\times m}\) from the left and with a matrix \(B\in \mathbb {R}^{m\times n}\) from the right via

and

In such a way, we obtain for all \(b\in \mathbb {R}^n\):

Furthermore, for \(a,b\in \mathbb {R}^n\) it holds

end especially for \(a=b\):

Hence, for all \(a,b\in \mathbb {R}^n\):

by induction over n, and, especially for \(a=b\):

The entries of  are, by definition, linear combinations of \(b_i\,b_j\), the entries of \(b\otimes b\). Interestingly, for \(n\ge 3\) also the converse holds true, i.e., the entries of \(b\otimes b\) are linear combinations of the entries of
are, by definition, linear combinations of \(b_i\,b_j\), the entries of \(b\otimes b\). Interestingly, for \(n\ge 3\) also the converse holds true, i.e., the entries of \(b\otimes b\) are linear combinations of the entries of  which will be assertion of the subsequent lemma. Moreover, we will use this as a key observation to achieve the existence of linear combinations in
which will be assertion of the subsequent lemma. Moreover, we will use this as a key observation to achieve the existence of linear combinations in  for \(n\ge 3\), so that we can follow the argumentation scheme presented in \(n=3\) dimensions, cf. [9], also in the higher-dimensional case.
for \(n\ge 3\), so that we can follow the argumentation scheme presented in \(n=3\) dimensions, cf. [9], also in the higher-dimensional case.
Lemma 2.3
For all \(b\in \mathbb {R}^n\) with \(n\ge 3\), we have:

denoting by L a corresponding constant coefficients linear operator.
Remark 2.4
There are no linear combinations (2.17) in \(n=2\) dimensions. Indeed, we only have

so that there are no linear expressions of \({b_1}^2\), \({b_2}^2\) nor of \(b_1b_2\) in terms of the sole entry of  .
.
Proof of Lemma 2.3by induction over \(n\ge 3\) For the base case \(n=3\), we have

and

Thus, for all \(b\in \mathbb {R}^3\)

and consequently from the expression (2.19) we conclude

Now, assume for the inductive step that for all \(\overline{b}\in \mathbb {R}^{n-1}\) with \(n\ge 4\) we have

For \(b\in \mathbb {R}^n\) we have

Surely,  by the expression (2.14). The induction hypothesis gives
by the expression (2.14). The induction hypothesis gives

hence, also  , so that finally
, so that finally

\(\square \)
By definition (2.11b), the entries of \(B\times _{n}b\) are linear combinations of the entries \(B_{ij}b_k\), i.e., of the entries of the matrix B multiplied with the entries of the vector b. For skew-symmetric matrices, also the converse holds true. This is the assertion of the next lemma.
Lemma 2.5
For all \(A\in \mathfrak {so}(n)\) and \(b\in \mathbb {R}^n\) with \(n\ge 2\), we have
-
(i)
\(A\times _{n}b = L(\mathfrak {a}_n (A) \otimes b)\)
-
(ii)
\(\mathfrak {a}_n (A) \otimes b = L(A\times _{n}b)\)
denoting by L a corresponding constant coefficients linear operator which can differ in both cases.
Proof
For \(A\in \mathfrak {so}(n)\) and \(b\in \mathbb {R}^n\), we have

and on the other hand

Thus, the conclusions of the lemma follow by induction over the dimension n. Indeed, for the base case \(n=2\) we have
which establishes (i) and (ii) of the lemma for \(n=2\).
For the inductive step, let us assume that the statement of the lemma holds for all \(\overline{A}\in \mathfrak {so}(n-1)\) and all \(\overline{b}\in \mathbb {R}^{n-1}\), i.e., it holds:
-
(i)
\(\overline{A}\times _{n-1}\overline{b} = L(\mathfrak {a}_{n-1}(\overline{A}) \otimes \overline{b})\) and
-
(ii)
\(\mathfrak {a}_{n-1} (\overline{A}) \otimes \overline{b} = L(\overline{A}\times _{n-1}\overline{b})\).
Thus, returning to \(A\in \mathfrak {so}(n)\) and \(b\in \mathbb {R}^n\) we have by the expressions (2.26) and (2.27), respectively,
-
(i)
\(\overline{A}\times _{n-1}\overline{b} = L(\mathfrak {a}_{n} (A) \otimes b)\) and
-
(ii)
\(\mathfrak {a}_{n-1}(\overline{A}) \otimes \overline{b} = L(A\times _{n} b)\)
and the conclusion of part (i) of the lemma follows then from the definition of the generalized cross product, indeed,
On the other hand, we have
so that, \(b_n\cdot \overline{A} = L(A\times _{n} b)\) and also \(b_n\cdot \mathfrak {a}_{n-1}(\overline{A}) = L(A\times _{n} b)\) which by (2.27) implies that \(\overline{A\,e_n}\otimes \overline{b}= L(A\times _{n} b)\). This finishes the proof of (ii) since we have shown that all the entries of \(\mathfrak {a}_n (A) \otimes b\) can be written as linear combinations of the entries of \(A\times _{n}b\). \(\square \)
Remark 2.6
The identity (2.30) is not a new result, and usually it is expressed using coordinates:
However, we included the statement as well as the proof not only for the sake of completeness, but also since the use of the matrix representation of the generalized cross product allows us to give a coordinate-free proof and provides a deeper insight into the algebra needed in the present paper. \(\square \)
For a square matrix \(P\in \mathbb {R}^{n\times n}\), we can take the generalized cross product with a vector \(b\in \mathbb {R}^n\) both left and right, and simultaneously we obtain for the identity matrix

and for a general matrix \(P\in \mathbb {R}^{n\times n}\)

Thus, especially for a symmetric matrix \(S\in {\text {Sym}}(n)\) and a skew-symmetric matrix \(A\in \mathfrak {so}(n)\) we obtain
Observation 2.7
Let \(A\in \mathfrak {so}(n)\) and \(\alpha \in \mathbb {R}\). Then,  for \(b\in \mathbb {R}^n\backslash \{0\}\) implies \(A=0\) and \(\alpha =0\).
for \(b\in \mathbb {R}^n\backslash \{0\}\) implies \(A=0\) and \(\alpha =0\).
Proof
Taking the generalized cross product from the left on both sides of  gives
gives

so that taking the trace of the symmetric part on both sides we obtain

which implies \(\alpha =0\). Consequently, we moreover have \(A\times _{n}b=0\) which by Lemma 2.5 (ii) yields \(\mathfrak {a}_n(A)\otimes b =0\), and thus \(\mathfrak {a}_n(A)=0\) and \(A=0\). \(\square \)
2.2 Considerations from vector calculus
Subsequently, we make use of the algebraic behavior of the vector differential operator \(\nabla \) as a vector for formal calculations. So, the derivative and the divergence of a vector field \(a\in \mathscr {D}'(\Omega ,\mathbb {R}^n)\) can be seen as

In a similar way, the generalized curl is related to the generalized cross product

The latter expression gives a generalized row-wise matrix \({\text {Curl}}_{n}\) operator for \(B\in \mathscr {D}'(\Omega ,\mathbb {R}^{m\times n})\) via

This differential operator kills the Jacobian matrix of a vector field (a compatible field), indeed

since \(b\times _{n}b=0\) for all \(b\in \mathbb {R}^n\). Furthermore, for a scalar field \(\zeta \in \mathscr {D}'(\Omega ,\mathbb {R})\) we obtain

For \(P\in \mathscr {D}'(\Omega ,\mathbb {R}^{n\times m})\), we consider also the column-wise differential operator of first order coming from a cross product from the left, namely

which kills the transposed Jacobian \(({\text {D}}a)^T\).
It is clear that \({\text {Curl}}_{n} B=L({\text {D}}B)\), i.e., the entries of \({\text {Curl}}_{n} B\) are linear combinations of the entries of \({\text {D}}B\) for all \(B\in \mathscr {D}'(\Omega ,\mathbb {R}^{m\times n})\). However, for skew-symmetric matrix fields also the converse holds true:
Corollary 2.8
For all \(A\in \mathscr {D}'(\Omega ,\mathfrak {so}(n))\) with \(n\ge 2\) it holds: \({\text {D}}A=L({\text {Curl}}_{n}A)\).
It is a well-known result and follows from the linear expression (ii) in Lemma 2.5 replacing b by \(-\nabla \) as well as from its analogous statement written out in coordinates (2.31).
We now catch up with the crucial linear relation needed in our argumentation scheme.
Lemma 2.9
Let \(n\ge 3\), \(A\in \mathscr {D}'(\Omega ,\mathfrak {so}(n))\) and \(\zeta \in \mathscr {D}'(\Omega ,\mathbb {R})\). Then, the entries of  are linear combinations of the entries of
are linear combinations of the entries of  .
.
Remark 2.10
The statement is false in \(n=2\) dimensions. Indeed, with \(\alpha ,\zeta \in \mathscr {D}'(\Omega ,\mathbb {R})\) we have
so that
and we cannot extract \(\partial _1\partial _1\, \alpha \) from the components of (2.44).
Proof of Lemma 2.9
The proof is divided into the two observations
-
1.
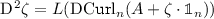 ,
, -
2.
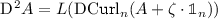
denoting by L a corresponding constant coefficients linear operator which can differ in both cases. To show that the entries of the Hessian \({\text {D}}^2 \zeta \) can be written as linear combinations of the entries of  , we introduce the following second-order derivative operator for square matrix fields \(P\in \mathscr {D}'(\Omega ,\mathbb {R}^{n\times n})\):
, we introduce the following second-order derivative operator for square matrix fields \(P\in \mathscr {D}'(\Omega ,\mathbb {R}^{n\times n})\):
in the style of the incompatibility operator known from the three-dimensional case. In regard of (2.32), we see

so that substituting b by \(-\nabla \) in Lemma 2.3 we obtain

Moreover, with regard to (2.34)\(_2\) we have for a skew-symmetric matrix field \(A\in \mathscr {D}'(\Omega ,\mathfrak {so}(n))\):
concluding for the 1. part that

where in the last step we have used that the entries of \(\mathbf{inc }_n P = - \nabla \times _{n}({\text {Curl}}_{n}P)\) are, of course, linear combinations of the entries from \({\text {D}}{\text {Curl}}_{n} P\).
To establish part 2, recall that the entries of \({\text {D}}A\) for a skew-symmetric matrix field are linear combinations of the entries of \({\text {Curl}}_{n}A\), giving

The conclusion follows by taking the \(\partial _j\)-derivative of (2.50) together with the observation from the 1. part:

\(\square \)
In the last result of this section, we focus on the kernel of \({\text {dev}}_n{\text {sym}}\) and \({\text {Curl}}_{n}\):
Lemma 2.11
Let \(n\ge 3\), \(A\in L^p(\Omega ,\mathfrak {so}(n))\) and \(\zeta \in L^p(\Omega ,\mathbb {R})\). Then,  in the distributional sense if and only if there exists constant \(b\in \mathbb {R}^n\), \(d\in \mathbb {R}^{\frac{n(n-1)}{2}}\), \(\beta \in \mathbb {R}\) such that
in the distributional sense if and only if there exists constant \(b\in \mathbb {R}^n\), \(d\in \mathbb {R}^{\frac{n(n-1)}{2}}\), \(\beta \in \mathbb {R}\) such that  almost everywhere in \(\Omega \).
almost everywhere in \(\Omega \).
Remark 2.12
The “only if”-part is false in \(n=2\) dimensions. To see this, take in (2.43) \(\alpha \) and \(\zeta \) to be the real and imaginary part of a holomorphic function.
Proof of Lemma 2.11
For the “if”-part we have

Conversely,  in the distributional sense implies by (2.49):
in the distributional sense implies by (2.49):
thus,
for some \(b\in \mathbb {R}^n\), \(\beta \in \mathbb {R}\), \(B\in \mathbb {R}^{\frac{n(n-1)}{2}\times n}\) and \(d\in \mathbb {R}^{\frac{n(n-1)}{2}}\), and we have

as well as
where \(C\in \mathbb {R}^{\frac{n(n-1)}{2}\times n}\) has only possibly nonzero entries at those positions at which the matrix  has zeros. Hence, the condition,
has zeros. Hence, the condition,  gives:
gives:

implying that \(C\equiv 0\) and  almost everywhere in \(\Omega \). \(\square \)
almost everywhere in \(\Omega \). \(\square \)
Remark 2.13
The expression of the kernel follows also from the consideration for the classical trace-free Korn inequalities. Indeed, on simply connected domains, \({\text {Curl}}_{n}P\equiv 0\) implies that \(P={\text {D}}u\) for a vector field \(u\in W^{1,\,p}(\Omega ,\mathbb {R}^n)\). Thus, the condition \({\text {dev}}_n{\text {sym}}P\equiv 0\) reads \({\text {dev}}_n{\text {sym}}{\text {D}}u\equiv 0\), whose solutions are well known as infinitesimal conformal mappings, cf. [1, 3, 6, 12, 14,15,16].
2.3 Function spaces
Having above relations at hand, we can now catch up the arguments from [9]. Let \(\Omega \subseteq \mathbb {R}^n\); we start by defining the space
equipped with the norm
and its subspace \(W^{1,\,p}_0({\text {Curl}}_{n}; \Omega ,\mathbb {R}^{n\times n})\) as the completion of \(C^\infty _0(\Omega ,\mathbb {R}^{n\times n})\) in the \(W^{1,\,p}({\text {Curl}}_{n}; \Omega ,\mathbb {R}^{n\times n})\)-norm.
In our proofs, we shall use an important equivalence of norms due to Nečas [13, Théorème 1] valid on bounded Lipschitz domains, cf. also discussion in [9, 11] and the references cited therein.
Thus, in what follows \(\Omega \subset \mathbb {R}^n\) will be a bounded domain with Lipschitz boundary and we are allowed to define boundary conditions in the distributional sense, so that
where \(\nu \) stands for the outward unit normal vector field and \(\{\tau _l\}_{l=1,\ldots , n-1}\) denotes a moving tangent frame on \(\partial \Omega \), cf. [10]. Here, the generalized tangential trace \(P\times _{n} \nu \) is understood in the sense of \(W^{-\frac{1}{p},\, p}(\partial \Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\) which is justified by partial integration, so that its trace is defined by

having denoted by \(\widetilde{Q}\in W^{1,\,p'}(\Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\) any extension of Q in \(\Omega \), where \(\big \langle .,.\big \rangle _{\partial \Omega }\) indicates the duality pairing between \(W^{-\frac{1}{p},\,p}(\partial \Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\) and \(W^{1-\frac{1}{p'},\,p'}(\partial \Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\). Indeed, for smooth P and Q on \(\overline{\Omega }\) we have

where in \((*)\) we have used the fact that we only deal with linear combinations of partial derivatives and from the classical divergence theorem it holds
for a smooth scalar function \(\zeta \) on \(\overline{\Omega }\).
Further, following [11] we introduce also the space \(W^{1,\,p}_{\Gamma ,0}({\text {Curl}}_{n};\Omega ,\mathbb {R}^{n\times n})\) of functions with vanishing tangential trace only on a relatively open (non-empty) subset \(\Gamma \subseteq \partial \Omega \) of the boundary by completion of \(C^\infty _{\Gamma ,0}(\Omega ,\mathbb {R}^{n\times n})\) with respect to the \(W^{1,\,p}({\text {Curl}}_{n};\Omega ,\mathbb {R}^{n\times n})\)-norm.
3 Trace-free Korn inequalities for incompatible tensors in higher dimensions
With the auxiliary results in hand, we can now catch up with the higher-dimensional versions of the results presented in [9].
Lemma 3.1
Let \(n\ge 3\), \(\Omega \subset \mathbb {R}^n\) be a bounded Lipschitz domain and \(1<p<\infty \). Then, \(P\in \mathscr {D}'(\Omega ,\mathbb {R}^{n\times n})\), \({\text {dev}}_n{\text {sym}}P\in L^p(\Omega ,\mathbb {R}^{n\times n})\) and \({\text {Curl}}_{n} P \in W^{-1,\,p}(\Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\) imply \(P\in L^p(\Omega ,\mathbb {R}^{n\times n})\). Moreover, we have the estimate

with a constant \(c=c(n,p,\Omega )>0\).
Proof
We have to show that  follows from the assumptions of the lemma. By the linearity of differential operator \({\text {D}}{\text {Curl}}_{n}\) and the orthogonal decomposition
follows from the assumptions of the lemma. By the linearity of differential operator \({\text {D}}{\text {Curl}}_{n}\) and the orthogonal decomposition  holding in \(\mathscr {D}'(\Omega ,\mathbb {R}^{n\times n})\), we obtain
holding in \(\mathscr {D}'(\Omega ,\mathbb {R}^{n\times n})\), we obtain

Thus, by the assumed regularity of the right-hand side, it follows that the left-hand side belongs to \( W^{-2,\,p}(\Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}\times n})\). Furthermore, we have

By Lemma 2.9 we obtain  and an application of the Lions lemma resp. Nečas estimate [9, Thm. 2.7 and Cor. 2.8] to
and an application of the Lions lemma resp. Nečas estimate [9, Thm. 2.7 and Cor. 2.8] to  yield the conclusions. \(\square \)
yield the conclusions. \(\square \)
Eliminating the first term on the right-hand side of (3.1) gives:
Theorem 3.2
Let \(n\ge 3\), \(\Omega \subset \mathbb {R}^n\) be a bounded Lipschitz domain and \(1<p<\infty \). There exists a constant \(c=c(n,p,\Omega )>0\), such that for all \(P\in L^p(\Omega ,\mathbb {R}^{n\times n})\) we have
where the kernel is given by

Remark 3.3
This result does not directly extend to \(n=2\), since in that case the condition \({\text {dev}}_2{\text {sym}}{\text {D}}u\equiv 0\) becomes the system of Cauchy–Riemann equations \(\{u_{1,x}=u_{2,y} \ \wedge \ u_{1,y}=-u_{2,x} \}\) so that the corresponding nullspace is infinite-dimensional.
Proof of Theorem 3.2
The characterization of the kernel of the right-hand side gives

so that \(P\in K_{dS,C_n}\) if and only if  and
and  . Hence, (3.5) follows by virtue of Lemma 2.11 and the conclusion follows in a similar way to [9, Thm. 3.8]. \(\square \)
. Hence, (3.5) follows by virtue of Lemma 2.11 and the conclusion follows in a similar way to [9, Thm. 3.8]. \(\square \)
Remark 3.4
For compatible displacement gradients \(P={\text {D}}u\), we get back from (3.4) the quantitative version of the classical trace-free Korn’s inequality, cf. [3, 15, 16].
Finally, we examine the effect of tangential boundary conditions \(P\times _{n}\nu \equiv 0\).
Theorem 3.5
Let \(n\ge 3\), \(\Omega \subset \mathbb {R}^n\) be a bounded Lipschitz domain and \(1<p<\infty \). There exists a constant \(c=c(n,p,\Omega )>0\), such that for all \(P\in W^{1,\,p}_0({\text {Curl}}_{n}; \Omega ,\mathbb {R}^{n\times n})\) we have
Proof
We follow the same argumentation scheme as in the proof of [11, Theorem 3.5] and consider a sequence \(\{P_k\}_{k\in \mathbb {N}}\subset W^{1,\,p}_0({\text {Curl}}_{n};\Omega ,\mathbb {R}^{n\times n})\) converging weakly in \(L^p(\Omega ,\mathbb {R}^{n\times n})\) to some \(P^*\) so that \({\text {dev}}_n{\text {sym}}P^* = 0\) almost everywhere and \({\text {Curl}}_{n} P^* = 0\) in the distributional sense, i.e., \(P^*\in K_{dS,C_n}\). By (2.56) we obtain that \(\big \langle P^*\times _{n} (-\nu ),Q\big \rangle _{\partial \Omega }=0\) for all \(Q\in W^{1,\,p'}(\Omega ,\mathbb {R}^{n\times \frac{n(n-1)}{2}})\). However, the boundary condition \(P^*\times _{n}\nu =0\) is also valid in the classical sense, since \(P^*\in K_{dS,C_n}\) has an explicit representation. Using the explicit representation of  , we conclude using Observation 2.7 that, in fact, \(P^*\equiv 0\):
, we conclude using Observation 2.7 that, in fact, \(P^*\equiv 0\):

\(\square \)
Remark 3.6
Estimate (3.6) should persist also in \(n=2\) dimensions. So, the case \(p=2\) is already contained in [1]. However, for the general case \(p\in (1,\infty )\) we need a different approach and it will be the subject of a forthcoming note.
Remark 3.7
For compatible \(P={\text {D}}u\) we recover from (3.6) a tangential trace-free Korn inequality.
Remark 3.8
For \(n\ge 3\), the previous results also hold true for tensor fields with vanishing tangential trace only on a relatively open (non-empty) subset \(\Gamma \subseteq \partial \Omega \) of the boundary, cf. discussion in [11]. But, this is not the case in \(n=2\) dimensions. Indeed, already the trace-free version of Korn’s first inequality (1.1) with only partial boundary condition is false in the \(n=2\) case, cf., e.g., the counterexample contained in [1, section 6.6].
References
Bauer, S., Neff, P., Pauly, D., Starke, G.: Dev-Div- and DevSym-DevCurl-inequalities for incompatible square tensor fields with mixed boundary conditions. ESAIM: Control, Optimisation and Calculus of Variations 22(1), 12–133 (2016)
Conti, S., Garroni, A.: Sharp rigidity estimates for incompatible fields as a consequence of the Bourgain Brezis div-curl result. Comptes Rendus. Mathématique, Tome 359(2), 155–160 (2021). https://doi.org/10.5802/crmath.161, https://comptes-rendus.academiesciences.fr/mathematique/articles/10.5802/crmath.161/
Dain, S.: Generalized Korn’s inequality and conformal Killing vectors. Calc. Var. Partial. Differ. Equ. 25(4), 535–540 (2006)
Fuchs, M., Schirra, O.: An application of a new coercive inequality to variational problems studied in general relativity and in Cosserat elasticity giving the smoothness of minimizers. Arch. Math. 93(6), 587–596 (2009)
Gmeineder, F., Spector, D.: On Korn-Maxwell-Sobolev Inequalities. J. Math. Anal. Appl. 502, 125226 (2021) https://doi.org/10.1016/j.jmaa.2021.125226
Jeong, J., Neff, P.: Existence, uniqueness and stability in linear Cosserat elasticity for weakest curvature conditions. Math. Mech. Solids 15(1), 78–95 (2010)
Lauteri, G., Luckhaus, S.: “Geometric rigidity estimates for incompatible fields in dimension \(\ge \) 3” (2017). arXiv: 1703.03288 [math.AP]
Lewintan, P., Müller, S., Neff, P.: “Korn inequalities for incompatible tensor fields in three space dimensions with conformally invariant dislocation energy”. To appear in Calc. Var. Partial. Differ. Equ. (2021)
Lewintan, P., Neff, P.: “\(L^{p}\)-trace-free generalized Korn inequalities for incompatible tensor fields in three space dimensions”. submitted (2020). arXiv: 2004.05981 [math.AP]
Lewintan, P., Neff, P.: “Nečas-Lions lemma revisited: An \(L^{p}\)-version of the generalized Korn inequality for incompatible tensor fields”. Math. Methods Appl. Sci. (2021). https://doi.org/10.1002/mma.7498
Lewintan, P., Neff, P.: “\(L^{p}\)-versions of generalized Korn inequalities for incompatible tensor fields in arbitrary dimensions with \(p\)-integrable exterior derivative”. To appear in Comptes Rendus. Mathématique (2021)
Neff, P., Jeong, J., Ramezani, H.: Subgrid interaction and micro-randomness - novel invariance requirements in infinitesimal gradient elasticity. Int. J. Solids Struct. 46(25–26), 4261–4276 (2009)
Nečas, J.: “Sur les normes équivalentes dans \(W^{(k)}_p (\Omega )\) et sur la coercivité des formes formellement positives”. Équations aux dérivées partielles. Les Presses de l’Université de Montreal, pp. 102–128 (1966)
Reshetnyak, Y.G.: Estimates for certain differential operators with finite-dimensional kernel. Siberian Math. J. 11(2), 315–326 (1970)
Reshetnyak, Y.G.: Stability Theorems in Geometry and Analysis. Springer Science+Business Media Dordrecht (1994)
Schirra, O.D.: New Korn-type inequalities and regularity of solutions to linear elliptic systems and anisotropic variational problems involving the trace-free part of the symmetric gradient. Calc. Var. Partial. Differ. Equ. 43(1), 147–172 (2012)
Smith, K.T.: Formulas to represent functions by their derivatives”. Math. Ann. 188, 53–77 (1970)
Acknowledgements
The authors thank the referees for their valuable comments. This work was initiated in the framework of the Priority Programme SPP 2256 “Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials” funded by the Deutsche Forschungsgemeinschaft (DFG, German research foundation), Project ID 422730790. The second author was supported within the project “A variational scale-dependent transition scheme–from Cauchy elasticity to the relaxed micromorphic continuum” (Project ID 440935806). Moreover, both authors were supported in the Project ID 415894848 by the Deutsche Forschungsgemeinschaft.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lewintan, P., Neff, P. \(L^p\)-trace-free version of the generalized Korn inequality for incompatible tensor fields in arbitrary dimensions. Z. Angew. Math. Phys. 72, 127 (2021). https://doi.org/10.1007/s00033-021-01550-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-021-01550-6


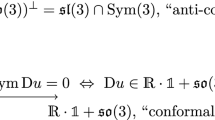


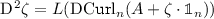 ,
,