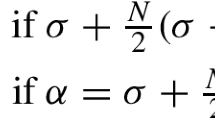Abstract
The chemotaxis May–Nowak model
is considered in a bounded domain \(\Omega \subset \mathbb {R}^n (n\ge 1)\) with homogeneous Neumann boundary conditions and the parameters \(D_u,D_v,D_w,r>0\). The chemotactic sensitivity function and the conversion function are given by \(f\left( s\right) =K_{f}\left( 1+s\right) ^{-\alpha }\) and \(g(s) = K_{g} s^{\beta }\) for all \(s > 0\), respectively, where \(K_{f}\in \mathbb {R}\), \(K_{g}, \alpha , \beta >0\). The global boundedness of solution is shown if the following case holds:
Moreover, for the large time behavior of the global smooth bounded solution, the basic reproduction number \(R_{0}:=K_{g}r^{\beta }\) has an important effect (Lai and Zou in Bull Math Biol 76:2806-2833, 2014; Wang et al. in Nonlinear Anal RWA 33:253-283, 2017), and system has the infection-free steady state if \(0<R_0<1\) and the coexistence equilibrium steady state if \(R_0>1\) (Korobeinikov in Bull Math Biol 66:879-883, 2004). By constructing an appropriate energy function, under the conditions that \(K_f\) and \(K_g\) are appropriately mild, it is shown that: \(\bullet \) If \(R_0\in (0,1)\), then any global bounded solution converges to \(\left( r, 0, 0\right) \) as \(t\rightarrow \infty \); \(\bullet \) If \(R_0\in (1,\infty )\), \(\beta =1\), then any global bounded solution converges to \(\bigg ( \frac{1}{K_g}, r-\frac{1}{K_g}, r-\frac{1}{K_g} \bigg )\) as \(t\rightarrow \infty \).
Similar content being viewed by others
References
Bai, X., Winkler, M.: Equilibration in a fully parabolic two-species chemotaxis system with competitive kinetics. Indiana Univ. Math. J. 65, 553–583 (2016)
Bellomo, N., Bellouquid, A., Tao, Y., Winkler, M.: Toward a mathematical theory of Keller–Segel models of pattern formation in biological tissues. Math. Models Methods Appl. Sci. 25, 1663–1763 (2015)
Bellomo, N., Painter, K.J., Tao, Y., Winkler, M.: Occurrence vs. absence of taxis-driven instabilities in a May–Nowak model for virus infection. SIAM J. Appl. Math. 79, 1990–2010 (2019)
Bellomo, N., Tao, Y.: Stabilization in a chemotaxis model for virus infection. Discrete Contin. Dyn. Syst. Ser. S. 13, 105–117 (2020)
Bonhoeffer, S., May, R.M., Shaw, G.M., Nowak, M.A.: Virus dynamics and drug therapy. Proc. Natl. Acad. Sci. 94, 6971–6976 (1997)
Campos, D., Méndez, V., Fedotov, S.: The effects of distributed life cycles on the dynamics of viral infections. J. Theor. Biol. 254, 430–438 (2008)
Friedman, A.: Partial Differential Equations. Holt, Rinehart and Winston, New York (1969)
Fuest, M.: Boundedness enforced by mildly saturated conversion in a chemotaxis-May–Nowak model for virus infection. J. Math. Anal. Appl. 472, 1729–1740 (2019)
Hethcote, H.W.: The mathematics of infectious diseases. SIAM Rev. 42, 599–653 (2000)
Hirata, M., Kurima, S., Mizukami, M., Yokota, T.: Boundedness and stabilization in a two-dimensional two-species chemotaxis-Navier–Stokes system with competitive kinetics. J. Differ. Equ. 263, 470–490 (2017)
Horstmann, D., Winkler, M.: Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215, 52–107 (2005)
Hu, B., Lankeit, J.: Boundedness of solutions to a virus infection model with saturated chemotaxis. J. Math. Anal. Appl. 468, 344–358 (2018)
Ishida, S., Seki, K., Yokota, T.: Boundedness in quasilinear Keller–Segel systems of parabolic-parabolic type on non-convex bounded domains. J. Differ. Equ. 258, 2993–3010 (2014)
Jones, E., Roemer, P., Raghupathi, M., Pankavich, S.: Analysis and simulation of the three-component model of HIV dynamics. SIAM Undergr. Res. Online 7, 89–105 (2014)
Keller, E.F., Segel, L.A.: Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 26, 399–415 (1970)
Korobeinikov, A.: Global properties of basic virus dynamics models. Bull. Math. Biol. 66, 879–883 (2004)
Lai, X., Zou, X.: Repulsion effect on superinfecting virions by infected cells. Bull. Math. Biol. 76, 2806–2833 (2014)
Lions, J.L., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications, vol. 1. Springer, Berlin (2012)
Liu, D., Tao, Y.: Boundedness in a chemotaxis system with nonlinear signal production. Appl. Math. J. Chin. Univ. Ser. B. 31, 379–388 (2016)
Mizoguchi, N., Souplet, P.: Nondegeneracy of blow-up points for the parabolic Keller–Segel system. Ann. Inst. H. Poincaré Anal. Non Linéaire. 31, 851–875 (2014)
Nirenberg, L.: An extended interpolation inequality. Ann Scuo. Norm. Sup Pisa. 20, 733–737 (1966)
Nowak, M.A., Bangham, C.R.: Population dynamics of immune responses to persistent viruses. Science 272, 74–79 (1996)
Nowak, M., May, R.M.: Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford University Press, London (2000)
Pan, X., Wang, L.: Improvement of conditions for boundedness in a fully parabolic chemotaxis system with nonlinear signal production. C. R. Mathématique. (2020) to appear
Pan, X., Wang, L.: On a quasilinear fully parabolic two-species chemotaxis system with two chemicals. Discrete Contin. Dyn. Syst. Ser. B. (2021). https://doi.org/10.3934/dcdsb.2021047
Perelson, A.S., Neumann, A.U., Markowitz, M., Leonard, J.M., Ho, D.D.: HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science 271, 1582–1586 (1996)
Stancevic, O., Angstmann, C., Murray, J.M., Henry, B.I.: Turing patterns from dynamics of early HIV infection. Bull. Math. Biol. 75, 774–795 (2013)
Tao, Y., Wang, Z.: Competing effects of attraction vs. repulsion in chemotaxis. Math. Models Methods Appl. Sci. 23, 1–36 (2013)
Tao, Y., Winkler, M.: Boundedness in a quasilinear parabolic-parabolic Keller-Segel system with subcritical sensitivity. J. Differ. Equ. 252, 692–715 (2012)
Wang, L., Mu, C.: A new result for boundedness and stabilization in a two-species chemotaxis system with two chemicals. Discrete Contin. Dyn. Syst. Ser. B. 25, 4585–4601 (2020)
Wang, L., Li, Y., Mu, C.: Boundedness in a parabolic-parabolic quasilinear chemotaxis system with logistic source. Discrete Contin. Dyn. Syst. 34, 789–802 (2014)
Wang, L., Mu, C., Zheng, P.: On a quasilinear parabolic-elliptic chemotaxis system with logistic source. J. Differ. Equ. 256, 1847–1872 (2014)
Wang, W., Ma, W., Lai, X.: Repulsion effect on superinfecting virions by infected cells for virus infection dynamic model with absorption effect and chemotaxis. Nonlinear Anal. RWA 33, 253–283 (2017)
Wei, X., Ghosn, S.K., Taylor, M.E., Johnson, V.A.A., Emini, E.A., Deutsch, P., Lifson, J.D., Bonhoeffer, S., Nowak, M.A., Hahn, B.H., Saag, M.S., Shaw, G.M.: Viral dynamics in human immunodeficiency virus type 1 infection. Nature 373, 117–122 (1995)
Winkler, M.: A critical blow-up exponent in a chemotaxis system with nonlinear signal production. Nonlinearity 31, 2031–2056 (2018)
Winkler, M.: Aggregation vs. global diffusive behavior in the higher-dimensional Keller–Segel model. J. Differ. Equ. 248, 2889–2905 (2010)
Winkler, M.: Boundedness in a chemotaxis-May–Nowak model for virus dynamics with mildly saturated chemotactic sensitivity. Acta Appl. Math. 163, 1–17 (2019)
Winkler, M.: Boundedness in the higher-dimensional parabolic-parabolic chemotaxis system with logistic source. Commun. Partial Differ. Equ. 35, 1516–1537 (2010)
Winkler, M.: Does a ‘volume-filling effect’ always prevent chemotactic collapse? Math. Methods Appl. Sci. 33, 12–24 (2010)
Winkler, M.: Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller–Segel system. J. Math. Pures Appl. 100, 748–767 (2013)
Xiang, T.: How strong a logistic damping can prevent blow-up for the minimal Keller–Segel chemotaxis system? J. Math. Anal. Appl. 459, 1172–1200 (2018)
Acknowledgements
The authors thank the anonymous referee for his/her positive and useful comments, which helped him improve further the exposition of the paper. This work is supported by the Chongqing Research and Innovation Project of Graduate Students (No. CYS20271).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Pan, X., Wang, L. & Hu, X. Boundedness and stabilization of solutions to a chemotaxis May–Nowak model. Z. Angew. Math. Phys. 72, 52 (2021). https://doi.org/10.1007/s00033-021-01491-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-021-01491-0