The Whittaker Functional Is a Shifted Microstalk

Abstract

For a smooth projective curve X and reductive group G, the Whittaker functional on nilpotent sheaves on $Bun _G(X)$ is expected to correspond to global sections of coherent sheaves on the spectral side of Betti geometric Langlands. We prove that the Whittaker functional calculates the shifted microstalk of nilpotent sheaves at the point in the Hitchin moduli where the Kostant section intersects the global nilpotent cone. In particular, the shifted Whittaker functional is exact for the perverse t-structure and commutes with Verdier duality. Our proof is topological and depends on the intrinsic local hyperbolic symmetry of $Bun _G(X)$. It is an application of a general result relating vanishing cycles to the composition of restriction to an attracting locus followed by vanishing cycles.

1 Introduction

Let X be a smooth projective complex curve, G a complex reductive group with Langlands dual $G^\vee$.

1.1 Main Result

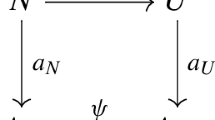
The Betti variant [3] of the geometric Langlands conjecture [1, 2, 9] says there should be an equivalence

$$\begin{aligned} Sh _{\Lambda }(Bun _G(X)) \simeq Ind Coh _{\mathcal {N}}(Loc _{G^{\vee }}(X)) \end{aligned}$$

(1.1)

compatible with natural structures (Hecke operators, parabolic induction, cutting and gluing curves...) on each side.

In this paper, we will only be concerned with the left-hand automorphic side, $Sh _{\Lambda }(Bun _G(X))$, the (dg derived) category of sheaves with singular support [8] in $\Lambda$. Here $\Lambda = h^{-1}(0) \subset T^*Bun _G(X)$ is the global nilpotent cone, the closed conic Lagrangian [2, 6, 10] given by the zero-fiber of the Hitchin system $h:T^*Bun _G(X)\rightarrow \mathfrak {c}^*_G(X)$.

The Kostant section $\kappa : \mathfrak {c}^*_G(X) \rightarrow T^*Bun _G(X)$ to the Hitchin system has image $K = \kappa ( \mathfrak {c}^*_G(X) )$ a closed (non-conic) Lagrangian that intersects $\Lambda$ transversely at a smooth point $\lambda \in \Lambda$. Informally speaking, following paradigms from T-duality applied to Hitchin systems, one expects the “Lagrangian A-brane” K to correspond to the space-filling “coherent B-brane” $\mathcal {O}_{Loc _{G^{\vee }}(X)}$. If K were to define a nilpotent sheaf $\mathcal {F}_K\in Sh _{\Lambda }(Bun _G(X))$, one would expect the corepresented functor $Hom (\mathcal {F}_K, -)$ to give the microstalk of nilpotent sheaves at the intersection point $\lambda = K \cap \Lambda$. Thus under T-duality, one would expect the microstalk at $\lambda$ to correspond to the global sections functor $\Gamma (Loc _{G^{\vee }}(X), -) \simeq Hom (\mathcal {O}_{Loc _{G^{\vee }}(X)}, -)$.

Explicitly describing the nilpotent sheaf $\mathcal {F}_K$ corepresenting the microstalk of nilpotent sheaves at $\lambda$ is a difficult problem. But our main result, Theorem 3.3.4, confirms the traditional Whittaker functional

(1.2)

indeed calculates the (shifted) microstalk at $\lambda = df(\rho ^{\vee }(\omega ))$ of nilpotent sheaves. Here we first pull back along

$$\begin{aligned} i: Bun _N^{\omega }(X) \rightarrow Bun _G(X) \end{aligned}$$

(1.3)

and then take vanishing cycles for a particular function

$$\begin{aligned} f: Bun _N^{\omega }(X) \rightarrow \mathbb {A}^1. \end{aligned}$$

(1.4)

We will recall the notation and further details in Section 3.1.¹

We also calculate the shift: the Whittaker functional is the usual exact microstalk (with respect to the perverse t-structure) after a shift by $\dim _{\rho ^{\vee }(\omega )} Bun _{B^-}(X)$. This exactness of the shifted Whittaker functional was recently obtained by Færgeman-Raskin [5] and we were in part motivated by giving a geometric explanation of their results. Our proof of exactness only uses the hyperbolic symmetry of $Bun _G(X)$, as opposed to tools from geometric Langlands. Our general result, Theorem 2.2.2, may be applicable outside of representation theory. As will be explained in Section 3.4, our arguments easily extend to the case of tame ramification.

Remark 1.1.1

The Whittaker functional is corepresented by the (non nilpotent) Whittaker sheaf $i_!f^* \Psi$ where $\Psi$ is a $\mathbb {G}_m$-equivariant version of the Artin-Schreier sheaf (see for example [11]). Let us pretend that the singular support of $f^*\Psi$ were the graph of the differential $\Gamma _{df} \subset T^*Bun _N^{\omega }(X)$. This is of course nonsense because singular support is a closed conic Lagrangian. But it is motivated by the observation that $f^* \Psi$ corepresents vanishing cycles for f. Accepting this, we would then expect the singular support of the Whittaker sheaf to be the shifted conormal bundle $T^*_{Bun _N^{\omega }(X)} Bun _G(X) + df \subset T^*Bun _G(X)$ which coincides with the Kostant section $K \subset T^*Bun _G(X)$.

1.2 Overview

Here is a brief overview of the sections of the paper.

In Sect. 2.2, we establish the general result, Theorem 2.2.2, that in the presence of hyperbolic $\mathbb {C}^\times$-symmetry on a complex manifold Y, the !-restriction to the attracting locus $i:Y^{>0} \rightarrow Y$ of a point $y_0\in Y$, followed by vanishing cycles $\phi _{f, y_0}$ for a function f on $Y^{>0}$ is naturally isomorphic to vanishing cycles $\phi _{F, y_0}$ for a suitable extension F of f to Y. Adjunction provides a natural map

(1.6)

To show Eq. 1.6 is an isomorphism, we corepresent the respective functionals by !-extensions of constant sheaves on regions $V \subset W \subset Y$. The cone of the map Eq. 1.6 is corepresented by the !-extension of the “difference” $k_{W \setminus V}$. We show the cone vanishes on sheaves with hyperbolic symmetry since $W \setminus V$ is foliated by its intersection with $\mathbb {R}^{>0}$-orbits entering through its closed $*$-boundary and exiting through its open !-boundary.

Next we fix a singular support $\Lambda \subset T^*Y$, and study the vanishing cycles $\phi _{F, y_0}$ for the extended function F. In Theorem 2.2.2 we required F to be maximally negative definite in the repelling directions. Now we also ask for the graph of its differential to intersect $\Lambda$ transversely. In Sect. 2.3, we show that such an extension F exists if the shifted conormal $T^*_{Y^{>0}} Y + df$ intersects $\Lambda$ cleanly in smooth points of $\Lambda$ and the dimension of the clean intersection is not too large. In this case, we show that $\phi _{F, y_0}$ is exact after a Maslov index shift which we calculate in terms of the dimension of the clean intersection.

In Sect. 3.1, we specialize to the situation of $Bun _G(X)$ and define the Whittaker functional. We add level structure to uniformize (a quasicompact open substack of) $Bun _G(X)$ by a scheme. In Sect. 3.2, we recall the intrinsic hyperbolic action from [4] so as to apply Theorem 2.2.2. In Sect. 3.3, we interpret the shifted conormal bundle as the Kostant slice to see that it intersects the nilpotent cone cleanly. Then we calculate the Maslov index shift in terms of the dimension of the clean intersection.

2 General Results

2.1 Some Microlocal Sheaf Theory

Fix a field k. By a sheaf of k-modules, we will mean an object of the dg derived category of sheaves of k-modules.

Let Y be a real analytic manifold and $F:Y\rightarrow \mathbb {R}$ a real-valued smooth function. We define the vanishing cycles

(2.1)

by first !-restricting to $F \ge 0$ and then $*$-restricting to $F = 0$. Further $*$-restricting to a point $y_0$ gives a functional

(2.2)

We view the functional Eq. 2.2 as a measurement of a sheaf associated to the covector $dF(y_0) \in T^*Y$. The singular support $ss (\mathcal {F})\subset T^*Y$ of a sheaf $\mathcal {F}$ on Y is the closure of those covectors $\xi _0 \in T^*Y$ for which there exists a function F with $F(y_0) = 0$, $dF(y_0) = \xi _0$, and $\phi _{F, y_0}(\mathcal {F}) \not \simeq 0$.

Let $\Lambda \subset T^*Y$ be a subanalytic closed conic Lagrangian and $Sh _{\Lambda }(Y)$ the category of sheaves with singular support in $\Lambda$. Recall there is a subanalytic stratification of Y so that any sheaf with singular support in $\Lambda$ is weakly constructible for the stratification. By adjunction, !-restriction to $F \ge 0$ is corepresented by the !-extension $k_{F \ge 0}$. The stalk at a point $y_0$ is corepresented by the !-extension $k_{B'}$ from a sufficiently small open ball $B' \subset Y$ around $y_0$, see Lemma 8.4.7 of [8]. Therefore vanishing cycles is corepresented by

(2.3)

where $k_{B' \cap \{F \ge 0\}}$ is !-extended along the boundary of the open ball $B'$ and $*$-extended along the closed boundary $F = 0$.

Proposition 7.5.3 of [8] says that for a smooth point $\xi _0 \in \Lambda$, and any function F such that the graph $\Gamma _{dF}$ of its differential intersects $\Lambda$ transversely at $\xi _0$, the shifted vanishing cycles $\phi _{F, y_0}[ind /2]$ is independent of F (up non-canonical isomorphism), only depending on $\xi _0$. Here $ind /2$ denotes half the Maslov index of three Lagrangians in the symplectic vector space $T_{\xi _0}T^*Y$: the tangent to the graph $\Gamma _{dF}$, the tangent to the singular support $\Lambda$, and the tangent to the cotangent fiber $T_{y_0}^*Y$. We call $\phi _{F, y_0}[ind /2]$ the microstalk functional at $\xi _0$.

If Y is complex analytic, and $f:Y\rightarrow \mathbb {C}$ is holomorphic, then there is a traditional vanishing cycles functor

(2.4)

which we normalize so that it is exact with respect to the perverse t-structure (see [8], Corollary 10.3.13). Taking the stalk at a point $y_0$ gives a functional

(2.5)

If $\Lambda \subset T^*Y$ is complex subanalytic then on $Sh _{\Lambda }(Y)$ the complex and real vanishing cycles functionals are related by $\phi _{f, y_0} \simeq \phi _{{\text {Re}} f, y_0}$ (see [8] Exercise VIII.13). If also the intersection $\Gamma _{df} \cap \Lambda$ is zero-dimensional, then $\phi _f: Sh _{\Lambda }(Y) \rightarrow Sh (f = 0)$ takes values in sheaves with zero dimensional support, so after taking the stalk, $\phi _{f, y_0}$ is still exact.

Singular support behaves well under smooth pullback and pushforward along closed embeddings. For a map $\pi : Z\rightarrow Y$, consider the natural Lagrangian correspondence

(2.6)

If $\pi$ is smooth, then $ss (\pi ^!-) = d\pi (\pi ^{-1} ( ss (-)))$; if $\pi$ is a closed embedding, then $ss (\pi _!-) = \pi (d\pi ^{-1}( ss (-)))$ (see [8, Propositions 5.4.4 and 5.4.5]).

2.2 Restriction to the Attracting Locus Then Vanishing Cycles

Let Y be a complex analytic manifold and $\Lambda \subset T^*Y$ be a subanalytic closed conic Lagrangian singular support condition.

It is not true in general pullback along a closed embedding followed by vanishing cycles can be interpreted as vanishing cycles.

Example 2.2.1

Let $k_{y = x^2}$ be the pushforward to $\mathbb {A}^2$ of the constant sheaf on a parabola and let $i: \mathbb {A}^1 \rightarrow \mathbb {A}^2$ be the inclusion of the axis $y = 0$. Then $i^! k_{y = x^2}$ is a skyscraper at $0 \in \mathbb {A}^1$ and hence has nonzero vanishing cycles $\phi _{x, 0} i^! k_{y = x^2} \not \simeq 0$. On the other hand, we have the vanishing $\phi _{x, 0} k_{y = x^2} \simeq 0$ since the level-sets of x are transverse to $y=x^2$.

Suppose we have a $\mathbb {C}^{\times }$-action on Y. Let $Y^0\subset Y$ denote the fixed locus, $Y^{\ge 0} \rightarrow Y$ the attracting locus, and $Y^{\le 0} \rightarrow Y$ the repelling locus. Suppose $y_0 \in Y^0$ is a fixed point. Let $Y^{> 0} \rightarrow Y$ be the attracting locus of $y_0$, and $Y^{< 0} \rightarrow Y$ the repelling locus of $y_0$.

Let $f: Y^{>0} \rightarrow \mathbb {C}$ be a $\mathbb {C}^{\times }$-equivariant function where $\mathbb {C}^{\times }$ acts linearly on the target $\mathbb {C}$ with some weight. The Whittaker functional

(2.7)

is defined by pulling back along

(2.8)

and then taking vanishing cycles for the function f at the point $y_0$.

We wish to compare the Whittaker functional with directly taking vanishing cycles on Y without pulling back to $Y^{>0}$ first. To define vanishing cycles on Y, we need a function on Y extending f.

Using local coordinates choose (a germ near $y_0$ of) a real-valued smooth function $F:Y\rightarrow \mathbb {R}$ such that

• $F|_{Y^{>0}} = {\text {Re}} f$,

• $F|_{Y^{\le 0} \setminus y_0} < 0$.

The $\mathbb {C}^{\times }$-action provides a splitting $T^*_{y_0}Y \simeq T^*_{y_0}Y^{\le 0} \oplus T^*_{y_0}Y^{> 0}$. The second condition says that F has a local maximum at $y_0 \in Y^{\le 0}$ so $dF(y_0)$ lies in the second summand of the splitting. The first condition implies $dF(y_0) = d{\text {Re}} f(y_0) \in T^*_{y_0}Y^{> 0}$.

Having chosen such a function F, the vanishing cycles functor

(2.9)

is corepresented by the !-extension $k_V$ of the constant sheaf on

$$\begin{aligned} V := B' \cap \{F \ge 0\}, \end{aligned}$$

(2.10)

where $B'\subset Y$ is a small open ball around $y_0$, see Fig. 1.

By adjunction, the !-restriction along $i: Y^{> 0} \rightarrow Y$ is internally corepresented

$$\begin{aligned} i^! (-) \simeq \underline{Hom }(k_{Y^{>0}}, -) \end{aligned}$$

(2.11)

by the !-extension $k_{Y^{>0}}$ of the constant sheaf on $Y^{>0}$. So the Whittaker functional is corepresented

$$\begin{aligned} \phi _{f, y_0} i^!( -) = Hom (k_{Y^{>0} \cap B \cap \{{\text {Re}} f \ge 0\}}, -) \end{aligned}$$

(2.12)

by the !-extension $k_{Y^{>0} \cap B \cap \{{\text {Re}} f \ge 0\}}$ of the constant sheaf on

$$\begin{aligned} Y^{>0} \cap B \cap \{{\text {Re}} f \ge 0\}, \end{aligned}$$

(2.13)

where $B\subset Y^{>0}$ is a small open ball around $y_0$, see Fig. 2.

By Lemma 8.4.7 of [8], deforming $Y^{>0}$ to a very small closed tube does not change the functor Eq. 2.12. More precisely the Whittaker functional

$$\begin{aligned} \phi _{f, y_0} i^!( -) = Hom (k_{W}, -) \end{aligned}$$

(2.14)

is corepresented by the !-extension $k_{W}$ of the constant sheaf on

$$\begin{aligned} W := B \cap T \cap \{F \ge 0\}, \end{aligned}$$

(2.15)

where $T\subset Y$ is a very small closed tube around $Y^{> 0}$, see Fig. 3. To apply Lemma 8.4.7 of [8] we chose $\varphi$ a distance function from $Y^{>0}$ and used that the sheaf $\underline{Hom }(k_{B \cap \{F \ge 0\}}, -)$ has compact support. The tube depends on the ball, so T needs to be very small compared to B.

Fig. 1

Structure of $k_V$ where $V = B' \cap \{F \ge 0\}$

Fig. 2

Structure of $k_{Y^{>0} \cap B \cap \{{\text {Re}} f \ge 0\}}$

Fig. 3

Structure of $k_W$ where $W = B \cap T \cap \{F \ge 0\}$

Finally, taking $B'$ small compared to B and T gives an inclusion $V \subset W$ inducing a canonical map $k_V\rightarrow k_W$, and hence a canonical map on corepresented functors

(2.16)

We say a sheaf $\mathcal {F}$ on Y is $\mathbb {C}^{\times }$-monodromic if it is locally constant along each $\mathbb {C}^{\times }$-orbit.²

Theorem 2.2.2

If $\mathcal {F} \in Sh _{\Lambda }(Y)$ is $\mathbb {C}^{\times }$-monodromic (and has singular support in some subanalytic closed conic Lagrangian $\Lambda$) then the map Eq. 2.16 induces an equivalence

(2.17)

Proof

The kernel of the map Eq. 2.16 is corepresented by the !-extension $k_{W \setminus V}$ of the constant sheaf on $W \setminus V$. We will show that $W \setminus V$ is foliated by flow lines for the action of $\mathbb {R}^{>0} \subset \mathbb {C}^{\times }$ entering through its $*$-boundary and exiting through its !-boundary.

Note the zero locus of the Euler vector field v generating the $\mathbb {R}_{>0}$-action is the fixed locus $Y^0$. Since $F|_{Y^0 \setminus y_0} < 0$ and $y_0$ is not in the closure of $W \setminus V$, the vector field v never vanishes on the closure of $W\setminus V$.

Choose complex coordinate functions $(y^{< 0}_i, y^0_j, y^{> 0}_k)$ so that $\mathbb {C}^{\times }$ acts by $y^{<0}_i(z \cdot y) = z^{m_i} y^{< 0}_i(y)$ with negative weights $m_i < 0$, by $y^{> 0}_k(z \cdot y) = z^{n_k} y^{> 0}_k(y)$ with positive weights $n_k > 0$, and fixes the coordinates $y^0_j(z\cdot y) = y^0_j(y)$. Consider distance functions (for some metric) in these coordinates

$$\begin{aligned} d_{<0}(y) = \sum |y_i^{< 0}|^2, \qquad d_{>0}(y) = \sum |y_i^{>0}|^2, \qquad d_0(y) = \sum |y^0_i|^2. \end{aligned}$$

(2.18)

Note that acting by $z \in \mathbb {C}^{\times }$ with $|z| >1$ decreases $d_{<0}$ (when non-zero), increases $d_{>0}$ (when non-zero), and fixes $d_0$.

Observe we can take $W \setminus V$ to be defined by

$$\begin{aligned} F \ge 0,\qquad a \le d_{>0}< b,\qquad d_0 \le c, \qquad d_{<0} \le d \end{aligned}$$

(2.19)

where $c, d>0$ are small compared with $b>0$, and $a>0$ is small compared with c, d. The boundary components of $W \setminus V$ are given by the equations

$$\begin{aligned} F = 0, \qquad d_{>0} = a, \qquad d_{>0} = b, \qquad d_{<0} = c, \qquad d_0 = d. \end{aligned}$$

(2.20)

Observe that $k_{W \setminus V}$ is a !-extension along the $d_{>0} = b$ boundary component and a $*$-extension along all the other boundary components. Now we further observe how the Euler vector field v interacts with the boundary components:

• v is tangent to $\{F = 0\} \cap Y^{>0} = \{{\text {Re}} f = 0\}$ since if ${\text {Re}} f(y) = 0$, then for $z \in \mathbb {R}^{>0}$, we have ${\text {Re}} f(z\cdot y) = {\text {Re}} (z^n f(y)) = z^n{\text {Re}} f(y) = 0$. (Here we use $f: Y^{>0} \rightarrow \mathbb {C}$ is $\mathbb {C}^{\times }$-equivariant for a linear $\mathbb {C}^{\times }$-action on the target $\mathbb {C}$ by some weight n.)

• v is inward pointing on the rest of the face $F = 0$ away from $Y^{>0}$ since by assumption $F|_{Y^{\le 0} \setminus y_0} > 0$.

• v is inward pointing along the faces $d_{>0} = a$ and $d_{<0} = c$ and outward pointing along the face $d_{>0} = b$ because acting by $z\in \mathbb {R}^{>0}$, with $z>1$, decreases $d_{<0}$ and increases $d_{>0}$ where they are non-zero.

• v is tangent to the face $d_0 = d$ because acting by $z\in \mathbb {R}^{>0}$ fixes $d_0$.

We conclude $W \setminus V$ is foliated by flow segments for the action of $\mathbb {R}^{>0} \subset \mathbb {C}^{\times }$ entering through its $*$-boundary and exiting through its !-boundary. The kernel of $\phi _{f, y_0} i^! \mathcal {F} \rightarrow \phi _{F, y_0} \mathcal {F}$ is global sections of the sheaf $\underline{Hom }(k_{W \setminus V}, \mathcal {F})$. If $\mathcal {F}$ is $\mathbb {C}^\times$-monodromic, then the pushforward of $\underline{Hom }(k_{W \setminus V}, \mathcal {F})$ to the quotient $Y/\mathbb {R}_{>0}$ is already zero, so its global sections are zero. $\square$

2.3 Calculation of the Shift

As in Section 2.2, let $Y^{>0}$ be the attracting locus to $y_0$ and let $Y^{\le 0}$ be the repelling locus. In applying Theorem 2.2.2, we want to be able to interpret the vanishing cycles $\phi _{F, y_0}$ as a microstalk. To this end, we want to be able to choose a real valued function F on Y extending f on $Y^{>0}$ not only satisfying the required properties from Section 2.2 but also such that the graph of the differential $\Gamma _{dF}$ intersects the singular support transversely at a smooth point.

Proposition 2.3.1

Assume that the shifted conormal $T^*_{Y^{> 0}} Y + d f$ intersects $\Lambda$ cleanly and the dimension of the clean intersection is bounded above by

$$\begin{aligned} \dim (\Lambda \cap (T^*_{Y^{> 0}} Y + d f)) \le \dim Y^{\le 0}. \end{aligned}$$

(2.21)

Then there exists a function $F: Y \rightarrow \mathbb {R}$ satisfying the following properties

• $F|_{Y^{>0}} = {\text {Re}} f$,

• $F_{Y^{\le 0} \setminus y_0} < 0$,

• the graph $\Gamma _{dF}$ intersects $\Lambda$ transversely at a smooth point.

Proof

The first condition is equivalent to $(\Gamma _{dF})|_{Y^{> 0}} \subset (T^*_{Y^{> 0}} Y + d{\text {Re}} f)$. In other words, above $Y^{> 0}$ the graph $\Gamma _{dF}$ restricts to a section of the shifted conormal. By Eq. 2.21 it is possible to choose a section $(\Gamma _{dF})|_{Y^{>0}}$ of the shifted conormal intersecting $\Lambda \cap (T^*_{Y^{> 0}} Y + df)$ transversely. The remaining two conditions imply that $dF(y_0) = df(y_0)$ and only depend on $T_{df(y_0)}\Gamma _{dF}$ the tangent space to the graph. Therefore it is a matter of linear algebra to extend $(\Gamma _{dF})|_{Y^{>0}}$ to a transverse maximally negative definite section $\Gamma _{dF}$ over all of Y. Consider the space of graphical Lagrangian subspaces of $T_{df(y_0)}T^*Y$ containing $(\Gamma _{dF})|_{Y^{>0}}$. A generic such subspace will satisfy the third transversality condition. The second condition is open and using local coordinates nonempty. Therefore the desired F exists. $\square$

Choose a function $F: Y \rightarrow \mathbb {R}$ as in Proposition 2.3.1 so that $\phi _{F, y_0}$ calculates the microstalk at the intersection point $\Lambda \cap \Gamma _{dF}$.

Remark 2.3.2

(Real versus holomorphic tangent bundles) For a holomorphic function f on $Y^{>0}$ the differential $df(y) \in (T_y^*Y^{>0} \otimes _{\mathbb {R}} \mathbb {C})^{1, 0}$ lies in the holomorphic tangent bundle. Alternatively, we could take the differential of the real part $(d {\text {Re}} f) (y) \in T_y^*Y^{>0}$. We identify the holomorphic tangent bundle with the tangent bundle of the underlying real manifold by

(2.22)

where the second map is dual to the inclusion $T_yY^{>0} \hookrightarrow T_yY^{>0}\otimes _{\mathbb {R}} \mathbb {C}.$ Therefore we let $T^*Y^{>0}$ also denote the holomorphic tangent bundle. For a holomorphic function f, we are free to confuse df(y) with $d{\text {Re}} f(y)$. Moreover, the two shifted conormal bundles $T^*_{Y^{>0}} Y + df$ and $T^*_{Y^{>0}} Y + d{\text {Re}} f$ are identified inside $T^*Y$.

Moreover $\phi _{F, y_0}$ is exact up to a shift by the Maslov index of three Lagrangians

$$\begin{aligned} \lambda _{ vert } := T_{d f(y_0)} T^*_{y_0} Y, \quad \lambda := T_{d f(y_0)}\Lambda , \quad \lambda _F := T_{d f(y_0)}\Gamma _{dF} \end{aligned}$$

(2.23)

inside the symplectic vector space $T_{df(y_0)}T^*Y$.

Proposition 2.3.3

Assume that $\Lambda \subset T^*Y$ is a closed conic complex subanalytic Lagrangian preserved by the hyperbolic action, $F|_{Y^{>0}} = {\text {Re}} f$ is the real part of a $\mathbb {G}_m$-equivariant holomorphic function, on the repelling locus $F|_{Y^{\le 0}}$ is maximized at $y_0$ and the graph of dF intersects $\Lambda$ transversely at a smooth point. Then the vanishing cycles functor

(2.24)

is exact and commutes with the Verdier duality functor D.³

Proof

Vanishing cycles for F at $y_0$ is exact after a shift by $ind (\lambda _{ vert }, \lambda , \lambda _F)/2$, the Maslov index of three Lagrangrians defined in Eq. 2.23. This follows by Proposition 7.5.3 of [8] and the fact that vanishing cycles for a holomorphic function is exact. The index is calculated in Proposition 2.3.6. Since $\Gamma _{dF}$ intersects $\Lambda$ transversely at a smooth point, Eq. 2.24 is a microstalk and therefore commutes with Verdier duality by the following Proposition 2.3.4. $\square$

Below we prove the standard fact that in the complex analytic setting, microstalk at a smooth point of the singular support commutes with Verdier duality.

Proposition 2.3.4

If $\Lambda \subset T^*Y$ is a complex subanalytic closed conic Lagrangian then microstalk at a smooth point $\xi _0 \in \Lambda$ commutes with Verdier duality.

Proof

The microstalk category $Sh _{\Lambda }(Y)_{\xi _0}$ is defined in Section 6.1 of [8] by localizing with respect to all sheaves singular supported away from $\xi _0$. Moreover $Sh _{\Lambda }(Y)_{\xi _0}$ is invariant under contact transformations by Corollary 7.2.2 of [8]. Since $\xi _0$ is a smooth point of $\Lambda$, the proof of Corollary 1.6.4 of [7] gives a contact transformation taking a neighborhood of $\xi _0$ in $\Lambda$ to a neighborhood in the conormal bundle to a smooth hypersurface. Therefore $Sh _{\Lambda }(Y)_{\xi _0} = Vect$ by Proposition 6.6.1 of [8]. Since $\Lambda$ is complex subanalytic, Verdier duality on $Sh _{\Lambda }(Y)_{\xi _0}$ preserves singular support, see Exercise V.13 of [8]. Both the microstalk at $\xi _0$ and its conjugate by Verdier duality vanish on sheaves singular supported away from $\xi _0$, so they both factor through the microstalk category $Sh _{\Lambda }(Y)_{\xi _0} \simeq Vect$ and therefore coincide. $\square$

If $\Lambda$ is a smooth closed conic Lagrangian then it is the conormal to a smooth submanifold $\Lambda = T^*_ZY$ ([8] Exercise A.2) and the Maslov index of Eq. 2.23 is the signature of the Hessian of F restricted to Z. This is not the case in our application. Although the global nilpotent cone is smooth near $df(y_0)$, it is not smooth near $y_0$ in the zero section. But the Maslov index only depends on the tangent space to $\Lambda$ at $df(y_0)$. So to compute the index we will choose a submanifold Z whose conormal bundle is tangent to $\Lambda$ at $df(y_0)$ and then study the Hessian of $F|_Z$.

Proposition 2.3.5

Let $\Lambda \subset T^*Y$ be a closed conic Lagrangian that is smooth near $df(y_0)$ and preserved by the hyperbolic $\mathbb {G}_m$-action. Set $\lambda = T_{d f(y_0)}\Lambda$. Then there exists a hyperbolic $\mathbb {G}_m$-stable submanifold $Z \subset Y$ such that the tangent spaces coincide:

$$\begin{aligned} T_{df(y_0)}T_Z^*Y = \lambda . \end{aligned}$$

(2.25)

Proof

If $df(y_0) = 0$ is in the zero section, then by smoothness $\Lambda = T_Z^*Y$ is conormal to a smooth $\mathbb {G}_m$-equivariant submanifold Z, above a neighborhood of $y_0 \in Y$.

If $df(y_0) \ne 0$ is not in the zero section, then the tangent space to the conormal $T_{df(y_0)}T_Z^*Y$ is determined by the tangent space $T_{y_0}Z$ plus the quadratic order behavior of Z in the $df(y_0)$ codirection. Set $\rho = \lambda \cap \lambda _{ vert }$ regarded as a subspace of the vertical $\lambda _{ vert } = T^*_{y_0}Y$. (Note $\rho$ contains at least the tangent to the line through $df(y_0)$.) There are two different things that we could mean by the orthogonal of $\rho$: its symplectic orthogonal $\rho _{\perp } \subset T_{df(y_0)}T^*Y$, or its orthogonal under duality $\rho ^{\perp } \subset T_{y_0}Y$.

Let $\textsf{L}$ be the set of:

• Lagrangians $\lambda ' \subset T_{df(y_0)}T^*Y$ with vertical component $\lambda ' \cap \lambda _{ vert } = \rho$,

• or equivalently Lagrangians $\lambda '/\rho \subset \rho _{\perp }/\rho$ transverse to the vertical fiber.

Then $\textsf{L}$ is a torsor for the vector space of quadratic forms on $\rho ^{\perp }$. Indeed if we choose a reference Lagrangian $\lambda _0 \in \textsf{L}$ then we can identify $\rho _{\perp }/\rho = T^* \rho ^{\perp }$ using $\lambda _0/\rho$ as the zero section. A Lagrangian in $T^* \rho ^{\perp }$ transverse to the vertical fiber is the graph of a quadratic form on $\rho ^{\perp }$.⁴

Let $\textsf{G}$ be the set of germs of submanifolds $Z' \subset Y$ with tangent space $T_{y_0}Z' = \rho ^{\perp }$ up to quadratic order equivalence. This is a torsor for the space of quadratic forms from $\rho ^{\perp }$ to the normal space. Indeed if we choose a reference $[Z_0] \in \textsf{G}$ then quadratic germs in $\textsf{G}$ can be identified with the graphs of quadratic forms $T_{y_0}Z_0 \rightarrow (T_{Z_0}Y)_{y_0}$.

Taking the tangent space to the conormal bundle gives a map

(2.26)

There are two commuting $\mathbb {G}_m$ actions on $T^*Y$: the cotangent fiber scaling action and the Hamiltonian action induced by the hyperbolic action on Y. Neither action fixes the point $df(y_0)$. However there is some combination of the two actions which fixes $df(y_0)$ and therefore acts linearly on $T_{df(y_0)}T^*Y$. This is because $y_0$ is a fixed point and $f:Y^{>0} \rightarrow \mathbb {C}$ is $\mathbb {G}_m$-equivariant where $\mathbb {G}_m$ acts on $\mathbb {C}$ with some weight n. Therefore we get a $\mathbb {G}_m$-action on $\textsf{L}$ for which $\textsf{G} \rightarrow \textsf{L}$ is equivariant.⁵

First, choose any $\mathbb {G}_m$-stable germ $[Z_{0}] \in \textsf{G}$.⁶ This gives identifications $\textsf{L} \simeq Hom (Sym ^2(T_{y_0}Z_0), \mathbb {C})$ and $\textsf{G} \simeq Hom (Sym ^2(T_{y_0}Z_0), (T_{Y_0}Y)_{y_0})$ compatibly with all $\mathbb {G}_m$-actions (in particular the weight n action on $\mathbb {C}$). Then Eq. 2.26 is identified with

(2.27)

given by composition with $df:(T_{Z_0}Y)_{y_0} \rightarrow \mathbb {C}$.

Since $\Lambda \subset T^*Y$ is preserved by both $\mathbb {G}_m$-actions, its tangent space $\lambda$ is preserved by the combined action on $T_{df(y_0)}T^*Y$. Therefore the associated quadratic form $Sym ^2(T_{y_0}Z_0) \rightarrow \mathbb {C}$ is $\mathbb {G}_m$-equivariant. Lift it along Eq. 2.27 to a $\mathbb {G}_m$-equivariant quadratic form $Sym ^2(T_{y_0}Z_0) \rightarrow (T_{Z_0}Y)_{y_0}$. This gives a $\mathbb {G}_m$-equivariant germ $[Z] \in \textsf{G}$ whose conormal is $\lambda$.

It just remains to lift the $\mathbb {G}_m$-stable germ $[Z] \in \textsf{G}$ to a genuine $\mathbb {G}_m$-stable submanifold. Suppose [Z] is cut out from $Spec (\mathcal {O}_{Y, y_0}/\mathfrak {m}^3)$ by polynomials $\overline{f}_1, \dots \overline{f}_d \in \mathcal {O}_{Y, y_0}/\mathfrak {m}^3$ that are $\mathbb {G}_m$-eigenvectors and whose differentials at $y_0$ are linearly independent. Lift them to polynomials $f_1, \dots f_d$ in $\mathcal {O}_{Y, y_0}$ that are $\mathbb {G}_m$-eigenvectors. Then the lifts $f_1, \dots f_d$ cut out a $\mathbb {G}_m$-stable submanifold Z in a neighborhood of $y_0$ satisfying the desired $T_{df(y_0)}T_Z^*Y = \lambda$. $\square$

Now we are ready to replace $\Lambda$ by a conormal bundle and calculate the Maslov index.

Proposition 2.3.6

Under the same assumptions as Proposition 2.3.3, the Maslov half-index of the three Lagrangian subspaces Eq. 2.23 inside $T_{df(y_0)}T^*Y$ is

$$\begin{aligned} ind (\lambda _{ vert }, \lambda , \lambda _F)/2 = \dim Y^{\le 0} - \dim (\Lambda \cap (T^*_{Y^{>0}}Y + df)). \end{aligned}$$

(2.28)

Proof

Use Proposition 2.3.5 to choose a $\mathbb {G}_m$-stable submanifold Z such that $T_{df(y_0)}T^*_ZY = \lambda$. Since $df(y_0)$ vanishes on $T_{y_0}Z$, the Hessian of $F|_Z$ defines a quadratic form on $T_{y_0}Z$ and the sought after index

$$\begin{aligned} ind (\lambda _{ vert }, \lambda , \lambda _F)/2 = -sgn (Hess F|_Z) \end{aligned}$$

(2.29)

is the negative of the signature of that form. Since the graph $\Gamma _{dF}$ intersects $T_Z^*Y$ transversely, $Hess F|_Z$ is nondegenerate. By $\mathbb {G}_m$-equivariance $T_{y_0}Z = T_{y_0}Z^{>0} \oplus T_{y_0}Z^{\le 0}$ splits into attracting and repelling subspaces. By the assumption that $F|_{Z^{\le 0} - y_0} < 0$, it follows that the restriction $Hess F|_{Z^{\le 0}}$ is negative definite on the repelling $T_{y_0}Z^{\le 0}$. By the assumption that $F|_{Z^{>0}}$ is holomorphic it follows the restriction $Hess F|_{Z^{>0}}$ to $T_{y_0}Z^{>0}$ has signature 0.

Therefore the number of positive eigenvalues of $Hess F|_Z$ equals the number of positive eigenvalues of $Hess F|_{Z^{>0}}$ which is

$$\begin{aligned} (\dim Z^{>0} - null (Hess F|_{Z^{>0}})/2. \end{aligned}$$

(2.30)

Here $null (Hess F|_{Z^{>0}})$ is the multiplicity of 0 as an eigenvalue of the quadratic form. Since $Hess F|_Z$ is nondegenerate, the remaining eigenvalues are strictly negative. So the index is

$$\begin{aligned} ind (Hess F|_Z)/2 = -\dim Z^{\le 0} + null (Hess F|_{Z^{>0}}). \end{aligned}$$

(2.31)

It remains to compare the expression Eq. 2.31 with the dimension of the intersection of $\Lambda$ and the shifted conormal. Since the intersection is clean near $df(y_0)$, we can pass to tangent spaces before calculating the dimension of the intersection.

Let $\lambda _f = T_{df(y_0)}(T^*_{Y^{>0}} Y + df)$ be tangent to the shifted conormal, a fourth Lagrangian in $T_{df(y_0)}T^*Y$.

The codifferential of the inclusion of Z maps

(2.32)

and differentiating gives a linear map⁷

(2.33)

Since $\lambda \subset T_{df(y_0)}(T^*Y|_Z)$, we can calculate the dimension of $\lambda \cap \lambda _f$ from the rank and nullity of $\pi$ restricted to $\lambda \cap \lambda _f$.

By $\mathbb {G}_m$-invariance, Z intersects $Y^{>0}$ cleanly and so the inclusion $T_{df(y_0)} ((T^*_{Y^{>0}}Y + df)|_Z) \subset \lambda _f|_{T_{y_0}Z}$ is an equality. In other words, for the shifted conormal, passing to tangent spaces commutes with restriction to Z. Moreover the coderivative Eq. 2.32 maps $(T^*_{Y^{>0}}Y + df)|_Z$ smoothly to the shifted conormal bundle $T^*_{Z^{>0}}Z + df|_{Z^{>0}}$. By smoothness, passing to tangent spaces commutes with taking the image along $di^*$ and $\pi$. Therefore,

$$\begin{aligned} {\begin{matrix} \pi (\lambda _f|_{T_{y_0}Z}) &{}= T_{y_0}(T^*_{Z^{>0}}Z + df|_{Z^{>0}}) = T_{y_0}T^*_{Z^{>0}}Z + \Gamma _{Hess F|_{Z^{>0}}} \\ &{}= \{v \in \! T_{y_0}Z^{>0}, \xi \in \! T_{y_0}^*Z \text { such that } \xi (w) \!= (Hess F)(v, w) \text { for } w \!\in T_{y_0}Z^{>0}\}, \end{matrix}} \end{aligned}$$

(2.34)

is the conormal to $T_{y_0}Z^{>0} \subset T_{y_0} Z$ shifted by the graph of the Hessian of $F|_{Z^{>0}}$.

Moreover, $\lambda = \pi ^{-1}(\xi = 0)$, for $\xi$ the coordinate on $T_{y_0}^*Z$, is exactly the preimage in $T_{y_0}T^*Z$ under Eq. 2.33 of the zero section $T_{y_0}Z$. Therefore

$$\begin{aligned} \pi (\lambda \cap \lambda _f) = T_{y_0}Z \cap \pi (\lambda _f|_{T_{y_0}Z}) \end{aligned}$$

(2.35)

is the nullspace of $Hess F|_{Z^{>0}}$ inside the zero section. So the dimension of $\pi (\lambda \cap \lambda _f)$ is

$$\begin{aligned} rank \, (\pi |_{\lambda \cap \lambda _f}) = null (Hess F|_{Z^{>0}}). \end{aligned}$$

(2.36)

The kernel of $\pi |_{\lambda \cap \lambda _f}$ is $((T_{y_0}Z)^{\perp } \cap (T_{y_0}Y^{>0})^{\perp })$ inside the vertical $T^*_{y_0}Y \subset T_{df(y_0)}T^*Y$ of dimension

$$\begin{aligned} null (\pi |_{\lambda \cap \lambda _f}) = \dim Y^{\le 0} - \dim Z^{\le 0}. \end{aligned}$$

(2.37)

Combining Eqs. 2.36 and 2.37 gives

$$\begin{aligned} \dim (\lambda \cap \lambda _f) = \dim Y^{\le 0} - \dim Z^{\le 0} + null (Hess F|_{Z^{>0}}) \end{aligned}$$

(2.38)

which together with Eq. 2.31 gives the desired formula Eq. 2.28 for the shift. $\square$

Example 2.3.7

Let $Y = \mathbb {A}^2$ with hyperbolic action $z \cdot (x, y) = (zx, z^{-1} y)$. So i is the inclusion of $Y^{>0} = \{y = 0\}$.

The Whittaker functional of the skyscraper sheaf $k_0$ is

$$\begin{aligned} \phi _{x, 0} i^! k_{0} = \phi _{x, 0} k_0 = k. \end{aligned}$$

(2.39)

The singular support $\Lambda = T_0^* \mathbb {A}^2$ of the skyscraper intersects the shifted conormal bundle $(T_{Y^{>0}} \mathbb {A}^2 + dx)$ in the one dimensional space $(T_{y = 0}^* \mathbb {A}^2)_0 + dx$ so

$$\begin{aligned} \dim Y^{\le 0} - \dim (T_0^* \mathbb {A}^2 \cap (T_{Y^{>0}}^* \mathbb {A}^2 + dx)) = 0 \end{aligned}$$

(2.40)

and there is no shift.

The Whittaker functional of the perverse sheaf $k_{x = 0}[1]$ is

$$\begin{aligned} \phi _{x, 0} i^! k_{x = 0}[1] = \phi _{x, 0} k_{x = 0}[-1] = k[-1]. \end{aligned}$$

(2.41)

The resulting vector space becomes perverse after shifting by

$$\begin{aligned} \dim Y^{\le 0} - \dim (T^*_{x = 0} \mathbb {A}^2 \cap (T_{Y^{>0}}^* \mathbb {A}^2 + dx)) = 1 \end{aligned}$$

(2.42)

because the singular support $\Lambda = T^*_{x = 0} \mathbb {A}^2$ intersects the shifted conormal bundle in a single point.

3 Application to Automorphic Sheaves

Let X be a smooth connected projective complex curve with canonical bundle denoted by $\omega$. Let G be a complex reductive group with Borel subgroup $B\subset G$ with unipotent radical $N = [B,B]$ and universal Cartan $T=B/N$. For concreteness, we will fix a splitting $T\subset B$.

3.1 The Whittaker Functional Under Uniformization

Let $\rho ^{\vee }$ be half the sum of the positive coroots. Choose a square root $\omega ^{1/2}$ of the canonical bundle and consider the T-bundle $\rho ^{\vee }(\omega ):= 2\rho ^{\vee }(\omega ^{1/2})$. Its key property is that for every simple root $\alpha$, the associated line bundle $\rho ^{\vee }(\omega ) \times _T \mathbb {C}_{\alpha } = \omega ^{\langle \rho ^{\vee }, \alpha \rangle } = \omega$ is canonical. Let $Bun _N^{\omega }(X)$ be the moduli of B-bundles on X whose underlying T-bundle is $\rho ^{\vee }(\omega )$. Thus $Bun _N^{\omega }(X)$ classifies maps $X\rightarrow pt /B$ such that the composition with $pt /B\rightarrow pt /T$ classifies the T-bundle $\rho ^{\vee }(\omega )$. Such maps factor through the classifying space of $B \times _T 2\rho ^{\vee }(\mathbb {G}_m) \simeq N \rtimes \mathbb {G}_m$ as in the diagram:

(3.1)

So alternatively $Bun _N^{\omega }(X)$ is represented by maps to $pt /(N \rtimes \mathbb {G}_m)$ such that the composition to $pt /\mathbb {G}_m$ classifies $\omega ^{1/2}$.

The semidirect product $N \rtimes \mathbb {G}_m$ mentioned above is formed by letting $z \in \mathbb {G}_m$ act on N by conjugation by $2\rho ^{\vee }(z) \in T$. In other words, $N \rtimes \mathbb {G}_m \subset B$ is the subgroup of the Borel generated by N and $2\rho ^{\vee }(\mathbb {G}_m)$. Consider the action of $N \rtimes \mathbb {G}_m$ on $\mathfrak {n}^*$ by

$$\begin{aligned} z \cdot X = Ad _{2\rho ^{\vee }(z)}(z^2 X), \end{aligned}$$

(3.2)

the product of scaling and the adjoint T-action.

Proposition 3.1.1

The cotangent bundle $T^*Bun _N^{\omega }(X)$ is represented by maps $X \rightarrow \mathfrak {n}^*/(N \rtimes \mathbb {G}_m)$, where we quotient by the Eq. 3.2 action, such that the composition $X \rightarrow pt /\mathbb {G}_m$ classifies the line bundle $\omega ^{1/2}$.

Proof

By definition $Bun _N^{\omega }(X)$ is a fiber of the smooth (but not representable) map $p:Bun _B(X) \rightarrow Bun _T(X)$. The relative tangent complex of p is $( \pi _* \mathfrak {b}_{F^{univ }}[1]\rightarrow \pi _*\mathfrak {t}_{F^{univ }}) \simeq \pi _* \mathfrak {n}_{F^{univ }}[1]$ given by pushing forward vector bundles associated to the universal B-bundle $F^{univ }$ along $\pi : X \times Bun _B(X) \rightarrow Bun _B(X)$. The tangent complex of $Bun _N^{\omega }(X)$ is the restriction $\pi _* \mathfrak {n}_{F^{univ }}|_{Bun _N^{\omega }(X)}[1]$. Taking the stalk at a point $F \in Bun _N^{\omega }(X)$ gives the tangent space $T_F Bun _N^{\omega }(X) = H^1(\mathfrak {n}_F)$. By Serre duality the cotangent space is

$$\begin{aligned} T^*_FBun _N^{\omega }(X) = H^0(\mathfrak {n}^*_F \otimes \omega ). \end{aligned}$$

(3.3)

Here $\mathfrak {n}^*_F$ is the vector bundle obtained from F via the adjoint action of B on $\mathfrak {n}^*$. Whereas $\mathfrak {n}^*_F \otimes \omega$ is obtained from F via $N \rtimes \mathbb {G}_m$ acting on $\mathfrak {n}^*$ by Eq. 3.2.

So giving a cotangent vector in $T_F^* Bun _N^{\omega }(X)$ is equivalent to lifting the classifying map $X \rightarrow pt /(N \rtimes \mathbb {G}_m)$ of the bundle F to a map $X \rightarrow \mathfrak {n}^*/(N \rtimes \mathbb {G}_m)$. It was important that we modified the adjoint B-action on $\mathfrak {n}^*$ by also scaling so as to incorporate the canonical twist from Serre duality. $\square$

Let $f: Bun _N^{\omega }(X) \rightarrow \mathbb {A}^1$ be the function given by the sum of the functions

(3.4)

induced by projection onto each simple root space $N \rightarrow N/[N,N] \rightarrow \mathbb {G}_a$. The graph of its differential $\Gamma _{df} \subset T^* Bun _N^{\omega }(X)$ is represented by

$$\begin{aligned} \psi /(N \rtimes \mathbb {G}_m) \subset \mathfrak {n}^*/(N \rtimes \mathbb {G}_m) \end{aligned}$$

(3.5)

where $\psi : \mathfrak {n} \rightarrow \mathfrak {n}/[\mathfrak {n}, \mathfrak {n}] \rightarrow \mathbb {A}^1$ is given by summing over the simple root spaces. To see that the expression $\psi /(N \rtimes \mathbb {G}_m)$ makes sense we need to check that $\psi$ is invariant under the $(N \rtimes \mathbb {G}_m)$-action. Indeed $\psi$ factors through the abelianization so it is N-invariant. Furthermore the adjoint action of $2\rho ^{\vee }(z)$ scales the $\alpha _i$ simple root space component of $\psi$ by $z^{-\langle 2\rho ^{\vee }, \alpha _i\rangle } = z^{-2}$ cancelling out the $\mathbb {G}_m$-scaling action.

Let $Bun _G(X)$ be the moduli of G-bundles on X. Recall the cotangent bundle of $Bun _G(X)$ is the moduli of Higgs bundles

$$\begin{aligned} T^* Bun _G(X) \simeq \{E, \sigma \in H^0(\mathfrak {g}^*_E \otimes \omega )\} \end{aligned}$$

(3.6)

classifying maps $X\rightarrow \mathfrak {g}^*/(G\times \mathbb {G}_m)$ such that the composition to $pt /\mathbb {G}_m$ classifies the line bundle $\omega$. The global nilpotent cone $\Lambda \subset T^*Bun _G(X)$ is the moduli of everywhere nilpotent Higgs bundles

$$\begin{aligned} \Lambda = \{E, \sigma \in H^0(\mathcal {N}^*_E \otimes \omega )\} \end{aligned}$$

(3.7)

classifying maps $X\rightarrow \mathcal {N}^*/(G\times \mathbb {G}_m)$ such that the composition to $pt /\mathbb {G}_m$ classifies the line bundle $\omega$.

The Whittaker functional

(3.8)

is !-pullback along the natural induction map

(3.9)

followed by vanishing cycles for f at the point $\rho ^{\vee }(\omega )$. Note one could alternatively take global sections rather than stalk of the vanishing cycles $\phi _{f}$, but this will give the same result by the contraction principle ([8] Proposition 3.7.5).

To apply our general results, we would like to locally uniformize the moduli in play and replace them by smooth schemes. To this end, fix a closed point $x \in X$.

First, by taking n large enough, we may factor i through a closed embedding followed by a smooth projection

(3.10)

Here $Bun ^{\omega }_{G, N}(X, nx)$ is the moduli space of G-bundles on X with a B-reduction on the nth order neighborhood $D_n(x)$ whose underlying T-bundle is $\rho ^{\vee }(\omega )|_{D_n(x)}$. The maps factoring i are the natural induction maps; the second is clearly a smooth projection, and we will see momentarily that the first is a closed embedding.

Next, introduce the moduli $Bun _{G}^{\omega }(X, nx)$ classifying G-bundles on X with a reduction on the nth order neighborhood $D_n(x)$ to the $\mathbb {G}_m$-bundle $\omega ^{1/2}$ via the inclusion $2\rho ^{\vee }:\mathbb {G}_m \rightarrow T \subset G$.⁸ Form the following induction diagram with a Cartesian square.

(3.11)

Thus $Bun _N^{\omega }(X, nx)$ classifies objects of $Bun _N^{\omega }(X)$ with a reduction on $D_n(x)$ to the $\mathbb {G}_m$-bundle $\omega ^{1/2}$ via the inclusion $2\rho ^{\vee }:\mathbb {G}_m \rightarrow T \subset B$.

Take a quasi-compact open substack $U \subset Bun _G(X)$ containing the image of $Bun _N^{\omega }(X)$. Then for n sufficiently large, $Bun _G^{\omega }(X, nx)|_U$ is a scheme. Futhermore, at $F \in Bun _N^{\omega }(X, nx)$, for n sufficiently large, the codifferential

(3.12)

is surjective since $H^1(\mathfrak {n}^{\perp }_F \otimes \omega (nx)) = 0$. Moreover, we can choose $n \gg 0$ once and for all uniformly over $Bun _N^{\omega }(X)$ by quasi-compactness.

Thus for n sufficiently large, since $i'$ is a map between smooth schemes with surjective codifferential, it is locally a closed embedding. Applying contraction for the natural $\mathbb {G}_m$-action considered below, we see $i'$ is in fact a closed embedding. Also, $Bun _N^{\omega }(X) \rightarrow Bun ^{\omega }_{G, N}(X, nx)$ is a closed embedding because $i'$ is a base-change of it via a surjective map.

The cotangent bundle $T^* Bun _G^{\omega }(X, nx)$ classifies data

$$\begin{aligned} T^* Bun _G^{\omega }(X, nx) = \{E, E|_{D_n(x)} \simeq G \times _T \rho ^{\vee }(\omega )|_{D_n(x)}, \sigma \in H^0(\mathfrak {g}^*_E \otimes \omega (nx))\}. \end{aligned}$$

(3.13)

Singular support behaves well under smooth pullback. So if $\mathcal {F}$ is a sheaf on $Bun _G(X)$ with singular support in the nilpotent cone

$$\begin{aligned} \Lambda = \{E, \sigma \in H^0(\mathcal {N}^*_E \otimes \omega ) \} \end{aligned}$$

(3.14)

then the singular support of its smooth pullback to $Bun _G^{\omega }(X, nx)$ lies in

$$\begin{aligned} \Lambda ' \!=\! \Lambda \times _{Bun _G(X)} Bun _G^{\omega }(X, nx) \!=\! \{E, E|_{D_n(x)}\! \simeq \! G \times _T \rho ^{\vee }(\omega )|_{D_n(x)}, \sigma \!\in \! H^0(\mathcal {N}^*_E \otimes \omega ) \}. \end{aligned}$$

(3.15)

3.2 Hyperbolic Symmetry

To apply Theorem 2.2.2, we seek a $\mathbb {G}_m$-action for which $i':Bun _N^{\omega }(X, nx) \rightarrow Bun _G^{\omega }(X, nx)$ is the attracting locus for the bundle $\rho ^{\vee }(\omega )$. Let $f': Bun _N^{\omega }(X, nx) \rightarrow \mathbb {A}^1$ be the pullback of f to the uniformized moduli space. To apply Theorem 2.2.2 we also need $f'$ to be $\mathbb {G}_m$-equivariant for some $\mathbb {G}_m$ action on $\mathbb {A}^1$ (which will turn out to have weight 2).

An automorphism $\alpha \in Aut (G)$ induces an automorphism of $Bun _G(X)$ by twisting the G-actions on the underlying bundles. A G-bundle E goes to the G-bundle $\alpha E$ with the same total space but the old action of g on E is replaced by the new action of $\alpha (g)$ on $\alpha E$.⁹ If the automorphism of G is inner, say it is given by conjugation by $h \in G$, then the action on $Bun _G(X)$ is entirely stacky in the sense that it is trivial on the set of isomorphism classes of points. Indeed the multiplication by h map $h:E \rightarrow \alpha E$ intertwines the original action with the twisted one.

Suppose now that the automorphism $\alpha$ of G is trivial on T. Then $\alpha$ also induces an automorphism of $Bun _G^{\omega }(X, nx)$ with level structure. A G-bundle E with canonically twisted trivialization $\phi : E|_{D_n(X)} \xrightarrow {\sim } G \times _T \rho ^{\vee }(\omega )|_{D_n(x)}$ goes to the G-bundle $\alpha E$ with trivialization

(3.16)

The final map is trivial on the $\rho ^{\vee }(\omega )$ factor and is well defined because we assumed that the automorphism $\alpha : G \rightarrow G$ is right T-invariant. For example if $\alpha (g) = hgh^{-1}$ is an inner automorphism and $h \in T$, then we get an automorphism of $Bun _G^{\omega }(X, nx)$ that preserves the underlying bundle and changes the trivialization by conjugation by h. In other words $\alpha$ acts along the fibers of $Bun _G^{\omega }(X, nx) \rightarrow Bun _G(X)$.

Remark 3.2.1

For simplicity ignore the canonical twist and suppose that G is semisimple so we have one point uniformization,

$$\begin{aligned} Bun _G(X, nx) = K_n \setminus G(K_x) / G(X - x). \end{aligned}$$

(3.17)

Here $K_n \subset G(\mathcal {O}_x)$ consists of matrices that are the identity to nth order. Then the inner automorphism $\alpha (g) = h g h^{-1}$ sends a double coset $K_n g G(X - x)$ to $K_n h g h^{-1} G(X - x) \simeq K_n h g G(X - x)$. Since $h^{-1}$ is a constant function we could absorb it into $G(X - x)$, so alternatively the action is given by changing the trivialization by left multiplication.

Let $z \in \mathbb {G}_m$ act on G and B by conjugation by $\rho ^{\vee }(z) \in T/Z(G)$ in the torus of the adjoint group. This gives a $\mathbb {G}_m$-action on the moduli spaces of bundles for which the natural maps between moduli spaces are equivariant.

Proposition 3.2.2

(4.7 of [4]) Restrict to the connected component of $Bun _B(X, nx)$ and $Bun _T(X, nx)$ indexed by the coweight $(2g-2)\rho ^{\vee }$. Then for n sufficiently large, $Bun _B(X, nx)$ is the attracting locus to $Bun _T(X, nx)$ in an open neighborhood of $Bun _T(X, nx)$ inside $Bun _G^{\omega }(X, nx)|_U$.

Proof

The $\mathbb {G}_m$-action contracts $Bun _B(X, nx)$ to $Bun _T(X, nx)$ because $\rho ^{\vee }(\mathbb {G}_m)$ contracts B to T. Indeed if F is a B-bundle then acting by $\rho ^{\vee }(z)$ gives a bundle with the same total space but b acting by $\rho ^{\vee }(z)b\rho ^{\vee }(z)^{-1}$. As $z \rightarrow 0$, the conjugate $\rho ^{\vee }(z)b\rho ^{\vee }(z)^{-1}$ approaches an element of T so the B-bundle approaches one induced from a T-bundle.

It remains to check $Bun _B(X, nx)$ is the full attracting locus in an open neighborhood of $Bun _T(X, nx)$ inside $Bun _G^{\omega }(X, nx)$. This is because $p:Bun _B(X, nx) \rightarrow Bun _G^{\omega }(X, nx)|_U$ is a closed embedding (we are implicitly restricting to the connected component containing $\rho ^{\vee }(\omega )$ and choosing n large) so p is a closed embedding into the attracting locus. Since $Bun _B(X, nx)$ is smooth, it suffices to show that p is also an open embedding into a neighborhood of the attracting locus about $Bun _T(X, nx)$. This follows because the derivative over $L \in Bun _T(X, nx)$, given by the natural map

(3.18)

maps isomorphically into the non-negative $\mathbb {G}_m$-weight spaces. $\square$

Since $p: Bun _B^{\omega }(X, nx) \rightarrow Bun _T^{\omega }(X, nx)$ is $\mathbb {G}_m$-equivariant, the fiber $Bun _N^{\omega }(X, nx)$ also admits a $\mathbb {G}_m$-action. But the action on $Bun _N^{\omega }(X, nx)$ changes the bundles not just the trivializations because conjugation by $\rho ^{\vee }(\mathbb {G}_m)$ is an outer automorphism of N.

Proposition 3.2.3

The function $f: Bun _N^{\omega }(X) \rightarrow \mathbb {A}^1$ is $\mathbb {G}_m$-equivariant.

Proof

For each positive simple root, projection onto that root space $N \rightarrow \mathbb {G}_a$ is $\mathbb {G}_m$-equivariant for the $\rho ^{\vee }$ action on N and the scaling action on $\mathbb {G}_a$. Under uniformization

$$\begin{aligned} Bun _{\mathbb {G}_a}^{\omega }(X) = \mathcal {O}_x dt \setminus K_xdt / \omega (X - x) = H^1(X, \omega ) \times BH^0(X, \omega ) \end{aligned}$$

(3.19)

the scaling action on $\mathbb {G}_a$ induces an action that scales the gluing data in $K_xdt$. The residue map $K_x dt \rightarrow \mathbb {A}^1$ descends to the map $Bun _{\mathbb {G}_a}^{\omega }(X) \rightarrow \mathbb {A}^1$ which is $\mathbb {G}_m$-equivariant. Since f is defined as the sum over positive simple roots of

(3.20)

it is $\mathbb {G}_m$-equivariant. $\square$

We are interested in sheaves on $Bun _G^{\omega }(X, nx)$ pulled back from $Bun _G(X)$ so they will certainly be $\mathbb {G}_m$-equivariant. Alternatively, having singular support in $\Lambda ' \subset T^*Bun _G^{\omega }(X, nx)$, implies constructibility along the orbits of this $\mathbb {G}_m$-action.

Applying Theorem 2.2.2 for $Y = Bun _G^{\omega }(X, nx)$, $y_0 = \rho ^{\vee }(\omega )$ with its canonical level structure, $Y^{> 0} = Bun _N^{\omega }(X, nx)$, and $Y^{\le 0} = Bun _{B^-}(X, nx)$ gives the following. Let $f'$ be the pullback to $Bun _N^{\omega }(X, nx)$ of f.

Proposition 3.2.4

There is an isomorphism of functors

$$\begin{aligned} \phi _{f', \rho ^{\vee }(\omega )} i'^! = \phi _{F, \rho ^{\vee }(\omega )}: Sh _{\Lambda '}(Bun _G^{\omega }(X, nx)) \rightarrow Vect . \end{aligned}$$

(3.21)

Here F is a real valued extension of $f'$ as in Theorem 2.2.2 satisfying $F|_{Bun _N^{\omega }(X, nx)} = {\text {Re}} f'$ and $F|_{Bun _{B^-}^{\omega }(X, nx) - \rho ^{\vee }(\omega )} < 0$.

Vanishing cycles commutes with smooth pullback, so $\phi _{f, \rho ^{\vee }(\omega )} i^!$ and $\phi _{f', \rho ^{\vee }(\omega )}i'^!$ agree up to a shift

$$\begin{aligned} \phi _{f, \rho ^{\vee }(\omega )}i^! [2n\dim N] \simeq \phi _{f', \rho ^{\vee }(\omega )} i'^! \pi ^!. \end{aligned}$$

(3.22)

Therefore we are free to pull everything back to $Bun _G^{\omega }(X, nx)$ where F is defined. Note that !-pullback along

(3.23)

is not exact, but by smoothness $\pi ^![-n \dim G]$ is.

3.3 Microstalk Along the Kostant Section

Now we will explain how the shifted conormal is the Kostant section of the Hitchin fibration and therefore intersects the global nilpotent cone transversely in a single smooth point.

Proposition 3.3.1

Inside $T^* Bun _G(X)$ the shifted conormal bundle $T^*_{Bun _N^{\omega }(X)}Bun _G(X)$ $+ df$¹⁰ intersects the global nilpotent cone $\Lambda$ transversely at a smooth point.

Proof

The shifted conormal bundle consists of cotangent vectors $X \rightarrow \mathfrak {g}^*/(N \rtimes \mathbb {G}_m)$ in $(T^*Bun _G(X))|_{Bun _N^{\omega }(X)}$ such that the composition

(3.24)

lands in $\psi /(N \rtimes \mathbb {G}_m)$. Therefore $T^*_{Bun _N^{\omega }(X)}Bun _G + df$ is represented by the Kostant section

(3.25)

We used the homomorphism

$$\begin{aligned} N \rtimes \mathbb {G}_m \rightarrow G \times \mathbb {G}_m, \qquad n \rtimes z \mapsto (n \cdot 2\rho ^{\vee }(z), z^2). \end{aligned}$$

(3.26)

This is a section of the characteristic polynomial map $\mathfrak {g}^*/(G \times \mathbb {G}_m) \rightarrow \mathfrak {c}^* / \mathbb {G}_m$ which represents the Hitchin map

(3.27)

Let $T^* Bun _G(X)^{reg }$ be the regular locus, represented by $\mathfrak {g}^{*, reg }/(G \times \mathbb {G}_m) \subset \mathfrak {g}^*/(G \times \mathbb {G}_m)$. It is an open substack of $T^* Bun _G(X)$ because $\mathfrak {g}^{*, reg } \subset \mathfrak {g}^*$ is open and X is proper. The Hitchin fibration h is smooth after restricting to this regular locus. Since $\psi + \mathfrak {n}^{\perp } \subset \mathfrak {g}^{*, reg }$ consists of regular elements the Kostant section is contained in $T^* Bun _G(X)^{reg }$. After restricting to $T^* Bun _G(X)^{reg }$, the Kostant section is a section of a smooth projection so intersects every fiber, in particular the global nilpotent cone, transversely at a smooth point. $\square$

Since i is not a closed embedding we factored it through $Bun _N^{\omega }(X) \rightarrow Bun _{G, N}^{\omega }(X, nx)$.

Proposition 3.3.2

Inside $T^* Bun _{G, N}^{\omega }(X, nx)$, the shifted conormal bundle

$$\begin{aligned} \Lambda _f'' := df + T^*_{Bun _N^{\omega }(X)} Bun ^{\omega }_{G, N}(X, nx) \end{aligned}$$

(3.28)

intersects the global nilpotent cone

$$\begin{aligned} \Lambda '' = \Lambda \times _{Bun _G(X)} Bun ^{\omega }_{G, N}(X, nx) \end{aligned}$$

(3.29)

transversely at a single smooth point.

Proof

The nilpotent cone $\Lambda ''$ is contained inside¹¹

$$\begin{aligned} \mu ^{-1}(0)/N := T^* Bun _G(X) \times _{Bun _G(X)} Bun ^{\omega }_{G, N}(X, nx). \end{aligned}$$

(3.30)

Whereas we claim that the shifted conormal $\Lambda _f''$ intersects $\mu ^{-1}(0)/N$ transversely. By the previous Proposition 3.3.1,

$$\begin{aligned} \Lambda _f'' \cap (\mu ^{-1}(0)/N) = df + T^*_{Bun _N^{\omega }(X)} Bun _G(X) \end{aligned}$$

(3.31)

intersects $\Lambda ''$ transversely inside $\mu ^{-1}(0)/N$ at a single smooth point of $\Lambda ''$. Therefore $\Lambda _f''$ and $\Lambda ''$ intersect transversely as desired.

To see the claim that $\Lambda _f''$ and $\mu ^{-1}(0)/N$ intersect transversely we need to check that their tangent spaces at $df(\rho ^{\vee }(\omega ))$ together span the whole $T_{df(\rho ^{\vee }(\omega ))} T^* Bun _{G, N}^{\omega }(X, nx)$. Projecting onto the horizontal directions, $T_{df(\rho ^{\vee }(\omega ))} T^* Bun _{G, N}^{\omega }(X, nx)$ fits into a short exact sequence

$$\begin{aligned} 0 \rightarrow T^*_{\rho ^{\vee }(\omega )} Bun _{G, N}^{\omega }(X, nx) \rightarrow T_{df(\rho ^{\vee }(\omega ))} T^* Bun _{G, N}^{\omega }(X, nx) \rightarrow T_{\rho ^{\vee }(\omega )} Bun _{G, N}^{\omega }(X, nx) \rightarrow 0. \end{aligned}$$

(3.32)

The tangent space to $\mu ^{-1}(0)/N$ surjects onto $T_{\rho ^{\vee }(\omega )} Bun _{G, N}^{\omega }(X, nx)$ so it suffices to show that the tangent spaces to $\Lambda _f''$ and $\mu ^{-1}(0)/N$ intersected with the vertical subspace $T^*_{\rho ^{\vee }(\omega )} Bun _{G, N}^{\omega }(X, nx)$ together span the whole $T^*_{\rho ^{\vee }(\omega )} Bun _{G, N}^{\omega }(X, nx)$. The vertical part of the tangent space to $\Lambda _f''$ is the conormal space $(T^*_{Bun _N^{\omega }(X)} Bun _{G, N}^{\omega }(X,$$nx))_{\rho ^{\vee }(\omega )}$, which is by definition the kernel in a short exact sequence

$$\begin{aligned} 0 \rightarrow (T^*_{Bun _N^{\omega }(X)} Bun _{G, N}^{\omega }(X, nx))_{\rho ^{\vee }(\omega )} \rightarrow T^*_{\rho ^{\vee }(\omega )} Bun _{G, N}^{\omega }(X, nx) \rightarrow T^*_{\rho ^{\vee }(\omega )} Bun _N^{\omega }(X) \rightarrow 0. \end{aligned}$$

(3.33)

The vertical part of the tangent space to $\mu ^{-1}(0)/N$ is $T^*_{\rho ^{\vee }(\omega )} Bun _G(X)$ which surjects onto the cokernel $T^*_{\rho ^{\vee }(\omega )} Bun _N^{\omega }(X)$. So together the tangent spaces to $\Lambda _f''$ and $\mu ^{-1}(0)/N$ span $T^*_{\rho ^{\vee }(\omega )} Bun _{G, N}^{\omega }(X, nx)$.

$\square$

Pulling back to $i':Bun _N^{\omega }(X, nx) \rightarrow Bun _G^{\omega }(X, nx)$ the intersection is no longer transverse but still clean.

Proposition 3.3.3

Inside $T^* Bun _G^{\omega }(X, nx)$, the shifted conormal bundle

$$\begin{aligned} \Lambda _f' := T^*_{Bun _N^{\omega }(X, nx)} Bun _G^{\omega }(X, nx) + df' \end{aligned}$$

(3.34)

intersects the global nilpotent cone $\Lambda '$ cleanly along smooth points. The intersection is $n \dim N$ dimensional.

Proof

Both $\Lambda '$ and $\Lambda _f'$ live inside

$$\begin{aligned} \mu ^{-1}(\mathfrak {n}^{\perp }) := T^*Bun ^{\omega }_{G, N}(X, nx) \times _{Bun ^{\omega }_{G, N}(X, nx)} Bun _G^{\omega }(X, nx) \subset T^*Bun _G^{\omega }(X, nx) \end{aligned}$$

(3.35)

and are pulled back from $\Lambda ''$ and $\Lambda _f''$ respectively along

(3.36)

By the previous Proposition 3.3.2, $\Lambda '$ and $\Lambda '_f$ intersect transversely inside $\mu ^{-1}(\mathfrak {n}^{\perp })$ and the dimension of intersection is $n \dim N$, the relative dimension of $\pi$. Therefore they intersect cleanly inside the full $T^*Bun _G^{\omega }(X, nx)$. $\square$

Therefore by Proposition 2.3.3, the Whittaker functional

$$\begin{aligned} \phi _{f', \rho ^{\vee }(\omega )} i'^! \simeq \phi _{F, \rho ^{\vee }(\omega )} \end{aligned}$$

(3.37)

is a shifted microstalk and

$$\begin{aligned} \phi _{f', \rho ^{\vee }(\omega )} i'^![\dim _{\rho ^{\vee }(\omega )} Bun _{B^-}(X, nx) - n\dim N] \end{aligned}$$

(3.38)

is exact and commutes with Verdier duality. Descending from $Bun _G^{\omega }(X, nx)$ back to $Bun _G(X)$ we get that $\phi _{f, \rho ^{\vee }(\omega )}$ is exact after shifting by

$$\begin{aligned} 2n\dim N - n\dim G + \dim _{\rho ^{\vee }(\omega )} Bun _{B^-}(X, nx) - n\dim N = \dim _{\rho ^{\vee }(\omega )} Bun _{B^-}(X). \end{aligned}$$

(3.39)

Reassuringly, this expression is independent of n, the amount of uniformization. We have proved:

Theorem 3.3.4

The shifted Whittaker functional

$$\begin{aligned} \phi _{f, \rho ^{\vee }(\omega )} i^! [\dim _{\rho ^{\vee }(\omega )} Bun _{B^-}(X)] \end{aligned}$$

(3.40)

calculates microstalk. In particular Eq. 3.40 is exact and commutes with Verdier duality.

The result that the Whittaker functional is exact and commutes with Verdier duality was also obtained in [5]. Let’s recall where all of the shifts came from in our arguments:

• The $2n \dim N$ shift appears from Eq. 3.22 as the difference between vanishing cycles for f on $Bun _N^{\omega }(X)$ versus !-pullback to $Bun _N^{\omega }(X, nx)$ followed by vanishing cycles for the lifted function $f'$.

• The $-n \dim G$ shift came from the fact that !-pullback along $\pi : Bun _G^{\omega }(X, nx) \rightarrow Bun _G(X)$ is not exact but $\pi ^![-n\dim G]$ is.

• The $\dim _{\rho ^{\vee }(\omega )} Bun _{B^-}(X, nx)$ shift is the dimension of $Y^{\le 0}$ appearing in Proposition 2.3.3.

• The $-n \dim N$ shift is minus the dimension of $\Lambda \cap (T^*_{Y^{> 0}}Y + df)$ appearing in Proposition 2.3.3.

3.4 The Whittaker Functional in the Presence of Tame Ramification

In this section we extend Theorem 3.3.4 the case of tame ramification at a finite subset of points $S \subset X$. Let $Bun _N^{\omega (S)}(X, S)$ be the moduli of B-bundles such that the underlying T-bundle is $\rho ^{\vee }(\omega (S))$ plus a trivialization of the fibers at the marked points S. The Whittaker function is given by summing up

(3.41)

over simple roots, see Section 2.5 of [11]. There is a map

(3.42)

to the moduli of G-bundle with $N^-$-reductions at S.

The cotangent space

$$\begin{aligned} T^*Bun _{G, N^-}(X, S) = \{E, F_S, \sigma \in H^0(\mathfrak {g}^*_E \otimes \omega (S)) | res _S(\sigma ) \in \mathfrak {b}^*_{F_S} \} \end{aligned}$$

(3.43)

is the moduli of G-bundles E with an $N^-$-reduction $F_S$ at S plus a Higgs field $\sigma \in H^0(\mathfrak {g}^*_E \otimes \omega (S))$ whose residue at S is in $\mathfrak {b}^*$ with respect to $F_S$. The Hitchin map

(3.44)

sends a Higgs field to its characteristic polynomial plus an ordering of the eigenvalues at the points of S. Let $\Lambda = h^{-1}(0)$ be the nilpotent cone in $T^*Bun _{G, N^-}(X, S)$.

The cotangent space $T^* Bun _{G, N^-}(X, S)$ is represented by maps $X \rightarrow \mathfrak {g}^*/G \times \mathbb {G}_m$ such that the underlying $\mathbb {G}_m$-bundle is $\omega (S)$, plus a lifting at the marked points $S \rightarrow \mathfrak {b}^*/N^-$. We identified $\mathfrak {b}^* = (\mathfrak {n}^-)^{\perp }$ using the Killing form. Below we list the other relevant cotangent spaces together with the pairs of spaces representing them:

Theorem 3.4.1

The shifted Whittaker functional

(3.45)

calculates microstalk. In particular Eq. 3.45 is exact and commutes with Verdier duality.

Proof

By looking at cotangent spaces we see that $Bun _N^{\omega (S)}(X, S)$ is the full attracting locus in $Bun _{G, N^-}(X, S)$. Moreover the shifted conormal maps isomorphically to the Hitchin base under

(3.46)

because the above composition is represented by the map of pairs

(3.47)

Therefore the shifted conormal intersects the global nilpotent cone $\Lambda$ transversely at a single smooth point. The result now follows by uniformizing $Bun _{G, N^-}(X, S)$ by a scheme and then applying Proposition 2.3.3. $\square$