Tilted biorthogonal ensembles, Grothendieck random partitions, and determinantal tests

Abstract

We study probability measures on partitions based on symmetric Grothendieck polynomials. These deformations of Schur polynomials introduced in the K-theory of Grassmannians share many common properties. Our Grothendieck measures are analogs of the Schur measures on partitions introduced by Okounkov (Sel Math 7(1):57–81, 2001). Despite the similarity of determinantal formulas for the probability weights of Schur and Grothendieck measures, we demonstrate that Grothendieck measures are not determinantal point processes. This question is related to the principal minor assignment problem in algebraic geometry, and we employ a determinantal test first obtained by Nanson in 1897 for the $4\times 4$ problem. We also propose a procedure for getting Nanson-like determinantal tests for matrices of any size $n\ge 4$, which appear new for $n\ge 5$. By placing the Grothendieck measures into a new framework of tilted biorthogonal ensembles generalizing a rich class of determinantal processes introduced by Borodin (Nucl Phys B 536:704–732, 1998), we identify Grothendieck random partitions as a cross-section of a Schur process, a determinantal process in two dimensions. This identification expresses the correlation functions of Grothendieck measures through sums of Fredholm determinants, which are not immediately suitable for asymptotic analysis. A more direct approach allows us to obtain a limit shape result for the Grothendieck random partitions. The limit shape curve is not particularly explicit as it arises as a cross-section of the limit shape surface for the Schur process. The gradient of this surface is expressed through the argument of a complex root of a cubic equation.

1 Introduction

1.1 Random partitions from symmetric functions

The study of random integer partitions involving probability weights expressed through symmetric polynomials has been a long-standing topic in integrable probability and related fields [13, 22]. Asymptotic analysis of various measures on partitions produced law of large numbers and asymptotic fluctuation results in many stochastic models describing complex real-world phenomena, including longest increasing subsequences [9, 57, 83], interacting particle systems [46], random growth models [10], random polymer models [30, 67, 75], random matrices [12], and geometry [69, 72].

One of the earliest studied ensembles of random partitions based on symmetric functions is the Schur measure introduced in [70]. The Schur measure probability weights have the form

$$\begin{aligned} \mathop {\textrm{Prob}}(\lambda ):=\frac{1}{Z} \underbrace{\frac{ \det [x_j^{\lambda _i+N-i}]_{i,j=1}^{N}}{\prod _{1\le i<j\le N}(x_i-x_j)}}_{s_\lambda (x_1,\ldots ,x_N )} \underbrace{\frac{ \det [y_j^{\lambda _i+N-i}]_{i,j=1}^{N}}{\prod _{1\le i<j\le N}(y_i-y_j)}}_{s_\lambda (y_1,\ldots ,y_N )}. \end{aligned}$$

(1.1)

Here $\lambda =(\lambda _1\ge \cdots \ge \lambda _N\ge 0 )$ are integer partitions which we think of as our random objects, $x_i,y_j\ge 0$ with $x_iy_j<1$ are parameters of the measure. The quantities $s_\lambda (x_1,\ldots ,x_N )$ and $s_\lambda (y_1,\ldots ,y_N )$ in (1.1) are the well-known Schur symmetric polynomials in the variables $x_1,\ldots ,x_N$ and $y_1,\ldots ,y_N$, respectively, indexed by the same partition $\lambda$. The probability normalizing constant $Z=\prod _{i,j=1}^{N}(1-x_iy_j)^{-1}$ has a product form thanks to the Cauchy summation identity for Schur polynomials.

The Schur measures are particularly tractable thanks to their determinantal structure, which allows expressing correlation functions

$$\begin{aligned} \rho (a_1,\ldots ,a_m )&:=\mathop {\textrm{Prob}}\Bigg ( \text {the random set }\nonumber \\&\quad \left\{ \lambda _i+N-i \right\} \subset \mathbb {Z}_{\ge 0} \text { contains each } a_1,\ldots ,a_m \Bigg ) \end{aligned}$$

(1.2)

of an arbitrary order m as $m\times m$ determinants $\det [K(a_i,a_j)]_{i,j=1}^m$ of a fixed correlation kernel K(a, b), where $a,b\in \mathbb {Z}_{\ge 0}$. The kernel has a double contour integral form, readily amenable to asymptotic analysis by steepest descent.

Over the past two decades, Schur measures have been generalized to other families of symmetric polynomials, including Macdonald polynomials [7] and their degenerations such as Jack [12], Hall–Littlewood [15, 23], and q-Whittaker polynomials [22, 62]. More recently, these efforts have extended to symmetric rational functions (like spin q-Whittaker and spin Hall–Littlewood functions) arising as partition functions of integrable (in the sense of the Yang–Baxter equation) vertex models [3, 20, 24, 28]. The vertex model approach also naturally included distinguished nonsymmetric polynomials powering the structure of multispecies stochastic systems [4, 29].

While these more general symmetric polynomials and rational functions share many properties with the Schur polynomials, the technique of determinantal point processes does not straightforwardly extend. This has led to several interesting alternative approaches, including eigenoperators [7] and duality [8], which brought multiple contour integral formulas for expectations of observables. Recently [44] presented a direct mapping between q-Whittaker and cylindric Schur measures [17] preserving specific observables. Since the latter measures are determinantal, this allows for employing determinantal process methods for the asymptotic analysis of these observables.

1.2 Grothendieck measures on partitions

Our primary focus is on Grothendieck measures on partitions whose probability weights are expressed through the Grothendieck symmetric polynomials:

$$\begin{aligned} \mathop {\textrm{Prob}}(\lambda ) :=\frac{1}{Z'} \underbrace{ \frac{\det \bigl [ x_i^{\lambda _j+N-j}(1-\beta x_i)^{j-1}\bigr ]_{i,j=1}^{N} }{\prod _{1\le i<j\le n}(x_i-x_j)} }_{G_\lambda (x_1,\ldots ,x_N )} \underbrace{\frac{ \det \bigl [ y_i^{\lambda _j+N-j}(1-\beta y_i^{-1})^{N-j}\bigr ]_{i,j=1}^{N} }{\prod _{1\le i<j\le n}(y_i-y_j)}}_ {\overline{G}_\lambda (y_1,\ldots ,y_N )}.\nonumber \\ \end{aligned}$$

(1.3)

Here $x_i,y_j$, and $\beta$ are parameters such that $x_i,y_j\ge 0$, $x_iy_j<1$, and $\beta \le \min _{1\le i\le N}(x_i^{-1},y_i)$. The latter condition implies that the probability weights are nonnegative. The Grothendieck symmetric polynomials $G_\lambda (x_1,\ldots ,x_N )$ and $\overline{G}_\lambda (y_1,\ldots ,y_N )$ are one-parameter deformations of the Schur polynomials appearing in the K-theory of Grassmannians. The normalizing constant is $Z'= \prod _{i=1}^{N}(1-x_i\beta )^{N-1} \prod _{i,j=1}^N(1-x_iy_j)^{-1}$. When $\beta =0$, the Grothendieck measure (1.3) reduces to the Schur measure (1.1). We refer to [27, 31, 35, 58, 84], and [41] for details, properties, and various multiparameter generalizations of Grothendieck polynomials. All methods of the present paper apply in a setting when there are multiple $\beta _j$’s (see the polynomials $G_\lambda$ and $\overline{G}_\lambda$ in (3.3) in the text). However, in the Introduction and asymptotic analysis, we restrict to the case of the homogeneous $\beta _j$’s.

In this paper, we obtain two main results for the Grothendieck measures:

• We show that despite the determinant representation of their probability weights, Grothendieck measures do not possess a determinantal structure of correlations. This observation may appear unexpected given the similarity of Grothendieck probability weights compared to the Schur measures.

• We establish a link between Grothendieck random partitions and Schur processes, the latter being determinantal point processes on a two-dimensional lattice. We perform this connection within an extended framework of tilted biorthogonal ensembles, which we introduce. This connection provides an essential structure for the Grothendieck measures. It enables us to derive formulas expressing their correlations through sums of Fredholm determinants and prove limit shape results.

We formulate these results in the remainder of the Introduction.

Remark 1.1

It was observed in [20, Sections 8.3 and 8.4] that the $q=0$ specialization of spin Hall–Littlewood polynomials produces determinantal partition functions of vertex models which resemble the Grothendieck polynomials $G_\lambda$ in (1.3). Most of the machinery for computing expectations of observables of the form $q^{\textrm{height}}$ breaks down for $q=0$, so it is not immediately clear whether vertex models are applicable in the analysis of Grothendieck measures. Moreover, limit shape results are not yet established for random partitions with spin Hall–Littlewood weights or their $q=0$ degenerations (see, however, [5] for limit shapes of Macdonald random partitions in another regime, as $q,t\rightarrow 1$).

1.3 Absence of determinantal structure

Theorem 1.2

For certain fixed N and values of parameters $x_i,y_j$, and $\beta$, the correlations (1.2) of the Grothendieck measures do not possess a determinantal form. That is, there does not exist a function $K:\mathbb {Z}_{\ge 0}^{2}\rightarrow \mathbb {C}$ for which $\rho (a_1,\ldots ,a_m )=\det [K(a_i,a_j)]_{i,j=1}^m$ for all m and all pairwise distinct $a_1,\ldots ,a_m\in \mathbb {Z}_{\ge 0}$.

We show the nonexistence of a correlation kernel K by constructing an explicit polynomial in the correlation functions $\rho (a_1,\ldots ,a_m )$, which vanishes identically if the correlation functions have a determinantal form (we call such polynomials determinantal tests). We then show that for a specific choice of parameters, $N=2$, $x_i=y_j=1/2$, $\beta =-1$, the determinantal test does not vanish. While for Theorem 1.2, we only need a specific choice of parameters, we expect the absence of determinantal structure to hold for generic parameters in the Grothendieck measures.

The problem of finding a kernel representing all correlations $\rho (a_1,\ldots ,a_m )$ in a determinantal form is the same as the well-known principal minor assignment problem in algebraic geometry. This problem seeks an $n\times n$ matrix whose all principal (diagonal) minors are given, but such an underlying matrix does not exist for all choices of (prospective) principal minors. Therefore, one has to find relations between principal minors. These relations are polynomial, and each may be used as a determinantal test. The variety of $n\times n$ principal minors becomes complicated already for $n=4$ (it is minimally generated by 65 polynomials of degree 12), but for Theorem 1.2, it suffices to show that one generating polynomial does not vanish. In fact, the determinantal test we employ in our proof was written down by Nanson in 1897 for $4\times 4$ matrices [66]. In Sect. 4.2, we discuss the rich history of the principal minor assignment problem and several instances of its rediscovery within the study of determinantal point processes. In Sects. 4.3 and 4.4, we present a self-contained derivation of the Nanson’s determinantal test and suggest a generalization of the Nanson’s test to matrices of arbitrary size. This generalization appears new.

1.4 Tilted biorthogonal ensembles

To connect Grothendieck measures to Schur processes, which are determinantal processes on the two-dimensional integer lattice, we consider a more general framework of tilted biorthogonal ensembles, which is inspired by a talk of Kenyon [48]. The ordinary biorthogonal ensembles introduced in [21] are measures on partitions with probability weights of the form

$$\begin{aligned} \mathop {\textrm{Prob}}(\lambda )=\frac{1}{Z} \det \bigl [ \Phi _i(\ell _j) \bigr ]_{i,j=1}^{N} \det \bigl [ \Psi _i(\ell _j) \bigr ]_{i,j=1}^{N}, \qquad \ell _j:=\lambda _j+N-j, \end{aligned}$$

(1.4)

where $\Phi _i,\Psi _j$ are given functions, and Z is the normalizing constant. Biorthogonal ensembles are determinantal processes on $\mathbb {Z}_{\ge 0}$ in the same sense as the Schur measures. Moreover, when $\Phi _i(k)=x_i^k$, $\Psi _j(k)=y_j^k$, the weights (1.4) coincide with (1.1).

We “tilt” the biorthogonal ensemble (1.4) by inserting j-dependent difference operators into the determinants.¹ When $\Phi _i(k)=x_i^k$, $\Psi _j(k)=y_j^k$, the action of these operators results in the factors $(1-\beta x_i)^{j-1}$ and $(1-\beta y_i^{-1})^{N-j}$ in (1.3). In general, we apply the operator $(D)^{j-1}$ to $\Phi _i(\ell _j)$, where $Df(k)=f(k)-\beta f(k+1)$, and $(D^{\dagger })^{N-j}$ to $\Psi _i(\ell _j)$, where $D^{\dagger }f(k)=f(k)-\beta f(k-1)\textbf{1}_{k\ge 1}$. Here and throughout the paper, $\textbf{1}_{A}$ stands for the indicator of an event or a condition A. We arrive at the following measure on partitions:

$$\begin{aligned}{} & {} \mathop {\textrm{Prob}}(\lambda )=\frac{1}{Z'} \det \bigl [ (D)^{j-1}\Phi _i(\ell _j) \bigr ]_{i,j=1}^{N} \det \bigl [ (D^{\dagger })^{N-j}\Psi _i(\ell _j) \bigr ]_{i,j=1}^{N}, \qquad \nonumber \\{} & {} \quad \ell _j= \lambda _j+N-j. \end{aligned}$$

(1.5)

For details, we refer to Sect. 2.1 in the text.

The action of D is the same as the multiplication by the matrix $T_\beta (k,l):=\textbf{1}_{l=k}-\beta \hspace{1pt}\textbf{1}_{l=k-1}$, and $D^{\dagger }$ is the multiplication by $T_\beta$ on the opposite side. Using this, we identify (Theorem 2.3) the joint distribution of $(\ell _1>\cdots >\ell _N )$ under the tilted biorthogonal ensemble with that of the points $(x_1^1>\cdots >x^N_N )$ in the two-dimensional ensemble $\{x^m_j:1\le m,j\le N \}$ which has probability weights proportional to

$$\begin{aligned} \det \left[ \Phi _i(x^1_j) \right] _{i,j=1}^N \biggl (\hspace{1pt}\prod _{m=1}^{N-1} \det \left[ T_{\beta }(x^m_i,x^{m+1}_j) \right] _{i,j=1}^{N} \biggr ) \det \left[ \Psi _i(x^{N}_j) \right] _{i,j=1}^N. \end{aligned}$$

(1.6)

The two-dimensional process has probability weights given by products of determinants. Thus, it is determinantal thanks to the well-known Eynard–Mehta theorem [26, 34], see also [18, Theorem 4.2].

The above identification allows us to write down certain Fredholm determinantal formulas for marginal distributions and correlation functions of tilted biorthogonal ensembles; see Sect. 2.5 and Proposition 2.7 in particular.

When $\Phi _i(k)=x_i^k$ and $\Psi _j(k)=y_j^k$ for all i, j, the two-dimensional determinantal process (1.6) becomes the Schur process whose correlation kernel has a double contour integral form [73]. The particular specializations of the Schur process parameters are given in Sect. 3.3 in the text. Our Schur process has nonnegative probability weights only for $\beta <0$, and this is the case we restrict to in our asymptotic analysis (see Sect. 1.5). The case $\beta =0$ is covered by standard results on Schur measures. It is plausible that our results on the Grothendieck limit shape still apply to values of $\beta >0$, even if probabilities in the two-dimensional process are negative, as long as the Grothendieck probability weights (1.3) remain nonnegative. See Conjecture 5.10 for details.

Remark 1.3

(Application to the five-vertex model) In [48], Kenyon expressed certain distributions arising in the five-vertex model (see also [32]) as tilted biorthogonal ensembles. It would be very interesting to apply our results to the asymptotic analysis of the five-vertex model, but there are three clear obstacles. First, the two-dimensional process for the five-vertex model is not the Schur process but rather a multiparameter analog of the more complicated model of lozenge tilings of the hexagon (see, e.g., [37, 77] for the determinantal structure of the original tilings of the hexagon). One does not have as elegant expressions for the correlation kernel in the case of multiple parameters. Second, the probability weights in the two-dimensional process are complex-valued. This makes probabilistic identification of limit shapes problematic; see also the discussion in Sect. 5.4.4. Third, for the five-vertex model, the multiple parameters $x_i,y_j$ are solutions to the Bethe equations. This makes a potential asymptotic analysis even more intricate (see, however, [78] and [14] for a related analysis of TASEP on the ring).

1.5 Limit shape

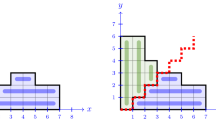
Consider Grothendieck random partitions (1.3) with homogeneous parameters $x_i\equiv x>0$, $y_j\equiv y>0$, such that $xy<1$ and $\beta <0$. Let us draw Young diagrams of our Grothendieck random partitions in the (u, v) coordinate system rotated by $45^\circ$, see Fig. 1, left. Each partition is encoded by a piecewise linear function $v=\mathfrak {W}_N(u)$ with derivatives $\pm 1$ and integer maxima and minima. Since our partitions have at most N parts, we almost surely have $\mathfrak {W}_N(u)\ge |u|$ for all u, $\mathfrak {W}_N(u)= |u|$ if |u| is large enough, and $\mathfrak {W}_N(u)\le u+2N$ if $u\ge -N$.

Theorem 1.4

Fix the parameters $x,y,\beta$ as above. There exists a continuous, piecewise differentiable, 1-Lipschitz function $\mathfrak {W}(u)= \mathfrak {W}(u\mid x,y,\beta )$ with $\mathfrak {W}(u)\ge |u|$ and $\mathfrak {W}(u)=|u|$ if |u| is large enough, such that

$$\begin{aligned} \lim _{N\rightarrow +\infty }\frac{\mathfrak {W}_N(u N)}{N}=\mathfrak {W}(u),\qquad u\in \mathbb {R}, \end{aligned}$$

where the convergence is pointwise in probability. See Fig. 1, right, for an illustration.

Fig. 1

Left: The Young diagram for $\lambda =(6,6,5,3,1,1)$ in the coordinate system rotated by $45^\circ$. The diagonal line $v=u+2N$ represents the upper boundary of the shape of $\lambda$. Right: An example of a limit shape $\mathfrak {W}(u)$ of the Grothendieck random partition for $x=1/3$, $y=1/5$, and $\beta =-25$. We added a horizontal line to highlight the staircase frozen facet where the limit shape $\mathfrak {W}(u)$ is horizontal. An exact sample of a random partition corresponding to the limit shape on the right is given in Fig. 9, right (see also Sect. 5.5 for a discussion of how to sample Grothendieck random partitions)

The first limit shape result for random partitions (with Plancherel measure, which is a particular case of Schur measures) was obtained by Logan–Shepp [57] and Vershik–Kerov [83]. We do not have an analytic formula for our shapes $\mathfrak {W}(u)$ in contrast to this classical VKLS shape. Let us briefly describe how $\mathfrak {W}(u)$ is related to the limit surface of the Schur process. We used this connection to numerically plot all our examples; see Sect. 5.4 for details and more discussion.

Let $\{x^m_j:1\le m,j\le N \}$ be distributed according to the Schur process as in (1.6). Define the height function $H_N(a,t):=\#\{j:x^t_j\ge a \}$, where $(a,t)\in \mathbb {Z}_{\ge 0}\times \left\{ 1,\ldots ,N \right\}$. Using the standard steepest descent analysis of the correlation kernel of the Schur process (dating back to [73], see also [71, Section 3]), one can show that $H_N$ has a limit shape $\mathfrak {H}(\xi ,\tau ) = \lim \limits _{N\rightarrow \infty }N^{-1}\hspace{1pt}H_N(\lfloor \xi N \rfloor ,\lfloor \tau N \rfloor )$, where $(\xi ,\tau )\in \mathbb {R}_{\ge 0} \times [0,1]$. The gradient of $\mathfrak {H}$ is expressed through arguments of the complex root $z_c=z_c(\xi ,\tau )$ of a certain cubic equation depending on $(\xi ,\tau )$ and our parameters $(x,y,\beta )$, see (5.7) and (5.9) for the formulas.

The identification between Grothendieck random partitions and the slice $(x_1^1>\cdots >x^N_N )$ of the Schur process (see Sect. 1.4) helps to express the Grothendieck limit shape $\mathfrak {W}(u)$ through $\mathfrak {H}(\xi ,\tau )$. Namely, let $\mathfrak {L}(\tau )$ be an auxiliary function defined from the implicit equation

$$\begin{aligned} \mathfrak {H} \left( \mathfrak {L}(\tau ),\tau \right) =\tau \quad \text {for all }\tau \in [0,1]. \end{aligned}$$

(1.7)

In other words, the three-dimensional parametric curve $(\mathfrak {L}(\tau ),\tau ,\tau )$ is the cross-section of the Schur process limit shape surface $\eta =\mathfrak {H}(\xi ,\tau )$ in the $(\xi ,\tau ,\eta )$ coordinates by the plane $\eta =\tau$. From the Schur process limit shape result, we have $\mathfrak {L}(\tau )=1-\tau +\lim \limits _{N\rightarrow \infty }N^{-1}\lambda _{\lfloor N\tau \rfloor }$ (the shift by $1-\tau$ comes from $\ell _j=\lambda _j+N-j$, see (1.5)). Then the Grothendieck limit shape curve $(u,\mathfrak {W}(u))$ as in Fig. 1, right, has the following parametrization through $\mathfrak {L}(\tau )$:

$$\begin{aligned} u=\mathfrak {L}(\tau )-1,\qquad \mathfrak {W}=\mathfrak {L}(\tau )-1+2\tau . \end{aligned}$$

The functions $\mathfrak {L}(\tau )$ and $\mathfrak {W}(u)$ satisfy differential equations involving the root $z_c(\xi ,\tau )$, see (5.17)–(5.18). However, the implicit equation (1.7) turns out to be more convenient for plotting the shapes.

The flat, “frozen”, facets of the Schur limit shape surface (where the gradient is at a vertex of its allowed triangle, see (5.5)) lead to the three possible flat facets of $\mathfrak {W}(u)$, where $\mathfrak {W}'(u)$ is equal to $-1,0$, or 1, respectively. The derivatives $\pm 1$ occur when $\mathfrak {W}(u)=|u|$ outside of the curved part of the limit shape. The facet $\mathfrak {W}'(u)=0$ always arises for sufficiently negative $\beta$ (Lemma 5.6). In this facet, the random partition develops the deterministic frozen staircase behavior, that is, $\lambda _i=\lambda _{i+1}+1$ for all i in some interval of order N. See the horizontal part of the limit shape in Fig. 1, right.

Besides limit shapes, the study of random partitions often involves fluctuations in various regimes (at the edge, in the bulk, and global Gaussian fluctuations). It would be interesting to obtain fluctuation results for Grothendieck random partitions in these regimes and compare them to the classical case of the Plancherel random partitions [9, 16, 45, 47]. The tilted nature of the cross-section leading to Grothendieck measures seems to be affecting all Grothendieck fluctuations except the edge ones. Indeed, for any fixed k, $(\lambda _1,\ldots ,\lambda _k)$ have the same joint distribution as $(\mu ^1_1,\ldots ,\mu ^k_k )$, where the partitions $\mu ^1,\ldots ,\mu ^k$ for a Schur process. Moreover, we have $|\mu ^j_j-\mu ^1_j|\le j$ for all j (see Sect. 5.3.3 for details). Therefore, we expect that the joint distribution of $(\lambda _j-cN)/(\sigma N^{1/3})$, $j=1,\ldots ,k$, should converge to the Airy$_2$ point process, just like for the Plancherel measure. We also expect that the bulk fluctuations are not given by the same discrete sine process as in the Plancherel case. It would be interesting to compute the correlations of the Gaussian limit, and compare them to the Plancherel case.

1.6 Outline

In Sect. 2, we introduce the framework of tilted biorthogonal ensembles and show that they are cross-sections of two-dimensional determinantal processes. The correlation kernel of the latter is given by the Eynard–Mehta theorem. In Sect. 3, we specialize tilted biorthogonal ensembles to Grothendieck measures on partitions and write down the correlation kernel of the corresponding two-dimensional Schur process in a double contour integral form (specializing the results of [73]). In Sect. 4, we prove Theorem 1.2 that Grothendieck measures are not determinantal point processes. Section 4.2 provides a brief historical account of the relation between the determinantal structure of probability measures and the principal minor assignment problem. Finally, in Sect. 5, we establish limit shape results for Schur processes and Grothendieck random partitions and illustrate these results by several plots and exact sampling simulations.

2 Tilted biorthogonal ensembles

In this section, we present the main framework for measures on particle configurations in $\mathbb {Z}_{\ge 0}$ given by a certain product of determinants, and discuss their characteristics.

2.1 Definition of the ensemble

Fix N, and let $\Phi _k$, $\Psi _k$, $k=1,\ldots ,N$, be arbitrary complex-valued functions on $\mathbb {Z}_{\ge 0}$. Fix additional complex parameters $\beta _1,\beta _2,\ldots ,\beta _{N-1}$. Let us define the following operators acting on finitely supported functions on $\mathbb {Z}_{\ge 0}$:

$$\begin{aligned} D_k^{(r)}f(k):=f(k)-\beta _r f(k+1),\qquad D_k^{(r)\dagger }f(k):=f(k)-\beta _r f(k-1)\hspace{1pt}\textbf{1}_{k\ge 1}, \end{aligned}$$

(2.1)

where $r=1,\ldots ,N-1$. These operators are conjugate to each other with respect to the bilinear form $\sum _{k=0}^{\infty }f(k)g(k)$ on finitely supported functions on $\mathbb {Z}_{\ge 0}$. Denote

$$\begin{aligned} D_\ell ^{[a,b)}:=D_{\ell }^{(a )}D_{\ell }^{(a+1 )}\ldots D_{\ell }^{( b-1 )}, \end{aligned}$$

(2.2)

and similarly for other types of segments and the conjugate operators $D_\ell ^{[a,b)\dagger }$. Clearly, $D_{\ell }^{[1,1)}$ is the identity operator.

Assign the following weights to N-point configurations on $\mathbb {Z}_{\ge 0}$:

$$\begin{aligned} \mathscr {W}_{\vec \beta }(X):=\det \bigl [ D_{\ell _j}^{[1,j)}\Phi _i(\ell _j) \bigr ]_{i,j=1}^{N} \det \bigl [ D_{\ell _j}^{[j,N)\dagger }\Psi _i(\ell _j) \bigr ]_{i,j=1}^{N}, \end{aligned}$$

(2.3)

where $X=(\ell _1> \ell _2> \cdots > \ell _N\ge 0 )$. If the number of points in X is not N, then set $\mathscr {W}_{\vec \beta }(X)=0$. Assume that the series for the partition function for the weights (2.3),

$$\begin{aligned} \mathscr {Z}_{\vec \beta }:=\sum _{X=(\ell _1> \ell _2> \cdots > \ell _N\ge 0 )} \mathscr {W}_{\vec \beta }(X) \end{aligned}$$

converges and is nonzero.²

Definition 2.1

The normalized weights

$$\begin{aligned} \mathscr {M}_{\vec \beta }(X) = \mathscr {W}_{\vec \beta }(X)/\mathscr {Z}_{\vec \beta } \end{aligned}$$

(2.4)

define a probability measure on N-particle configurations on $\mathbb {Z}_{\ge 0}$. We call this measure the $\vec \beta$-tilted N-point biorthogonal ensemble.

The term “probability measure” here refers to the fact that the sum of the normalized weights is equal to 1. The weights are generally complex-valued but become nonnegative real numbers in the specializations we discuss later.

When $\beta _j\equiv 0$, the operators (2.1) become identity operators, and the tilted biorthogonal ensemble turns into the usual biorthogonal ensemble with probability weights proportional to

$$\begin{aligned} \det \bigl [ \Phi _i(\ell _j) \bigr ]_{i,j=1}^{N} \det \bigl [ \Psi _i(\ell _j) \bigr ]_{i,j=1}^{N}. \end{aligned}$$

(2.5)

Biorthogonal ensembles were introduced and studied in [21], see also [18, Section 4] for a summary of formulas.

2.2 Normalization

Let us compute the normalizing constant $\mathscr {Z}_{\vec \beta }$:

Proposition 2.2

We have

$$\begin{aligned} \mathscr {Z}_{\vec \beta }=\det \bigl [ G_{ij}(\vec \beta ) \bigr ]_{i,j=1}^{N}, \end{aligned}$$

(2.6)

where

$$\begin{aligned} G_{ij}(\vec \beta ):=\sum _{k=0}^\infty \Psi _j(k)\hspace{1pt}D_k^{[1,N)}\Phi _i(k). \end{aligned}$$

(2.7)

Proof

Observe that for any $0\le a\le b$, we have the following summation by parts:

$$\begin{aligned} \sum _{k=a}^b f(k)\hspace{1pt}D^{(r)\dagger }_k g(k)- \sum _{k=a}^b g(k)\hspace{1pt}D^{(r)}_kf(k) = \beta _r g(b)\hspace{1pt}f(b+1) - \beta _r f(a)\hspace{1pt}g(a-1)\hspace{1pt}\textbf{1}_{a\ge 1}.\nonumber \\ \end{aligned}$$

(2.8)

We have

$$\begin{aligned} \begin{aligned} \mathscr {Z}_{\vec \beta }&= \sum _{\ell _1>\ell _2>\cdots>\ell _N\ge 0 } \Bigl (D_{\ell _1}^{[1,1)} \ldots D_{\ell _N}^{[1,N)} \det \bigl [ \Phi _i(\ell _j) \bigr ]_{i,j=1}^{N} \Bigr )\\&\quad \Bigl ( D_{\ell _N}^{[N,N)\dagger }\ldots D_{\ell _1}^{[1,N)\dagger } \det \bigl [ \Psi _i(\ell _j) \bigr ]_{i,j=1}^{N} \Bigr ) \\ {}&= \sum _{\ell _1>\ell _2>\cdots >\ell _N\ge 0 } \det \bigl [ \Psi _i(\ell _j) \bigr ]_{i,j=1}^{N} \, D_{\ell _1}^{[1,N)} D_{\ell _2}^{[1,N)} \ldots D_{\ell _N}^{[1,N)} \det \bigl [ \Phi _i(\ell _j) \bigr ]_{i,j=1}^{N}, \end{aligned} \end{aligned}$$

where we moved each of the operators $D_{\ell _j}^{[j,N)\dagger }$ to the other function and observed that the presence of the determinants eliminates the boundary terms arising from (2.8). Writing

$$\begin{aligned} D_{\ell _1}^{[1,N)} D_{\ell _2}^{[1,N)} \ldots D_{\ell _N}^{[1,N)} \det \bigl [ \Phi _i(\ell _j) \bigr ]_{i,j=1}^{N} = \det \Bigl [ D_{k}^{[1,N)}\Phi _i(k)\hspace{1pt}\Big \vert _{k=\ell _j} \hspace{1pt}\Bigr ]_{i,j=1}^{N}, \end{aligned}$$

we can use the Cauchy–Binet summation to replace the sum of products of two determinants over $\ell _1>\ell _2>\cdots >\ell _N\ge 0$ by the determinant of single sums. $\square$

2.3 Two-dimensional process

We will show in Sect. 4 that a $\vec \beta$-tilted N-point biorthogonal ensemble on $\mathbb {Z}_{\ge 0}$ is not necessarily a determinantal point process, even though its probability weights are products of determinants.

On the other hand, each $\vec \beta$-tilted biorthogonal ensemble can be embedded into a two-dimensional determinantal point process on $\mathfrak {X}:=\mathbb {Z}_{\ge 0}\times \left\{ 1,\ldots ,N \right\}$. A similar construction for TASEP first appeared in [11] (and was later exploited to construct the KPZ fixed point [63]). The embedding which we describe below in this subsection is suggested in the talk by Kenyon [48].

This process lives on particle configurations $X^{2d}=\{x^m_j :1\le m,j\le N \}$ satisfying

$$\begin{aligned} x^m_N<x^m_{N-1}<\cdots<x^m_2<x^m_1,\qquad 1\le m\le N. \end{aligned}$$

(2.9)

Denote $|x^m|:=x^m_1+\cdots +x^m_N$. Let

$$\begin{aligned} T_\beta (x,y):=\textbf{1}_{y=x}-\beta \hspace{1pt}\textbf{1}_{y=x-1},\qquad x,y\in \mathbb {Z}_{\ge 0}. \end{aligned}$$

One readily sees that

$$\begin{aligned} \det [T_\beta (x^m_i,x^{m+1}_j)]_{i,j=1}^N= (-\beta )^{|x^m|-|x^{m+1}|} \prod _{j=1}^{N}\textbf{1}_{x^{m}_j-x^{m+1}_j=\hspace{1pt}0\text { or } 1}. \end{aligned}$$

(2.10)

Using the given notation, assign (possibly complex) weights to configurations $X^{2d}$:

$$\begin{aligned}{} & {} \mathscr {W}_{\vec \beta }^{2d}(X^{2d}):=\det \left[ \Phi _i(x^1_j) \right] _{i,j=1}^N \biggl (\hspace{1pt}\prod _{m=1}^{N-1}\nonumber \\{} & {} \quad \det \left[ T_{\beta _m}(x^m_i,x^{m+1}_j) \right] _{i,j=1}^{N} \biggr ) \det \left[ \Psi _i(x^{N}_j) \right] _{i,j=1}^N.\nonumber \\ \end{aligned}$$

(2.11)

In the proof of the next statement and throughout the rest of the section, we use the notation “$*$” for discrete convolution of functions on $\mathbb {Z}_{\ge 0}$, and assume that all series thus arising converge absolutely. For example, we write $(f*h)(x)=\sum _{y=0}^{\infty }f(x,y)h(y)$ for functions f(x, y) and h(x). See also [18, Section 4] for further examples of this notation.

Theorem 2.3

The normalizing constant of the two-dimensional distribution

$$\begin{aligned} \mathscr {Z}_{\vec \beta }^{2d}:=\sum _{X^{2d}} \mathscr {W}_{\vec \beta }^{2d}(X^{2d}) \end{aligned}$$

is equal to the one-dimensional normalizing constant $\mathscr {Z}_{\vec \beta }$ given by (2.6)–(2.7). Moreover, under the normalized two-dimensional probability distribution $\mathscr {M}^{2d}_{\vec \beta }(X^{2d}):=\mathscr {W}_{\vec \beta }^{2d}(X^{2d})/\mathscr {Z}_{\vec \beta }$, the marginal distribution of $x^1_1>x^2_2>\cdots >x^N_N$ coincides with that of $\ell _1>\ell _2>\cdots \ell _N$ under $\mathscr {M}_{\vec \beta }$.

For complex-valued probabilities, the coincidence of marginal distributions means that for any finitely supported function f in N variables, we have

$$\begin{aligned} \sum _{X^{2d}=\{x^m_j\}} f(x^1_1,\ldots ,x^N_N )\hspace{1pt}\mathscr {M}_{\vec \beta }^{2d}(X^{2d}) = \sum _{X=(\ell _1>\cdots >\ell _N\ge 0 )} f(\ell _1,\ldots ,\ell _N )\hspace{1pt}\mathscr {M}_{\vec \beta }(X). \end{aligned}$$

(2.12)

Proof of Theorem 2.3

By the Cauchy–Binet summation, we have

$$\begin{aligned} \mathscr {Z}^{2d}_{\vec \beta }= \det \bigl [ \Phi _i * T_{\beta _1} * \ldots * T_{\beta _{N-1}} * \Psi _j \bigr ]_{i,j=1}^{N}. \end{aligned}$$

Next, for any function h(y) on $\mathbb {Z}_{\ge 0}$ we have $(h*T_{\beta _r})(y)=h(y)-\beta _r h(y+1)=D^{(r)}_y h(y)$. By (2.7), this implies the first claim about the normalizing constant.

The second claim essentially follows from the LGV (Lindstrom–Gessel–Viennot) lemma, which expresses the partition function of nonintersecting path collections in a determinantal form [40, 54]. By the first claim, it suffices to prove (2.12) for unnormalized weights $\mathscr {W}^{2d}_{\vec \beta }$ and $\mathscr {W}_{\vec \beta }$. Next, the weights $\mathscr {W}^{2d}_{\vec \beta }(X^{2d})$ (2.11) and $\mathscr {W}_{\vec \beta }(X)$ (2.3) are multilinear in $(\Phi _1,\ldots ,\Phi _N; \Psi _1,\ldots ,\Psi _N )$, so it suffices to prove the summation identity in the case of delta functions

$$\begin{aligned} \Phi _i(x)=\textbf{1}_{x=k_i},\qquad \Psi _i(x)=\textbf{1}_{x=k_i'}, \qquad i=1,\ldots ,N, \end{aligned}$$

where $k_1>\cdots >k_N\ge 0$ and $k_1'>\cdots >k_N'\ge 0$ are arbitrary but fixed. With this choice of $\Phi _i,\Psi _i$, the distribution of $X^{2d}$ is the same as the distribution of the nonintersecting path ensemble on the graph shown in Fig. 2, where the paths connect $k_1,\ldots ,k_N$ to $k_1',\ldots ,k_N'$.

Then the marginal distribution of $\ell _1,\ldots ,\ell _N$ can be expressed through the product of two determinants: One for the nonintersecting paths connecting $k_1,\ldots ,k_N$ to $\ell _1,\ldots ,\ell _N$, and the other one for the nonintersecting paths from $\ell _1,\ldots ,\ell _N$ to $k_1',\ldots ,k_N'$. These determinants are immediately identified with the two determinants in (2.3), and so we are done. $\square$

Fig. 2

The directed graph with vertices $\mathbb {Z}_{\ge 0}\times \left\{ 1,\ldots ,N \right\}$ and edges which can be vertical (with weight 1) or diagonal (with weight $-\beta _m$, $m=1,\ldots ,N$). We consider an ensemble of N nonintersecting paths connecting $k_1,\ldots ,k_N$ to $k_1',\ldots ,k_N'$. The particles $x^m_j$ encode the intersections of the paths with the m-th horizontal line, $m=1,\ldots ,N$

2.4 Determinantal kernel

The two-dimensional ensemble $X^{2d}$ defined in Sect. 2.3 is a determinantal point process. This means that for any $p\ge 1$ and pairwise distinct points $(y_i,t_i)\in \mathbb {Z}_{\ge 0}\times \left\{ 1,\ldots ,N \right\}$, $i=1,\ldots ,p$, we have

$$\begin{aligned} \sum _{\begin{array}{c} X^{2d}:X^{2d} \text { cointains each}\\ (y_i,t_i),\ i=1,\ldots ,p \end{array}} \mathscr {M}^{2d}_{\vec \beta }(X^{2d}) =\det \bigl [ K_{\vec \beta }^{2d}(y_i,t_i;y_j,t_j) \bigr ]_{i,j=1}^{p}. \end{aligned}$$

(2.13)

Here $K_{\vec \beta }^{2d}(x,t;y,s)$ is a function called the correlation kernel. Both the determinantal structure and an expression for the correlation kernel follow from the well-known Eynard–Mehta theorem [26, 34], see also [18, Theorem 4.2].

Proposition 2.4

The correlation kernel (2.13) for the point process $X^{2d}$ has the form

$$\begin{aligned} K_{\vec \beta }^{2d}(x,t;y,s)= & {} -\textbf{1}_{t>s} \left( T_{\beta _s}*\ldots *T_{\beta _{t-1}} \right) (y,x) \nonumber \\{} & {} + \sum _{i,j=1}^{N} G_{ji}^{-1}(\vec \beta )\cdot D_x^{[1,t)} \Phi _i(x) \cdot D_y^{[s,N)\dagger }\Psi _j(y). \end{aligned}$$

(2.14)

Proof

By [18, Theorem 4.2], the correlation kernel has the form

$$\begin{aligned} K_{\vec \beta }^{2d}(x,t;y,s)= & {} -\textbf{1}_{t>s} \left( T_{\beta _s}*T_{\beta _{s+1}}*\ldots *T_{\beta _{t-1}} \right) (y,x) \\{} & {} + \sum _{i,j=1}^{N} G_{ji}^{-1}(\vec \beta )\cdot \bigl ( \Phi _i*T_{\beta _1}*\ldots * T_{\beta _{t-1}} \bigr )(x) \cdot \\{} & {} \bigl ( T_{\beta _s}*\ldots * T_{\beta _{N-1}}*\Psi _j \bigr )(y). \end{aligned}$$

As in the proof of Theorem 2.3, we can rewrite the convolutions with the $T_\beta$’s as applications of the difference operators (2.1):

$$\begin{aligned}{} & {} \bigl (\Phi _i*T_{\beta _1}*\ldots * T_{\beta _{t-1}}\bigr )(x) = D_x^{[1,t)} \Phi _i(x);\qquad \\{} & {} \bigl ( T_{\beta _s}*\ldots * T_{\beta _{N-1}}*\Psi _j \bigr )(y) =D_y^{[s,N)\dagger }\Psi _j(y). \end{aligned}$$

This completes the proof. $\square$

Note that the variables $t,s\in \left\{ 1,\ldots ,N \right\}$ in the correlation kernel (2.14) correspond to the vertical coordinates in Fig. 2 which increases from top to bottom. We use this convention throughout the rest of the paper.

Remark 2.5

From the fact that $x^j_j=\ell _j$, $j=1,\ldots ,N$, as joint distributions (where the $x^j_j$’s come from $\mathscr {M}_{\vec \beta }^{2d}$ and the $\ell _j$’s come from $\mathscr {M}_{\vec \beta }$), one may think that the probabilities $\mathscr {M}_{\vec \beta }$ are expressed through the correlation kernel $K_{\vec \beta }^{2d}$ as

$$\begin{aligned} \mathscr {M}_{\vec \beta }(\ell _1,\ldots ,\ell _N )= \det \bigl [ K_{\vec \beta }^{2d}(\ell _i,i;\ell _j,j) \bigr ]_{i,j=1}^{N},\qquad \ell _1>\cdots >\ell _N. \end{aligned}$$

(2.15)

However, identity (2.15) is generally false when $\ell _{i+1}=\ell _i+1$ for some i. Indeed, this is because the correlation event in the right-hand side of (2.15) includes more configurations of nonintersecting paths (as in Fig. 2) than just the ones with $x^j_j=\ell _j$ for all $j=1,\ldots ,N$. One can check that if $\ell _j-\ell _{j+1}\ge 2$ for all $j=1,\ldots ,N$, then identity (2.15) holds.

2.5 Marginals and correlations of the tilted biorthogonal ensemble

Fix $k\ge 1$ and $\mathcal {I}=\{i_1<\cdots <i_k \}\subset \left\{ 1,\ldots ,N \right\}$. Let $a_{\mathcal {I}}=(a_{i_1}>\cdots >a_{i_k}\ge 0 )$ be a fixed integer vector, and also let $X_{\mathcal {I}}=(\ell _{i_1}>\cdots >\ell _{i_k} \ge 0)$ be a random vector, which is a marginal of the $\vec \beta$-tilted biorthogonal ensemble $\mathscr {M}_{\vec \beta }(X)$ defined by (2.3)–(2.4). Using Theorem 2.3 and Proposition 2.4, we can express the probability $\mathscr {M}_{\vec \beta }(X_{\mathcal {I}}=a_{\mathcal {I}})$ through the correlation kernel $K^{2d}_{\vec \beta }$ in a polynomial way.

We use the following statement adapted to our space $\mathfrak {X}=\mathbb {Z}_{\ge 0}\times \left\{ 1,\ldots ,N \right\}$:

Lemma 2.6

([79, Theorem 2]) Fix a finite number of disjoint subsets of $\mathfrak {X}$ and denote them by $B_1,\ldots ,B_p$. Let $B=B_1\cup \cdots \cup B_p$. For a determinantal point process on $\mathfrak {X}$ with kernel K, let $\#_{B_i}$ be the random number of points of the process which belong to $B_i$. Then we have the following identity of generating functions in $z_1,\ldots ,z_p$:

$$\begin{aligned} \mathbb {E} \bigl ( z_1^{\#_{B_1}}\ldots z_p^{\#_{B_p}} \bigr )= \det \Bigl ( \textbf{1}-\chi _{_B} \sum _{i=1}^{p}(1-z_i)\cdot K \cdot \chi _{_{B_i}} \Bigr ), \end{aligned}$$

(2.16)

where $\textbf{1}$ is the identity operator, in the right-hand side there is a Fredholm determinant, and $\chi _{_B},\chi _{_{B_i}}$ are the indicator functions of these subsets.

In our applications, the sets $B_i$ will be finite, and thus the Fredholm determinants in (2.16) are simply finite-dimensional determinants of the corresponding block matrices. In general, the right-hand side of (2.16) is an infinite series, see, for example, [79, Remark 3].

To illustrate the general formula of Proposition 2.7, let us first look at the case $k=1$. For fixed a and i, the event $\ell _i=a$ is equivalent to $\#_{B_i(a)}=N-i$, $\#_{C_i(a)}=1$, where

$$\begin{aligned}{} & {} B_i(a):=\left\{ 0,1,\ldots ,a-1 \right\} \times \left\{ i \right\} ,\qquad C_i(a):=\left\{ a \right\} \times \left\{ i \right\} , \nonumber \\{} & {} \qquad F_i(a):=B_i(a)\cup C_i(a).\nonumber \\ \end{aligned}$$

(2.17)

Indeed, for $\ell _i=x^i_i=a$, we need to have exactly $N-i$ points of the configuration $X^{2d}$ to the left of a, and exactly one point at a. Thus, we can write by Lemma 2.6:

$$\begin{aligned} \mathscr {M}_{\vec \beta }(\ell _i=a)= [z^{N-i}w]\det \Bigl ( \textbf{1} - (1-z)\chi _{_{F_i(a)}}K^{2d}_{\vec \beta } \chi _{_{B_{i}(a)}} - (1-w)\chi _{_{F_i(a)}}K^{2d}_{\vec \beta } \chi _{_{C_{i}(a)}} \Bigr ), \end{aligned}$$

(2.18)

where $[z^{N-i}w]$ is the operator of taking the coefficient of a polynomial by $z^{N-i}w$. The matrix in the right-hand side (2.18) has dimensions $(a+1)\times (a+1)$ and looks as

$$\begin{aligned} \begin{bmatrix} 1+(z-1)K(0;0)&{} (z-1)K(0;1)&{}\ldots &{} (w-1)K(0;a)\\ (z-1)K(1;0)&{} 1+(z-1)K(1;1)&{}\ldots &{} (w-1)K(1;a)\\ \cdots &{}\cdots &{}\cdots &{} \cdots \\ (z-1)K(a-1;0)&{} (z-1)K(a-1;1)&{}\ldots &{} (w-1)K(a-1;a) \\ (z-1)K(a;0)&{} (z-1)K(a;1)&{}\ldots &{} 1+(w-1)K(a;a) \end{bmatrix}, \end{aligned}$$

where we abbreviated $K(x;y)=K^{2d}_{\vec \beta }(x,i;y,i)$.

Finally, to get the correlation function, we simply have to sum (2.18) over all $i=1,\ldots ,N$:

$$\begin{aligned} \mathscr {M}_{\vec \beta }(X \text { contains } a)= & {} \sum _{i=1}^{N} [z^{N-i}w]\det \Bigl ( \textbf{1} - (1-z)\chi _{_{F_i(a)}}K^{2d}_{\vec \beta } \chi _{_{B_{i}(a)}} \nonumber \\{} & {} + (1-w)\chi _{_{F_i(a)}}K^{2d}_{\vec \beta } \chi _{_{C_{i}(a)}} \Bigr ). \end{aligned}$$

(2.19)

Notice that this is a polynomial in the entries $K^{2d}_{\vec \beta }(x,t;y,s)$ of the correlation kernel (2.14).

The next statement for general k follows from an argument for several points which is analogous to the above computations:

Proposition 2.7

For arbitrary $k\ge 1$ and $\mathcal {I}=\{i_1<\cdots <i_k \}$, the marginal distribution of $X_{\mathcal {I}}$ under $\mathscr {M}_{\vec \beta }$ has the form

$$\begin{aligned} \mathscr {M}_{\vec \beta }(X_{\mathcal {I}}= & {} a_{\mathcal {I}})= [z_1^{N-i_1}\ldots z_{k}^{N-i_k} w_1\ldots w_k ] \det \biggl ( \textbf{1} - \chi _{_{F_{\mathcal {I}}(a_{\mathcal {I}})}}\sum _{p=1}^k (1-z_p) K^{2d}_{\vec \beta }\chi _{_{B_{i_p}(a_{i_p})}} \nonumber \\{} & {} + \chi _{_{F_{\mathcal {I}}(a_{\mathcal {I}})}}\sum _{p=1}^k (1-w_p)K^{2d}_{\vec \beta }\chi _{_{C_{i_p}(a_{i_p})}} \biggr ). \end{aligned}$$

(2.20)

Here the square matrix has dimensions $\sum _{p=1}^{k}(a_{i_p}+1)$, the union of all the sets is denoted by $F_{\mathcal {I}}(a_{\mathcal {I}}):=\bigcup _{p=1}^{k}\left( B_{i_p}(a_{i_p})\cup C_{i_p}(a_{i_p}) \right)$, and the determinant is a polynomial in the entries of the correlation kernel $K^{2d}_{\vec \beta }$.

The correlation functions of $\mathscr {M}_{\vec \beta }$ are finite sums of determinants of the form (2.20). Namely, for any k and any pairwise distinct $a_1,\ldots ,a_k \in \mathbb {Z}_{\ge 0}$, we have

$$\begin{aligned} \mathscr {M}_{\vec \beta }(X \text { contains } a_1,\ldots ,a_k )= \sum _{\begin{array}{c} \mathcal {I}=\{1\le i_1<\cdots <i_k\le N \} \end{array}} \mathscr {M}_{\vec \beta }\left( X_{\mathcal {I}}=\{a_1,\ldots ,a_k \} \right) . \end{aligned}$$

3 Grothendieck random partitions

Here, we specialize the setup of $\vec \beta$-tilted biorthogonal ensembles developed in Sect. 2 to Grothendieck random partitions. A crucial feature in this special case is that the corresponding two-dimensional ensemble $X^{2d}$ becomes the well-known Schur process introduced in [73].

3.1 Specialization of tilted biorthogonal ensemble

Fix $N\ge 1$ and parameters $x_1,\ldots ,x_N,y_1,\ldots ,y_N$ such that $|x_iy_j|<1$ for all i, j, and specialize

$$\begin{aligned} \Phi _i(k)=x_i^k,\qquad \Psi _j(k)=y_j^k,\qquad k\in \mathbb {Z}_{\ge 0}. \end{aligned}$$

(3.1)

Then the operators (2.1) act as

$$\begin{aligned} D_k^{(r)}\Phi _i(k)=x_i^k(1-\beta _r x_i),\qquad D_k^{(r)\dagger }\Psi _j(k)=y_j^k(1-\beta _r y_j^{-1}\textbf{1}_{k\ge 1}). \end{aligned}$$

(3.2)

For a configuration $X=(\ell _1>\cdots >\ell _N\ge 0 )$, denote $\lambda _j:=\ell _j+j-N$, $j=1,\ldots ,N$, so $\ell _j=\lambda _j+N-j$. Clearly, we have $\lambda =(\lambda _1\ge \cdots \ge \lambda _N\ge 0 )$, and $\lambda$ is an integer partition with at most N parts. The $\vec \beta$-tilted biorthogonal weight (2.3) specializes to

$$\begin{aligned} \begin{aligned} \mathscr {W}_{\vec \beta ;\textrm{Gr}}(\lambda )&= \det \bigl [ x_i^{\lambda _j+N-j}(1-\beta _1x_i)\ldots (1-\beta _{j-1}x_i) \bigr ]_{i,j=1}^{N} \\&\quad \times \det \bigl [ y_i^{\lambda _j+N-j}(1-\beta _j y_i^{-1})\ldots (1-\beta _{N-1}y_i^{-1}) \bigr ]_{i,j=1}^{N}. \end{aligned} \end{aligned}$$

Observe that in the second determinant, the operators $D_{\ell _j}^{[j,N)\dagger }$ are applied in $\ell _1,\ldots ,\ell _{N-1}$, which are strictly positive. Therefore, the special case $k=0$ in $D_k^{(r)\dagger }$ in (3.2) does not occur.

The normalizing constant in Proposition 2.2 becomes

$$\begin{aligned} \begin{aligned} \mathscr {Z}_{\vec \beta ;\textrm{Gr}}&= \det \Bigl [ \frac{(1-\beta _1x_i)\ldots (1-\beta _{N-1}x_i) }{1-x_iy_j} \Bigr ]_{i,j=1}^{N} \\&= \frac{ \prod _{i=1}^{N}\prod _{r=1}^{N-1} (1-x_i\beta _r)}{\prod _{i,j=1}^N(1-x_iy_j)} \hspace{1pt}\prod _{1\le i<j\le N}(x_i-x_j)(y_i-y_j), \end{aligned} \end{aligned}$$

where the matrix elements are geometric sums, see (2.7), and the well-known Cauchy determinant is evaluated in a product form.

Let us denote

$$\begin{aligned} G_\lambda (x_1,\ldots ,x_N ):= & {} \frac{\det \bigl [ x_i^{\lambda _j+N-j}(1-\beta _1x_i)\ldots (1-\beta _{j-1}x_i) \bigr ]_{i,j=1}^{N}}{\prod _{1\le i<j\le N}(x_i-x_j)}; \nonumber \\ \overline{G}_\lambda (y_1,\ldots ,y_N ):= & {} \frac{\det \bigl [ y_i^{\lambda _j+N-j}(1-\beta _j y_i^{-1})\ldots (1-\beta _{N-1}y_i^{-1}) \bigr ]_{i,j=1}^{N}}{\prod _{1\le i<j\le N}(y_i-y_j)}. \end{aligned}$$

(3.3)

Since $\lambda _j+N-j\ge N-j$ and in the matrix elements in $\overline{G}_\lambda$ there are $N-j$ factors of the form $(1-\beta _r y_i^{-1})$, we see that both $G_\lambda$ and $\overline{G}_\lambda$ are symmetric polynomials in N variables. We thus see that the $\vec \beta$-tilted biorthogonal ensemble with the specialization (3.1) has the form

$$\begin{aligned} \mathscr {M}_{\vec \beta ;\textrm{Gr}}(\lambda ) = \frac{\prod _{i,j=1}^N(1-x_iy_j)}{\prod _{i=1}^{N}\prod _{r=1}^{N-1}(1-x_i\beta _r)} \hspace{1pt}G_\lambda (x_1,\ldots ,x_N )\hspace{1pt}{\overline{G}}_{\lambda }(y_1,\ldots ,y_N ). \end{aligned}$$

(3.4)

We call (3.4) the (multiparameter) Grothendieck measure on partitions. This distribution is analogous to the Schur measure introduced in [70] which is a particular case of $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ for $\beta _r\equiv 0$.

Note that the probability weights (3.4) may be complex-valued. In Sect. 3.2 we discuss conditions on the parameters $x_i,y_j,\beta _r$ which make the weights nonnegative real.

3.2 Grothendieck polynomials and positivity

Here, we comment on the relations between the polynomials $G_\lambda ,{\overline{G}}_\lambda$ and Grothendieck polynomials appearing in the literature. We also discuss the nonnegativity of the measure $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ (3.4) on partitions.

Grothendieck polynomials are well-known in algebraic combinatorics and geometry, going back to at least [58], see also [27]. Their one-parameter $\beta$-deformations appeared in [35]. The recent paper [41] introduced and studied the most general (to date) deformations called refined canonical stable Grothendieck polynomials $\textsf {G}_\lambda (x_1,\ldots ,x_N;\vec \alpha ,\vec \beta )$. These objects generalize most known Grothendieck-like polynomials in the literature, in particular, the ones in [27, 35], as well as more recent extensions in, e.g., [31, 84]. The refined canonical stable Grothendieck polynomials $\textsf {G}_\lambda (x_1,\ldots ,x_N;\vec \alpha ,\vec \beta )$ depend on two sequences of parameters $\vec \alpha =(\alpha _1,\alpha _2,\ldots )$ and $\vec \beta =(\beta _1,\beta _2,\ldots )$, and are defined as

$$\begin{aligned} \textsf {G}_\lambda (x_1,\ldots ,x_N;\vec \alpha ,\vec \beta ) :=\frac{\det \biggl [ x_i^{\lambda _j+N-j} \dfrac{(1-\beta _1x_i)\ldots (1-\beta _{j-1}x_i)}{(1-\alpha _1 x_i)\ldots (1-\alpha _{\lambda _j}x_i) } \biggr ]_{i,j=1}^{N}}{\prod _{1\le i<j\le N}(x_i-x_j)}. \end{aligned}$$

(3.5)

Note that for nonzero $\alpha _j$’s, $\textsf {G}_\lambda (x_1,\ldots ,x_N;\vec \alpha ,\vec \beta )$ are not polynomials but rather are generating series in the $x_j$’s. When $\alpha _j=0$ for all j (which drops the word “canonical” from the terminology), expressions (3.5) become polynomials and reduce to our $G_\lambda$’s from (3.3). The polynomials $\overline{G}_\lambda$ in (3.3) are expressed through the $G_{\lambda }$’s as follows. Denote $\beta _r^{rev}:=\beta _{N-r}$, $r=1,\ldots ,N-1$, and $\lambda ^{rev}:=(0\ge -\lambda _N\ge -\lambda _{N-1}\ge \cdots \ge -\lambda _1 )$. Then, one readily sees that

$$\begin{aligned} \overline{G}_{\lambda }(x_1,\ldots ,x_N \mid \vec \beta )= G_{\lambda ^{rev}}(x_1^{-1},\ldots ,x_{N}^{-1}\mid \vec \beta ^{rev} ), \end{aligned}$$

(3.6)

where we explicitly indicated the dependence on the parameters $\beta _r$. Moreover, since $G_\lambda$ satisfies the index shift property $G_{\lambda +(1,\ldots ,1 )}(x_1,\ldots ,x_N )=x_1\ldots x_N \cdot G_{\lambda }(x_1,\ldots ,x_N )$, one can shift the negative coordinates $\lambda ^{rev}$ to obtain a nonnegative partition.

The sum to one property of the Grothendieck measure $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ (3.4) is equivalent to the following Cauchy-type summation identity for the polynomials (3.3):

$$\begin{aligned}{} & {} \sum _{\lambda =(\lambda _1\ge \cdots \ge \lambda _N\ge 0 )} G_{\lambda }(x_1,\ldots ,x_N ) \hspace{1pt}\overline{G}_{\lambda }(y_1,\ldots ,y_N ) = \frac{ \prod _{i=1}^{N}\prod _{r=1}^{N-1} (1-x_i\beta _r)}{\prod _{i,j=1}^N(1-x_iy_j)}, \qquad \nonumber \\{} & {} \quad |x_iy_j|<1. \end{aligned}$$

(3.7)

It is instructive to compare this identity to Cauchy identities for Grothendieck symmetric functions, for example, see [84, (36)] or [41, Corollary 3.6]. The latter identities involve sums of products in the form $\textsf {G}_\lambda \hspace{1pt}\textsf {g}_\lambda$, where $\textsf {g}_\lambda$ are the dual Grothendieck symmetric functions. The products in the right-hand side of these summation identities have the form $\prod _{i,j=1}^{\infty }(1-x_iy_j)^{-1}$, and a possible analogue in our case would be $\prod _{i,j=1}^{\infty }\frac{1-x_i\beta _j}{1-x_iy_j}$. However, in this paper, we will not explore a symmetric function extension of the identity (3.7).

Let us now discuss the nonnegativity of the probability weights $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ (3.4). Using the tableau formula for $G_\lambda$ (for example, [41, Corollary 4.5]) and the relation (3.6) between $G_\lambda$ and $\overline{G}_\lambda$, we see that the probability weights $\mathscr {M}_{\vec \beta ;\textrm{Gr}}(\lambda )$ are nonnegative for all $\lambda$ when the parameters satisfy

$$\begin{aligned} x_i\ge 0,\quad y_j\ge 0,\quad \beta _r\le 0;\qquad |x_iy_j|<1; \qquad 1\le i,j\le N,\quad 1\le r\le N-1. \end{aligned}$$

(3.8)

Indeed, under (3.8) we have nonnegativity (and even Schur-nonnegativity, cf. [41, Theorem 4.3]) of $G_\lambda$ and $\overline{G}_\lambda$, as well as the convergence of the series (3.7).

Furthermore, we can extend the nonnegativity range of the Grothendieck measures to certain positive values of $\beta _r$:

Proposition 3.1

Let $x_i,y_j\ge 0$ and $\beta _r\le x_i^{-1}$, $\beta _r\le y_j$ for all i, j, r. Then the Grothendieck polynomials $G_\lambda (x_1,\ldots ,x_N )$ and $\overline{G}_{\lambda }(y_1,\ldots ,y_N )$ defined by (3.3) are nonnegative.

Proof

We consider only the case $G_\lambda$, as $\overline{G}_\lambda$ is completely analogous. For a nonnegative function f on $\mathbb {Z}_{\ge 0}$ we have under our conditions:

$$\begin{aligned} D_k^{(r)}f(k) = f(k)-\beta _r f(k+1) \ge f(k)-x_r^{-1} f(k+1). \end{aligned}$$

Therefore, replacing $\beta _r$ by $x_r^{-1}$ in the application of $D_k^{(r)}$ can only decrease the result.

The Grothendieck polynomial $G_\lambda (x_1,\ldots ,x_N )$ is obtained by applying the operators $D_k^{(r)}$ to the Schur polynomial $s_\lambda (x_1,\ldots ,x_N )$:

$$\begin{aligned} G_\lambda (x_1,\ldots ,x_N ) = \dfrac{ \det \bigl [ D_{\ell _j}^{[1,j)} x_i^{\ell _j}\Bigr ]_{i,j=1}^{N}}{\prod _{1\le i<j\le N}(x_i-x_j)} = D_{\ell _1}^{[1,1)}\dots D_{\ell _N}^{[1,N)} s_{\lambda }(x_1,\ldots ,x_N ). \end{aligned}$$

It follows that $G_\lambda (x_1,\ldots ,x_N ) \ge G_\lambda (x_1,\ldots ,x_N )\bigl |_{\beta _r = x_r^{-1}\text { for all } r}$. On the other hand, when $\beta _r=x_r^{-1}$ for all r, the matrix in the numerator in $G_\lambda$ (3.3) becomes triangular, and we have

$$\begin{aligned} \det \bigl [ x_i^{\ell _j}(1-x_i/x_1)\ldots (1-x_i/x_{j-1}) \bigr ]_{i,j=1}^N =x_1^{\ell _1}\ldots x_N^{\ell _N} \prod _{1\le i<j\le N}\left( 1-\tfrac{x_j}{x_i} \right) . \end{aligned}$$

Cancelling the product over i, j with the denominator in $G_\lambda$, we see that after the substitution, the resulting expression $G_\lambda (x_1,\ldots ,x_N )\bigl |_{\beta _r = x_r^{-1}\text { for all } r}$ is clearly nonnegative. This completes the proof. $\square$

Proposition 3.1 implies that the Grothendieck probability weights $\mathscr {M}_{\vec \beta ;\textrm{Gr}}(\lambda )$ are nonnegative for all $\lambda$ when the parameters satisfy the extended conditions

$$\begin{aligned} x_i\ge & {} 0,\quad y_j\ge 0,\quad \beta _r\le x_i^{-1},\quad \beta _r\le y_j; \quad |x_iy_j|<1; \quad 1\le i,j\le N,\quad \nonumber \\ 1\le & {} r\le N-1. \end{aligned}$$

(3.9)

3.3 Two-dimensional Schur process and its correlation kernel

By Theorem 2.3, the Grothendieck measure is embedded into the two-dimensional ensemble $X^{2d}$ (2.9). Our specialization (3.1) implies that $X^{2d}$ is distributed as the Schur process. Schur processes are a vast family of determinantal point processes on the two-dimensional lattice introduced and studied in [73].

Assume that the parameters satisfy (3.8), and define $\mu _i^m:=x^m_i+i-N$, $i,m=1,\ldots ,N$, where the particles $x^m_i$ come from the two-dimensional ensemble $X^{2d}$. Clearly, each $\mu ^m=(\mu ^m_1\ge \cdots \ge \mu ^m_N\ge 0)$ is a partition with at most N parts. From (2.10)–(2.11) we conclude that the probability weight of the tuple of partitions $(\mu ^1,\ldots ,\mu ^N)$ is

$$\begin{aligned}{} & {} \mathscr {M}_{\vec \beta ;\textrm{Gr}}^{2d}( \mu ^1,\ldots ,\mu ^N ) \propto s_{\mu ^1}(x_1,\ldots ,x_N ) \nonumber \\{} & {} \quad \times s_{(\mu ^1)'/(\mu ^2)'}(-\beta _1)\ldots s_{(\mu ^{N-1})'/(\mu ^{N})'}(-\beta _{N-1})\hspace{1pt}s_{\mu ^{N}}(y_1,\ldots ,y_N ). \end{aligned}$$

(3.10)

Here $(\mu ^{m})'/(\mu ^{m+1})'$ denote skew transposed partitions, and we used a basic property of skew Schur functions evaluated at a single variable (for example, see [60, Chapter I.5]):

$$\begin{aligned} \det \left[ T_{\beta _m}(x^m_i,x^{m+1}_j) \right] _{i,j=1}^{N}= s_{(\mu ^{m})'/(\mu ^{m+1})'}(-\beta _{m}). \end{aligned}$$

From Theorem 2.3 we immediately get:

Proposition 3.2

The Grothendieck measure $\mathscr {M}_{\vec \beta ;\textrm{Gr}}(\lambda )$ (3.4) is embedded into the Schur process (3.10) in the sense that the joint distributions of the integer N-tuples $\{\lambda _i\}_{i=1,\ldots ,N }$ and $\{\mu _i^i \}_{i=1,\ldots ,N }$ coincide.

Remark 3.3

While the Schur process (3.10) is not a nonnegative measure for $\beta _r>0$, the Grothendieck measures (3.4) are still nonnegative probability measures under the more relaxed conditions (3.9). Consequently, we will primarily focus on the case when the parameters satisfy the more restrictive conditions (3.8). However, in Sect. 5.4 we will also consider the question of limit shapes for Grothendieck measures with positive $\beta _r$’s (which do not correspond to nonnegative Schur processes).

As shown in [73], the correlation kernel of the Schur process (3.10) has a double contour integral form. The alternative proof of this result given in [26, Theorem 2.2] proceeds from the general kernel $K^{2d}_{\vec \beta }$ (2.14) and involves an explicit inverse matrix $G^{-1}(\vec \beta )$ which is available thanks to the Cauchy determinant. Let us record this double contour integral kernel:

Proposition 3.4

The correlation kernel for the Schur process $X^{2d}=\{x^m_i:1\le m,i\le N\}$ containing the Grothendieck measure $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ (3.4) has the form

(3.11)

where $a,b\in \mathbb {Z}_{\ge 0}$, $t,s \in \left\{ 1,\ldots ,N \right\}$,

$$\begin{aligned} F_t(z):=\prod _{i=1}^{N}\frac{1-z^{-1}y_i}{1-zx_i}\hspace{1pt}\prod _{r=t}^{N-1} \frac{1}{1-\beta _r z^{-1}}, \end{aligned}$$

(3.12)

and the integration contours in (3.11) are positively oriented simple closed curves around 0 satisfying the following conditions:

• (1) $|z|>|w|$ for $t\le s$ and $|z|<|w|$ for $t>s$;

• (2) On the contours it must be that $|\beta _r|<|z|<x_i^{-1}$ and $|w|>y_i$ for all i and r.

The integration contours in Proposition 3.4 exist only under certain conditions on the parameters $x_i,y_j$, and $\beta _r$, for example, it must be that $|\beta _r|<x_i^{-1}$ for all i, r. When these conditions on the parameters are violated, we should deform the integration contours to take the same residues. In other words, we can analytically continue the kernel by declaring that the double contour integral in (3.11) is always equal to the sum of the same residues: first take the sum of the residues in w at 0, all $y_i$’s, and at z if $t>s$; then take the sum of the residues of the resulting expression in z at 0 and all $\beta _r$’s.

Fig. 3

Graphical representation of the Schur process (3.10). Arrows indicate the diagram inclusion relations

Proof of Proposition 3.4

It is well-known that determinantal correlation kernels for the Schur measures and processes have double contour integral form, see [70, 73]. Namely, the generating function for the Schur process kernel has the form

$$\begin{aligned} \sum _{a,b\in \mathbb {Z}} K^{\text {Schur process}}(a,t;b,s)\hspace{1pt}z^{a}w^{-b-1}= \frac{1}{z-w}\frac{\Phi (t,z)}{\Phi (s,w)}, \end{aligned}$$

(3.13)

where $\Phi (t,z)$ are is a function which is read off from the specializations in the Schur process, and the generating series in (3.13) is expanded differently depending on whether $t\le s$ or $t>s$. This difference in expansion is that we assume either $|z|>|w|$ or $|z|<|w|$, which can be ultimately traced back to the normal ordering of the fermionic operators $\psi (z),\psi ^*(w)$ in the notation of [73, Section 2.3.4]. Formula (3.13) is the same as [73, Theorem 1], up to switching from half-integers to integers in the indices a, b.

Let us remark that it is not immediate how to adapt the generating function (3.13) to a particular specialization of the Schur process (that is, how to select the integration contours to pick out the correct coefficients). In general, one could use the contour integrals from [46] (see also [13, Remark 2 after Theorem 5.3]) or [26, Theorem 2.2], but here for convenience let us briefly record a “user’s manual” for such an adaptation. There are three principles:

• First, start with the Schur measures ($t=s$). By [70, Theorem 2], the contours must satisfy $|z|>|w|$ for $t=s$.

• Second, on the integration contours for all t, s, all denominators in the integrand should expand as geometric series in a natural way as $\frac{1}{1-\xi }=\sum _{n=0}^{\infty }\xi ^n$.

• The first two principles allow to select the integration contours for $t=s$, and it only remains to determine their ordering ($|z|>|w|$ or $|z|<|w|$) for $t \ne s$. This is done by inspecting how the specializations of the Schur measures at $t=s$ change with t.

Let us implement these principles for our Schur process (3.10). Its graphical representation is given in Fig. 3. Each $\mu ^t$ distributed as the Schur measure with probability weights

$$\begin{aligned} \propto s_{\mu ^{t}}(x_1,\ldots ,x_N ) s_{\mu ^t}(-\hat{\beta }_t,\ldots ,-{\hat{\beta }}_{N-1};y_1,\ldots ,y_N ). \end{aligned}$$

(3.14)

Here the notation $-{\hat{\beta }}_i$ means that these are “dual” parameters, that is, they correspond to transpositions of the Young diagrams. Moreover, we unified a number of these “dual” parameters with the usual parameters $y_i$ in the second Schur function (see, e.g., [13, Section 2] for details). The weights (3.14) follows from the weights (3.10) and the skew Cauchy identity for Schur functions.

Now, from (3.14) and [70, Theorem 2], we see that the functions in the integrand for $t=s$ are given by

$$\begin{aligned} F_t(z)=\frac{H_{(x_1,\ldots ,x_N )}(z)}{ H_{-\hat{\beta }_t,\ldots ,-{\hat{\beta }}_{N-1}; y_1,\ldots ,y_N }(z^{-1})}= \prod _{i=1}^{N}\frac{1-z^{-1}y_i}{1-zx_i}\hspace{1pt}\prod _{r=t}^{N-1} \frac{1}{1-\beta _r z^{-1}}, \end{aligned}$$

(3.15)

where $H_\rho (z)=\sum _{n\ge 0}z^n\hspace{1pt}s_{(n)}(\rho )$ is the single-variable Cauchy kernel for a specialization $\rho$ of Schur functions. The second equality in (3.15) follows from the Cauchy identity, and is precisely the expression (3.12) for $F_t(z)$. Thus, using the first two principles above, we get all the conditions on the contours in our Proposition 3.4 for $t=s$. In particular, the second condition $|\beta _r|<|z|<x_i^{-1}$, $|w|>y_i$ follows from requiring the expansion of

$$\begin{aligned} \frac{F_t(z)}{F_s(w)}= \prod _{i=1}^{N}\frac{1-z^{-1}y_i}{1-zx_i} \prod _{i=1}^{N} \frac{1-wx_i}{1-w^{-1}y_i} \hspace{1pt}\frac{ \prod _{r=s}^{N-1} (1-\beta _r w^{-1}) }{ \prod _{r=t}^{N-1} (1-\beta _r z^{-1}) } \end{aligned}$$

as geometric series. Observe that to get the integral (3.11), we also needed to shift the indices (a, b) by $N-\frac{1}{2}$ compared to formulas in [70, 73]. Indeed, in these references the point configuration associated to a partition $\mu$ is $\left\{ \mu _i-i+\frac{1}{2} \right\} _{i\in \mathbb {Z}_{\ge 1}}$, while we work with $\left\{ \mu _i+N-i \right\} _{i=1}^{N}$.

Extending our formula (3.11) to $t \ne s$ in a natural way leaves only the question of the ordering of the integration contours ($|z|>|w|$ or $|z|<|w|$) for $t\ne s$. This can be resolved by comparing (3.15) with [73, (20)]. We see that $H_{-\hat{\beta }_t,\ldots ,-{\hat{\beta }}_{N-1}; y_1,\ldots ,y_N }(z^{-1})$ should be matched to the product $\prod _{m<t}\phi ^+[m](z^{-1})$. In the latter product, increasing t will increase the number of factors, which is opposite to how the number of factors depends on t in (3.15). Thus, we must choose $|z|>|w|$ for $t\le s$, which is opposite to [73, Theorem 1]. This completes the proof. $\square$

4 Absence of determinantal structure

The Grothendieck measure $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ (3.4) has probability weights expressed as products of two determinants. This structure is very similar to that of biorthogonal ensembles (2.5), which are well-known determinantal point processes. However, this section shows that the Grothendieck measures are not determinantal point processes. This question is deeply linked to the principal minor assignment problem from linear algebra and algebraic geometry. We describe this problem in Sect. 4.1, and discuss its long history in Sect. 4.2. Then in Sect. 4.3, we present a self-contained derivation of a determinantal test for minors of a $4\times 4$ matrix originally obtained by Nanson in 1897 [66], and in Sect. 4.4 we extend this test to matrices of arbitrary size. Finally, in Sect. 4.5, we apply the original Nanson’s test to show that the Grothendieck measures are not determinantal.

4.1 Principal minor assignment problem

Let A be an $n\times n$ complex matrix. To it, we associate $2^{n}$ principal minors $A_I=\det [A_{i_a,i_b}]_{a,b=1}^{|I|}$, where I runs over all subsets of $\left\{ 1,\ldots ,n \right\}$, and |I| is the number of elements in I. This includes the empty minor $A_{\varnothing }=1$. The map $\mathbb {C}^{n^2}\rightarrow \mathbb {C}^{2^n}$, $A\rightarrow ( A_I )_{I\subseteq \left\{ 1,\ldots ,n \right\} }$, is called the affine principal minor map. The (affine) principal minor assignment problem [42, 56] aims to characterize the image under this map in $\mathbb {C}^{2^n}$. Denote this image by $\mathcal {A}_n\subset \mathbb {C}^{2^n}$. This complex algebraic variety is closed and has dimension $n^2-n+1$ [56, 81].

For $n\le 3$, the dimension of $\mathcal {A}_n$ is equal to $2^n-1$, (full available dimension because $A_{\varnothing }=1$), but starting with $n=4$, $\mathcal {A}_n$ becomes very complicated. Indeed, by [56, Theorem 2], the prime ideal of the (13-dimensional) variety $\mathcal {A}_4$ is minimally generated by 65 polynomials of degree 12 in the $A_I$’s.

Let us translate the principal minor assignment problem into the language of point processes. Let $\mathscr {M}$ be a point process on $\mathbb {Z}_{\ge 0}$, that is, a probability measure on point configurations in $\mathbb {Z}_{\ge 0}$. This measure may have complex weights, but has to be normalized to have total probability mass 1, and has to be bounded in absolute value by a nonnegative probability measure on point configurations in $\mathbb {Z}_{\ge 0}$. The base space for the point process may be arbitrary and is not necessarily finite, and here we take $\mathbb {Z}_{\ge 0}$ for an easier future application. For each finite subset $I\subset \mathbb {Z}_{\ge 0}$ consider the correlation function

$$\begin{aligned} \rho _I = \mathscr {M}\left( \text {the random point configuration contains all points from } I \right) . \end{aligned}$$

It is natural to ask whether the point process $\mathscr {M}$ is determinantal, that is, whether there exists a kernel K(x, y), $x,y\in \mathbb {Z}_{\ge 0}$, such that for any finite $I\subset \mathbb {Z}_{\ge 0}$ we have $\rho _I=\det [K(a,b)]_{a,b\in I}$. A clear necessary condition for the process to be determinantal is as follows:

Proposition 4.1

If the process $\mathscr {M}$ is determinantal, then for any $n\ge 1$ and any n-point subset $\textsf {J}\subset \mathbb {Z}_{\ge 0}$, the vector $(\rho _I:I\subseteq \textsf {J}) \in \mathbb {C}^{2^n}$ belongs to the image $\mathcal {A}_n$ under the principal minor map.

Thus, if for some n and some n-point $\textsf {J}\subset \mathbb {Z}_{\ge 0}$ the vector $(\rho _I:I\subseteq \textsf {J}) \in \mathbb {C}^{2^n}$ does not belong to $\mathcal {A}_n$, then the process $\mathscr {M}$ is not determinantal. Due to the complicated nature of $\mathcal {A}_n$ for $n\ge 4$, checking that a vector belongs to $\mathcal {A}_n$ is hard. However, to show that some vector $(\rho _I)$ does not belong to $\mathcal {A}_n$, it suffices to find a polynomial in the ideal of $\mathcal {A}_n$ that does not vanish on $(\rho _I)$. This leads us to the following definition:

Definition 4.2

Fix $n\ge 4$. A determinantal test of order n is any element in the ideal of $\mathcal {A}_n$, that is, a polynomial in the indeterminates $(A_I:I\subset \left\{ 1,\ldots ,n \right\} )$ which vanishes if the $A_I$’s are principal minors of some matrix A.

Thus, to show that the process $\mathscr {M}$ is not determinantal, it suffices to show that there exists $\textsf {J}\subset \mathbb {Z}_{\ge 0}$ and a determinantal test which does not vanish on the vector $(\rho _I:I \subset \textsf {J})$. Let us describe an example of such a test of order 4 which we call the Nanson’s test as it first appeared in 1897 in [66]. First, we need another definition:

Definition 4.3

Let $A=(a_{ij})$ be a complex $n\times n$ matrix, and fix $I\subseteq \left\{ 1,\ldots ,n \right\}$ with $|I|=k\ge 2$. For a k-cycle $\pi \in S_n$ with support I (there are $(k-1)!$ such cycles), define $t_\pi (A) :=\prod _{i:i\ne \pi (i)}a_{i,\pi (i)}$. Let the cycle-sum [56] be

$$\begin{aligned} T_I :=\sum _{\text {all } k-\text {cycles } \pi \text { with support } I}t_\pi (A). \end{aligned}$$

(4.1)

The cycle-sums are the same as cluster functions in the terminology of [82], and they can be expressed through the principal minors $A_I$ as follows:

$$\begin{aligned} T_I=\sum _{I=I_1\sqcup \cdots \sqcup I_m }(-1)^{k+m}(m-1)!\hspace{1pt}A_{I_1}\cdots A_{I_m}, \end{aligned}$$

(4.2)

where the sum is taken over all set partitions of I into exactly m nonempty parts. For example,

$$\begin{aligned} \begin{aligned} T_{ \left\{ 1,2,3 \right\} }&=a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} \\ {}&= 2 A_{ \left\{ 1 \right\} } A_{ \left\{ 2 \right\} } A_{ \left\{ 3 \right\} } -\left( A_{ \left\{ 1 \right\} }A_{ \left\{ 2,3 \right\} } + A_{ \left\{ 2 \right\} }A_{ \left\{ 1,3 \right\} } + A_{ \left\{ 3 \right\} }A_{ \left\{ 1,2 \right\} } \right) + A_{ \left\{ 1,2,3 \right\} }. \end{aligned} \end{aligned}$$

Definition 4.4

The Nanson’s determinantal test is a polynomial $\mathfrak {N}_4$ of order 4 in the indeterminates $T_I$ which has the form

$$\begin{aligned} \mathfrak {N}_{4}= \frac{1}{2}\det \begin{bmatrix} T_{123} T_{14} &{}\quad T_{124} T_{13} &{}\quad T_{134} T_{12} &{}\quad 2 T_{12} T_{13} T_{14} T_{234}+T_{123} T_{124} T_{134} \\ T_{124} T_{23} &{}\quad T_{123} T_{24} &{}\quad T_{234} T_{12} &{}\quad 2 T_{12} T_{23} T_{24}T_{134} +T_{123} T_{124} T_{234} \\ T_{134} T_{23} &{}\quad T_{234}T_{13} &{}\quad T_{123} T_{34} &{}\quad 2 T_{13} T_{23} T_{34}T_{124} + T_{123} T_{134} T_{234} \\ T_{234}T_{14} &{}\quad T_{134} T_{24} &{}\quad T_{124} T_{34} &{}\quad 2 T_{14} T_{24} T_{34} T_{123}+T_{124} T_{134} T_{234} \end{bmatrix},\nonumber \\ \end{aligned}$$

(4.3)

where we abbreviated $T_{ij}=T_{ \left\{ i,j \right\} }$, and so on. By (4.2), $\mathfrak {N}_4$ is also a polynomial in the indeterminates $A_I$.

One readily verifies (for example, using computer algebra) that $\mathfrak {N}_4$ is indeed a determinantal test:

Proposition 4.5

If for all $I\subseteq \left\{ 1,2,3,4 \right\}$ we replace the indeterminates $T_I$’s in (4.3) by the cycle-sums (4.1) coming from a $4\times 4$ matrix A, then the polynomial $\mathfrak {N}_4$ (4.3) vanishes identically.

We apply Nanson’s test $\mathfrak {N}_4$ to show that the Grothendieck measures are not determinantal in Sect. 4.5.

4.2 On the history of the principal minor assignment problem

Let us briefly discuss the rich history and variants of the principal minor assignment problem. Within this history, we can observe at least two instances where similar questions were independently formulated and addressed in the context of algebra (on the original principal minor assignment) and probability (concerning determinantal processes). We hope that these two research avenues will become increasingly aware of one another.

The problem itself dates to the late 19th century work of MacMahon [59], with initial results due to Muir [64, 65] and Nanson [66]. In particular, Nanson has partially solved the $4\times 4$ principal minor assignment problem, and obtained the determinantal test $\mathfrak {N}_4$ (4.3). He also obtained four other tests algebraically independent from $\mathfrak {N}_4$ (which enter the list of 65 polynomials in Lin–Sturmfels [56]). The question of relations on principal minors is investigated by Stouffer [81], and in particular he showed that the dimension of $\mathcal {A}_n$ is $n^2-n+1$.

Another question related to the principal minor assignment problem, when it has a solution, concerns the relationship between two $n\times n$ complex matrices A, B with the same principal minors. Under various natural conditions, it has been shown that the matrix A should be diagonally conjugate either to B, or to $B^{\textrm{transpose}}$. Here “diagonally conjugate” means $A=DBD^{-1}$, where D is a nondegenerate diagonal matrix. This question was first addressed in the context of the principal minors assignment problem by Loewy [55]. More recently, Stevens [80] and Mantelos [61] investigated essentially the same question within the context of determinantal processes, seemingly unaware of Loewy’s work.

Griffin–Tsatsomeros [39] proposed algorithms for finding the solution of the principal minor assignment problem (that is, the matrix A), which are computationally fast for particular subclasses of matrices. While this does not yield explicit polynomial determinantal tests, an algorithm can be used to (numerically) demonstrate that a point process is not determinantal. In our application to Grothendieck measures in Sect. 4.5 we do not use an algorithm like in [39], but rather perform a symbolic computation based on the Nanson’s test $\mathfrak {N}_4$.

A particularly well-understood case of the principal minor assignment problem assumes that the initial complex $n\times n$ matrix A is Hermitian symmetric. Holtz–Sturmfels [43] and Oeding [68] use the additional hyperdeterminantal structure of the variety formed by principal minors to solve the assignment problem set-theoretically. More recently, Al Ahmadieh and Vinzant [1, 2] considered the principal minor assignment problem over other rings and explored connections to stable polynomials. These latter works represent the current state of the art of the principal minor assignment problem from an algebraic perspective. In particular, [2, Theorem 8.1] is a strong and unexpected negative result.

Finally, let us mention that there are several natural generalizations of the principal minor assignment problem, as considered by Borodin–Rains [26, Section 4] and independently by Lin–Sturmfels [56] (unaware at the time of the work by Borodin–Rains). These variants allow more general conditional and/or Pfaffian structure of the correlation functions $\rho _I$. A conditional determinantal process, by definition, has correlation functions $\rho _I=\det \left[ K(a,b) \right] _{a,b\in I\cup S}$, where $S=\left\{ n+1,\ldots ,n+m \right\}$, and $I \subseteq \left\{ 1,\ldots , n \right\}$. In other words, it is a usual determinantal process on $\left\{ 1,\ldots ,n,n+1,\ldots ,n+m \right\}$ conditioned to have particles at each of the points $n+1,\ldots ,n+m$. In the terminology of [56], the conditional determinantal structure is the same as the projective principal minor assignment problem, a more natural setting for algebraic geometry. The projective variety analog of $\mathcal {A}_n$ for $n=4$ is more complicated, with 718 generating polynomials. The Pfaffian and conditional Pfaffian structures (considered in [26]; they are motivated, in particular, by real and quaternionic random matrix ensembles) are defined similarly to the determinantal ones, but with determinants replaced by Pfaffians. The $n=4$ conditional Pfaffian (projective) variety analog of $\mathcal {A}_n$ is even more complicated than the determinantal one, and experimentation suggests [26] that a corresponding test could have degree 1146.

It would be interesting to develop determinantal and Pfaffian tests for conditional processes (as well as for further generalizations involving, for example, $\alpha$-determinants and permanents), but we leave these directions for future work.

4.3 A self-contained derivation of Nanson’s determinantal test

Here we present a self-contained derivation of Nanson’s determinantal test polynomial $\mathfrak {N}_4$ (4.3). This argument differs slightly from Nanson’s original work [66] and was obtained independently by the second author (unaware of the principal minor assignment problem) over a decade ago [76]. Here we see another instance of the disconnect between the principal minor assignment problem and determinantal processes (complementing the two cases discussed in Sect. 4.2). In Sect. 4.4, we discuss how our derivation of $\mathfrak {N}_4$ can be adapted to obtain Nanson-like higher-order determinantal tests.

We aim to explain where the polynomial $\mathfrak {N}_4$ (4.3) comes from. Checking that it is indeed a determinantal test is a direct verification (Proposition 4.5), and we do not focus on this here.

Assume that we are given the cluster functions $T_I$ (4.2), where I runs over subsets of $\left\{ 1,2,3,4 \right\}$ with $\ge 2$ elements. The $T_I$’s are polynomials in the minors $A_I$, but working with the $T_I$’s is much more convenient. Let us use the $T_I$’s to try finding the matrix elements $a_{ij}$ of the original matrix A.

Throughout the rest of this section, we will abbreviate expressions like $T_{ \left\{ 1,2 \right\} }$ as $T_{12}$. Note that all the $T_I$’s are symmetric in the indices. Assume that $a_{1i}\ne 0$ for all $i=2,3,4$, and conjugate the matrix by the diagonal matrix with the entries $d_i=\textbf{1}_{i=1}+a_{1i}\textbf{1}_{i\ne 1}$. Then we have for the conjugated matrix (denoted by ${\tilde{A}}=(\tilde{a}_{ij})$):

$$\begin{aligned} {\tilde{a}}_{1i}=\frac{d_1}{d_i}\hspace{1pt}a_{1i}=1,\qquad i=2,3,4. \end{aligned}$$

(4.4)

With this notation, we have $T_{1i}={\tilde{a}}_{i1}$ and

$$\begin{aligned} T_{ij}={\tilde{a}}_{ij}{\tilde{a}}_{ji},\qquad T_{1ij}=\tilde{a}_{ij}T_{1j}+{\tilde{a}}_{ji}T_{1i}. \end{aligned}$$

(4.5)

The second identity in (4.5) is by the definition of the cluster function (4.1), simplified thanks to (4.4). Equations (4.5) allow to find ${\tilde{a}}_{ij}T_{1j}$ and ${\tilde{a}}_{ji}T_{1i}$ as two distinct roots of a quadratic equation. We thus have

$$\begin{aligned} {\tilde{a}}_{ij}T_{1j}=\frac{T_{1ij}+R_{ij}}{2}, \qquad \tilde{a}_{ji}T_{1i}=\frac{T_{1ij}- R_{ij}}{2}, \end{aligned}$$

(4.6)

where we denoted $R_{ij}:=\pm \sqrt{T_{1ij}^2-4T_{1i}T_{1j}T_{ij}}$. Observe that $R_{ij}$ contains an unknown sign that we cannot determine a priori (it may also depend on i and j), but up to sign $R_{ij}$ is symmetric in i, j.

Let us substitute (4.6) into the following identity (which is again an instance of (4.1)):

$$\begin{aligned} T_{234}={\tilde{a}}_{23}{\tilde{a}}_{34}{\tilde{a}}_{42}+ {\tilde{a}}_{24}\tilde{a}_{43}{\tilde{a}}_{32}. \end{aligned}$$

As a result, we obtain the following identity involving three square roots $R_{23},R_{34},R_{24}$ with unknown signs:

$$\begin{aligned} 8T_{12}T_{13}T_{14}T_{234}= & {} \left( T_{123}+R_{23} \right) \left( T_{124}+R_{24} \right) \left( T_{134}+R_{34} \right) \nonumber \\{} & {} + \left( T_{123}-R_{23} \right) \left( T_{124}-R_{24} \right) \left( T_{134}-R_{34} \right) . \end{aligned}$$

(4.7)

Note that (4.7) does not contain the matrix elements ${\tilde{a}}$. Thus, it is an algebraic (but not yet polynomial) identity on the cluster functions $T_I$. Simplifying (4.7), we see that

$$\begin{aligned} 4T_{12}T_{13}T_{14}T_{234}-T_{123}T_{124}T_{143} -T_{123}R_{24}R_{34} - T_{124}R_{23}R_{34} - T_{134}R_{23}R_{24} =0. \end{aligned}$$

(4.8)

The left-hand side contains three summands with irrationalities $R_{24}R_{34}, R_{23}R_{34}$, and $R_{23}R_{24}$ with uncertain signs. By choosing all possible eight combinations of the signs for $R_{23},R_{34},R_{24}$, we see that there are only four possible combinations of signs in (4.8). Thus, by multiplying together all these four expressions with different signs, we can get rid of irrationality and obtain a polynomial in the $T_I$’s:

$$\begin{aligned}{} & {} \bigl ( 4T_{12}T_{13}T_{14}T_{234}-T_{123}T_{124}T_{143} -T_{123}R_{24}R_{34} - T_{124}R_{23}R_{34} - T_{134}R_{23}R_{24} \big ) \nonumber \\{} & {} \quad \times \bigl ( 4T_{12}T_{13}T_{14}T_{234}-T_{123}T_{124}T_{143} +T_{123}R_{24}R_{34} + T_{124}R_{23}R_{34} - T_{134}R_{23}R_{24} \big ) \nonumber \\{} & {} \quad \times \bigl ( 4T_{12}T_{13}T_{14}T_{234}-T_{123}T_{124}T_{143} -T_{123}R_{24}R_{34} + T_{124}R_{23}R_{34} + T_{134}R_{23}R_{24} \big ) \nonumber \\{} & {} \quad \times \bigl ( 4T_{12}T_{13}T_{14}T_{234}-T_{123}T_{124}T_{143} + T_{123}R_{24}R_{34} - T_{124}R_{23}R_{34} \nonumber \\{} & {} \quad + T_{134}R_{23}R_{24} \big ) =0. \end{aligned}$$

(4.9)

Clearly, expanding the left-hand side of (4.9) squares all the quantities $R_{ij}$. Thus, the resulting identity is polynomial in the $T_I$’s, and, moreover, all unknown signs present in the R’s disappear.

One can check (for example, using computer algebra) that the resulting polynomial (4.9) in the $T_I$’s has 19 summands, and it is symmetric in the indices 1, 2, 3, 4. One can also verify that this polynomial divided by the common factor $256T_{12}^2T_{13}^2T_{14}^2$ is exactly the same as the Nanson’s test $\mathfrak {N}_4$ (4.3). This concludes our derivation of the Nanson’s determinantal test of order four.

4.4 Procedure for higher-order Nanson tests

Adapting the derivation of the test $\mathfrak {N}_4$ given in Sect. 4.3, one can produce concrete determinantal tests $\mathfrak {N}_{n}$ for minors of general $n\times n$ matrices, where $n\ge 4$. Let us explain the necessary steps for general n without going into full detail. We have from (4.1):

$$\begin{aligned} T_{2,3,\ldots ,n }= \sum _{(n-1)-\text {cycles } \sigma \text { on } \{2,\ldots ,n\}} {\tilde{a}}_{\sigma (2)\sigma (3)}\ldots \tilde{a}_{\sigma (n-1)\sigma (n)}{\tilde{a}}_{\sigma (n)\sigma (2)}. \end{aligned}$$

(4.10)

For every $i<j$, let us substitute the solutions (4.6), so (4.10) becomes

$$\begin{aligned} 2^{n-1} T_{12}\ldots T_{1n} T_{2,\ldots ,n} = \sum _{\sigma } \prod _{i=2}^{\circlearrowright n}\left( T_{1\sigma (i)\sigma (i+1)}+(-1)^{\textbf{1}_{\sigma (i)>\sigma (i+1)}} R_{\sigma (i)\sigma (i+1)} \right) .\nonumber \\ \end{aligned}$$

(4.11)

Here the sum is also over $(n-1)$-cycles $\sigma$ on $\left\{ 2,\ldots ,n \right\}$, and “$\circlearrowright$” means that the product is cyclic in the sense that $n+1$ is identified with 2. We see that (4.11) is an algebraic identity on the $T_I$’s which does not contain the matrix elements ${\tilde{a}}_{ij}$.

Opening up the parentheses in (4.11), one readily sees that all terms with an odd number of the factors $R_{ij}$ cancel out, while the terms with an even number of the factors $R_{ij}$ appear twice. Therefore, we can continue (4.11) as

$$\begin{aligned} 2^{n-2} T_{12}\ldots T_{1n} T_{2,\ldots ,n} - \sum _{\begin{array}{c} \text { non-oriented } (n-1)-\text {cycles} \\ \tau \text { on } \left\{ 2,\ldots ,n \right\} \end{array}} \ \prod _{i=2}^{\circlearrowright n} T_{1\tau (i)\tau (i+1)}=\textsf {RHS}. \end{aligned}$$

(4.12)

Here $\textsf {RHS}$ is a sum over non-oriented $(n-1)$ cycles $\tau$ on $\left\{ 2,\ldots ,n \right\}$, where the summands are $(n-1)$-fold cyclic products of the quantities $T_{1ij}$ and $R_{ij}$ with a nonzero even number of the R’s, and each such monomial has coefficient $\pm 1$. More precisely, the sign is determined by the number of descents $\tau (i)>\tau (i+1)$ in $\tau$ for which the monomial contains $R_{\tau (i)\tau (i+1)}$ (and not $T_{1\tau (i)\tau (i+1)}$).

Next, in $\textsf {RHS}$ there are $\left( {\begin{array}{c}n-1\\ 2\end{array}}\right)$ possible elements $R_{ij}$, and each of them contains an unknown sign in front of the square root. Let us take the product over those of the $2^{\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) }$ possible sign combinations which lead to the different $\textsf {RHS}$’s. Expanding this product removes all irrationalities and unknown signs, and produces a polynomial (denoted by $\mathfrak {N}_n$) in the cluster functions $T_I$, where I runs over subsets of $\left\{ 1,\ldots ,n \right\}$ with $\ge 2$ elements. We call $\mathfrak {N}_n$ the Nanson-like determinantal test of order n.

For example, for $n=5$ identity (4.12) has the form (recall that the quantities $T_{1ij}$ and $R_{ij}$ are symmetric in i, j):

$$\begin{aligned}&8T_{12}T_{13}T_{14}T_{15}T_{2345} -T_{24}T_{43}T_{35}T_{52} -T_{23}T_{34}T_{45}T_{52} -T_{23}T_{35}T_{54}T_{42} \\&\quad =R_{24} R_{25} R_{34} R_{35} - R_{23} R_{25} R_{34} R_{45} + R_{23} R_{24} R_{35} R_{45} \\&\qquad + R_{34} R_{45} T_{123} T_{125} + R_{24} R_{35} T_{125} T_{134} + R_{23} R_{45} T_{125} T_{134}\\&\qquad + R_{24} R_{45} T_{123} T_{135} + R_{25} R_{34} T_{124} T_{135} + R_{23} R_{35} T_{124} T_{145} \\&\qquad + R_{23} R_{34} T_{125} T_{145} - R_{23} R_{25} T_{134} T_{145} - R_{23} R_{24} T_{135} T_{145}\\&\qquad - R_{35} R_{45} T_{123} T_{124} - R_{34} R_{35} T_{124} T_{125} - R_{25} R_{45} T_{123} T_{134}\\&\qquad - R_{25} R_{35} T_{124} T_{134} - R_{23} R_{45} T_{124} T_{135}- R_{24} R_{34} T_{125} T_{135} \\&\qquad - R_{24} R_{25} T_{134} T_{135} - R_{25} R_{34} T_{123} T_{145}- R_{24} R_{35} T_{123} T_{145}. \end{aligned}$$

In the right-hand side, there are $2^{\left( {\begin{array}{c}4\\ 2\end{array}}\right) }=64$ possible signs in the $R_{ij}$’s, but they lead to “only” 32 distinct identities. Multiplying all these 32 expressions similarly to (4.9) and recalling the definition of the R’s leads to a polynomial in the $T_I$’s with no irrationality. This produces the determinantal test $\mathfrak {N}_5$.

4.5 Application to Grothendieck measures and proof of Theorem 1.2

In this subsection we employ the Nanson determinantal test $\mathfrak {N}_4$ to prove Theorem 1.2 from Introduction. That is, we will show that the Grothendieck measure on partitions $\mathscr {M}_{\vec \beta ; \textrm{Gr}}(\lambda )$ (3.4) is not determinantal as a point process on $\mathbb {Z}_{\ge 0}$ with points $\ell _j=\lambda _N+N-j$, $j=1,\ldots ,N$.

We focus on the case $N=2$ and look at correlations $\rho _I^{\textrm{Gr}}$ of the random point configuration $\{\ell _1,\ell _2\}=\{\lambda _1+1,\lambda _2\}$ for all subsets $I\subseteq \left\{ 0,1,2,3 \right\}$. Moreover, we will set $\beta _1=\beta$, $x_1=x_2=x$, and $y_1=y_2=y$. Clearly, $\rho ^{\textrm{Gr}}_I=0$ if $|I|=3$ or 4. Moreover, we have $\rho ^{\textrm{Gr}}_{\varnothing }=1$, and for two-point subsets we have (where $i>j$):

$$\begin{aligned} \rho ^{\textrm{Gr}}_{ \{i,j \} }= & {} \mathscr {M}_{\vec \beta ; \textrm{Gr}}\bigl ( (i-1,j) \bigr ) \nonumber \\= & {} \frac{(1-x y)^4}{(1-x\beta )^2}\hspace{1pt}\hspace{1pt}x^{i+j-1} y^{i+j-2} \left( \beta x (i-j-1)-i+j\right) \left( (j-i) (y-\beta )-\beta \right) ,\nonumber \\ \end{aligned}$$

(4.13)

where we used (3.3)–(3.4), and took the limits as $x_2\rightarrow x_1=x$ and $y_2\rightarrow y_1=y$.

To compute one-point correlations, we employ Proposition 2.7 and the correlation kernel $K^{2d}_{\vec \beta ;\textrm{Gr}}$ of the ambient Schur process (Proposition 3.4). We have by Proposition 2.7 (specifically, by its particular case (2.19))

$$\begin{aligned} \rho ^{\textrm{Gr}}_{ \left\{ i \right\} }= & {} [z^{1}w]\det \Bigl ( \textbf{1} - (1-z)\chi _{[0,i]}K^{2d}_{\vec \beta ;\textrm{Gr}}(\cdot ,1;\cdot ,1) \chi _{[0,i)} \nonumber \\{} & {} + (1-w) \chi _{[0,i]}K^{2d}_{\vec \beta ;\textrm{Gr}}(\cdot ,1;\cdot ,1) \chi _{ \left\{ i \right\} } \Bigr ) \nonumber \\{} & {} + [z^{0}w]\det \Bigl ( \textbf{1} - (1-z)\chi _{[0,i]}K^{2d}_{\vec \beta ;\textrm{Gr}}(\cdot ,2;\cdot ,2) \chi _{[0,i)} \nonumber \\{} & {} + (1-w) \chi _{[0,i]}K^{2d}_{\vec \beta ;\textrm{Gr}}(\cdot ,2;\cdot ,2) \chi _{ \left\{ i \right\} } \Bigr ). \end{aligned}$$

(4.14)

This yields formulas for $\rho ^{\textrm{Gr}}_{ \left\{ i \right\} }$, $i=0,1,2,3$, namely,

$$\begin{aligned} \rho ^{\textrm{Gr}}_{ \left\{ 0 \right\} }&= 1-x^2 y^2 ; \nonumber \\ \rho ^{\textrm{Gr}}_{ \left\{ 1 \right\} }&= x^2 y^2(1-x^2y^2)+\frac{(1-x y)^4}{(1-\beta x)^2} ; \nonumber \\ \rho ^{\textrm{Gr}}_{ \left\{ 2 \right\} }&= x^4y^4(1-x^2y^2)+ \frac{x (1-x y)^4 \left( \beta (\beta x-2)+x y^2+y (4-2 \beta x)\right) }{(1-\beta x)^2} ; \nonumber \\ \rho ^{\textrm{Gr}}_{ \left\{ 3 \right\} }&= x^6 y^6(1-x^2y^2) \nonumber \\&+ \frac{x^2 y (1-x y)^4 \left( x^2 y^3+y \left( \beta ^2 x^2-8 \beta x+9\right) +2 \beta (2 \beta x-3)-2 x y^2 (\beta x-2)\right) }{(1-\beta x)^2} . \end{aligned}$$

(4.15)

Remark 4.6

These one-point correlation functions $\rho ^{\textrm{Gr}}_{ \left\{ i \right\} }$ can be also computed without using the finite-dimensional Fredholm-like determinants (4.14). Namely,

$$\begin{aligned} \rho ^{\textrm{Gr}}_{ \left\{ i \right\} } = \sum _{j=0}^{i-1} \mathscr {M}_{\vec \beta ; \textrm{Gr}}\bigl ( (i-1,j) \bigr ) + \sum _{j=i}^{\infty } \mathscr {M}_{\vec \beta ; \textrm{Gr}}\bigl ( (j,i) \bigr ), \end{aligned}$$

and the infinite sum is explicit because the summands have the form (4.13). However, this simplification of correlation functions works only for small N and small order of correlation functions. We will use the full two-dimensional determinantal kernel to obtain asymptotics of Grothendieck random partitions in Sect. 3.

Plugging the correlation functions (4.13), (4.15) into the Nanson test (4.3) (with the help of the representation of cluster functions via minors (4.2)), we find

$$\begin{aligned} \mathfrak {N}_4= \beta ^4 x^{34} y^{30} (1-x y)^{42} (1+x y)^2 P_{14}(xy) +O\left( \beta ^5\right) ,\qquad \beta \rightarrow 0, \end{aligned}$$

(4.16)

where $P_{14}(xy)$ is a certain degree 14 polynomial in the single variable xy. We see that $\mathfrak {N}_4$ vanishes at $\beta =0$, as it should be because then the Grothendieck measure reduces to the Schur measure which is determinantal. On the other hand, for $\beta \ne 0$ the test does not vanish in general. For example, at $x=y=1/2$, we have

$$\begin{aligned} \begin{aligned}&\mathfrak {N}_4= \frac{(\beta -4) (\beta -1) \beta ^4}{(\beta -2)^{32}} \hspace{1pt}Q_3(\beta ) Q_5(\beta ) Q_7(\beta ) Q_9(\beta ), \\&\frac{(\beta -2 )^{32}}{(\beta -4 ) (\beta -1 ) \beta ^4} \hspace{1pt}\mathfrak {N}_4\Big \vert _{x=y=1/2,\ \beta =-1}\approx 0.00005021> 0, \end{aligned} \end{aligned}$$

where $Q_3,Q_5,Q_7,Q_9$ are certain polynomials in $\beta$ of degrees 3, 5, 7, 9, respectively. Since the Nanson determinantal test does not vanish for these values of $x,y,\beta$, this implies Theorem 1.2 from Introduction.

5 Limit shape of Grothendieck random partitions

In this section we employ the standard steepest descent asymptotic analysis of the correlation kernel of the Schur process (for example, explained in [71, Section 3]) to derive the limit shape result for Grothendieck random partitions.

5.1 Limit shape of the Schur process

In this subsection we assume that all the parameters $x_i,y_j,\beta _r$ are homogeneous and satisfy (3.8), that is, for all i, j, r we have

$$\begin{aligned} x_i=x,\quad y_j=y,\quad \beta _r=\beta ; \qquad x>0,\quad y>0,\quad xy<1,\quad \beta <0. \end{aligned}$$

(5.1)

We require the parameters be nonzero, otherwise the measure degenerates and may not produce asymptotic limit shapes.

Under conditions (5.1), the Schur process $\mathscr {M}^{2d}_{\vec \beta ;\textrm{Gr}}$ (3.10) is a well-defined probability measure on integer arrays $X^{2d}=\{x_i^m:1\le m,i\le N\}$. With each such array, we associate a height function on $\mathbb {Z}_{\ge 0}\times \left\{ 1,\ldots ,N \right\}$ as follows:

$$\begin{aligned} H_N(a,t):=\#\left\{ j:x^t_j\ge a \right\} , \qquad a\in \mathbb {Z}_{\ge 0},\quad t=1,\ldots ,N. \end{aligned}$$

(5.2)

In words, $H_N(a,t)$ is the number of particles of the configuration $X^{2d}$ at level t which are to the right of a. In particular, we have

$$\begin{aligned} H_N(x^t_t,t)=t,\qquad t=1,\ldots ,N. \end{aligned}$$

(5.3)

The following limit shape result for the Schur process can be obtained in a standard manner via the steepest descent analysis of the correlation kernel $K_{\vec \beta ;\textrm{Gr}}^{2d}$ (3.11)–(3.12). We refer to [10, 33, 53, 73, 74] for similar steepest descent arguments.

Theorem 5.1

(Limit shape for Schur processes) There exists a function $\mathfrak {H}(\xi ,\tau )$ in $\xi \in \mathbb {R}_{\ge 0}$, $\tau \in [0,1]$, depending on the parameters $x,y,\beta$ (5.1) such that in probability,

$$\begin{aligned} \lim _{N\rightarrow +\infty }\frac{H_N\left( \lfloor \xi N \rfloor ,\lfloor \tau N \rfloor \right) }{N} = \mathfrak {H}(\xi ,\tau ). \end{aligned}$$

(5.4)

The function $\mathfrak {H}(\xi ,\tau )$ is continuous, piecewise differentiable, weakly decreases in both $\xi$ and $\tau$, and its gradient $\nabla \mathfrak {H}= (\partial _\xi \mathfrak {H},\partial _\tau \mathfrak {H})$ belongs to the triangle

$$\begin{aligned} -1\le \partial _\xi \mathfrak {H}\le 0, \qquad -1\le \partial _\tau \mathfrak {H}\le 0, \qquad \partial _\tau \mathfrak {H}\ge \partial _\xi \mathfrak {H}. \end{aligned}$$

(5.5)

See Fig. 4 for an illustration.

Fig. 4

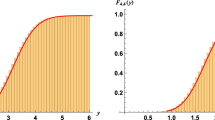
An example of the frozen boundary curve in the $(\xi ,\tau )$ coordinates, and an example of several up-diagonal paths as in Fig. 2 serving as the level lines for the pre-limit height function $H_N$ (5.2). There are no up-diagonal paths in the frozen zones Ia-b, so $\nabla \mathfrak {H}=(0,0)$. In zone II, the paths go diagonally, so $\nabla \mathfrak {H}=(-1,-1)$. Finally, in zone III, the paths go vertically, so $\nabla \mathfrak {H}=(-1,0)$. These frozen zone gradients correspond to the vertices of the triangle (5.5). In this example, we have $x=1/3$, $y=1/5$, $\beta =-6$. For other values of parameters, zones Ib and II may be present. Zone III is always present, see Lemma 5.4

Throughout the rest of this subsection we will give an idea of proof of Theorem 5.1 together with the necessary formulas for the gradient $\nabla \mathfrak {H}$. The integrand in the kernel $K_{\vec \beta ;\textrm{Gr}}^{2d}$ (3.11) can be rewritten as

$$\begin{aligned} \frac{e^{N \bigl (S\bigl (z;\tfrac{a}{N},\tfrac{t}{N}\bigr ) - S\bigl (w;\tfrac{b}{N},\tfrac{s}{N}\bigr )\bigr )}}{z-w}, \end{aligned}$$

where

$$\begin{aligned} S(z;\xi ,\tau ):=-(\xi -1)\log z+\log (1-z^{-1}y)-\log (1-zx)-(1-\tau )\log (1-\beta z^{-1}).\nonumber \\ \end{aligned}$$

(5.6)

The critical point equation $\frac{\partial }{\partial z}\hspace{1pt}S(z;\xi ,\tau )=0$ is equivalent to a cubic polynomial equation on z:

$$\begin{aligned}{} & {} \xi x z^3 -(\xi +\beta x (\xi +\tau -1)+(\xi +1) x y-1)z^2 \nonumber \\{} & {} \quad + (\beta (\xi +\tau +\xi x y+\tau x y-2)+\xi y)z- \beta y (\xi +\tau -1) =0. \end{aligned}$$

(5.7)

The region in the $(\xi ,\tau )$ plane where (5.7) has two complex conjugate nonreal roots is called the liquid region $\mathcal {L}$. Inside it, the gradient $\nabla \mathfrak {H}(\xi ,\tau )$ belongs to the interior of the triangle (5.5). In Fig. 4, $\mathcal {L}$ is the region inside the frozen boundary curve which we denote by $\partial \mathcal {L}$. For $(\xi ,\tau )\in \mathcal {L}$, denote by $z_c=z_c(\xi ,\tau )$ the unique root of (5.7) in the upper half complex plane. This is a critical point of the function S (5.6).

We forgot a standard steepest descent analysis of the kernel $K_{\vec \beta ;\textrm{Gr}}^{2d}$ which would constitute a detailed proof of Theorem 5.1. Instead, we briefly explain how to derive explicit formulas for the gradient $\nabla \mathfrak {H}$. We need only the a priori assumption (which would follow from the steepest descent) that this gradient depends on the critical point $z_c$ in a harmonic way when $z_c$ belongs to the upper half-plane. When the point $(\xi ,\tau )$ approaches the boundary of the liquid region, the critical points $z_c$ and $\bar{z}_c$ merge and become a real double critical point which is a double root of the cubic equation (5.7). Therefore, the frozen boundary curve $\partial \mathcal {L}$ can be obtained in parametric form by solving the equations

$$\begin{aligned} \frac{\partial }{\partial z}\hspace{1pt}S(z;\xi ,\tau )= \frac{\partial ^2}{\partial z^2}\hspace{1pt}S(z;\xi ,\tau )=0, \end{aligned}$$

(5.8)

in $(\xi ,\tau )$, and taking $z_c={\bar{z}}_c\in \mathbb {R}$ as a parameter. Equivalently, $\partial \mathcal {L}$ is the discriminant curve of the cubic equation (5.7). See (5.20) for this parametrization of the frozen boundary curve (we do not an explicit parametrization just yet).

We are only interested in the “physical” part of the frozen boundary which lives in the half-infinite rectangle $(\xi ,\tau )\in [0,\infty )\times [0,1]$, and so not all values of $z_c={\bar{z}}_c\in \mathbb {R}$ correspond to points of the frozen boundary $\partial \mathcal {L}$. Modulo this remark, we get the following trichotomy of the frozen zones:

Proposition 5.2

(Frozen zone trichotomy) Depending on the location of the double critical point, we have:

• If $\partial \mathcal {L}$ is adjacent to zones Ia or Ib, then $z_c={\bar{z}}_c>0$.

• If $\partial \mathcal {L}$ is adjacent to zone II, then $\beta<z_c={\bar{z}}_c<0$.

• If $\partial \mathcal {L}$ is adjacent to zone III, then $z=\bar{z}_c<\beta$.

Parts of $\partial \mathcal {L}$ bounding zones Ia-b are asymptotically formed by up-diagonal paths. In particular, the slope of these parts of $\partial \mathcal {L}$ in the $(\xi ,\tau )$ coordinates cannot exceed 1. One can check that in Fig. 4, the rightmost part of the frozen boundary $\partial \mathcal {L}$ is not linear and has slope slightly less than 1. On the other hand, the boundaries of zones II and III are not formed by our up-diagonal paths. Instead, one should use suitably chosen “dual paths” defined through the complement of the particle configuration $X^{2d}=\{x^m_j\}$.

Using Proposition 5.2, one can show that inside the liquid region, we have the following expressions for the gradient of the limit shape in terms of the critical point $z_c(\xi ,\tau )$:

$$\begin{aligned} \partial _\xi \hspace{1pt}\mathfrak {H}(\xi ,\tau )= -\frac{\mathop {\textrm{Arg}}z_c(\xi ,\tau )}{\pi },\qquad \partial _\tau \hspace{1pt}\mathfrak {H}(\xi ,\tau )= \frac{\mathop {\textrm{Arg}}\bigl (z_c(\xi ,\tau )-\beta \bigr )-\mathop {\textrm{Arg}}z_c(\xi ,\tau )}{\pi }.\nonumber \\ \end{aligned}$$

(5.9)

That is, $1+\partial _\xi \hspace{1pt}\mathfrak {H}$ and $-\partial _\tau \hspace{1pt}\mathfrak {H}$ are the normalized angles of the triangle in the complex plane with vertices $0,\beta$, and $z_c$, adjacent to 0 and $z_c$, respectively (recall that both partial derivatives are negative). See Fig. 5 for an illustration.

Fig. 5

Triangle in the complex plane with vertices $0,\beta$, and $z_c$. When $z_c$ approaches the real line at $(0,+\infty )$, $(\beta ,0)$, and $(-\infty ,\beta )$, we have, respectively, $\nabla \mathfrak {H}=(0,0)$, $\nabla \mathfrak {H}=(-1,-1)$, and $\nabla \mathfrak {H}=(-1,0)$

Remark 5.3

From the cubic equation $\frac{\partial }{\partial z}\hspace{1pt}S(z;\xi ,\tau )=0$, one can readily check that the complex critical point $z_c(\xi ,\tau )$ satisfies the following version of the complex Burgers equation:

$$\begin{aligned} \frac{\partial z_c(\xi ,\tau )}{\partial \xi }= \left( 1-\frac{z_c(\xi ,\tau )}{\beta } \right) \frac{\partial z_c(\xi ,\tau )}{\partial \tau }. \end{aligned}$$

(5.10)

We refer to [52] for general details on how the complex Burgers equation arises for limit shapes of planar dimer models.

5.2 From Schur to Grothendieck limit shapes

From the limit shape result for the Schur process (Theorem 5.1), we readily get the limit shape of Grothendieck random partitions. Indeed, recall from Proposition 3.2 that the shifted random variables $\ell _i=\lambda _i+N-i$, $i=1,\ldots ,N$, under the Grothendieck measure $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ (3.4) are equal in distribution to the particle coordinates $x^i_i=\mu ^i_i+N-i$ corresponding to the random partitions under the Schur process $\mathscr {M}^{2d}_{\vec \beta ;\textrm{Gr}}$ (3.10). The Schur process possesses a limit shape, so when i grows proportionally to N, the random variables $x^i_i$ also scale proportionally to N. More precisely, Theorem 5.1 and the observation (5.3) imply that for all $\tau \in [0,1]$ we have

$$\begin{aligned} \frac{x^{i}_i}{N}\rightarrow \mathfrak {L}(\tau ),\qquad i=\lfloor \tau N \rfloor , \qquad N\rightarrow +\infty , \end{aligned}$$

(5.11)

where the convergence is in probability. Here $\mathfrak {L}(\tau )$ is a weakly decreasing function satisfying the equation

$$\begin{aligned} \mathfrak {H} \left( \mathfrak {L}(\tau ),\tau \right) =\tau \quad \text {for all }\tau \in [0,1], \end{aligned}$$

(5.12)

where $\mathfrak {H}(\xi ,\tau )$ is the limit shape of the Schur process. In other words, the shape $\mathfrak {L}(\tau )$ is the cross-section of the Schur process limit shape surface $\eta =\mathfrak {H}(\xi ,\tau )$ in the $(\xi ,\tau ,\eta )$ coordinates by the plane $\eta =\tau$.

Lemma 5.4

The function $\mathfrak {L}(\tau )$, $\tau \in [0,1]$, is continuous and is uniquely determined by equation (5.12) and by continuity at the endpoints $\tau =0,1$. In particular, $\mathfrak {L}(1)=0$.

Proof

Observe that $\mathfrak {H}(\xi ,\tau )$ strictly decreases in $\xi$ as long as $\mathfrak {H}\ne 0,1$. Indeed, $\mathfrak {H}$ is strictly monotone in the liquid region thanks to the first of the identities in (5.9). In the frozen zones, we have $\partial _\xi \hspace{1pt}\mathfrak {H}=0$ only in zones Ia-b, and there we have $\mathfrak {H}=0$ in Ia or $\mathfrak {H}=1$ in Ib. Indeed, $\partial _{\xi } \mathfrak {H}=0$ implies $z_c(\xi , \tau ) \in \mathbb {R}$, see (5.9). Since we only consider the “physical” part $(\xi ,\tau )\in [0,\infty )\times [0,1]$, it follows that $(\xi ,\tau )$ must lie on the frozen boundary. This implies that the function $\mathfrak {L}(\tau )$ is determined by (5.12) uniquely for $\tau \ne 0,1$, and is continuous.

For $\tau =0$, is it natural to set $\mathfrak {L}(0)=\max \{\xi :\mathfrak {H}(\xi ,0)=0 \}$ by continuity. For $\tau =1$, it suffices to show that $(\mathfrak {L}(\tau ),\tau )$ for $\tau$ close to 1 must belong to the frozen zone III and not Ib. For $\tau =1$, the critical point equation (5.7) has a root $z=\beta$ independently of $\xi$. The discriminant of the remaining quadratic equation is negative for

$$\begin{aligned} \frac{2}{1+\sqrt{xy}}<1+\xi <\frac{2}{1-\sqrt{xy}}. \end{aligned}$$

In particular, the discriminant is positive for $\xi$ close to zero, so the point $(\xi ,\tau )=(0,1)$ lies in a frozen zone. By looking at the value of $z_c={\bar{z}}_c$ at a point of the adjacent frozen boundary, one can verify that the neighborhood of $(\xi ,\tau )=(0,1)$ is always in zone III. Thus, $\mathfrak {H}(\xi ,1)$ is strictly monotone in $\xi$ in this neighborhood. Setting $\mathfrak {L}(1)=0$, we get the continuity of $\mathfrak {L}(\tau )$ at $\tau =0$, as desired. $\square$

We arrive at the following limit shape result for Grothendieck random partitions:

Theorem 5.5

Let $\lambda =(\lambda _1,\ldots ,\lambda _N )$ be the Grothendieck random partition distributed as $\mathscr {M}_{\vec \beta ;\textrm{Gr}}$ (3.4) with parameters $x,y,\beta$ as in (5.1) (in particular, $\beta <0$). For any fixed $\tau \in [0,1]$ we have the convergence in probability:

$$\begin{aligned} \frac{\lambda _{\lfloor \tau N \rfloor }}{N}\rightarrow \mathfrak {L}(\tau )+\tau -1,\qquad N\rightarrow +\infty , \end{aligned}$$

(5.13)

where the function $\mathfrak {L}(\tau )$ is defined before Lemma 5.4.

In particular, the shift by $\tau -1$ in (5.13) comes from $\lambda _i=\ell _i+i-N$, $i=1,\ldots ,N$. When we need to indicate the dependence of $\mathfrak {L}(\tau )$ on the parameters, we will write $\mathfrak {L}(\tau \mid x,y,\beta )$.

To help visualize the Grothendieck limit shape determined by the function $\mathfrak {L}(\tau )$, we employ the coordinate system rotated by $45^\circ$ (for illustration, see Fig. 1, left, in the Introduction). In this way, Young diagrams and their limit shapes become functions $\mathfrak {W}(u)$, $u\in \mathbb {R}$, satisfying

$$\begin{aligned} |\mathfrak {W}(u)-\mathfrak {W}(v)|\le |u-v|,\qquad \mathfrak {W}(u)=|u| \quad \text {for all large enough } |u|. \end{aligned}$$

(5.14)

Define the norm of a continuous Young diagram by

$$\begin{aligned} \Vert \mathfrak {W}\Vert :=\frac{1}{2}\int _{-\infty }^{+\infty }\left( \mathfrak {W}(u)-|u| \right) du. \end{aligned}$$

(5.15)

Before the limit, the functions $\mathfrak {W}_N(u)$ corresponding to Young diagrams $\lambda$ with at most N rows are piecewise linear with derivatives $\pm 1$ and integer maxima and minima. Note that $\Vert \mathfrak {W}_N\Vert =|\lambda |$ is the number of boxes in the Young diagram.

The space of all functions satisfying (5.14) is called the space of continuous Young diagrams by Kerov, see [49, Chapter 4].³ Young diagrams in the coordinate system rotated by $45^\circ$ were first considered in connection with the Vershik–Kerov–Logan–Shepp (VKLS) limit shape of Plancherel random partitions, see [57, 83].

Let the pre-limit continuous Young diagrams $\mathfrak {W}_N(u)$ correspond to the Grothendieck random partitions with parameters $(x,y,\beta )$. The convergence (5.13) in Theorem 5.5 implies the pointwise convergence in probability as $N\rightarrow +\infty$ of the rescaled functions $\frac{1}{N}\hspace{1pt}\mathfrak {W}_N(uN)$ to a limit shape. This limit shape is a continuous Young diagram $u\mapsto \mathfrak {W}(u)$ which has parametric form

$$\begin{aligned} u=\mathfrak {L}(\tau )-1,\qquad \mathfrak {W}=\mathfrak {L}(\tau )-1+2\tau , \qquad \tau \in [0,1]. \end{aligned}$$

(5.16)

This parametric form follows from the change of coordinates from $\left( \tau ,\mathfrak {L}(\tau )+\tau -1 \right)$ to $(u,\mathfrak {W}(u))$ under the $45^\circ$ rotation. When we need to indicate the dependence of $\mathfrak {W}(u)$ on the parameters of the Grothendieck measure, we will write $\mathfrak {W}(u\mid x,y,\beta )$. Thus, we have established Theorem 1.4 from the Introduction.

In Sect. 5.4 we present graphs of the limit shapes (5.16) for several choices of parameters $(x,y,\beta )$ of the Grothendieck measure.

5.3 Properties of Grothendieck limit shapes

Here let us make several general observations in connection with the limit shape result for Grothendieck random partitions (Theorem 5.5).

5.3.1 Differential equations

Differentiating (5.12) in $\tau$, we see that $\mathfrak {L}(\tau )$ satisfies the differential equation $\mathfrak {L}'(\tau )= \frac{1-\partial _\tau \hspace{1pt}\mathfrak {H}(\mathfrak {L}(\tau ),\tau )}{\partial _\xi \hspace{1pt}\mathfrak {H}(\mathfrak {L}(\tau ),\tau )}$. In terms of the critical point, with the help of (5.9), this equation has the form

$$\begin{aligned} \mathfrak {L}'(\tau ) = -\frac{\pi -\mathop {\textrm{Arg}}\bigl (z_c(\mathfrak {L}(\tau ),\tau )-\beta \bigr ) + \mathop {\textrm{Arg}}z_c(\mathfrak {L}(\tau ),\tau )}{\mathop {\textrm{Arg}}z_c(\mathfrak {L}(\tau ),\tau )}. \end{aligned}$$

(5.17)

Here $z_c=z_c(\xi ,\tau )$ is the root of the cubic equation (5.7) in the upper half plane if $(\xi ,\tau )$ belongs to the liquid region. When $(\xi ,\tau )$ is in a frozen zone, $z_c$ should be taken real such that the arguments in (5.9) give the gradient $\nabla \mathfrak {H}$ in this frozen zone. We refer to the trichotomy in Proposition 5.2, see also Fig. 4 for an illustration.

The limit shape continuous Young diagram $\mathfrak {W}(u)$ (5.16) in the $45^\circ$ rotated coordinate system satisfies a more symmetric differential equation

$$\begin{aligned} \mathfrak {W}'(u)= \frac{\pi -\mathop {\textrm{Arg}}\bigl (z_c\left( u+1,\frac{\mathfrak {W}(u)-u}{2}\right) -\beta \bigr ) - \mathop {\textrm{Arg}}z_c\left( u+1,\frac{\mathfrak {W}(u)-u}{2}\right) }{\pi -\mathop {\textrm{Arg}}\bigl (z_c\left( u+1,\frac{\mathfrak {W}(u)-u}{2}\right) -\beta \bigr ) + \mathop {\textrm{Arg}}z_c\left( u+1,\frac{\mathfrak {W}(u)-u}{2}\right) }. \end{aligned}$$

(5.18)

We remark that the root $z_c(\xi ,\tau )$ of the cubic equation (5.7) depends on $(\xi ,\tau )$ in a nonlinear and somewhat implicit manner. Therefore, it may be challenging to extract useful information about the Grothendieck limit shape from the differential equations (5.17)–(5.18). Even for producing the plots in Sect. 5.4 we relied not on these differential equations, but rather on the original implicit equation (5.12).

5.3.2 Staircase frozen facet

Observe that when $(\xi ,\tau )$ is in the frozen zone II, we have $\nabla \mathfrak {H}=(-1,-1)$, which corresponds to taking $z_c$ from $(\beta ,0)$. Thus, in this frozen zone we have from (5.17) and (5.18):

$$\begin{aligned} \mathfrak {L}'(\tau )=-\frac{1}{2},\qquad \mathfrak {W}'(u)=0. \end{aligned}$$

(5.19)

Notice that for (5.19) to hold, the point $(\mathfrak {L}(\tau ),\tau )$ of the Grothendieck limit shape must belong to the frozen zone II. In fact, this is possible for certain choices of the parameters $(x,y,\beta )$, namely, when $\beta$ is sufficiently large in the absolute value:

Lemma 5.6

Let the parameters $(x,y,\beta )$ satisfy (5.1). For any fixed x, y, there exists $\beta _0<0$ such that for all all $\beta <\beta _0$, the frozen zone II extends through the whole horizontal strip $\xi >0$, $0<\tau <1$ in the $(\xi ,\tau )$ coordinates. See Fig. 6 for an illustration.

Fig. 6

Frozen boundary curve in the full space $\mathbb {R}^2$ with $x=1/3$, $y=1/5$, $\beta =-25$. As $\beta$ decays to $-\infty$, the cusp point goes to infinity along the main diagonal in the first quadrant in the coordinates $(\xi ,1-\tau )$

Proof

An explicit parametrization of the frozen boundary curve by $z\in \mathbb {R}$ is obtained by solving the double critical point equations (5.8). This parametrization has the form

$$\begin{aligned} \xi= & {} \frac{(1-x y) \left( y \left( \beta +x z^2-2 z\right) +z^2 (1-\beta x)\right) }{(1-x z)^2 (y-z)^2},\quad \nonumber \\ \tau= & {} 1+ (z-\beta )^2\hspace{1pt}\frac{(1-x y) \left( y-x z^2\right) }{(-\beta ) (1-x z)^2 (y-z)^2}. \end{aligned}$$

(5.20)

One can check the following facts about the frozen boundary curve $\partial \mathcal {L}$ in the whole space $(\xi ,\tau )\in \mathbb {R}^2$:

• $\partial \mathcal {L}$ is tangent to the horizontal coordinate line at a unique point $(\xi ,1)$ with $\xi >0$. This point corresponds to $z=\beta$ which is a double zero of $\tau -1$. Substituting $z=\beta$ into $\xi$ produces a positive quantity.

• $\partial \mathcal {L}$ is tangent to the vertical coordinate line at a unique point $(0,\tau )$ with $\tau <1$. This point corresponds to $z\rightarrow \infty$. Taking this limit in $\tau$ shows that the tangent point has $\tau <1$.

• The slope of the curve $\partial \mathcal {L}$ in the coordinates $(\xi ,1-\tau )$ (as in Fig. 4) is

  $$\begin{aligned} -\frac{\partial \tau /\partial z}{\partial \xi /\partial z}=1-\frac{z}{\beta }, \end{aligned}$$

  which changes sign only at $z=\beta$ and $z=\infty$.

• For $z=y$ and $z=1/x$, the curve $\partial \mathcal {L}$ goes to infinity in two different asymptotic directions. For $z\rightarrow y$ we have $\xi ,1-\tau \rightarrow -\infty$, and for $z\rightarrow 1/x$ we have $\xi ,1-\tau \rightarrow +\infty$. Each of these asymptotic directions has degree 2, that is, there are exactly two components of $\partial \mathcal {L}$ escaping to infinity in each of the first and the third quadrants in the coordinates $(\xi ,1-\tau )$.

Now let us look at the “cusp” point of $\partial \mathcal {L}$, that is, where the third derivative of $S(z;\xi ,\tau )$ vanishes along with the first two. In Fig. 4, the cusp is at the tip of the frozen zone II. Let us show that the cusp point is always unique and exists in the full space $(\xi ,\tau )\in \mathbb {R}^{2}$. Take $\frac{\partial ^3}{\partial z^3}\hspace{1pt}S(z;\xi ,\tau )$, and substitute into it $\xi ,\tau$ as in (5.20). We obtain a rational function in z and the parameters $(x,y,\beta )$ whose numerator is a cubic polynomial

$$\begin{aligned} \textsf {P}(z)= z^3 x (1 + x y - x\beta ) - 3z^2xy +3zx y \beta + y (y -\beta - x y \beta ). \end{aligned}$$

The discriminant of $\textsf {P}(z)$ is $-27\hspace{1pt}x^2 y^2 (1-x\beta )^2 (1-x y)^2 (y-\beta )^2$, which is manifestly negative. Therefore, there is a unique real root z of $\textsf {P}(z)$, and it corresponds to the cusp point.

Let us look at the behavior of the cusp point for large negative $\beta$. We have

$$\begin{aligned} \textsf {P}(z) = \textsf {P}_0(z)\beta +O(1),\qquad \beta \rightarrow -\infty , \quad \text {where}\quad \textsf {P}_0(z):=-x^2 z^3+3 x y z-y (1+x y). \end{aligned}$$

The polynomial $\textsf {P}_0(z)$ has a unique real root, denote it by $z_0$. Clearly, the root of $\textsf {P}(z)$ becomes close to $z_0$ as $\beta \rightarrow -\infty$. Next, for $z=z_0$, we have

$$\begin{aligned} \xi =1-\tau +O(1)= \frac{(1-x y) \left( y-x z_0^2\right) }{(1-x z_0)^2 (y-z_0)^2}\hspace{1pt}\beta +O(1),\qquad \beta \rightarrow -\infty . \end{aligned}$$

Since $\textsf {P}_0(-\sqrt{y/x})>0$ and the coefficient by $z^3$ in $\textsf {P}_0$ is negative, we see that $y-x z_0^2>0$. This inequality implies that the cusp point of $\partial \mathcal {L}$ goes to infinity along the main diagonal in the first quadrant in the coordinates $(\xi ,1-\tau )$.

We conclude that for large $\beta$, four components of the frozen boundary escape as $\xi ,1-\tau \rightarrow +\infty$, and two components escape as $\xi ,1-\tau \rightarrow -\infty$. Together with the tangence properties observed at the beginning of the proof, this implies that each horizontal line at height $\tau$, $\tau \in [0,1]$, intersects the frozen boundary precisely four times. The frozen zone II is between the middle two intersections. This completes the proof. $\square$

By Lemma 5.6, if $|\beta |$ is sufficiently large and $\beta <0$, the limit shape of the Grothendieck random partition always has a part where the derivative satisfies (5.19). In particular, the density of the particles $\ell _i$ is $\frac{1}{2}$. We call the part of the Grothendieck limit shape where (5.19) holds the staircase frozen facet.

Let us discuss how the partition $\lambda$ looks in the staircase facet. For the two-dimensional Schur process, in zone II the up-diagonal paths are densely packed and move diagonally. In terms of the particle configuration $X^{2d}=\{x_i^m:1\le m,i\le N\}$, this means that

$$\begin{aligned} x^{m+1}_i=x^m_i-1,\qquad x^m_{i+1}=x^m_i-1. \end{aligned}$$

Thus, for the coordinates $\lambda _i$ and $\ell _i=\lambda _i+N-i$ of the Grothendieck random partition, where $\ell _i=x^i_i$ in distribution (Proposition 3.2), we have in the staircase facet:

$$\begin{aligned} \ell _{i+1} =\ell _i-2,\qquad \lambda _{i+1} =\lambda _i-1. \end{aligned}$$

Thus, in this facet, the Young diagram $\lambda$ locally looks like a staircase with no fluctuations. This justifies the name “staircase frozen facet”. In the $45^\circ$ rotated coordinates, the limit shape $\mathfrak {W}(u\mid x,y,\beta )$ of $\lambda$ is horizontal in this facet. We refer to Sect. 5.4 for illustrations of staircase facets.

5.3.3 Reduction to Schur measures and Plancherel limit shapes

Observe that for all $\beta \le 0$, under the Schur process $\mathscr {M}^{2d}_{\vec \beta ;\textrm{Gr}}$ (3.10), the marginal distribution of the partition $\mu ^N$ is simply the Schur measure with probability weights

$$\begin{aligned} (1-xy)^{N^2}\hspace{1pt}s_{\mu ^N}(\underbrace{x,\ldots ,x}_N )\hspace{1pt}s_{\mu ^{N}}(\underbrace{y,\ldots ,y}_N ). \end{aligned}$$

(5.21)

When $\beta =0$, the weights $(-\beta )$ of the diagonal edges in the directed graph in Fig. 2 vanish. Thus, for $\beta =0$, all up-diagonal paths must go vertically, and almost surely $\mu ^m=\mu ^N$ for all $m=1,\ldots , N$. This implies that for fixed x, y and as $\beta \nearrow 0$, the limit shape $\mathfrak {W}(u\mid x,y,\beta )$ of the Grothendieck random partition $\lambda _i=\mu ^i_i$ converges to that of the Schur measure (5.21). Denote the latter limit shape by $\mathfrak {S}_{\tau =1}(u)$. It depends on the parameters x, y only through their product, and is independent of $\beta$.

On the other hand, the marginal distribution of the partition $\mu ^{1}$ is the following Schur measure:

$$\begin{aligned} (1-xy)^{N^2}(1-x\beta )^{-N(N-1)} s_{\mu ^1}(\underbrace{x,\ldots ,x}_N)\hspace{1pt}s_{\mu ^1}(\underbrace{y,\ldots ,y}_N;\underbrace{-\hat{\beta },\ldots ,-{\hat{\beta }}}_{N-1} ), \end{aligned}$$

(5.22)

where $(-{\hat{\beta }},\ldots ,-{\hat{\beta }} )$ is the dual specialization (e.g., see [13, Section 2] for the definition). Denote the limit shape of $\mu ^1$ by $\mathfrak {S}_{\tau =0}(u)$. It depends on all our parameters $x,y,\beta$.

Using, for example, the Robinson–Schensted–Knuth correspondence [36, 51], one can show that the expected numbers of boxes in the partitions $\mu ^N$ and $\mu ^1$ are, respectively,

$$\begin{aligned} \mathbb {E}|\mu ^N|=\frac{N^2xy}{1-xy},\qquad \mathbb {E}|\mu ^1|=\frac{N^2xy}{1-xy}-N(N-1)\beta y. \end{aligned}$$

Dividing by $N^2$ (which comes from rescaling both coordinate directions of the continuous Young diagram by $N^{-1}$), we see that the norms (5.15) of the limit shapes are

$$\begin{aligned} \Vert \mathfrak {S}_{\tau =1}\Vert =\frac{xy}{1-xy},\qquad \Vert \mathfrak {S}_{\tau =0}\Vert =\frac{xy}{1-xy}-\beta y. \end{aligned}$$

When x, y are small, $\Vert \mathfrak {S}_{\tau =1}\Vert$ is of order xy, and the rescaled limit shape

$$\begin{aligned} \frac{1}{\sqrt{xy}}\hspace{1pt}\mathfrak {S}_{\tau =1}\left( u\sqrt{xy}\right) \end{aligned}$$

converges to the celebrated Vershik–Kerov–Logan–Shepp (VKLS) curve

$$\begin{aligned} \Omega (u):={\left\{ \begin{array}{ll} \frac{2}{\pi } \left( u \arcsin (\frac{u}{2}) + \sqrt{4 - u^2}\right) ,&{} |u|\le 2;\\ |u|,&{}|u|>2. \end{array}\right. } \end{aligned}$$

(5.23)

Note that $\Vert \Omega \Vert =1$.

By Proposition 3.2 and Theorem 5.5, the Grothendieck random partition $\lambda$ should have a limit shape which is between those of $\mu ^1$ and $\mu ^N$. When $-\beta y\ll xy\ll 1$, the limit shapes of $\mu ^1$ and $\mu ^N$ should be close to each other and to the VKLS shape (5.23). Together with numerical experimentation in Sect. 5.4, this prompts the following conjecture:

Conjecture 5.7

Let $x,y\searrow 0$ and $\beta =\beta (x)\nearrow 0$ such that $-\beta (x)\ll x$. Then the rescaled Grothendieck limit shape $\frac{1}{\sqrt{xy}}\hspace{1pt}\mathfrak {W}(u\sqrt{xy}\mid x,y,\beta (x))$ converges to the VKLS shape $\Omega (u)$.

Consider another regime when $x,y\searrow 0$ but $\beta =\beta (y) \rightarrow -\infty$ such that $-\beta y$ is fixed. This change in $\beta$ does not affect $\mu ^N$, and the norm of $\mathfrak {S}_{\tau =1}$ goes to zero. After rescaling, $\mathfrak {S}_{\tau =1}$ is close to VKLS shape. The limit shape of $\mu ^1$ at $\tau =0$, on the other hand, grows macroscopically, but one can show that $\mathfrak {S}_{\tau =0}$ still contains a Plancherel-like part at scale xy in the neighborhood of $u=1$. In the two-dimensional Schur process picture, for $\beta \rightarrow -\infty$ the up-diagonal paths strongly prefer to go diagonally. Therefore, we expect that in this regime, the Grothendieck limit shape contains a (shifted) Plancherel-like part. However, numerical experimentation Sect. 5.4 suggests that this shape is not exactly the VKLS shape. Let us formulate a conjecture:

Conjecture 5.8

Let $x,y\searrow 0$ and $\beta =\beta (y)=-K/y$, where $K>0$ is fixed. There exists $K_0>0$ such that for all $K>K_0$, in the $O(\sqrt{xy})$-neighborhood of $u=1$, the Grothendieck limit shape $\mathfrak {W}(u\mid x,y,\beta (y))$ is close to

$$\begin{aligned} \frac{u+1}{2}+\frac{\sqrt{xy}}{2}\hspace{1pt}\Omega _{(K)}\left( \frac{u-1}{\sqrt{xy}} \right) , \end{aligned}$$

(5.24)

where $\Omega _{(K)}$ is a suitable K-dependent deformation of the VKLS shape $\Omega$. We expect that as $K\rightarrow -\infty$, the shapes $\Omega _{(K)}$ approach $\Omega$.

We have formulated Conjectures 5.7 and 5.8 only for limit shapes, but similar Plancherel-like behavior should arise for Grothendieck random partitions themselves.

5.4 Grothendieck limit shape plots

The limit shape surface $\mathfrak {H}(\xi ,\tau )$ of the two-dimensional Schur process has the normal vector $\nabla \mathfrak {H}(\xi ,\tau )$. This gradient is expressed through the solution $z_c(\xi ,\tau )$ to the cubic equation (5.7), see (5.9). However, $\mathfrak {H}(\xi ,\tau )$ itself is not explicit, making it necessary to employ numerical integration to graph the surface. This is achieved by integrating the gradient along the $\xi$ direction, starting from $+\infty$ and moving towards the point $(\xi ,\tau )$.

Recall that the Grothendieck limit shape $\mathfrak {L}(\tau )$ is the cross-section of the Schur process limit shape surface $\eta =\mathfrak {H}(\xi ,\tau )$ in the $(\xi ,\tau ,\eta )$ coordinates, at the plane $\eta =\tau$. This cross-section is not explicit either. Therefore, we need to solve numerically the implicit equation (5.12) to get the desired function $\mathfrak {L}(\tau )$. After obtaining $\mathfrak {L}(\tau )$, we use it to graph the shape $\mathfrak {W}(u)$ in the coordinate system rotated by $45^\circ$ using the parametric representation (5.16).

We remark that the differential equations (5.17) and (5.18) for $\mathfrak {L}(\tau )$ or $\mathfrak {W}(u)$, respectively, are not very useful for graphing directly, as they cannot be solved explicitly. While a numerical solution of these differential equations is possible, it would require specific convergence estimates, which we avoid with our more direct approach.

We implement a cubic equation solver in Python to find the roots $z_c(\xi ,\tau )$ along a regular grid of $(\xi ,\tau )$, utilizing the code from [50]. Then (also with Python) we perform direct numerical integration of the $\xi$-gradient of the height function (5.9). After that we solve the implicit equation (5.12). This procedure yields the values of $\mathfrak {W}(u)$ along a non-regular grid in u, which is sufficient for graphing the limit shape of Grothendieck random partitions. Our Python code is available at [38].

Remark 5.9

Here we do not perform probabilistic simulations of Grothendieck random partitions, but rather focus on numerically graphing the Grothendieck limit shapes which exist due to Theorem 5.5.

Next we descibe the resulting plots of Grothendieck limit shapes. The images are located at the end of the paper.

Fig. 7

Graphs with $x=1/3$, $y=1/5$, $\beta =-6$. See Sect. 5.4 for description

5.4.1 Basic example ($x=1/3,\,y=1/5,\,\beta =-6$)

First, we take the same parameters as in Fig. 4. In Fig. 7, the left pane displays the limit shape surface $\mathfrak {H}$ for the Schur process (red), the plane $\eta =\tau$ (blue), and the curve $(\mathfrak {L}(\tau ),\tau ,\tau )$ in the cross-section. The top right pane shows the projection of the cross-section onto the bottom coordinate plane $(\xi ,1-\tau )$, and also includes the frozen boundary curve. The frozen boundary is the same as in Fig. 4. The bottom right pane presents the limit shape of Grothendieck random partitions in the coordinates $(u,\mathfrak {W}(u))$. The limit shape $\mathfrak {W}(u)$ always lies below the line $u+2$, as the number of nonzero parts in the Grothendieck random partition is limited to at most N.

Fig. 8

Graphs with $x=1/3$, $y=1/5$, $\beta =-25$. See Sect. 5.4 for description

Fig. 9

Exact samples of the Grothendieck random partitions with $N=50$ and parameters $x=1/3$, $y=1/5$, and $\beta =-6$ (left plot) or $\beta =-25$ (right plot). See Sect. 5.5 for a discussion of the sampling mechanism. We observe that the samples follow the limit shapes from Figs. 7 and 8, as it should be. In particular, notice the staircase frozen facet on the right plot

5.4.2 Large negative beta ($x=1/3,\,y=1/5,\,\beta =-25$)

Second, we consider the case of large negative $\beta$. In the top left pane in Fig. 8, we have zoomed in around the flat section of the surface $\mathfrak {H}$ (red). The blue plane corresponds to $\eta =\tau$, and the black meshed plane extends the zone II frozen facet of $\mathfrak {H}$ which has $\nabla \mathfrak {H}=(-1,-1)$. We see that the intersection of the blue plane with the red surface is a straight line in this neighborhood. The bottom left pane displays the projection of the cross-section, similar to Fig. 7. By Lemma 5.6, the black curve must traverse through zone II. On the right pane, we added a horizontal line to highlight the staircase frozen facet where the limit shape $\mathfrak {W}(u)$ is horizontal.

Fig. 10

Graphs of $\mathfrak {W}(u)$ with $x=y=1/40$ and $\beta =-1/40$ (round), $\beta =-1/250$ (yellow squares), and $\beta =-1/1600$ (green squares). We also added the scaled VKLS curve $\sqrt{xy}\,\Omega (u/\sqrt{xy})$. See Sect. 5.4 for more detail

Fig. 11

Graph of $\mathfrak {W}(u)$ with $x=y=1/100$ and $\beta =-1/1000$ and the scaled VKLS curve $\sqrt{xy}\,\Omega (u/\sqrt{xy})$. See Sect. 5.4 for more detail

5.4.3 Plancherel-like behavior for small negative beta

In Figs. 10 and 11 we numerically support Conjecture 5.7 that the rescaled Grothendieck limit shape converges to the VKLS shape $\Omega (u)$ (5.23) as $x,y\rightarrow 0$ such that $\beta \ll x$. In Fig. 10 the parameters $x=y=1/40$ are fixed. As $\beta$ gets close to zero (we chose three orders, $(xy)^{\frac{1}{2}}, (xy)^{\frac{3}{4}}$, and xy), we see that the plots of $\mathfrak {W}(u)$ get closer to the VKLS shape. Moreover, Fig. 11 demonstrates that for smaller $x=y=1/100$, taking $\beta =1/1000$ (order $(xy)^{\frac{3}{4}}$), makes the shape $\mathfrak {W}(u)$ closer than for $x=y=1/40$. Indeed, we have for the uniform norms:

$$\begin{aligned} \begin{aligned} (xy)^{-\frac{1}{2}}\cdot \bigl \Vert \mathfrak {W}(\cdot \mid x,y,\beta ) - \sqrt{xy}\,\Omega \left( \cdot /\sqrt{xy}\right) \bigr \Vert _C \bigg \vert _{x=y=1/40,\,\beta =1/250}&\approx 0.10; \\ (xy)^{-\frac{1}{2}}\cdot \bigl \Vert \mathfrak {W}(\cdot \mid x,y,\beta ) - \sqrt{xy}\,\Omega \left( \cdot /\sqrt{xy}\right) \bigr \Vert _C \bigg \vert _{x=y=1/100,\,\beta =1/1000}&\approx 0.06; \\ (xy)^{-\frac{1}{2}}\cdot \bigl \Vert \mathfrak {W}(\cdot \mid x,y,\beta ) - \sqrt{xy}\,\Omega \left( \cdot /\sqrt{xy}\right) \bigr \Vert _C \bigg \vert _{x=y=1/900,\,\beta =1/27000}&\approx 0.044, \end{aligned} \end{aligned}$$

which suggests that these expressions should decay to zero.

Fig. 12

Graphs with $x=y=1/40$ and $\beta =-120$. On the right, we added the shifted and scaled VKLS shape (given by (5.24) with $\Omega _{(K)}$ replaced by $\Omega$ (5.23)). The Grothendieck limit shape apparently is not close to the shifted and scaled VKLS shape. See Sect. 5.4 for more detail

5.4.4 Plancherel-like behavior for large negative beta

In Fig. 12, we consider the regime of Conjecture 5.8, and take $x=y=1/40$, $\beta =-120$, so $-\beta y=3$. The Grothendieck limit shape $\mathfrak {W}(u)$ has a staircase frozen facet, and to the right of it we observe a curved part of size $O(\sqrt{xy})$. Zooming in, we see that this part of $\mathfrak {W}(u)$ does not seem to be close to the shifted and scaled VKLS shape, see Fig. 12, right.

5.4.5 Positive beta ($x=1/3,\,y=1/5,\,\beta =1/12$)

By Proposition 3.1, the Grothendieck measure $\mathscr {M}_{\vec \beta ;\textrm{Gr}}(\lambda )$ on partitions is also nonnegative for $0\le \beta <\min (x^{-1},y)$. Setting $\beta >0$ makes the corresponding two-dimensional Schur process (3.10) a signed probability measure. However, in this case we can still define the surface $\mathfrak {H}(\xi ,\tau )$ using the root $z_c(\xi ,\tau )$ of the cubic equation (5.7). Then we can define the curve $\mathfrak {L}(\tau )$ as the solution of the implicit equation (5.12), and finally obtain a shape $\mathfrak {W}(u)$ via (5.16). This leads to the following conjecture:

Conjecture 5.10

The curve $\mathfrak {W}(u)=\mathfrak {W}(u\mid x,y,\beta )$ is well-defined by the procedure described above for all $\beta <\min (x^{-1},y)$. Moreover, this curve $\mathfrak {W}(u)$ is the limit shape of the random partitions distributed according to the Grothendieck measure with homogeneous parameters (5.1) in the $45^\circ$ rotated coordinate system.

In Fig. 13, we numerically support Conjecture 5.10 by considering parameters $x=1/3$, $y=1/5$, $\beta =1/12$. We plot the surface $\mathfrak {H}(\xi ,\tau )$ in Fig. 13, top left. In the bottom left pane we plot the curve $\mathfrak {L}(\tau )$ together with the “frozen boundary”. An interesting feature is that here $\mathfrak {L}(\tau )$ is tangent to this “frozen boundary”. Finally, in Fig. 13, right, we plot the conjectural limit shape $\mathfrak {W}(u\mid \frac{1}{3},\frac{1}{5},\frac{1}{12})$. From additional numerical examples we also noticed that as $\beta \nearrow \min (x^{-1},y)$, we have $\Vert \mathfrak {W}(\cdot \mid x,y,\beta )\Vert \rightarrow 0$.

Fig. 13

Graphs with $x=1/3$, $y=1/5$, and $\beta =1/12$. The two graphs on the right do not correspond to a nonnegative probability measure on two-dimensional point configurations. However, we conjecture that the Grothendieck measures still converge to the limit shape $\mathfrak {W}(u)$ on the right. See Sect. 5.4 and Conjecture 5.10 in particular for details

5.5 Exact sampling Grothendieck random partitions by Schur dynamics

It is known that Schur processes can be exactly sampled using push-block type dynamics or Robinson–Schensted–Knuth (RSK) correspondences. We refer to [10, 13, 19, 62, Section 4], or [6] for various expositions of general sampling mechanisms for Schur processes. An application to our Schur process $\mathscr {M}^{2d}_{\vec \beta ;\textrm{Gr}}$ (3.10) is implemented in Python [38, file RSK_code.py] and follows the RSK dynamics on interlacing arrays as in [62]. We only work with homogeneous parameters, but a straightforward modification would cover the fully inhomogeneous case. The results of the simulation are given in Fig. 9.

Let us briefly describe our sampling mechanism in terms of semistandard Young tableaux (which are in a well-known bijection with interlacing arrays). Start from an empty Young tableau $T(0)=\varnothing$.

In the first stage, insert into this tableau an $N\times N$ matrix A of independent geometric random variables with distribution $\textrm{Prob}(\xi =k)= (1-xy)\cdot (xy)^{k}$, $k=0,1,2,\ldots$ using the classical RSK correspondence [51]. This procedure is performed in N steps, and in each t-th step we form the word $1^{A_{t1}}\ldots N^{A_{tN}}$, where $A_{ij}\in \mathbb {Z}_{\ge 0}$ are the elements of the matrix A, and powers of letters mean repetition. This word is then inserted into the Young tableau $T(t-1)$ using the usual RSK insertion. After these N steps, the shape of our Young tableau T(N) is distributed according to the Schur measure (5.21) with specializations $(x,x,\ldots ,x)$ and $(y,y,\ldots ,y )$.

In the second stage, take an $(N-1)\times N$ matrix of independent Bernoulli random variables with distribution $\textrm{Prob}(\eta =1)=-\beta x/(1-\beta x)$, and insert it into the tableau T(N) using the dual RSK correspondence. This procedure is performed in $N-1$ steps, and in each s-th step we form the word $1^{B_{s1}}\ldots N^{B_{sN}}$ (where $B_{ij}\in \left\{ 0,1 \right\}$ are the elements of B), and insert it into the Young tableau $T(N+s-1)$ using the dual RSK insertion. An implementation of the dual RSK insertion for semistandard Young tableaux (equivalently, interlacing arrays of integers) that we used is the algorithm $\mathscr {Q}_{\textrm{row }}^{q=0}[-\hat{\beta }]$ from [62, Section 4.3]. After these $N-1$ steps, the shape of our Young tableau $T(2N-1)$ is distributed according to the Schur measure (5.22) with specializations $(x,x,\ldots ,x)$ and $(y,y,\ldots ,y;-{\hat{\beta }},\ldots ,-\hat{\beta })$.

To obtain the Grothendieck random partition, one has to track different parts of the shape of the evolving Young tableau $T(N+s-1)$. Namely, set

$$\begin{aligned} \lambda _{N-s+1}=T(N+s-1)_{N-s+1},\qquad s=1,2,\ldots ,N, \end{aligned}$$

(5.25)

where $T(N+s-1)_j$ means the j-th part of the shape of the Young tableau.

Proposition 5.11

The distribution of the random Young diagram $\lambda =(\lambda _1,\ldots ,\lambda _N )$ defined by (5.25) coincides with the Grothendieck measure (1.3) with homogeneous parameters $x_i=x$, $y_j=y$, $\beta _r=\beta$.

Proof

The joint distribution of the shapes of the semistandard Young tableaux $T(N+s-1)$, $s=1,\ldots ,N$, is given by the Schur process $\mathscr {M}^{2d}_{\vec \beta ;\textrm{Gr}}$ (3.10) (with homogeneous parameters), where the shape of $T(N+s-1)$ is $\mu ^{N-s+1}$. Indeed, this statement follows from the general Schur dynamics result [19, Theorem 10] (where instead of the push-block dynamics one can use the Robinson–Schensted–Knuth one, cf. [25, 62]). With this identification, the desired claim follows from Proposition 3.2. $\square$