Abstract
As a quantum affinization, the quantum toroidal algebra \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\) is defined in terms of its “left” and “right” halves, which both admit shuffle algebra presentations (Enriquez in Transform Groups 5(2):111–120, 2000; Feigin and Odesskii in Am Math Soc Transl Ser 2:185, 1998). In the present paper, we take an orthogonal viewpoint, and give shuffle algebra presentations for the “top” and “bottom” halves instead, starting from the evaluation representation \({U_q({\dot{{\mathfrak {gl}}}}_n)}\curvearrowright {{\mathbb {C}}}^n(z)\) and its usual R-matrix \(R(z) \in \text {End}({{\mathbb {C}}}^n \otimes {{\mathbb {C}}}^n)(z)\) (see Faddeev et al. in Leningrad Math J 1:193–226, 1990). An upshot of this construction is a new topological coproduct on \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\) which extends the Drinfeld–Jimbo coproduct on the horizontal subalgebra \({U_q({\dot{{\mathfrak {gl}}}}_n)}\subset {U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1. The affine quantum group \({U_q({\dot{{\mathfrak {sl}}}}_n)}= U_q({\widehat{{\mathfrak {sl}}}}_n)\) (hats will be replaced by points in the present paper) has the following two presentations:
-
as the affinization of \(U_q({\mathfrak {sl}}_n)\)
-
as the Drinfeld–Jimbo quantum group whose Dynkin diagram is an n-cycle
However, the two presentations above yield different bialgebra structures on \({U_q({\dot{{\mathfrak {sl}}}}_n)}\), which is evidenced by the fact that the coproduct in the first bullet is only topological (i.e. \(\Delta \) is an infinite sum, which only makes sense in a certain completion). Moreover, the two bullets above yield different triangular decompositions of \({U_q({\dot{{\mathfrak {sl}}}}_n)}\) into positive, Cartan, and negative halves:
The two decompositions above are quite different: the positive subalgebra \(U_q^\rightarrow ({\dot{{\mathfrak {sl}}}}_n)\) of (1.1) is generated by Drinfeld’s elements \(e_{i,k}\) over all \(1 \le i < n\) and \(k \in {{\mathbb {Z}}}\), while the positive subalgebra \(U_q^\uparrow ({\dot{{\mathfrak {sl}}}}_n)\) of (1.2) is generated by the Drinfeld–Jimbo elements \(\{e_i\}_{i \in {{\mathbb {Z}}}/n{{\mathbb {Z}}}}\). The connection between these two presentations was given in [1].
1.2. The main purpose of the present paper is to extend the description above to the quantum toroidal algebra \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\), which is defined as in the first bullet above:
This construction naturally comes with a triangular decomposition (see Sect. 3.12 for an overview of the quantum toroidal algebra, as well as of our conventions):
Our \({{\widetilde{U}}_{q,{{\overline{q}}}}^\leftarrow (\ddot{{\mathfrak {gl}}}_n)}\) and \({{\widetilde{U}}_{q,{{\overline{q}}}}^\rightarrow (\ddot{{\mathfrak {gl}}}_n)}\) are the “Borel” subalgebras of the quantum toroidal algebra, and they explicitly arise as tensor products:
There is a well-known topological coproduct of \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\), which preserves the subalgebras (1.4) and (1.5), and extends the (almost) cocommutative coproduct on the “vertical” subalgebra:
The main goal of this paper is to define another decomposition into subalgebras:
(see Corollary 3.29). We will explicitly construct the tensor factors of (1.7) as:
where the “horizontal” subalgebra:
will be the quantum group in the RTT presentation ( [7]). Moreover, we endow \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\) with a new topological coproduct which preserves the subalgebras (1.8), (1.9), and extends the usual (Drinfeld–Jimbo) coproduct on \({U_q({\dot{{\mathfrak {gl}}}}_n)}\subset {U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\).
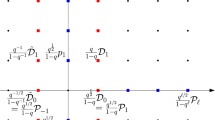
1.3. To represent the aforementioned decompositions pictorially, we will recall that the quantum toroidal algebra is graded by \({{{{\mathbb {Z}}}}^n}\times {{\mathbb {Z}}}\), where \({{{{\mathbb {Z}}}}^n}\) is the root lattice of \({U_q({\dot{{\mathfrak {sl}}}}_n)}\) and \({{\mathbb {Z}}}\) is the affinization direction. Then the following picture indicates the various subalgebras of \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\), by displaying which degrees they live in:
In the particular case \(n=1\), the quantum toroidal algebra is isomorphic to the well-known Ding–Iohara–Miki algebra [4, 11] a.k.a. the elliptic Hall [2, 17] algebra, on which the universal cover of \(SL_2({{\mathbb {Z}}})\) acts by automorphisms. With respect to this action, the decomposition (1.7) is obtained from the decomposition (1.3) by applying the automorphism corresponding to rotation by 90 degrees. However, in the general n case, the algebras featuring in the two decompositions are not isomorphic to each other, which is sensible given the fact that the grading axes \({{{{\mathbb {Z}}}}^n}\) and \({{\mathbb {Z}}}\) are quite different (Fig. 1).
1.4. To describe \({U_{q,{{\overline{q}}}}^\rightarrow (\ddot{{\mathfrak {gl}}}_n)}\) of (1.4), let us consider the vector space:
of rational functions which satisfy the wheel conditions (as in [8, 10]): namely that such rational functions have at most simple poles at \(z_{ia} q^2 - z_{i+1,b}\) (for all i, a, b) and that the residue at such a pole is divisible by \(z_{i a'} - z_{i+1,b}\) and \(z_{ia} - z_{i+1,b'}\) for all \(a' \ne a\) and \(b' \ne b\). The vector space (1.11) is called a shuffle algebra, akin to the classical construction of Feigin and Odesskii concerning certain elliptic algebras ( [10]). Explicitly, the product on (1.11) is constructed using the rational function (3.40), see Definition 3.16. An algebra homomorphism was constructed in [6]:
and it was shown to be an isomorphism in [14]. Similarly, \({U_{q,{{\overline{q}}}}^\leftarrow (\ddot{{\mathfrak {gl}}}_n)}\cong {{\mathcal {S}}}^-:= ({{\mathcal {S}}}^+)^\text {op}\).
To describe the subalgebras \(U^\uparrow _{q,{\bar{q}}}(\ddot{{\mathfrak {gl}}}_n)\) and \(U^\downarrow _{q,{\bar{q}}}(\ddot{{\mathfrak {gl}}}_n)\) of (1.8)–(1.9), we will introduce a new kind of shuffle algebra (let V be an n-dimensional vector space):
and the algebra structure on the RHS is constructed using the R-matrix (4.1), see Propositions 4.5 and 4.6. By definition, the subspace (1.12) precisely consists of \(\text {End}(V^{\otimes k})\)-valued rational functions which have at most simple poles at \(z_a {{\overline{q}}}^2 - z_b\) (for all a, b) and whose residue at such a pole satisfies the conditions outlined in Definition 4.8. The subalgebra \({{\mathcal {A}}}^{-}\) is defined similarly, but with \({{\overline{q}}}^{-1} q^{-n}\) instead of \({{\overline{q}}}\).
Theorem 1.5
There exist injective algebra homomorphisms:
Denoting the images of these maps by \(U^\uparrow _{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)\) and \(U^\downarrow _{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)\) yields the decompositions featuring in (1.7), (1.8), (1.9). Moreover, there exist topological coproducts on the subalgebras:
which extend the Drinfeld–Jimbo coproduct on the horizontal subalgebra (1.10), and realize \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\) as the Drinfeld double of its subalgebras (1.13) and (1.14).
We emphasize the fact that \({U_{q,{{\overline{q}}}}^\uparrow (\ddot{{\mathfrak {gl}}}_n)}\) is not the same as the “vertical subalgebra” that was studied in [9] and numerous other works. The latter construction has to do with \({U_q({\dot{{\mathfrak {sl}}}}_n)}\) presented as the affinization of \(U_q({\mathfrak {sl}}_n)\) and thus implicitly breaks the symmetry among the vertices of the cyclic quiver. Meanwhile, our construction takes the “horizontal subalgebra” \({U_q({\dot{{\mathfrak {gl}}}}_n)}\) and its evaluation representation \(V = {{\mathbb {C}}}^n(z)\) as an input, and outputs half of the quantum toroidal algebra.
More generally, starting from a quantum group \(U_q({{\mathfrak {g}}})\) and a representation V endowed with a unitary R-matrix, one may ask if the double shuffle algebra:
(defined as in Sect. 2) is related to the quantum group \(U_q({\dot{{{\mathfrak {g}}}}})\). Theorem 1.5 deals with the case \({{\mathfrak {g}}}= {\dot{{\mathfrak {gl}}}}_n\) and \(V = {{\mathbb {C}}}^n(z)\). If something along these lines is true in affine types other than A, we venture to speculate that the algebra (1.15) might be related to the extended Yangians of [18], appropriately q-deformed and doubled.
1.6. The structure of the present paper is the following:
-
In Sect. 2, we construct a shuffle algebra \({{\mathcal {A}}}^+\) starting from a vector space V and a unitary R-matrix \(\in \text {End}(V^{\otimes 2})\) (see also [12]). By adding certain elements, we construct the extended shuffle algebra \({\widetilde{{{\mathcal {A}}}}}^+\), which admits a coproduct. From two such extended shuffle algebras, we construct their Drinfeld double \({{\mathcal {A}}}\).
-
In Sect. 3, we recall the quantum group \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\) and its PBW presentation from [15]. This will allow us to construct the decomposition (1.7) as algebras.
-
In Sect. 4, we construct a version of the shuffle algebra of Sect. 2 that corresponds to the R-matrix with spectral parameter (4.1), thus yielding (1.12).
-
In Sect. 5, we construct the extended version of the shuffle algebra of Sect. 4, endow it with a topological coproduct, and construct a PBW basis of it.
-
In Sect. 6, we construct a bialgebra pairing between two copies of the extended shuffle algebras of Sect. 5. The corresponding Drinfeld double will precisely match \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\), thus completing the proof of Theorem 1.5.
I would like to thank Pavel Etingof, Sachin Gautam, Victor Kac, Andrei Okounkov, and Alexander Tsymbaliuk for many valuable conversations, and all their help along the years. I gratefully acknowledge the NSF grants DMS–1600375, DMS–1760264 and DMS–1845034, as well as support from the Alfred P. Sloan Foundation.
1.7. Given a finite-dimensional vector space V, we will often write elements \(X \in \text {End}(V^{\otimes k})\) as \(X_{1...k}\) in order to point out the set of indices of X. If \(V = {{\mathbb {C}}}^n\), then:
for certain coefficients, where \(E_{ij} \in \text {End}(V)\) denotes the matrix with entry 1 on row i and column j, and 0 everywhere else. For any permutation \(\sigma \in S(k)\), we write:
where \(\sigma \curvearrowright V^{\otimes k}\) by permuting the factors (therefore, the effect of conjugating (1.16) by \(\sigma \) is to replace the indices \(i_1,\ldots ,j_k\) by \(i_{\sigma (1)},\ldots ,j_{\sigma (k)}\)). Moreover, we will write:
if we wish to set apart the first i tensor factors from the last \(k-i\) tensor factors of X. There is an implicit summation in the right-hand side of (1.18) which we will not write down, much alike Sweedler notation. For any \(a \in {{\mathbb {N}}}\), we will write:
(the number \(k \ge a\) will always be clear from context). More generally, for any \(X \in \text {End}(V^{\otimes k})\) and any collection of distinct natural numbers \(a_1,\ldots ,a_k\), write:
(the number \(N \ge a_1,\ldots ,a_k\) will always be clear from context) for the image of X under the map \(\text {End}(V^{\otimes k}) \rightarrow \text {End}(V^{\otimes N})\) that sends the i-th factor of the domain to the \(a_i\)-th factor of the codomain, and maps to the unit in all factors \(\ne \{a_1,\ldots ,a_k\}\).
2 Shuffle algebras and R-matrices
2.1. The main goal of the present section is to study shuffle algebras associated to the data contained in the four bullets below:
-
a vector space V, assumed finite-dimensional for simplicity
-
an element (R-matrix) \(R \in \text {Aut}(V^{\otimes 2})\) satisfying the Yang–Baxter equation:
$$\begin{aligned} R_{12} R_{13} R_{23} = R_{23} R_{13} R_{12} \end{aligned}$$(2.1) -
an element \({\widetilde{R}}\in \text {Aut}(V^{\otimes 2})\) satisfying:
$$\begin{aligned} {\widetilde{R}}_{21} {\widetilde{R}}_{31} R_{23} = R_{23} {\widetilde{R}}_{31} {\widetilde{R}}_{21} \end{aligned}$$(2.2)$$\begin{aligned} R_{12} {\widetilde{R}}_{31} {\widetilde{R}}_{32} = {\widetilde{R}}_{32} {\widetilde{R}}_{31} R_{12} \end{aligned}$$(2.3) -
a scalar f so that:
$$\begin{aligned} R_{12} R_{21} = f \cdot \text {Id}_{V \otimes V} = R_{21} R_{12} \end{aligned}$$(2.4)
The present section will be concerned with developing a certain algebraic framework in the generality above, while Sect. 4 will deal with the particular case of:
and \({\widetilde{R}}(x) = R_{21}\left( x^{-1} {{\overline{q}}}^{-2} \right) \), for a parameter \({{\overline{q}}}\). Many Propositions in the current section have counterparts in Sect. 4, and we will only prove such statements once.
2.2. We will represent the tensor product \(V^{\otimes k}\) as k labeled dots on a vertical line, and certain elements of \(\text {End}(V^{\otimes k})\) will be represented as braids between two such collections of k labeled dots situated on parallel vertical lines (the labels will not change along strands, so they will be represented pictorially as colors). Specifically, the crossings below represent either the automorphisms R or \({\widetilde{R}}\), with indices given by the labels of the strands (which are inherited from the labels of their endpoints) (Fig. 2).
The strands are represented either as straight or squiggly lines, because we wish to indicate whether the picture in question refers to either R or \({\widetilde{R}}\). Compositions are always read left-to-right, for example the following equivalence of isotopy classes of braids underlies the Yang–Baxter relation (2.1).
We will equivalate braids connected by the Reidemeister III type moves above.
2.3. The following construction (when \({\widetilde{R}}_{12} = R_{21}\)) bears similarities with that of Sect. 5.2 of [12], itself a dual version of the construction of [7]. We will then construct an extended shuffle algebra which admits a coproduct and bialgebra pairing, and then define the corresponding Drinfeld double.
Proposition 2.4
For \(V, R, {\widetilde{R}}\) as in Sect. 2.1, the assignment:
Footnote 1 yields an associative algebra structure on the vector space (Figs. 3, 4, 5):
with unit \(1 \in \text {End} (V^{\otimes 0})\). We will call (2.6) the “shuffle product”.
We note that the second line of (2.6) can be represented by the braid in Fig. 6, depicted here for \(k=2\), \(l=2\) and \((a_1,a_2) = (1,3)\), \((b_1,b_2) = (2,4)\).
The following equivalences underlie equations (2.2) and (2.3), respectively:
Proof
The associativity of multiplication (2.6) is pictorially summarized by the equivalence of the braids in Figs. 7 and 8. Indeed, in Fig. 7, one can pull the straight red strands to the left of the blue-green crossings, the squiggly red strands below the blue-green crossings, and the straight green strands above the red-blue crossings. This procedure is simply a succession of the Reidemeister III moves of Figs. 3,4 and 5, which in the end produces the braid in Fig. 8. \(\square \)
2.5. A tensor \(X \in \text {End}(V^{\otimes k})\) is called symmetric if for all permutations \(\sigma \in S(k)\):
where \(\sigma X \sigma ^{-1}\) is defined in (1.17), and \(R_\sigma \in \text {End}(V^{\otimes k})\) is any braid lift of \(\sigma \) (i.e. any braid connecting the i-th endpoint on the right with the \(\sigma (i)\)-th endpoint on the left). Choosing one braid lift of \(\sigma \) over another is just the ambiguity of choosing \(R_{ab}\) over \(R_{ba}^{-1}\) for any crossing between the strands labeled a and b. Since (2.4) says that these two endomorphisms differ by a scalar, the ambiguity does not affect (2.8).
Pictorially, the right-hand side of (2.8) is represented by the following braid (Fig. 9):
The symmetrization of any tensor \(X \in \text {End}(V^{\otimes k})\) is defined as:
It is easy to see that the symmetrization of an abitrary tensor is symmetric.
Proposition 2.6
The shuffle product of Proposition 2.4 preserves the vector space:
consisting of symmetric tensors. We will call \({{\mathcal {A}}}^+\) the shuffle algebra.
Proof
Let \(A_{1...k} \in \text {End}(V^{\otimes k})\) and \(B_{1...l} \in \text {End}(V^{\otimes l})\) be any symmetric tensors. A permutation \(\mu \in S(k+l)\) is called a (k, l)-shuffle if:
Because of the diagram (depicted for \(k=2\), \(l=2\), \((a_1,a_2) = (1,3)\), \((b_1,b_2) = (2,4)\)):
it is easy to see that the definition (2.6) can be restated as:
where:
For any \(\tau \in S(k) \times S(l)\) standardly embedded in \(S(k+l)\), we have:
which can be seen from the fact that the braid below:
is equivalent to \(\Phi \) (since we can cancel the braids representing \(R_\tau \) and \(R_\tau ^{-1}\) by pulling them through the symmetric tensors A and B). Then (2.12) implies:
Since any \(\sigma \in S(k+l)\) can be written uniquely as \(\mu \circ \tau \), where \(\mu \) is a (k, l)-shuffle and \(\tau \in S(k) \times S(l) \subset S(k+l)\), the formula above yields:
(we have used the fact that \(R_{\mu \tau } = R_\mu \cdot \mu R_\tau \mu ^{-1}\), times a product of scalars (2.4)). Since the symmetrization of any tensor is symmetric, this concludes the proof (Figs. 10, 11, 12, 13). \(\square \)
By analogy with formula (2.14), one has the following:
where \(\Psi = A_{l+1...l+k} \Big [{\widetilde{R}}_{l+1,l}... {\widetilde{R}}_{l+k,1} \Big ] B_{1...l} \Big [R_{l+k,1}... R_{l+1,l} \Big ]\). The proof is analogous.
2.7. Let us fix a basis \(v_1,\ldots ,v_n\) of V and write \(E_{ij}\) for the matrix unit with a single 1 at the intersection of row i and column j, and 0 elsewhere.
Definition 2.8
Consider the extended shuffle algebra:
In order to concisely state the relations, we encode the new generators \(s_{ij}\), \(t_{ij}\) into:
and the required relations take the form:
as well as:
\(\forall X_{1...k} \in \text {End} (V^{\otimes k}) \subset {{\mathcal {A}}}^+\). The latter two formulas should be interpreted as identities in \({\widetilde{{{\mathcal {A}}}}}^+ \otimes \text {End} (V)\), where the latter copy of V is the one represented by index 0.Footnote 2
Proposition 2.9
The following assignments make \({\widetilde{{{\mathcal {A}}}}}^+\) into a bialgebra:
while for all \(X = X_{1...k} \in \text {End} (V^{\otimes k}) \subset {{\mathcal {A}}}^+ \subset {\widetilde{{{\mathcal {A}}}}}^+\) for \(k \ge 1\), we set \(\varepsilon (X) = 0\) and:
where the notation \(X_{1...k} = X_{1...i} \otimes X_{i+1...k}\) is explained in (1.18).
Proof
The facts that the counit extends to an algebra homomorphism, and that it interacts appropriately with the coproduct, are easy to see. In order to show that the coproduct extends to an algebra homomorphism:
we must show that (2.21), (2.22), (2.23) respect relations (2.16)–(2.20), as well as formula (2.6) for the shuffle product. To this end, note that:
An analogous argument shows that \(\Delta (T_1 T_2 R) = \Delta (R T_2 T_1)\). As for (2.18):
Let us now apply the coproduct to the left-hand side of (2.19):
The last line above equals \(\Delta \)(RHS of (2.19)), so we are done. The computation showing that \(\Delta \) respects relation (2.20) is analogous, and therefore left to the interested reader. As for the shuffle product itself, we must show that \(\Delta (A_{1...k} * B_{1...l}) = \Delta (A_{1...k}) * \Delta (B_{1...l})\). Applying formulas (2.6) and (2.23) implies:
In the next-to-last row of the expression above, we may apply (2.18) in order to move the T’s to the right and the S’s to the left. Afterwards, we apply (2.19) and (2.20) to move the S’s to the left of \(A_{a_1...a_d}\) and the T’s to the right of \(B_{b_1...b_e}\):
Finally, we may use (2.16) and (2.17) to move the outermost products of \(R_{a_ib_j}\) past the S’s and the T’s, at the cost of re-ordering the latter:
The right-hand side is simply \(\Delta \) applied to the RHS of (2.6), as we needed to prove. \(\square \)
2.10. Let us consider two copies of the extended shuffle algebra, denoted \({\widetilde{{{\mathcal {A}}}}}^+\), \({\widetilde{{{\mathcal {A}}}}}^-\), defined as in the previous subsections with respect to the same R, but with:
where \(\text {End}(V^{\otimes k}) {\mathop {\rightarrow }\limits ^{\dagger _{s}}}\text {End}(V^{\otimes k})\) denotes the transposition of the s-tensor factor:
It is an elementary exercise to show that if properties (2.2)–(2.3) hold for \({\widetilde{R}}^+ = {\widetilde{R}}\), then they also hold for \({\widetilde{R}}^-\) given by formula (2.25). We will now define a pairing:
which respects the bialgebra structure in the following sense:
We will henceforth write \(X^\pm \) for the copy of an arbitrary \(X \in \text {End}(V^{\otimes k})\) in \({\widetilde{{{\mathcal {A}}}}}^\pm \). The analogous notation will apply to \(S^\pm , T^\pm \in {\widetilde{{{\mathcal {A}}}}}^\pm \otimes \text {End}(V)\).
Proposition 2.11
The assignments:
and for all \(X,Y \in \text {End} (V^{\otimes k})\):
(the pairings between \(X^+\), \(Y^-\) on one side and \(S^+, T^+, S^-, T^-\) on the other side are defined to be 0) generate a bialgebra pairing (2.27) satisfying (2.28)–(2.29).
Proof
The data provided are sufficient to completely define the pairing, in virtue of (2.28) and (2.29). The thing that we need to check is that the defining relations of the extended shuffle algebras, namely (2.16)–(2.20) and the definition of the shuffle product in (2.6), are preserved by the pairing. For (2.16), we have:
and:
We leave the analogous formulas when (2.16) is replaced by (2.17), or when the roles of the two arguments of the pairing are switched, as exercises to the reader. As for (2.18), we have:
The analogous formulas when \(S_3^-\) is replaced by \(T_3^-\), or when the roles of the arguments of the pairing are switched, are left as exercises to the interested reader. To prove that (2.19) pairs correctly with elements of \({{\mathcal {A}}}^-\), note that (2.23) implies:
where “other terms” stands for summands in which \(Y_{1...k}^-\) has a non-zero number of indices on either side of the \(\otimes \) sign. Then we claim that:
where \(\text {Tr}_{V^{\otimes k}}\) denotes trace with respect to the indices \(1,\ldots ,k\) only (therefore the expression above is valued in \(\text {End}(V)\), corresponding to the index 0). The equality between the two rows of (2.33) is proved as follows: because both sides are bilinear in the tensors \(X_{1...k}\) and \(Y_{1...k}\), it suffices to prove that they are equal for:
for arbitrary \(i_a,j_a,i_a',j_a' \in \{1,\ldots ,n\}\). In this case, the equality between the two rows of (2.33) is a straightforward exercise, which is performed by expanding \(S_a^\pm \) and \(T_a^\pm \) in terms of the elementary matrices \(E_{ij}\), and using (2.29), (2.30), (2.31). Similarly, because \(\varepsilon (S^+_0) = \text {Id}\), one sees that:
We conclude that relation (2.19) is preserved by the pairing. The proof that (2.20) is preserved by the pairing is analogous, and left as an exercise to the reader.
Before proving that the pairing (2.32) intertwines the shuffle product with the coproduct, let us show that the trace pairing is symmetric, in the sense that:
for all symmetric tensors \(X,Y \in \text {End}(V^{\otimes k})\) and all tensors \(A,B \in \text {End}(V^{\otimes k})\). Indeed, (2.34) follows from the fact that \(\forall \sigma \in S(k)\), we have:
where the latter equality is the conjugation invariance of trace. Property (2.35) is proved likewise. As a consequence of (2.15) and (2.34), proving formula (2.28) for \(a = A^+\), \(b = B^+\) and \(c = Y^-\) boils down to the following equality:
which we will now prove. We have:
where the phrase “other terms” denotes summands whose second tensor factor has a non-zero number of indices on either side of the \(\otimes \) sign. Because of this, formula (2.29) when one of b and c is either \(S^-\) or \(T^-\) (which we have already checked yields a consistent bialgebra pairing) implies that:
Therefore, the RHS of (2.36) is precisely equal to the LHS of (2.36), as required. Similarly, proving (2.29) for \(a = X^+\), \(b = A^-\), \(c = B^-\) boils down to the equality:
The equality (2.37) is proved by analogy with (2.36), so we skip the details. \(\square \)
2.12. Proposition 2.11 allows us to define the Drinfeld double:
such that \({\widetilde{{{\mathcal {A}}}}}^+ \cong {\widetilde{{{\mathcal {A}}}}}^+ \otimes 1\) and \({\widetilde{{{\mathcal {A}}}}}^{-, \text {op},{\text {coop}}} \cong 1 \otimes {\widetilde{{{\mathcal {A}}}}}^{-, \text {op}, {\text {coop}}}\) are sub-bialgebras of \({{\mathcal {A}}}\) (“op” and “coop” denote the opposite algebra and coalgebra structure, respectively), and the commutation of elements coming from the two factors is governed by:
for all \(a \in {\widetilde{{{\mathcal {A}}}}}^+\) and \(b \in {\widetilde{{{\mathcal {A}}}}}^{-, \text {op},{\text {coop}}}\). Let us now spell out formula (2.39) when a and b are among the generators of the double algebra (2.38). The quadratic relations (2.16)–(2.20) hold as stated between the \(+\) generators, and hold with the opposite multiplication between the − generators. As for the relations that involve one of the \(+\) generators and one of the − generators, we have:
Proposition 2.13
We have the following formulas in \({{\mathcal {A}}}\):
as well as:
where \(\cdot _+ = \cdot \) and \(\cdot _- = \cdot ^{\text {op} }\) (the opposite multiplication in \({{\mathcal {A}}}\)). Finally, we have:
\(\forall \ i,j,i',j' \in \{1,\ldots ,n\}\), where \(E_{ij}^\pm \) are elements in the \(k=1\) summand of (2.7).
Proof
Let us now prove the first formula in (2.40) and leave the second one and (2.41) as exercises for the reader. Since:
formula (2.39) for \(a = S_2^+\) and \(b = S_1^-\) implies:
Using (2.30) to evaluate the pairing implies precisely the first formula in (2.40).
Let us now prove (2.42) and leave the analogous formula (2.43) as an exercise. We will do so in the case \(\pm = +\), as \(\pm = -\) just involves the opposite of all relations.
where “other terms” stands for terms which have a non-zero number of indices on either side of the \(\otimes \) sign, so they pair trivially with \(S^-\). Meanwhile, \(\Delta (S^-)\) is given by (2.46). Applying (2.39) for \(a = X_{1...k}^+\) and \(b_0 = S^-\) yields:
Formulas (2.28), (2.30) and (2.31) transform the formula above precisely into (2.42).
As for (2.44), consider relation (2.23) for \(k=1\) and \(X = E^+_{ij}\):
as well as the \((\text {op},{\text {coop}})\) version of the above equality that holds in \({\widetilde{{{\mathcal {A}}}}}^{-,\text {op},{\text {coop}}}\):
Then (2.44) follows from (2.39) for \(a = E_{ij}^+\) and \(b = E_{i'j'}^-\). \(\square \)
3 Quantum toroidal \({\mathfrak {gl}}_n\)
In the present section, we will define quantum affine and toroidal \({\mathfrak {gl}}_n\), and recall (in Sects. 3.12–3.30) a generators-and-relations presentation for the latter, which will play a big role in the subsequent sections. As for quantum affine \({\mathfrak {gl}}_n\), we recall its Drinfeld–Jimbo presentation in Sects. 3.2–3.3, and its RTT presentation in Sects. 3.31–3.35. We also note that Sects. 3.5–3.11 serve as a bridge between the Drinfeld–Jimbo and RTT presentations; the reader who is familiar with our notation and conventions may skip this bridge, but otherwise it will serve as useful motivation for the subsections that follow.
3.1. Fix \(n>1\), and let us start with a few notational remarks. The symbol \(\delta \) will refer to several different notions throughout the present paper. Specifically, the main usage of \(\delta \) is the following “mod n” variant of the Kronecker symbol:
We will write \(\delta _{j \text { mod }g}^i\) if we need the notion above for congruences modulo another number g instead of n. Moreover, if \(i,j,i',j' \in {{\mathbb {Z}}}\), we will write:
The ordinary Kronecker symbol will be denoted by \({\tilde{\delta }}_j^i\), and it takes the value 1 if and only if \(i = j\) as integers, and 0 otherwise. Finally, we will use the notation:
for the formal \(\delta \) series. Since the various uses of \(\delta \) will arise in different contexts, we hope this abuse of notation will not cause confusion.
3.2. Let \({\dot{{\mathfrak {sl}}}}_n\) be the Kac-Moody Lie algebra of type \({\widehat{A}}_{n-1}\). The corresponding Drinfeld–Jimbo quantum groupFootnote 3 is defined to be the associative algebra:
modulo the fact that c is central, as well as the following relations for all \(i,j \in {{\mathbb {Z}}}/n{{\mathbb {Z}}}\) and \(s,s' \in \{1,\ldots ,n\}\) (by setting \(\psi _{s+n} = c\psi _s\), we extend the notation \(\psi _s\) to all \(s \in {{\mathbb {Z}}}\)):
(note that relation (3.6) must be amended in the case \(n=2\), but we will not need the modification in question). We also consider the q-deformed Heisenberg algebra:
where c is central, and the \(p_{\pm k}\) satisfy the commutation relation:
Then we will consider the algebra:
which serves as an affine q-version of the Lie algebra isomorphism \({\mathfrak {gl}}_n \cong {\mathfrak {sl}}_n \oplus {\mathfrak {gl}}_1\).
3.3. We can make \({U_q({\dot{{\mathfrak {gl}}}}_n)}\) into a bialgebra by using the counit \(\varepsilon (c) = 1\), \(\varepsilon (\psi _s) = 1\), \(\varepsilon (x_i^\pm ) = 0\), \(\varepsilon (p_k) = 0\) and the coproduct given by \(\Delta (c) = c \otimes c\) and:
Moreover, the sub-bialgebras:
are endowed with a bialgebra pairing:
generated by properties (2.28), (2.29) and:
and all other parings between generators are 0. It is well-known that \({U_q({\dot{{\mathfrak {gl}}}}_n)}\) is the Drinfeld double corresponding to the data (3.18) (modulo the identification of the symbols \(\psi _s,c\) in the two factors of (3.18)). The algebra \({U_q({\dot{{\mathfrak {gl}}}}_n)}\) is \({{{{\mathbb {Z}}}}^n}\)-graded:
where \({\varvec{\varsigma }}^i = \underbrace{(0,\ldots ,0,1,0,\ldots ,0)}_{\text {1 on }i\text {--th position}}\) and \({\varvec{\delta }}= (1,\ldots ,1)\).
Remark 3.4
The elements \(x_i^\pm \) of \({U_q({\dot{{\mathfrak {gl}}}}_n)}\) are called simple (root) generators, while the elements \(p_{\pm k}\) are called imaginary (root) generators. Up to constant multiples, these are all the primitive elements of \({U_q({\dot{{\mathfrak {gl}}}}_n)}\) (see Definition 3.8).
3.5. We will now give a different incarnation of the bialgebra (3.10), which is obtained by combining the results of [3] and [5]. We will use the notation of [14].
Definition 3.6
Consider the algebra:
where c is central, and the quadratic relations (3.98)–(3.97) will be explained later.
The algebra \({{\mathcal {E}}}\) is a bialgebra with respect to the counit \(\varepsilon (\psi _s) = \varepsilon (c) = 1, \forall s\) and \(\varepsilon (f_{\pm [i;j)}) = 0, \forall i<j\), as well as the coproduct \(\Delta (c) = c \otimes c\) and:
where the notation \(\psi _s\) is extended to all \(s \in {{\mathbb {Z}}}\) by \(\psi _{s+n} = c\psi _s\). The sub-bialgebras:
are endowed with a bialgebra pairing:
generated by properties (2.28), (2.29) and:
where the right-most delta symbol is defined in (3.2). With respect to the pairing (3.25), the algebra \({{\mathcal {E}}}\) is isomorphic to the Drinfeld double \({{\mathcal {E}}}^{\ge } \otimes {{\mathcal {E}}}^{\le }\) modulo the identification of \(\psi _s, c\) in the two tensor factors. The algebra \({{\mathcal {E}}}\) is \({{{{\mathbb {Z}}}}^n}\)-graded:
where \([i;j) = {\varvec{\varsigma }}^i + \cdots + {\varvec{\varsigma }}^{j-1} \in {{{{\mathbb {N}}}}}^n\) (we write \({\varvec{\varsigma }}^k = {\varvec{\varsigma }}^{k \text { mod }n}\)).
3.7. The subalgebras:
are graded by \(\pm {{{{\mathbb {N}}}}}^n\), and we will write \({{\mathcal {E}}}_{\pm {{\textbf{d}}}}\) for their graded pieces, for all \({{\textbf{d}}}\in {{{{\mathbb {N}}}}}^n\). The dimensions of these graded pieces are given by the following formula:
In fact, ordered products of the various \(f_{\pm [i;j)}\) give rise to a PBW basis of \({{\mathcal {E}}}^\pm \) ( [14]).
Definition 3.8
An element \(x \in {{\mathcal {E}}}_{\pm {{\textbf{d}}}}\) is called primitive if:
It is easy to see that any sum of primitive elements is primitive. With this in mind, we will write \({{\mathcal {E}}}_{\pm {{\textbf{d}}}}^{\text {prim} } \subset {{\mathcal {E}}}_{\pm {{\textbf{d}}}}\) for the vector subspace of primitive elements.
As shown in [15, Lemma 2.3], we have:
for various \(i \in {{\mathbb {Z}}}/n{{\mathbb {Z}}}\) and \(k \in {{\mathbb {N}}}\). Therefore, up to scalar multiples, there is a unique choice of primitive elements:
which will be called simple and imaginary (respectively) primitive generators of \({{\mathcal {E}}}\). Comparing this with Remark 3.4 yields the following:
Theorem 3.9
[14] Any choice of simple and imaginary primitive elements (3.29) of \({{\mathcal {E}}}\) gives rise to an isomorphism of \({{{{\mathbb {Z}}}}^n}\)-graded bialgebras \({U_q({\dot{{\mathfrak {gl}}}}_n)}\cong {{\mathcal {E}}}\).
3.10. As is clear from the Theorem above, understanding the bialgebra structure of \({{\mathcal {E}}}\) boils down to controlling the up-to-scalar ambiguity in choosing the primitive elements. To do this, we consider a formal parameter \({{\overline{q}}}\) and define linear functionals:
for all \((i < j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\), satisfying the following properties:
and (let \({{\overline{q}}}_+ = {{\overline{q}}}\) and \({{\overline{q}}}_- = (q^n {{\overline{q}}})^{-1}\)):
We henceforth fix the elements (3.29) by making the choice of [15], namely:
\(\forall k > 0\), \(i,s \in {{\mathbb {Z}}}/n{{\mathbb {Z}}}\). The fact that the right-hand side of (3.34) does not depend on s is a consequence of the \({{\mathbb {Z}}}/n{{\mathbb {Z}}}\)-invariance of the elements \(p_{\pm k}\), see [14].
3.11. It is easy to note that the bialgebra \({U_q({\dot{{\mathfrak {gl}}}}_n)}\cong {{\mathcal {E}}}\) possesses an antipodeFootnote 4
In terms of the generators \(f_{\pm [i;j)}\), we may write:
where the elements \({\bar{f}}_{\pm [i;j)}\) are inductively defined in terms of \(f_{\pm [i;j)}\) by the formulas:
Alternatively, the elements \({\bar{f}}_{\pm [i;j)}\) are completely determined by their coproduct:
and by their values under the linear maps (3.30):
Since \({{\mathcal {E}}}\cong {U_q({\dot{{\mathfrak {gl}}}}_n)}\), we will use the notation \(f_{\pm [i;j)}\) (respectively \({\bar{f}}_{\pm [i;j)}\)) for the elements of either algebra. These elements will be called root generators of either algebra \({{\mathcal {E}}}\cong {U_q({\dot{{\mathfrak {gl}}}}_n)}\), because [i; j) are positive roots of the affine \(A_n\) root system.
3.12. Affinizations of quantum groups are defined by replacing each generator \(x_i^\pm \) as in Sect. 3.2 by an infinite family of generators \(\{x_{i,k}^\pm \}_{k \in {{\mathbb {Z}}}}\). To define affinizations explicitly, let us consider variables z as being colored by an integer i, denoted by “\(\text {col }z\)”. Then we may define the following color-dependent rational function:
for any variables z, w of colors i and j respectively.
Definition 3.13
The quantum toroidal algebra is:
In order to spell out the defining relations in the quantum toroidal algebra, let us consider the series \(x_i^\pm (z) = \sum _{k \in {{\mathbb {Z}}}} \frac{x_{i,k}^\pm }{z^k}\) and \(\varphi _s^\pm (w) = \frac{\psi _{s+1}^{\pm 1}}{\psi _s^{\pm 1}} + \sum _{k=1}^\infty \frac{\varphi _{s,k}^\pm }{w^{\pm k}}\), and set:
and, for \(j \in \{i-1,i+1\}\):
for all choices of \(\pm , \pm ', i, j\), where the variables z and w have color i and j, respectively, for the purpose of defining the rational function \(\zeta \) (when \(n=2\), one needs to modify (3.47) similarly to how one needs to modify (3.6)). Note that we extend the index i to arbitrary integers, by applying the convention:
We consider the subalgebras \({U_{q,{{\overline{q}}}}^\pm (\ddot{{\mathfrak {gl}}}_n)}\subset {U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\) generated by \(\{x^\pm _{i,k}\}^{i \in {{\mathbb {Z}}}/n{{\mathbb {Z}}}}_{k \in {{\mathbb {Z}}}}\).
Remark 3.14
In the notation of Sect. 1.2, we have \({U_{q,{{\overline{q}}}}^+(\ddot{{\mathfrak {gl}}}_n)}= {U_{q,{{\overline{q}}}}^\rightarrow (\ddot{{\mathfrak {gl}}}_n)}\) and \({U_{q,{{\overline{q}}}}^-(\ddot{{\mathfrak {gl}}}_n)}= {U_{q,{{\overline{q}}}}^\leftarrow (\ddot{{\mathfrak {gl}}}_n)}\), but we will henceforth use the ± notation.
3.15. Let us now recall the classic shuffle algebra realization of \({U_{q,{{\overline{q}}}}^\pm (\ddot{{\mathfrak {gl}}}_n)}\). Consider variables \(z_{ia}\) of color i, for various \(i \in \{1,\ldots ,n\}\) and \(a \in {{\mathbb {N}}}\). We call a function \(R(z_{11}...,z_{1d_1},\ldots ,z_{n1}...,z_{nd_n})\) color-symmetric if it is symmetric in \(z_{i1},\ldots ,z_{id_i}\) for all \(i \in \{1,\ldots ,n\}\) separately. Depending on the context, the symbol “Sym” will refer to either color-symmetric functions in variables \(z_{ia}\), or to the symmetrization operator:
Let \({{\textbf{d}}}! = d_1!...d_n!\). The following construction arose in the context of quantum groups in [6], by analogy to the work of Feigin-Odesskii on certain elliptic algebras.
Definition 3.16
Consider the vector space:
and endow it with an associative algebra structure, by setting \(R*R'\) equal to:
Let \({{\mathcal {S}}}^+\) the subalgebra of \({{\mathcal {V}}}\) generated by \(\{ z_{i1}^k \}^{1\le i \le n}_{k \in {{\mathbb {Z}}}}\) and we let \({{\mathcal {S}}}^- = \left( {{\mathcal {S}}}^+ \right) ^\text {op} \).
The algebras \({{\mathcal {S}}}^\pm \) are graded by \(\pm {{{{\mathbb {N}}}}}^n\times {{\mathbb {Z}}}\), where \(\deg R(...,z_{i1},\ldots ,z_{id_i},...) = (\pm {{\textbf{d}}}, k)\) if \({{\textbf{d}}}= (d_1,..,d_n)\), while k denotes the homogeneous degree of R. We will write \({{\mathcal {S}}}_{\pm {{\textbf{d}}}}\) for the graded pieces of \({{\mathcal {S}}}^\pm \) with respect to the \(\pm {{{{\mathbb {N}}}}}^n\) direction only.
Theorem 3.17
[14] The subalgebras \({{\mathcal {S}}}^\pm \) coincide with the \({{\mathbb {Q}}}(q,{{\overline{q}}}^{\frac{1}{n}})\)-vector subspaces of \({{\mathcal {V}}}\) consisting of rational functions \(R(...,z_{ia},...)\) that satisfy:
where r is any Laurent polynomial which vanishes at the specializations:
for any \(i \in \{1,\ldots ,n\}\). This vanishing property is the natural analogue of the wheel conditions studied in [8, 10]. By convention, we set \(z_{n+1,a} = z_{1a} {{\overline{q}}}^{-2}\), \(z_{0a} = z_{na} {{\overline{q}}}^2\).
It is a well-known fact (see [6]) that \({{\mathcal {S}}}^\pm \cong {U_{q,{{\overline{q}}}}^\pm (\ddot{{\mathfrak {gl}}}_n)}\). In order to obtain the entire quantum toroidal algebra and not just its halves, define the double shuffle algebra:
where:
Therefore, there is a isomorphism:
given by sending \(\left( z_{i1}^k \right) ^\pm \leadsto x_{i,k}^\pm , \ \varphi _{i,k}^\pm \leadsto \varphi _{i,k}^\pm , \ \psi _s \leadsto \psi _s, c \leadsto c, {\bar{c}}\leadsto {\bar{c}}\).
3.18. Let us consider the following halves of \({{\mathcal {S}}}\):
For \({{\textbf{e}}}, {{\textbf{d}}}\in {{{{\mathbb {N}}}}}^n\), we will write \({{\textbf{e}}}\le {{\textbf{d}}}\) if \(e_i \le d_i\) for all \(i \in \{1,\dots ,n\}\). With this in mind, the algebras (3.51) and (3.52) are endowed with topological coproducts:
Remark 3.19
To think of (3.53) as a tensor, we expand the right-hand side in non-negative powers of \(z_{ia} / z_{i'a'}\) for \(a\le e_i\), \(e_{i'} < a'\), thus obtaining an infinite sum of monomials. In each of these monomials, we put the symbols \(\varphi ^+_{i,d}\) to the very left of the expression, then all powers of \(z_{ia}\) with \(a\le e_i\), then the \(\otimes \) sign, and finally all powers of \(z_{ia}\) with \(a>e_i\). The powers of the central element \({\bar{c}}_1 = {\bar{c}}\otimes 1\) are placed in the first tensor factor. The resulting expression will be a power series, and therefore lies in a completion of \({{\mathcal {S}}}^\ge \otimes {{\mathcal {S}}}^\ge \). The same argument applies to (3.54).
There exists a pairing between the halves \({{\mathcal {S}}}^\ge \) and \({{\mathcal {S}}}^\le \), given by:
for any \(R^+ \in {{\mathcal {S}}}_{{{\textbf{d}}}}\) and \(R^- \in {{\mathcal {S}}}_{-{{\textbf{d}}}}\) (we refer the reader to [14] or [15] for details).
3.20. In [14, 15], we constructed a PBW basis of \({{\mathcal {S}}}^\pm \cong {U_{q,{{\overline{q}}}}^\pm (\ddot{{\mathfrak {gl}}}_n)}\). More precisely we construct particular elements of \({{\mathcal {S}}}^\pm \) called “PBW generators”, indexed by a totally ordered set, and claim that a linear basis of \({{\mathcal {S}}}^\pm \) is given by ordered products of the PBW generators. In the case of the algebra \({{\mathcal {E}}}^\pm \cong {U_q^\pm ({\dot{{\mathfrak {gl}}}}_n)}\), we have already seen in Sect. 3.7 that the PBW generators of \({{\mathcal {E}}}^\pm \) are indexed by:
It should come as no surprise that the PBW generators of \({{\mathcal {S}}}^\pm \) are indexed by:
If we write \(\mu = \frac{j-i}{k}\), we will find it more useful to index the PBW generators by:
such that \(\frac{j-i}{\mu } \in {{\mathbb {Z}}}\). For any choice of \(i<j\) and \(\mu \) as above, we define:
In order to think of the RHS of (3.56) and (3.57) as shuffle elements, we relabel the variables \(z_i,\ldots ,z_{j-1}\) according to the following rule \(\forall a \in \{i,\ldots ,j-1\}\):
where \({\bar{a}}\) is the residue class of a in the set \(\{1,\ldots ,n\}\) (and the precise value of \(\bullet _a \in {{\mathbb {N}}}\) is immaterial due to the “Sym” in (3.56)–(3.57)). If \(\frac{j-i}{\mu } \notin {{\mathbb {Z}}}\), the LHS of (3.56) and (3.57) are defined to be 0. We will occasionally write:
where \(k = \frac{j-i}{\mu }\), in order to indicate the fact that \(\deg A_{\pm [i;j)}^{(\pm k)}, B_{\pm [i;j)}^{(\pm k)}= \pm ([i;j), k)\).
3.21. We will now define an algebra \({{\mathcal {D}}}\) that is isomorphic to \({{\mathcal {S}}}\cong {U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\), much like the algebra \({{\mathcal {E}}}\) was isomorphic to \({U_q({\dot{{\mathfrak {gl}}}}_n)}\) (see Theorem 3.9). The first step is to define an infinite family of the latter algebras. Specifically, for any coprime \((a,b) \in {{\mathbb {Z}}}\times {{\mathbb {N}}}\), define:
where \(g = \gcd (n,a)\). The root generators of (3.59) are parametrized by:
However, we choose to replace a triple (u, v, r) as above by:
and therefore we will use the following notation for the root generators of (3.59):
for any indices i, j, which are connected to u, v, r by (3.60). Note that we allow \(i>j\) in formula (3.60), via the convention:
Moreover, formula (3.60) implies that \(k:= (j-i) \frac{b}{a}\) is an integer, so we will write:
We make the convention that \(f_{[i;j)}^{(k)} = {\bar{f}}_{[i;j)}^{(k)} = 0\) if \(k = (j-i) \frac{b}{a} \notin {{\mathbb {Z}}}\).
3.22. For any \((i,j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) and \(k \in {{\mathbb {N}}}\), let us write \(\mu = \frac{j-i}{k}\). The assignment:
makes \({{\mathcal {E}}}_\mu \) into a \({{{{\mathbb {Z}}}}^n}\times {{\mathbb {Z}}}\) graded algebra. For all \({{\textbf{d}}}\in {{{{\mathbb {Z}}}}^n}\), we will write \({{\mathcal {E}}}_{\mu |{{\textbf{d}}}}\) for its degree \({{\textbf{d}}}\times {{\mathbb {Z}}}\) graded piece. Consider two invertible central elements \(c,{\bar{c}}\), and recall the Cartan elements \(\psi _1,\ldots ,\psi _n\) of \({{\mathcal {E}}}_\infty = {{\mathcal {E}}}\). As \(\mu \) ranges over \({{\mathbb {Q}}}\sqcup \infty \), we will identify the central elements of the algebras \({{\mathcal {E}}}_\mu \) according to the rule:
and identify the Cartan elements of the algebras \({{\mathcal {E}}}_\mu \) according to the rule:
where \(g = \gcd (n,a)\). Hence we have the following relation:
where \(\langle \cdot , \cdot \rangle \) is the bilinear form on \({{\mathbb {Z}}}^n\) determined by \(\langle {\varvec{\varsigma }}^i, {\varvec{\varsigma }}^j \rangle = \delta _{i}^{j} - \delta _{i}^{j+1}\).
We henceforth extend the scalars in \({{\mathcal {E}}}_\mu \) from \({{\mathbb {Q}}}(q)\) to \({{\mathbb {Q}}}(q,{{\overline{q}}}^{\frac{1}{n}})\). The following is an obvious consequence of the structure defined in Sects. 3.5–3.11.
Proposition 3.23
For any \(\mu \), the algebra \({{\mathcal {E}}}_\mu \) has a coproduct \(\Delta _\mu \), for whichFootnote 5:
Footnote 6\(\forall (i,j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) such that \(\frac{j-i}{\mu } \in {{\mathbb {N}}}\). For all such i, j, we have linear maps:
that satisfy property (3.31) and:
3.24. Let us consider the subalgebras \({{\mathcal {E}}}^\pm _\mu \subset {{\mathcal {E}}}_\mu \) generated by those elements (3.63) where the sign of k is equal to ±. As in (3.29), we obtain the following elements:
\(\forall \mu = \frac{a}{b} \in {{\mathbb {Q}}}\sqcup \infty \). These elements are all primitive for the coproduct \(\Delta _\mu \) and satisfy:
for any u, v, s. We may use the notation:
to emphasize the fact that \(\deg p_{{{\textbf{d}}}}^{(k)} = ({{\textbf{d}}},k) \in {{{{\mathbb {Z}}}}^n}\times {{\mathbb {Z}}}\). Let us write:
for all \(i \in {{\mathbb {Z}}}\), and recall that \(\delta _i^j = 1\) if \(i \equiv j\) modulo n, and 0 otherwise.
Definition 3.25
Consider the algebras:
whose generators, by the discussion above, are denoted by:
Whenever \(d:= \det \begin{pmatrix} k &{} k' \\ j-i &{} nl \end{pmatrix}\) satisfies \(|d| = \gcd (k',nl)\), we impose the relation:
and whenever \(\det \begin{pmatrix} k &{} k' \\ j-i &{} j'-i' \end{pmatrix} = \gcd (k+k',j+j'-i-i')\), we impose:
where \(\mu = \frac{j+j'-i-i'}{k+k'}\).
3.26. Let us write \({{\mathcal {D}}}^0 = {{\mathcal {E}}}_\infty \), and use the notation \(p^{(0)}_{\pm [i;i+1)}\) and \(p_{\pm k{\varvec{\delta }}, 1}^{(0)}\) for its simple and imaginary generators, respectively, as defined in Sect. 3.24.
Definition 3.27
Let us define the double of the algebras (3.73) as:
where:
and:
Relations (3.77)–(3.81) are sufficient to describe all the commutation relations between the three tensor factors of (3.76), because the algebras \({{\mathcal {D}}}^\pm \) are generated by:
(we will prove this in Proposition 3.42). Therefore, relations (3.77)–(3.81) allow us to “reorder” any product of elements from the subalgebras \({{\mathcal {D}}}^+\), \({{\mathcal {D}}}^0\), \({{\mathcal {D}}}^-\), i.e. to write said product as a sum of products of elements from \({{\mathcal {D}}}^+\), \({{\mathcal {D}}}^0\), \({{\mathcal {D}}}^-\), in this order.
Theorem 3.28
[15] There is an isomorphism \({{\mathcal {D}}}\cong {{\mathcal {S}}}\).
Proof
(sketch, see [15, Theorem 5.7, Proposition 5.8] for detailsFootnote 7) The subalgebra:
is isomorphic to \({{\mathcal {E}}}_\mu \) of (3.59) for all \(\mu \in {{\mathbb {Q}}}\sqcup \infty \), by sending:
if \(\mu > 0\) or \(\mu = \infty \), and:
if \(\mu < 0\). Similarly, \({{\mathcal {T}}}_0:= {{\mathcal {S}}}^0\) is isomorphic to a tensor product of n Heisenberg algebras. As in Sect. 3.24, this allows us to construct the images of the simple and imaginary generators:
In [15], we showed that the simple and imaginary generators \(X_{...}^{...} \in {{\mathcal {S}}}\) defined above satisfy relations (3.74)–(3.75) and (3.77) –(3.81) with p’s replaced by X’s, hence we obtain an algebra homomorphism:
This map is an isomorphism because ordered products of the elements \(f_{[i;j)}^\mu \) (respectively their images under the assignments (3.83)–(3.86)) in increasing order of \(\mu \) were shown in [15] (respectively [14]) to form a linear basis of \({{\mathcal {D}}}\) (respectively \({{\mathcal {S}}}\)). \(\square \)
Corollary 3.29
If we combine (3.50) with (3.87), we obtain an isomorphism:
Let us define:
and consider the usual triangular decomposition (see (3.16) and (3.17)):
Then the algebras
yield the decomposition \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}= {{\widetilde{U}}_{q,{{\overline{q}}}}^\uparrow (\ddot{{\mathfrak {gl}}}_n)}\otimes {{\widetilde{U}}_{q,{{\overline{q}}}}^\downarrow (\ddot{{\mathfrak {gl}}}_n)}\) of (1.7).
3.30. The purpose of the remainder of the present paper is to make:
into bialgebras, in such a way that \({{\mathcal {D}}}\) becomes their Drinfeld double. This will be done by recasting \({{\mathcal {D}}}^\pm \) as a new type of shuffle algebra, as described in Sect. 1.4. With this in mind, we will prove the following more explicit version of Theorem 1.5.
Theorem 1.5 (explicit): If \({{\mathcal {A}}}^+\) and \({{\mathcal {A}}}^-\) are the shuffle algebras that will be introduced in Definitions 4.8and 6.2, respectively, then we have algebra isomorphisms:
Moreover, the extended algebras \({\widetilde{{{\mathcal {A}}}}}^+ = {{\mathcal {A}}}^+ \otimes {U_{q,{{\overline{q}}}}^\ge (\ddot{{\mathfrak {gl}}}_n)}\) and \({\widetilde{{{\mathcal {A}}}}}^- = {{\mathcal {A}}}^- \otimes {U_{q,{{\overline{q}}}}^\le (\ddot{{\mathfrak {gl}}}_n)}\) defined in (6.6) have topological bialgebra structures and a bialgebra pairing between them, such that the Drinfeld double:
is isomorphic to \({{\mathcal {D}}}\) (and hence also with \({{\mathcal {S}}}\) and \({U_{q,{{\overline{q}}}}(\ddot{{\mathfrak {gl}}}_n)}\)) as an algebra.
3.31. In the remainder of this section, we will study the algebra \({{\mathcal {E}}}\cong {U_q({\dot{{\mathfrak {gl}}}}_n)}\) in more detail, and fill the gaps left in the discussion above. Let us consider the following matrix-valued rational function called an R-matrix with parameter x:
where \(E_{ij} \in \text {End}({{\mathbb {C}}}^n)\) denotes the \(n \times n\) matrix with a single 1 at the intersection of row i and column j, and zeroes everywhere else. We will now give an alternate version of Definition 3.6, and afterwards show how to match notations:
Definition 3.32
[3] Consider the algebra:
where:
Footnote 8 where \(Z_1 = Z \otimes \text {Id} \) and \(Z_2 = \text {Id} \otimes Z\) for any symbol Z, and:
The series S(x), T(y) are the transposes of the series denoted \(T^-(x)\), \(T^+(y)\) in [14], which explains the discrepancy between our conventions and those of loc. cit.
3.33. We will write \(\psi _k = s_{[k;k)}^{-1} = t_{[k;k)} \in {{\mathcal {E}}}\) for all \(1 \le k \le n\), and set:
\(\forall 1 \le i \le n\) and \(i \le j \in {{\mathbb {Z}}}\). We will extend our notation to all integers by setting:
\(\forall i \le j, \forall k\). It is elementary to see that relations (3.91)–(3.93) can be rewritten as:
for all \(\pm , \pm ' \in \{+,-\}\) and \({{\textbf{d}}}\in \pm {{{{\mathbb {N}}}}}^n\pm ' {{{{\mathbb {N}}}}}^n\). We will not need to spell out the coefficients in (3.97) explicitly, but they can easily be obtained by expanding (3.91)–(3.93) as power series in x/y and equating matrix coefficients of every \(E_{ij} \otimes E_{i'j'}\). In particular, an important special case of relation (3.97) reads:
The bialgebra (and Drinfeld double) structure on \({{\mathcal {E}}}= {{\mathcal {E}}}^\ge \otimes {{\mathcal {E}}}^\le \) from (3.20)–(3.22) can be presented in terms of the matrix-valued power series (3.94)–(3.95) as:
where \(\cdot \) denotes matrix multiplication (i.e. the formula \(E_{ij} \cdot E_{i'j'} = \delta _j^{i'} E_{ij'}\)), and \(c_1 = c \otimes 1\), \(c_2 = 1 \otimes c\). It is straightforward to check that these coproducts respect relations (3.91)–(3.93), i.e. extend to well-defined coproducts on the algebra \({{\mathcal {E}}}\).
3.34. The pairing (3.26) takes the form:
with R expanded in non-negative powers of \(\frac{y}{x}\). It is elementary to show (see [14] for details) that (3.101) generates a bialgebra pairing, i.e. it intertwines the product with the coproduct on \({{\mathcal {E}}}\), and that \({{\mathcal {E}}}\) is the Drinfeld double of its halves with respect to this pairing. Moreover, we claim that the linear maps (3.30) which were used to normalize primitive elements of \({{\mathcal {E}}}\) can be recovered from the assignment:
Indeed, we define:
as the coefficients of the maps \(\alpha ^\pm \), appropriately renormalized as follows:
Then it is elementary to observe that the bialgebra property (2.28)–(2.29) of the pairing, together with definition (3.102), imply the multiplicativity property (3.31).
3.35. We will henceforth write \(S^+(x) = S(x)\) and \(T^-(x) = T(x)\), so we have:
as elements of \({{\mathcal {E}}}\otimes \text {End}({{\mathbb {C}}}^n)[[x^{\pm 1}]]\). We define series \(S^-(x)\) and \(T^+(x)\) by:
where \(D = \text {diag}(q^2,\ldots ,q^{2n})\) and \(\dagger \) denotes the transpose operation \(E_{ij}^\dagger = E_{ji}\). The coefficients of these series will be denoted by:
It is straightforward to show that formulas (3.106) and (3.107) imply (3.36). The following identities are easy to prove, as consequences of (3.91), (3.92), (3.93):
3.36. In the present subsection, we will show how to rewrite relations (3.77)–(3.80) between the generators of \({{\mathcal {D}}}^+\), \({{\mathcal {D}}}^0\), \({{\mathcal {D}}}^-\) in terms of the series \(S^\pm (x)\) and \(T^\pm (x)\).
Proposition 3.37
Under the substitution:
for all \(1\le i,j\le n\) and \(d \in {{\mathbb {Z}}}\), the following relations hold in \({{\mathcal {D}}}\):
for any \(X^+(z) \in \text {End} ({{\mathbb {C}}}^n)[z^{\pm 1}]\), where \(f(x) = \frac{(1-xq^2)(1-xq^{-2})}{(1-x)^2}\).
We emphasize the fact that \(X^+(z)\) does not denote a generating series, but is instead a placeholder for \(E_{ji}z^d\) for all \(i,j \in \{1,\dots ,n\}\) and \(d \in {{\mathbb {Z}}}\). Thus, to understand the meaning of relations (3.115)–(3.118), let us spell out the first of these. Letting \(S^+(w) = \sum _{u,v}^{k \ge 0} s^+_{[u;v+nk)} \frac{E_{uv}}{w^{k}}\) and \(X(z) = \frac{E_{ij}}{z^d}\), formula (3.115) reads:
where r and \(r'\) are the coefficients of the power series expansions:
Equating the coefficients of \(... \otimes \frac{E_{uv}}{w^k}\) in the two sides of (3.119) yields the identity:
which is a relation in the algebra \({{\mathcal {D}}}\), once we perform the substitution (3.114).
Proof
We will only prove relation (3.115), and leave the analogous formulas (3.116)–(3.118) as exercises to the reader. Let us rewrite (3.115) as:
(note that we are using (4.6)). If we let \(A:{{\mathcal {E}}}\rightarrow {{\mathcal {E}}}\) denote the antipode, then (3.99) implies \(A^{-1}(S(w)) = S(w/c)^{-1}\). With this in mind, relation (3.120) reads:
where for any \(e \in {U_q^\ge ({\dot{{\mathfrak {gl}}}}_n)}\), we write:
Indeed, when \(e = S(w)\), the right-hand sides of (3.122) and (3.123) match the LHS and RHS of (3.120), respectively, due to (3.101). It is easy to see that the operations \(\spadesuit \) and \(\clubsuit \) are additive in e. Moreover, as a consequence of the properties of the antipode and bialgebra pairing (respectively), we have the following identities:
Since \({{\mathcal {E}}}^+\) is generated by the \(p_{l{\varvec{\delta }}, 1}^{(0)}\)’s and \(p_{[s;s+1)}^{(0)}\)’s, formula (3.121) is equivalent to:
When \(e = p_{l{\varvec{\delta }}, 1}^{(0)}\) (whose coproduct is \(\Delta (e) = e \otimes 1 + c^{-l} \otimes e\)), relation (3.124) reads:
Formulas (3.70) and (3.102)–(3.104) imply that the pairings in the right-hand side of the formula above are equal to \(z^l{{\overline{q}}}^l\) and \(-z^l {{\overline{q}}}^{-l}\), respectively, hence we obtain:
If we plug \(X^+(z) = E_{ji} z^d {{\overline{q}}}^{\frac{2i}{n}}\) into the equation above and use the correspondence (3.114), the formula above reduces to (3.77) for \(\pm = +\). Similarly, if we plug \(e = p_{[s;s+1)}^{(0)}\) into (3.124), then the resulting formula reduces to (3.79) for \(\pm = +\).
\(\square \)
By analogy with Proposition 3.37, we have the following result (whose proof is quite close to the one above, hence left as an exercise to the reader):
Proposition 3.38
Under the substitution:
the following relations hold in \({{\mathcal {D}}}\) (recall that \(\cdot _\text {op} \) denotes the opposite product):
for any \(X^-(z) \in \text {End} ({{\mathbb {C}}}^n)[z^{\pm 1}]\), where \(D = \text {diag} (q^2,\ldots ,q^{2n})\).
Finally, let us perform both substitutions (3.114) and (3.125) simultaneously:
(for any \(X \in \text {End}({{\mathbb {C}}}^n)[z^{\pm 1}]\), we use the notation \(X^+\) and \(X^-\) to differentiate among the matrices representing \(p_{[i,j+nd)}^{(+ 1)}\) and \(p_{[i,j+nd)}^{(- 1)}\), respectively). Then we have:
as an immediate consequence of formula (3.81) (we set \(s^\pm _{[i;j)} = t^\pm _{[i;j)} = 0\) if \(i>j\)).
3.39. We will now prove a useful Lemma about the structure of the algebra \({{\mathcal {E}}}^+\) of Sect. 3.7. Let us write \(\text {LHS}_{{\textbf{d}}}\) for the quantity in the left-hand side of (3.97), when the signs are \(\pm = \pm ' = +\). Then we have:
In Sect. 5, we will find ourselves in the situation of having an algebra \({{\mathcal {B}}}^+\) and wanting to construct an algebra isomorphism \(\Upsilon : {{\mathcal {E}}}^+ \cong {{\mathcal {B}}}^+\). Of course, the straightforward way to do this is to construct elements:
declare that \(\Upsilon (f_{[i;j)}) = f'_{[i;j)}\), and directly check that \(\Upsilon (\text {LHS}_{{\textbf{d}}}) = 0\), \(\forall {{\textbf{d}}}\in {{{{\mathbb {N}}}}}^n\). However, such a check is not handy in our situation, and we will instead rely on some additional structure. More precisely, we will prove the following.
Lemma 3.40
Assume \({{\mathcal {B}}}^+\) is a \({{{{\mathbb {N}}}}}^n\)-graded \({{\mathbb {Q}}}(q)\)-algebra, such that:
Footnote 9 is a bialgebra. Assume there exist elements \(0 \ne f'_{[i;j)} \in {{\mathcal {B}}}_{[i;j)}\) and linear maps:
such that the analogues of (3.21), (3.31), (3.32) hold. If:
then the map \({{\mathcal {E}}}^+ {\mathop {\rightarrow }\limits ^{\Upsilon }}{{\mathcal {B}}}^+\), \(\Upsilon (f_{[i;j)}) = f'_{[i;j)}\) is an injective algebra homomorphism.
Proof
Let us consider the left-hand side of (3.97) with \(f'_{[i;j)}\) instead of the \(f_{[i;j)}\):
To show that \(\Upsilon \) is an algebra homomorphism, we would need to show that \(\text {LHS}_{{\textbf{d}}}' = 0\), which we will prove by induction on \({{\textbf{d}}}\in {{{{\mathbb {N}}}}}^n\). The base case \({{\textbf{d}}}= 0\) is trivial, so we will only prove the induction step. We have:
where the middle terms denoted by the ellipsis are equal to \(\Upsilon \otimes \Upsilon \) applied to the middle terms of \(\Delta (\text {LHS}_{{\textbf{d}}})\). Since the latter are 0 (by using \(\text {LHS}_{{\textbf{d}}}= 0\) in \({{\mathcal {E}}}^+\) and the induction hypothesis), we conclude that \(\text {LHS}'_{{\textbf{d}}}\) is primitive. Moreover, the analogues of (3.31) and (3.32) imply that:
Therefore, the assumption (3.131) implies that \(\text {LHS}'_{{\textbf{d}}}= 0\) for all \({{\textbf{d}}}\), thus establishing the fact that \(\Upsilon \) is a well-defined algebra homomorphism. To show that \(\Upsilon \) is injective, assume that its kernel is non-empty. Since \(\Upsilon \) preserves degrees, we may choose \(0 \ne x \in {{\mathcal {E}}}^+\) of minimal degree \({{\textbf{d}}}\in {{{{\mathbb {N}}}}}^n\) such that \(\Upsilon (x) = 0\). Since \(\Upsilon \) preserves the coproduct and is injective in degrees \(<{{\textbf{d}}}\) (by the minimality of \({{\textbf{d}}}\)), we conclude that x is primitive. However, since \(\Upsilon \) intertwines the linear maps \(\alpha _{[i;j)}\) with \(\alpha '_{[i;j)}\), we conclude that x is also annihilated by the linear maps \(\alpha _{[i;j)}\). However, [15, Lemma 3.11] tells us that under these circumstances, we must have \(x = 0\). \(\square \)
Since an injective linear map of finite-dimensional vector spaces \(\Phi : V_1 \hookrightarrow V_2\) is an isomorphism if \(\dim V_2 \le \dim V_1\) (as well as the similar statement in the graded case, if \(V_1\) and \(V_2\) have finite-dimensional graded pieces which are preserved by \(\Phi \)) we obtain the following:
Corollary 3.41
If the assumption of Lemma 3.40 holds, and moreover, if \(\dim {{\mathcal {B}}}_{{\textbf{d}}}\le \) the RHS of (3.27) for all \({{\textbf{d}}}\in {{{{\mathbb {N}}}}}^n\), then \(\Upsilon : {{\mathcal {E}}}^+ \cong {{\mathcal {B}}}^+\) is an isomorphism.
Proposition 3.42
The \({{\mathbb {Q}}}(q,{{\overline{q}}}^{\frac{1}{n}})\)-algebra \({{\mathcal {D}}}^\pm \) is generated by the elements:
Proof
Without loss of generality, let \(\pm = +\). We will prove that \(p_{[i;j)}^{(k)}\) (resp. \(p_{l{\varvec{\delta }},r}^{(k')}\)) lies in the subalgebra generated by the elements (3.132) for all choices of indices i, j, l, r, by induction on k (respectively \(k'\)). To this end, let us choose a lattice triangle of minimal area with the vector \((j-i,k)\) (respectively \((nl,k')\)) as an edge:

In the case of the picture on the left, namely that of the element \(p_{[i;j)}^{(k)}\), the minimality of the area of the triangle implies that:
Recall that \(i \not \equiv j\) mod n. If \(a \equiv j-i\) modulo n, then relation (3.74) gives us:
while if \(a \not \equiv j-i\) modulo n, then relation (3.75) gives us:
In either of the two formulas above, the induction hypothesis implies that the left-hand side lies in the algebra generated by the elements (3.132). Therefore, so does the right-hand side, and the induction step is complete.
The case of the picture on the right, namely that of the element \(p_{l{\varvec{\delta }}, r}^{(k')}\), is proved analogously. We will therefore only sketch the main idea, and leave the details to the interested reader. As shown in [15, Lemma 4.2], relation (3.75) implies for all u:
where \(\mu = \frac{k'}{nl}\), and \({\tilde{p}}_{[v;v+x)}^{(y)} = \sum _{v' \in {{\mathbb {Z}}}/n{{\mathbb {Z}}}} p_{[v';v'+x)}^{(y)} \cdot \left[ q^{-\delta _x^0} \delta _{v'}^v + \delta _x^0(q-q^{-1}) \frac{{{\overline{q}}}^{\frac{2}{n} \cdot \overline{y(v-v')}}}{{{\overline{q}}}^2-1} \right] \). By the induction hypothesis, the left-hand side of the expression above lies in the subalgebra generated by the elements (3.132), hence so does the right-hand side, which we henceforth denote \(\text {RHS}\). Clearly, \(\text {RHS}\in {{\mathcal {B}}}_\mu ^+\), and it can therefore be expressed as a sum of products of the simple and imaginary generators:
By the induction hypothesis, all products of more than one simple or imaginary generator lie in the subalgebra generated by the elements (3.132). We conclude that \(\sum _{r} \alpha _{u}^r \cdot p^\mu _{l{\varvec{\delta }}, r}\) also lies in the same algebra, for all \(u \in \{1,\ldots ,n\}\). Since the matrix \(\alpha ^r_u\) has full rank (as shown in [15]), we conclude that \(p^\mu _{l{\varvec{\delta }}, r}\) also lies in the subalgebra generated by the elements (3.132), precisely what we needed to show. \(\square \)
4 The shuffle algebra with spectral parameters
4.1. We will now generalize the construction of Sect. 2 by allowing the coefficients of matrices in \(\text {End}(V^{\otimes k})\) to be rational functions. We will recycle all the notations from Sect. 2, so fix a basis of a n-dimensional vector space V, and let:
be given by formula (3.88). For a parameter \({{\overline{q}}}\), we define:
It is well-known that R(x) satisfies the Yang–Baxter equation with parameter:
and it is easy to show that \({\widetilde{R}}(z)\) satisfies the following analogue of (2.2)–(2.3):
Finally, we note that the R-matrix (3.88) is (almost) unitary, in the sense that:
where:
It is easy to see that “half” of the rational function f(x) could have been absorbed in the definition of R(x), thus making R(x) to be unitary on the nose, but we will prefer our current conventions.
4.2. We will represent elements of \(\text {End}(V^{\otimes k})(z_1,\ldots ,z_k)\) as braids on k strands. The only difference between the present setup and that of Sect. 2 is that each strand carries not only a label \(i \in \{1,\ldots ,k\}\) but also a variable \(z_i\). With this in mind, we make the convention that the endomorphism corresponding to a positive crossing of strands labeled a and b, endowed with variables \(z_a\) and \(z_b\) respectively, is:
Because of (4.2), we can represent both R and \({\widetilde{R}}\) as crossings of braids of the same kind (i.e. we do not need the dichotomy of straight strands versus squiggly strands, of Sect. 2.2) if we remember to change the variable on one of our strands. We will always write the variable next to every braid. For example, the braids:
represent the following compositions \(\in \text {End}(V^{\otimes 2}) (z_1,z_2)\):
respectively. The variable does not change along a strand, except at a box.
4.3. We make an unusual convention on residues of rational functions, by stipulating that \(\frac{\alpha }{\alpha - x}\) has residue 1 at \(x=\alpha \) (instead of the more usual \(-\alpha \)). With this in mind, note that R(x) has a pole at \(x = 1\), with residue \((q - q^{-1}) \cdot (12)\). Thus:
where (12) denotes the permutation operator of the two factors. Pictorially, the endomorphism (4.8) will be represented by two black dots indicating a color change (recall that the color encodes the index \(\in \{1,\ldots ,k\}\) of a strand) between two strands:
The equality of braids depicted in Fig. 13 means that one can move the black dots as far left or as far right as we wish, no matter how many other strands we pass over or under. Explicitly, the equality depicted above reads:
which is a true identity (Fig. 14). Finally, we note that due to formula (4.6), we can always change a crossing in a braid, at the cost of multiplying with the function (4.7):
4.4. The following is proved just like Proposition 2.4, so we leave it as an exercise.
Proposition 4.5
Let \(A = A_{1...k}(z_1,\ldots ,z_k)\), \(B = B_{1...l}(z_1,\ldots ,z_l)\). The assignment:
yields an associative algebra structure on the vector space:
with unit \(1 \in \text {End} _{{{\mathbb {Q}}}(q,{{\overline{q}}}^{\frac{1}{n}})}(V^{\otimes 0})\). We call (4.9) the “shuffle product”.
Proposition 4.6
The shuffle product above preserves the vector space:
consisting of tensors \(X = X_{1...k}(z_1,\ldots ,z_k)\) which simultaneously satisfy:
-
\(X = \displaystyle \frac{x(z_1,\ldots ,z_k)}{\prod _{1\le i \ne j \le k} (z_i - z_j {{\overline{q}}}^2)}\) for some \(x \in \text {End} _{{{\mathbb {Q}}}(q,{{\overline{q}}}^{\frac{1}{n}})}(V^{\otimes k})[z_1^{\pm 1},\ldots ,z_k^{\pm 1}]\).
-
X is symmetric, in the sense that:
$$\begin{aligned} X = R_\sigma \cdot (\sigma X \sigma ^{-1}) \cdot R_{\sigma }^{-1} \end{aligned}$$(4.10)\(\forall \sigma \in S(k)\), where \(R_\sigma = R_\sigma (z_1,\ldots ,z_k)\) is any braid lift of the permutation \(\sigma \), and:
$$\begin{aligned} \sigma X \sigma ^{-1} = X_{\sigma (1)...\sigma (k)}(z_{\sigma (1)},\ldots ,z_{\sigma (k)}) \end{aligned}$$
Proof
The fact that the shuffle product (4.9) preserves the vector space of symmetric tensors is proved word-for-word as in Proposition 2.6. Therefore, it remains to prove that if A and B have no poles other than simple poles at \(z_i = z_j {{\overline{q}}}^2\), then \(A * B\) has the same property. Besides simple poles at \(z_i = z_j {{\overline{q}}}^2\) (which we allow), the R-matrices in the right-hand side of (4.9) only produce simple poles at \(z_i = z_j\), so it remains to show that the residues at the latter poles vanish.
We will show that any symmetric tensor \(X = X_{1...k}(z_1,\ldots ,z_k)\) with at most a simple pole at \(z_1 = z_k\) is actually regular there. Without loss of generality, we will prove the vanishing of the residue at \(z_1 = z_k\). Since only the indices/variables 1 and k will play an important role in the following, we will use ellipses... for the indices/variables \(2,\ldots ,k-1\). Let us consider (4.10) in the particular case \(\sigma = (1k)\):
where \(Y(z_1,\ldots ,z_k) = X(z_1,\ldots ,z_k) \cdot (z_1-z_k)\) is regular at \(z_1 = z_k\). We may choose:
Since the residue of \(R_{1k} \left( \frac{z_1}{z_k} \right) \) at \(z_1 = z_k\) is \((q-q^{-1})\cdot (1k)\), the residue of (4.11) is:
(above, we wrote \(x = z_1 = z_k\) and canceled an overall scalar factor of \(q-q^{-1}\)). We may move the permutation (1k) to the very right of the equations above, obtaining:
After canceling all the R factors and the permutation operators (1k), we are left with \(Y_{1...k}(x,\ldots ,x) = 0\), which implies that X was regular at \(z_1 = z_k\) to begin with. \(\square \)
4.7. For a rational function \(X(z_1,\ldots ,z_k)\) with at most simple poles, we let:
be the rational function in \(y,z_{i+1},\ldots ,z_k\) obtained by successively taking the residue at \(z_2 = z_1 {{\overline{q}}}^2\), then at \(z_3 = z_1 {{\overline{q}}}^4\),..., then at \(z_i = z_1 {{\overline{q}}}^{2(i-1)}\) and finally relabeling the variable \(z_1 \leadsto y\). More generally, for any collection of natural numbers:
we will write:
for the rational function in \(y_1,..,y_u\) obtained by applying the iterated residue (4.12) construction for the collections of variables indexed by \(\{c_1,c_1+1,\ldots ,c_2-1\}\),..., \(\{c_u,c_u+1,\ldots ,c_{u+1}-1\}\). Moreover, we write:
for any collection of potentially non-commuting symbols \(x_1,\ldots ,x_k\).
Definition 4.8
Let \({{\mathcal {A}}}^+ \subset {{\mathcal {A}}}^+_\text {big}\) be the subspace of tensors \(X = X_{1...k}(z_1,\ldots ,z_k)\) such that for any composition \(k = \lambda _1+\cdots +\lambda _u\) we have (let \(\lambda _s = c_{s+1}-c_s\), \(\forall s\)):
for some tensor \(X^{(\lambda _1,\ldots ,\lambda _u)} \in \text {End} (V^{\otimes u})(y_1,\ldots ,y_u)\).
Pictorially, the RHS of (4.13) may be represented as follows:
The RHS of (4.13) for \(u=2\), \(\lambda _1 = 4\), \(\lambda _2 = 3\)
Note the symbol “blue over blue” to the right of Fig. 15. Given two colors \(\gamma _1\) and \(\gamma _2\), placing \(\gamma _1\) over \(\gamma _2\) is a prescription that indicates that the braid in question be multiplied by the product of \(f(y/y')\), where y (respectively \(y'\)) goes over all variables on strands whose left endpoint has color \(\gamma _1\) (respectively \(\gamma _2\)), and the leftmost endpoint with variable y is above the leftmost endpoint with variable \(y'\). This is meant to account for the product of f’s on the second line of (4.13).
Remark 4.9
When \(n=1\), we may identify \(1 \times 1\) matrices with scalars, and so elements of the shuffle algebra are merely symmetric rational functions in \(z_1,\dots ,z_k\) with at most simple poles at \(z_i = z_j {{\overline{q}}}^2\). The shuffle product (4.9) takes the form
where
Meanwhile, the wheel conditions (4.13) for the composition \(1+\cdots +1+2\) impose the following restriction on a rational function \(X(z_1,\dots ,z_k)\):
where the function in the round brackets can only have simple poles at \(z_i-z_j{{\overline{q}}}^{\pm 2}\) and \(z_i - z_{k-1}{{\overline{q}}}^{-2,0,2,4}\) for all \(i < j \in \{1,\dots ,k-1\}\) (see Proposition 4.11). Therefore, the residue above vanishes when we set \(z_i = z_{k-1} q^{-2}\) or \(z_i = z_{k-1} q^{2} {{\overline{q}}}^{2}\), which in our notations and normalization is precisely the wheel condition of [8].
Proposition 4.10
The vector subspace \({{\mathcal {A}}}^+\) of Definition 4.8 is preserved by the shuffle product (and will henceforth be called the “shuffle algebra”).
Proof
Assume that two matrix-valued rational functions A and B in k and l variables, respectively, satisfy the wheel condition (4.13). To prove that their shuffle product \(A*B\) also satisfies the wheel condition, we must take the iterated residue of the right-hand side of (4.9) at:
for any composition \(k+l = \lambda _1+\cdots +\lambda _u\). We will show that, at such a specialization, each summand in the RHS of (4.9) has the form predicated in the RHS of (4.13), so we henceforth fix a shuffle \(a_1<...<a_k\), \(b_1<...<b_l\). Because \({\widetilde{R}}(z)\) has a simple pole at \(z = {{\overline{q}}}^{-2}\), the only way such a shuffle can have a non-zero residue is if:
for some choice of \(r_s \in \{c_s,\ldots ,c_{s+1}-1\}\) for all \(s \in \{1,\ldots ,u\}\). We will indicate this choice by using the following colors for the strands of our braids:

With this in mind, the summand of (4.9) corresponding to our chosen shuffle is represented by the following braid (to keep the pictures reasonable, we will only depict the case \(u=2\), but the modifications that lead to the general case are straightforward; although we only depict a single blue and green strand in each of the u groups, the reader may obtain the general case by replacing each of them with any number of parallel blue and green strands, respectively):
The black dots in the middle of the braid appear because the variables on the braids in question are set equal to each other in the iterated residue. By sliding the black dots as far to the right as possible (which is allowed, due to Fig. 13), we obtain (Figs. 16, 17):
One readily notices that certain pairs of braids are twisted twice around each other, and these twists can be canceled up to a factor of \(f(y/y')\) (due to the identity in Fig. 14), where y and \(y'\) are the variables on the braids in question. Keeping in mind that the variables on the red strands are modified to the right of the red boxes, this yields the braid in Fig. 18. Note that the black dots on the right side of Fig. 18 yield the same permutation as the black dots on the right side of the braid in Fig. 15, due to the following identity:
in the symmetric group S(k). Therefore, the braid in Fig. 18 is precisely of the form predicated in the right-hand side of (4.13), which concludes our proof. \(\square \)
Proposition 4.11
For any \(X \in {{\mathcal {A}}}^+\) and any composition \(k = \lambda _1 +... + \lambda _u\), the tensor \(Y = X^{(\lambda _1,\ldots ,\lambda _u)}\) that appears in (4.13) has at most simple poles at:
for all \(1 \le s < t \le u\) and any \(0 \le d < \lambda _s\). Moreover, if \(\lambda _s = \lambda _t\) then:
for any braid lift \(R_{(st)} = R_{(st)}(y_1,\ldots ,y_u)\) of the transposition (st).Footnote 10
Proof
Let us first prove the statement about the poles of Y. In the course of this proof, all poles will be counted with multiplicities, in the sense that whenever we refer to a “set of poles”, the reader should assume this means “multiset of poles”. Because of the first bullet of Proposition 4.6, which determines the allowable poles of \(X \in {{\mathcal {A}}}^+\), the left-hand side of (4.13) has a simple pole at:
On the other hand, the right-hand side of (4.13) has a double pole at:
because of the f factors, and a simple pole at:
because of the simple pole of R(z) at \(z=1\). Eliminating the multiset of poles in (4.17) and (4.18) from the multiset of poles in (4.16) yields the allowable poles of \(Y(y_1,\ldots ,y_u)\), and it is elementary to see that they are precisely of the form (4.14).
As for (4.15), we will prove it pictorially. To keep the pictures legible, we will only show the case \(u=2\) (hence \((s,t) = (1,2)\)), but the reader may easily generalize the argument. Because of property (4.10), the tensor \(X(y_s,y_s{{\overline{q}}}^2,\ldots ,y_t,y_t{{\overline{q}}}^2,...)\) (which is represented by a braid akin to Fig. 15) is also equal to the following braid: (we ignore the scalar-valed rational functions f in the diagrams above, as they commute with all the braids involved). The braid called \(R_\sigma \) interchanges the two collections of \(\lambda _s = \lambda _t\) braids corresponding to the variables \(y_s {{\overline{q}}}^{2*}\) and \(y_t {{\overline{q}}}^{2*}\). Although we could choose the crossings of \(R_\sigma \) arbitrarily, the choice we make above is that the two red strands cross above all other ones, then the two blue strands next to the red strands cross above all remaining ones, then the two blue strands next to the previous blue strands cross etc. In virtue of Fig. 13, we may move the black dots to the very right of the picture above, obtaining the braid below (Figs. 19, 20):
Then we pull the red strands as far up as possible, and notice that the blue strands are all unlinked, thus yielding the braid in Fig. 21 below. The red strands in Fig. 21 correspond to the endomorphism:
which we may equate with Y due to the braid equivalences described above. \(\square \)
4.12. The shuffle algebra \({{\mathcal {A}}}^+\) has a “vertical” and a “horizontal” grading:
where \({\varvec{\delta }}= (1,\ldots ,1)\) and the grading on \(\text {End}(V)\) is defined by:
We will find it convenient to extend the notation \(E_{ij}\) to all \(i,j \in {{\mathbb {Z}}}\), according to:
where \({\bar{i}}\) denotes the residue class of i in the set \(\{1,\ldots ,n\}\).Footnote 11 Then formulas (4.20) and (4.21) hold for arbitrary integer indices \(i_1,j_1,\ldots ,i_k,j_k\) and i, j. We will denote the graded pieces of the shuffle algebra by:
and refer to \(({{\textbf{d}}},k)\) as the degree of homogeneous elements. Finally, we write:
for any \({{\textbf{d}}}= (d_1,\ldots ,d_n) \in {{\mathbb {Z}}}\) and refer to the number:
as the slope of the matrix-valued rational function \(f(z_1,\ldots ,z_k) E_{i_1j_1} \otimes \cdots \otimes E_{i_kj_k}\). We will consider the partial ordering on \({{\mathbb {Z}}}^n\) given by:
5 The extended shuffle algebra with spectral parameter
5.1. We will now replicate the construction of Sect. 2.7 in the situation of the R–matrix with spectral parameter (3.88).
Definition 5.2
Consider the extended shuffle algebra:
In order to concisely state the relations, it makes sense to package the new generators \(s_{[i;j)}\) into the following matrix-valued generating function:
We impose the following analogues of relations (2.16) and (2.19):
for any \(X = X_{1...k}(z_1,\ldots ,z_k) \in {{\mathcal {A}}}^+ \subset {\widetilde{{{\mathcal {A}}}}}^+\).
Note that the grading on \({{\mathcal {A}}}^+\) extends to one on \({\widetilde{{{\mathcal {A}}}}}^+\), by setting:
The series S(x) defined above is supposed to match the homonymous series in (3.94).
5.3. We may also consider the elements \(t_{[i;j)} \in {\widetilde{{{\mathcal {A}}}}}^+\) defined by (3.107), where:
Then it is a straightforward computation (which we leave as an exercise to the interested reader) to see that (5.1), (5.2) imply analogues of (2.17), (2.18), (2.20):
Therefore, we conclude that the series S(x) and T(x) satisfy the same relations as in Definition 2.8 (modified in order to account for the variables \(z_i\)), even though the s’s and the t’s are not independent of each other anymore. We will write:
for all \(i \in \{1,\dots ,n\}\) and note that formulas (5.1) imply that:
\(\forall X \in {\widetilde{{{\mathcal {A}}}}}^+\), where \(\langle \cdot , \cdot \rangle \) is the bilinear form on \({{\mathbb {Z}}}^n\) given by \(\langle {\varvec{\varsigma }}^i, {\varvec{\varsigma }}^j \rangle = \delta _{i}^{j} - \delta _{i}^{j+1}\).
5.4. Consider the following topological coproduct on the algebra \({\widetilde{{{\mathcal {A}}}}}^+\), which is the natural analogue of the coproduct studied in Proposition 2.9:
(hence \(\Delta (T(x)) = \left( T(x) \otimes 1 \right) \cdot (1 \otimes T(x))\) by (3.107)) and:
for all \(X_{1...k}(z_1,\ldots ,z_k) \in {{\mathcal {A}}}^+ \subset {\widetilde{{{\mathcal {A}}}}}^+\). The fact that \(\Delta \) defined above gives rise to a coasociative coalgebra structure which respects the algebra structure is proved by analogy with Proposition 2.9, and we leave the details to the interested reader.
Remark 5.5
Because S(x) is a power series in x, the coproduct defined above takes values in a completion of \({\widetilde{{{\mathcal {A}}}}}^+ \otimes {\widetilde{{{\mathcal {A}}}}}^+\). Specifically, to make sense of the second line of (5.10), we must expand the rational function:
for \(z_1,\ldots ,z_i \ll z_{i+1},\ldots ,z_k\), then collect all tensors of the form \(X_{1...i}(z_1,\ldots ,z_i)\) to the left of \(\otimes \), and all tensors of the form \(X_{i+1,\ldots ,k}(z_{i+1},\ldots ,z_k)\) to the right of \(\otimes \). See [13, Equation (4.4)] for an analogous situation, which corresponds to our case \(n=1\).
5.6. Given \(X \in {{\mathcal {A}}}^+\), we will represent its degree \(\deg X = ({{\textbf{d}}},k)\) on a 2 dimensional lattice, via the projection \(({{\textbf{d}}},k) \twoheadrightarrow (|{{\textbf{d}}}|,k)\), and hence assign to X the lattice point \((|{{\textbf{d}}}|,k)\). Similarly, we will assign to the tensor \(X_1 \otimes X_2\) the two-segment path:
The intersection of the arrows, namely \((|{{\textbf{d}}}_2|,k_2)\), is called the hinge of \(X_1 \otimes X_2\). Recall the definition of slope in (4.24).
Definition 5.7
Let \(\mu \in {{\mathbb {Q}}}\). We let \({{\mathcal {A}}}_{\le \mu }^+ \subset {{\mathcal {A}}}^+\) be the set of those X such that:
where \(\Delta _\mu (X)\) consists only of summands \(X_1 \otimes X_2\) with \(\text {slope } X_2 = \mu \) (we also choose to include the summand \(X \otimes 1\) in \(\Delta _\mu (X)\)). In terms of the pictorial definitions of hinges in Fig. 22, \(X \in {{\mathcal {A}}}^+_{\le \mu }\) if and only if all summands in \(\Delta (X)\) have hinge at slope \(|{{\textbf{d}}}|/k \le \mu \) as measured from the origin.
We will say that an element of \({{\mathcal {A}}}^+_{\le \mu }\) has slope \(\le \mu \). Since having slope \(\le \mu \) is an additive property, \({{\mathcal {A}}}^+_{\le \mu }\) is a vector space. Let us define its graded pieces:
and note that \({{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k} \ne 0\) only if \(|{{\textbf{d}}}| \le k \mu \).
Proposition 5.8
For any \(\mu \in {{\mathbb {Q}}}\), the subspace \({{\mathcal {A}}}^+_{\le \mu }\) is a subalgebra of \({{\mathcal {A}}}^+\), and:
for all \(X,Y \in {{\mathcal {A}}}^+_{\le \mu }\).
Proof
Note that degree is multiplicative, i.e. (assume the LHS is non-zero):
Therefore, if \(\Delta (X) = X_1 \otimes X_2\) and \(\Delta (Y) = Y_1 \otimes Y_2\) with \(\text {slope}\ X_2, \text {slope}\ Y_2 \le \mu \), then \(\text {slope}\ X_2 Y_2 \le \mu \). Since \(\Delta (XY) = X_1 Y_1 \otimes X_2 Y_2\), this implies the conclusion. \(\square \)
5.9. Our reason for introducing slopes and the algebras \({{\mathcal {A}}}^+_{\le \mu }\) is that \(\{{{\mathcal {A}}}_{\le \mu | {{\textbf{d}}},k}\}_{\mu \in {{\mathbb {Q}}}}\) yield a filtration of \({{\mathcal {A}}}_{{{\textbf{d}}},k}\) by finite-dimensional vector spaces.
Lemma 5.10
The dimension of \({{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k}\) as a vector space over \({{\mathbb {Q}}}(q,{{\overline{q}}}^{\frac{1}{n}})\) is at most the number of unordered collections:
where:
-
\(\lambda _s \in {{\mathbb {N}}}\) with \(\sum _{s=1}^u \lambda _s = k\)
-
\((i_s,j_s) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) with \(\sum _{s=1}^u [i_s;j_s) = {{\textbf{d}}}\)
-
\(j_s - i_s \le \mu \lambda _s\) for all \(s \in \{1,\ldots ,u\}\)
In (5.74), we will show that the dimension of \({{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k}\) is in fact equal to the number of unordered collections (5.13). The argument below follows that of [8, 13, 14].
Proof
To any partition \(\lambda = (\lambda _1 \le ... \le \lambda _u)\) of \(k \in {{\mathbb {N}}}\), we associate the linear map:
Consider the dominance partial ordering \(\lambda ' > \lambda \) on partitions.Footnote 12, and define:
Since \({{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k}^{(k)} = {{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k}\), then the desired bound on \(\dim {{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k}\) would follow from:
for any \(\lambda = (\lambda _1 \le ... \le \lambda _u)\). Above, “quasi-ordered” means that collections \(\{(i_1,j_1),\ldots ,(i_u,j_u)\}\) are considered only up to arbitrarily swapping any \((i_a,j_a)\) and \((i_b,j_b)\) for which \(\lambda _a=\lambda _b\). By Proposition 4.11, any \(Y \in \text {Im } \varphi _\lambda \) is of the form:
However, if \(Y = \varphi _\lambda (X)\) for some \(X \in {{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k}^{\lambda }\), we claim that Y is a Laurent polynomial. Indeed, let us show that Y is regular at \(y_s {{\overline{q}}}^{2d} - y_t {{\overline{q}}}^{-2}\). We have:
where \(\lambda '\) is obtained from \(\lambda \) by replacing \(\lambda _s\) and \(\lambda _t\) by \(\lambda _s-d-1\) and \(\lambda _t+d+1\). The right-hand side of the expression above vanishes because \(X \in {{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},k}^{\lambda }\) and \(\lambda '>\lambda \). Similarly, one can show that the residue of Y vanishes at \(y_s {{\overline{q}}}^{2d} - y_t {{\overline{q}}}^{2\lambda _t}\) for any \(s<t\) and \(0 \le d < \lambda _s\). This precisely implies that Y is a Laurent polynomial:
Since the matrices R and \({\widetilde{R}}\) have total degree 0, the horizontal degree of Y is equal to that of X, namely \({{\textbf{d}}}\), so we conclude that the only summands with non-zero coefficient in (5.16) satisfy:
Finally, the slope condition on X implies an analogous slope condition on Y: in each variable \(y_s\), we have:
Therefore, the number of coefficients that one gets to choose in (5.16) is at most the number of collections \((j_s = \alpha _s + n h_s, i_s = \beta _s)\) satisfying the conditions in the right-hand side of (5.14) (we only take quasi-ordered collections because of (4.15)). \(\square \)
5.11. Definition 4.8 of the shuffle algebra allows us to associate to any \(X = X_{1...k}(z_1,\ldots ,z_k) \in {{\mathcal {A}}}^+\) the matrix-valued power series \(X^{(k)}(y) \in \text {End}(V)[y^{\pm 1}]\) (namely the object arising in (4.13) for the composition (k) of k).
Proposition 5.12
For any \(A \in {{\mathcal {A}}}_{{{\textbf{d}}},k}\) and \(B \in {{\mathcal {A}}}_{{{\textbf{e}}},l}\), we have:
where \(e_n\) is the last component of the vector \({{\textbf{e}}}= (e_1,\ldots ,e_n) \in {{{{\mathbb {Z}}}}^n}\).
Proof
The proof is precisely the \(u=1\) case of the proof of Proposition 4.10, since the equality of braids therein indicates the fact that:
Since \(B \in {{\mathcal {A}}}_{{{\textbf{e}}},l}\), formulas (4.20) and (4.21) imply the homogeneity property:
As R–matrices are invariant under rescaling variables, the rational function \(B^{(l)}(y)\) of (4.13) also satisfies \(B^{(l)}(y \xi ) = \xi ^{e_n} B^{(l)}(y)\). Then (5.18) implies (5.17). \(\square \)
For all \((i, j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\), define the linear maps:
(recall that \(E_{ij} = E_{{\bar{i}}{\bar{j}}} y^{\left\lfloor \frac{i-1}{n} \right\rfloor - \left\lfloor \frac{j-1}{n} \right\rfloor }\)).
Corollary 5.13
For any \(k,l \in {{\mathbb {N}}}\) and \((i,j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\), we have:
whenever \(\deg A = ([s;j),k)\) and \(\deg B = ([i;s),l)\) for some s between i and j. If such an s does not exist, then the RHS of (5.20) is set equal to 0, by convention.
Proof
The corollary is an immediate consequence of (5.17) and (5.19). The only thing we need to check is that the power of \({{\overline{q}}}\) is the same in the left as in the right-hand sides of (5.20), which happens due to the elementary identity:
since if \({{\textbf{e}}}= [i;s)\), then \(e_n = \left\lfloor \frac{s-1}{n} \right\rfloor - \left\lfloor \frac{i-1}{n} \right\rfloor \).
\(\square \)
5.14. Let \({{\mathcal {B}}}_{\mu |{{\textbf{d}}}} = {{\mathcal {A}}}_{\le \mu |{{\textbf{d}}},\frac{|{{\textbf{d}}}|}{\mu }}\). Particular importance will be given to the subalgebra:
We will call \({{\mathcal {B}}}_\mu ^+\) a slope subalgebra. As a consequence of Proposition 5.8, the leading order term \(\Delta _\mu \) of (5.11) restricts to a coproduct on the extended subalgebra:
Lemma 5.15
If \(X \in {{\mathcal {B}}}_\mu ^+\) is primitive with respect to the coproduct \(\Delta _\mu \), and:
for all \((i,j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) such that \(\deg X \in [i;j) \times {{\mathbb {N}}}\), then \(X = 0\).
Proof
The assumption \(X \in {{\mathcal {B}}}^+_\mu \) implies that \(\deg X = ({{\textbf{d}}},k)\) with:
As we observed in the proof of Lemma 5.10, it suffices to show that \(\varphi _\lambda (X) = 0\) for all partitions \(\lambda \), which we will do in reverse dominance order of the partition \(\lambda \). The base case is when \(\lambda = (k)\), which is satisfied because \(\varphi _{(k)}(X) = 0\) is precisely the content of the assumption (5.23). For a general partition \(\lambda \ne (k)\), we may invoke the induction hypothesis to conclude that \(\varphi _{\lambda '}(X) = 0\) for all partitions \(\lambda ' > \lambda \), and in this case \(\varphi _\lambda (X)\) takes the form of (5.16). However, the fact that X is a primitive element requires every summand appearing in the RHS of (5.16) to satisfy:
for all \(1 \le s \le u\) (we have \(u > 1\), since \(\lambda \ne (k))\). However:
This yields a contradiction, hence \(\varphi _\lambda (X) = 0\), thus completing the induction step. \(\square \)
5.16. We will now construct particular elements of \({{\mathcal {B}}}_\mu ^+\), which together with Lemma 5.10 will yield a PBW basis of the shuffle algebra, leading to the proof of Theorem 1.5. Consider the following notion of symmetrization, analogous to (2.9):
where \(R_\sigma \) is the product of \(R_{ij} \left( \frac{z_i}{z_j} \right) \) associated to any braid lift of \(\sigma \). For instance:
lifts the longest element \(\omega _k \in S(k)\). Consider the matrix-valued rational functions:
which have, up to scalar, the same simple pole and residue as \({\widetilde{R}}(x)\):
(see formula (4.8)). Moreover, it is easy to check the following identity:
In the following, we will invoke (4.22) and (4.23) by writing:
for all \(a \in \{1,\ldots ,k\}\), \(b,c \in {{\mathbb {Z}}}\) (in the RHS, the non-trivial term is on the a-th spot).
Proposition 5.17
For any \((i,j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) and \(\mu \in {{\mathbb {Q}}}\) such that \(k = \frac{j-i}{\mu } \in {{\mathbb {N}}}\), set:
where \(s_a = j - \lceil \mu a \rceil \), \(s'_a = j - \lfloor \mu a \rfloor \). Then \(F_{[i;j)}^\mu , {\bar{F}}_{[i;j)}^\mu \in {{\mathcal {B}}}_\mu ^+\), and:
where we set \(F_{[i;j)}^\mu = {\bar{F}}_{[i;j)}^\mu = 0\) if \(\frac{j-i}{\mu } \notin {{\mathbb {N}}}\).
Proof
Note that if Q, \({\bar{Q}}\) were replaced by \({\widetilde{R}}\) in formulas (5.31), (5.32), then the right-hand sides of the aforementioned formulas would precisely equal:
The fact that the shuffle elements (5.35) satisfy the wheel conditions is simply a consequence of iterating Proposition 4.10 a number of \(k-1\) times. As far as the elements \(F_{[i;j)}^\mu \), \({\bar{F}}_{[i;j)}^\mu \) are concerned, the fact that they satisfy the wheel conditions is proved similarly with the fact that (5.35) satisfies the wheel conditions: this is because Proposition 4.10 uses the fact that \(\text {Res}_{x = {{\overline{q}}}^{-2}} {\widetilde{R}}(x)\) is a multiple of the permutation matrix, and we have already seen in (5.29) that the residues of Q(x), \({\bar{Q}}(x)\), \({\widetilde{R}}(x)\) are the same up to scalar. We leave the details to the interested reader.
Let us prove that the shuffle elements (5.31) and (5.32) lie in \({{\mathcal {B}}}_\mu ^+\). We will only prove the former case, since the latter case is analogous. We have:
where X is the expression on the second line of (5.31). Since F has degree ([i; j), k) with \(j-i = \mu k\), it remains to prove that F has slope \(\le \mu \). To this end, for any \(l \in \{0,\ldots ,k\}\) we need to look at the first l tensor factors of \(\text {Sym}\ R_{\omega _k} X\) and isolate the terms of minimal \(|\text {hdeg}|\). If Y is a k–tensor, we will henceforth use the phrase “initial degree of Y” instead of “total \(|\text {hdeg}|\) of the first l factors of Y”. Because:
for all indices a and b, we obtain the following easy (but very useful) fact:
Claim 5.18
For any \(1 \le a \ne b \le k\), multiplying a k–tensor Y by:
(either on the left or on the right) cannot decrease the minimal initial degree of Y.
Therefore, it suffices to compute the minimal initial degree of:
for any permutation \(\sigma \) of \(\{1,\ldots ,k\}\). Claim 5.18 implies that the minimal initial degree (henceforth denoted “m.i.d.”) comes from the various \(E_{s_{a-1}s_a}\) factors:
where \(A = \{\sigma ^{-1}(1),\ldots ,\sigma ^{-1}(l)\}\) and the number \(\#\) counts those \(a \in A\) such that \(a - 1 \notin A\). This number appears in the right-hand side of (5.40) because \(Q(\infty )\) has 0 on the diagonal, by definition. It is elementary to show that:
if A splits up into consecutive blocks of integers:
with \(0 \le \alpha _1\), while \(\beta _s < \alpha _{s+1}\) for all s, and \(\beta _t \le k\). Since:
we conclude that \(F \in {{\mathcal {A}}}^+_{\le \mu }\). Because \(|\text {hdeg }F| = j-i\) and \(\text {vdeg }F = k\), then \(F \in {{\mathcal {B}}}^+_\mu \).
Moreover, the terms of minimal initial degree in F correspond to those situations where we have equality in all the inequalities above, and these require \(\mu l \in {{\mathbb {Z}}}\) and:
Let us now compute the summands which achieve the minimal initial degree in:

where the notation \(E^{(u...v)}_{c_{u-1}|c_u|...|c_{v-1}|c_v}\) is shorthand for:
If the terms with the squiggly red underline were not present in (5.44), then we would conclude that the terms of minimal initial degree would be precisely:
and upon symmetrization, this would almost imply (5.33). However, we must deal with the contribution of the terms with the squiggly red underline. As we have seen in the discussion above (specifically (5.37) and (5.38)), these factors only contribute a diagonal matrix to the terms of minimal initial degree. Specifically, if:
(above, \(y_{l} = s_{l} = x_{l+1}\) in all summands with non-zero coefficient) then the terms of minimal initial degree in \(R_{\omega _k} X\) yield the following value for the coproduct (5.11):
where the various \(\psi _a^{\pm 1}\) factors arise from the diagonal terms of the series S(x), T(x) (see (5.10), (5.11)). Using (5.8), we may move the product of \(\psi \)’s on the left to join the product of \(\psi \)’s in the middle, at the cost of cancelling the powers of q:
As a consequence of the following straightforward claim:
Claim 5.19
The quantity (5.45) is a sum of tensors \(E_{x_uy_u} \otimes \cdots \otimes E_{x_v y_v}\) where:
for any \(r \in {{\mathbb {Z}}}/n{{\mathbb {Z}}}\).
we may rewrite (5.47) as:
Upon symmetrization with respect to those permutations \(\sigma \in S(k)\) which preserve the set \(\{1,\ldots ,l\}\), this yields precisely (5.33). \(\square \)
5.20. According to Lemma 5.15, the elements \(F_{[i;j)}^\mu , {\bar{F}}_{[i;j)}^\mu \in {{\mathcal {B}}}_\mu ^+\) are completely determined by the coproduct relations (5.33) and (5.34), together with their value under the linear functionals (5.19). Let us therefore compute the latter:
Proposition 5.21
For any \((i,j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) and \(\mu \in {{\mathbb {Q}}}\) such that \(\frac{j-i}{\mu } \in {{\mathbb {N}}}\), we have:
for any \((u,v) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) such that \([u;v) = [i;j)\).
Proof
Recall that \(F = F_{[i;j)}^\mu \) is given by the symmetrization (5.36), namely:
where \(R_\sigma \) is an arbitrary braid which lifts the permutation \(\sigma \). Of the k! summands in the right-hand side, only the one corresponding to the identity permutation is involved in the iterated residue of F at \(z_k = z_{k-1} {{\overline{q}}}^2\),..., \(z_2 = z_1 {{\overline{q}}}^2\), hence we obtain:
(in \(E_{bc}^{(a)} = E_{{\bar{b}}{\bar{c}}}^{(a)} z_a^{\left\lfloor \frac{b-1}{n} \right\rfloor - \left\lfloor \frac{c-1}{n} \right\rfloor }\), we must specialize \(z_a = y {{\overline{q}}}^{2a-2}\)). Note that:
due to (4.3). Since \({\widetilde{R}}\) is given by (4.2) and \(\underset{x={{\overline{q}}}^{-2}}{\text {Res}} Q(x) = q^{-1} \cdot (12)\), we have:
If we move the permutations \((b-1,b)\) all the way to the right, then we obtain:
With this in mind, (4.13) implies that:
Given formula (5.19) and the elementary identity:
we conclude (5.48). Formula (5.49) is proved analogously. \(\square \)
5.22. Let \(a\in {{\mathbb {Z}}}\) and \(b \in {{\mathbb {N}}}\) be coprime, set \(g = \gcd (n,a)\) and:
Recall the discussion in Sect. 3.21, in which the algebra:
was graded by \({{{{\mathbb {Z}}}}^n}\times {{\mathbb {Z}}}\), and its root generators were indexed as:
Comparing (3.21) and (3.32) with (5.33) and (5.48), respectively, Lemma 3.40 implies that there exists a bialgebra homomorphism:
Lemma 5.10 for \(|{{\textbf{d}}}| = k \mu \) implies that:
The right-hand side above is precisely equal to the dimension of the algebra \({{\mathcal {E}}}^+_\mu \) in degree \({{\textbf{d}}}\), so Corollary 3.41 implies:
Proposition 5.23
For any \(\mu \in {{\mathbb {Q}}}\), the map \(\Upsilon _\mu : {{\mathcal {E}}}_\mu ^+ \rightarrow {{\mathcal {B}}}_\mu ^+\) is an isomorphism.
5.24. Since \({{\mathcal {B}}}_\mu ^+\) is isomorphic to the algebra \({{\mathcal {E}}}_\mu ^+\), we may present it instead in terms of simple and imaginary generators (see Sect. 3.24 for the notation):
Since \(\Upsilon _\mu \) preserves the maps \(\alpha _{[u;v)}\), we have:
for all \((u,v) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\). By (5.48) and (5.49), the simple generators are given by:
if \(\gcd (j-i,\mu (j-i)) = 1\), but we do not know a closed formula for the imaginary generators (5.56). We will sometimes use the notation:
if \(j-i = \mu k\), \(nl = \mu k'\), in order to emphasize the fact that \(\deg P_{{{\textbf{d}}}}^{(k)} = ({{\textbf{d}}},k)\). Set:
if \(j = i + nl\) and \(\gcd (k,j-i)=1\). The reason for this (rather unusual) choice is to unify notation in what follows. Indeed, under the aforementioned assumptions, the numbers \(a = j-i\) and \(b = k\) are coprime. Since n|a, we have \(g = \gcd (n,a) = n\) and so the corresponding slope subalgebra \({{\mathcal {B}}}^+_\mu \) is isomorphic to \({U_q^+({\dot{{\mathfrak {gl}}}}_1)}^{\otimes n}\). This slope algebra does not have simple generators (only imaginary ones), so in (5.58) we are effectively relabeling its first imaginary generator as if it were a simple generator.
Theorem 5.25
We have an algebra isomorphism:
where \({{\mathcal {D}}}^+\) is the explicit algebra of Definition 3.25.
5.26. To prove Theorem 5.25, we need to show that the simple and imaginary generators of \({{\mathcal {B}}}_\mu ^+\) satisfy the analogues of relations (3.74) and (3.75). We recall the discussion of hinges from Sect. 5.6, and the fact (Definition 5.7) that a shuffle element X having slope \(\le \mu \) means that all the hinges of the terms in \(\Delta (X)\) are situated left of the ray of slope \(\mu \) from the origin (“left” refers to the usual direction in the lattice plane). We will also say that a point is “strictly left” of the ray of slope \(\mu \) to indicate that the point in question is not allowed to lie on the ray.
Proposition 5.27
Assume \(\gcd (j-i,k) = 1\), and consider the lattice triangle T: uniquely determined as the triangle of maximal area situated completely to the left of the vector \((j-i,k)\), which does not contain any lattice points inside. Let \(\mu \) denote the slope of one of the edges of T, as indicated in the pictures above. Then:
where \(\bullet = k- \frac{j-v+u-i}{\mu }\).
Proof
Due to (5.57), we may replace all P’s by F’s in formula (5.60). We will refine the proof of Proposition 5.17, so we will freely adapt the notations therein: let F and X be given by (5.36). The summands of \(\Delta (F)\) with leftmost possible hinge correspond to those tensors of minimal initial degree, which is:
(the notation \(\alpha _s,\beta _s\) is as in relation (5.41)). If we let \(y:= \sum _{s=1}^t (\beta _s - \alpha _s) = \# A\), where \(A = \{\sigma ^{-1}(1),\ldots ,\sigma ^{-1}(l)\}\), then it is easy to see that the lattice point (x, y) lies on the boundary or to the left of the lattice triangle T. This implies that all hinges of summands of \(\Delta (F)\) lie on the boundary or to the left of the triangle T. The boundary cases correspond to equality in (5.61), and they explicitly are:
-
for the picture on the left in Fig. 23: \(A = \{1,\ldots ,\beta \} \sqcup \{\alpha +1,\ldots ,k\}\) where \(\beta < \alpha \) have the property that \(\mu \alpha , \mu \beta \in {{\mathbb {Z}}}\)
-
for the picture on the right in Fig. 23: \(A = \{\alpha +1,\ldots ,\beta \}\) where \(\alpha < \beta \) have the property that \(\mu \alpha , \mu \beta \in {{\mathbb {Z}}}\)
We will only treat the situation in the first bullet (i.e. in the picture on the left), because that of the second bullet is analogous and will not be used in the present paper. Recall that \(\text {m.i.d. }Y\) stands for the terms of minimal initial degree of a k–tensor Y, i.e. the smallest value of the total \(|\text {hdeg}|\) of the first l tensor factors of Y (for fixed \(l \le k\)). We will now show that the terms of minimal initial degree give rise precisely to the tensors on the second line of (5.60). Explicitly, we have:

where the symbol \(E^{(u...v)}_{c_{u-1} |... | c_v}\) is defined in (5.45). As we have seen in the latter part of Proposition 5.17, the terms with the squiggly red underline contribute certain powers of q to the minimal initial degree of \(R_{\omega _k} X\). Specifically, let:
(we note that \(x_1 = j\), \(y_\beta = s_\beta = x_{\beta + 1}\), \(y_\alpha = s_\alpha = x_{\alpha +1}\), \(y_k = i\) in all summands above that have non-zero coefficient). Then \(\text {m.i.d. }\Delta (R_{\omega _k}X)\), which differs by certain powers of \(\psi _s^{\pm 1}\) from \(\text {m.i.d. }R_{\omega _k}X\), is given by:
Before we move on, we must explain three issues concerning the expression above: the power of q labeled “conjugation”, why \(y_\alpha = x_{\alpha +1} = s_\alpha \) were increased by 1, and why the factor \(-q^{-2}\) arose. The first issue, namely the power of q, appeared from the diagonal terms of arbitrary conjugation matrices \(R_\sigma \) and \(R_{\sigma }^{-1}\) as in (5.25), where \(\sigma \) is any permutation which switches the variables \(\{\beta +1,\ldots ,\alpha \}\) and \(\{\alpha +1,\ldots ,k\}\) (this is because in the definition of the coproduct, the variables to the left of the \(\otimes \) sign must all have smaller indices than the variables to the right of the \(\otimes \) sign). The latter two issues happened because of the presence of \(Q_{\alpha , \alpha +1}(z_{\alpha }/z_{\alpha +1})\) in the fourth squiggle. Because \(Q_{\alpha , \alpha +1}(\infty )\) has 0 on the diagonal, its contribution of minimal initial degree comes from the immediately off-diagonal terms, which are:
Therefore, for any indices u and v, we have:
Using (5.8), we may move certain \(\psi \) factors around in (5.62), in order to cancel the powers of q with underbraces beneath:
As a consequence of Claim 5.19, we may write the expression above as:
Symmetrizing the expression above with respect to all permutations \(\sigma \in S(k)\) which fix the set A gives rise to \(\text {m.i.d. }\Delta (F)\). To obtain the expression on the second line of (5.60), it remains to establish the formulas below (let \(u = s_\alpha + 1\) and \(v = s_\beta \)):
To prove the formulas above, we start with an easy computation:
Claim 5.28
We have the identity:
where \({\bar{E}}^{(u...v)}_{c_{u-1}|...|c_v} = \prod _{a=u}^{v} \left[ {\widetilde{R}}_{ua} \left( \frac{z_{u}}{z_a} \right) ... {\widetilde{R}}_{a-2,a} \left( \frac{z_{a-2}}{z_a} \right) {\bar{Q}}_{a-1,a} \left( \frac{z_{a-1}}{z_a} \right) E^{(a)}_{c_{a-1} c_a} {{\overline{q}}}^{\frac{2\overline{c_a}}{n}} \right] \).
Let us first show how the Claim allows us to complete the proof of the Proposition. Because of (5.67), formula (5.66) is equivalent to:
Then (5.64), (5.65), (5.68) follow from (5.31), (5.32) and the formulas below:
which are all straightforward consequences of our assumption on the triangle T. This completes the proof of formula (5.60) for the picture on the left in Fig. 23 (as we said, the case of the picture on the right is analogous, and left to the interested reader). As for Claim 5.28, we start with the following identity:
for all \(i,j,t \in {{\mathbb {Z}}}\). Indeed, by plugging in (5.27)–(5.28), formula (5.69) reads:
which is elementary. Identity (5.67) follows by \(k-1\) applications of (5.69). \(\square \)
Proof
of Theorem 5.25: As a consequence of Proposition 5.23, the assignment
yields an algebra homomorphism \({{\mathcal {E}}}^+_\mu \rightarrow {{\mathcal {A}}}^+\), for any \(\mu \in {{\mathbb {Q}}}\). To extend this to a homomorphism:
we need to prove that formulas (3.74) and (3.75) hold with p, f replaced by P, F. In order to show that (3.74) holds in this setup, let us first show that the linear maps \(\alpha _{[u;v)}\) take the same value on both sides of the equation. By (5.20), we have:
\(\forall u,v\). Therefore, Lemma 5.15 reduces the equality (3.74) to showing that:
We may depict the degree vectors of the elements \(P_{[i;j)}^{(k)}\), \(P_{l{\varvec{\delta }}, r}^{(k')}\), \(P_{[i;j+nl)}^{(k+k')}\) as:

We need to show that all the hinges of summands of \(\Delta (\text {LHS}\text { of }(\text {3.74}))\) are to the left the vector \((j-i+nl,k+k')\). Since coproduct is multiplicative, the hinges of \(\Delta (XY)\) are all among the sums of hinges of \(\Delta (X)\) and \(\Delta (Y)\), as vectors in \({{\mathbb {Z}}}^2\). By definition, the hinges of \(\Delta (P_{[i;j)}^{(k)})\) and \(\Delta (P_{l{\varvec{\delta }}, r}^{(k')})\) lie to the left of the vectors \((j-i,k)\) and \((nl,k')\), respectively. The sum of any two such hinges lies to the left of the parallelogram in the picture, except for the sum of the two hinges below:
Therefore, \(\Delta (P_{[i;j)}^{(k)}P_{l{\varvec{\delta }}, r}^{(k')})\) and \(\Delta (P_{l{\varvec{\delta }}, r}^{(k')}P_{[i;j)}^{(k)})\) both have a hinge at the point \((nl,k')\), but the corresponding summand in both coproducts is:
We conclude that this summand vanishes in \(\Delta (\text {LHS}\text { of } (3.74))\), which therefore has all the hinges to the left of \((j-i+nl,k+k')\). This completes the proof of (3.74).
Let us now prove (3.75) by induction on \(k+k'\) (the base case \(k+k' = 1\) is trivial). Recall that \(\mu = \frac{j+j'-i-i'}{k+k'}\), and let us represent the degrees of \(P_{[i;j)}^{(k)}\) and \(P_{[i';j')}^{(k')}\) as:

We have the following formulas, courtesy of Proposition 5.27:
where the ellipsis denotes terms whose hinges lie to the left of the line of slope \(\mu \) (this convention will remain in force for the remainder of this proof), and \(\bullet \) denotes the natural number which makes the two sides of the expressions above have the same vertical degree. Letting \(\text {LHS}\) denote the left-hand side of (3.75), we have:

Relation (5.8) allows us to move \(\psi \)’s around, and show that the expression with the squiggly underline vanishes, while the expression on the second line yields:
If we are only interested in the leading term \(\Delta _\mu \) of the coproduct, we may neglect the terms represented by the ellipsis. The induction hypothesis allows us to replace the term in square brackets by the RHS of (3.75) for \((i,j,k) \mapsto (u,v,\bullet )\), hence:
Let \(\gamma _{i'j'k'}(s) \in {{\mathbb {Q}}}(q,{{\overline{q}}}^{\frac{1}{n}})\) denote the constant in the round brackets on the second line above. By (5.33) and (5.34), notice that the formula above matches \(\Delta _\mu (\text {RHS})\). By Lemma 5.15, to prove that \(\text {LHS}= \text {RHS}\), it suffices to show that the two sides of equation (3.75) take the same values under the maps (5.19). To this end:
where \(d = \gcd (k+k',j+j'-i-i')\), while (5.20), (5.48) and (5.49) imply:
The equality between the right-hand sides of (5.71) and (5.72) was established in [15, Claim 4.6]. This concludes the proof of (3.75), so there exists an algebra homomorphism \(\Upsilon ^+\) as in (5.70). In the remainder of this proof, we need to show that \(\Upsilon ^+\) is an isomorphism. As explained in [15] (following the similar argument of [2]), one may use relations (3.74) and (3.75) to express an arbitrary product of the generators (5.55) and (5.56) as a linear combinations of products of the form:
where \(\{x^{(i)}_\mu \}\) go over any linear basis of \({{\mathcal {B}}}_\mu ^+\), and \(\prod ^\rightarrow _\mu \) is taken in increasing order of \(\mu \).
Claim 5.29
The elements (5.73) are all linearly independent in \({{\mathcal {A}}}^+\).
Let us first show how the Claim above completes the proof of the Theorem. The linear independence of the elements (5.73) implies that:
for all \(\mu \), k, \({{\textbf{d}}}\) (indeed, (3.27) implies that the number of products \(\prod _{\rho \le \mu } x_\rho ^{(i)}\) is precisely equal to the number in the RHS of (5.74)). Combining (5.74) with Lemma 5.10, we conclude that the products (5.73) actually form a linear basis of \({{\mathcal {A}}}^+\). This implies that \(\Upsilon ^+\) is an isomorphism, since Definition 3.25 says that the same products also form a linear basis of \({{\mathcal {D}}}^+\).
Let us now prove Claim 5.29. For any \(\mu \), we assume that the basis vectors \(x_\mu ^{(i)}\) of \({{\mathcal {B}}}_\mu ^+\) are ordered in non-decreasing order of \(|\text {hdeg}|\), i.e.:
Now suppose we have a non-trivial linear relation among the various products (5.73). We may rewrite this hypothetical relation as:
where all terms in the RHS have \(i' < i\). Since the coproduct is multiplicative, then all the hinges of \(\Delta (XY)\) are sums of hinges of \(\Delta (X)\) and hinges of \(\Delta (Y)\), as vectors in \({{\mathbb {Z}}}^2\). Therefore, \(\Delta (\text {LHS}\text { of }(5.76))\) has a single summand with hinge at the lattice point:
and the corresponding summand is precisely:
where \(\psi \) stands for a certain (unimportant) product of \(\psi _a^{\pm 1}\)’s. Meanwhile, the coproduct of the RHS of (5.76) can only have a hinge at a lattice point (5.77) if \(|\text {hdeg }x_\mu ^{(i)}| = |\text {hdeg }x_{\mu }^{(i')}|\). The corresponding summand in the coproduct is:
Since \(x_\mu ^{(i)}\) cannot be expressed as a linear combination of \(x_\mu ^{(i')}\) with \(i' < i\), the right-hand sides of expressions (5.78) and (5.79) cannot be equal. This contradiction implies that there can be no relation (5.76), which proves Claim 5.29. \(\square \)
Corollary 5.30
The algebra \({{\mathcal {A}}}^+\) is generated by the \(\text {vdeg }= 1\) elements:
The corollary is an immediate consequence of Proposition 3.42 and Theorem 5.25. In [16, Theorem 1.2 and Definition 2.3], we will construct explicit quadratic relations satisfied by the generators \(E_{ij} \in {{\mathcal {A}}}^+\), in the language of formal series.
6 The double shuffle algebra with spectral parameters
In the previous section, we constructed the extended shuffle algebra corresponding to the R–matrix with spectral parameters (3.88). We will now take two such extended shuffle algebras and construct their double, as was done in Sects. 2.10 and 2.12 for R–matrices without spectral parameters. This will conclude the proof of Theorem 1.5.
6.1. Let \({{\overline{q}}}_+ = {{\overline{q}}}\) and \({{\overline{q}}}_- = q^{-n} {{\overline{q}}}^{-1}\). If \({\widetilde{R}}^+(x) = {\widetilde{R}}(x)\) is given by (4.2), then:
is given by:
Note that we have the equality:
where \(D = \text {diag}(q^2,\ldots ,q^{2n}) \in \text {End}(V)\).
Definition 6.2
The shuffle algebra \({{\mathcal {A}}}^-\) is defined just like in Definition 4.8, using \({{\overline{q}}}_-\) instead of \({{\overline{q}}}\), and the multiplication (4.9) uses \({\widetilde{R}}^-\) instead of \({\widetilde{R}}\).
Because of (6.2), the map:
is a \({{\mathbb {Q}}}(q)\)–linear algebra isomorphism. The following elements of \({{\mathcal {A}}}^-\) are the images of the elements (5.31)–(5.32) under \(\Phi \), times a factor of \({{\overline{q}}}_-^{\frac{2{\bar{j}}-2{\bar{i}}}{n}}\):
where \(s_a = j - \lceil \mu a \rceil \), \(s'_a = j - \lfloor \mu a \rfloor \), \(Q^- = D_2 Q D_2^{-1} |_{{{\overline{q}}}\mapsto {{\overline{q}}}_-}\), \({\bar{Q}}^- = D_2 {\bar{Q}}D_2^{-1}|_{{{\overline{q}}}\mapsto {{\overline{q}}}_-}\).
6.3. In Definition 5.2, we defined the extended shuffle algebra by introducing new generators. We will now add two more central elements c and \({\bar{c}}\), and define instead:
where:
for any \(X^\pm = X^\pm _{1...k}(z_1,\ldots ,z_k) \in {{\mathcal {A}}}^\pm \subset {\widetilde{{{\mathcal {A}}}}}^\pm \), where:
If we define the series \(T^\pm (x)\) by (3.106) and (3.107), then (6.8) is equivalent to:
6.4. The algebras \({\widetilde{{{\mathcal {A}}}}}^\pm \) are graded by \({{{{\mathbb {Z}}}}^n}\times {{\mathbb {Z}}}\), with:
where \({{\textbf{d}}}\in {{{{\mathbb {Z}}}}^n}\) is defined according to (4.20). We write \(\deg X = (\text {hdeg }X, \text {vdeg }X)\) to specify the components of the degree vector in \({{{{\mathbb {Z}}}}^n}\) and \({{\mathbb {Z}}}\), respectively. The reason why we introduced central elements c and \({\bar{c}}\) to the algebras (6.6) is to twist the coproduct. Specifically, let \(\Delta _{\text {old}}\) be the coproduct of (5.9)–(5.10), and define:
by the formulas \(\Delta (c) = c \otimes c\), \(\Delta ({\bar{c}}) = {\bar{c}}\otimes {\bar{c}}\), as well as:
Since \(\deg X\) is multiplicative in X, the fact that \(\Delta _{\text {old}}\) is coassociative and an algebra homomorphism implies the analogous statements for the coproduct \(\Delta \).
6.5. We must now prove an analogue of Proposition 2.11, but the main difficulty in doing so is (2.32): given \(X, Y \in \text {End}(V^{\otimes k})(z_1,\ldots ,z_k)\), we can still define the trace of XY, but the answer will be a rational function in \(z_1,\ldots ,z_k\). To obtain a number, one must integrate out the variables \(z_1,\ldots ,z_k\), and the choice of contours will be crucial.
Let us consider the following expressions, for any \(\sigma \in S(k)\):
Explicitly, the product in \(R_\sigma \) is taken by following the crossings in the positive braid lifting the permutation \(\sigma \), while \({\overline{R}}_\sigma \) is defined as \(\sigma R_{\sigma ^{-1}} \sigma ^{-1}\). It is elementary to prove the following equation for all \(\sigma \in S(k)\):
where \(\omega _k\) denotes the longest permutation. We may use \({\overline{R}}_\sigma ^{-1}\) instead of \(R_\sigma \) in (5.25) because they both lift the permutation \(\sigma \), and thus we obtain:
for all \(I_1,\ldots , I_k \in \text {End}(V)[z^{\pm 1}] \subset {{\mathcal {A}}}^\pm \). By Corollary 5.30, any element of \({{\mathcal {A}}}^\pm \) is a linear combination of the shuffle elements (6.12), for various \(I_1,\ldots ,I_k\).
Proposition 6.6
There is a pairing (of vector spaces):
given by:
for all \(I_1,\ldots ,I_k, J_1,\ldots ,J_k \in \text {End} (V)[z^{\pm 1}]\) and all \(X^\pm \in {{\mathcal {A}}}^\pm \). The notation:
refers to the iterated residue of F at 0: first in \(z_1\), then in \(z_2\),..., finally in \(z_k\).
Note that the pairing \(\langle X^+, Y^- \rangle \) is only non-zero for pairs of elements of opposite degrees, i.e. \(X^+ \in {{\mathcal {A}}}_{{{\textbf{d}}},k}\) and \(Y^- \in {{\mathcal {A}}}_{-{{\textbf{d}}},-k}\) for various \(({{\textbf{d}}},k) \in {{{{\mathbb {Z}}}}^n}\times {{\mathbb {N}}}\).
Proof
Formula (6.14) is well-defined as a linear functional in the second argument, while (6.15) is well-defined as a linear functional in the first argument. Therefore, to show that (6.13) is well-defined as a linear functional in both arguments, we only need to show that (6.14) and (6.15) produce the same result when \(X^\pm \) is of the form (6.12) (this statement implicitly uses Corollary 5.30, which states that any element in \({{\mathcal {A}}}^\pm \) is a linear combination of the elements (6.12)). To this end, we have:
and:
By using the cyclic property of the trace and the straightforward identity:
(which uses (4.6)) we may rewrite the formulas above as:
and:
If we replace \(\sigma \mapsto \sigma ^{-1}\) and replace \(z_a \mapsto z_{\sigma (a)}\) in the latter formula, then it precisely matches (6.19) (this uses the fact that \(\text {Tr}(Y) = \text {Tr}(\sigma Y \sigma ^{-1})\) for any tensor Y), up to the fact that the order of the contours changes:
Therefore, we may conclude that (6.16) equals (6.17) (which is what we need to prove), once we show that we may change the contours of the integral (6.19):
The integrand of (6.19) has three kinds of poles:
-
\(z_i = z_j q^{\pm 2}\) if \(i<j\) and \(\sigma ^{-1}(i) < \sigma ^{-1}(j)\), which arise from the zeroes of f(x)
-
\(z_i {{\overline{q}}}_+^2 = z_j\) if \(i<j\), which arise from the poles of \({\widetilde{R}}^+(x)\)
-
\(z_i {{\overline{q}}}_-^2 = z_j\) if \(\sigma ^{-1}(i) < \sigma ^{-1}(j)\), which arise from the poles of \({\widetilde{R}}^-(x)\)
(note that the terms \(R_{\sigma \omega _k}\) and \(R_{\sigma ^{-1}\omega _k}\) do not produce poles at \(z_i=z_j\) in the integrand (6.19), because such poles are canceled by the denominator of f). As we move the contours as in (6.21), the only poles encountered involve \(z_i\) and \(z_j\) for \(i<j\) and \(\sigma ^{-1}(i) > \sigma ^{-1}(j)\), so already the poles in the first bullet do not come up. Meanwhile, the poles in the second bullet may come up, and in the remainder of this proof, we will show that the corresponding residue is 0 (the situation of the poles in the third bullet is analogous, so we skip it). To this end, recall that:
by the definition of \({\widetilde{R}}^-\) in (6.1). This implies the identity:
for any \(A, B \in \text {End}(V)\). Taking the residue at \(z = {{\overline{q}}}^{-2}\), we obtain:
We may generalize the formula above to:
\(\forall i \ne j\) and \(A, B \in \text {End}(V^{\otimes k-1})\). Formula (6.22) implies (6.23) because none the indices, other than the i–th and j–th, play any role in the vanishing of the trace.

We will use (6.23) to prove that the residue of the integrand of (6.19) at \(z_i {{\overline{q}}}_+^2 = z_j\) vanishes. Let us consider the expression on the second line of (6.19) for \(\sigma = \omega _k\) and take its residue at \(z_i {{\overline{q}}}_+^2 = z_j\). The corresponding quantity is precisely represented by Braid 1 on the previous page (we draw braids top-to-bottom instead of left-to-right, for better legibility), if we make the convention that the variable on each strand is multiplied by \({{\overline{q}}}_+^2\) and \({{\overline{q}}}_-^2\) (respectively) as soon as it reaches the first and the second (respectively) box on the strand in question. Braids 1,2,3 and 4 are equivalent due to Reidemeister moves and the move in Fig. 13. Braids 4 and 5 do not represent equal endomorphisms of \(V^{\otimes k}\), but they are equal upon taking the trace (since \(\text {Tr}(AB) = \text {Tr}(BA)\)). Finally, Braids 5 and 6 are equal due to Reidemeister moves. The crossing between the blue and green strands in Braid 6 represents \({\widetilde{R}}^-_{ij}({{\overline{q}}}^2)\), and we will call the portion of the braid above (respectively below) this crossing A (respectively B). Then identity (6.23) applies, thus showing that Braid 6 has zero trace, precisely what we needed to prove.
Strictly speaking, the argument just given covers the case \(i=2\), \(j=4\) and \(k=5\), but it is obvious that we may replace the strands labeled 1,3,5 by any number of parallel strands, thus yielding the situation of arbitrary i, j, k. More crucial is the fact that we have only shown the vanishing of the residue at \(z_i {{\overline{q}}}_+^2 = z_j\) of the \(\sigma = \omega _k\) summand of (6.19). The case of general \(\sigma \) would require one to insert the positive braid representing the permutation \(\sigma \omega _k\) at the middle of the braids above and the positive braid representing the permutation \(\sigma ^{-1}\omega _k\) at the bottom of the braids above. The braid moves involved are analogous to the ones just performed, with the idea being to move the crossing between the blue and green strands to the very left of all other crossings. We leave the visual depiction of this fact to the interested reader, but we stress the fact that we only need to check the vanishing of the residue for those \(i<j\) such that \(\sigma ^{-1}(i) > \sigma ^{-1}(j)\). This implies that the green and blue strands do not cross except at the two points already depicted in the braids above, and this is what allows the argument to carry through. \(\square \)
Proposition 6.7
There exists a bialgebra pairing:
generated by (6.13) and:
(all rational functions above are expanded as power series in the region \(|x| \ll |y|\)).
Proof
The proof follows that of Proposition 2.11 very closely, so we will only sketch the main ideas and leave the details as an exercise to the reader. Take any:
and define \(\langle ab, c \rangle \) to be the RHS of (2.28). Then if \(\sum _{i} a_i b_i = 0\) holds in \({\widetilde{{{\mathcal {A}}}}}^+\), we must show that the pairing:
thus defined is 0. If at least one of a, b, c is a coefficient of either \(S^\pm (x)\) or \(T^\pm (x)\), then the statement in question is proved just like in Proposition 2.11, if one is careful to expand x around \(\infty ^{\pm 1}\) (since (6.14)–(6.15) also involve integrals, we need to stipulate that x should be closer to \(\infty ^{\pm 1}\) than any of the variables \(z_1,..,z_k\)).
The remaining case is when a, b, c are all in \({{\mathcal {A}}}^\pm \), and we must prove that:
for all \(A_{1...k}(z_1,\ldots ,z_k), B_{1...l}(z_1,\ldots ,z_l) \in {{\mathcal {A}}}^+\) and \(Y_{1...k+l}(z_1,\ldots ,z_{k+l}) \in {{\mathcal {A}}}^-\). By Corollary 5.30, it suffices to consider \(A = I_1 *... * I_k\) and \(B = I_{k+1} *... * I_{k+l}\) for various \(I_1,\ldots ,I_{k+l} \in \text {End}(V)[z^{\pm 1}]\). In this case, we may rewrite (6.14) as:
by reversing the order of the tensor factors of \(V^{\otimes k}\) and relabeling the variables \(z_a \mapsto z_{k+1-a}\), as well as using the symmetry property (4.10) of X. Then we have:
Meanwhile, the right-hand side of (6.27) is computed just like the right-hand side of (2.36), with the specification that \(\Delta (Y)\) is expanded in the region when the first k tensor factors are much smaller than the last l tensor factors. Thus, we obtain:
We may move \({\overline{R}}_{\omega _k}\) to the very right of the expression above, and obtain precisely (6.29). This completes the proof of the fact that the pairing (6.24) respects (2.28). The situation of (2.29) is analogous, so we leave it as an exercise to the reader. \(\square \)
6.8. Having proved Proposition 6.7, we may construct the Drinfeld double:
We will often use the notation \(\psi _i = (s^+_{[i;i)})^{-1}\).
Proposition 6.9
We have the following commutation relations in the algebra \({{\mathcal {A}}}\):
if \(X^\pm = X_{1...k}^\pm (z_1,\ldots ,z_k) \in {{\mathcal {A}}}^\pm \), where we recall that \(\cdot _+ = \cdot \) and \(\cdot _- = \cdot ^{\text {op} }\). Finally:
(we set \(s^\pm _{[i;j)} = t^\pm _{[i;j)} = 0\) if \(i>j\)).
Proof
Formulas (6.31) and (6.32) are proved just like (2.42) and (2.43) (the presence of c is due to the twist in the coproduct (6.10)), and so we leave them as exercises to the interested reader. As far as (6.33) is concerned, we note the definition (6.11) of the coproduct implies the following analogue of formula (2.47):
in \({\widetilde{{{\mathcal {A}}}}}^+\), as well as the following analogue of (2.48):
in \({\widetilde{{{\mathcal {A}}}}}^{-,\text {op},{\text {coop}}}\). Then (6.33) is simply an application of (2.39). \(\square \)
Proof
of Theorem 1.5 (in the formulation of subsection 3.30): Let us write:
for the subalgebra generated by the coefficients of the series \(S^\pm (x)\) and \(T^\pm (x)\). Then \({{\mathcal {A}}}^0\) is isomorphic to the subalgebra \({{\mathcal {D}}}^0\) of Sect. 3.26, because they are both isomorphic to the algebra \({{\mathcal {E}}}\) of Definition 3.32. Moreover, Theorem 5.25 (and its analogue when \({{\mathcal {A}}}^+\) is replaced by \({{\mathcal {A}}}^-\)) give rise to algebra isomorphisms:
Putting the preceding remarks together yields an isomorphism of vector spaces:
where the first isomorphism holds by definition, and the last isomorphism follows from (6.30). To show that \(\Upsilon \) is an algebra isomorphism, one needs to show that:
for all \(a,b \in {{\mathcal {D}}}\). By Proposition 3.42, we may assume that:
for various \(x_i,x_i' \in {{\mathcal {D}}}^+\) of \(\text {vdeg }= 1\), \(y_i,y_i' \in {{\mathcal {D}}}^-\) of \(\text {vdeg }= -1\), and \(\alpha ,\beta \in {{\mathcal {D}}}^0\). To compute the left-hand side of (6.37), one takes:
and uses relations  to write it as:
to write it as:
for various \(x_i'' \in {{\mathcal {D}}}^+\) of \(\text {vdeg }= 1\), \(y_i'' \in {{\mathcal {D}}}^-\) of \(\text {vdeg }= -1\), and \(\gamma \in {{\mathcal {D}}}^0\). Similarly:
can be expressed using relations  as:
as:
where the coefficients and the various \(x_i'',y_i'',\gamma \) are the same ones as in (6.38). The reason for the latter fact is that the squiggly underlined relations above match each other pairwise. By its very definition in (6.36), \(\Upsilon \) applied to the right-hand side of (6.38) is precisely the right hand side of (6.39), thus completing the proof. \(\square \)
6.10. We will now study the bialgebra pairing between \({\widetilde{{{\mathcal {A}}}}}^+\) and \({\widetilde{{{\mathcal {A}}}}}^-\) in more detail, with the goal of proving certain formulas that will be used in [16]. Let us consider the restriction of the pairing (6.24) to the following subalgebras:
for all \(\mu \in {{\mathbb {Q}}}\sqcup \infty \).
Proposition 6.11
For all \(\mu \in {{\mathbb {Q}}}\sqcup \infty \), the pairing (6.40) is a bialgebra pairing, i.e. it intertwines the product with the coproduct \(\Delta _\mu \), in the sense of (2.28)–(2.29).
Proof
Let us prove (2.28), and leave (2.29) as an exercise to the interested reader. Take formula (6.27), which we already proved in the course of Proposition 6.7:
If we let \(A^+,B^+ \in {{\mathcal {B}}}_\mu ^+\) and \(Y^- \in {{\mathcal {B}}}_\mu ^-\), then our task is equivalent to showing that the formula above holds with \(\Delta \) replaced by \(\Delta _\mu \). Since \(Y^- \in {{\mathcal {B}}}_\mu ^-\), we have:
(the reason why the formula above differs from (5.11) is that slope lines are reflected across the horizontal line when going from \({{\mathcal {A}}}^+\) to \({{\mathcal {A}}}^-\), due to opposite vertical grading conventions). All the summands in the right-hand side of (6.42) other than \(\Delta _\mu (Y^-)\) pair trivially with \(B^+ \otimes A^+\), for degree reasons. This implies that (6.41) holds with \(\Delta \) replaced by \(\Delta _\mu \). \(\square \)
As a consequence of Proposition 6.11, the Drinfeld double:
defined with respect to the coproduct \(\Delta _\mu \), will be a subalgebra of the algebra \({{\mathcal {A}}}\) of (6.30). Moreover, the following diagram commutes, for all \(\mu \in {{\mathbb {Q}}}\sqcup \infty \):

where the vertical map on the left is the natural double of the isomorphism \(\Upsilon _\mu \) of Proposition 5.23, and the vertical map on the right is the isomorphism \(\Upsilon \) of (6.36).
6.12. Let us consider any \(\mu \in {{\mathbb {Q}}}\sqcup \infty \). As we have seen in Sect. 3.21, the subalgebra \({{\mathcal {E}}}_\mu \subset {{\mathcal {D}}}\) is generated by the elements:
which satisfy the coproduct relations of Proposition 3.23, as well as formulas (3.65)–(3.66) for their images under the maps \(\alpha _{\pm [i;j)}\). When we pass the elements above through the vertical isomorphisms of diagram (6.43), we obtain:
defined in (5.31)–(5.32) when the sign is \(+\), and in (6.4)–(6.5) when the sign is −. As proved for the case \(\pm = +\) in Proposition 5.17 (the case \(\pm = -\) is analogous, and we leave it as an exercise to the interested reader), the elements \(F,{\bar{F}}\) satisfy the analogous coproduct relations as \(f,{\bar{f}}\). Similarly, we have the following formulas:
where the linear maps:
are given by:
Recall that \(X^{(k)}(y) \in \text {End}(V)[y^{\pm 1}]\) was defined by Fig. 15, for any \(X \in {{\mathcal {A}}}_k\). Meanwhile, for any \(Y \in {{\mathcal {A}}}_{-k}\), the symbol \(Y^{(k)}(y)\) is defined analogously, but with \({{\overline{q}}}\) replaced by \({{\overline{q}}}_-\), and the operators \(D_1...D_k\) placed in front of the braid in Fig. 15. Formulas (6.44)–(6.45) were proved when \(\pm = +\) in Proposition 5.17, and the case when \(\pm = -\) is an analogous exercise that we leave to the interested reader.
6.13. As we have seen in Sect. 3.24, the subalgebra \({{\mathcal {E}}}_\mu \) is also generated by the primitive elements:
where \(\mu = \frac{a}{b}\) with \(\gcd (a,b) = 1\), \(b \ge 0\) and \(g = \gcd (n,a)\). These primitive elements satisfy formulas (3.69)–(3.70). When we pass the elements above through the vertical isomorphisms of diagram (6.43), we obtain:
The elements (6.47) are primitive for the coproduct \(\Delta _\mu \), and moreover satisfy the following analogues of formulas (3.69) and (3.70):
6.14. Proposition 3.23 gives us formulas for the coproducts of the elements (3.63). Meanwhile, the elements (3.71) are primitive, so there are no intermediate terms in their coproduct. Therefore, we may apply relation (2.39) between the two halves of the bialgebra \({{\mathcal {B}}}_\mu \), and obtain the following formulas:
for all \((i,j),(i',j') \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) such that \(j-i=j'-i' \in {{\mathbb {N}}}\mu \). Similarly, we have:
for all \(l \in {{\mathbb {Z}}}\) and \((i',j') \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) such that \(nl = j'-i' \in {{\mathbb {N}}}\mu \), and \(r \in {{\mathbb {Z}}}/g{{\mathbb {Z}}}\) where \(g = \gcd (n,\text {numerator } \mu )\). Similar formulas were worked out in [15] between the p and \(f,{\bar{f}}\) generators in \({{\mathcal {E}}}_\mu \), but with explicit numbers instead of the pairings in the right-hand side. Therefore, the fact that \(\Upsilon _\mu \) is an isomorphism implies the following explicit formulas for the pairings above:
for all applicable indices. Comparing the formulas above with (6.48)–(6.49) yields:
Proposition 6.15
For any \((i,j) \in \frac{{{\mathbb {Z}}}^2}{(n,n){{\mathbb {Z}}}}\) and \(k \in {{\mathbb {N}}}\) such that \(\mu = \frac{j-i}{k}\), we have:
for all \(X \in {{\mathcal {B}}}_\mu ^+\) and \(Y \in {{\mathcal {B}}}_{\mu }^-\).
Proof
We will only prove (6.55) as it will be used in [16], and leave the analogous formula (6.54) as an exercise to the interested reader. Comparing formulas (6.48), (6.49) with (6.51), (6.53) shows us that formula (6.55) holds when Y is one of the primitive generators of \({{\mathcal {B}}}_\mu ^-\). Therefore, all that remains to show is that if (6.55) holds for \(Y,Y' \in {{\mathcal {B}}}_\mu ^-\), then it also holds for \(Y * Y'\). This follows by comparing:
with (3.31). \(\square \)
Notes
The meaning of the indexing sets in the three products of R’s or \({\widetilde{R}}\)’s is that the factors in:
$$\begin{aligned} {\widetilde{R}}_{a_1b_l}... {\widetilde{R}}_{a_kb_1} \end{aligned}$$are taken in any order such that \((a_i,b_j)\) is to the left of \((a_{i'},b_j)\) if \(i<i'\) and to the right of \((a_i,b_{j'})\) if \(j<j'\). The text “only if \(a_i < b_j\)” or “only if \(a_i > b_j\)” under such a product means that only those pairs of indices \((a_i,b_j)\) satisfying the respective inequalities occur in the product.
We write \(f_{ij} = f_{ji}\) for the scalar \(f \in \text {Aut}(V \otimes V)\), interpreted as an element of \(\text {Aut}(V^{\otimes k})\) via the inclusion of the i-th and j-th tensor factors. This notation will come in handy in Sect. 5, when \(f_{ij}\) will be a scalar-valued rational function in the variable \(z_i/z_j\).
We note that the algebra defined below is slightly larger than the usual quantum group, since the Cartan part of the latter is generated by the ratios \(\frac{\psi _i}{\psi _j}\), instead of \(\psi ^{\pm 1}_1,\ldots ,\psi _n^{\pm 1}\) themselves.
The antipode is a bialgebra anti-automorphism \(A:: {{\mathcal {E}}}\rightarrow {{\mathcal {E}}}\) obeying certain compatibility conditions with the product, coproduct and pairing. We choose to write A(x) instead of the more common S(x) so as to not confuse the antipode with the series S(x) of Sect. 3.31.
The notation \(s \in \{i,\ldots ,j\}\) means “s runs between i and j”, for either \(i<j\) or \(i>j\).
Note that the slope \(\mu \) in loc. cit. is actually \(\frac{1}{\mu }\) in our notation.
In the formula above, \(\langle \cdot , \cdot \rangle \) is the bilinear form on \({{\mathbb {Z}}}^n\) given by \(\langle {\varvec{\varsigma }}^i, {\varvec{\varsigma }}^j \rangle = \delta _{i}^{j} - \delta _{i}^{j+1}\)
Although we will not need it, formula (4.15) admits the following generalization for any \(X \in {{\mathcal {A}}}^+\) and any composition \(\lambda = (\lambda _1,\ldots ,\lambda _u)\) of k:
$$\begin{aligned} X^{\lambda }_{...,s,...t,...}(...,y_s,\ldots ,y_t,...) = R_{(st)} \cdot X^{\lambda '}_{...,t,...s,...}(...,y_t,\ldots ,y_s,...) \cdot R_{(st)}^{-1} \end{aligned}$$where \(\lambda '\) denotes the composition obtained from \(\lambda \) by switching the s-th and the t-th entries.
More generally, we will extend the notation above to a k-fold tensor, by the rule:

as elements of \(\text {End}(V^{\otimes k}) [z_1^{\pm 1},\ldots , z_k^{\pm 1}]\)
Recall that \(\lambda = (\lambda _1 \le .. \le \lambda _u) \le \lambda ' = (\lambda '_1 \le ... \le \lambda '_v)\) if \(\lambda _u+\cdots +\lambda _{u-s+1} \le \lambda '_v+... +\lambda '_{v-s+1}\) for all s, but \(\lambda _u+\cdots +\lambda _1 = \lambda '_v+\cdots +\lambda '_1\).
References
Beck, J.: Braid group action and quantum affine algebras. Commun. Math. Phys. 165, 555–568 (1994)
Burban, I., Schiffmann, O.: On the Hall algebra of an elliptic curve, I. Duke Math. J. 161(7), 1171–1231 (2012)
Ding, J., Frenkel, I.: Isomorphism of two realizations of quantum affine algebra \(U_q({\widehat{{{\mathfrak{gl} }}}}_n)\). Commun. Math. Phys. 156(2), 277–300 (1993)
Ding, J., Iohara, K.: Generalization of Drinfeld quantum affine algebras. Lett. Math. Phys. 41(2), 181–193 (1997)
Drinfeld, V.G.: A new realization of Yangians and quantized affine algebras. Soviet Math. Dokl. 36, 212–216 (1988)
Enriquez, B.: On correlation functions of Drinfeld currents and shuffle algebras. Transform. Groups 5(2), 111–120 (2000)
Faddeev, L., Reshetikhin, N., Takhtajan, L.: Quantization of Lie groups and Lie algebras. Leningrad Math. J. 1, 193–226 (1990)
Feigin, B., Hashizume, K., Hoshino, A., Shiraishi, J., Yanagida, S.: A commutative algebra on degenerate \(\mathbb{C}\mathbb{P}^1\) and MacDonald polynomials. J. Math. Phys. 50(9) (2009)
Feigin, B., Jimbo, M., Miwa, T., Mukhin, E.: Representations of quantum toroidal \({{\mathfrak{gl} }}_n\). J. Algebra 380, 78–108 (2013)
Feigin, B., Odesskii, A.: Vector bundles on elliptic curve and Sklyanin algebras, Topics in Quantum Groups and Finite-Type Invariants. Am. Math. Soc. Transl. Ser. 2, 185 (1998). Am. Math. Soc. 65–84
Miki, K.: A \((q, \gamma )\) analog of the \(W_{1+\infty }\) algebra. J. Math. Phys. 48(12) (2007)
Mudrov, A.I.: Reflection equation and twisted Yangians. J. Math. Phys. 48, 093501 (2007)
Neguț, A.: Shuffle algebra revisited. Int. Math. Res. Not. 2014(22), 6242–6275 (2014)
Neguț, A.: Quantum toroidal and shuffle algebras. Adv. Math. 372, 107288 (2020)
Neguț, A.: PBW basis for \({U_{q,{\overline{q}}}(\ddot{{{\mathfrak{gl} }}}_n)}\). Transform. Groups (2022). https://doi.org/10.1007/s00031-022-09696-x
Neguț, A.: Deformed \(W\)-algebras in type \(A\) for rectangular nilpotent. Commun. Math. Phys. 389, 153–195 (2022)
Schiffmann, O.: Drinfeld realization of the elliptic Hall algebra. J. Algebr. Comb. 35(2), 237–262 (2012)
Wendlandt, C.: The \(R\)-matrix presentation for the Yangian of a simple lie algebra. Commun. Math. Phys. 363(1), 289–332 (2018)
Funding
’Open Access funding provided by the MIT Libraries’
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neguț, A. A tale of two shuffle algebras. Sel. Math. New Ser. 30, 62 (2024). https://doi.org/10.1007/s00029-024-00941-7
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-024-00941-7