Abstract
It is well known that braided monoidal categories are the categorical algebras of the little two-dimensional disks operad. We introduce involutive little disks operads, which are \({\mathbb {Z}}_2\)-orbifold versions of the little disks operads. We classify their categorical algebras and describe these explicitly in terms of a finite list of functors, natural isomorphisms and coherence equations. In dimension two, the categorical algebras are braided monoidal categories with an anti-involution together with a pointed module category carrying a universal solution to the (twisted) reflection equation. Examples of these are obtained from the categories of representations of a ribbon Hopf algebra with an involution and a quasi-triangular coideal subalgebra, such as a quantum group and a quantum symmetric pair coideal subalgebra.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we introduce and study the operad of involutive little disks. We show that its operations naturally encode the symmetries of quantum groups and quantum symmetric pairs. Quantum groups are of course well-studied and known to have myriad connections to other parts of mathematics. Only in recent years, however, have quantum symmetric pairs come to the forefront of research on quantum groups.
A quantum symmetric pair consists of a quantum group together with a subalgebra that quantizes the subgroup of fixed points of some given involution. In the 90s, examples of quantum symmetric pairs were constructed on a case-by-case basis by Noumi, Sugitani and Dijkhuizen using solutions to the reflection equation [59,60,61]. This equation, sometimes called the ‘boundary Yang–Baxter equation’, was introduced by Cherednik in the context of particle scattering on a half line [20] and Sklyanin’s study of quantum integrable systems with non-periodic boundary conditions [45, 63]. The motivation of the work of Noumi–Sugitani–Dijkhuizen was to study q-orthogonal polynomials (e.g. Askey–Wilson polynomials [4], Macdonald polynomials [53] and Koornwinder polynomials [44]) as zonal spherical functions on quantum symmetric spaces; a field which is sometimes called ‘quantum harmonic analysis’ [22, 42, 43]. A complete classification of quantum symmetric pairs was later achieved by Letzter [46,47,48]. Kolb then extended the theory of quantum symmetric pairs to include Kac–Moody algebras, with examples such as twisted q-Yangians and q-Onsager algebras [39].
In recent years the reflection equations appeared in a more methodical way in the theory of quantum symmetric pairs. Kolb and Stokman showed that an invertible solution to a type A reflection equation is exactly a character of the reflection equation algebra \({\mathcal {O}}_q (\text {SL}_n)\) [41]. From such a character they construct a coideal subalgebra of the quantum group. Their method recovers the type AIII/AIV quantum symmetric pairs, see Table 1, streamlining the approach of Noumi–Sugitani–Dijkhuizen. Furthermore, Balagovic and Kolb showed that any pair in Letzter’s classification carries a canonical solution to a reflection equation, called a universal K-matrix [8, 40]. Such solutions can be used for applications to low-dimensional topology in the spirit of the celebrated Reshetikhin–Turaev knot invariants [64, 65].
A categorical approach to the reflection equations, as well as Letzter’s classification of quantum symmetric pairs, allowed for applications to geometric representation theory. Jordan and Ma used quantum symmetric pairs to construct representations of the double affine braid group and of the double affine Hecke algebra of type \(C^{\vee }C_n\) [35]. Ehrig and Stroppel showed that translation functors in parabolic category \({\mathcal {O}}\) in type D categorify the action of a quantum symmetric pair [25]. The same result was shown to hold in type B by Bao and Wang [12]. Further work by Bao and Wang on type AIII/AIV quantum symmetric pairs shows such quantum symmetric pairs admit a canonical basis [10]. Furthermore, they have a geometric interpretation through the geometry of partial flag varieties of type B/C [9], and are Schur–Weyl dual to Hecke algebras of type B [11].
One of the fundamental properties of the Drinfeld–Jimbo quantum group is that it is a quasi-triangular Hopf algebra: it has a universal R-matrix providing solutions to the Yang–Baxter equation. We can rephrase this by saying that the category of finite dimensional modules of a quantum group is a braided monoidal category. In this paper we introduce a categorical framework, called a \({\mathbb {Z}}_2\)-braided pair, which exactly encodes the structure of the universal K-matrix of a quantum symmetric pair; analogous to how a braided monoidal category encodes the R-matrix.
It is well known that braided monoidal categories are exactly the categorical algebras over the so-called \(E_2\)-operad [24, 28, 66].Footnote 1 Recall that the \(E_2\)-operad, or operad of little two-dimensional disks, is a topological operad whose operations are parametrized by the different embeddings of a disjoint union of disks into a larger disk. In the identification of categorical \(E_2\)-algebras with braided monoidal categories the braiding (i.e. the universal R-matrix) is interpreted as an operation rotating two disks in the plane. In this paper we propose an interpretation for the universal K-matrix of Balagovic and Kolb in terms of \({\mathbb {Z}}_2\)-orbifoldFootnote 2 disks rotating around each other, see Fig. 3. This naturally leads us to consider an operadic perspective on quantum symmetric pairs in which the \(E_2\)-operad is replaced by an \({\mathbb {Z}}_2\)-orbifold analogue. We therefore introduce the \({\mathbb {Z}}_2{\mathcal {D}}_2\)-operad of involutive little two-dimensional disks, and study its categorical algebras. Our main result is that \({\mathbb {Z}}_2\)-braided pairs are exactly the categorical \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebras.
Recall that an \(E_2\)-algebra A can be used to construct invariants of surfaces by computing the so-called factorization homology of the surface with coefficients in A [5, 52]. In [14, 15], the authors compute the surface invariants of factorization homology with coefficients in the braided monoidal category of quantum group representations. These invariants produce quantizations of the character variety of the surfaces (the moduli space of local systems on that surface). In Sect. 1.3 we explain forthcoming work in which we compute the factorization homology of \({\mathbb {Z}}_2\)-orbifold surfaces with coefficients in the \({\mathbb {Z}}_2\)-braided pair of representations of a quantum symmetric pair. Thereby, we will construct invariants of surfaces \(\Sigma \) with an involution and actions of the associated orbifold braid groups \(B_n[\Sigma /{\mathbb {Z}}_2]\). We expect that these invariants give quantizations of the character varieties of orbifold surfaces with isolated \({\mathbb {Z}}_2\)-singularities.
1.1 Summary of results
We introduce the notion of a \({\mathbb {Z}}_2\)-braided pair, which is central to our results. A \({\mathbb {Z}}_2\)-braided pairs consists of a braided monoidal category, a module category and some extra structure which we now recount. See Sect. 3 for the definitions of braided monoidal category and module category.
Definition 1.1
(Definition 3.1)
-
1.
A \({\mathbb {Z}}_2\)-monoidal pair consists of a monoidal category \({\mathcal {A}}\) endowed with an anti-monoidal involution \(\Phi : {\mathcal {A}}\rightarrow {\mathcal {A}}^{\otimes \text {-op}}\), t: \(\Phi ^2 \cong \text {id}_{{\mathcal {A}}}\), together with a module category \({\mathcal {M}}\) over \({\mathcal {A}}\) and a distinguished object
 .
. -
2.
A \({\mathbb {Z}}_2\)-braided pair consists of a \({\mathbb {Z}}_2\)-monoidal pair \(({\mathcal {A}},{\mathcal {M}})\) together with a braiding \(\sigma : \otimes \cong \otimes ^{op}\) on \({\mathcal {A}}\) such that \(\Phi \) is braided, as well as a family of natural isomorphisms \(\kappa _{M,X}: M\otimes X \rightarrow M \otimes \Phi (X)\) for all \(M \in {\mathcal {M}}, X \in {\mathcal {A}}\) satisfying the coherence diagrams of Figs. 7 and 8.
-
3.
A \({\mathbb {Z}}_2\)-symmetric pair is a \({\mathbb {Z}}_2\)-braided pair such that \(\sigma ^2 = \text {id}\) and \(\kappa ^2 = \text {id}\).
We will call the natural isomorphism \(\kappa \) the \({\mathbb {Z}}_2\)-cylinder braiding as its topological interpretation is the braid around the singular point in the orbifold cylinder \([D^2/{\mathbb {Z}}_2]\) (see Fig. 1). Crucially, Definition 1.1 implies that the \({\mathbb {Z}}_2\)-cylinder braiding \(\kappa \) and the braiding \(\sigma \) satisfy the \(\Phi \)-twisted reflection equation (1.10.1).
Remark 1.2
The notion of a \({\mathbb {Z}}_2\)-braided pair is very close to the notion of a \(\Phi \)-braided module category of [40, Remark 3.15] and braided module category of [17]. However, in the definition of \({\mathbb {Z}}_2\)-braided pair we had to impose additional requirements to match the topology of the \({\mathbb {Z}}_2{\mathcal {D}}_2\)-operad. For a precise comparison see Remarks 3.2 and 3.6.
(Left) The isotopy of operations in \({\mathbb {Z}}_2{\mathcal {D}}_2\) corresponding to the \({\mathbb {Z}}_2\)-cylinder braiding \(\kappa \). The operations are embeddings of the form \({\mathbb {D}}\amalg {\mathbb {D}}_* \rightarrow {\mathbb {D}}_*\). (Right) A coloured braid encoding the isotopy up to homotopy (colour figure online)
Our main result interprets the axioms in Definition 1.1 via topological operads \({\mathbb {Z}}_2{\mathcal {D}}_n\). These operads have two colours \({\mathbb {D}}\) and \({\mathbb {D}}_*\), that represent the free quotient \((D^n \amalg D^n) /{\mathbb {Z}}_2\) where \({\mathbb {Z}}_2\) swaps the disks, and the orbifold quotient \(D^n/{\mathbb {Z}}_2\) where \({\mathbb {Z}}_2\) acts by rotations (see Fig. 4). The operations in \({\mathbb {Z}}_2{\mathcal {D}}_n\) are parametrized by equivariant embeddings of disjoint unions of the orbifold disks \({\mathbb {D}}\) and \({\mathbb {D}}_*\) into each other. Consider a categorical \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra \(({\mathcal {A}},{\mathcal {M}})\), where \({\mathcal {A}}\) corresponds to \({\mathbb {D}}\) and \({\mathcal {M}}\) corresponds to \({\mathbb {D}}_*\). Disjoint unions of the disk \({\mathbb {D}}\) embed into \({\mathbb {D}}\), which determines a multiplication structure on \({\mathcal {A}}\). Moreover, \({\mathbb {D}}\) embeds into \({\mathbb {D}}_*\), but not conversely. This determines an \({\mathcal {A}}\)-module structure on \({\mathcal {M}}\). Our main result is the following classification, relating the categorical \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras to Definition 1.1.
Theorem 1.3
(Theorem 6.14) Let \(\mathbf Cat \) denote the 2-category of categories.
-
1.
A \({\mathbb {Z}}_2{\mathcal {D}}_1\)-algebra in \(\mathbf{Cat } \) is exactly a \({\mathbb {Z}}_2\)-monoidal pair.
-
2.
A \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebra in \(\mathbf Cat \) is exactly a \({\mathbb {Z}}_2\)-braided pair.
-
3.
Let \(n\ge 3\). A \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra in \(\mathbf Cat \) is exactly a \({\mathbb {Z}}_2\)-symmetric pair.
Remark 1.4
We stated the main theorem in terms of \(\mathbf{Cat }\) for simplicity. We prove the main theorem for \(\mathbb {k}\)-linear categorical algebras since \(\mathbb {k}\)-linear categories provide a more natural setting for representation theory, see e.g. [26]. However, our proofs are readily adaptable to Cat, where they yield the above result.
Convention
We refer to plain categories with a tensor product as monoidal categories, whereas we refer to \(\mathbb {k}\)-linear categories with a tensor product as tensor categories.Footnote 3
Remark 1.5
We use \(\infty \)-categories to define \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras in general. Since Cat is only a 2-category we will delay discussing the \(\infty \)-categorical foundations to Sect. 6. The reader only interested in applications to representation theory can safely avoid reading that section.
Remark 1.6
Recall that for \(n\ge 3\) a categorical \(E_n\)-algebra is the same thing as a categorical \(E_\infty \)-algebra (i.e. a symmetric monoidal category). This is an instance of the Baez–Dolan stabilisation hypothesis [7]. As one would expect from the stabilisation hypothesis, categorical \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras also stabilise when \(n\ge 3\).
All our examples of \({\mathbb {Z}}_2\)-braided pairs are obtained from the theory of Hopf algebras. Namely, the categories of representations of quasi-triangular Hopf algebras provide important examples of braided monoidal categories. A standard source of module categories are then the coideal subalgebras of the Hopf algebra. Recall that a coideal subalgebra B of a Hopf algebra H is a subalgebra \(B \subset H\) for which \(\Delta (B) \subset B \otimes H\). Following [40], we call a coideal subalgebra quasi-triangular if it has a universal K-matrix, see Definition 3.3.
Proposition 1.7
(Proposition 3.5 see also [8, Remark 4.13] and [40, §2.2].) Let H be a ribbon Hopf algebra with involution \(\phi : H \rightarrow H\) and let B be a quasi-triangular coideal subalgebra of H. Then \((H\text {-mod}_{\text {f.d.}},B\text {-mod}_{\text {f.d.}})\) naturally defines a \({\mathbb {Z}}_2\)-braided pair.
The main results [8, Corollary 9.6] and [40, Corollary 3.14] state that the quantum symmetric pair coideal subalgebra is quasi-triangular. As a corollary we then have:
Corollary 1.8
Any quantum symmetric pair together with the standard ribbon element of the quantum group satisfies the hypothesis of Proposition 1.7.
In order to prove Theorem 1.3 we establish various coherence theorems which may be of independent interest. A priori, to specify a categorical \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra one needs to provide an infinite amount of data, corresponding to the infinitely many operations in the operad \({\mathbb {Z}}_2{\mathcal {D}}_n\), the isotopies between these operations, the isotopies between isotopies, and so on. Theorem 1.3 states all this data can be reduced to the finite list of functors, isomorphisms and equations in Definition 1.1. Concretely, one needs to show that all the functors and natural isomorphisms one can construct using these generators make the correct diagrams commute, as specified by the operad \({\mathbb {Z}}_2{\mathcal {D}}_n\). This is exactly the content of a coherence theorem. We can state our coherence results informally as follows:
Theorem 1.9
Let \(({\mathcal {A}},{\mathcal {M}})\) be a \({\mathbb {Z}}_2\)-monoidal/braided/symmetric pair. By a coherence diagram we mean a diagram in \({\mathcal {A}}\) or \({\mathcal {M}}\) constructed using the functors and natural isomorphisms that are part of Definition 1.1.
-
1.
Any coherence diagram in a \({\mathbb {Z}}_2\)-monoidal pair commutes. (Theorem 4.19)
-
2.
A coherence diagram in a \({\mathbb {Z}}_2\)-braided pair commutes if the underlying braids agree.Footnote 4 (Theorem 4.18)
-
3.
Any coherence diagram in a \({\mathbb {Z}}_2\)-symmetric pair commutes. (Theorem 4.20)
1.2 Quantum symmetric pairs and the reflection equations
An infinitesimal symmetric pair \(({\mathfrak {g}},{\mathfrak {g}}^{\theta })\) consists of a complex semisimple Lie algebra \({\mathfrak {g}}\) and a sub Lie algebra \({\mathfrak {g}}^{\theta } \subset {\mathfrak {g}}\) fixed by some involutive automorphism \(\theta : {\mathfrak {g}}\rightarrow {\mathfrak {g}}\). Irreducible symmetric pairsFootnote 5 were classified by Araki [3]. The classification of type A symmetric pairs is recorded in Table 1.
A quantum symmetric pair \(({\mathcal {U}}_q({\mathfrak {g}}),{\mathcal {C}}_{\mathbf{c }} ({\mathfrak {g}}^{\theta }))\) should then be a quantization of the pair \(({\mathcal {U}}({\mathfrak {g}}), {\mathcal {U}}({\mathfrak {g}}^{\theta }))\).
Notation
Notation for quantum symmetric pairs varies in the literature. Some authors denote the coideal subalgebra by \({\mathcal {B}}_{\mathbf{c }}\). The c denotes a multi-parameter as there can be multi-parameter families of quantizations of \(U({\mathfrak {g}}^\theta )\).
It turns out that requiring \({\mathcal {C}}_{\mathbf{c }} ({\mathfrak {g}}^{\theta })\) to be a sub-Hopf algebra of \({\mathcal {U}}_q({\mathfrak {g}})\) is too strong a requirement, rather this quantization will be a (left) coideal subalgebra i.e. a subalgebra satisfying \(\Delta ({\mathcal {C}}_{\mathbf{c }} ({\mathfrak {g}}^{\theta })) \subset {\mathcal {C}}_{\mathbf{c }} ({\mathfrak {g}}^{\theta })\otimes {\mathcal {U}}_q({\mathfrak {g}})\).
1.2.1 The reflection equation and cylinder braids
The first constructions of quantum symmetric pairs in [22, 60, 61] depended crucially on solutions to various versions of the reflection equation:
where R denotes a given solution of the Yang–Baxter equation. Like the Yang–Baxter equation, the reflection equation has an interpretation in low-dimensional topology, see Fig. 2. Similar to the Reshetikhin–Turaev invariants, one can use solutions of the reflection equation to construct knot invariants [64, 65].
Solutions to the \({\mathfrak {g}}{\mathfrak {l}}_n\)-reflection equation were studied by Donin, Mudrov and Kulish [23] and completely classified by Mudrov [57]. It turns out such solutions can be viewed as characters of the reflection equation algebra \({\mathcal {O}}_q(G)\). In [41], characters of the reflection equation algebra are used to reconstruct the type AIII/AIV quantum symmetric pairs of Noumi–Sugitani–Dijkhuizen.
Remark 1.10
The reflection equation algebra \({\mathcal {O}}_q(G)\) is an (equivariant) quantization of the Semenov-Tian-Shansky Poisson bracket on \({\mathcal {O}}(G)\) [58]. This algebra goes by many names: Majid’s braided dual of \({\mathcal {U}}_q({\mathfrak {g}})\) [55], the quantum-loop algebra [1] and is isomorphic to the locally finite part of \({\mathcal {U}}_q({\mathfrak {g}})\) via the Rosso form [41, Proposition 2.8].
1.2.2 The reflection equations revisited
Recall that various versions of the reflection equation appeared in the works [22, 59,60,61]. It was only later realised by Balagovic and Kolb, through their algebraic construction of universal K-matrices, that there is a general framework of twisted reflection equations which unifies all different reflection equations [8, Remark 9.7]. For a quasi-triangular Hopf algebra H with coideal subalgebra B one fixes an additional Hopf algebra involution \(\phi \) of H, such that \((\phi \otimes \phi )(R) = R\), called the twist. A (\(\phi \)-twisted) universal K-matrix is a universal solution to the \(\phi \)-twisted reflection equation:
where \(R^\phi = (\phi \otimes 1)(R)\) and \(R^{\phi ,\phi } = (\phi \otimes \phi )(R) = R\).
Remark 1.11
The twist \(\phi \) for a given quantum symmetric pair is determined by the Dynkin data that characterises it in Araki’s classification [3]. See Table 1 for twists in type A.
Remark 1.12
Quantum symmetric pairs for which the twist is trivial, \(\phi = \text {id}\), have universal K-matrices that provide solutions to the untwisted reflection equation (1.9.1). This explains why in [41] characters of \({\mathcal {O}}_q(G)\) could only be used to construct quantum symmetric pairs of type AIII/AIV: such characters solve the untwisted reflection equation.
The twist is naturally built into the categorical framework of \({\mathbb {Z}}_2\)-braided pairs via the involution \(\Phi \). Recall from Fig. 1 that we can interpret the \({\mathbb {Z}}_2\)-cylinder braiding in the operad \({\mathbb {Z}}_2{\mathcal {D}}_2\) as a coloured braid. The twisted reflection equation is then naturally interpreted in the operad \({\mathbb {Z}}_2{\mathcal {D}}_2\) as an isotopy of coloured braids, see Fig. 3. Therefore, we can now recognise that the twists \(\phi \), which had an algebraic origin but lacked intrinsic topological meaning, are an integral part of the topological interpretation of quantum symmetric pairs.
1.3 Outlook: factorization homology and quantum symmetric pairs
The constructions in this paper are the first step in a program where quantum symmetric pairs are used for applications to low-dimensional topology. The next steps will involve (developing and) applying a general framework called factorization homology.
Factorization homology was first introduced by Lurie [51, 52] as a topological variant of the chiral homology of Beilinson–Drinfeld [13], and was further developed by Francis, Ayala and Tanaka [5, 6]. Nowadays there is a large body of literature on factorization homology and related ideas, see e.g. [2, 21, 31,32,33, 56]. See [30] for a survey. The formalism of factorization homology, in its simplest form, takes as input an \(E_n\)-algebra \({\mathcal {A}}\) in a symmetric monoidal higher category \({\mathcal {C}}\) and associates to every framed n-manifold M an invariant denoted \(\int _M {\mathcal {A}}\). We will informally explain the assignment. Following [5], we view the manifold as glued from all the framed disks embedding into M, and view the \(E_n\)-algebra \({\mathcal {A}}\) as a functor \({\mathcal {A}}: {\mathcal {D}}isk^{\text {fr}}_n \rightarrow {\mathcal {C}}\) from some higher category of framed disks into \({\mathcal {C}}\). The invariant is then defined as follows:
We record some key properties of factorization homology:
-
1.
Factorization homology is uniquely characterised by an excision property. After decomposing a manifold along a collared boundary, one can compute the global invariant of the manifold in terms of the invariants of the pieces [5, §3.5].Footnote 6
-
2.
The invariant is functorial with respect to embeddings. In particular \(\text {Diff}^{\mathrm{fr}}(M)\) acts on \(\int _M {\mathcal {A}}\). Moreover, for a categorical \(E_n\)-algebra \({\mathcal {A}}\) and \(X_1, \ldots , X_n \in {\mathcal {A}}\) the braid group \(B_n(M)\) acts on an associated object \(\int _M (X_1 \otimes \cdots \otimes X_n) \in \int _M {\mathcal {A}}\).
-
3.
There are many versions of factorization homology e.g. for oriented manifolds and manifolds with singularities [5, 6].
-
4.
For a given \(E_n\)-algebra \({\mathcal {A}}\), the factorization homology of n-manifolds with coefficients in \({\mathcal {A}}\) defines a fully extended n-dimensional TQFT [62].
Most relevant to our work are the applications of factorization homology to representation theory via the factorization homology of braided tensor categories as developed in [14, 15]. In [14, 15], the authors compute invariants of genus g framed and oriented surfaces using factorization homology with coefficients in the braided tensor category of quantum group representations. For example, the invariant assigned to the annulus is the category of representations of the reflection equation algebra \({\mathcal {O}}_q(G)\) and the invariant assigned to the torus is the category of strongly equivariant quantum \({\mathcal {D}}\)-modules on G. Via Key Property (2) the authors obtain braid group actions of oriented surfaces. Such surface braid group actions were previously constructed by ‘generators and relations’ methods in [34] and used to construct representations of the type A double affine Hecke algebra (abbreviated DAHA). The type A DAHA, due to Cherednik [19], is a quotient of the group algebra of the torus braid group \(B_n(T)\) by additional Hecke relations. The braid group actions constructed in [14, 15] recover the surface braid group actions of [34] and provide an intrinsic topological explanation for their existence.
To connect these developments to our work on quantum symmetric pairs and the \({\mathbb {Z}}_2{\mathcal {D}}_2\)-operad we make the following observation. The colimit formula (1.12.1) defining factorization homology is motivated by the fact that a n-manifold M is covered by disks \(D^n\). Correspondingly, a \({\mathbb {Z}}_2\)-orbifold surface \([\Sigma /{\mathbb {Z}}_2]\) with isolated singularities is covered by the orbifold disks \({\mathbb {D}}\) and \({\mathbb {D}}_*\), which appear in the definition of the operad \({\mathbb {Z}}_2{\mathcal {D}}_2\). Hence it is natural to associate invariants to such orbifold surfaces constructed from a \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebra via a formula like Eq. (1.12.1). In the follow-up paper [68] we make this idea precise by introducing \(\Gamma \)-equivariant factorization homology, where \(\Gamma \) can be an arbitrary finite group.
Recall that in [35] representations of the type \(C^\vee C_n\) DAHA were constructed using quantum symmetric pairs of type AIII/AIV. These constructions were made using a generators and relations approach alike [34], and similarly lacked a topological interpretation. The DAHA of type \(C^\vee C_n\) arises as a quotient of the orbifold surface braid group \(B_n[T^2/{\mathbb {Z}}_2]\), where the \({\mathbb {Z}}_2\) action on the torus \(T^2\) is induced by rotating the fundamental domain. In future work we hope to recover the DAHA representations in [35] from the braid group actions arising in the equivariant factorization homology of the orbifold torus \([T^2/{\mathbb {Z}}_2]\) with coefficients in a quantum symmetric pair. Moreover, the general construction of equivariant factorization homology will allow us to immediately generalise the constructions in [35] to other quantum symmetric pairs, not necessarily of type AIII/AIV. This provides important motivation for our work on quantum symmetric pairs and factorization homology.
1.4 Organisation
The contents of this article are laid out as follows.
In Sect. 2 we introduce and study the operads \({\mathbb {Z}}_2{\mathcal {D}}_n\). We first recall the definition of orbifold configuration spaces and then define the operads \({\mathbb {Z}}_2{\mathcal {D}}_n\). We compute the homotopy type of the spaces of operations of the operads \({\mathbb {Z}}_2{\mathcal {D}}_n\) in terms of orbifold configuration spaces.
In Sect. 3 we introduce \({\mathbb {Z}}_2\)-monoidal pairs, \({\mathbb {Z}}_2\)-braided pairs and \({\mathbb {Z}}_2\)-symmetric pairs. Moreover, we prove Proposition 1.7.
Section 4 is a technical section where we prove Theorem 1.9. The reader uninterested in methods for proving a coherence result can safely skip the section. To prove the theorem we follow the ‘strictification implies coherence’ approach of Joyal and Street [37].
Section 5 is devoted to proving Theorem 1.3, though two further results from Sect. 6 are needed to complete the proof. We begin by defining the 2-category \(\mathbf Rex \) and the Deligne–Kelly tensor product. We then use the coherence results of Sect. 4 to assign categorical \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras for \(n=1\), \(n=2\), \(n\ge 3\) to respectively \({\mathbb {Z}}_2\)-monoidal, \({\mathbb {Z}}_2\)-braided and \({\mathbb {Z}}_2\)-symmetric pairs. We also construct assignments in the opposite direction.
Finally, in Sect. 6 we recall the definitions in [52] of algebras over \(\infty \)-operads. We show that in the special case of \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras in \(\mathbf Rex \) we recover the definition of categorical \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras we gave in Sect. 5. We conclude by finishing the proof of Theorem 1.3 by showing that the assignments constructed in Sect. 5 are inverse equivalences.
1.5 A note to the reader
It is well known that categorical \(E_2\)-algebras are braided monoidal categories. For a proof in the strict setting see [66], and for a proof using Dunn Additivity see [52]. As there is no Dunn Additivity for \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebras we had to directly prove that categorical \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebras are \({\mathbb {Z}}_2\)-braided pairs. A subset of our arguments can be used to give a direct proof that categorical \(E_2\)-algebras are braided monoidal categories. As we are unaware of such a proof in the literature, this may be of independent interest.
2 The involutive little disks operad
2.1 Orbifold configuration spaces
Orbifold configuration spaces will be fundamental to our understanding of the \({\mathbb {Z}}_2{\mathcal {D}}_n\)-operads. We now recall the definitions of configuration spaces for manifolds and global quotient orbifolds and their associated braid groups.
Definition 2.1
Let \(\Sigma \) be some surface.
-
1.
The configuration space of k ordered points in \(\Sigma \) is denoted \(F_n(\Sigma )\) and defined as
$$\begin{aligned} F_k (\Sigma ) := \big \{ (z_1,\ldots ,z_k) \in \Sigma ^{\times k} \mid z_i \ne z_j \text { if } i \ne j \big \}. \end{aligned}$$The symmetric group \(S_k\) acts freely on \(F_k(\Sigma )\) by swapping points.
-
2.
The configuration space of k unordered points in \(\Sigma \) is denoted \(C_k(\Sigma )\) and defined to be the quotient space \(C_k(\Sigma ) := F_k(\Sigma )/S_k\).
-
3.
The braid group on n strands of \(\Sigma \) is denoted \(B_k(\Sigma )\) and defined to be the fundamental group \( \pi _1 C_k(\Sigma )\).
Recall that for a given group \(\pi \) an Eilenberg–MacLane space of type \(K(\pi ,1)\) is a topological space S that has trivial homotopy groups except \(\pi _1(S) \cong \pi \).
Example 2.2
[27] Recall the following classical examples of Eilenberg–MacLane spaces:
-
1.
The space \(C_k({\mathbb {R}}^2)\) is a \(K(B_k,1)\) where \(B_k\) is Artin’s braid group.
-
2.
The space \(C_k({\mathbb {R}}^2{\setminus } \text {pt})\) is a \(K(B^{\text {cyl}}_k,1)\) where \(B^{\text {cyl}}_k\) is the cylinder braid group.
Proposition 2.3
[16] The group \(B^{\text {cyl}}_k\) of cylinder braids admits a presentation with generators \(\sigma _1, \ldots , \sigma _k\), \(\kappa \) and relations
We now give a definition of orbifold configuration spaces. The definition is a slight adaptation of the ‘orbit configuration spaces’ of Xicoténcatl [69].Footnote 7
Definition 2.4
Let \(\Gamma \) be a finite group acting smoothly and faithfully on a surface \(\Sigma \). Denote \(\Sigma _{\text {free}} \subset \Sigma \) the subset of smooth points i.e. the subset of points where \(\Gamma \) acts freely.
-
1.
The configuration space of k ordered smooth points in the orbifold \([\Sigma /\Gamma ]\) is denoted \(F_k[\Sigma {/}\Gamma ]\) and defined as
$$\begin{aligned} F_k [\Sigma {/}\Gamma ] := \big \{ (z_1,\ldots ,z_n)\in (\Sigma _{\text {free}})^{\times k} \mid \Gamma \cdot z_i \cap \Gamma \cdot z_j = \emptyset \text { if } i \ne j \big \}. \end{aligned}$$There is a natural free \(\Gamma ^{\times k} \rtimes S_k\) action on \(F_k[\Sigma /\Gamma ]\).
-
2.
The configuration space of k unordered smooth points in \([\Sigma {/}\Gamma ]\) is denoted \(C_k[\Sigma /\Gamma ]\) and defined to be the quotient space \(F_k [\Sigma {/}\Gamma ] {/}\Gamma ^{\times k} \rtimes S_k\).
-
3.
The braid group on k strands in the orbifold \([\Sigma {/}\Gamma ]\) is denoted \(B_k[\Sigma {/}\Gamma ]\) and defined to be the fundamental group\(\pi _1 C_n[\Sigma {/}\Gamma ]\).
The following two \({\mathbb {Z}}_2\)-global quotients will be our central examples throughout:
Example 2.5
Fix a dimension \(n\ge 1\). Let \(D^n\) denote the open unit disk in \({\mathbb {R}}^n\). Let \({\mathbb {Z}}_2\) act on \({\mathbb {R}}^n\) via the sign representation. We have an induced action on \(D^n\).
-
1.
Let \({\mathbb {D}}_*\) denote the topological space \(D^n\) equipped with the \({\mathbb {Z}}_2\) action given by the sign action.
-
2.
Let \({\mathbb {D}}\) denote the topological space \(D^n \amalg D^n\) equipped with the \({\mathbb {Z}}_2\) action given by combining the sign action with swapping the two disks.
The spaces for \(n=2\) are illustrated in Fig. 4.
Lemma 2.6
Let \({\mathbb {D}}\) and \({\mathbb {D}}_*\) be the orbifolds defined above for dimension \(n=2\).
-
1.
The space \(C_k[{\mathbb {D}}^2/{\mathbb {Z}}_2]\) is a \(K(B_k,1)\).
-
2.
The space \(C_k[{\mathbb {D}}^2_*/{\mathbb {Z}}_2]\) is a \(K(B^{\text {cyl}}_k,1)\).
Proof
As the proofs are identical we will do both at once. Let \(\Sigma \) be either \({\mathbb {D}}\) or \({\mathbb {D}}_*\). The projection \(F_k[\Sigma {/}\Gamma ] \rightarrow F_n(\Sigma _{free}{/}\Gamma )\) descends to a \(S_k\)-equivariant homeomorphism \(F_k[\Sigma /\Gamma ]{/}\Gamma ^{\times k} \cong F_k(\Sigma _{free}{/}\Gamma )\). Hence \(C_k[\Sigma {/}\Gamma ] \cong C_k(\Sigma _{free}{/}\Gamma )\) are naturally homeomorphic. Thus we reduce to the classical cases of Example 2.2. \(\square \)
2.2 Definition of the operad
Let \(n \ge 1\) denote some dimension.
Notation
We will use the following notation throughout without further comment:
-
1.
To differentiate between the two copies of \(D^n\) in \({\mathbb {D}}\) we will write \({\mathbb {D}}= D^n_b \amalg D^n_r\). For a map \(f: {\mathbb {D}}\rightarrow X\) we will write \(f_b = f|_{D^n_b} : D^n_b \rightarrow X\) and \(f_r = f|_{D^n_r} : D^n_r \rightarrow X\) for the restrictions. We will write \(\mathbf{0 }_b\) for the center of \(D^n_b \subset {\mathbb {D}}\).
-
2.
We will view maps whose source is a disjoint union of spaces as collections of component maps, e.g. viewing \(f: {\mathbb {D}}^{\amalg k} \rightarrow {\mathbb {D}}\) as a collection \((f^i: {\mathbb {D}}\rightarrow {\mathbb {D}})_{i=1}^k\).
An embedding \(f: D^n \rightarrow D^n\) is called rectilinear if it is of the form \(f(x,y) = (\lambda x + t_x, \lambda y + t_y)\) for some \(\lambda , t_x, t_y \in {\mathbb {R}}\). We will call an embedding \(f: {\mathbb {D}}\rightarrow {\mathbb {D}}\), and \(f: {\mathbb {D}}\rightarrow {\mathbb {D}}_*\) rectilinear if the restrictions \(f_r\) and \(f_b\) are rectilinear. We will say an embedding \(f:{\mathbb {D}}^{\amalg k} \amalg {\mathbb {D}}_*^{\amalg m} \rightarrow {\mathbb {D}}_*\), or \(f: {\mathbb {D}}^{\amalg k} \amalg {\mathbb {D}}_*^{\amalg m} \rightarrow {\mathbb {D}}\), is equivariant rectilinear if the component maps \(f_i\) are rectilinear and \({\mathbb {Z}}_2\)-equivariant.
We will now define a topological coloured operad \({\mathbb {Z}}_2{\mathcal {D}}_n\) with two colours \({\mathbb {D}}\) and \({\mathbb {D}}_*\) and which has spaces of operations
Operadic composition is defined in the obvious way: compose the embeddings. Concretely, one inserts a configurations of disks into disks; an example in dimension two is illustrated in Fig. 5.
Remark 2.7
Equivariance requires an embedding to map a \({\mathbb {Z}}_2\)-fixed point to a \({\mathbb {Z}}_2\)-fixed point. Therefore, \({\mathbb {Z}}_2{\mathcal {D}}_n( {\mathbb {D}}^{\amalg k} \amalg {\mathbb {D}}_*^{\amalg m}, {\mathbb {D}}) = \emptyset \) if \(m>0\) and \({\mathbb {Z}}_2{\mathcal {D}}_n( {\mathbb {D}}^{\amalg k} \amalg {\mathbb {D}}_*^{\amalg m}, {\mathbb {D}}_*) = \emptyset \) if \(m>1\).
It remains to address the topology on the sets of operations 2.6.1 and 2.6.2. For a rectilinear embedding \(f: D^n \rightarrow D^n\) we write r(f) for the radius of the disk \(f(D^n)\). We define maps
that record the positions of the centers and the radii. These maps are clearly injections. We induce the subspace topology on the sets of operations, where \({\mathbb {R}}^k\) has the Euclidean topology. This endows \({\mathbb {Z}}_2{\mathcal {D}}_n\) with the structure of a topological operad.
Definition 2.8
The topological coloured operad \({\mathbb {Z}}_2{\mathcal {D}}_n\), described above, with two colours \({\mathbb {D}}\) and \({\mathbb {D}}_*\) and operation spaces 2.6.1 and 2.6.2 is called the involutive little n-disks operad.
2.3 The homotopy type of the spaces of operations
The connection between configuration spaces and the \({\mathbb {Z}}_2{\mathcal {D}}_n\)-operad is established in the following easy but nevertheless important result.
Proposition 2.9
The maps
that forget the radii define homotopy equivalences.
Proof
Easy adaptation of the usual proof for the \(E_n\)-operad and \(F_k({\mathbb {R}}^2)\).Footnote 8 \(\square \)
Remark 2.10
By Proposition 2.9 we can encode isotopies in \({\mathbb {Z}}_2{\mathcal {D}}_n({\mathbb {D}}^{\amalg k}, {\mathbb {D}}_*)\) up to homotopy as paths in \(F_k[{\mathbb {D}}/{\mathbb {Z}}_2]\). Paths in \(F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) are naturally drawn as coloured braids, see e.g. Figs. 1 and 3.
In dimension one the configuration spaces \(F_k[{\mathbb {D}}/{\mathbb {Z}}_2]\) and \(F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) are particularly easy to describe. To a point \(p\in F_1[{\mathbb {D}}/{\mathbb {Z}}_2]\) we assign a value
and to a configuration \(x = (x_1,\ldots ,x_k) \in F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) we assign a permutation \(\sigma _x \in S_k\) recording the order of the disks in \(D^1_b\), see Fig. 6. More precisely, \(\sigma _x\) is the unique permutation in \(S_k\) for which the inequalities
hold.
Lemma 2.11
The map
is a homotopy equivalence.
Proof
Easy. \(\square \)
Similarly, to a point \(x \in F_1[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) we can assign a value
so that for every \(x \in F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) there is a unique \(\sigma _x \in S_k\) satisfying Eq. (2.10.2).
Lemma 2.12
The map
defines a homotopy equivalence.
Proof
Easy. \(\square \)
3 \({\mathbb {Z}}_2\)-braided pairs
Before we state our definitions we fix notation and remind the reader of some standard definitions in categorical representation theory, for more details and background see [26]. A monoidal category is a category \({\mathcal {A}}\) together with a tensor product functor \(\otimes : {\mathcal {A}}\times {\mathcal {A}}\rightarrow {\mathcal {A}}\), a unit object  and natural isomorphisms
and natural isomorphisms

for \(X,Y,Z\in {\mathcal {A}}\) satisfying the Mac Lane triangle and pentagon axioms. A braided monoidal category is a monoidal category \({\mathcal {A}}\) together with a natural isomorphism \(\sigma \), called the braiding,
for \(X,Y\in {\mathcal {A}}\) satisfying the Joyal–Street hexagon axioms. A monoidal functor between monoidal categories \({\mathcal {A}}\) and \({\mathcal {B}}\) consists of a functor \(\Psi : {\mathcal {A}}\rightarrow {\mathcal {B}}\) together with natural isomorphisms

for \(X,Y \in {\mathcal {A}}\) satisfying unit and associativity axioms. A monoidal functor \(\Psi \) between braided monoidal categories is called braided if it preserves the braiding i.e. \(\Psi (\sigma _{{\mathcal {A}}}) = \sigma _{{\mathcal {B}}}\). A (right) \({\mathcal {A}}\)-module category over a monoidal category \({\mathcal {A}}\) is a category \({\mathcal {M}}\) together with an action functorFootnote 9 \(\text {act}: {\mathcal {M}}\times {\mathcal {A}}\rightarrow {\mathcal {M}}, (M,X) \mapsto M \otimes X\) and natural isomorphisms

for \(M \in {\mathcal {M}}\) and \(X,Y \in {\mathcal {A}}\) satisfying a unit and associativity axiom. We call a module category \({\mathcal {M}}\) pointed if it has a distinguished object  .
.
Notation
For a monoidal category \({\mathcal {A}}\) we have the opposite monoidal category \({\mathcal {A}}^{\otimes \text {-op}}\), which is the category \({\mathcal {A}}\) with the reversed order tensor product \(\otimes ^{\text {op}}\) i.e. \(X \otimes ^{\text {op}} Y := Y \otimes X\).
Definition 3.1
-
1.
An anti-involution \(\Phi \) of a monoidal category \({\mathcal {A}}\) consists of a monoidal functor \((\Phi ,\Phi _2,\Phi _0): {\mathcal {A}}\rightarrow {\mathcal {A}}^{\otimes \text {-op}}\) and a monoidal isomorphism \(t: \Phi ^2 \Rightarrow \text {id}_{{\mathcal {A}}}\) such that \(\Phi (t_X) = t_{\Phi (X)}\).
-
2.
A \({\mathbb {Z}}_2\)-monoidal pair consists of a monoidal category \({\mathcal {A}}\) together with an anti-involution \(\Phi \), and a pointed \({\mathcal {A}}\)-module category \({\mathcal {M}}\).
-
3.
A \({\mathbb {Z}}_2\)-braided pair consists of a \({\mathbb {Z}}_2\)-monoidal pair \(({\mathcal {A}},{\mathcal {M}})\) with the following additional structures. The category \({\mathcal {A}}\) is braided monoidal so that \(\Phi \) is braided, together with natural isomorphisms \(\kappa _{M,X}: M\otimes X \rightarrow M \otimes \Phi (X)\) such that the diagrams in Figs. 7 and 8 commute for all \(M\in {\mathcal {M}}\) and \(X,Y \in {\mathcal {A}}\). The natural isomorphism \(\kappa \) is called the \({\mathbb {Z}}_2\)-cylinder braiding.
Remark 3.2
The definition of a \({\mathbb {Z}}_2\)-braided pair is a \({\mathbb {Z}}_2\)-equivariant version of the braided module categories of Brochier [17]. A braided module category over a braided monoidal category \({\mathcal {A}}\) consists of an \({\mathcal {A}}\)-module category \({\mathcal {M}}\) together with a natural isomorphism \(\gamma : M \otimes X \rightarrow M \otimes X\) for \(X\in {\mathcal {A}}, M\in {\mathcal {M}}\) satisfying axioms BP1 and BP2, but where the functor \(\Phi = \text {id}_{{\mathcal {A}}}\) is trivial and replacing \(\Phi _2\) by the braiding \(\sigma \) in axiom BP2.
Many important examples of \({\mathbb {Z}}_2\)-braided pairs come from the representation theory of quasi-triangular Hopf algebras, and their coideal subalgebras.
Notation
For an algebra A we denote with \(A\text {-mod}\) the category of A-modules, and \(A\text {-mod}_{\text {f.d.}}\) the category of finite dimensional A-modules.
Recall that for a quasi-triangular Hopf algebra H the category \(H\text {-mod}\) is naturally a braided monoidal category. A coideal subalgebra \(B\subset H\) is a subalgebra so that \(\Delta (B) \subset B \otimes H\). The category \(B\text {-mod}\) is then naturally a module category over \(H\text {-mod}\). To obtain a \({\mathbb {Z}}_2\)-braided pair \((H\text {-mod},B\text {-mod})\) we need some further structure on H and B.
Definition 3.3
[40, Definition 2.7] Let H be a quasi-triangular Hopf algebra with universal R-matrix \(R\in H\), a Hopf algebra involution \(\phi : H \rightarrow H\) such that \((\phi \otimes \phi )(R) = R\) and \(B\subset H\) a coideal subalgebra. The coideal subalgebra B is called quasi-triangular if there exists an invertible element \(K \in B \otimes U\) satisfying
Here \(R^\phi := \phi \otimes \text {id}(R)\). Note \(R^\phi = \text {id}\otimes \phi (R)\) also. We call K the universal K-matrix.
The raison d’être of universal K-matrices is that they provide solutions to the twisted reflection equation
Recall that a balancing on a braided monoidal category \({\mathcal {A}}\) is a natural isomorphism \(\theta : \text {id}_{{\mathcal {A}}} \Rightarrow \text {id}_{{\mathcal {A}}}\) satisfying
for all \(M,N \in {\mathcal {A}}\). A ribbon Hopf algebra is a quasi-triangular Hopf algebra H together with a ribbon element i.e. a central invertible element \(\nu \in H\) such that the natural isomorphism \(\theta : \text {id}_{H\text {-mod}} \Rightarrow \text {id}_{H\text {-mod}}\) defined by acting with \(\nu \) gives a balancing on \(H\text {-mod}\).
Remark 3.4
For a braided monoidal category \({\mathcal {A}}\) both \((\text {id}_{{\mathcal {A}}},\sigma )\) and \((\text {id}_{{\mathcal {A}}},\sigma ^{-1})\) define monoidal functors \({\mathcal {A}}\rightarrow {\mathcal {A}}^{\otimes \text {-op}}\). The balancing axiom 3.3.1 expresses that \(\theta : (\text {id}_{{\mathcal {A}}},\sigma ^{-1}) \cong (\text {id}_{{\mathcal {A}}},\sigma )\) is a monoidal isomorphism. Consequently also \((\text {id}_{{\mathcal {A}}},\sigma ^2) \cong (\text {id}_{{\mathcal {A}}},\text {id})\) monoidally.
Proposition 3.5
Let H be a ribbon Hopf algebra, together with a be a Hopf algebra involution \(\phi \) that preserves R and v, and a quasi-triangular coideal subalgebra B. Then \((H\text {-mod},B\text {-mod})\) is canonically equipped with the structure of a \({\mathbb {Z}}_2\)-braided pair.
Proof
The category \(H\text {-mod}\) is braided monoidal since H is quasi-triangular. The involution \(\phi : H \rightarrow H\) defines a functor \(\Phi : M \mapsto M^\phi \), where \(M^{\phi }\) is the H-module where the H-action is twisted by \(\phi \). Since \(\phi \) is an Hopf algebra involution that preserves R, the functor  is a braided monoidal functor. We equip \(\Phi \) with the structure of an anti-involution via
is a braided monoidal functor. We equip \(\Phi \) with the structure of an anti-involution via

The monoidal functor  squares to
squares to  . The balancing \(\theta \) then gives a monoidal isomorphism \(t:\Phi ^2 \cong \text {id}_{{\mathcal {A}}}\) by Remark 3.4. Since \(\phi (\nu ) = \nu \) we also have \(\Phi (\theta ) = \theta _{\Phi }\). As B is a right coideal subalgebra the category \(B\text {-mod}\) inherits the structure of a right module category over \(H\text {-mod}\) with pointing
. The balancing \(\theta \) then gives a monoidal isomorphism \(t:\Phi ^2 \cong \text {id}_{{\mathcal {A}}}\) by Remark 3.4. Since \(\phi (\nu ) = \nu \) we also have \(\Phi (\theta ) = \theta _{\Phi }\). As B is a right coideal subalgebra the category \(B\text {-mod}\) inherits the structure of a right module category over \(H\text {-mod}\) with pointing  .
.
Action by the universal K-matrix defines the \({\mathbb {Z}}_2\)-cylinder braiding. \(\square \)
As explained in the introduction, examples are provided by quantum symmetric pairs.
Remark 3.6
Given a braided monoidal category \({\mathcal {A}}\), the notion of a \({\mathbb {Z}}_2\)-braided pair \(({\mathcal {A}},{\mathcal {M}})\) is very close to the notion of a \(\Phi \)-braided module category of [40]. Recall that a \(\Phi \)-braided module category over \({\mathcal {A}}\) consists of an \({\mathcal {A}}\)-module category \({\mathcal {M}}\), a braided monoidal equivalence  and a family of natural isomorphisms \(\kappa _{M,X}: M\otimes X\rightarrow M \otimes \Phi (X)\) for \(X\in {\mathcal {A}}\) and \(M \in {\mathcal {M}}\) satisfying the axioms BP1 and BP2 in Figs. 7 and 8.Footnote 10
and a family of natural isomorphisms \(\kappa _{M,X}: M\otimes X\rightarrow M \otimes \Phi (X)\) for \(X\in {\mathcal {A}}\) and \(M \in {\mathcal {M}}\) satisfying the axioms BP1 and BP2 in Figs. 7 and 8.Footnote 10
The difference is that in a \({\mathbb {Z}}_2\)-braided pair \(\Phi \) is required to be anti-monoidal and involutive. Given a \(\Phi \)-braided module category \({\mathcal {M}}\) over \({\mathcal {A}}\) such that the underlying functor \(\Phi \) is strictly involutive, then the pair \(({\mathcal {A}},{\mathcal {M}})\) defines a \({\mathbb {Z}}_2\)-braided pair exactly if \({\mathcal {A}}\) admits a balancing.Footnote 11
Definition 3.7
A \({\mathbb {Z}}_2\)-symmetric pair is a \({\mathbb {Z}}_2\)-braided pair \(({\mathcal {A}},{\mathcal {M}})\) such that
for all \(M\in {\mathcal {M}}\), \(X,Y\in {\mathcal {A}}\).
Examples of \({\mathbb {Z}}_2\)-symmetric pairs are provided by infinitesimal symmetric pairs.
Example 3.8
Let \({\mathfrak {g}}\) be a complex semisimple Lie algebra and let \(\theta : {\mathfrak {g}}\rightarrow {\mathfrak {g}}\) be an involution with fixed points \({\mathfrak {g}}^{\theta }\). We can decompose \(\theta = J \phi (-) J^{-1}\) for an outer automorphisms \(\phi \) and \(J \in G\).Footnote 12 Then \((U({\mathfrak {g}})\text {-mod}_{\text {f.d.}},U({\mathfrak {g}}^{\theta })\text {-mod}_{\text {f.d.}})\) is a \({\mathbb {Z}}_2\)-symmetric pair where \(\Phi (M) = M^\phi \) and acting with J defines \(\kappa \).
4 Coherence results
A coherence theorem asserts all diagrams of a certain class commute. Most famously, Mac Lane’s coherence theorem for monoidal categories states any diagramFootnote 13 in a monoidal category \({\mathcal {A}}\) commutes. An important consequence is that the a-priori different (parenthesized) tensor products \(X_1 \otimes \cdots \otimes X_n\) of objects \(X_1,\ldots , X_n \in {\mathcal {A}}\) are canonically isomorphic. In a braided monoidal category \({\mathcal {A}}\) coherence is more subtle. It is not true that all diagrams commute, for example \(\sigma ^2 \ne \text {id}\) in general. Thinking of \(\sigma \) as the simple braid on two strands provides intuition: the double braid and the trivial braid are different braids. This can be made precise: one associates a diagram of braids to a diagram in \({\mathcal {A}}\) by interpreting \(\sigma \) as the generators of a braid group \(B_n\). The Joyal–Street Coherence Theorem then states that a diagram in a braided monoidal category commutes if the associated diagram of braids commutes [37]. We will now prove a coherence theorem (1.9) for \({\mathbb {Z}}_2\)-braided pairs.
4.1 Coherence in the strict setting
We will now precisely state the coherence theorem, and prove it in a strict setting. Recall that a monoidal category is called strict if \(\alpha = \text {id}\), \(\rho = \text {id}\) and \(\lambda =\text {id}\).
Definition 4.1
Let \(({\mathcal {A}},{\mathcal {M}})\) be a \({\mathbb {Z}}_2\)-monoidal pair.
-
1.
We call the \({\mathbb {Z}}_2\)-monoidal pair strict if \({\mathcal {A}}\) is a strict monoidal category with a strict anti-involution \(\Phi \), and \({\mathcal {M}}\) is a strict module category.Footnote 14
-
2.
We call a \({\mathbb {Z}}_2\)-braided pair (or \({\mathbb {Z}}_2\)-symmetric pair) strict if the underlying \({\mathbb {Z}}_2\)-monoidal pair is strict.
We have the following simple, but important result:
Lemma 4.2
Let \(({\mathcal {A}},{\mathcal {M}})\) be a strict \({\mathbb {Z}}_2\)-braided pair.
-
1.
The braiding \(\sigma \) satisfies the Yang–Baxter equation
$$\begin{aligned}&\displaystyle (\sigma _{Y,Z} \otimes \text {id}_X) \circ (\text {id}_Y \otimes \sigma _{X,Z}) \circ (\sigma _{X,Y} \otimes \text {id}_Z) \\&\displaystyle = \\&\displaystyle (\text {id}_Z \otimes \sigma _{X,Y}) \circ (\sigma _{X,Z} \otimes \text {id}_Y) \circ (\text {id}_X \otimes \sigma _{Y,Z}) \end{aligned}$$for all \(X,Y,Z\in {\mathcal {A}}\).
-
2.
The \({\mathbb {Z}}_2\)-cylinder braiding \(\kappa \) satisfies the twisted reflection equation
$$\begin{aligned}&\displaystyle (\text {id}_M \otimes \sigma _{\Phi (Y),\Phi (X)}) \circ (\kappa _{M,Y}\otimes \text {id}_X) \circ (\text {id}_M \otimes \sigma _{\Phi (X),Y}) \circ (\kappa _{M,X} \otimes \text {id}_Y) \\&\displaystyle = \\&\displaystyle (\kappa _{M,X} \otimes \text {id}_Y) \circ (\text {id}_M \otimes \sigma _{\Phi (Y),X}) \circ (\kappa _{M,Y} \otimes \text {id}_X)\circ (\text {id}_M \otimes \sigma _{X,Y}) \end{aligned}$$for any \(M\in {\mathcal {M}}\) and \(X,Y \in {\mathcal {A}}\).
Proof
The proof that the braiding satisfies the Yang–Baxter equation is standard, see e.g. [26, 8.1.10]. To prove part (2) we observe that in the following diagram

the subdiagrams commute by naturality of \(\kappa \), the BP2 axiom and the fact that \(\Phi \) is a braided monoidal functor. Commutativity of the outer sides follows and expresses that \(\kappa \) satisfies the twisted reflection equation. \(\square \)
Before stating the coherence theorem we introduce some notation and definitions.
Notation
For natural isomorphisms \(F_1 \xrightarrow {\beta } F_2\), \(G_1\xrightarrow {\gamma } G_2\) with composite functors \(G_i \circ F_i\) we write \(\gamma * \beta : G_1 \circ F_1 \rightarrow G_2 \circ F_2\) for the horizontal composition. For natural isomorphisms \(F \xrightarrow {\beta } G \xrightarrow {\gamma } H\) we write \(\gamma \circ \beta \) or \(\gamma \beta \) for the (vertical) composition \(F \rightarrow H\).
Definition 4.3
Let \(({\mathcal {A}},{\mathcal {M}})\) be a \({\mathbb {Z}}_2\)-braided pair. A structural isomorphism in \({\mathcal {A}}\) (respectively \({\mathcal {M}}\)) is a natural isomorphism in \({\mathcal {A}}\) (respectively \({\mathcal {M}}\)) constructed as a vertical and horizontal composition of the natural isomorphisms: \(\text {id}_{\text {id}_{{\mathcal {A}}}}, \alpha ,\lambda ,\rho ,\text {id}_\Phi , \text {id}_{\otimes },\) \(\Phi _2,\Phi _0,t\) (and \(\text {id}_{\text {id}_{{\mathcal {M}}}}, \text {id}_{\text {act}}, a, r, \kappa \)) and their inverses.
Any structural isomorphism f in \({\mathcal {A}}\) is a natural isomorphism between functors with domain \({\mathcal {A}}^{\times n}\) and codomain \({\mathcal {A}}\) for some \(n\ge 0\). To a structural isomorphism f with a given presentation as a vertical/horizontal composition we can associate its underlying braid on n strands, denoted \(\beta _f \in B_n\), by interpreting instances of the braiding \(\sigma \) as simple braids, and doubling strings for instances of \(\text {id}_{\otimes }\). See Fig. 9 for two illustrated examples.
Remark 4.4
Note that the assignment of the underlying braid depends on the presentation of the structural isomorphism.
Similarly a structural isomorphism f in \({\mathcal {M}}\) is a natural isomorphism between functors with domain \({\mathcal {M}}\times {\mathcal {A}}^{\times n}\) and codomain \({\mathcal {M}}\) for some \(n\ge 0\). To such f together with a given presentation we can associate its underlying cylinder braid on n strands, denoted \(\beta _f \in B^{\text {cyl}}_n\), by interpreting instances of the braiding \(\sigma \) and \({\mathbb {Z}}_2\)-cylinder braiding \(\kappa \) as the generators \(\sigma \) and \(\kappa \) in \(B^{\text {cyl}}_n\), and doubling strings for instances of \(\text {id}_{\otimes }\).
Remark 4.5
By axioms BP1 and BP2 of Figs. 7 and 8 one can change the presentation of a structural isomorphism in \({\mathcal {M}}\) so that only one string is involved in an instance of the \({\mathbb {Z}}_2\)-cylinder braiding at a time but without changing the underlying braid.
Proposition 4.6
Let \(({\mathcal {A}},{\mathcal {M}})\) be a strict \({\mathbb {Z}}_2\)-braided pair and consider two parallel structural isomorphisms \(f,g: T_1 \Rightarrow T_2\) in \({\mathcal {A}}\) (or \({\mathcal {M}}\)). Then \(f=g\) if \(\beta _f = \beta _g\).
Proof
As both cases are analogous we will only give the proof for f and g in \({\mathcal {M}}\), The non-trivial components of the presentations of f and g consist of instances of \(\sigma \), \(\kappa \) and \(\text {id}_{\otimes }\), \(\text {id}_{\Phi }\). By Remark 4.5 we can change the presentation of f and g so that the underlying braids only braid two strings at a time without changing the underlying braid.Footnote 15 As \(\beta _f = \beta _g\) one can relate the presentations of the braids \(\beta _f\) and \(\beta _g\) via repeated applications of the cylinder braid relations 2.3.1 and 2.3.2. Using that \(\Phi \) is braided and strict we can then also rewrite the presentations of f and g into each other by applying the cylinder braid relations. By Lemma 4.2 it follows that \(f=g\). \(\square \)
We will now prove coherence for general \({\mathbb {Z}}_2\)-braided pairs by showing that one can replace a \({\mathbb {Z}}_2\)-braided pair (up to appropriate equivalence) by a strict \({\mathbb {Z}}_2\)-braided pair.
4.2 Strictification of the braided monoidal category
The strictification of \({\mathcal {A}}\) will move in two steps: first strictifying the tensor product on \({\mathcal {A}}\) and then strictifying the involution \(\Phi \).
Notation
Let \({\mathcal {A}}\) be a monoidal category, recall that \({\mathcal {A}}\) can be seen as a right \({\mathcal {A}}\)-module category in a canonical way. We denote this module category by \({\mathcal {A}}_{{\mathcal {A}}}\). For two right \({\mathcal {A}}\)-module categories \({\mathcal {M}}_1\) and \({\mathcal {M}}_2\) we denote by \(\text {Fun}_{{\mathcal {A}}}({\mathcal {M}}_1,{\mathcal {M}}_2)\) the category of right \({\mathcal {A}}\)-module functors, and morphisms of right \({\mathcal {A}}\)-module functors. For definitions see [26, ch. 7].
Definition 4.7
Let \({\mathcal {A}}\) be a monoidal category. We denote by \({\mathcal {A}}^{st}\) the strict monoidal category \(\text {Fun}_{{\mathcal {A}}}({\mathcal {A}}_{{\mathcal {A}}},{\mathcal {A}}_{{\mathcal {A}}})\). The tensor product on objects is given by composition of functors (denoted by \(\circ \)), with unit object the identity functor. The tensor product on morphisms is given by horizontal composition of natural transformations (denoted by \(\; * \;\)).
Proposition 4.8
[37, Proposition 1.3] Let \({\mathcal {A}}\) be a monoidal category. The monoidal functor \((L,L_2,L_0): {\mathcal {A}}\rightarrow {\mathcal {A}}^{st}\) defined by \(L(X) = (X\otimes -,\alpha _{X,-,-})\), \((L_2)_{X,Y} = \alpha _{X,Y,-}\), and \(L_0 = l_-\) is a monoidal equivalence.
Convention
We will use the following fact implicitly throughout: If F is a monoidal functor so that the functor underlying F is an equivalence, then any quasi-inverse \(F^{-1}\) is naturally monoidal, and the natural isomorphisms \(1 \Rightarrow F^{-1}F\) and \(FF^{-1} \Rightarrow 1\) are monoidal isomorphisms [26, 2.4.10]. Moreover, the natural isomorphisms can be chosen to satisfy the triangle identities of an adjunction [54, §4.4].
We now transport the anti-involution along the equivalence to the strict category.
Lemma 4.9
1. Let \(\alpha : F_1 \rightarrow F_2\) be a monoidal isomorphism, and let H, G be monoidal functors. The natural isomorphism \(\text {id}_H* \alpha *\text {id}_G: HF_1G \Rightarrow HF_2G\) is monoidal.
2. Let \(F: {\mathcal {A}}\rightarrow {\mathcal {B}}\) be an equivalence of monoidal categories, \(\Phi : {\mathcal {A}}\rightarrow {\mathcal {A}}^{\otimes \text {-op}}\) a monoidal functor and \(t: \Phi ^2 \Rightarrow \text {id}_{{\mathcal {A}}}\) an isomorphism of monoidal functors. Then there exists a anti-involution \(\Psi : {\mathcal {B}}\rightarrow {\mathcal {B}}^{\otimes \text {-op}}\), \(\pi : \Psi ^2 \Rightarrow \text {id}_{{\mathcal {B}}}\) such that \(\Psi \circ F \cong F \circ \Phi \) are monoidally isomorphic and the diagram

commutes.
Proof
The first statement is an easy verification. For the second claim we define \(\Psi := F \Phi F^{-1}\). As a composite of monoidal functors it is monoidal. Similarly, as a composite of adjoint equivalences it is an adjoint equivalence. One easily verifies the natural isomorphism \(\pi \) can defined as the composite
\(\square \)
We strictify the anti-involution using homotopy orbits, a method we adapted from [29].
Definition 4.10
Let \({\mathcal {A}}\) be a strict monoidal category, with an anti-involution \((\Psi ,\Psi _2,\Psi _0)\), \(\pi : \Psi ^2 \Rightarrow \text {id}_{{\mathcal {A}}}\). The category \({\mathcal {A}}_{{\mathbb {Z}}_2}\) has as objects quadruples
where \(X_i \in {\mathcal {A}}\) and \(\eta _i\) are isomorphisms in \({\mathcal {A}}\) such that the left diagram in Fig. 10 commutes for \(i=0,1\). A morphism
consists of a pair \(f_i: X_i \rightarrow Y_i\) of morphisms in \({\mathcal {A}}\) such that the right diagram of Fig. 10 commutes for \(i=0,1\).
Notation
We will write \(\vec {X}\) for a quadruple \((X_0,X_1,\eta _0,\eta _1)\), or use vector notation \(\left( \begin{bmatrix} X_0 \\ X_1 \end{bmatrix}, \begin{bmatrix} \eta _0 \\ \eta _1 \end{bmatrix}\right) \). We will sometimes refer to \(X_i\) (resp. \(\eta _i\)) the object (resp. morphism) components of \(\vec {X}\).
Lemma 4.11
The category \({\mathcal {A}}_{{\mathbb {Z}}_2}\) is strictly monoidal with tensor product
and unit  . Moreover, the functor \(\vec {\Psi }: {\mathcal {A}}_{{\mathbb {Z}}_2} \rightarrow {\mathcal {A}}_{{\mathbb {Z}}_2}\) defined by
. Moreover, the functor \(\vec {\Psi }: {\mathcal {A}}_{{\mathbb {Z}}_2} \rightarrow {\mathcal {A}}_{{\mathbb {Z}}_2}\) defined by
is a strict anti-monoidal functor such that \(\vec {\Psi }^2 = \text {id}\) is a monoidal isomorphism.
Proof
A straightforward calculation. \(\square \)
We can now prove a strictification theorem for monoidal categories with an anti-involution.
Proposition 4.12
1. The functor
defines an equivalence of categories.
2. The maps

equip \(\Omega \) with the structure of a monoidal functor.
3. The natural transformation \(\begin{bmatrix} \text {id}\\ \pi \end{bmatrix}: \vec {\Psi } \circ \Omega \Rightarrow \Omega \circ \Psi \) defines a monoidal isomorphism such that the diagram

commutes.
Proof
Let us first prove \(\Omega \) defines an equivalence. To see \(\Omega (X)\) defines an object, we observe that indeed \(\Psi (\text {id}) \circ \pi ^{-1}_X = \pi ^{-1}_X\) and \(\Psi (\pi _X^{-1}) \circ \text {id}= \pi ^{-1}_{\Psi (X)}\). That \(\Omega (f)\) defines a morphism is clear. To show \(\Omega \) is an equivalence we will check it’s fully faithful and essentially surjective. Faithfulness is clear. For fullness, let \(\vec {f}: \Omega (X) \rightarrow \Omega (Y)\) be any morphism. We have

by definition of \(\vec {f}\) being a morphism. Then \(\vec {f} = \Omega (f_0)\). Finally, \(\Omega \) is essentially surjective since for any \(\vec {X}\) we have the isomorphism \(\begin{bmatrix} \text {id}\\ \eta _0 \end{bmatrix}:\vec {X} \rightarrow \Omega (X_0)\).
The assertions of (2) are all easy checks that follow from \(\pi \), \(\Psi _2\), \(\Psi _0\) being natural isomorphisms and monoidality of \(\pi \) and \(\Psi \).
Finally, to prove part (3) we note that the maps \(\begin{bmatrix} \text {id}\\ \pi \end{bmatrix}: \Omega \circ \Psi \Rightarrow \varepsilon \circ \Omega \) define the components of a natural isomorphism. Monoidality can be checked componentwise, and is inherited from \(\text {id}\) and \(\pi \) e.g. the diagram

commutes since \(\pi \) is monoidal. The diagram in the theorem commutes since \(\Omega (\pi ) = (\pi , \Psi (\pi )) = (\pi , \pi _{\Psi }) = \varepsilon ( (\text {id},\pi ) ) \circ (\text {id},\pi )_{\Psi }\), where the second equality holds by assumption of \(\Psi \) being an anti-involution. \(\square \)
We can also transport the braiding \(\sigma \) on \({\mathcal {A}}\) to the strictification.
Lemma 4.13
[37, Example 2.4].
-
1.
Let \({\mathcal {A}}\) and \({\mathcal {A}}\) be monoidal categories and let \((F,\mu ): {\mathcal {A}}\rightarrow {\mathcal {A}}\) be a monoidal equivalence. If \({\mathcal {A}}\) is braided, there is a unique braiding on \({\mathcal {A}}\) making F braided monoidal.
-
2.
A monoidal equivalence F is braided monoidal iff its quasi-inverse \(F^{-1}\) is braided monoidal.
4.3 Strictification of the module category
We will strictify \({\mathcal {M}}\) by replacing it by the category \({\mathcal {M}}^{st} := \text {Fun}_{{\mathcal {A}}}({\mathcal {A}},{\mathcal {M}})\). This category is a strict module category over \({\mathcal {A}}^{st}\) where the action is defined by precomposition i.e. \(\text {act}(F,S) := F \circ S\) for \(F \in {\mathcal {M}}^{st}\), \(S \in {\mathcal {A}}^{st}\).
Lemma 4.14
Let \({\mathcal {M}}\) be a right \({\mathcal {A}}\)-module category. The functor \({\overline{L}}: {\mathcal {M}}\rightarrow {\mathcal {M}}^{st}\) defined by \({\overline{L}}(M) = (M\otimes -, (a)_{M,-,-})\) is an equivalence of categories.
Proof
Standard, see [26, Remark 7.2.4]. \(\square \)
The equivalences \({\overline{L}}\) and L intertwine the actions of \({\mathcal {A}}\) and \({\mathcal {A}}^{st}\) on \({\mathcal {M}}\) and \({\mathcal {M}}^{st}\) respectively.
Lemma 4.15
Let \(L: {\mathcal {A}}\rightarrow {\mathcal {A}}^{st}\), and \({\overline{L}}: {\mathcal {M}}\rightarrow {\mathcal {M}}^{st}\) be as above. There exist natural isomorphisms \(({\overline{L}}_2)_{M,X}: {\overline{L}}(M \otimes X) \cong {\overline{L}}(M) \circ L(X)\) for \(M\in {\mathcal {M}}\) and \(X\in {\mathcal {A}}\) such that the diagrams

commute for any \(M\in {\mathcal {M}}\), \(X,Y\in {\mathcal {A}}\).
Proof
The natural isomorphism \({\overline{L}}_2\) is defined as follows
To check if the diagrams of natural transformations commutes we need to check if the components commute. If we evaluate the functors on some \(D \in {\mathcal {A}}\) the first diagram becomes the pentagon axiom of the module category \({\mathcal {M}}\), whereas the second diagram becomes the triangle axiom of the module category. Thus the components define commuting diagrams for any D, and hence the diagrams of natural transformations commute. \(\square \)
Notation
We denote the quasi-inverse of \((L,L_2,L_0)\) by \((R,R_2,R_0)\) and let \(\eta : 1 \Rightarrow RL\) and \(\varepsilon : LR \rightarrow 1\) be the monoidal isomorphisms of the equivalence L. Similarly, we have \(\overline{\eta }: 1 \Rightarrow {\overline{R}}{\overline{L}}\), \(\overline{\varepsilon }: {\overline{L}}{\overline{R}}\Rightarrow 1\).
Lemma 4.16
Let \(R: {\mathcal {A}}^{st} \rightarrow {\mathcal {A}}\), and \({\overline{R}}: {\mathcal {M}}^{st} \rightarrow {\mathcal {M}}\) be as above. There exist natural isomorphisms \(({\overline{R}}_2)_{F,S}: {\overline{R}}(F \circ S) \cong {\overline{R}}(F) \otimes R(S)\) for \(F\in {\mathcal {M}}^{st}\) and \(S\in {\mathcal {A}}^{st}\) such that the diagram

commutes for any \(F\in {\mathcal {M}}^{st}\), \(S,T\in {\mathcal {A}}^{st}\).
Proof
Since \({\overline{L}}\) is full and faithful we can define isomorphisms \(({\overline{R}}_2)_{M,X}: {\overline{R}}(M\circ X) \Rightarrow {\overline{R}}(M) \otimes R(X)\) via the diagram

Then by naturality of \({\overline{L}}_2\) and \(\varepsilon \), \(\overline{\varepsilon }\) we have \({\overline{L}}({\overline{R}}_2)\circ LR( \alpha * \beta ) = L(R(\alpha )* R(\beta )) \circ {\overline{L}}({\overline{R}}_2)\). Faithfulness of \({\overline{L}}\) then implies naturality of \({\overline{R}}_2\). Consider the diagram

We wish to show the upper inner hexagon commutes. The other subdiagrams commute by definition of \({\overline{R}}_2\), naturality of \({\overline{L}}_2\) and Lemma 4.15. The outside of the diagram commutes since \(\varepsilon : LR \Rightarrow \text {id}\) is monoidal. Therefore, the inner hexagon commutes. Faithfulness of \({\overline{L}}\) implies \({\overline{R}}_2\) has the required property. \(\square \)
Note that the category \({\mathcal {M}}^{st}\) is also a strict module category over \({\mathcal {A}}^{st}_{{\mathbb {Z}}_2}\) with action \(F \cdot \vec {X} := F \circ X_0\), for \(\vec {X} = (X_0,X_1,\eta _0,\eta _1) \in {\mathcal {A}}^{st}_{{\mathbb {Z}}_2}\), and \(F \in {\mathcal {M}}^{st}\). Lemma 4.15 holds mutatis mutandis for the composite \(\Omega L\) and \({\overline{L}}\). To strictify the \({\mathbb {Z}}_2\)-braided pair it remains to transport the \({\mathbb {Z}}_2\)-cylinder braiding along the equivalences to \({\mathcal {A}}^{st}\) and \({\mathcal {A}}^{st}_{{\mathbb {Z}}_2}\).
Proposition 4.17
Let \(({\mathcal {A}}, {\mathcal {M}})\) be a \({\mathbb {Z}}_2\)-braided pair. There is a \({\mathbb {Z}}_2\)-cylinder braiding K on \(({\mathcal {A}}^{st},{\mathcal {M}}^{st})\) such that the diagram

commutes for any \(M \in {\mathcal {M}}\) and \(X \in {\mathcal {A}}\).
Proof
Let \(U\in {\mathcal {M}}^{st}\) and \(S, T \in {\mathcal {A}}^{st}\). Since \({\overline{R}}\) is full and faithful the diagram

defines the components \(K_{U,S}\) uniquely. Naturality of \(\eta , {\overline{R}}_2\) and \(\kappa \) implies that \({\overline{R}}(K) \circ {\overline{R}}(\alpha \; * \;\beta ) = {\overline{R}}(\alpha \; * \;\Psi (\beta )) \circ {\overline{R}}(K)\). Faithfulness of \({\overline{R}}\) then implies naturality of K. To show K defines a \({\mathbb {Z}}_2\)-cylinder braiding we need to check it satisfies axioms BP1 and BP2. We consider the diagram in Fig. 11. We wish to show the inner octagon commutes. The outer diagram commutes since \(\kappa \) is a \({\mathbb {Z}}_2\)-cylinder braiding. The other subdiagrams commute by naturality, Lemma 4.16, definition of K, and R being braided monoidal. We conclude the inner octagon commutes. By faithfulness of \({\overline{R}}\) we find that K satisfies axiom BP1. Similarly, one can write down a diagram to show K also satisfies BP2. We leave this to the reader, or see [67]. It remains to show K satisfies the diagram in the Proposition. Let \(M\in {\mathcal {M}}\), \(X \in {\mathcal {A}}\) and consider the diagram

The subdiagrams commute by naturality, the triangle identity, the definition of \({\overline{R}}_2\), and the definition of K. Therefore the outer diagram commutes, which is what we wished to show. \(\square \)
Finally, we transport the \({\mathbb {Z}}_2\)-cylinder braiding from \({\mathcal {A}}^{st}\) to \({\mathcal {A}}^{st}_{{\mathbb {Z}}_2}\). Namely, let \(\vec {S} = (S_0,S_1,\eta _0^S, \eta _1^S)\in {\mathcal {A}}^{st}_{{\mathbb {Z}}_2}\) and \(F \in {\mathcal {M}}^{st}\) we define \(\vec {K}_{F,\vec {S}}\) as the composite
One easily verifies that \(\vec {K}\) is a \({\mathbb {Z}}_2\)-cylinder braiding. Thus \(({\mathcal {A}}^{st}_{{\mathbb {Z}}_2},{\mathcal {M}}^{st})\) is a strict \({\mathbb {Z}}_2\)-braided pair.
4.4 Coherence as a corollory to strictification
Our strictification results now yield the coherence theorem as an easy corollary.
Theorem 4.18
Let \(({\mathcal {A}},{\mathcal {M}})\) be a \({\mathbb {Z}}_2\)-braided pair and consider two parallel structural isomorphisms \(T_1 \xrightarrow {f,g} T_2\) in \({\mathcal {A}}\) (or \({\mathcal {M}}\)). Then \(f=g\) if the underlying (cylinder) braids are equal \(\beta _f = \beta _g\).
Proof
We will provide the proof when f and g are structural isomorphisms with a given presentation in \({\mathcal {M}}\). The case of structural isomorphisms in \({\mathcal {A}}\) is analogous and left to the reader. We consider the diagram with sides \({\overline{L}}(f)\) and \({\overline{L}}(g)\) in \({\mathcal {M}}^{st}\). The presentation of f and g consists of a vertical composition of horizontal compositions of the \(a,\kappa ,r\), etcetera. Below each arrow of the presentation we build a rectangle using the diagrams in Propositions 4.8, 4.12.3, 4.17, Lemmas 4.9.2, 4.15 and 4.16 and so that we obtain a prism of natural isomorphisms. The lower face of the prism consists of two structural isomorphisms \(f^{st}\) and \(g^{st}\) in \({\mathcal {A}}^{st}_{{\mathbb {Z}}_2}\), whereas the upper face of the prism is our original diagram containing f and g. It is clear from these rectangles that if \(\beta _f= \beta _g\), then also \(\beta _{f^{st}}=\beta _{g^{st}}\). By assumption \(\beta _f=\beta _g\) so that Proposition 4.6 implies that \(f^{st} = g^{st}\). Then \({\overline{L}}(f)= {\overline{L}}(g)\) follows since the prism has vertical faces consisting of commutative diagrams of isomorphisms, and we just proved that the lower face commutes. By faithfulness of \({\overline{L}}\) we conclude \(f=g\). \(\square \)
We also have the following two coherence results:
Theorem 4.19
Let \(({\mathcal {A}},{\mathcal {M}})\) be a strict \({\mathbb {Z}}_2\)-monoidal pair, any two parallel structural isomorphisms are equal.
Proof
This is clear in a strict \({\mathbb {Z}}_2\)-monoidal pair since all horizontal composition of identities are identities. Now we deduce coherence from the strictification results, following the technique of the proof of Theorem 4.18. \(\square \)
Theorem 4.20
Let \(({\mathcal {A}},{\mathcal {M}})\) be a strict \({\mathbb {Z}}_2\)-symmetric pair, any two parallel structural isomorphisms are equal.
Proof
Note that the strictification \(({\mathcal {A}}^{st}_{{\mathbb {Z}}_2},{\mathcal {M}}^{st})\) is a strict \({\mathbb {Z}}_2\)-symmetric pair. We leave the proof, an easy adaptation of the proofs of Proposition 4.6 and Theorem 4.18, to the reader. \(\square \)
5 Classifying categorical algebras
Notation
Let \(\mathbb {k}\) be a field. We denote with \(\mathbf Vect \) the category of \(\mathbb {k}\)-vector spaces.
We now analyse categorical algebras in \(\mathbf Rex \), a setting of \(\mathbb {k}\)-linear categories well suited to higher algebra. By a \(\mathbb {k}\)-linear category we mean a category enriched over \(\mathbf Vect \). We introduce \(\mathbf Rex \) following the exposition given in [14].
Notation
We denote with \(\mathbf Vect _{\text {f.d.}}\) the \(\mathbb {k}\)-linear category of finite dimensional \(\mathbb {k}\)-vector spaces.
Notation
For a (higher) category \({\mathcal {C}}\) and \(X,Y\in {\mathcal {C}}\) we sometimes write \({\mathcal {C}}(X,Y)\) for \(\text {Hom}_{{\mathcal {C}}}(X,Y)\).
Recall that a functor is called right exact if it preserves finite colimits. A category is essentially small if it is equivalent to a small category.Footnote 16
Definition 5.1
\(\mathbf Rex \) is the 2-category of \(\mathbb {k}\)-linear essentially small categories that admit finite colimits with morphisms being right exact functors and 2-morphisms being natural isomorphisms.
Example 5.2
For any \(\mathbb {k}\)-algebra A the category \(A\text {-mod}_{\text {f.d.}}\) is in \(\mathbf Rex \).
For \({\mathcal {C}}, {\mathcal {D}}, {\mathcal {E}}\) k-linear we let \(\text {Bilin}({\mathcal {C}}\times {\mathcal {D}}, {\mathcal {E}})\) denote the category of \(\mathbb {k}\)-bilinear functors from \({\mathcal {C}}\times {\mathcal {D}}\) to \({\mathcal {E}}\) that preserve finite colimits in each variable separately.
Definition 5.3
The Deligne–Kelly tensor product \({\mathcal {C}}\boxtimes {\mathcal {D}}\) for \({\mathcal {C}},{\mathcal {D}}\in \mathbf Rex \) is uniquely characterised by the natural equivalence
For existence of the Deligne–Kelly tensor product see e.g. [49, §2.4].
Example 5.4
If A and B are \(\mathbb {k}\)-algebras then \(A\text {-mod}_{\text {f.d.}}\boxtimes B \text {-mod}_{\text {f.d.}}\simeq (A \otimes _{\mathbb {k}} B)\text {-mod}_{\text {f.d.}}\).
Convention
From now on any functor between categories in \(\mathbf Rex \) will be assumed to be \(\mathbb {k}\)-linear and right exact without further comment.
Two operations in \({\mathbb {Z}}_2{\mathcal {D}}_n\) are called isotopic if there is a path in the space of operations connecting them; we will refer to this path as an isotopy. If \(\beta : g\Rightarrow g'\) is an isotopy of operations and \((\gamma _i: f_i \Rightarrow h_i)_{i=1}^k\) a collection of isotopies then we call the associated isotopy
the horizontal composition. A 2-isotopy between two isotopies is a homotopy between the two paths in the space of operations.
Notation
For a permutation \(\sigma \in S_k\) we abuse notation by also writing \(\sigma \) for the induced permutation maps \(\sigma : {\mathbb {D}}^{\amalg k} \rightarrow {\mathbb {D}}^{\amalg k}\) and \(\sigma : {\mathcal {A}}^{\boxtimes k} \rightarrow {\mathcal {A}}^{\boxtimes k}\) where \({\mathcal {A}}\in \mathbf Rex \). More generally, for a collection of operations \((f_i)_{i=1}^{k}\) (resp. functors \((F_i)_{i=1}^{k}\)) in a composite \(\sigma \circ (\amalg _i f_i)\) and \(\sigma \circ (\boxtimes _i F_i)\) the map (resp. functor) \(\sigma \) permutes the codomains of the \(f_i\) (resp. \(F_i\)).
Definition-Proposition 5.5
An \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra F in \(\mathbf Rex \) is a choice of categories \({\mathcal {A}}, {\mathcal {M}}\in \mathbf Rex \) together with assignments
-
1.
For every operation f assigned functors F(f) as follows
$$\begin{aligned}&f \in {\mathbb {Z}}_2{\mathcal {D}}_n( {\mathbb {D}}^{\amalg k}, {\mathbb {D}}) \mapsto F(f): {\mathcal {A}}^{\boxtimes k} \rightarrow {\mathcal {A}},\\&f \in {\mathbb {Z}}_2{\mathcal {D}}_n( {\mathbb {D}}_* \amalg {\mathbb {D}}^{\amalg k}, {\mathbb {D}}_*) \mapsto F(f): {\mathcal {M}}\boxtimes {\mathcal {A}}^{\boxtimes k} \rightarrow {\mathcal {M}}, \\&f \in {\mathbb {Z}}_2{\mathcal {D}}_n( {\mathbb {D}}^{\amalg k}, {\mathbb {D}}_*) \mapsto F(f): {\mathcal {A}}^{\boxtimes k} \rightarrow {\mathcal {M}}. \end{aligned}$$where \({\mathcal {A}}^{\boxtimes 0 }:= \mathbf Vect _{\text {f.d.}}\).
-
2.
For every isotopy between compositions of operations \((g,(f_i)_{i=1}^k,h)\) and permutation \(\sigma \in S_k\) an assigned natural isomorphism as follows

Subject to the conditions that:
-
(i)
identity operations get assigned identity functors,
-
(ii)
for every operation f the constant isotopies

get assigned the identity natural isomorphism \(\text {id}_{F(f)}\),
-
(iii)
and for every diagram of operations and isotopies

such that there exists a 2-isotopy between the composite isotopies filling the square then the following equation holds between the assigned natural isomorphisms
$$\begin{aligned} \Big ( \text {id}_{F(m)} * (\text {id}_{\sigma _h} * \boxtimes _n F(\beta _n) \Big ) \; \circ \; F(\alpha ) = \Big ( F(\delta ) * (\text {id}_{\sigma _f} * \boxtimes _j \text {id}_{F(f_j)}) \Big ) \; \circ \; F(\gamma ). \end{aligned}$$(5.5.1)
Remark 5.6
We will view \({\mathbb {Z}}_2{\mathcal {D}}_n\) as an \(\infty \)-operad to define \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras in general. Definition-Proposition 5.5 unpacks that definition for \(\mathbf Rex \). The proof is delayed until Sect. 6.
Various special cases of condition (iii) determine the ‘pseudofunctoriality’ of \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras:
Lemma 5.7
Let F be a \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra in \(\mathbf Rex \).
-
1.
Let \(\alpha : f \simeq g\) be an isotopy between operations, then

and

are assigned the same natural isomorphism denoted \(F(\alpha )\).
-
2.
Let \(\alpha ^{-1}\) denote the inverse isotopy of \(\alpha : f\simeq g\), then \(F(\alpha ^{-1}) = F(\alpha )^{-1}\).
-
3.
If \(\alpha \) and \(\beta \) are isotopies that are 2-isotopic, then \(F(\alpha ) = F(\beta )\).
-
4.
For any choice of composite \(\beta \circ \alpha \) of two isotopies \(\beta \), \(\alpha \) we have \(F(\beta \circ \alpha ) = F(\beta ) \circ F(\alpha )\).
-
5.
The constant isotopy

is assigned a natural isomorphism
$$\begin{aligned} F\big (m \circ (\sigma _g \circ \amalg _n g_n) \big ) \cong F(m) \circ \big (\sigma _g \circ \boxtimes _n F(g_n) \big ). \end{aligned}$$ -
6.
The two composites of natural isomorphisms between \(F\big (m \circ (\sigma _g \circ \amalg _n g_n) \circ (\sigma _f \circ \amalg _i f_j))\) and \(F(m) \circ \big (\sigma _g \circ \boxtimes _n F(g_n) \big ) \circ \big (\sigma _f \circ \boxtimes _j F(f_j))\) are equal.
-
7.
The diagram

commutes.
Convention
A right exact functor \(F: \mathbf Vect _{\text {f.d.}}\rightarrow {\mathcal {C}}\) in \(\mathbf Rex \) is uniquely determined by the image of \(\mathbb {k}\in \mathbf Vect _{\text {f.d.}}\). We will identify F with \(F(\mathbb {k}) \in {\mathcal {C}}\) without further comment.
In the coming three subsections we will construct assignments of \(\mathbb {k}\)-linear categorical \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras for \(n=1\), \(n=2\), \(n\ge 3\) out of \(\mathbb {k}\)-linear \({\mathbb {Z}}_2\)-monoidal, \({\mathbb {Z}}_2\)-braided, \({\mathbb {Z}}_2\)-symmetric pairs, and vice versa. That these assignments are inverse equivalences is shown in Sect. 6.
Remark 5.8
We delay proving the assignments are equivalences because we don’t want to write down all the data here that determines an isomorphism of \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras in \(\mathbf Rex \).
5.1 \({\mathbb {Z}}_2\)-tensor pairs versus \({\mathbb {Z}}_2{\mathcal {D}}_1\)-algebras
By a tensor category we will a monoidal category \({\mathcal {A}}\) such that \({\mathcal {A}}\in \mathbf Rex \) and \(\otimes \in \text {Bilin}({\mathcal {A}}\times {\mathcal {A}}, {\mathcal {A}})\).
Remark 5.9
By definition of the Deligne–Kelly product \(\boxtimes \) the tensor product \(\otimes \) corresponds to a functor \(\otimes : {\mathcal {A}}\boxtimes {\mathcal {A}}\rightarrow {\mathcal {A}}\). A tensor category is thus exactly an \(E_1\)-algebra in \(\mathbf Rex \).
A right module category over a tensor category \({\mathcal {A}}\) is an \({\mathcal {A}}\)-module category \({\mathcal {M}}\) such that \({\mathcal {M}}\in \mathbf Rex \) and \(\text {act}\in \text {Bilin}({\mathcal {M}}\times {\mathcal {A}}, {\mathcal {M}})\).
Definition 5.10
A \({\mathbb {Z}}_2\)-tensor pair consists of a tensor category \({\mathcal {A}}\) with an anti-involution \(\Phi \) and a right \({\mathcal {A}}\)-module category \({\mathcal {M}}\) with a pointing  .
.
Remark 5.11
One obtains a \({\mathbb {Z}}_2\)-monoidal pair from a \({\mathbb {Z}}_2\)-tensor pair by forgetting \(\mathbb {k}\)-enrichment. As forgetting \(\mathbb {k}\)-enrichment is faithfulFootnote 17 Theorems 4.18, 4.19, 4.20 automatically yield coherence theorems for their \(\mathbb {k}\)-linear tensor category analogues.
Proposition 5.12
To a \({\mathbb {Z}}_2{\mathcal {D}}_1\)-algebra F in \(\mathbf Rex \) there is an associated \({\mathbb {Z}}_2\)-tensor pair \(({\mathcal {A}}_F,{\mathcal {M}}_F)\).
Proof
We set \({\mathcal {A}}_F := {\mathcal {A}}\) and \({\mathcal {M}}_F := {\mathcal {M}}\). Consider the fixed operations \(f_\otimes \), \(\text {id}_{\mathbb {D}}\), \(f_\Phi \),  , \(f_\text {act}\), \(\text {id}_{{\mathbb {D}}_*}\),
, \(f_\text {act}\), \(\text {id}_{{\mathbb {D}}_*}\),  in Table 2. The operations are assigned functors that for which we introduce the following suggestive notation, respectively: \(\otimes \), \(\text {id}_{{\mathcal {A}}}\), \(\Phi \),
in Table 2. The operations are assigned functors that for which we introduce the following suggestive notation, respectively: \(\otimes \), \(\text {id}_{{\mathcal {A}}}\), \(\Phi \),  , \(\text {act}\), \(\text {id}_{{\mathcal {M}}}\) and
, \(\text {act}\), \(\text {id}_{{\mathcal {M}}}\) and  . Note that by Definition-Proposition 5.5 (i) the functors \(\text {id}_{{\mathcal {A}}}\) and \(\text {id}_{{\mathcal {M}}}\) are indeed the identity functors on \({\mathcal {A}}\) and \({\mathcal {M}}\).
. Note that by Definition-Proposition 5.5 (i) the functors \(\text {id}_{{\mathcal {A}}}\) and \(\text {id}_{{\mathcal {M}}}\) are indeed the identity functors on \({\mathcal {A}}\) and \({\mathcal {M}}\).
Next we need to show there exist natural isomorphisms \(\alpha , \lambda ,\rho ,\Phi _2,\Phi _0,t,r,a\) that are part of the definition of a \({\mathbb {Z}}_2\)-tensor pair. One can define all the isomorphisms analogously, therefore we only define \(\alpha \) leaving the others to the reader. Consider the composite operations \(f_{\otimes } \circ (f_{\otimes } \amalg \text {id}_{\mathbb {D}})\) and \(f_{\otimes } \circ (\text {id}_{{\mathbb {D}}} \amalg f_{\otimes })\). Observe that the two composites define isotopic operations since they lie in the same connected components lying over \((0,0,0,\text {id}) \in \{0,1\}^{\times 3} \times S_3\) in the notation of Lemma 2.11. Choose an isotopy \(f_{\alpha }\) between them, then by Lemma 5.7.1 we have an associated natural isomorphism \(F\big (f_{\alpha }): F(f_{\otimes } \circ (f_{\otimes } \amalg \text {id}_{\mathbb {D}}) \big ) \cong F\big (f_{\otimes } \circ (\text {id}_{{\mathbb {D}}} \amalg f_{\otimes }\big )\). Using the natural isomorphisms of Lemma 5.7.5 we can define a natural isomorphism \(\alpha \) by requiring that the diagram

commutes.
To show that our functors and natural isomorphisms equip \(({\mathcal {A}},{\mathcal {M}})\) with the structure of a \({\mathbb {Z}}_2\)-tensor pair, we need to check that the natural isomorphisms satisfy the defining equations of a \({\mathbb {Z}}_2\)-tensor pair. Since all such equations can be treated similarly, we will verify one case in detail leaving the others to the reader. We will verify that \(\alpha \), \(\lambda \) and \(\rho \) satisfy the triangle axiom of a monoidal category. By definition the triangle axiom requires that for every \(X,Y \in {\mathcal {A}}\) the diagram

commutes. This is equivalent to asking that the equation

holds. Let us consider the isotopy \(\text {id}_{f_{\otimes }} * (\text {id}_{\text {id}_{{\mathbb {D}}}} \amalg f_\rho )\) and choose a composite isotopy  . Note that both these isotopies are paths between the same operations, and recall that by Lemmas 2.9 and 2.11 the space of operations \({\mathbb {Z}}_2{\mathcal {D}}_n({\mathbb {D}}^3,{\mathbb {D}})\) contracts onto a discrete space. We conclude the two isotopies are 2-isotopic, so that their assigned natural isomorphisms are equal by Lemma 5.7.3. Now consider the diagram
. Note that both these isotopies are paths between the same operations, and recall that by Lemmas 2.9 and 2.11 the space of operations \({\mathbb {Z}}_2{\mathcal {D}}_n({\mathbb {D}}^3,{\mathbb {D}})\) contracts onto a discrete space. We conclude the two isotopies are 2-isotopic, so that their assigned natural isomorphisms are equal by Lemma 5.7.3. Now consider the diagram

and note that the arrows \(\cong \) are unambiguous by Lemma 5.7 part 6. Then all inner squares commute by Lemma 5.7 and the definitions of \(\lambda \), \(\rho \) and \(\alpha \). The inner triangle commutes by Lemma 5.7 parts 3 and 4. Hence the outer sides of the diagram commute which expresses Eq. (5.12.1) holds. \(\square \)
Theorem 5.13
To a \({\mathbb {Z}}_2\)-tensor pair \(({\mathcal {A}},{\mathcal {M}})\) there is an associated \({\mathbb {Z}}_2{\mathcal {D}}_1\)-algebra \(F_{({\mathcal {A}},{\mathcal {M}})}\) in \(\mathbf Rex \).
Proof
We will abbreviate \(F_{({\mathcal {A}},{\mathcal {M}})}\) by F. First we define the assignment of functors to embeddings. To do that we introduce some notation. Recall we can assign a tuple \((\varepsilon _1,\ldots ,\varepsilon _k) \in \{0,1\}^{\times k}\) and a permutation \(\sigma \in S_k\) to operations via the Lemmas 2.9, 2.11 and 2.12. We denote \(\Phi ^0 := \text {id}_{{\mathcal {A}}}\) and \(\Phi ^1 := \Phi \), and  and \(\otimes _n := \otimes \circ (\otimes _{n-1} \boxtimes \text {id}_{{\mathcal {A}}}): {\mathcal {A}}^{\boxtimes n} \rightarrow {\mathcal {A}}\).
and \(\otimes _n := \otimes \circ (\otimes _{n-1} \boxtimes \text {id}_{{\mathcal {A}}}): {\mathcal {A}}^{\boxtimes n} \rightarrow {\mathcal {A}}\).
We can then define the associated functors to operations in \({\mathbb {Z}}_2{\mathcal {D}}_n( {\mathbb {D}}^{\amalg k}, {\mathbb {D}})\) by
and define the associated functors to operations in \({\mathbb {Z}}_2{\mathcal {D}}_n( {\mathbb {D}}^{\amalg k}, {\mathbb {D}}_*)\) by

and define the associated functors to operations in \({\mathbb {Z}}_2{\mathcal {D}}_n({\mathbb {D}}_* \amalg {\mathbb {D}}^{\amalg k}, {\mathbb {D}}_*)\) by
Note this assignment satisfies Definition-Proposition 5.5 (i).
Next we will assign the natural isomorphisms. To an isotopy between operations \(g \circ (\sigma _f \circ (\amalg f_j))\) and h we will assign a structural isomorphisms between the assigned functors \(F(g) \circ (\sigma \circ (\boxtimes F(f_j))\) and F(h). Combining Theorem 4.19 and Remark 5.11 we know there is at most one structural isomorphism between two given functors. Hence to unambiguously specify the assignment it suffices to show that there exists a structural isomorphism. We will only discuss one particular case of an assignment, leaving the others to the reader since they are all analogous. Consider operations \(g \circ (\sigma _F\circ (\amalg _j f_j))\) and h with codomain \({\mathbb {D}}\) that are isotopic. Note that then all the \(f_j\) must also be operations with codomain \({\mathbb {D}}\). We consider their images under the maps of Lemmas 2.9 and 2.11:
As \(g \circ (\sigma _f\circ (\amalg _j f_j)) \simeq h\) and \({\mathbb {Z}}_2{\mathcal {D}}_n({\mathbb {D}}^k,{\mathbb {D}})\) contracts onto the discrete space \(\{0,1\}^{\times k}\times S_k\) we find
Hence F(h) and \(F(g)\circ (\sigma _f \circ (\boxtimes _j F(f_j)))\) multiply a tuple of objects \((X_1,\ldots ,X_k)\) in \({\mathcal {A}}\) in the same order, and with the same distribution of \(\Phi \)’s (modulo 2). Then we can define a structural isomorphism between F(h) and \(F(g) \circ (\boxtimes _j F(f_j))\) via repeated applications of \(\alpha , \Phi _2\), and t (and possibly \(\Phi _0\), \(\lambda \) and \(\rho \) in case one or more of the \(k_j=0\)).
Note that property (ii) of Definition-Proposition 5.5 is satisfied by our assignment of natural isomorphisms. It remains to check condition (iii). Consider a diagram of isotopies and operations as in condition (iii) together with a 2-isotopy. The two sides of Eq. (5.5.1) are structural isomorphisms by construction of our assignments. Thus the two sides are parallel structural isomorphisms. Then they must agree by Theorem 4.19 combined with Remark 5.11. \(\square \)
5.2 \({\mathbb {Z}}_2\)-braided pairs versus \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebras
Definition 5.14
A \({\mathbb {Z}}_2\)-braided tensor pair is a \({\mathbb {Z}}_2\)-tensor pair \(({\mathcal {A}},{\mathcal {M}})\) together with a braiding \(\sigma \) on \({\mathcal {A}}\), such that \(\Phi \) is braided monoidal, and a natural isomorphism
such that the diagrams of Figs. 7 and 8 commute for all \(M\in {\mathcal {M}}\), \(X,Y \in {\mathcal {A}}\).
To study categorical \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebras we will make use of an ordering on \({\mathbb {R}}^2\) that subdivides the spaces of operations.
Definition 5.15
Let \({\mathbb {D}}\) and \({\mathbb {D}}_*\) be of dimension \(n >1\).
-
1.
For \(x = (x_1,\ldots ,x_n)\), \(y = (y_1,\ldots ,y_n) \in {\mathbb {R}}^n\). We write \(x<y\) iff \(x_1 < x_2\) or there exists \(i>1\) such that \(x_1 = y_1,x_2 = y_2,\ldots , x_i = y_i\) and \(x_{i+1} < y_{i+1}\).
-
2.
To \(x = (x_1,\ldots ,x_k) \in F_k [{\mathbb {D}}/{\mathbb {Z}}_2]\) or \(x = (x_1,\ldots ,x_k) \in F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) we assign \((\varepsilon _1,\ldots ,\varepsilon _k)\in \{0,1\}^{\times k}\) as in 2.10.1 respectively 2.11.1.
-
3.
For \(x \in F_k [{\mathbb {D}}/{\mathbb {Z}}_2]\) or \(x\in F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) Eq. (2.10.2) defines a unique \(\sigma \in S_k\).
Remark 5.16
Note that the assignments
of Definition 5.15 do not define continuous maps.
Lemma 5.17
Let \(n=2\) and \(k\ge 0\) and fix basepoints of the spaces \(F_k[{\mathbb {D}}/{\mathbb {Z}}_2]\) and \(F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\).
-
1.
To a path \(\gamma \) in \(F_k[{\mathbb {D}}/{\mathbb {Z}}_2]\) there is a canonically associated braid \([\gamma ] \in B_n\) such that \([\gamma _1 * \gamma _2] = [\gamma _1][\gamma _2]\) and \([\gamma ^{-1}] = [\gamma ]^{-1}\).
-
2.
To a path \(\gamma \) in \(F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) there is a canonically associated braid \([\gamma ] \in B^{\text {cyl}}_n\) such that \([\gamma _1 * \gamma _2] = [\gamma _1][\gamma _2]\) and \([\gamma ^{-1}] = [\gamma ]^{-1}\).
Proof
We will prove part two, and leave part one to the reader as the proof is analogous. Consider the non-continuous projection
and observe that the set-theoretic fibers of p define contractible subspaces \(\{F^i\}_{i=0}^N\) of \(F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\). Let \(\{x_1,\ldots ,x_N: x_i \in F^i\}\) denote the \({\mathbb {Z}}_2^{\times k} \times S_k\) orbit of the basepoint of \(F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\). Given a path \(\gamma \) in \(F_k[{\mathbb {D}}_*/{\mathbb {Z}}_2]\) with endpoints \(\gamma _0 \in F^{i_0}\) and \(\gamma _1 \in F^{i_1}\) we choose a path \(e_0\) lying in \(F^{i_0}\) from \(x_{i_0}\) to \(\gamma _0\) and a path \(e_1\) lying \(F^{i_1}\) from \(\gamma _1\) to \(x_{i_1}\). Recall that we have the quotient map
we then define
Since the subspaces \(F^i\) are contractible one easily verifies the assignment is independent of the choice of \(e_0\) and \(e_1\) and respects composition and inversion. \(\square \)
Remark 5.18
Consequently, Lemma 5.17 together with the homotopy equivalences of Proposition 2.9 allows us to associate braids to isotopies of operations in \({\mathbb {Z}}_2{\mathcal {D}}_2\). Moreover, note that 2-isotopic isotopies are assigned the same braids.
Proposition 5.19
To a \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebra F in \(\mathbf Rex \) there is an associated \({\mathbb {Z}}_2\)-braided tensor pair \(({\mathcal {A}}_F,{\mathcal {M}}_F)\).
Proof
We set \({\mathcal {A}}_F := {\mathcal {A}}\) and \({\mathcal {M}}_F := {\mathcal {M}}\). Consider the fixed operations \(f_\otimes \), \(f_\Phi \), \(f_\text {act}\), in Fig. 12, the identity operations \(\text {id}_{\mathbb {D}}\) and \(\text {id}_{{\mathbb {D}}_*}\) and the unique operations  and
and  . These operations are by F assigned functors that we denote respectively \(\otimes \), \(\Phi \), \(\text {act}\), \(\text {id}_{{\mathcal {A}}}\),\(\text {id}_{{\mathcal {M}}}\),
. These operations are by F assigned functors that we denote respectively \(\otimes \), \(\Phi \), \(\text {act}\), \(\text {id}_{{\mathcal {A}}}\),\(\text {id}_{{\mathcal {M}}}\),  , and
, and  . Note that by Definition-Proposition 5.5 (i) the functors \(\text {id}_{{\mathcal {A}}}\) and \(\text {id}_{{\mathcal {M}}}\) are indeed the identity functors on \({\mathcal {A}}\) and \({\mathcal {M}}\).
. Note that by Definition-Proposition 5.5 (i) the functors \(\text {id}_{{\mathcal {A}}}\) and \(\text {id}_{{\mathcal {M}}}\) are indeed the identity functors on \({\mathcal {A}}\) and \({\mathcal {M}}\).
Next we need to show there exist natural isomorphisms \(\alpha \), \(\lambda \), \(\rho \), \(\sigma \), \(\Phi _2\), \(\Phi _0\), t, r, a, \(\kappa \) that are part of the definition of a \({\mathbb {Z}}_2\)-braided tensor pair. Our strategy is as follows. To define a structural isomorphism \(\eta \), we choose an isotopy \(\gamma \) such that the associated braid \([\gamma ]\) is equal to the underlying braid \(\beta _\eta \), and then define \(\eta \) as the induced isomorphism of \(F(\gamma )\). Let us treat the case of \(\sigma \), leaving the others to the reader. Consider the ‘swap’ permutation \(\tau = (12) \in S_2\). We choose the isotopy \(i_\sigma \) from \(f_\otimes \) to the composite operation \(f_\otimes \circ (\tau \circ (\text {id}_{\mathbb {D}}\amalg \text {id}_{\mathbb {D}}))\), given by rotating the disks 180 degrees around each other. By definition of \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebra the assignment \(F(i_\sigma )\) is a natural isomorphism from \(\otimes = F(f_\otimes )\) to \(\otimes \circ (\tau \circ ( \text {id}_{{\mathcal {A}}} \boxtimes \text {id}_{{\mathcal {A}}}) = \otimes ^{op}\). We then define \(\sigma := F(i_\sigma )\).
It remains to check that the natural isomorphisms satisfy the defining equations of a \({\mathbb {Z}}_2\)-braided tensor pair. As in the proof of Theorem 5.12 one easily deduces that the equations hold from the existence of various 2-isotopies. For example, consider axiom BP1. The isotopy of coloured braids drawn there can easily be ‘fattened’ to give a 2-isotopy in \({\mathbb {Z}}_2{\mathcal {D}}_2({\mathbb {D}}^{\amalg 2} \amalg {\mathbb {D}}_*,{\mathbb {D}}_*)\). The existence of this 2-isotopy implies \(a, \Phi _2,\kappa \) and \(\sigma \) satisfy axiom BP1. We leave the details to the reader. \(\square \)
Theorem 5.20
To a \({\mathbb {Z}}_2\)-braided tensor pair \(({\mathcal {A}},{\mathcal {M}})\) there is an associated \({\mathbb {Z}}_2{\mathcal {D}}_2\)-algebra \(F_{({\mathcal {A}},{\mathcal {M}})}\) in \(\mathbf Rex \).
Proof
We will abbreviate \(F_{({\mathcal {A}},{\mathcal {M}})}\) by F. Via Definition 5.15 we can assign a permutation \(\sigma \in S_k\) and a tuple \((\varepsilon _1,\ldots ,\varepsilon _k) \in \{0,1\}^{\times k}\) to an operation f. We then assign functors F(f) to operations via the formulae in Eqs. (5.13.1)–(5.13.3).
Next we assign natural isomorphisms to isotopies. To an isotopy \(\gamma \) between operations \(g \circ (\sigma _f \circ (\amalg f_j))\) and h we will assign a structural isomorphisms between the assigned functors \(F(g) \circ (\sigma \circ (\boxtimes F(f_j))\) and F(h), as we did in the proof of Theorem 5.13. Via Lemma 5.17 and Remark 5.18 we have an associated braid \([\gamma ]\) to \(\gamma \). Recall that by Theorem 4.18 there is at most one structural isomorphism between \(F(g) \circ (\sigma \circ (\boxtimes F(f_j))\) and F(h) that has underlying braid \([\gamma ]\). Hence to specify the assignment it suffices to show that there exists such a structural isomorphism. Existence is an easy case-by-case analysis similar to the one in Theorem 5.13 that we leave to the reader.
Property (ii) of Definition-Proposition 5.5 is satisfied by our assignment. It remains to check condition (iii). Consider a diagram of isotopies and operations as in condition (iii) together with a 2-isotopy. The two sides of Eq. (5.5.1) are structural isomorphisms by construction of our assignments and by definition of structural isomorphism. Moreover, the assigned braids of both sides are equal by Lemma 5.17 and Remark 5.18. Hence, Eq. (5.5.1) holds by Theorem 4.18 combined with Remark 5.11. \(\square \)
5.3 \({\mathbb {Z}}_2\)-symmetric pairs versus \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras
Definition 5.21
A \({\mathbb {Z}}_2\)-braided tensor pair \(({\mathcal {A}},{\mathcal {M}})\) is called a \({\mathbb {Z}}_2\)-symmetric tensor pair if
for all \(M\in {\mathcal {M}}, X, Y \in {\mathcal {A}}\).
Proposition 5.22
Let \(n\ge 3\). To a \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra F in \(\mathbf Rex \) there is an associated \({\mathbb {Z}}_2\)-symmetric tensor pair \(({\mathcal {A}}_F,{\mathcal {M}}_F)\).
Proof
As the proof is very similar to Proposition 5.19 we will be brief. The n-dimensional analogues of the operations, isotopies and 2-isotopies in the proof of Proposition 5.19 define the structure of a \({\mathbb {Z}}_2\)-braided pair on \({\mathcal {A}}_F := {\mathcal {A}}\) and \({\mathcal {M}}_F:= {\mathcal {M}}\). Denote the isotopies \(i_\sigma \), \(i_\kappa \), \(i_t\) that are mapped by F to the natural isomorphisms \(\sigma \), \(\kappa \) and t. For \(n\ge 3\) there now exist 2-isotopies
in \({\mathbb {Z}}_2{\mathcal {D}}_n\) enforcing the equations \(\sigma ^2 = \text {id}\) and \((1\otimes t) \circ \kappa ^2 = \text {id}\). \(\square \)
Theorem 5.23
Let \(n\ge 3\). To a \({\mathbb {Z}}_2\)-symmetric tensor pair \(({\mathcal {A}},{\mathcal {M}})\) there is an associated \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra \(F_{({\mathcal {A}},{\mathcal {M}})}\) in \(\mathbf Rex \).
Proof
As the proof is very similar to Theorems 5.13 and 5.20 we will be brief. Via Definition 5.15 we can assign a permutation \(\sigma \in S_k\) and a tuple \((\varepsilon _1,\ldots ,\varepsilon _k) \in \{0,1\}^{\times k}\) to an operation f. We then assign functors F(f) to operations via the formulae in Eqs. (5.13.1)–(5.13.3). For an isotopy \(\gamma \) between operations \(g \circ (\sigma _f \circ (\amalg f_j))\) and h it is not hard to show that there exists a structural isomorphism between the assigned functors \(F(g) \circ (\sigma \circ (\boxtimes F(f_j))\) and F(h). Theorem 4.20 combined with Remark 5.11 then imply this assignment is unique, and satisfies Definition-Proposition 5.5. \(\square \)
6 General algebras
To define algebras in the (2, 1)-category \(\mathbf Rex \) over the topological operad \({\mathbb {Z}}_2{\mathcal {D}}_n\) we employ the language of \((\infty ,1)\)-categories. Our model of \((\infty ,1)\)-categories is given by quasi-categories, also known as \(\infty \)-categories.Footnote 18 Our references are [50, 52].
6.1 Higher categories and higher operads
Before recalling the definition of \(\infty \)-operads we first adopt a different perspective on topogical operads.
Notation
Let \(\text {Fin}_*\) denoted the skeletal category of finite pointed sets.Footnote 19
Definition 6.1
[52, 2.1.1.7] Let \({\mathcal {O}}\) be a topological coloured operad with operation spaces \({\mathcal {O}}(c_1 \otimes \cdots \otimes c_k,c)\) for colours \(c,c_i\). The topological category \({\mathcal {O}}^{\otimes }\) has as objects finite sequences of colours of \({\mathcal {O}}\) and a morphism \(\{c_1,\ldots ,c_k\} \rightarrow \{d_1,\ldots ,d_m\}\) is a collection
where f is a morphism in \(\text {Fin}_*\).Footnote 20
Remark 6.2
The category \({\mathcal {O}}^{\otimes }\) has a canonical forgetful functor \({\mathcal {O}}^{\otimes } \rightarrow \text {Fin}_*\) which one can use to reconstruct the operad \({\mathcal {O}}\) out of \({\mathcal {O}}^{\otimes }\).
One obtains the associated \(\infty \)-operad by taking the (homotopy) coherent nerve \(\text {N}\) of \({\mathcal {O}}^{\otimes }\).Footnote 21 To apply the homotopy coherent nerve to a topological category one needs to change enrichment to simplicial sets via the singular chains functor.
Convention
We will change enrichment from topological to simplicial without comment.
It is worthwhile to remind ourselves of some of the low-dimensional simplices of \(\text {N}{\mathcal {C}}\).
Example 6.3
Let \({\mathcal {C}}\) be a simplicially enriched category, and denote \(\circ \) (resp. \(*\)) the horizontal composition in \({\mathcal {C}}\) of vertices (resp. edges). The coherent nerve \(\text {N}{\mathcal {C}}\) is a simplicial set with vertices being the objects of \({\mathcal {C}}\), 1-simplices being the morphisms of \({\mathcal {C}}\), 2-simplices being diagrams of the form

and a 3-simplex consists of

Notation
We denote \(\text {N}{\mathcal {O}}^{\otimes }\) as \(N^\otimes ({\mathcal {O}})\) and call it the operadic nerve of \({\mathcal {O}}\) [52, 2.1.1.23].
Remark 6.4
\(\text {N}^{\otimes } ({\mathcal {O}})\) is an \(\infty \)-category with a canonical functor \(q: \text {N}^{\otimes } ({\mathcal {O}}) \rightarrow \text {N}\text {Fin}_*\).Footnote 22
To describe the special properties of the map q we recall some further definitions. A map \(f: [n] \rightarrow [m]\) is called inert if for all \(0< i \le m\) there is a unique \(j \in [n]\) such that \(f(j)=i\).
Example 6.5
For given k and \(1\le i \le n\) we denote by \(\rho ^i: [k] \rightarrow [1]\) the inert map in \(\text {Fin}_*\) that sends i to 1 and the rest to 0.
A morphism \(f: X\rightarrow Y\) in \({\mathcal {O}}^{\otimes }\) is q-coCartesian if and only for every \(Z\in {\mathcal {O}}^{\otimes }\) the diagram

is a homotopy pullback.Footnote 23
Example 6.6
A morphism \((f,f_i)\) in \(\text {N}^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n)\) lying over an inert morphism f is q-coCartesian if and only if each \(f_i\) is isotopic to either \(\text {id}_{\mathbb {D}}\) or \(\text {id}_{{\mathbb {D}}_*}\).
Notation
For \(f: [m] \rightarrow [n]\) denote \(\text {Map}_{{\mathcal {O}}^{\otimes }}^{f}(X,Y)\) the union of connected components of \(\text {Map}_{{\mathcal {O}}^{\otimes }}(X,Y)\) lying over f.
Notation
We denote with \({\mathcal {O}}^{\otimes }_{[n]}\) the subcategory of \({\mathcal {O}}^{\otimes }\) consisting of lists of length n and morphisms lying over \(\text {id}_{[n]}\).
Proposition 6.7
[52, 2.1.1.27] For any topological operad \({\mathcal {O}}\) the functor \(q: \text {N}^{\otimes } ({\mathcal {O}}) \rightarrow \text {N}\text {Fin}_*\) defines an \(\infty \)-operad i.e.
-
1.
For any \(f: [m] \rightarrow [k]\) and \(X \in {\mathcal {O}}^{\otimes }_{[m]}\) there is an object \(Y \in {\mathcal {O}}^{\otimes }_{[k]}\) and q-coCartesian morphism \(f_!: X \rightarrow Y\) lying over f.
-
2.
Let \(X \in {\mathcal {O}}^{\otimes }_{[m]}\), \(Y \in {\mathcal {O}}^{\otimes }_{[k]}\) and choose q-coCartesian morphism \(\rho ^i_!:Y \rightarrow Y_i\) lying over the \(\rho _i: [k] \rightarrow [1]\). Then the induced map
$$\begin{aligned} \text {Map}_{{\mathcal {O}}^{\otimes }}^f(X,Y) \rightarrow \prod _{1\le i \le k} \text {Map}_{{\mathcal {O}}^{\otimes }}^{\rho ^i \circ f}(X,Y_i) \end{aligned}$$is a homotopy equivalence.
-
3.
For any \(X_1,\ldots ,X_k \in {\mathcal {O}}^{\otimes }\) there is a \(X \in {\mathcal {O}}^{\otimes }_{[k]}\) and q-coCartesian morphisms \(\rho ^i_!:X \rightarrow X_i\) lying over \(\rho ^i\).
Definition 6.8
Let \(p:{\mathcal {O}}^{\otimes } \rightarrow \text {N}\text {Fin}_*\) be an \(\infty \)-operad. A \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra in \({\mathcal {O}}^{\otimes }\) is a map of \(\infty \)-operads from \({\mathbb {Z}}_2{\mathcal {D}}_n\) to \({\mathcal {O}}^{\otimes }\) i.e. a functor \(F: \text {N}^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n) \rightarrow {\mathcal {O}}^{\otimes }\) such that \(p \circ F = q\) and F sends q-coCartesian morphisms lying over inert morphisms to p-coCartesian morphisms.
Remark 6.9
A symmetric monoidal \(\infty \)-category \({\mathcal {C}}^{\otimes } \rightarrow \text {N}\text {Fin}_*\) is a special kind of \(\infty \)-operad [52, 2.0.0.7], so that Definition 6.8 provides a notion of \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra in \({\mathcal {C}}^{\otimes }\).
Remark 6.10
If \({\mathcal {O}}^{\otimes } = N^{\otimes }({\mathcal {O}})\) for some topological operad \({\mathcal {O}}\) then a \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra in \({\mathcal {O}}^{\otimes }\) corresponds to a homotopy coherent algebra in \({\mathcal {O}}\) over \({\mathbb {Z}}_2{\mathcal {D}}_n\).
Definition 6.11
Let \({\mathcal {O}}^{\otimes }\) be an \(\infty \)-operad. The \(\infty \)-category of \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras in \({\mathcal {O}}\), denoted \(\text {Alg}_{{\mathbb {Z}}_2{\mathcal {D}}_n}({\mathcal {O}})\), is the full subcategory of
with objects the \(\infty \)-operad maps.Footnote 24
6.2 Categorical algebras revisited
Recall that \(\mathbf Rex \) has natural isomorphisms as 2-morphisms. Hence \(\mathbf Rex \) is a (2, 1)-category i.e. a category enriched over groupoids. We can view \(\mathbf Rex \) as a simplicially enriched category by base-changing enrichment along the nerve functor \(\text {N}: \text {Grpds} \rightarrow \text {sSet}\).
Definition 6.12
The \(\infty \)-operad \(p: \text {N}^{\otimes }(\mathbf Rex ) \rightarrow \text {N}\text {Fin}_*\) is the operadic nerve of the simplicial operad whose colours are the objects of \(\mathbf Rex \) and which has operations spacesFootnote 25
Since \(\mathbf Rex \) is a (2,1)-category the operadic nerve allows a simple description as it is 3-coskeletal. Let us briefly recall this notion. Denote \(\Delta _n \subset \Delta \) the full subcategory generated by \([0],[1],\ldots ,[n]\). For a simplicial set the restriction to \(\Delta _n\) defines a truncation functor
A simplicial set X is called n-coskeletal if for any simplicial set Y the natural map
is a bijection.Footnote 26
Definition-Proposition 6.13
[18, Proposition 4.1] Let \({\mathcal {C}}\) be a 2-category. The coherent nerve \(\text {N}{\mathcal {C}}\) is the 3-coskeletal simplicial set with vertices the objects of \({\mathcal {C}}\), 1-simplices the morphisms of \({\mathcal {C}}\), 2-simplices the diagrams of the form

and 3-simplices are ‘commutative tetrahedra’ of the form

where commutativity means that the diagram

commutes.Footnote 27
We will now prove Definition-Proposition 5.5 by showing \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebras in \(N^{\otimes }(\mathbf Rex )\) are exactly determined by the list of data specified there.
Proof of Definition-Proposition 5.5
Let \(F: \text {N}^{\otimes } ({\mathbb {Z}}_2{\mathcal {D}}_n ) \rightarrow \text {N}^{\otimes } (\mathbf Rex )\) be a map of \(\infty \)-operads. We denote \({\mathcal {A}}:= F({\mathbb {D}})\) and \({\mathcal {M}}:= F({\mathbb {D}}_*)\). Without loss of generality we may assume \(F (X_1,\ldots X_k) = (F(X_1),\ldots , F(X_k))\). By Property (2) in Proposition 6.7 the functor F is completely determined by its value on n-simplices in which the edge between vertices \(n-1\) and n is a map lying over some \(f:[k] \rightarrow [1]\). Such a map is exactly an operation in \({\mathbb {Z}}_2{\mathcal {D}}_n\). The value of F on such 1-, 2-, and 3-simplices are on the nose the assignments of Definition-Proposition 5.5. The further restrictions on identity operations and trivial isotopies in Definition 5.5 correspond to F commuting with the simplicial maps between 1-,2- and 3-simplices. Now recall that the nerve of any 2-category is 3-coskeletal i.e.
Hence by Eq. (6.13.1) the functor F is completely determined by an assignment as in Definition 5.5. Conversely, we observe that starting from such an assignment the associated functor F is a map of \(\infty \)-operads. Indeed, this is clear from Example 6.6 since these q-coCartesian morphisms are assigned either \(\text {id}_{{\mathcal {A}}}\) or \(\text {id}_{{\mathcal {M}}}\) which are of course p-coCartesian. \(\square \)
We will conclude by showing that the assignments in Sect. 5 are inverse equivalences.
Theorem 6.14
-
1.
The assignments
$$\begin{aligned}&F \mapsto ({\mathcal {A}}_F,{\mathcal {M}}_F) \text { of Proposition}~5.12\\&({\mathcal {A}},{\mathcal {M}}) \mapsto F_{({\mathcal {A}},{\mathcal {M}})} \text { of Theorem}~5.13 \end{aligned}$$are inverse equivalences.
-
2.
The assignments
$$\begin{aligned}&F \mapsto ({\mathcal {A}}_F,{\mathcal {M}}_F) \text { of Proposition}~5.20,\\&({\mathcal {A}},{\mathcal {M}}) \mapsto F_{({\mathcal {A}},{\mathcal {M}})} \text { of Theorem}~5.19 \end{aligned}$$are inverse equivalences.
-
3.
The assignments
$$\begin{aligned}&F \mapsto ({\mathcal {A}}_F,{\mathcal {M}}_F) \text { of Proposition}~5.22,\\&\quad ({\mathcal {A}},{\mathcal {M}}) \mapsto F_{({\mathcal {A}},{\mathcal {M}})} \text { of Theorem}~5.23 \end{aligned}$$are inverse equivalences.
Proof
The three proofs are identical, so we will prove all three statements at once. First observe that the composite assignment
by construction gives back \(({\mathcal {A}},{\mathcal {M}})\) on the nose. Conversely, let us show that a \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra F is isomorphic to the \({\mathbb {Z}}_2{\mathcal {D}}_n\)-algebra \(F_{({\mathcal {A}}_F,{\mathcal {M}}_F)}\) as objects in \(\text {Alg}_{{\mathbb {Z}}_2{\mathcal {D}}_n}(\mathbf Rex )\). We will abbreviate \(F_{({\mathcal {A}}_F,{\mathcal {M}}_F)}\) by G. Since \(\text {N}^{\otimes }(\mathbf Rex )\) is 3-coskeletal, we find that a morphism \(\eta : F \rightarrow G\) is completely determined by specifying:
-
for each 1-simplex \(f: X \rightarrow Y\) in \(N^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n)\) a 1-simplex \(\eta (f): F(X) \rightarrow G(Y)\) in \(N^{\otimes }(\mathbf Rex )\),
-
for each 2-simplex \(\alpha : h \simeq g \circ f\) in \(N^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n)\) 2-simplices
$$\begin{aligned} \eta ^F(\alpha ): \eta (h) \Rightarrow \eta (g) \circ F(f), \quad \eta ^G(\alpha ): \eta (h) \Rightarrow G(g) \circ \eta (f) \end{aligned}$$in \(N^{\otimes }(\mathbf Rex )\),
-
so that for every 3-simplex in \(N^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n)\), in the notation of Definition-Proposition 6.13, Eqs. (6.14.1)–(6.14.3) hold.
$$\begin{aligned} (\eta ^F(\delta ) * \text {id}) \circ \eta ^F (\gamma )&= (\text {id}* F(\beta ))\circ \eta ^F(\alpha ), \end{aligned}$$(6.14.1)$$\begin{aligned} (\eta ^G(\delta ) * \text {id}) \circ \eta ^F(\gamma )&= (\text {id}* \eta ^F(\beta )) \circ \eta ^G(\alpha ), \end{aligned}$$(6.14.2)$$\begin{aligned} (G (\delta ) * \text {id}) \circ \eta ^G(\gamma )&= (\text {id}* \eta ^G(\beta )) \circ \eta ^G(\alpha ). \end{aligned}$$(6.14.3)
By Property (2) in Proposition 6.7 it suffices to define \(\eta \) on operations and \(\eta ^F,\eta ^G\) on isotopies between operations. We set \(\eta (f) := F(f)\) for all operations, and set \(\eta ^F(\alpha ) := F(\alpha )\) for isotopies. To define \(\eta ^G(\text {id}_f)\) we must construct a natural isomorphism \(F(f) \Rightarrow G(f)\). The operation f lies in the contractible fiber of one of the projections
and note that there exists an operation \(f_0\) in the fiber that is a horizontal/vertical composite of the fixed operations \(f_\otimes \), \(f_\text {act}\), \(f_\Phi \),  ,
,  of Proposition 5.12 (or 5.19 or 5.22). Let us choose a path in the fiber from f to \(f_0\). This defines an isotopy \(\gamma _f: f \simeq f_0\) which we view as a 1-simplex in \(\text {N}^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n)\). We define \(\eta ^G (\text {id}_f)\) to be the composite natural isomorphism
of Proposition 5.12 (or 5.19 or 5.22). Let us choose a path in the fiber from f to \(f_0\). This defines an isotopy \(\gamma _f: f \simeq f_0\) which we view as a 1-simplex in \(\text {N}^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n)\). We define \(\eta ^G (\text {id}_f)\) to be the composite natural isomorphism
More generally, we define \(\eta ^G\) for an isotopy \(\alpha : h \simeq g\circ f\) as the horizontal composition
It remains to show \(\eta \) defines an isomorphism. By writing out the definitions of G and \(\eta \) in terms of F one shows Eqs. (6.14.1)–(6.14.3) hold. For example, Eq. (6.14.1) follows immediately from functoriality of F. For the details see [67]. To show that \(\eta \) is an isomorphism it suffices to show its components \(\eta (\text {id}_X)\) for all \(X \in \text {N}^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n)\) are equivalences [36, Theorem C]. This clearly holds as \(\eta (\text {id}_X) = \text {id}_{F(X)}\). \(\square \)
Notes
See [52, Example 5.1.2.4] for a modern version of this result phrased in the terminology of higher categories and operads.
By \({\mathbb {Z}}_2\)-orbifold we mean a manifold with a faithful \({\mathbb {Z}}_2\)-action possibly with fixed points.
To be precise we moreover assume a tensor category is finitely cocomplete, and that the tensor product functor is \(\mathbb {k}\)-bilinear and preserves finite colimits in each variable, see Sect. 5.1.
The underlying braid of a natural isomorphism is obtained by interpreting instances of the braiding \(\sigma \) and \(\kappa \) as generators of the cylinder braid group \(B_n^{\text {cyl}}\) (Definition 2.3).
A symmetric pair is called irreducible if it cannot be obtained as the symmetric pair associated to a non-trivial product of two symmetric pairs.
The colimit in Eq. (1.12.1) is difficult to compute and typically computed via excision in practice.
The difference between our definition and [69] is that we restrict to smooth points.
For the usual proof for the \(E_n\)-operad and \(F_k({\mathbb {R}}^2)\) see e.g. [52, Lemma 5.1.1.3].
Typically the action functor is denoted \(\otimes \), we write \(\text {act}\) to avoid confusion with the tensor product on \({\mathcal {A}}\).
Where \(\Phi _2\) is replaced by \(\sigma \) in BP2.
In that case we can define the anti-involution via
 with \(t: \Phi ^2 \cong \text {id}\) being the balancing.
with \(t: \Phi ^2 \cong \text {id}\) being the balancing.Here G is the Lie group integrating \({\mathfrak {g}}\). Note that decompositions of involutions of semisimple Lie algebras are not unique in general.
More precisely, any diagram constructed out of the associator \(\alpha \) and unitors \(\lambda \) and \(\rho \) and \(\otimes \).
Thus \(\alpha \), \(\lambda \), \(\rho \), a, r, \(\Phi _2\),\(\Phi _0\) and t are required to be identities.
Besides Remark 4.5 we are using the analogous observation about the hexagon axioms for the braiding.
A category is called small if it has a set of objects and a set of morphisms rather than proper classes.
Two morphisms in a \(\mathbb {k}\)-linear category are equal iff they are equal in the underlying plain category.
Simplicial sets satisfying the weak Kan condition of Boardman–Vogt.
\(\text {Fin}_*\) has objects [k] for \(k\in {\mathbb {Z}}_{\ge 0}\) and a morphism \(f:[k] \rightarrow [m]\) is map \(f:\{0,\ldots ,k\} \rightarrow \{0,\ldots ,m\}\) that sends 0 tot 0.
The composition of morphisms in \({\mathcal {O}}^{\otimes }\) is induced from the operadic composition in \({\mathcal {O}}\). The morphism spaces in \({\mathcal {O}}^{\otimes }\) are canonically unions of products of operation spaces of \({\mathcal {O}}\).
See e.g. [50, §1.1.5] for the definition of the coherent nerve (also known as the simplicial nerve).
\(\text {Fin}_*\) is a discrete topological category so that the coherent nerve of \(\text {Fin}_*\) agrees with the usual nerve.
Recall that \(\text {Fun}(\text {N}^{\otimes }({\mathbb {Z}}_2{\mathcal {D}}_n),{\mathcal {O}}^{\otimes })\) is just the inner hom of simplicial sets.
The Deligne–Kelly tensor product can be used to define an operadic structure as it defines a symmetric monoidal structure on the (2, 1)-category \(\mathbf Rex \) [38].
In fact, there is an adjunction \(\text {cosk}_n: [\Delta _n^{op},\text {Set}] \leftrightharpoons [\Delta ^{op},\text {Set}]: \text {tr}_n\) and n-coskeletal sets are exactly those for which \(X \cong \text {cosk}_n\text {tr}_n X\).
This simplicial set is sometimes called the geometric nerve of the 2-category and is due to R. Street.
References
Alekseev, A.Y., Schomerus, V.: Representation theory of Chern–Simons observables. Duke Math. J. 85(2), 447–510 (1996)
Andrade, R.: From manifolds to invariants of En-algebras. ProQuest LLC, Ann Arbor, MI. Thesis (Ph.D.), Massachusetts Institute of Technology (2010)
Araki, S.: On root systems and an infinitesimal classification of irreducible symmetric spaces. J. Math. Osaka City Univ. 13(1), 1–34 (1962)
Askey, R., Wilson, J.: Some Basic Hypergeometric Orthogonal Polynomials that Generalize Jacobi Polynomials. Volume 54 of Memoirs of the American Mathematical Society. AMS, Providence (1985)
Ayala, D., Francis, J.: Factorization homology of topological manifolds. J. Topol. 8(4), 1045–1084 (2015)
Ayala, D., Francis, J., Tanaka, H.L.: Factorization homology of stratified spaces. Sel. Math. (New Ser.) 23(1), 293–362 (2017)
Baez, J.C., Dolan, J.: Higher-dimensional algebra and topological quantum field theory. J. Math. Phys. 36(11), 6073–6105 (1995)
Balagović, M., Kolb, S.: Universal K-matrix for quantum symmetric pairs. J. Reine Angew. Math. 747, 299–353 (2019)
Bao, H., Kujawa, J., Li, Y., Wang, W.: Geometric Schur duality of classical type. Preprint: arXiv:1404.4000 (2014)
Bao, H., Wang, W.: Canonical bases arising from quantum symmetric pairs. Invent. Math. 213(3), 1099–1177 (2018)
Bao, H., Wang, W., Watanabe, H.: Multiparameter quantum Schur duality of type B. Preprint: arXiv:1609.01766 (2016)
Bao, H., Wang, W.: A New Approach to Kazhdan–Lusztig Theory of Type \(B\) via Quantum Symmetric Pairs. Astérisque, p. vii+134. Société Mathématique de France, Paris (2018)
Beilinson, A., Drinfeld, V.: Chiral Algebras. Volume 51 of AMS Colloquium Publications. AMS, Providence, RI (2004)
Ben-Zvi, D., Brochier, A., Jordan, D.: Integrating quantum groups over surfaces. J. Topol. 11(4), 873–916 (2018)
Ben-Zvi, D., Brochier, A., Jordan, D.: Quantum character varieties and braided module categories. Sel. Math. (NewSer.) 24(5), 4711–4748 (2018)
Brieskorn, E.: Die Fundamentalgruppe des Raumes der regulären Orbits einer endlichen komplexen Spiegelungsgruppe. Invent. Math. 12, 57–61 (1971)
Brochier, A.: Cyclotomic associators and finite type invariants for tangles in the solid torus. Algebr. Geom. Topol. 13(6), 3365–3409 (2013)
Bullejos, M., Faro, E., Blanco, V.: A full and faithful nerve for 2-categories. Appl. Categ. Struct. 13(3), 223–233 (2005)
Cherednik, I.: Double Affine Hecke Algebras. Volume 319 of London Mathematical Society Lecture Note Series. Cambridge University Press, Cambridge (2005)
Cherednik, I.V.: Factorizing particles on a half line, and root systems. Teor. Mat. Fiz. 61(1), 35–44 (1984)
Costello, K., Gwilliam, O.: Factorization Algebras in Quantum Field Theory. Volume 31 of New Mathematical Monographs, vol. 1. Cambridge University Press, Cambridge (2017)
Dijkhuizen, M.S.: Some remarks on the construction of quantum symmetric spaces. Acta Appl. Math. 44(1–2), 59–80 (1996). (Representations of Lie groups, Lie algebras and their quantum analogues)
Donin, J., Kulish, P.P., Mudrov, A.I.: On a universal solution to the reflection equation. Lett. Math. Phys. 63(3), 179–194 (2003)
Dunn, G.: Lax operad actions and coherence for monoidal \(N\)-categories, \(A_\infty \) rings and modules. Theory Appl. Categ. 3(4), 50–84 (1997)
Ehrig, M., Stroppel, C.: Nazarov–Wenzl algebras, coideal subalgebras and categorified skew Howe duality. Adv. Math. 331, 58–142 (2018)
Etingof, P., Gelaki, S., Nikshych, D., Ostrik, V.: Tensor Categories. Volume 205 of Mathematical Surveys and Monographs. A.M.S., Providence, RI (2015)
Fadell, E., Neuwirth, L.: Configuration spaces. Math. Scand. 10, 111–118 (1962)
Fiedorowicz, Z.: The symmetric bar construction. https://people.math.osu.edu/fiedorowicz.1/symbar.ps.gz (Unpublished). Accessed 2 Sept 2017
Galindo, C.: Coherence for monoidal \(G\)-categories and braided \(G\)-crossed categories. J. Algebra 487, 118–137 (2017)
Ginot, G.: Notes on factorization algebras, factorization homology and applications. In: Calaque, D., Strobl, T. (eds.) Mathematical Aspects of Quantum Field Theories. Mathematical Physics Studies, pp. 429–552. Springer, Cham (2015)
Ginot, G., Tradler, T., Zeinalian, M.: Higher Hochschild homology, topological chiral homology and factorization algebras. Commun. Math. Phys. 326(3), 635–686 (2014)
Gwilliam, O.: Factorization algebras and free field theories. ProQuest LLC, Ann Arbor, MI. Thesis (Ph.D.), Northwestern University (2012)
Horel, G.: Factorization homology and calculus à la Kontsevich Soibelman. J. Noncommut. Geom. 11(2), 703–740 (2017)
Jordan, D.: Quantum \(D\)-modules, elliptic braid groups, and double affine Hecke algebras. Int. Math. Res. Not. IMRN 11, 2081–2105 (2009)
Jordan, D., Ma, X.: Quantum symmetric pairs and representations of double affine Hecke algebras of type \(C^\vee C_n\). Sel. Math. (New Ser.) 17(1), 139–181 (2011)
Joyal, A.: The theory of quasi-categories and its applications (in preparation)
Joyal, A., Street, R.: Braided tensor categories. Adv. Math. 102(1), 20–78 (1993)
Kelly, G.M.: Elementary observations on \(2\)-categorical limits. Bull. Aust. Math. Soc. 39(2), 301–317 (1989)
Kolb, S.: Quantum symmetric Kac–Moody pairs. Adv. Math. 267, 395–469 (2014)
Kolb, S.: Braided module categories via quantum symmetric pairs. Preprint: arXiv:1705.04238 (2017)
Kolb, S., Stokman, J.V.: Reflection equation algebras, coideal subalgebras, and their centres. Sel. Math. (New Ser.) 15(4), 621–664 (2009)
Koornwinder, T.H.: Orthogonal polynomials in connection with quantum groups. In: Nevai, P. (ed.) Orthogonal Polynomials (Columbus, OH, 1989). Volume 294 of NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, pp. 257–292. Kluwer Academic Publishers, Dordrecht (1990)
Koornwinder, T.H.: The addition formula for little \(q\)-Legendre polynomials and the \({\rm SU}(2)\) quantum group. SIAM J. Math. Anal. 22(1), 295–301 (1991)
Koornwinder, T.H.: Askey–Wilson polynomials for root systems of type \(BC\). In: Richards, D.S.P. (ed.) Hypergeometric Functions on Domains of Positivity, Jack Polynomials, and Applications (Tampa, FL, 1991). Volume 138 of Contemporary Mathematics, pp. 189–204. American Mathematical Society, Providence, RI (1992)
Kulish, P.P., Sklyanin, E.K.: Algebraic structures related to reflection equations. J. Phys. A 25(22), 5963–5975 (1992)
Letzter, G.: Symmetric pairs for quantized enveloping algebras. J. Algebra 220(2), 729–767 (1999)
Letzter, G.: Coideal subalgebras and quantum symmetric pairs. In: Montgomery, S., Schneider, H.-J. (eds.) New Directions in Hopf Algebras. Volume 43 of Mathematical Sciences Research Institute Publications, pp. 117–165. Cambridge University Press, Cambridge (2002)
Letzter, G.: Quantum symmetric pairs and their zonal spherical functions. Transform. Groups 8(3), 261–292 (2003)
López Franco, I.: Tensor products of finitely cocomplete and abelian categories. J. Algebra 396, 207–219 (2013)
Lurie, J.: Higher Topos Theory. Princeton University Press, Princeton (2009)
Lurie, J.: On the classification of topological field theories. In: Jerison, D., Mazur, B., Mrowka, T., Schmid, W., Stanley, R.P., Yau, S.-T. (eds.) Current Developments in Mathematics, 2008, pp. 129–280. International Press, Somerville, MA (2009)
Lurie, J.: Higher algebra. http://www.math.harvard.edu/~lurie/papers/HA.pdf (2017). Accessed 24 Apr 2018
Macdonald, I.G.: Orthogonal polynomials associated with root systems. In: Nevai, P. (ed.) Orthogonal Polynomials (Columbus, OH, 1989). Volume 294 of NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, pp. 311–318. Kluwer Academic Publishers, Dordrecht (1990)
MacLane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics, vol. 5, 2nd edn. Springer, Berlin (1997)
Majid, S.: Foundations of Quantum Group Theory. Cambridge University Press, Cambridge (1995)
Morrison, S., Walker, K.: Blob homology. Geom. Topol. 16(3), 1481–1607 (2012)
Mudrov, A.: Characters of \({\cal{U}}_q(gl(n))\)-reflection equation algebra. Lett. Math. Phys. 60(3), 283–291 (2002)
Mudrov, A.: On quantization of the Semenov-Tian-Shansky Poisson bracket on simple algebraic groups. Algebra i Analiz 18(5), 156–172 (2006)
Noumi, M.: Macdonald’s symmetric polynomials as zonal spherical functions on some quantum homogeneous spaces. Adv. Math. 123(1), 16–77 (1996)
Noumi, M., Dijkhuizen, M.S., Sugitani, T.: Multivariable Askey–Wilson polynomials and quantum complex Grassmannians. In: Ismail, M.E.H., Masson, D.R., Rahman, M. (eds.) Special Functions, \(q\)-series and Related Topics (Toronto, ON, 1995). Volume 14 of Fields Institute Communications, pp. 167–177. American Mathematical Society, Providence, RI (1997)
Noumi, M., Sugitani, T.: Quantum symmetric spaces and related \(q\)-orthogonal polynomials. In: Wolf, K.B. (ed.) Group Theoretical Methods in Physics (Toyonaka, 1994), pp. 28–40. World Scientific Publishing, River Edge, NJ (1995)
Scheimbauer, C.I.: Factorization homology as a fully extended topological field theory. Ph.D. thesis, ETH Zürich (2014)
Sklyanin, E.K.: Boundary conditions for integrable quantum systems. J. Phys. A 21(10), 2375–2389 (1988)
Tom Dieck, T.: Categories of rooted cylinder ribbons and their representations. J. Reine Angew. Math. 494, 35–63 (1998)
Tom Dieck, T., Häring-Oldenburg, R.: Quantum groups and cylinder braiding. Forum Math. 10(5), 619–639 (1998)
Wahl, N.: Ribbon braids and related operads. Ph.D. thesis, University of Oxford (2001). http://www.maths.ox.ac.uk/research/theses/
Weelinck, T.A.N.: Quantum symmetric pairs in topological field theory. Ph.D. thesis, University of Edinburgh (to appear)
Weelinck, T.A.N.: Equivariant factorization homology of global quotient orbifolds. Preprint: arXiv:1810.12021 (2018)
Xicoténcatl, M.: On configuration spaces of orbits of points and their loop space homology. Morfismos 1(1), 13–26 (1997)
Acknowledgements
First and foremost, I wish to thank David Jordan for his invaluable guidance. I would also like to thank Stefan Kolb for patiently answering many questions about quantum symmetric pairs. Finally, thanks to the anonymous referee for their careful reading and helpful remarks. This work was supported by the Engineering and Physical Sciences Research Council (Grant Number 1633460). This work was also supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 637618).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.



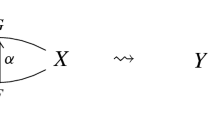
 .
.


















 with
with