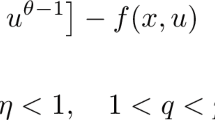Abstract
We use the variational concept of \({\Gamma}\)-convergence to prove existence, stability and exhibit the geometric structure of four families of stationary solutions to the singularly perturbed parabolic equation \({u_t=\epsilon^2 {\rm div}(k\nabla u)+f(u,x)}\), for \({(t,x)\in \mathbb{R}^+\times\Omega}\), where \({\Omega\subset\mathbb{R}^n}\), \({n\geq 1}\), supplied with no-flux boundary condition. The novelty here lies in the fact that the roots of the bistable function f are not isolated, meaning that the graphs of its roots are allowed to have contact or intersect each other along a Lipschitz-continuous (n − 1)-dimensional hypersurface \({\gamma \subset \Omega}\); across this hypersurface, the stable equilibria may have corners. The case of intersecting roots stems from the phenomenon known as exchange of stability which is characterized by \({f(\cdot,x)}\) having only two roots.
Similar content being viewed by others
References
Angenent S. B., Mallet-Paret J., Peletier L. A.: Stable transition layers in a semilinear boundary value problem. J. Differ. Equations, 67, 212–242 (1987)
Butuzov V. F., Nefedov N. N., Schneider K. R.: Singularly perturbed elliptic problems in the case of exchange of stabilities. J. Differ. Equations, 169, 373–395 (2001)
Butuzov V. F.: On the stability and domain of attraction of asymptotically non-smooth stationary solutions to a singularly perturbed parabolic equation. Computational Mathematics and Mathematical Physics, 46, 413–424 (2006)
Butuzov, V. F., Nefedov, N. N.: Schneider, K. R.: Singularly perturbed problems in case of exchange of stabilities, Journal of Mathematical Sciences, 121 No. 1, 1973–2079 (2004).
Consul, N., Sola-Morales, J.: Stability of local minima and stable nonconstant equilibria, J. Differ. Equations, 157, 61–81 (1999).
do Nascimento, A. S.: Stable transition layers in a semilinear diffusion equation with spatial inhomogeneities in N-dimensional domains, J. Differ. Equations, 190, 16–38 (2003).
do Nascimento, A. S.: Reaction-diffusion induced stability of spatially inhomogeneous equilibrium with boundary layer formation, J. Differ. Equations, 108 No. 2, 296–325 (1994).
do Nascimento, A. S.: Stable stationary solutions induced by spatial inhomogeneity via \({\Gamma}\)-convergence, Bull. Braz. Math. Soc., 29 No.1, 75–97 (1998).
do Nascimento, A. S.: On the role of diffusivity in some stable equilibria of a diffusion equation, J. Differ. Equations,155 No. 2, 231–244 (1999).
do Nascimento, A. S., Sônego, M.: The roles of diffusivity and curvature in patterns on surfaces of revolution, J. Math. Anal. Appl., 412, 1084–1096 (2014).
do Nascimento A. S., Sônego, M.: Stable stationary solutions to a singularly perturbed diffusion problem in two-dimensional domains, Advanced Nonlinear Studies, 15, 363–376 (2015).
Evans, L., Gariepy, R.: Measure Theory and Fine Properties of Functions, Studies in Advanced Mathematics, CRC Press (1992).
Fusco G., Hale J. K.: Stable equilibria in a scalar parabolic equations with variable diffusion. SIAM J. Math. Anal., 16, 1154–1164 (1985)
Giusti E.: Minimal Surfaces and Functions of Bounded Variation, Birkhauser-Australia (1984).
Henry, D.: Geometric theory of semilinear parabolic equations, Springer Lecture Notes in Mathematics, v. 840 (1981).
Hale J. K., Rocha, C.: Bifurcations in a parabolic equation with variable diffusion, Nonlinear Anal., 9 No. 5 479–494 (1985).
Hale J. K., Vegas J.: A nonlinear parabolic equation with varying domain. Arch. Ration. Mech. An., 86, 99–123 (1984)
Karali, G., Sourdis, C.: Radial and bifurcating non-radial solutions for a singular perturbation problem in the case of exchange of stabilities, Ann. I. H. Poincare-AN., 29, 131–170 (2012).
Karali, G., Sourdis, C.: Resonance phenomena in a singular perturbation problem in the case of exchange of stability, Commun. Part. Diff. Eq., 37 No.9, 1620–1667 (2012).
Kohn, R. V., Sternberg, P.: Local minimizers and singular perturbations, P Edinburgh Math. Soc., 111 (A), 69–84 (1989).
Matano H.: behavior and stability of solutions of semilinear diffusion equations. Publ. Res. Inst. Math. Sci., 15(2), 401–454 (1979)
Nakashima, K.: Stable transition layers in a balanced bistable equation, Differential and Integral Equations, 13 No. 7–9, 1025–1038 (2000).
Sternberg P.: The effect of a singular perturbation on nonconvex variational problems. Arch. Ration. Mech. An., 101, 209–260 (1988)
Ziemer, W. P.: Weakly Differentiable Functions, Springer-Verlag (1989).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
do Nascimento, A.S., Sônego, M. Stable equilibria of a singularly perturbed reaction–diffusion equation when the roots of the degenerate equation contact or intersect along a non-smooth hypersurface. J. Evol. Equ. 16, 317–339 (2016). https://doi.org/10.1007/s00028-015-0304-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00028-015-0304-4