Abstract
We construct examples and families of locally Hermitian ovoids of the generalized quadrangle \(H(3,q^2)\). We also obtain a computer classification of all locally Hermitian ovoids of \(H(3,q^2)\) for \(q \le 4\), and compare the obtained classification for \(q=3\) with the classification of all ovoids of H(3, 9) which is also obtained by computer.
Similar content being viewed by others
Notes
If \(\gcd (a,q^2-1)\), then \(a^{-1}\) denotes the inverse of a modulo \(q^2-1\).
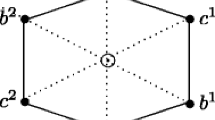
Note that the group generated by the automorphisms mentioned under (G1), (G5), (G6), (G7) induces the full group of automorphisms of L stabilizing B.
References
A. Bishnoi and B. De Bruyn. On generalized hexagons of order \((3,t)\) and \((4,t)\) containing a subhexagon. European J. Combin. 62 (2017), 115–123.
A. E. Brouwer and H. A. Wilbrink. Ovoids and fans in the generalized quadrangle \(Q(4,2)\). Geom. Dedicata 36 (1990), 121–124.
R. H. Bruck. Finite nets. I. Numerical invariants. Canadian J. Math. 3 (1951), 94–107.
A. Bruen. Spreads and a conjecture of Bruck and Bose. J. Algebra 23 (1972), 519–537.
A. Cossidente, G. L. Ebert, G. Marino and A. Siciliano. Shult sets and translation ovoids of the Hermitian surface. Adv. Geom. 6 (2006), 523–542.
A. Cossidente, G. Lunardon, G. Marino and O. Polverino. Hermitian indicator sets. Adv. Geom. 7 (2007), 357–373.
B. De Bruyn. Computer code for “On ovoids of the generalized quadrangle \(H(3,q^2)\)”. Available online from http://cage.ugent.be/geometry/preprints.php.
J. W. P. Hirschfeld and J. A. Thas. General Galois geometries. Springer Monographs in Mathematics. Springer, 2016.
N. L. Johnson, V. Jha and M. Biliotti. Handbook of finite translation planes. Pure and Applied Mathematics 289. Chapman & Hall/CRC, 2007.
R. Lidl and H. Niederreiter. Finite fields. Encyclopedia of Mathematics and its Applications 20. Cambridge University Press, 1997.
S. E. Payne and J. A. Thas. Finite generalized quadrangles. EMS Series of Lectures in Mathematics. European Mathematical Society (EMS), Zürich, 2009.
Sage Mathematics Software (Version 6.3), The Sage Developers, 2014, http://www.sagemath.org.
F. A. Sherk and G. Pabst. Indicator sets, reguli, and a new class of spreads. Canad. J. Math. 29 (1977), 132–154.
E. E. Shult. Problems by the wayside. Discrete Math. 294 (2005), 175–201.
J. A. Thas. Semi-partial geometries and spreads of classical polar spaces. J. Combin. Theory Ser. A 35 (1983), 58–66.
J. A. Thas and S. E. Payne. Spreads and ovoids in finite generalized quadrangles. Geom. Dedicata 52 (1994), 227–253.
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.7.5, 2014. (http://www.gap-system.org)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Marni Mishna
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Determination of Some \(E_l(q^2)\)’s
Determination of Some \(E_l(q^2)\)’s
If \(\lambda x^e\) is an I-monomial of \({{\mathbb {F}}}_{q^2}[x]\), then the map \(x \mapsto \lambda x^e\) is bijective and hence \(gcd(e,q^2-1)=1\). Also, as \(\frac{\lambda x^e- \lambda 0^e}{x-0} = \lambda x^{e-1} \not \in {{\mathbb {F}}}_q\) for all \(x \in {{\mathbb {F}}}_{q^2}^*\), we have \(\lambda \not \in {{\mathbb {F}}}_q\) and \(gcd(e-1,q^2-1) \not = 1\). For each prime power \(q \le 32\), we computed all I-monomials \(\lambda x^e\), see [7]. If we denote by \(E(q^2)\) the set of all \(e \in \{ 1,2,\ldots ,q^2-1 \}\) for which there exists an I-monomial of \({{\mathbb {F}}}_{q^2}[x]\) of the form \(\lambda x^e\), then we have
-
\(E(2^2)=\{ 1 \}\),
-
\(E(3^2)=\{ 1,3,5 \}\),
-
\(E(4^2)=\{ 1 \}\),
-
\(E(5^2)=\{ 1,5,7,13 \}\),
-
\(E(7^2)=\{ 1,7,17,25 \}\),
-
\(E(8^2)=\{ 1,4,10,16,19 \}\),
-
\(E(9^2)=\{ 1,3,9,11,27,41,51 \}\),
-
\(E(11^2)=\{ 1,11,13,37,61 \}\),
-
\(E(13^2)=\{ 1,13,29,85 \}\),
-
\(E(16^2) = \{ 1 \}\),
-
\(E(17^2)=\{ 1,17,19,37,91,109,145 \}\),
-
\(E(19^2)=\{ 1,19,181 \}\),
-
\(E(23^2)=\{ 1,23,25,49,97,169,265 \}\),
-
\(E(25^2)=\{ 1,5,25,53,125,313,365 \}\),
-
\(E(27^2)=\{1,3,9,27,29,57,81,99,113,243,281,365,393,477,603 \}\),
-
\(E(29^2)=\{ 1,29,31,271,421 \}\),
-
\(E(31^2)=\{ 1,31,481 \}\),
-
\(E(32^2) = \{ 1,4,16,34,64,67,256,331,397 \}\).
More generally, if \(l \in {{\mathbb {N}}}^*\), then \(E_l(q^2)\) denotes the set of all subsets \(\{ e_1,e_2,\ldots ,e_l \} \subseteq {{\mathbb {N}}}^*\) such that \(1 \le e_1< e_2< \cdots < e_l \le q^2-1\) and there exist \(\lambda _1,\lambda _2,\ldots ,\lambda _l \in {{\mathbb {F}}}_{q^2}^*\) such that \(x \mapsto \sum _{i=1}^l \lambda _i x^{e_i}\) is an I-permutation of \({{\mathbb {F}}}_{q^2}\). We denote by \(E_l'(q^2)\) the subset of \(E_l(q^2)\) consisting of all \(\{ e_1,e_2,\ldots ,e_l \} \subseteq {{\mathbb {N}}}^*\) satisfying the above conditions but with the extra requirement that \(\lambda _1 \not \in {{\mathbb {F}}}_q\) if \(e_1=1\). If \(I \in E_l(q^2) {\setminus } E_l'(q^2)\) for some \(l \in {{\mathbb {N}}}^*\), then \(l \ge 2\), \(1 \in I\) and \(I {\setminus } \{ 1 \} \in E_{l-1}'(q^2)\) by construction (C5). Conversely, by construction (C5) we know that if \(l \ge 2\) and \(I \in E_{l-1}'(q^2)\) with \(1 \not \in I\), then \(I \cup \{ 1 \} \in E_l(q^2)\). If one is interested in finding only one representative for each equivalence class of I-polynomials, it suffices to consider the sets \(E_l'(q^2)\). With the aid of a computer, we found all sets \(E_2'(q^2)\) for \(q \le 9\) and all sets \(E_3'(q^2)\) for \(q \le 5\) [7]:
-
\(E_2'(2^2) = E_2'(3^2) = \{ \}\),
-
\(E_2'(4^2) = \{ \{ 1,4 \} , \{ 2,8 \} \}\),
-
\(E_2'(5^2) = \{ \{ 1,5 \} , \{ 7,19 \} \}\),
-
\(E_2'(7^2) = \{ \{ 1,7 \} , \{ 5,17 \} , \{ 5,29 \} , \{17,41 \} \}\),
-
\(E_2'(8^2) = \{ \{ 1,8 \} , \{ 2,16 \} , \{ 4,32 \} , \{ 16,37 \} \}\),
-
\(E_2'(9^2) = \{ \{ 1,9 \} , \{ 3,27 \} , \{ 11,27 \}, \{ 21,61 \} , \{ 29,61 \} , \{ 31,71 \} \}\),
-
\(E_3'(2^2) = E_3'(3^2) = \{ \}\),
-
\(E_3'(4^2) = \{ \{ 1,6,11 \} \}\),
-
\(E_3'(5^2) = \{ \{ 1,7,13 \},\{ 1,9,17 \},\{ 3,11,19 \}\}\).
For additive I-polynomials, the corresponding ovoids of \(H(3,q^2)\) are translation ovoids related to so-called semifield spreads of \(\mathrm{PG}(3,q)\), see [5]. These spreads and their related semifields have extensively been discussed in the literature, see, e.g. [9].
Let us now turn our attention to non-additive I-monomials of \({{\mathbb {F}}}_{q^2}[x]\) with \(q \le 32\), non-additive I-binomials of \({{\mathbb {F}}}_{q^2}[x]\) with \(q \le 9\) and non-additive I-trinomials of \({{\mathbb {F}}}_{q^2}[x]\) with \(q \le 5\). We have verified by computer that for each \(q = p^h \le 32\) and each \(e \in E(q^2)\) not being a power of p, there exists up to equivalence a unique I-polynomial of the form \(\lambda x^e\). These I-monomials have been listed in Table 3. In this table, \(\alpha \) is a primitive element of \({{\mathbb {F}}}_{q^2}\) that is a root of the polynomial mentioned in Table 4.
We have also verified that each subset of \(E_2'(q^2)\), \(q=p^h \le 9\), and each subset of \(E_3'(q^2)\), \(q=p^h \le 5\), not entirely consisting of powers of p, is associated with either one or two I-polynomials (up to equivalence). These have been listed in Table 5. Also here, \(\alpha \) is a primitive element of \({{\mathbb {F}}}_{q^2}\) that is a root of the polynomial mentioned in Table 4.
Finally, we wish to mention that we found more subsets of the \(E_l(q^2)\)’s than the ones mentioned above. Through ad hoc searches we found, for instance, that \(\{ 1,17,33 \} \in E_3'(7^2)\) and \(\{ 1,7,13,19 \} \in E_4'(5^2)\).
Rights and permissions
About this article
Cite this article
De Bruyn, B. On Ovoids of the Generalized Quadrangle \(H(3,q^2)\). Ann. Comb. 25, 495–514 (2021). https://doi.org/10.1007/s00026-021-00538-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00026-021-00538-3