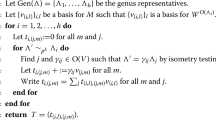Some Remarks on the Saito Kurokawa Lift for Orthogonal Forms

Abstract

Duke and Imamoglu showed that the Saito–Kurokawa lift for Siegel modular forms can in an elegant manner be obtained from a converse theorem by Imai using spectral analysis of the hyperbolic Laplacian. In an earlier paper we gave a simplified approach without any appeal to spectral analysis. Here we want to show, that this generalizes to some orthogonal groups of signature $(2,m+2)$ with $m>2$.

1 Introduction

There is a well-known correspondence between classical modular forms contained in the Kohnen space and the Maass Spezialschar of Siegel modular forms, called the Saito–Kurokawa-Lift. Kojima [6] and Krieg [3] found an Hermitian analogue of this lifting. Sugano [12] generalized this lifting to orthogonal modular forms. In the case of Siegel modular forms Duke and Imamoglu in [1] gave an alternative proof for the lift using a converse theorem of Imai [2]. In [9] we applied the method of Duke and Imamoglu to the Hermitian case.

Recently we gave simpler proofs for the Saito–Kurokawa lift, see [7, 8], where we may skip the analysis of the spectral Koecher-Maass series. The crucial point in our proof is the observation, that the partial Mellin transform of the Saito–Kurokawa-lift of f coincides with a theta lift of f matched with an Eisenstein series, which can easily be evaluated by applying the Rankin Selberg method. The purpose of the present paper is to show how this proof may be generalized to $\mathrm{O}(2,m+2)$ with $m>1$.

2 Siegel Theta Series

Let S be an even integral positive definite matrix of degree $m\in {{\mathbb {N}}}$ with maximal integral lattice $\Lambda _0={{\mathbb {Z}}}^m$ and let $\Lambda _1={{\mathbb {Z}}}\times \Lambda _0\times {{\mathbb {Z}}}$ be the even lattice with respect to

$$\begin{aligned} S_1=\left( \begin{array}{ccc}{}&{}{}&{}{1}\\ {}&{}{-S}&{}{}\\ {1}&{}{}&{}{}\end{array}\right) . \end{aligned}$$

For later purposes we also introduce the even lattice $\Lambda _2={{\mathbb {Z}}}\times \Lambda _1\times {{\mathbb {Z}}}$ with respect to

$$\begin{aligned} S_2=\left( \begin{array}{ccc}{}&{}{}&{}{1}\\ {}&{}{S_1}&{}{}\\ {1}&{}{}&{}{}\end{array}\right) . \end{aligned}$$

As usual the dual lattice of $\Lambda _i$ is given by

$$\begin{aligned} {\hat{\Lambda }}_i =\{{\mu }\in {{\mathbb {Q}}}^{m+2i}:S_i{\mu }\in {{\mathbb {Z}}}^{m+2i}\}. \end{aligned}$$

The corresponding quadratic forms on $V_i={{\mathbb {R}}}\otimes \Lambda _i$ are denoted by $Q_i=\frac{1}{2}S_i$. We use the common notation $Q_i[U]:=U^tQ_iU$ for any real matrix U. $Q_2$ has signature $(2,m+2)$ and $Q_1$ has signature $(1,m+1)$. Further remark that $Q_1^+=\frac{1}{2}\left( \begin{array}{ccc}{1}&{}{}&{}{}\\ {}&{}{S}&{}{}\\ {}&{}{}&{}{1}\end{array}\right)$ is a majorant of $Q_1$ in the sense of Siegel i.e. $Q_1^+$ is symmetric and positive definite and $Q_1^+ Q_1^{-1}Q_1^+=Q_1$. Any other majorant P is given by $P=Q_1^+[\sigma ]$ with $\sigma \in \mathrm{O}(Q_1)$.

There is a Siegel’s theta function for each element $\mathbf{r}$ from the discriminant group ${{\mathcal {D}}}={\hat{\Lambda }}_1/\Lambda _1$ which for $z=x+iy \in {{\mathbb {H}}}$ and P a majorant of $Q_1$ is given by

$$\begin{aligned} \Theta (\mathbf{r},z, P):=y^{\frac{m+2}{4}}\sum _{{\nu }\equiv \mathbf{r}(\mathrm{mod}\,\Lambda _1)} e(xQ_1[{\nu }]+iyP[\nu ]). \end{aligned}$$

With this we build a vector-valued theta function

$$\begin{aligned} {\varvec{\Theta }}(z,P)=(\Theta (\mathbf{r},z,P))_{\mathbf{r}\in {{\mathcal {D}}}}. \end{aligned}$$

Siegel’s theta function can be constructed using the Weil representation as was done by Shintani [11]. From this it becomes evident, see [11], Proposition 1.6, that for $\gamma \in \mathrm{SL}(2,{{\mathbb {Z}}})$ there is a transformation formula

$$\begin{aligned} {\varvec{\Theta }}(\gamma z,P)= j_{-m/2}(\gamma ,z) \chi (\gamma ){\varvec{\Theta }}(z,P) \end{aligned}$$

with the automorphy factor $j_{-m/2}(\gamma ,z)=\left( \frac{cz+d}{c\bar{z}+d}\right) ^{-m/4}$ and a unitary matrix $\chi (\gamma )=(\chi _{\mathbf{r,s}}(\gamma ))_{\mathbf{r,s}\in {{\mathcal {D}}}}$ .

Lemma 2.1

For $\gamma =\left( \begin{array}{rr}\in&\mathrm{SL}(2,{{\mathbb {Z}}})\end{array}\right)$ one has

$$\begin{aligned}&\chi _\mathbf{r,s}(\gamma )\\&\quad =\left\{ \begin{array}{ll} e\left( \frac{m}{8}\right) |\det (2cQ_1)|^{-\frac{1}{2}}\sum _{g\in \Lambda /c\Lambda }e\left( \frac{aQ_1[g+\mathbf{r}]-2\mathbf{s}^tQ_1[g+\mathbf{r}]+dQ_1[\mathbf{s}]}{c}\right) ,&{}c\ne 0\\ e\left( abQ_1[\mathbf{r}]\right) &{} c=0,a\mathbf{r}=\mathbf{s}\\ 0&{} c=0,a\mathbf{r}\ne \mathbf{s}. \end{array} \right. \end{aligned}$$

$\square$

This was originally shown by Siegel [10], Hilfssatz 1.

3 Orthogonal Modular Forms

Siegel modular forms can be regarded as modular forms on $\mathrm{O}(2,3)$, the Hermitian case corresponds to $\mathrm{O}(2,4)$ . Here we shall also consider forms on $\mathrm{O}(2,m+2)$ with $m>2$.

3.1 The Tube Domain

There is a symmetric space associated to $\mathrm{O}(Q_2,{{\mathbb {R}}})$, a model is given by the tube domain

$$\begin{aligned} {{\mathcal {H}}}=\{{{\mathcal {Z}}}=(z_1,w,z_2)^t\in {{\mathbb {C}}}^{m+2}: \Im {z_1}, \Im {z_2}>0, w\in {{\mathbb {C}}}^m, Q_1[\Im {{\mathcal {Z}}}]>0\}. \end{aligned}$$

In order to understand the action of the orthogonal group on this space one may regard the zero space ${{\mathcal {N}}}=\{(a,{{\mathcal {Z}}},b)^t\in {{\mathbb {C}}}^{m+4}: Q_2[(a,{{\mathcal {Z}}},b)^t]=0\}$ on which $\mathrm{O}(Q_2,{{\mathbb {R}}})$ acts by matrix multiplication. The condition $Q_2[(a,{{\mathcal {Z}}},b)^t]=0$ then is equivalent to $ab=-Q_1[{{\mathcal {Z}}}]$.

One finds, that for ${{\mathcal {Z}}}\in {{\mathcal {H}}}$ and $g\in \mathrm{O}(Q_2,{{\mathbb {R}}})$ matrix multiplication gives

$$\begin{aligned} g\cdot \left( \begin{array}{c}{- Q_1 [{\mathcal {Z}}]}\\ {{{\mathcal {Z}}}}\\ {1}\end{array}\right) = b(g,{{\mathcal {Z}}}) \left( \begin{array}{c}{-Q_1 [g\langle {{\mathcal {Z}}}\rangle ]}\\ {g\langle {{\mathcal {Z}}} \rangle }\\ {1}\end{array}\right) \end{aligned}$$

with some uniquely determined tuple $(b(g,{{\mathcal {Z}}}),g\langle {{\mathcal {Z}}}\rangle )$. The factor $b(g,{{\mathcal {Z}}})$ is an automorphy factor, it satisfies the chain rule $b(gh,{{\mathcal {Z}}})=b(g,h\langle {{\mathcal {Z}}}\rangle )b(h,{{\mathcal {Z}}})$.

The map $g:{{\mathcal {Z}}}\rightarrow g\langle {{\mathcal {Z}}}\rangle$ induces a transitive action of the real orthogonal group $\mathrm{O}(Q_2,{{\mathbb {R}}})$ on ${{\mathcal {H}}}\cup -{{\mathcal {H}}}$ as a group of biholomorphic automorphisms. Define $\mathrm{O}^+(Q_2,{{\mathbb {R}}})\}$ to be the subgroup stabilizing ${{\mathcal {H}}}$.

For $h\in \mathrm{O}(Q_1,{{\mathbb {R}}})$ we have a natural injection $\iota : h\rightarrow \left( \begin{array}{ccc}{1}&{}{}&{}{}\\ {}&{}{h}&{}{}\\ {}&{}{}&{}{1}\end{array}\right)$ of $\mathrm{O}(Q_1)$ into $\mathrm{O}(Q_2)$, we denote by $\mathrm{O}^+(Q_1,{{\mathbb {R}}})$ the preimage of $\mathrm{O}^+(Q_2,{{\mathbb {R}}})$. The action of $\iota (h)$ corresponds to matrix multiplication ${{\mathcal {Z}}}\rightarrow h {{\mathcal {Z}}}$. $\mathrm{O}^+(Q_1,{{\mathbb {R}}})$ acts transitively on the subspace of purely imaginary elements $i{{\mathcal {Y}}}\in {{\mathcal {H}}}$ with $Q_1[{{\mathcal {Y}}}]=1$ (so $Q_1[i{{\mathcal {Y}}}]=-1$) by matrix multiplication, this corresponds to the set

$$\begin{aligned} {{\mathbb {H}}}_{m+1}=\{{{\mathcal {Y}}}=(y_1,v,y_2)^t\in {{\mathbb {R}}}^{m+2}: y_1, y_2 >0, v\in {{\mathbb {R}}}^m, Q_1[{{\mathcal {Y}}}]=1\}. \end{aligned}$$

Observe that $(y_1,v,y_2)\in {{\mathbb {H}}}_{m+1}$ implies $y_1=(1+Q_0[v])y_2^{-1}$. So for any ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$ there is some $S_{{{\mathcal {Y}}}}\in \mathrm{O}^+(Q_1,{{\mathbb {R}}})$ with $S_{{{\mathcal {Y}}}}e={{\mathcal {Y}}}$ where $e=(1,0..,0,1)^t\in HH_{m+1}.$

3.2 Modular Forms

Let

$$\begin{aligned} \mathrm{O}(\Lambda _i)=\{M\in \mathrm{O}(Q_i,{{\mathbb {R}}}): M\Lambda _i=\Lambda _i\}. \end{aligned}$$

The orthogonal modular group is now defined as

$$\begin{aligned} \Gamma :=\mathrm{O}^+(Q_2,{{\mathbb {R}}})\cap \mathrm{O}(\Lambda _2) \end{aligned}$$

which can be shown to be generated by

$$\begin{aligned} J=\left( \begin{array}{ccccc}{}&{}{}&{}{}&{}{}&{}-1\\ {}&{}{}&{}{}&{}-1&{}{}\\ {}&{}{}&{}{E_m}&{}{}&{}\\ {}&{}-1&{}{}&{}{}&{}{}\\ {}-1&{}{}&{}{}&{}{}&{}{} \end{array}\right) \quad n(\zeta )=\left( \begin{array}{ccc}{1}&{}{-\zeta ^{t}S_1}&{}{-Q_1[\zeta ]}\\ {}&{}{E_{m+2}}&{}{\zeta }\\ {}&{}{}&{}{1}\end{array}\right) ,\quad \zeta \in {{\mathbb {Z}}}^{m+2} \end{aligned}$$

and

$$\begin{aligned}\{\iota (U): U\in \mathrm{O}(\Lambda _1)\}\cap {\mathrm {O}}^+(Q_2,{{\mathbb {R}}}).\end{aligned}$$

By $\Gamma _1$ we denote the subgroup of $\mathrm{O}^+(Q_1,{{\mathbb {R}}})$ consisting of all U such that $\iota (U)\in \Gamma$. A holomorphic function F on ${{\mathcal {H}}}$ is a holomorphic modular form of weight $k\in {{\mathbb {Z}}}$ with respect to $\Gamma$ if

$$\begin{aligned} F(\gamma \langle {{\mathcal {Z}}}\rangle )=b^k(\gamma ,{{\mathcal {Z}}})F({{\mathcal {Z}}}) \end{aligned}$$

(1)

for all $\gamma \in \Gamma$. This space is denoted by $M_k(\Gamma )$. Especially note that

$$\begin{aligned} F(U {{\mathcal {Z}}})=F( {{\mathcal {Z}}})\end{aligned}$$

(2)

for $U \in \Gamma _1.$

Further

$$\begin{aligned} n(\zeta )\cdot \left( \begin{array}{c}{-Q_1[{{\mathcal {Z}}}]}\\ {{{\mathcal {Z}}}}\\ {1}\end{array}\right) = \left( \begin{array}{c}{-Q_1[{{\mathcal {Z}}}]-\zeta ^tS_1{{\mathcal {Z}}}-Q_1[\zeta ]}\\ {{{\mathcal {Z}}}+\zeta }\\ {1} \end{array}\right) = \left( \begin{array}{c}{-Q_1[{{\mathcal {Z}}}+\zeta ]}\\ {{{\mathcal {Z}}}+\zeta }\\ {1}\end{array}\right) . \end{aligned}$$

Therefore $n(\zeta )\langle {{\mathcal {Z}}}\rangle = {{\mathcal {Z}}}+\zeta$ and each holomorphic modular form $F({{\mathcal {Z}}})$ admits an absolutely convergent Fourier development

$$\begin{aligned} F({{\mathcal {Z}}})=\sum _{{{\mathcal {T}}}\in {\hat{\Lambda }}_1, Q_1[{{\mathcal {T}}}]\ge 0}A({{\mathcal {T}}})e({{\mathcal {T}}}^tS_1{{\mathcal {Z}}}). \end{aligned}$$

(3)

Note, that the Koecher-principle is valid, and therefore we only have summands for ${{\mathcal {T}}}=(y_1,v,y_2)^t$ with $y_1,y_2,Q_1[{{\mathcal {T}}}]\ge 0$. See e.g. [4, Thm. 2].

For short we write $L:=\{{{\mathcal {T}}}=(y_1,v,y_2)^t\in {\hat{\Lambda }}_1: y_1,y_2,Q_1[{{\mathcal {T}}}]\ge 0\}, L^+=L\cap \{{{\mathcal {T}}}\in {\hat{\Lambda }}_1: Q_1[{{\mathcal {T}}}]> 0 \}$ and $L_n:=L\cap \{{{\mathcal {T}}}\in {\hat{\Lambda }}_1: qQ_1[{{\mathcal {T}}}]=n \}$. Here q denotes the level of the lattice $\Lambda _1$. If ${{\mathcal {T}}}\in L$ then for $U\in \Gamma _1$ also $U{{\mathcal {T}}}\in L$ and because of (2) the Fourier coefficients satisfy the unimodularity property

$$\begin{aligned} A({{\mathcal {T}}})=A(U{{\mathcal {T}}}). \end{aligned}$$

(4)

4 Saito–Kurokawa Lift

By $S(k-\frac{m}{2},\chi )$ we denote the space of vector-valued cusp forms of weight $k-\frac{m}{2}$ that transform according to the representation ${\chi }$ of $\mathrm{SL}(2,{{\mathbb {Z}}})$

$$\begin{aligned} {f}\left( \frac{az+b}{cz+d}\right) =(cz+d)^{k-\frac{m}{2}}{\chi }\left( \left( \begin{array}{rr} a &{} b\\ c &{} d \end{array}\right) \right) {f}(z)\end{aligned}$$

for $\left( \begin{array}{rr} a &{} b\\ c &{} d \end{array}\right) \in \mathrm{SL}(2,{{\mathbb {Z}}})$. Any $f=(f_\mathbf{r})\in S({k-m/2},{\chi })$ has Fourier expansions of its components

$$\begin{aligned} f_\mathbf{r}(z)=\sum _{n>0,n\in qQ_1[\mathbf{r}+\Lambda _1]}a_\mathbf{r}(n)e(nz/q).\end{aligned}$$

For even $k>\frac{m}{2}$ we define for $f\in S({k-m/2},\chi )$ the function $F({{\mathcal {Z}}})$ on ${{\mathcal {H}}}$ by

$$\begin{aligned} F({{\mathcal {Z}}})=\sum _{{{\mathcal {T}}}\in L} A({{\mathcal {T}}})e({{\mathcal {T}}}^tS_1{{\mathcal {Z}}}) \end{aligned}$$

(5)

where $A({{\mathcal {T}}})=\sum _{d|\varepsilon ({{\mathcal {T}}})}d^{k-1}a^{*}(\frac{qQ_1[{{\mathcal {T}}}]}{d^{2}})$ with $\varepsilon ({{\mathcal {T}}})=\mathrm{max}\{l\in {{\mathbb {N}}}:{{\mathcal {T}}}/l\in L\}$ and

$$\begin{aligned} a^{*}(n)={\sum _{{\begin{array}{c}{} \mathbf{r}\\ {n\in qQ_1[\mathbf{r}+\Lambda _1]}\\ {}\end{array}}}}a_\mathbf{r}(n). \end{aligned}$$

$F({{\mathcal {Z}}})$ is called the Saito Kurokawa lift of f. The main purpose of this paper is to present a short proof for the following

Theorem 4.1

Assume that k is an even number and $k-\frac{m}{2}>0$. Let $f\in S({k-m/2},\chi )$ with $F({{\mathcal {Z}}})$ the corresponding Saito–Kurokawa lift. Then $F({{\mathcal {Z}}})$ is an element of $S_k(\Gamma )$, where $S_k(\Gamma )$ shall denote the subspace of $M_k(\Gamma )$ consisting of forms for which the Fourier coefficients $A({{\mathcal {T}}})=0$ whenever $Q_1[{{\mathcal {T}}}]=0$.

For the proof we shall show that for ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$ the Mellin transform

$$\begin{aligned} {\tilde{F}}({i{\mathcal {Y}}},s)=\int _0^{\infty }F(iu^{\frac{1}{2}}{{\mathcal {Y}}})u^{s-1}du\end{aligned}$$

satisfies a functional equation

$$\begin{aligned} {\tilde{F}}({i{\mathcal {Y}}},s)={\tilde{F}}({i{\mathcal {Y}}},k-s) \end{aligned}$$

(6)

and then use a converse theorem. The functional equation may result from corresponding equations for the spectral Koecher-Maass series. This was elaborated by Imai in [2] and used by Duke and Imamoglu in [1].

Here we use a shorter argument as we already did in [7, 8]. It results from the observation that ${\tilde{F}}({i{\mathcal {Y}}},s)$ is a theta lift of f matched with a real-analytic Eisenstein series, see (10). The analytic properties of the Eisenstein series, especially its functional equation, carry over to ${\tilde{F}}({{\mathcal {Y}}},s)$.

5 Proof of the Theorem

5.1 Mellin Transform of Unimodular Invariant Fourier Series

Now let us assume, that an absolutely convergent Fourier series

$$\begin{aligned} F({{\mathcal {Z}}})=F(\tau ,w,z)=\sum _{{{\mathcal {T}}}\in L}A({{\mathcal {T}}})e({{\mathcal {T}}}^tS_1{{\mathcal {Z}}}) \end{aligned}$$

on ${{\mathcal {H}}}$ with the property (4) is given, not necessarily coming from a modular form. Such a Fourier series we call unimodular invariant.

The unimodular invariance implies

$$\begin{aligned} F(U{{\mathcal {Z}}})=F({{\mathcal {Z}}})\end{aligned}$$

if $U\in \Gamma _1$.

We further assume, that for ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$ the partial Mellin transform

$$\begin{aligned} {\tilde{F}}({i{\mathcal {Y}}},s)=\int _0^{\infty }F\left( iu^{\frac{1}{2}}{{\mathcal {Y}}}\right) u^{s-1}du \end{aligned}$$

(7)

exists for $\Re (s)$ sufficiently large and Mellin inversion can be applied. We remind the reader that Mellin inversion can be applied if F is continuous and the integral is absolutely convergent in some strip $a<\Re (s)<b$.

5.2 A Converse Theorem

For our proof of the Saito–Kurokawa lift we shall employ the following converse theorem which for the case of Siegel modular forms can be found in [2].

Proposition 5.1

Let F be defined by an absolutely convergent unimodular Fourier series as in (3) where the Fourier coefficients are of at most polynomial growth $A({{\mathcal {T}}})\ll Q_1[{{\mathcal {T}}}]^a$, with some $a>0$, and $A({{\mathcal {T}}})=0$, if $Q_1[{{\mathcal {T}}}]=0$. If for each ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$ the partial Mellin transform ${\tilde{F}}({{\mathcal {Y}}},s)$ fulfills the following three conditions:

• (i) it is entire as a function of s

• (ii) it tends to zero as $\Im s\rightarrow \pm \infty$ uniformly in every vertical strip

• (iii) it satisfies the functional equation

  $$\begin{aligned} {\tilde{F}}({{\mathcal {Y}}},s)=(-1)^k {\tilde{F}}({{\mathcal {Y}}},k-s)\end{aligned}$$

  (8)

then $F({{\mathcal {Z}}})$ is a modular form of weight k.

Proof

We have to check the transformation formula (1) for the generators of the group $\Gamma$. By our assumptions on F we merely have to show that

$$\begin{aligned} F(J{{\mathcal {Z}}})=Q_1[{{\mathcal {Z}}}]^kF({{\mathcal {Z}}}). \end{aligned}$$

(9)

Following [5, Lemma 1.6, p. 48], it is enough to show the transformation property for the imaginary parts $i{{\mathcal {W}}}\in {{\mathcal {H}}}$. Each $i{{\mathcal {W}}}\in {{\mathcal {H}}}$ can be written as $t^{\frac{1}{2}}{{\mathcal {Y}}}$ with ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$ and suitable $t>0$. We use Mellin inversion, which is valid for $\Re s>c$, for some suitable $c\in {{\mathbb {R}}}$, and obtain

$$\begin{aligned} F(it^{\frac{1}{2}}{{\mathcal {Y}}})= & {} \frac{1}{2\pi i}\int _{\Re s= c}{\tilde{F}}({{\mathcal {Y}}},s)t^{-s}ds =\frac{(-1)^k}{2\pi i}\int _{\Re s= c}{\tilde{F}}({{\mathcal {Y}}},k-s)t^{-s}ds\\= & {} \frac{(-1)^k}{2\pi i}\int _{\Re s= k-c}{\tilde{F}}({{\mathcal {Y}}},s)t^{-k+s}ds\\= & {} \frac{(-1)^kt^{-k}}{2\pi i}\int _{\Re s= k-c}{\tilde{F}}({{\mathcal {Y}}},s)\left( \frac{1}{t}\right) ^{-s}ds\\= & {} (-t)^{-k}F(it^{-\frac{1}{2}}{{\mathcal {Y}}}). \end{aligned}$$

Here we moved the path of integration back to $\Re s=c$, which is possible because ${\tilde{F}}({{\mathcal {Y}}},s)$ is entire and tends to zero as $\Im s\rightarrow \pm \infty$ uniformly in every vertical strip. The matrix

$$\begin{aligned} V=\left( \begin{array}{ccc}{}&{}{}&{}{1}\\ {}&{}{-E_{m}}&{}{}\\ {1}&{}{}&{}{}\end{array}\right) \end{aligned}$$

is in $\mathrm{O}^+(Q_1,{{\mathbb {R}}})\cap \mathrm{GL}(m+2,{{\mathbb {Z}}})$ and

$$\begin{aligned} J\langle it^{\frac{1}{2}}{{\mathcal {Y}}}\rangle = it^{-\frac{1}{2}}V{{\mathcal {Y}}}. \end{aligned}$$

Unimodularity implies $F(it^{-\frac{1}{2}}{{\mathcal {Y}}})=F(it^{-\frac{1}{2}}V{{\mathcal {Y}}})=F(J\langle it^{\frac{1}{2}}{{\mathcal {Y}}}\rangle )$ so the above equality $F(it^{\frac{1}{2}}{{\mathcal {Y}}})=(-t)^{-k}F(it^{-\frac{1}{2}}{{\mathcal {Y}}})$ is equivalent to

$$\begin{aligned} F(J{it^{\frac{1}{2}}{\mathcal {Y}}})=(-t)^kF(it^{\frac{1}{2}}{{\mathcal {Y}}}). \end{aligned}$$

$\square$

5.3 Rankin–Selberg Integral

The proof of the theorem is complete if we can verify (i)-(iii) of Proposition 5.1. This will be accomplished by the Proposition below which relates the partial Mellin transform to a Rankin-Selberg integral involving the f and the Theta series for some special majorants $P_{{\mathcal {Y}}}$ which owe their relevance to the followig

Lemma 5.1

Let ${{\mathcal {T}}}\in L^+$, ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$. Then

• (i) ${{\mathcal {T}}}^tS_1{{\mathcal {Y}}}> 0$

• (ii) $({{\mathcal {T}}}^tS_1{{\mathcal {Y}}})^2= 2Q_1^+[S^{-1}_{{{\mathcal {Y}}}}][{{\mathcal {T}}}]+2 Q_1[{{\mathcal {T}}}]$.

Remark The matrix $P_{{\mathcal {Y}}}:=Q_1^+[S^{-1}_{{{\mathcal {Y}}}}]$ is a majorant for $Q_1$ since $S^{-1}_{{{\mathcal {Y}}}}\in \mathrm{O}(Q_1)$.

Proof

(i) Let ${{\mathcal {Y}}}=((1+Q_0[v])y^{-1},v,y)$ with $y>0$. Then $e^tS_1{{\mathcal {Y}}} =(1+Q_0[v])y^{-1}+y>0$. Since ${{\mathcal {T}}}^0:={{\mathcal {T}}}/{\sqrt{Q_1[{{\mathcal {T}}}]}}\in {{\mathbb {H}}}_{m+1}$ we can choose $S_{{{\mathcal {T}}}^0}\in \mathrm{O}(Q_1;{{\mathbb {R}}})$, such that $S_{{{\mathcal {T}}}^0}e={{\mathcal {T}}}^0$. Therefore

$$\begin{aligned} {{\mathcal {T}}}^tS_1{{\mathcal {Y}}}=\sqrt{Q_1[{{\mathcal {T}}}]}e^tS^t_{{{\mathcal {T}}}^0}S_1{{\mathcal {Y}}}=\sqrt{Q_1[{{\mathcal {T}}}]}e^tS_1S^{-1}_{{{\mathcal {T}}}^0}{{\mathcal {Y}}}>0 \end{aligned}$$

since $S^{-1}_{{{\mathcal {T}}}^0}{{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$.

(ii)

$$\begin{aligned} ({{\mathcal {T}}}^tS_1{{\mathcal {Y}}})^2= & {} {{\mathcal {T}}}^tS_1 {{\mathcal {Y}}} {{\mathcal {Y}}}^tS_1{{\mathcal {T}}}= {{\mathcal {T}}}^tS_1 S_{{{\mathcal {Y}}}}ee^tS_{ {{\mathcal {Y}}}}^tS_1{{\mathcal {T}}}\\= & {} {{\mathcal {T}}}^t S_{{{\mathcal {Y}}}}^{-t}S_1ee^tS_1S_{ {{\mathcal {Y}}}}^ {-1}{{\mathcal {T}}}\\= & {} {{\mathcal {T}}}^t S_{{{\mathcal {Y}}}}^{-t}ee^tS_{ {{\mathcal {Y}}}}^{-1}{{\mathcal {T}}}. \end{aligned}$$

The statement follows since $ee^t=S_1^++S_1$. $\square$

For $f=(f_\mathbf{r})\in S({k-m/2},{\chi })$ and ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$ we define

$$\begin{aligned} {{\mathcal {S}}}_f({{\mathcal {Y}}},s):= \int _{\mathrm{SL}(2,{{\mathbb {Z}}})\backslash {{\mathbb {H}}}}y^{\frac{k}{2}-\frac{m}{4}}f(z)^t \overline{{\varvec{\Theta }}(z,P_{{\mathcal {Y}}})} E_{-k}(z,s)\frac{dxdy}{y^2} \end{aligned}$$

(10)

where

$$\begin{aligned} E_{l}(z,s)=\sum _{T=\left( \begin{array}{cc}{a}&{}{b}\\ {c}&{}{d}\end{array}\right) \in \Gamma _{\infty }\backslash \mathrm{SL}(2,{{\mathbb {Z}}})}y_T^se^{-il\arg (cz+d)} \end{aligned}$$

is the real analytic Eisenstein series for $\mathrm{SL}(2,{{\mathbb {Z}}})$ of weight $l\in {{\mathbb {Z}}}$. As a function of s the Eisenstein series $E_{l}(z,s)$ has an analytic continuation to the whole complex plane. If $l\ne 0$ then $\zeta (2s)E_{l}(z,s)$ is an entire function in s and it satisfies the functional equation

$$\begin{aligned} E_{l}(z,s)=\phi _{l}(s)E_{l}(z,1-s) \end{aligned}$$

with $\phi _{l}(s)=\frac{i^{-l}2^{2-2s}\pi \Gamma (2s-1)\zeta (2s-1)}{\zeta (2s)\Gamma (s-\frac{l}{2})\Gamma (s+\frac{l}{2})}.$

The integral exists for any s which is not a pole of the Eisenstein series, since f is a cusp form and $P_{{\mathcal {Y}}}>0$. We now arrive at the announced Proposition.

Proposition 5.2

Let F be the Saito–Kurokawa lift of f as above. Then F is defined by a unimodular convergent Fourier series as in (3) where the Fourier coefficients are of at most polynomial growth and $A({{\mathcal {T}}})=0$, if $Q_1[{{\mathcal {T}}}]=0$. Furthermore for ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$ the partial Mellin transform ${\tilde{F}}({{\mathcal {Y}}},s)$ has the following properties:

• (i) Let ${{\mathcal {T}}}\in L^+$, ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$. Then For all $s\in {{\mathbb {C}}}$ with $\Re s$ sufficiently large, we have as an identity of meromorphic functions

  $$\begin{aligned} {\tilde{F}}({i{\mathcal {Y}}},s) =\frac{1}{2}\pi ^{-\frac{1}{2}-s}\Gamma (s+\frac{1}{2})\zeta (2s-k+1){{\mathcal {S}}}_f({{\mathcal {Y}}},s-\frac{k-1}{2}). \end{aligned}$$

• (ii) Let ${{\mathcal {T}}}\in L^+$, ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$. Then The Mellin transform ${\tilde{F}}(i{{\mathcal {Y}}},s)$ extends to an entire function in s and it satisfies the functional equation

  $$\begin{aligned} {\tilde{F}}(i{{\mathcal {Y}}},k-s)={\tilde{F}}(i{{\mathcal {Y}}},s). \end{aligned}$$

• (iii) Let ${{\mathcal {T}}}\in L^+$, ${{\mathcal {Y}}}\in {{\mathbb {H}}}_{m+1}$. Then ${\tilde{F}}(i{{\mathcal {Y}}},s)$ tends to zero as $\Im s\rightarrow \pm \infty$ uniformly in every vertical strip.

Proof

Absolute convergence of the defining series is guaranteed from the estimate $A({{\mathcal {T}}})\ll Q_1^a({{\mathcal {T}}})$ which in turn follows from well-known estimates for the Fourier coefficients of cusp forms. Also the condition of unimodularity is fulfilled due to the special form of the Fourier coefficients. As in [2], p.910f we conclude that the partial Mellin transform exists for $\Re s$ sufficiently large. The Rankin Selberg integral is evaluated as usual by unfolding the fundamental domain.

$$\begin{aligned} {{\mathcal {S}}}_f({{\mathcal {Y}}},s-\frac{k-1}{2})= & {} \int _0^{\infty }\int _0^1 f(z)^t\overline{{\varvec{\Theta }}(z,P_{{\mathcal {Y}}})} y^{s-(k-1)/2-2}dxdy \\= & {} 2\int _0^{\infty }\sum _{n>0}a^{*}(n)\sum _{{{\mathcal {T}}}\in L_n}e^{- \pi y ({{\mathcal {T}}}^tS_1{{\mathcal {Y}}})^2}y^{s-1}dy\\= & {} \frac{2q^s}{\pi ^{s}}\Gamma (s)\sum _{n>0} \frac{a^{*}(n)}{n^s}\sum _{{{\mathcal {T}}}\in L^+}\frac{1}{(({{\mathcal {T}}}^0)^tS_1{{\mathcal {Y}}})^{2s}}. \end{aligned}$$

We used that $\sum _{{{\mathcal {T}}}\in {\hat{\Lambda }}_1, qQ_1[{{\mathcal {T}}}]=n}=2\sum _{{{\mathcal {T}}}\in L_n}$ and the notation ${{\mathcal {T}}}^0=\sqrt{Q_1[{{\mathcal {T}}}]}^{-1} {{\mathcal {T}}}$. On the other hand

$$\begin{aligned} \int _0^{\infty }F(iu^{\frac{1}{2}}{{\mathcal {Y}}})u^{s-1}du= & {} \sum _{{{\mathcal {T}}}\in L^+}A({{\mathcal {T}}})\int _0^{\infty }e^{-2\pi \sqrt{u}({{\mathcal {T}}}^tS_1{{\mathcal {Y}}})}u^{s-1}du\\= & {} \frac{2q^s}{(2\pi )^{2s}} \Gamma (2s)\sum _{n>0}\frac{1}{n^s}\sum _{{{\mathcal {T}}}\in L_n}\frac{A({{\mathcal {T}}})}{(({{\mathcal {T}}}^0)^tS_1{{\mathcal {Y}}})^{2s}}\\= & {} \frac{2q^s}{(2\pi )^{2s}}\Gamma (2s)\sum _{n>0}\frac{\sum _{d^2|n}d^{k-1}a^{*}(n/d^2)}{n^s}\\&\times \,\sum _{{{\mathcal {T}}}\in L_{n/d^2}}\frac{1}{(({{\mathcal {T}}}^0)^tS_1{{\mathcal {Y}}})^{2s}}\\. \end{aligned}$$

If we use the identity $\zeta (2s-k+1)\sum _{n>0}\frac{c(n)}{n^s}=\sum _{n>0}\frac{\sum _{d^2|n}d^{k-1}c(n/d^2)}{n^s}$ and $\frac{\Gamma (2s)}{\Gamma (s)}=\frac{2^{2s-1}}{\sqrt{\pi }}\Gamma (s+\frac{1}{2})$, the statement of (i) follows for all s with $\Re s$ sufficiently large.

(ii) Since f is a cusp form the Rankin Selberg integral gives a meromorphic continuation for ${\tilde{F}}({{\mathcal {Y}}},s)$ as function of s to the whole complex plane. It is entire since $\zeta (2s-k+1)E_{-k}(z,s-k/2+1/2)$ is an entire function for even positive weight and the poles of $\Gamma (s+1/2)$ at $s=-1/2-n$ for $n\in {{\mathbb {N}}}$ are annihilated by the zeroes of the zeta function. Here it is important to notice, that k is even. The functional equation follows from that of the Eisenstein series and the well-known functional equation for the $\zeta$-function after some elementary calculations.

(iii) follows from the Phragmen–Lindelöf theorem. $\square$