Revisiting Multiple-Scattering Principles in a Crustal Waveguide: Equipartition, Depolarization and Coda Normalization

Abstract

Seismic waves radiated by small crustal earthquakes are prone to multiple mode conversions caused by reflection and transmission at interfaces, and scattering by small-scale heterogeneities in the bulk of the medium. The goal of this study is to clarify the complex interplay between volume scattering and interface reflections in crustal waveguides and how it will impact the crustal energy propagation. To carry out this task, we have incorporated a rigorous description of wave polarization in the context of Monte–Carlo simulations of the multiple-scattering process by introducing a five-dimensional Stokes vector. To shed light on the wave content of the regional short-period seismic wavefield, we investigate the asymptotic partitioning of seismic energy onto P, SV and SH polarizations in the coda, as well as the angular distribution of energy flux in the waveguide. In full elastic space, equipartition theory predicts that (1) the energy ratio between P- and S-wave energies tends to $\beta ^3/(2\alpha ^3)$, (2) an equal distribution of energy among SV- and SH-waves and (3) that energy fluxes are isotropic. In the presence of interfaces, we find that the isotropy of the wavefield is systematically broken and that energy ratios are shifted to the detriment of P-waves and in favor of SV-waves in a non-absorbing medium. This implies that a residual polarization is preserved in the waveguide. Through an extensive parametric study, we illustrate in detail how the anisotropy of the wavefield, the partitioning ratios and the shear wave polarization depend on the crustal attenuation parameters. The role of the initial polarization at the source has also been examined. In the case of an explosion and a shear dislocation with equal magnitude, we find that the energy level in the coda can differ by more than one order of magnitude when the effect of crustal scattering becomes very weak compared to reflections or transmissions at interfaces. When comparing different shear dislocation mechanisms, we find that the energy level in the coda can differ by up to 60%. While equipartition, depolarization and coda normalization remain fundamental guides to our understanding of the coda, their application requires a good a priori knowledge of the attenuation properties of the crust.

Appendices

Appendices

Basic Scattering Formulas

1.1 Scattering Amplitudes

We consider a continuous medium with small fluctuations of the elastic parameters (see the main text for further details). The scattering amplitudes $f_{**}$ can be found in Sato et al. (2012, p. 142). Because the specific intensities are expressed in frames that are attached to the scattering plane, the scattering amplitudes depend only on the scattering angle $\Theta$ when the scatterer is rotationally invariant. These scattering amplitudes are expressed as:

$$\begin{aligned} f_{PP}(\Theta ) &=\displaystyle \frac{k_P^2}{4\pi } \left[ \nu \left( -1+\cos \Theta +\frac{2}{\gamma ^2} \sin ^2 \Theta \right) - 2 + \frac{4}{\gamma ^2} \sin ^2 \Theta \right] {\tilde{\xi }} \left( 2k_P \sqrt{\frac{1-\cos \Theta }{2}} \right) \\ f_{PS}(\Theta ) &=\displaystyle \frac{-k_S^2 }{4\pi } \sin \Theta \left[ \nu \left( 1-\frac{2}{\gamma } \cos \Theta \right) - \frac{4}{\gamma } \cos \Theta \right] {\tilde{\xi }} \left( k_P \sqrt{1 - 2\gamma \cos \Theta + \gamma ^2} \right) \\ f_{SP}(\Theta ) &= \displaystyle \frac{k_P^2}{4\pi } \sin \Theta \left[ \nu \left( 1-\frac{2}{\gamma } \cos \Theta \right) - \frac{4}{\gamma } \cos \Theta \right] {\tilde{\xi }} \left( k_P \sqrt{1 - 2\gamma \cos \Theta + \gamma ^2} \right) \\ f_{\perp \perp }(\Theta ) &= \displaystyle \frac{k_S^2}{4\pi } \left[ \nu (\cos \Theta - \cos 2\Theta ) - 2\cos 2\Theta \right] {\tilde{\xi }} \left( 2k_S \sqrt{\frac{1-\cos \Theta }{2}} \right) \\ f_{\Vert \Vert }(\Theta ) &= \displaystyle \frac{k_S^2}{4\pi } \left[ \nu (\cos \Theta - 1) + 2\cos \Theta \right] {\tilde{\xi }} \left( 2k_S \sqrt{\frac{1-\cos \Theta }{2}} \right) . \end{aligned}$$

(23)

${\tilde{\xi }}$ is $k_P$ and $k_S$ are the P-wave and S-wave wavenumbers. $\gamma$ is the velocity ratio $\alpha /\beta$. We recall that $\nu$ is the Birch coefficient introduced in Eq. (1). We note the following reciprocity relation: $f_{SP} = -\frac{\beta ^2}{\alpha ^2} f_{PS}$.

1.2 Scattering Coefficients

To derive the scattering coefficients, we start from Eq. (6) which relates incident and scattered vectors in bases attached to the scattering plane. Suppose now that the scattering plane is oriented at an arbitrary angle $\Phi$ with respect to the fixed basis $(\varvec{x},\varvec{y},\varvec{z})$ with respect to which the incident Stokes vector is decomposed (see Fig. 2a). Noting that the unit normal vector to the scattering plane may be written as $\varvec{r} = \varvec{r}'= \varvec{p}' \wedge \varvec{p}/| \varvec{p}' \wedge \varvec{p}|$, we have:

$$\begin{aligned} \tan \Phi = \dfrac{\varvec{r} \cdot \varvec{y}}{\varvec{r} \cdot \varvec{x}} . \end{aligned}$$

(24)

The Stokes rotation matrix $\varvec{L}(\Phi )$, which expresses the Stokes vector in a new coordinate system (rotated by an angle $\Phi$ around the direction of propagation axis), can be written as (Turner & Weaver, 1994):

$$\begin{aligned} \varvec{L}(\Phi ) = \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \cos 2\Phi &{} \sin 2\Phi &{} 0 \\ 0 &{} 0 &{} -\sin 2\Phi &{} \cos 2\Phi &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{pmatrix} . \end{aligned}$$

(25)

The components $I_P$, $I_S$ and V are invariant under such a rotation. Note that $\varvec{L}(\Phi )=\varvec{L}(\Phi \pm \pi )$ so that the rotation angle is defined modulo $\pi$. The scattered Stokes vector $\varvec{S^{sc}}$ in the ($\varvec{r}', \varvec{l}', \varvec{p}'$) basis may be expressed as (see Fig. 2a):

$$\begin{aligned} \varvec{S^{sc}} = \varvec{F}(\Theta ) \varvec{L}(\Phi ) \varvec{S^i} \end{aligned}$$

(26)

where $\Theta$ is the scattering angle and $\Phi$ is the rotation angle to bring the $(\varvec{x},\varvec{y},\varvec{z})$ axes in coincidence with the $(\varvec{r},\varvec{l},\varvec{p})$ axes. From Eq. (26) we can deduce the expressions of the scattering coefficients. We first compute the total scattered intensities:

$$\begin{aligned}I_P^{sc} &= \displaystyle \frac{1}{R^2} \left( \langle |f_{PP} |^2 \rangle I_{P}^i + \frac{\alpha }{2\beta } \langle |f_{SP} |^2 \rangle (I_{S}^i - Q^i \cos 2 \Phi - U^i \sin 2 \Phi ) \right) \\ I_S^{sc} &= \displaystyle \frac{1}{R^2} \left( \frac{\beta }{\alpha } \langle |f_{PS} |^2 \rangle I_P^i + \frac{ \langle |f_{\perp \perp } |^2 + |f_{\Vert \Vert } |^2 \rangle }{2} I_S^i + \frac{\langle |f_{\perp \perp } |^2 - |f_{\Vert \Vert } |^2 \rangle }{2} (Q^i \cos 2 \Phi + U^i \sin 2 \Phi ) \right)\end{aligned}$$

(27)

In Eq. (27), the brackets indicate an average over the realization of the random medium. Note that for notational simplicity the dependence of the scattering amplitudes on $\Theta$ is implicit in Eq. (27) and following. Recalling that differential cross-sections $d\sigma _{**}/d\Omega$ are defined as the ratio between the energy scattered in a given direction per unit of solid angle and time, and the incident energy flux, we write:

$$\begin{aligned} \displaystyle \frac{d\sigma _{PP}}{d\Omega } &= \displaystyle \frac{I_P^{sc}}{I_P^i}\frac{dS}{d\Omega } \\ \displaystyle \frac{d\sigma _{PS}}{d\Omega } &=\displaystyle \frac{I_S^{sc}}{I_P^i}\frac{dS}{d\Omega } \\ \displaystyle \frac{d\sigma _{SP}}{d\Omega } &=\displaystyle \frac{I_P^{sc}}{I_S^i}\frac{dS}{d\Omega } \\ \displaystyle \frac{d\sigma _{SS}}{d\Omega } &= \displaystyle \frac{I_S^{sc}}{I_S^i}\frac{dS}{d\Omega }\end{aligned}$$

(28)

where the surface element is given by $dS = R^2d\Omega$. In turn, the scattering coefficients $g^{**}$ are related to the cross-sections by:

$$\begin{aligned} g^{**} = \displaystyle \frac{4\pi }{{\mathcal {V}}_{sc}} \frac{d\sigma _{**}}{d\Omega } \end{aligned}$$

(29)

We then deduce the following expressions of the differential scattering coefficients:

$$\begin{aligned} \displaystyle g^{PP}(\Theta , \Phi ) &=\displaystyle \frac{4 \pi }{{\mathcal {V}}_{sc}} \left\langle |f_{PP} |^2 \right\rangle \\ \displaystyle g^{PS}(\Theta , \Phi ) &= \displaystyle \frac{4 \pi }{{\mathcal {V}}_{sc}} \frac{\beta }{\alpha } \left\langle |f_{PS} |^2 \right\rangle \\ \displaystyle g^{SP}(\Theta , \Phi ) &= \displaystyle \frac{4 \pi }{{\mathcal {V}}_{sc}} \frac{\alpha }{2\beta } \left\langle |f_{SP} |^2 \right\rangle \left( 1 - \frac{Q^i \cos 2 \Phi - U^i \sin 2 \Phi }{I_{S}^i} \right) \\ \displaystyle g^{SS}(\Theta , \Phi ) &=\displaystyle \frac{4 \pi }{{\mathcal {V}}_{sc}} \left[ \frac{ \left\langle |f_{\perp \perp } |^2 + |f_{\Vert \Vert } |^2\right\rangle }{2} + \frac{\left\langle |f_{\perp \perp } |^2 - |f_{\Vert \Vert } |^2 \right\rangle }{2} \left( \frac{Q^i \cos 2 \Phi + U^i \sin 2 \Phi }{I_S^i} \right) \right] \end{aligned}$$

(30)

The case discussed in Sato et al. (2012) corresponds to an incident Stokes vector of the form: (0, 1, 1, 0, 0) (S-waves polarized along the $\varvec{x}$-axis). It may be readily verified that formulas (30) agree with the one given in Sato et al. (2012) in this case. In the case of an incident circular polarization (for example), the Stokes vector is of the form: $(0,1,0,0,\pm 1)$. Formulas (30) then predict that there is no azimuthal dependence of the differential scattering coefficients. From a physical point of view, this makes sense as both the medium and the incident wave are invariant by rotation about the propagation direction. We conclude that the scattering coefficients $g^{SP}$ and $g^{SS}$ depend on the incident polarization.

1.3 Rotation Angles for the Mueller Matrix

The Mueller matrix relates the incident and scattered Stokes vectors using a global convention to decompose the wavefields. Following previous works (Turner & Weaver, 1994), we introduce a global reference frame $(\varvec{x}, \varvec{y},\varvec{z})$ and a spherical basis $(\varvec{\theta }, \varvec{\phi }, \varvec{\rho })$ such that $\varvec{\theta }$, $\pmb { \phi }$ and $\varvec{\rho }$ are in the directions of increasing $\theta$ (co-latitude), $\phi$ (azimuth) and $\rho$ (distance from origin), respectively. With this convention, the derivation of the Mueller matrix requires the following steps: (1) rotate the incident Stokes vector from the $(\varvec{\theta },\pmb { \phi },\varvec{\rho })$ frame to the $(\varvec{r},\varvec{l},\varvec{p})$ frame attached to the scattering plane (note that $\varvec{p} = \varvec{\rho }$); (2) Apply the scattering matrix $\varvec{F}$; (3) rotate the scattered Stokes vector from the $(\varvec{r}',\varvec{l}',\varvec{p}')$ frame attached to the scattering plane to the $(\varvec{\theta }',\pmb {\phi }',\varvec{\rho }')$ frame (the primes refer to the scattered wave direction with $\varvec{\rho }' =\varvec{p}'$). The angle $\psi _1$ that realizes step (1) is defined by:

$$\begin{aligned} \tan (\psi _1) = \dfrac{\varvec{r} \cdot \varvec{\phi }}{\varvec{r} \cdot \varvec{\theta }}, \end{aligned}$$

(31)

where the unit normal vector to the scattering plane is given by:

$$\begin{aligned} \varvec{r} = \varvec{r}' = \dfrac{\varvec{p}' \wedge \varvec{p}}{|\varvec{p}' \wedge \varvec{p}|} . \end{aligned}$$

(32)

Using the definition of the scattering angle $\Theta$ we note: $|\varvec{p}' \wedge \varvec{p}| = \sin \Theta = \sqrt{1 - \cos ^2 \Theta }$ with:

$$\begin{aligned} \begin{array}{r c l} \cos \Theta = \sin \theta _1 \sin \theta _0 \cos (\phi _1-\phi _0) + \cos \theta _1 \cos \theta _0 . \end{array} \end{aligned}$$

(33)

From Eq. (31), we arrive after some algebra at:

$$\begin{aligned} \tan (\psi _1) = \dfrac{-\sin \theta _0 \cos \theta _1 + \cos \theta _0 \sin \theta _1 \cos (\phi _0 - \phi _1)}{\sin \theta _1 \sin (\phi _0 - \phi _1)}, \end{aligned}$$

(34)

The angle $\psi _2$ which brings $(\varvec{\theta }',\pmb {\phi }',\varvec{\rho }')$ in coincidence with $(\varvec{r}',\varvec{l}',\varvec{p}')$ is defined by

$$\begin{aligned} \begin{aligned} \tan (\psi _2) =&\dfrac{\varvec{r}' \cdot \pmb {\phi }'}{\varvec{r}' \cdot \varvec{\theta }'} \\ =&\dfrac{\sin \theta _1 \cos \theta _0 - \cos \theta _1 \sin \theta _0 \cos (\phi _0 - \phi _1)}{\sin \theta _0 \sin (\phi _0 - \phi _1)} \end{aligned} \end{aligned}$$

(35)

Note that rotation by an angle $-\psi _2$ needs to be applied to the scattered Stokes vector (see Eq. 9).

Construction of the Reflection Matrix at the Moho

The elements of the reflection matrices (11, 14 and 15) can be derived from the classical treatment of Aki and Richards (2002) by applying the superposition principle. Let us illustrate the method by deriving some typical Stokes parameters reflection coefficients for incident S-waves on the Moho.

The vertical $\varvec{z}$-axis is oriented downwards. In the spherical basis $(\varvec{\theta },\varvec{\phi }, \varvec{r})$, an arbitrarily polarized incident shear plane wave $\varvec{u}^i_S$ may be written as:

$$\begin{aligned} \varvec{u}^i_S = {\pmb {\theta }} A_{\theta } e^{-i \omega t +i\omega (z \cos j + x \sin j )/\beta _1 } + {\pmb {\phi }} A_{\phi } e^{-i \omega t +i\omega (z \cos j + x \sin j )/\beta _1 } \end{aligned}$$

(36)

with j the angle between $\varvec{r}$ and $\varvec{z}$. The $\pmb \theta$, $\pmb \phi$ components correspond to the usual SV and SH polarizations, respectively. In general the coefficients A may be complex to take into account possible phase shifts between the two components of the shear wave motion. The reflected S-wavefield $\varvec{u}^r_S$ may be written as:

$$\begin{aligned} \varvec{u}^r_S = \pmb {\theta _r} A_{\theta } \grave{S}\acute{S}_V e^{-i \omega t - i \omega (z \cos j - x \sin j)/\beta _1 } + \pmb {\phi _r} A_{\phi } \grave{S}\acute{S}_H e^{-i \omega t - i \omega (z \cos j - x \sin j)/\beta _1 } \end{aligned}$$

(37)

with $\pmb {\phi } = \pmb {\phi _r}$ and $\pmb {\theta _r}$ is the mirror image of $\pmb {\theta }$ by the interface. Let us now relate incident and reflected Stokes parameters. To do so, we consider an incident bundle of rays of typical angular aperture $d \Omega ^i_S = \sin j dj d\phi$ and denote by $N^i_S$ the number density of rays. In other words, the bundle contains $N^i_S d\Omega ^i_S$ statistically independent rays. Up to the common pre-factor $\rho _1 \beta _1 \omega ^2 N^i_S /2$, we have

$$\begin{aligned} \begin{aligned} I_S^i =&|A_{\theta }|^2 + |A_{\phi }|^2 \\ Q^i =&|A_{\theta }|^2 - |A_{\phi }|^2 \\ U^i =&2 \Re \mathrm {e}(A_{\theta } A_{\phi }^* ) \\ V^i =&2 \Im \mathrm {m}(A_{\theta } A_{\phi }^*) \end{aligned} \end{aligned}$$

(38)

for the incident waves, where the coefficients A represent the typical amplitudes of the rays in the bundle. Thanks to the assumption of statistical independence, the Stokes parameters are proportional to the ray density. We denote by $d\Omega ^r_S$ and $N^r_S$ the solid angle subtended by the reflected ray bundle and the number density of reflected rays, respectively. Up to the common pre-factor $\rho _1 \beta _1 \omega ^2 N^r_S /2$, the Stokes parameters of the reflected rays may be written as:

$$\begin{aligned} I_S^r & =|A_{\theta }|^2 |\grave{S}\acute{S}_V|^2 + |A_{\phi }|^2 |\grave{S}\acute{S}_H|^2 \\ Q^r &=|A_{\theta }|^2 |\grave{S}\acute{S}_V|^2 - |A_{\phi }|^2 |\grave{S}\acute{S}_H|^2 \\ U^r &=2 \Re \mathrm {e}(A_{\theta } A_{\phi }^* \grave{S}\acute{S}_V \grave{S}\acute{S}_H^*) \\ V^r &=2 \Im \mathrm {m}(A_{\theta } A_{\phi }^* \grave{S}\acute{S}_V \grave{S}\acute{S}_H^*) . \end{aligned}$$

(39)

Note that the angular aperture of the ray bundle is conserved for S-to-S reflection, i.e. $d\Omega ^i_S= d\Omega ^r_S$. This implies in turn $N^i_S=N^r_S$ since we keep track of a fixed set of rays. In Eq. (38), we have adopted a similar notation as Aki and Richards (2002) for the displacement reflection coefficients. For instance $\grave{S}\acute{S}_V$ represents the reflection coefficient for a downgoing SV-wave incident at the Moho reflected to an upgoing SV-wave. Due to a different convention for the definition of the upgoing SV wavefield, our displacement reflection coefficients involving an upgoing SV-waves differ by a sign from those given in Aki and Richards (2002). From Eqs. (38)–(39), we deduce the following relations between incident and reflected Stokes parameters:

$$\begin{aligned} I_S^r &=\dfrac{(I_S^i + Q^i)|\grave{S}\acute{S}_V|^2 }{2} + \dfrac{(I_S^i - Q^i)|\grave{S}\acute{S}_H|^2 }{2} \\ Q^r &=\dfrac{(I_S^i + Q^i)|\grave{S}\acute{S}_V|^2 }{2} - \dfrac{(I_S^i - Q^i)|\grave{S}\acute{S}_H|^2 }{2}\\ U^r &=\dfrac{(U^i + i V^i)\grave{S}\acute{S}_V \grave{S}\acute{S}_H^* }{2} + \dfrac{(U^i - i V^i)\grave{S}\acute{S}_V^* \grave{S}\acute{S}_H }{2} \\ V^r &=\dfrac{(-i U^i + V^i)\grave{S}\acute{S}_V \grave{S}\acute{S}_H^* }{2} + \dfrac{(iU^i + V^i)\grave{S}\acute{S}_V^* \grave{S}\acute{S}_H }{2} \end{aligned}$$

(40)

which agrees with the formulas given in the text. These results are valid for any incidence angle $0\le j < \pi /2$. From Eq. (40) we deduce:

$$\begin{aligned} (I^r_S)^2 - (Q^r)^2- (U^r)^2 - (V^r)^2 = \left( (I^i_S)^2 - (Q^i)^2 - (U^i)^2 - (V^i)^2 \right) |\grave{S}\acute{S}_v|^2 |\grave{S}\acute{S}_h|^2 \end{aligned}$$

(41)

This last Eq. shows that a fully polarized incident wave (i.e. such that $(I^i)^2 - (Q^i)^2 - (U^i)^2 - (V^i)^2=0$) remains fully polarized upon reflection.

When all the transmitted and refracted rays are in the propagation regime, the reflection coefficients for Stokes parameters are real. Furthermore, the off-diagonal reflection coefficients for U and V are equal to zero (because they are related to the imaginary part of the displacement reflection coefficients). As a consequence, an initially linearly polarized S-wave ($V^i=0$) will remain linearly polarized upon reflection ($V^r=0$).

When some rays are in the evanescent regime (which occurs when $\sin j > \beta _2/ \alpha _1$) the displacement reflection coefficients of SV-waves are complex and the Stokes parameters of reflected S-waves will exhibit a non-zero parameter V characteristic of elliptic polarizations. This elliptical polarization stems from the fact that the reflected SV and SH components are phase shifted with respect to one another due to their different reflection coefficients at the Moho.

Following the same line of reasoning, mode conversions may be treated with a notable difference related to Snell’s law. Consider again an incident bundle of plane S-waves (Eq. 36). The reflected P-wavefield of a single plane wave may be written as:

$$\begin{aligned} \varvec{u}^r_P = \pmb {r} A_{\theta } \grave{S}\acute{P} e^{-i \omega t - i \omega (z \cos i - x \sin i)/\alpha _1 } \end{aligned}$$

(42)

with $\sin i = \sin j \dfrac{\alpha _1}{\beta _1}$. Let us note that if any reflected (transmitted) ray is in the evanescent regime, the associated intensity reflection (transmission) coefficient is set to 0. To illustrate the idea, we note for instance that $R^{I}_{SV - P} = 0$ for $1/\alpha _1< p < 1/\beta _1$ (p is the ray parameter) both at the Moho and the free surface. Note that in the same range of ray parameters the reflection coefficients $R^{I}_{P - SV}$ is undefined (since P-waves are not propagating in this regime). With this in mind, we obtain for the intensity of the reflected set of P-wave rays:

$$\begin{aligned} I_P^r = \dfrac{\rho _1 \alpha _1 \omega ^2 N^r_P |\grave{S}\acute{P}|^2 |A_\theta |^2 }{ 2 } \end{aligned}$$

(43)

where $\grave{S}\acute{P}$ is the displacement reflection coefficient at the Moho. Using Eq. (38), we obtain:

$$\begin{aligned} I_P^r = \dfrac{ \alpha _1 |\grave{S}\acute{P}|^2 (I_S^i-Q^i) N^r_P}{ 2 \beta _1 N^i_S} \end{aligned}$$

(44)

Since we follow a given set of rays, the change in ray density is given by the ratio between the incident and reflected solid angles:

$$\begin{aligned} \dfrac{N^r_P}{N^i_S} = \dfrac{d\Omega ^i_S}{d\Omega ^r_P} \end{aligned}$$

(45)

where $d\Omega ^r_P$ denotes the solid angle subtended by the reflected P rays. Using Snell’s law, we find:

$$\begin{aligned} \dfrac{d \Omega ^i_S}{d \Omega ^r_P} = \dfrac{\beta _1^2 \cos i }{\alpha _1^2 \cos j } \end{aligned}$$

(46)

Reporting (46) into (44), we arrive at:

$$\begin{aligned} I_P^r = \dfrac{ \beta _1^2 R^E_{\grave{S}_V-\acute{P}} (I_S^i-Q^i)}{ 2 \alpha ^2_1 } \end{aligned}$$

(47)

where $R^E_{\grave{S}_V-\acute{P}} = \alpha _1 \cos i |\grave{S}\acute{P}|^2/ \beta _1 \cos j$ is the energy reflection coefficient as defined by Aki and Richards (2002). The formula is valid for any incident angle such that $\sin j < \dfrac{\beta _1}{\alpha _1}$. The change of ray divergence at the Moho is at the origin of the factor $\beta _1^2 / \alpha _1^2$ in Eq. (47). Note that this purely geometrical factor is automatically accounted for in the numerical simulations since the seismic phonons obey Snell’s law. In the text, we have lumped together the geometrical factor with the energy reflection coefficient to define $R^I_{\grave{S}_V-\acute{P}} = \beta _1^2 R^E_{\grave{S}_V-\acute{P}} / \alpha _1^2$.

Reflection of a Diffuse Field at the Free Surface

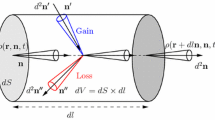
In this Appendix, we demonstrate that the free surface does not affect an equilibrated and isotropic wavefield. We recall that when this condition applies, we have equal amount of SV- and SH-waves incident at the free surface, which acts as a mirror for the latter. As a consequence, the isotropy of SH-waves is obviously preserved. The critical aspect pertains to the mode coupling between P- and SV-waves which strongly depends on the incidence angles. Let us illustrate the reasoning in the case of a beam of dowgoing P-waves at the free surface (see Fig. 14). This beam originates from the reflection of a set of upgoing P- and SV-wave rays. To properly quantify the contribution of SV-waves, two important physical effects have to be taken into account: mode conversions and focusing/defocusing of the beam of rays. We denote by $I_{P} (\varvec{n}^{i})$ and $I_{SV}(\varvec{n}^{j})$ the specific intensities of P- and SV-waves incident at the free surface. For the reflected P-waves we use the notation $I_{P} (\varvec{n}^{o})$. Note that the unit vectors $\varvec{n}^{i}$, $\varvec{n}^{j}$ and $\varvec{n}^{o}$ denoting the propagating direction of the rays are related by Snell’s law. The principle of energy conservation for P-waves may be expressed as follows:

$$\begin{aligned} I_{P} (\varvec{n}^{o}) |\varvec{n}^{o} \cdot \varvec{z} | d^2n^{o} = R^{E}_{\acute{P}{-}\grave{P}}(\varvec{n}^{i}) I_{P} (\varvec{n}^{i}) |\varvec{n}^{i} \cdot \varvec{z} | d^2n^{i} + R^{E}_{\acute{S}_{V}{-}\grave{P}}(\varvec{n}^{j}) I_{SV} (\varvec{n}^{j}) |\varvec{n}^{j} \cdot \varvec{z} | d^2n^{j} \end{aligned}$$

(48)

where $d^2n^{i,o,j}$ represent elementary solid angles (see Fig. 14) and the $R^{E}$ denote the energy reflection coefficients (see also the main text and Appendix B for further details). Using the notations of Aki and Richards (2002), they can be expressed in terms of the traditional displacement reflection coefficients as follows:

$$\begin{aligned} \begin{aligned} R^{E}_{\acute{P}{-}\grave{P}}(\varvec{n}^{i}) =&\acute{P} \grave{P}(\varvec{n}^{i}) ^{2} \\ R^{E}_{\acute{S}_{V}{-}\grave{P}}(\varvec{n}^{j}) =&1 -\acute{S}\grave{S}_{V} (\varvec{n}^{j})^{2} \end{aligned} \end{aligned}$$

(49)

Note that the displacement reflection coefficients are always real for the propagating waves considered in our model. We may now put the ratio between the reflected and incident energy densities in the form:

$$\begin{aligned} \dfrac{I_{P} (\varvec{n}^{o})}{I_{P} (\varvec{n}^{i})} & = \dfrac{\acute{P}\! \grave{P}(\varvec{n}^{i})^{2}|\varvec{n}^{i} \cdot \varvec{z} | d^2n^{i}}{|\varvec{n}^{o} \cdot \varvec{z} | d^2n^{o}}\\ &\quad + \dfrac{ I_{S} (\varvec{n}^{j})(1 -\acute{S}\!\grave{S}_V (\varvec{n}^{j}) ^{2})|\varvec{n}^{j} \cdot \varvec{z} | d^2n^{j} }{ I_{P} (\varvec{n}^{i}) | \varvec{n}^{o} \cdot \varvec{z} | d^2n^{o}} \end{aligned}$$

(50)

We may now apply Snell’s law to simplify this expression. For P-to-P reflection we clearly have: $|\varvec{n}^{i} \cdot \varvec{z} | d^2n^{i} = |\varvec{n}^{o} \cdot \varvec{z} | d^2n^{o}$. For S-to-P conversion we differentiate Snell’s law to obtain:

$$\begin{aligned} \dfrac{\cos i di}{\alpha _1} = \dfrac{\cos j dj}{\beta _1} \end{aligned}$$

(51)

where j is the incidence angle of SV-waves and i the reflection angle of P-waves. Combining (Eq. 51) with usual Snell’s law, we obtain:

$$\begin{aligned} \dfrac{|\varvec{n}^{j} \cdot \varvec{z} | d^2n^{j}}{| \varvec{n}^{o} \cdot \varvec{z} | d^2n^{o}} = \dfrac{\beta _1^2}{\alpha _1^2} \end{aligned}$$

(52)

Reporting the last result in Eq. (50) yields:

$$\begin{aligned} \dfrac{I_{P} (\varvec{n}^{o})}{I_{P} (\varvec{n}^{i})} = \acute{P}\!\grave{P}(\varvec{n}^{i})^{2} + \dfrac{\beta _1^2 I_{S} (\varvec{n}^{j}) (1 -{\acute{S}}\!{\grave{S}_{V}} (\varvec{n}^{j}) ^{2}) }{\alpha _1^2 I_{P} (\varvec{n}^{i})} \end{aligned}$$

(53)

For an equipartitioned upgoing wavefield, the specific intensities $I_{S} (\varvec{n}^{j})$ and $I_{P} (\varvec{n}^{i})$ are independent of the incidence angles and their ratio is equal to $\alpha _1^2/\beta _1^2$. Noting the symmetry relation $\acute{S} \grave{S}_V(\varvec{n}^{j}) ^{2} = \acute{P} \grave{P}(\varvec{n}^{i})^{2}$ (Aki & Richards, 2002), we arrive at the desired result:

$$\begin{aligned} I_{P} (\varvec{n}^{o}) = I_{P} (\varvec{n}^{i}) \end{aligned}$$

(54)

Following the same line of reasoning, the result can be extended to SV-waves. In conclusion, if the wavefield incident at the free surface is equipartitioned, so is the reflected wavefield.

Fig. 14

Energy balance at the free surface. The downgoing P-waves propagating around direction $\varvec{n}^{o}$ have two origins: reflection of P-waves with incidence direction $\varvec{n}^{i}$, or conversion of SV-waves with incidence direction $\varvec{n}^{j}$. The incidence angles of P- and S-waves are denoted by i and j, respectively. The elementary solid angles of incident P, incident S and reflected P-waves are denoted by $d^2\varvec{n}^{i}$, $d^2\varvec{n}^{j}$ and $d^2\varvec{n}^{o}$, respectively