1 Introduction

Observational seismology fundamentally relies on our ability to record seismic signals of interest with high fidelity and known orientations of the sensitive axes to a geographic coordinate system. Modern seismologists often record seismic signals using a force-feedback seismometer, where the electronics control the passband of the instrument as well as increase the dynamic range (Steim, 2015). These instruments have been successful tools for characterizing earthquakes as well as providing data for imaging the interior of the Earth. However, cases where instrumentation have been the source of anomalous signals compromise our ability to use seismic data in certain Earth studies (Ekström et al., 2006; Laske & Cotte, 2001). For example, orientation errors in seismometers can easily compromise our ability to identify off-angle incoming Rayleigh wave arrivals, which can be used to infer Earth structure (Laske, 1995). Similarly, differentiating between the effects of local geological structure and instrumentation errors can be hard (Eddy & Ekström, 2014). Errors in the reported sensitivity of a seismometer can compromise our ability to characterize the amplitudes of recorded waveforms used for structure studies (Dalton et al., 2008), and noise levels of the seismic instruments themselves can compromise the ability to make seismic observations (Ringler & Hutt, 2010).

In order to verify the sensitivity and orientation at long running stations in the Global Seismographic Network (GSN), network operators make use of a Sensitivity, Orientation, and location (SensorLoc) kit. These SensorLoc kits contain a Nanometrics Trillium Compact seismometer, digitizer, and fiber optic gyroscope. During maintenance visits to GSN seismic stations, a SensorLoc kit gets deployed to verify the azimuth of the sensors at the station as well as the sensitivity. Timing can also be verified because the SensorLoc kit is independent of the station. After a maintenance visit, the SensorLoc kit gets returned to the lab for calibration testing. This provides an independent check on the instrumentation at a station where the instruments might be running for long periods of time (Davis & Berger, 2012).

In previous work, we examined the precision to which compact seismometers can be oriented, calibrated, and characterized in a controlled environment in the Albuquerque Seismological Laboratory (ASL) underground vault (Ringler et al., 2017). Through repeatedly installing a Nanometrics Trillium Compact next to two additional identical sensors, we found that the orientations were stable to within 0.78° and that we could constrain sensitivity to 0.04% at the 99th percentile. At first glance, this is a promising result in terms of the robustness of constraining fundamental parameters of seismic instruments. However, in contrast to a typical field installation, the repeatedly installed sensor was aligned to the same north line, and the environment was exceptionally thermally stable (Doody et al., 2017). Additionally, since Nanometrics Trillium Compact instruments were used for the study, nothing could be said about the ability to record long-period (> 20 s) background seismic signals because the self-noise of these sensors exceeds ambient background noise levels at these periods.

In the Ringler et al. (2017) study, orientation precision was a measure of how well an instrument could be oriented to an inscribed line by eye. In contrast, during a normal field deployment, there is additional uncertainty with the actual orientation of the line, the techniques of different field engineers, and the method used to orient the seismometer to the north line (e.g., Ringler et al., 2013). Considering all factors, it was estimated that a real-world uncertainty of 2.4° for GSN deployments with a 99th percentile confidence. This agrees well with the 3° estimate at the 88th percentile observation interval attained by Ekström and Nettles (2018) for the Transportable Array in the conterminous U.S.

Beyond orientations, the mid-band sensitivity of a seismometer is another parameter that can change in response to local environmental conditions. For instance, during absolute calibrations of accelerometers, the temperature at which the calibration is carried out is suspected to be the largest driver of uncertainty for determining mid-band sensitivity (Anthony et al., 2017). Therefore, two seismometers that display identical mid-band sensitivities in the laboratory might change appreciably when one is installed in a polar or other cold environment and the other is installed in the tropics or other warm environment.

Finally, the sensitivity of instrumentation to various seismic and non-seismic noise sources can make testing instruments difficult. For example, testing instrumentation for performance in the GSN requires a low-noise vault that is isolated from non-seismic noise sources. This can be further complicated by local weather systems introducing time periods of elevated long-period noise. There can also be variability in the self-noise between like models of seismometers (e.g., Sleeman & Melichar, 2012). Identifying the variability among like models of sensors is further complicated by variability in the location where the instruments are installed, sometimes even when the instruments are located on the same pier (Rohde et al., 2017).

While it is well known that seismic instruments respond to local atmospheric drivers such as temperature (Doody et al., 2017) as well as pressure changes (e.g., Alejandro et al., 2020), some of the variations are not well constrained or have focused on improving only the long-period resolution of instruments. Recent work by Dybing et al. (2018) has suggested that local geology can produce variable noise levels through the excitation of the ground via wind-induced noise. Smith and Tape (2019) also observed local amplification of noise in central Alaska. This has also been observed by Xu and Yuan (2019), where three different locations were considered. This is in contrast to the model suggested by Sorrells (1971) that attenuation at depth is only weakly dependent on the material within which the sensor is emplaced. While much of this noise can be mitigated by deeper installations (Ringler et al., 2020), it is unclear how these noise levels vary when such deep installations are not plausible.

In order to look at the reproducibility and variability of seismic instrumentation parameters, we conduct an experiment by installing a Nanometrics Trillium T-360 and a Streckeisen STS-2.5 at five different locations at ASL. Our goal in this is to identify how repeatable various sensor parameters and noise levels are when the installation environment is not held constant. Instead of focusing on installations that have the extremely low-noise at periods greater than 100 s (e.g., Ringler et al., 2020), we focus on using high-quality instrumentation in a number of different settings. Many of these installations are more typical of a field deployment or a vault used in a regional network. By using high-quality instrumentation, we are not limited by instrument self-noise, which was the case in Ringler et al. (2017). We also do not focus on one particular seismic band but instead focus on a relatively broad seismic band of interest from 0.1 to 100 s period.

2 Methods and Data Collection

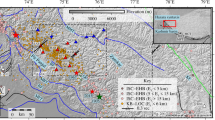
In order to look at the local variability across the ASL, we installed a Nanometrics T-360 GSN vault seismometer (network code XX, station code TST4, location code 00) along with a Streckeisen STS-2.5 vault seismometer (network code XX, station code TST4, location code 10) at five different locations (Fig. 1). The times and locations of the installations are given in Table 1. Both sensors were recorded on the same Quanterra Q330HR digitizer at each location in the experiment. The first location of installation was the West Underground Vault. Upon completing installations in the five different locations, we reinstalled both instruments one more time in the West Vault. We call this last installation “West Vault 2” throughout the rest of the manuscript. We compare data from these two vault sensors to the ASL reference Streckeisen STS-6 borehole seismometer, which is installed within a posthole in the cross tunnel between the East and West underground vaults (blue dot Fig. 1; network code GS, station code ALQ2, location code 00). In contrast to Ringler et al. (2017), all three of the broadband seismometers used in this study have self-noise levels below the Peterson (1993) New Low-Noise Model (NLNM) at periods less than 300 s; therefore, we are not limited by instrument noise at long-periods.

Fig. 1
figure 1

Locations of the different installations for our test (red circle) and the reference sensor (blue circle) at the Albuquerque Seismological Laboratory (location relative to the U.S. is in the bottom right). Location 1 is the West Vault, 2 the Cross tunnel, 3 the East Vault, 4 the Snake pit, and 5 the ANMO pit

Full size image
Table 1 Locations of the different deployments (first column), the start times of the deployments (second column), and the color used for plotting for the particular deployments (third column)
Full size table

For each installation, an ASL field engineer team scribed a north line using an iXblue Octans fiber optic gyroscope. Previous analysis of this orientation method has demonstrated that through use of an Octans, a north line can be scribed with a precision better than 0.1° (Ringler et al., 2013). At the latitude of ASL (39.94°), the Octans have an accuracy of 0.15/cos(latitude), which is approximately 0.18°. The field engineers then oriented both instruments to the scribed north line by eye without the use of an alignment jig. Finally, to avoid local thermal convection, fleece caps were placed on both sensors before covering them with foam boxes (Fig. 2). Upon installing the instruments and verifying the digitizer sensitivity, using a precision voltage supply, we did no further adjustments. At each location, the instruments recorded data for a seven-day period. We did not allow for any changes in the setup of the instruments between locations.

Fig. 2
figure 2

Different installations from our test. a West Vault, b the East Vault, c the Cross tunnel, d the Snake pit, and e the ANMO pit. Inset in (e) is the actual location of the sensors under the white fiberglass cover

Full size image

Upon acquiring the 40 samples per second (sps) data, we visually picked start and end times for each location (Table 1) based upon the seismometers showing signs of being “settled.” By “settled,” we mean that there were no longer transient signals on the sensors resulting from the field engineers moving around the sensors. From the seven days of data at each location, we used 4-h moving windows with 50% overlap to estimate the orientation, relative gain, and background noise as a function of period. We also estimated the incoherence self-noise, but ultimately did not use the results because they were not indictive of the self-noise of the instruments and instead followed background noise levels. Specifically, we perform our analysis for each of these metrics as follows:

2.1 Orientation

To estimate the relative orientations of each sensor, we decimated all data streams to 1 sps, removed the instrument response, removed the mean, applied a 4–8 s period bandpass filter, and finally applied a 5% cosine taper. We then estimated the relative orientation of the Nanometrics T-360 GSN and the Streckeisen STS-2.5 relative to the Streckeisen STS-6. This was done by minimizing the residual of the following cost function:

$$\mathrm{resi}(\theta )=\frac{\left|\sum_{t}x\left(\theta ,t\right)y(t)\right|}{\sqrt{\sum_{t}{x(\theta ,t)}^{2}}\sqrt{\sum_{t}{y(t)}^{2}}}-1$$
(1)

where x(\(\theta\),t) and y(t) denote the north components of instrument under test after being rotated by an angle \(\theta\) and the reference instrument, respectively. We have used t to denote the discrete time variable of our data so that the sums are taken over all samples in our window. We then estimated the relative orientation by finding the \(\theta\) that minimizes Eq. (1) using the Levenberg–Marquardt algorithm (Marquardt, 1963).

2.2 Relative Gains

Using the power spectral density (PSD) estimates described below, we estimate the relative gain between the sensors using the mean in the 4–8 s period band between the Streckeisen STS-6 reference and the other two sensors. This is a region where the background signal is well above the instrument self-noise (Fig. 3) and has been commonly used to infer the sensitivity of the instrument (e.g., Anthony et al., 2017).

Fig. 3
figure 3

Example vertical power spectral density (PSD) estimates and incoherent self-noise for the reference Streckeisen STS-6 (network GS, station ALQ2, location 00), the Nanometrics T-360 GSN (network XX, station TST4, location 00), and the Streckeisen STS-2.5 (network XX, station TST4, location 10) for October 13, 2020, starting at 12:45 UTC. All sensors were in the Albuquerque Seismological Laboratory (ASL) Cross tunnel. We have also included the Peterson (1993) New Low-/High-Noise Model (NLNM/NHNM, black)

Full size image

2.3 Background Noise and Self-Noise

With each 4-h window, we estimated the self-noise as well as the background noise using a Welch averaging of 214 data points with 28 points of overlap. For each averaged section, we applied a Hann taper and removed the mean. Finally, we removed the response and converted to units of dB relative to 1 (m/s2)2/Hz. Figure 3 shows an example of one of our PSD estimates. To estimate the self-noise, we used the three-sensor method developed by Sleeman et al. (2006), which attributes the incoherent signal of a seismometer to the noise level of that particular instrument. However, it should be pointed out that any incoherent signal among the instruments will be attributed to the self-noise of the instrument. For example, both sensor tilt (Rohde et al., 2017) and thermal variations (Doody et al., 2017) introduce incoherent signals on seismometers, and these non-seismic signals will contribute to self-noise estimates attained using the Sleeman et al. (2006) method. Additionally, in our self-noise estimates, we made no attempt to rotate components to mitigate incoherent signals (Tasič & Runovc, 2013, 2014). Finally, we note that the spatial separation of the reference STS-6 (about 15 m in Fig. 3) and the two instruments under test could further elevate the estimated self-noise levels, particularly at high-frequencies.

3 Results and Interpretation

3.1 Orientations

We find that our method for calculating relative orientations is able to estimate the relative sensor orientation between two sensors to within 0.1° when all sensors are located relatively close to one another (< 20 m) in the underground vaults (Fig. 4). However, orientation uncertainty between the reference STS-6 and both vault sensors increases noticeably to greater than 0.5° when the vault sensors are installed in the Snake pit or the ANMO pit. The ANMO pit is located nearby the GSN station ANMO (Albuquerque, New Mexico; Albuquerque Seismological Laboratory/USGS, 1988). Both instruments had very similar orientation errors suggesting that the scatter in our orientation methods are not limited by the model of instrument.

Fig. 4
figure 4

a Relative orientations between the Streckeisen STS-6 and Nanometrics T-360 GSN for the different deployments in this study (see Table 1) by day of year (doy). We have clipped the axes to be −2 to 2° and denoted the median orientation (−5.56°) for the first installation. b and c are the same as a, but for the Nanometrics T-360 GSN and Streckeisen STS-2.5 and the Streckeisen STS-6 and the Streckeisen STS-2.5, respectively

Full size image

This scatter is partially coming from reduced coherence as the distance between the reference sensor and the other two instruments increases. For example, Anthony et al. (2020a, 2020b) used the coherence methodology of Ringler et al. (2012) to determine the orientations and uncertainty of broadband seismometers installed in the ASL small-aperture posthole array using a reference sensor in the cross tunnel. The 95th percentile confidence interval of orientations increased with distance from the references sensor and reached 0.84° at a separation distance of 473 m. Anthony et al. (2020a, 2020b) also found that orientations between the reference vault and the postholes immediately outside the Snake pit could be oriented to 0.68° at the 95th confidence interval. In this study, there is more scatter in orientations from the sensors than was observed in Anthony et al. (2020a, 2020b). This suggests that there is an increase in the distortion of the waveforms in the surface vault sensors used in this study relative to the shallow burial sensors.

In addition to scatter between the two vault sensors and the reference increasing in the Snake pit and ANMO pit, the scatter in orientation between the two vault sensors themselves increases in these locations. In the four vault installs, the relative orientations between the two sensors are constrained to < 0.3° at the 95th percentile confidence. In the Snake pit, this scatter increases to 0.6° and in the ANMO pit to 0.7°. Because the distance between the vault sensors was nearly identical during all installations (Fig. 2), we attribute this difference to environmental factors. The ANMO pit in particular has poor thermal stability, and we could observe temperature-driven drifts in the time series of both sensors in this installation. Ultimately, this lack of thermal stability or other non-seismic driver could compromise our ability to identify the relative orientations between two seismometers even when they are co-located. This indicates that care must be taken to isolate SensorLoc kits from non-seismic noise sources when performing relative orientations at GSN sites.

Finally, the initial installation showed a human error, where the Nanometrics T-360 GSN was installed 4° off from the co-located STS-2.5 and 5.5° off from the reference STS-6. This is likely because the feet of the instrument do not perfectly align with the alignment arrows on the instrument. This is solely an operator error and not an issue with the instrument. However, such errors could easily be the cause in the outliers identified by Ekström and Nettles (2018, their Table 2) in a number of regional networks. As discussed in Ringler et al. (2013), using a fiber optic gyroscope to orient instruments helps remove uncertainty from the estimation of true north, but it does not remove uncertainty from operator error. We suggest that using mechanical jigs that engage with Octans may help to remove some of these human errors and could improve the precision to which we are able to align instruments.

3.2 Mid-Band Sensitivities

Upon estimating relative gains in the microseism band, we see that we are able to tightly constrain the sensitivities to well under 0.1% (Fig. 5). We did not observe any offsets in these sensitivities at any of the different locations. This suggests that the sensitivity of a seismometer is extremely stable over short time periods. This also implies that sensitivity errors identified in Ringler et al. (2015) and Pederson et al. (2019) originate not from installation errors, but instead either long-term drift of the instrument’s gain or poorly characterized metadata, such as not correcting for different digitizer input impedances (Anthony et al., 2018). This is consistent with our previous results on testing the Nanometrics Trillium Compact, where sensitivities of co-located instruments could be constrained to 0.04% at the 99th percentile confidence level (Ringler et al., 2017).

Fig. 5
figure 5

a Sensitivity ratios between sensors for the vertical component of the Streckeisen STS-6 and the Nanometrics Trillium 360 GSN in the West Vault (blue), the Cross tunnel (orange), the East Vault (green), the Snake pit (red), the ANMO pit (purple), and the second West Vault (brown). b and c are the same as a, but for the BH1 (north–south) and BH2 (east–west) components, respectively. d, e, and f are the same as a, b, and c, but for the Nanometrics T-360 GSN and the Streckeisen STS-2.5, respectively. g, h, and i are the same as a, b, and c, but for the Streckeisen STS-6 and the Streckeisen STS-2.5, respectively

Full size image

We also conducted digitizer tests at each location by inputting a known voltage to the digitizer to estimate the sensitivity of the digitizer in counts/V, but we did not analyze these because our sensitivity estimates were well within any reasonable tolerance, suggesting that the Quanterra Q330HR has a very stable sensitivity upon reboot.

3.3 Noise

We observed that the settling time in all locations was approximately the same, with the instrument coming to temperature within about 16 h (Fig. 6). The instruments were all able to record microseisms during this settling period because most of the settling is very long-period drift. We did not attempt to quantify the settling time because it can be difficult to identify when an instrument in actually considered “settled.”

Fig. 6
figure 6

a Vertical component time series data from the installation time to 16 h after for the Nanometrics T-360 GSN seismometer. b and c are the same as a, but for the north–south and east–west components, respectively

Full size image

In the 0.1–1 s period band, we found that the background noise levels were sensitive to location, with the ANMO pit and the Snake pit showing the highest noise levels relative to the reference sensor (Fig. 7). We see that this elevated noise is on all components of both instruments, and the elevated noise levels are relatively time independent. This is in contrast to the 1–30 s period band (Fig. 8d–f) where the background noise levels match that of the reference sensor very closely for all deployments in the study. In the 30–100 s period band, we see that all deployments have similar noise levels to the reference Streckeisen STS-6. This is in contrast to the horizontals where we see that horizontal components show elevated noise levels at many locations with the Snake pit and ANMO pit showing the largest deviation from the reference Streckeisen STS-6.

Fig. 7
figure 7

a Difference in dB between the Nanometrics T-360 GSN and the Streckeisen STS-6 reference sensor (circles) and the Streckeisen STS-2.5 and the Streckeisen STS-6 reference sensor (crosses) in the 0.1–1 s period band by day of year (doy). b and c are the same as a, but for the north–south and the east–west, respectively

Full size image
Fig. 8
figure 8

a Mean vertical power spectral density (PSD) estimates in the 0.1–1 s period band between the reference Streckeisen STS-6 on the horizontal axis and the Nanometrics T-360 GSN (circles) as well as the Streckeisen STS-2.5 (crosses) on the vertical axis for the different deployment locations. b and c are the same as a, but for the north–south and east–west components, respectively. d, e, and f are the same as a, b, and c, but for the 1–30 s period band. g, h, and i are the same as a, b, and c, but for the 30–100 s period band

Full size image

Because elevated noise levels recorded at 0.1–1 s when the sensors are installed in the Snake and ANMO pits are not isolated to the horizontal components, we do not attribute this observation to increased tilts in these environments. However, it is possible that this effect is coming from noise induced by wind exciting unconsolidated material around the instrument. Elevated noise from unconsolidated materials was also observed by Dybing et al. (2018). Dybing et al. (2018) used a method developed by Ziolkowski (1973) to predict elevated noise levels from unconsolidated materials. While the model of Ziolkowki (1973) focused on long-period noise, it is possible that their model could be applied to our 0.1–1 s period band, but the length scale would need to be identified in equation A22 of Ziolkowki (1973). Although cultural noise has been observed to be the dominant noise source at periods less than 1 s, it could be that the competency of the material ultimately limits the lower bound on the noise at the station. That is, during time periods of low cultural noise, we are limited by the geology in which the sensor is emplaced.

Our noise levels in all locations were very stable in the 1–30 s period band (Fig. 8d–f). Because this period band is dominated by marine microseisms, it is expected that over our short wavelength (Fig. 1) that the microseism will be uniform in amplitude. However, when using the 4–8 s period band for orientations at the locations with elevated noise (Snake pit and ANMO pit), we see that the spatial separation is compromising our ability to characterize the relative orientations (Fig. 4).

While we observed similar noise levels in the 1–30 s period band on all components, we only observed similar noise levels on the vertical component at periods from 30 to 100 s. Although it is well known that the horizontal components are sensitive to tilt, we see that the vertical components still provide low-noise data out to periods of 100 s. This suggests that even in relatively high-noise environments, it might be possible to achieve relatively low-noise vertical component long-period data when an instrument with sufficiently low self-noise is used (Fig. 8). Even though there will always be cost and power consumption considerations, this does suggest that using higher quality broadband seismometers in short-term deployments could help to record a larger portion of the seismic band. Whereas all three of the instruments used in this study are capable of recording signals well beyond 100 s period because they are all observatory quality instruments built for long-period observations, our results suggest that instruments with improved noise floors over that of small compact sensors could help to improve the bandwidth even when modest installation techniques are used.

4 Conclusion

We deployed two sensors at five different locations across the ASL. Although orientations were relatively good (e.g., less than a degree), there were cases of outliers due to human error. This suggests that to further improve orientations, we should examine incorporating mechanical jigs into sensor emplacement methodologies as well as the verification from multiple people installing the instrumentation to avoid such human error. We found that sensitivities are extremely tightly constrained and repeatable to within 1%. This suggests that upon identifying the sensitivity of the instrument over short time periods, the sensitivity is extremely stable. While previous work (Ringler et al., 2015) has identified cases of sensitivity errors, it is likely these errors come from long-term drift and not anything internal to the instrument when the instrument is operating correctly. We have also shown that local emplacement in different geology can easily produce changes in noise levels at periods less than 1 s. This warrants further investigation on noise levels as a function of surrounding material. It is unclear to what the spatial scale of the variable noise levels is constrained. We also found that vertical noise levels in the 30–100 s period band were largely insensitive to the local installation. This suggests that although horizontal noise levels can be easily improved by isolating the sensor in a deep vault, there is likely little noise improvement to be gained on the vertical component by further sensor isolation (over the period band in this study). Of course, at periods greater than 100 s, it has been shown that further sensor isolation can result in improved noise levels (Ringler et al., 2020).