Skip to main content
SpringerLink
Log in

Topological Modularity of Monstrous Moonshine

  • Published:
Annales Henri Poincaré Aims and scope Submit manuscript

Abstract

We explore connections among Monstrous Moonshine, orbifolds, the Kitaev chain and topological modular forms. Symmetric orbifolds of the Monster CFT, together with further orbifolds by subgroups of Monster, are studied and found to satisfy the divisibility property, which was recently used to rule out extremal holomorphic conformal field theories. For orbifolds by cyclic subgroups of Monster, we arrive at divisibility properties involving the full McKay–Thompson series. Orbifolds by non-abelian subgroups of Monster are further considered by utilizing the data of Generalized Moonshine.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Notes

  1. Holomorphic CFTs are tautologically (0,1) SQFTs with a trivial supersymmetric sector.

  2. In the absence of a global gravitational anomaly, the \(\text {S}_n\) permutation symmetry is non-anomalous [23].

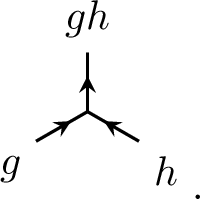
  3. An invertible field theory as introduced by Freed [38] is a topological quantum field theory with a unique vacuum. The characterization of the Arf invariant as a mod 2 index was given by Atiyah [39].

  4. The twisted denominator formula [30, 31] without inversion also figured in the work by Carnahan [40].

  5. In terms of topological defect lines, the h defect runs upwards in the time direction, the g defect runs toward the right in the space direction, and the group multiplication at a vertex reads

  6. While many conventions exist in the literature, e.g., Dijkgraaf, Vafa, Verlinde, Verlinde [44, (4.18)] or Dong and Mason [45, (1.4)], we choose to follow Tuite [43, (14)] closely since his paper contains many useful formulae for our computations.

  7. In terms of topological defect lines, we nucleate a loop of \(x \in G\) on the torus and perform the obvious moves to turn \(Z_h^g\) into \(Z_{xhx^{-1}}^{xgx^{-1}}\).

  8. Since group elements are labeled by integers in this subsection, to avoid confusion with the rth power of Z, we write \(Z^r_0\) instead of \(Z^r\) to denote the partition function with a temporal twist and no spatial twist.

  9. A sufficient condition for this property is if the outer automorphism group \(\text {Aut}(\mathbb {Z}_N\)) is a symmetry. Note that the CPT symmetry implies \(Z[\mathcal {T}]^r_0 = Z[\mathcal {T}]^{N-r}_0\). The author thanks Yifan Wang for a discussion.

  10. Conjugacy classes related by inversion must share the same McKay–Thompson series, as decreed by the CPT symmetry. All coincidences of the McKay–Thompson series can be explained this way, except for 27AB. The author thanks Yifan Wang for a discussion.

  11. See [50, 51] for a physics derivation of Monstrous Moonshine. The most nontrivial aspect of the Monstrous Moonshine [32] is that the McKay–Thompson series are Hauptmoduls of genus-zero subgroups of \(\text {PSL}(2,\mathbb {R})\). Since this property plays little role in the present pursuit, we make no further mention.

  12. Johnson-Freyd and Treumann [52] further showed that the \(\mathbb {Z}_{24}\) generated by \({V^\natural }\) is a direct summand of \(\text {H}^3(\mathbb {M},\text {U}(1))\), and \(\text {H}^3(\mathbb {M},\text {U}(1)) \ominus \mathbb {Z}_{24}\) has order dividing 4. The author thanks Theo Johnson-Freyd for explaining these results.

  13. While it is not true that the conjugacy classes \(\text {Cl}(g^r)\) only depend on \(\gcd (N,r)\) for every Monster group element g, it is true up to inversion. For instance, \(g\in \text {23A}\) and \(g^2\in \text {23B}\), despite \(\gcd (23,1) = \gcd (23,2) = 1\); however, because \(g^{-1}\in \text {23B}\), the conjugacy classes 23AB are related by inversion, and must share the same McKay–Thompson series by the CPT symmetry. The author thanks Yifan Wang for a discussion.

  14. It is important to series expand first in p and then in q.

  15. For a single copy \(n=1\), it is well-known that \({V^\natural }/{\langle {p\text {B}} \rangle }\) with \(p=2,3,5,7,13\) gives the Leech lattice CFT, with 24 spin-one conserved currents coming from the twisted sector; by contrast, (3.14) gives none.

  16. The (possible) class fusions for these subgroups were given in [54]. \(L_2(71)\) was proven to be a subgroup of \(\mathbb {M}\) by [55].

  17. For \(G = L_2(29), ~ \textrm{A}_5, ~ L_2(71)\), when computing the twisted sector of an order-2 element h, Gaiotto and Yin [33] only performed the partial projection by the cyclic subgroups \({\langle {h} \rangle } \cong \mathbb {Z}_{14}, ~ \mathbb {Z}_2, ~ \mathbb {Z}_{36}\) of the full centralizers \(\text {D}_{28}, ~ \mathbb {Z}_2 \times \mathbb {Z}_2, ~ \text {D}_{72}\), and obtained \(Z[{V^\natural }^{\otimes 2}/\text {S}_2 \times G]_{q^0} = 222, 3816, 112\), respectively. Using Norton’s Generalized Moonshine [34] data, we are able to uniquely determine the correct answers for \(L_2(29)\) and \(L_2(71)\), but not for \(\textrm{A}_5\) due to the author’s lack of knowledge of the class fusion(s) for \(\textrm{A}_5 < \text {C}_\mathbb {M}(h)\).

  18. The author thanks Scott Carnahan for correspondence and for sharing Norton’s data.

  19. See [7, 13, 59] for studies of the Conway CFT [58] in the context of TMF.

  20. The author thanks Theo Johnson-Freyd for a discussion.

  21. The series divisibility of pJ with base 24 instead of 12 can be explained by considering symmetric orbifolds of the TMF class \(j \Delta ^{-1}\), instead of \(j \Delta ^{-2}\) that is realized by Monster. This comment is due to Theo Johnson-Freyd.

References

  1. Witten, E.: Constraints on supersymmetry breaking. Nucl. Phys. B 202, 253 (1982)

    Article  ADS  MathSciNet  Google Scholar 

  2. Witten, E.: Elliptic genera and quantum field theory. Commun. Math. Phys. 109, 525 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  3. Douglas, C., Francis, J., Henriques, A., Hill, M.: Topological Modular Forms. Mathematical Surveys and Monographs, American Mathematical Society, Providence (2014)

    Book  Google Scholar 

  4. Segal, G.: What is an Elliptic Object?. London Mathematical Society Lecture Note Series, pp. 306–317. Cambridge University Press (2007)

  5. Stolz, S., Teichner, P.: What is an elliptic object?. London Mathematical Society Lecture Note Series, pp. 247–343. Cambridge University Press (2004)

  6. Stolz, S., Teichner, P.: Supersymmetric field theories and generalized cohomology. Mathematical foundations of quantum field theory and perturbative string theory 83, 279–340 (2011). arXiv:1108.0189

  7. Gaiotto, D., Johnson-Freyd, T.: Holomorphic SCFTs with small index. Can. J. Math. 74(2), 573–601 (2022). arXiv:1811.00589

    Article  MathSciNet  Google Scholar 

  8. Gukov, S., Pei, D., Putrov, P., Vafa, C.: 4-manifolds and topological modular forms. JHEP 05, 084 (2021). arXiv:1811.07884

  9. Gaiotto, D., Johnson-Freyd, T., Witten, E.: A Note on Some Minimally Supersymmetric Models in Two Dimensions (2019). arXiv:1902.10249

  10. Gaiotto and, D., Johnson-Freyd, T.: Mock Modularity and a Secondary Elliptic Genus (2019). arXiv:1904.05788

  11. Tachikawa, Y.: Topological modular forms and the absence of a heterotic global anomaly. PTEP 2022(4), 04A107 (2022). arXiv:2103.12211

  12. Tachikawa, Y., Yamashita, M.: Topological Modular Forms and the Absence of all Heterotic Global Anomalies (2021). arXiv:2108.13542

  13. Johnson-Freyd, T.: TMF and SQFT: questions and conjectures. Talk at ICTP conference. Generalized Cohomology and Physics (2021). https://indico.ictp.it/event/9639/other-view?view=ictptimetable

  14. Lin, Y.-H., Pei, D.: Holomorphic CFTs and Topological Modular Forms (2023). arXiv:2112.10724

  15. Höhn, G.: Selbstduale Vertexoperatorsuperalgebren und das Babymonster (Self-dual Vertex Operator Super Algebras and the Baby Monster) (1996). arXiv:0706.0236

  16. Höhn, G.: Conformal designs based on vertex operator algebras. Adv. Math. 217(5), 2301–2335 (2008). ([math/0701626])

    Article  MathSciNet  Google Scholar 

  17. Frenkel, I.B., Lepowsky, J., Meurman, A.: A natural representation of the Fischer-Griess Monster with the modular function J as character. Proc. Natl. Acad. Sci. 81(10), 3256–3260 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  18. Frenkel, I., Lepowsky, J., Meurman, A.: Vertex operator algebras and the monster. Pure Appl. Math. 134, 1 (1988)

    MathSciNet  Google Scholar 

  19. Witten, E.: Three-dimensional gravity revisited. arXiv:0706.3359

  20. Borcherds, R.E.: Automorphic forms on \(O_{s+2,2}(R)\) and infinite products. Inventiones mathematicae 120(1), 161–213 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  21. Dixon, L.J., Harvey, J.A., Vafa, C., Witten, E.: Strings on Orbifolds. Nucl. Phys. B 261, 678–686 (1985)

    Article  ADS  MathSciNet  Google Scholar 

  22. Dixon, L.J., Harvey, J.A., Vafa, C., Witten, E.: Strings on orbifolds. 2. Nucl. Phys. B 274, 285–314 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  23. Johnson-Freyd, T.: The moonshine anomaly. Commun. Math. Phys. 365(3), 943–970 (2019). [arXiv:1707.08388]

    Article  ADS  MathSciNet  Google Scholar 

  24. Schellekens, A.N.: Meromorphic \(c = 24\) conformal field theories. Commun. Math. Phys. 153, 159–186 (1993). [hep-th/9205072]

    Article  ADS  MathSciNet  Google Scholar 

  25. van Ekeren, J., Möller, S., Scheithauer, N.R.: Construction and classification of holomorphic vertex operator algebras. J. Reine Angew. Math. 2020(759), 61–99 (2020). [arXiv:1507.08142]

    Article  MathSciNet  Google Scholar 

  26. Möller, S., Scheithauer, N.: Dimension formulae and generalised deep holes of the Leech lattice vertex operator algebra. Ann. Math. 197(1), 221–288 (2023). [arXiv:1910.04947]

    Article  MathSciNet  Google Scholar 

  27. Höhn, G., Möller, S.: Systematic orbifold constructions of Schellekens’ vertex operator algebras from Niemeier lattices. J. Lond. Math. Soci. 106, 3162–3207 (2022). [arXiv:2010.00849]

    Article  MathSciNet  Google Scholar 

  28. van Ekeren, J., Lam, C.H., Möller, S., Shimakura, H.: Schellekens’ list and the very strange formula. Adv. Math. 380, 107567 (2021). [arXiv:2005.12248]

    Article  MathSciNet  Google Scholar 

  29. Dijkgraaf, R., Moore, G.W., Verlinde, E.P., Verlinde, H.L.: Elliptic genera of symmetric products and second quantized strings. Commun. Math. Phys. 185, 197–209 (1997). [hep-th/9608096]

    Article  ADS  MathSciNet  Google Scholar 

  30. Norton, S.P.: More on Moonshine. Computational Group Theory (1984)

  31. Borcherds, R.E.: Monstrous moonshine and monstrous lie superalgebras. Invent. Math. 109, 405–444 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  32. Conway, J.H., Norton, S.P.: Monstrous Moonshine. Bull. Lond. Math. Soc. 11(3), 308–339 (1979)

    Article  MathSciNet  Google Scholar 

  33. Gaiotto, D., Yin, X.: Near-Extremal CFTs From Orbifolds [Unpublished]. (2007)

  34. Norton, S.P.: Generalized moonshine. Proc. Symp. Pure Math 47, 208–209 (1987)

    Google Scholar 

  35. Dijkgraaf, R.: Discrete Torsion and Symmetric Products (1999). arXiv:hep-th/9912101

  36. Albert, J., Kaidi, J., Lin, Y.-H.: Topological Modularity of Supermoonshine (2022). arXiv:2210.14923

  37. Kitaev, A.Y.: Unpaired Majorana fermions in quantum wires. Phys. Usp. 44(10S), 131–136 (2001). [arXiv:cond-mat/0010440]

    Article  ADS  Google Scholar 

  38. Freed, D.S.: Short-range Entanglement and Invertible Field Theories (2014). arXiv:1406.7278

  39. Atiyah, M.F.: Riemann surfaces and spin structures. Annales scientifiques de l’École Normale Supérieure 4, 47–62 (1971)

    Article  MathSciNet  Google Scholar 

  40. Carnahan, S.: Generalized moonshine II: Borcherds products. Duke Math. J. 161, 893–950 (2012). [arXiv:0908.4223]

    Article  MathSciNet  Google Scholar 

  41. Abbott, R., Bray, J., Linton, S., Nickerson, S., Norton, S., Parker, R., Suleiman, I., Tripp, J., Walsh, P., Wilson, R.: Atlas of finite group representations-version 3 (2015). http://brauer.maths.qmul.ac.uk/Atlas/v3

  42. Bantay, P.: Characters and modular properties of permutation orbifolds. Phys. Lett. B 419, 175–178 (1998). [arXiv:hep-th/9708120]

    Article  ADS  MathSciNet  Google Scholar 

  43. Tuite, M.P.: Monstrous and Generalized Moonshine and Permutation Orbifolds, vol. 11 (2008). arXiv:0811.4525

  44. Dijkgraaf, R., Vafa, C., Verlinde, E.P., Verlinde, H.L.: The operator algebra of orbifold models. Commun. Math. Phys. 123, 485 (1989)

    Article  ADS  MathSciNet  Google Scholar 

  45. Dong, C.Y., Mason, G.: Nonabelian orbifolds and the boson-fermion correspondence. Commun. Math. Phys. 163, 523–559 (1994)

    Article  ADS  MathSciNet  Google Scholar 

  46. Bantay, P.: Symmetric products, permutation orbifolds and discrete torsion. Lett. Math. Phys. 63(3), 209–218 (2003). [arXiv:hep-th/0004025]

    Article  MathSciNet  Google Scholar 

  47. Baker, A.: Hecke operators as operations in elliptic cohomology. J. Pure Appl. Algebra 63(1), 1–11 (1990)

    Article  MathSciNet  Google Scholar 

  48. Ganter, N.: Hecke operators in equivariant elliptic cohomology and generalized moonshine. Groups Symmet. 47, 173–209 (2009). [arXiv:0706.2898]

    Article  MathSciNet  Google Scholar 

  49. Carnahan, S.: Generalized moonshine I: genus-zero functions. Algebra Number Theory 4(6), 649–679 (2010). [arXiv:0812.3440]

    Article  MathSciNet  Google Scholar 

  50. Paquette, N.M., Persson, D., Volpato, R.: Monstrous BPS-Algebras and the Superstring Origin of Moonshine. Commun. Num. Theor. Phys. 10(1), 433–526 (2016). [arXiv:1601.05412]

    Article  MathSciNet  Google Scholar 

  51. Paquette, N.M., Persson, D., Volpato, R., Algebras, B.P.S.: Genus zero, and the heterotic monster. J. Phys. A 50(41), 414001 (2017). [arXiv:1701.05169]

    Article  MathSciNet  Google Scholar 

  52. Johnson-Freyd, T., Treumann, D., et al.: Third homology of some sporadic finite groups, SIGMA. Symmetry, Integrability and Geometry: Methods and Applications 15, 059 (2019). arXiv:1810.00463

  53. Lin, Y.-H., Shao, S.-H.: \(\mathbb{Z} _N\) symmetries, anomalies, and the modular bootstrap. Phys. Rev. D 103(12), 125001 (2021). [arXiv:2101.08343]

    Article  ADS  Google Scholar 

  54. Norton, S.P., Wilson, R.A.: Anatomy of the Monster: II. Proc. Lond. Math. Soc. 84(3), 581–598 (2002)

    Article  MathSciNet  Google Scholar 

  55. Holmes, P.E., Wilson, R.A.: On subgroups of the Monster containing \(A_5\)’s. J. Algebra 319(7), 2653–2667 (2008)

    Article  MathSciNet  Google Scholar 

  56. Carnahan, S: Generalized Moonshine IV: Monstrous Lie algebras. arXiv:1208.6254

  57. The GAP Group: GAP—Groups, Algorithms, and Programming, Version 4.11.1 (2021)

  58. Duncan, J.F.: Super-moonshine for Conway’s largest sporadic group. Duke Math. J. 139(2), 255–315 (2007). ([math/0502267])

    Article  MathSciNet  Google Scholar 

  59. Johnson-Freyd, T.: Topological Mathieu Moonshine (2020). arXiv:2006.02922

  60. Duncan, J.F., Mack-Crane, S.: The moonshine module for Conway’s group. In: Forum of Mathematics, Sigma, vol. 3. Cambridge University Press (2015). arXiv:1409.3829

  61. Ganter, N.: Orbifold genera, product formulas and power operations. Adv. Math. 205(1), 84–133 (2006). [arXiv:math/0407021]

    Article  MathSciNet  Google Scholar 

  62. Barthel, T., Berwick-Evans, D., Stapleton, N.: Power operations in the Stolz–Teichner program. Geom. Topol. 26(4), 1773–1848 (2022). [arXiv:2006.09943]

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author thanks Jan Albert, Scott Carnahan, Chi-Ming Chang, Theo Johnson-Freyd, Justin Kaidi and Yifan Wang for discussions and comments on the draft.

Funding

This work was supported by the Simons Collaboration Grant on the Non-Perturbative Bootstrap.

Author information

Authors and Affiliations

  1. Jefferson Physical Laboratory, Harvard University, Cambridge, MA, 02138, USA

    Ying-Hsuan Lin

Authors
  1. Ying-Hsuan Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ying-Hsuan Lin.

Ethics declarations

Conflict of interest

The author has no relevant financial or non-financial interests to disclose.

Additional information

Communicated by Katrin Wendland.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, YH. Topological Modularity of Monstrous Moonshine. Ann. Henri Poincaré 25, 2427–2452 (2024). https://doi.org/10.1007/s00023-023-01352-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00023-023-01352-8

Search

Navigation