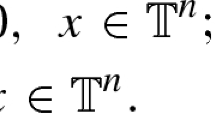Positive Measure of Effective Quasi-Periodic Motion Near a Diophantine Torus

Abstract

It was conjectured by Herman that an analytic Lagrangian Diophantine quasi-periodic torus ${\mathcal {T}}_0$, invariant by a real-analytic Hamiltonian system, is always accumulated by a set of positive Lebesgue measure of other Lagrangian Diophantine quasi-periodic invariant tori. While the conjecture is still open, we will prove the following weaker statement: there exists an open set of positive measure (in fact, the relative measure of the complement is exponentially small) around ${\mathcal {T}}_0$ such that the motion of all initial conditions in this set is “effectively” quasi-periodic in the sense that they are close to being quasi-periodic for an interval of time, which is doubly exponentially long with respect to the inverse of the distance to ${\mathcal {T}}_0$. This open set can be thought of as a neighborhood of a hypothetical invariant set of Lagrangian Diophantine quasi-periodic tori, which may or may not exist.

1 Introduction

We will be considering the dynamics in a neighborhood of an analytic Lagrangian Diophantine quasi-periodic torus ${\mathcal {T}}_0$ (DQP torus for short) invariant by a real-analytic Hamiltonian system. It is well known that without loss of generality, one may consider a real-analytic Hamiltonian $H: \mathbb {T}^d \times U \rightarrow {\mathbb {R}}$, with $\mathbb {T}^d:={\mathbb {R}}^d / {\mathbb {Z}}^d$ and $U\subset {\mathbb {R}}^d$ an open set containing the origin ($d \ge 2$ is an integer), of the form

$$\begin{aligned} H(\theta ,I)= \omega \cdot I + {\mathcal {O}}(|I|^2) \end{aligned}$$

(1.1)

where $\omega \in {\mathbb {R}}^d$ satisfies a Diophantine condition with exponent $\tau \ge d-1$ and constant $\gamma > 0$ (in short, $\omega \in DC(\tau , \gamma ))$: for all $k=(k_1,\dots ,k_d)\in {\mathbb {Z}}^{d}{\setminus } \{0\}$,

$$\begin{aligned} |\omega \cdot k| \ge \gamma |k|^{-\tau }, \quad |k|:=|k_1|+\cdots +|k_d|. \end{aligned}$$

Without loss of generality, we assume $|\omega |=1$. A fundamental object in the study of the dynamics near ${\mathcal {T}}_0= \mathbb {T}^d\times \{0\}$ is the so-called Birkhoff normal form ([2], see also [7] for a more recent treatment). For any $m \in {\mathbb {N}}$, $m \ge 2$, there exists a polynomial $N_m(I)=\omega \cdot I+{\mathcal {O}}(|I|^2)$ of degree m and an analytic symplectic transformation $\Psi _m(\theta , I) = (\theta + {\mathcal {O}}(|I|), I + {\mathcal {O}}(|I|^2))$ such that

$$\begin{aligned} H\circ \Psi _m(\theta , I) = N_{m} (I) + {\mathcal {O}}(|I|^{m+1}). \end{aligned}$$

(1.2)

Moreover, these constructions have a formal limit as $m \rightarrow + \infty$; there exists a formal power series N and a formal symplectic transformation $\Psi$ such that formally

$$\begin{aligned} H\circ \Psi (\theta , I) = N (I). \end{aligned}$$

The formal power series N is unique and is called the Birkhoff normal form (BNF for short, the formal mapping $\Psi$ is also unique upon normalization), and it was proved recently by Krikorian that generically it is divergent ([14], the corresponding statement for the transformation was proved much earlier by Siegel in [23]). Yet the existence of the truncated BNF $N_m$ for any $m \ge 2$ has several consequences.

Without further assumptions, given $r>0$ small enough, choosing an “optimal” order of truncation $m=m(r)$ (Poincaré “summation to the least term”), on a neighborhood of size r around the origin, the remainder in (1.2) ${\mathcal {O}}(|I|^{m+1})$ can be made exponentially small with respect to $(1/r)^a$ where $a=1/(\tau +1)$, leading to the following estimates for all solutions $(\theta (t),I(t))$ with initial conditions $(\theta _0,I_0)$ with $|I_0|<r$: there exist positive constants C and c independent of r and a vector $\omega (I_0) \in {\mathbb {R}}^d$ with ${|\omega (I_0)-\omega | \le Cr}$ such that

$$\begin{aligned} |\theta (t)-\theta _0-t\omega (I_0)| \le Cr, \quad |I(t)-I_0|\le Cr^2 \quad \text {for} \quad |t| \le \exp (cr^{-a}).\nonumber \\ \end{aligned}$$

(1.3)

We refer to the general theorem contained in [11] and references therein for earlier results (the elementary fact that one can also control the evolution of the angles was pointed out in [19]). Those estimates (1.3) can be understood as an effective stability of the quasi-periodic motion for an exponentially long interval of time. In general, those estimates cannot be improved: it follows from a recent construction of an unstable DQP torus in [9] that the action variables cannot be stable for a longer interval of time, but stronger results can be obtained if one imposes non-degeneracy conditions on the BNF.

First, the application of Nekhoroshev theory ([17, 18]) yields the stability of the action variables for a doubly exponentially long interval of time for all solutions with $|I_0|<r$ and r small enough:

$$\begin{aligned} |I(t)-I_0|\le Cr^2 \quad \text {for} \quad |t| \le \exp \exp (cr^{-a}). \end{aligned}$$

(1.4)

This was first proved by Morbidelli and Giorgilli in [15]) under a convexity assumption on N (that is, the quadratic part of $N_2$ is positive definite) and later in [3] under a generic “steepness” assumption on N (more precisely, it applies provided $N_{{\bar{m}}}$, where ${\bar{m}}$ depends only on d, avoids a semi-algebraic subset of positive codimension). Observe that in (1.4) only the time-scale of stability of the action variables is improved with respect to (1.3).

Applying classical KAM theory ([1, 13, 16])), provided the quadratic part of $N_2$ is non-degenerate (this is Kolmogorov non-degeneracy), for $r>0$ small enough there exists a set of DQP tori ${\mathcal {K}}_r$ in $\mathbb {T}^d \times \{|I|<r\}$ with positive Lebesgue measure. In fact, the relative measure of the complement of ${\mathcal {K}}_r$ is bounded by $\exp (-cr^{-a})$. KAM theory extends to more general non-degeneracy assumptions (see [22] for instance), and thus, the statement on the existence of positive measure of DQP tori remains true, provided that for some $m \ge 2$, the truncated BNF $N_m$ has the property that the local image of its gradient $\nabla N_m$ is not contained in any hyperplane of ${\mathbb {R}}^d$ (see [8] and also Theorem C for a more precise statement). Observe that when KAM theory applies, one can easily find an open set ${\mathcal {U}}_r$ in $\mathbb {T}^d \times \{|I|<r\}$ “centered around” ${\mathcal {K}}_r$ such that for solutions with initial condition $(\theta _0,I_0) \in {\mathcal {U}}$, the effective stability of the quasi-periodic motion for an exponentially long interval of time given by (1.3) is improved to a doubly exponentially long interval of time:

$$\begin{aligned} |\theta (t)-\theta _0-t\omega (I_0)| \le Cr, \quad |I(t)-I_0|\le Cr^2 \quad \text {for} \quad |t| \le \exp \exp (cr^{-a}).\nonumber \\ \end{aligned}$$

(1.5)

In [10], Herman conjectured that the conclusions of the application of KAM theory hold true without any non-degeneracy assumptions: more precisely, for H as in (1.1) with $\omega$ Diophantine, he asked whether there always exists, for $r>0$ small enough, a set of DQP tori ${\mathcal {K}}_r$ in $\mathbb {T}^d \times \{|I|<r\}$ with positive Lebesgue measure. In the case $d=2$ this follows from general results of Rüssmann ([21]) and Bruno ([5]) (the arithmetic condition on $\omega$ can be slightly weakened), but for $d\ge 3$ this is an open problem; the only general result is due to Eliasson, Fayad and Krikorian ([8]) who proved that ${\mathcal {T}}_0$ is always accumulated by other DQP tori but along an analytic submanifold, so with zero Lebesgue measure in general.

The aim of this paper is to prove that the following formal consequence of Herman’s conjecture holds true; for $r>0$ small enough, there exists an open set ${\mathcal {U}}_r$ in $\mathbb {T}^d \times \{|I|<r\}$, the complement of which has a relative measure bounded by $\exp (-cr^{-a})$, such that for solutions with the initial condition $(\theta _0,I_0) \in {\mathcal {U}}_r$, one has effective stability of the quasi-periodic motion for a doubly exponentially long interval as expressed in (1.5). This is the content of Theorem A. Of course, whether this set ${\mathcal {U}}_r$ actually contains a set of positive measure ${\mathcal {K}}_r$ of DQP tori is still an open question.

2 Main Results

To state precisely our main results, let us introduce some notations. Given $\rho >0$ and $r>0$, we consider complex domains

$$\begin{aligned} \mathbb {T}^d_{\rho }:=\left\{ \theta \in {\mathbb {C}}^d / {\mathbb {Z}}^d \; | \; |\mathop {\text{ Im }}\theta |< \rho \right\} , \quad {\mathcal {B}}_r:=\{ I\in {\mathbb {C}}^d \; | \; |I|< r \} \end{aligned}$$

with $\mathop {\text{ Im }}\theta :=(\mathop {\text{ Im }}\theta _1, \dots , \mathop {\text{ Im }}\theta _d)$, and we let $B_r:=\{ I\in {\mathbb {R}}^d \; | \; |I|< r \}={\mathcal {B}}_r \cap {\mathbb {R}}^d$. We denote by ${\mathcal {A}}_{\rho ,r}$ the Banach space of holomorphic bounded functions $f: \mathbb {T}^{d}_{\rho } \times {\mathcal {B}}_{r} \rightarrow {\mathbb {C}}$, which are real-valued for real arguments, equipped with the norm:

$$\begin{aligned} |f|_{\rho , r}:=\sup _{z\in \mathbb {T}^{d}_{\rho } \times {\mathcal {B}}_{r} }|f(z)|. \end{aligned}$$

Here’s our main result.

Theorem A

Assume $H \in {\mathcal {A}}_{\rho ,r_0}$ is as in (1.1) with $\rho >0$, $r_0>0$, and $\omega \in DC(\tau , \gamma )$. Then, there exist positive constants $r^*$, c and C which depend only on d, $\gamma$, $\tau$, $\rho$, $r_0$, $|H|_{\rho , r_0}$ and the BNF N such that for all $0<r<r^*$, there is an open set ${\mathcal {U}}_r \subseteq \mathbb {T}^d \times B_r$ with the measure estimate

$$\begin{aligned} \textrm{Leb}(\mathbb {T}^d \times B_r \setminus {\mathcal {U}}_r) < \textrm{Leb}(\mathbb {T}^d \times B_r)\exp (-c r^{-a}) \end{aligned}$$

(2.1)

and such that for any $(\theta _0, I_0)\in {\mathcal {U}}_r$, there exists $\omega (I_0)\in {\mathbb {R}}^d$ and the corresponding solution $(\theta (t), I(t))$ satisfies

$$\begin{aligned} |\theta (t)-\theta _0-t\omega (I_0)| \le Cr, \quad |I(t)-I_0|\le Cr^2 \quad \text {for} \quad |t| \le \exp \exp (cr^{-a}).\nonumber \\ \end{aligned}$$

(2.2)

Even though we did not state it, it will be clear from the proof that not only the vectors $\omega (I_0)$ are at a distance Cr from $\omega \in DC(\tau , \gamma )$ but also they are at an exponentially small distance $\exp (-cr^{-a})$ from a subset of vectors in $DC(\bar{\tau }, {\bar{\gamma }})$ for a proper choice of ${\bar{\tau }}>\tau$ and ${\bar{\gamma }}<\gamma$. To explain the dependence of the constants on the BNF and the strategy of the proof, recall that given $m \ge 2$, $N_m$ is the truncated BNF up to order m, and we extend this notation to $m=1$ by setting $N_1(I)=\omega \cdot I$. Now let $F_m=\nabla N_m$ be the gradient of $N_m$ for $m \ge 1$, which is a polynomial map of degree $m-1$ and define $V_m$ to be the vector space spanned by the partial derivatives of $F_m$ evaluated at the origin:

$$\begin{aligned} V_m:= \textrm{Vect}\{\partial _I^{\alpha } F_m(0), \; \alpha \in {\mathbb {N}}^d\}=\textrm{Vect}\{\partial _I^{\alpha } F_m(0), \; |\alpha | \le m-1\}. \end{aligned}$$

(2.3)

These vector spaces form a non-decreasing sequence, $V_m \subseteq V_{m+1}$ for $m \ge 1$, and they are contained in ${\mathbb {R}}^d$: consequently, this sequence is stationary, and we can define $m^*\ge 1$ to be the smallest integer such that $V_m=V_{m^*}:=V$, for all $m\ge m^*$. Obviously, the polynomial map $F_{m^*}: {\mathbb {R}}^d \rightarrow V$ is non-degenerate in the sense that its partial derivatives generate V, and the dependence of the constants on the BNF in Theorem A will only depend on $N_{m^*}$. To simplify the notations and statements in the sequel, we shall call “constants” any positive constant, which depends only on d, $\gamma$, $\tau$, $\rho$, $r_0$, $|H|_{\rho , r_0}$ and the truncated BNF $N_{m^*}$; in particular, a statement valid for $r>0$ small enough means that there exists a constant $r^*$ for which the statement is valid for all $0<r < r^*$. As we shall see, the main difficulty in proving Theorem A is when the dimension l of V satisfies $2 \le l \le d-1$ (which only occurs when $d \ge 3$) and the proof will consist in the following steps:

• (1) First, for $r>0$ small enough, we apply a BNF normalization up to optimal order $m=m(r)$

  $$\begin{aligned} H\circ \Psi _m(\theta , I) = N_{m} (I) + P_m(\theta ,I) \end{aligned}$$

  where the size of the remainder $P_m(\theta ,I)={\mathcal {O}}(|I|^{m+1})$ is bounded by $\mu =\exp (-c r^{-a})$. We shall deduce this from a general statement taken from [11], and this is the content of Theorem 1 in Sect. 3.

• (2) For any $r>0$ small enough, we have $m(r)\ge m^*$ and the polynomial mapping $F_{m(r)}=\nabla N_{m(r)}: {\mathbb {R}}^d \rightarrow V_{m(r)}=V$ is non-degenerate and close to $F_{m^*}$; using this and the fact that $V \cap DC(\tau ,\gamma )$ is non-empty (as it contains $\omega$), we will show that for some sufficiently large ${\bar{\tau }}>\tau$ and sufficiently small ${\bar{\gamma }}<\gamma$, the set $S_r$ of points $I_0 \in B_r$ for which $F_{m(r)}(I_0) \in DC({\bar{\tau }},{\bar{\gamma }})$ has positive measure (more precisely, we will show that the complement of this set has a measure bounded by a constant times a power of ${\bar{\gamma }}$). This will be stated in Proposition 1 in Sect. 4.

• (3) Consider the Hamiltonian ${\bar{H}}_r=H \circ \Psi _{m}$ with $m=m(r)$ given by the first step, restricted to the $\mu ^{1/2}$-neighborhood of the set $\mathbb {T}^d \times S_r$ given by the second step with the value ${\bar{\gamma }}=\mu ^{1/4}$. On this domain, ${\bar{H}}_r$ can be considered as a $\mu$-perturbation of an integrable Hamiltonian with frequencies in $DC({\bar{\tau }},{\bar{\gamma }})$ and by classical results on integrable normal form up to an exponentially small remainder (similar but slightly more general than Birkhoff normalization); there exists a transformation $\Phi$ such that ${\bar{H}}_r \circ \Phi$ is integrable up to a remainder, which is exponentially small in $(1/\mu )^{{\bar{a}}}$ for some ${\bar{a}}>0$. This will be the content of Theorem 2 in Sect. 5, which follows from a statement taken from [20].

• (4) The last step is a mere conclusion: ${\bar{H}}_r \circ \Phi =H \circ \Psi _{m} \circ \Phi$ is integrable up to an exponentially small remainder in $(1/\mu )^{\bar{a}}$ and thus doubly exponentially small in $(1/r)^{a}$. This will give stability estimates first for ${\bar{H}}_r \circ \Phi$, and then for H, for a time-scale which is doubly exponentially large in $(1/r)^{a}$. By the second step, the measure estimate of the solutions not covered by these stability estimates is a power of ${\bar{\gamma }}=\mu ^{1/4}$, and consequently, it is exponentially small in $(1/r)^{a}$. The corresponding details will be given in Sect. 6.

It remains to discuss the cases where the dimension l of V satisfies $l=1$ or $l=d$. In the first case, we do have $V={\mathbb {R}}\omega$ and the second step we described above is valid on a whole neighborhood of the origin and not only on a proper subset, and so are the estimates (2.2).

Theorem B

Assume $H \in {\mathcal {A}}_{\rho ,r_0}$ is as in (1.1) with $\omega \in DC(\tau , \gamma )$, and $V={\mathbb {R}}\omega$. Then, there exist positive constants c and C such that for r small enough, for any $(\theta _0, I_0)\in \mathbb {T}^d \times B_{r}$, there exists $\omega (I_0)\in {\mathbb {R}}^d$ and the corresponding solution $(\theta (t), I(t))$ satisfies

$$\begin{aligned} |\theta (t)-\theta _0-t\omega (I_0)| \le Cr, \quad |I(t)-I_0|\le Cr^2 \quad \text {for} \quad |t| \le \exp \exp (cr^{-a}). \end{aligned}$$

This result is in fact not surprising because it follows from a result proved independently by Rüssmann ([21]) and Bruno ([5]) that in this case, the transformation to the BNF actually converges and so H must be analytically conjugated to its linear part.

Now in the case $l=d$, we do have $V={\mathbb {R}}^d$; the BNF is actually non-degenerate and using only the first step of the scheme of the proof described above together with an abstract result of Rüssmann ([22]) we can be sure that the open set ${\mathcal {U}}_r$ in Theorem A actually contains a set ${\mathcal {K}}_r$ of DQP tori.

Theorem C

Assume $H \in {\mathcal {A}}_{\rho ,r_0}$ is as in (1.1) with $\omega \in DC(\tau , \gamma )$, and $V={\mathbb {R}}^d$. Then, there exists a constant $c>0$ such that for r small enough, there is a set ${\mathcal {K}}_r \subseteq \mathbb {T}^d \times B_{r}$ of DQP tori with the measure estimate

$$\begin{aligned} \textrm{Leb}(\mathbb {T}^d \times B_r \setminus {\mathcal {K}}_r) < \textrm{Leb}(\mathbb {T}^d \times B_r)\exp (-c r^{-a}). \end{aligned}$$

(2.4)

Again, this result is not new since the existence of a set of DQP tori with Lebesgue density one has been already proved in this context in [8]; yet, the extra information contained in Theorem C is the exponentially small measure (2.4), which shows that the abundance of tori is the same for Kolmogorov non-degenerate or Rüssmann non-degenerate BNF.

To conclude, let us point out that we have decided to focus on the dynamics near a DQP torus, but we expect our main result in Theorem A to be valid near a Diophantine elliptic fixed point (see [4] for results on double exponential stability near elliptic fixed points) with few modifications; indeed, the result we use in the first step is also known in this case (and follows again from [11]) and after performing such a transformation, upon removing a subset with exponentially small measure in phase space, one can use “non-singular” analytic action-angles coordinates and the rest of the proof follows exactly in the same way. Alternatively, one could only use elliptic coordinates but statements such as Proposition 2 and Theorem 2 would have to be re-proven in this setting. However, our proof does not extend to non-analytic Gevrey classes, and we do not know if our main result holds true in this context; this may be related to the fact that Herman’s conjecture is known to be false in these classes (see [8]).

3 BNF with Exponentially Small Remainder

We first recall the existence of a truncated BNF up to an exponentially small remainder. From now on, we denote by $\Pi _\theta$ (resp. $\Pi _I$) the projection onto angle components (resp. action components).

Theorem 1

Assume $H \in {\mathcal {A}}_{\rho ,r_0}$ is as in (1.1) with $\omega \in DC(\tau , \gamma )$. Then, there exist positive constants c and C such that for r small enough, there exists an analytic symplectic embedding $\Psi _r: \mathbb {T}^{d}_{\rho /2} \times {\mathcal {B}}_{3r} \longrightarrow \mathbb {T}^{d}_{\rho } \times {\mathcal {B}}_{4r}$ with the estimates

$$\begin{aligned} |\Pi _\theta \Psi _r-\textrm{Id}|_{\rho /2, 3r } \le Cr, \quad |\Pi _I \Psi _r-\textrm{Id}|_{\rho /2, 3r } \le Cr^2 \end{aligned}$$

(3.1)

such that

$$\begin{aligned} H \circ \Psi _{r}(\theta , I)= N_{m(r)}(I)+ P_{r}(\theta , I) \end{aligned}$$

for $m(r):=[c r^{-a}]$ with the estimates

$$\begin{aligned} |P_r|_{\rho /2, 3r} \le \exp (-cr^{-a}) \end{aligned}$$

(3.2)

and

$$\begin{aligned} |N_{m(r)}-N_m|_{3r} \le Cr^{m+1}, \quad 1 \le m \le m^*+1, \end{aligned}$$

(3.3)

where $m^*= \min \{m\in {\mathbb {N}}\; |\; V_{m}=V\}$.

This result follows from the general statement of Theorem 3.8 in [11], up to slight changes in the notation (for instance, we use $r=R^2$ and we can discard elliptic variables) and in the numerical constants involved, and with the following modifications that we now describe, which follow directly from the proof of Theorem 3.8 in [11]. In the following, we refer to the notation used in [11] to explain the differences in Theorem 1 with respect to Theorem 3.8 in [11].

First, in that reference, they have $N_r \ne N_{m(r)}$ but one can check that

$$\begin{aligned} N_r(I)=N_{m(r)}(I)+{\mathcal {O}}(|I|^{m(r)+1}), \end{aligned}$$

that is the difference between $N_r$ and $N_{m(r)}$ is flat up to order m(r); however, using this, an expansion of $N_r-N_{m(r)}$ into Taylor series (by analyticity) and Cauchy inequalities, one easily finds that $N_r-N_{m(r)}$ satisfies an estimate similar to the one for $P_r$ given in (3.2) (assuming $N_r$ is defined and bounded on a slightly larger domain, which can be assumed, and restricting c if necessary) and thus upon replacing $P_r$ by $P_r+N_r-N_{m(r)}$, we can indeed assume $N_r = N_{m(r)}$ without affecting (3.2) and (3.3).

The estimates on the distance to the identity stated in (3.1) are slightly better than those stated in Theorem 3.8 (in that reference, r is used to absorb the large positive constant C), but they clearly follow from the proof (indeed, $\Psi _r$ is obtained as a finite composition of transformations of the form $(\theta , I) \mapsto (\theta + {\mathcal {O}}(|I|), I + {\mathcal {O}}(|I|^2))$).

Finally, the estimate (3.3) is stated only for $m=2$ in [11] but holds true for any given “fixed” integer m such that $1 \le m \le m^*+1$ (clearly here r is small enough so that $2 \le m^*+1 \le m(r)$); indeed, and this is classical, such an estimate is obtained by applying m steps of Birkhoff normalization with “large” losses of widths of analyticity (depending on $r_0$ and $m^*$ but independent of r) and the remaining $m(r)-m$ steps with uniformly “small” losses.

4 Measure on the Set of Diophantine Points

In this section, we consider the integrable Hamiltonian $N_{m(r)}$, defined and analytic on the real domain $B_{3r}$ (so in particular $N_{m(r)}$ is smooth on the closed ball ${\bar{B}}_{2r}$), which is the truncated BNF given by Theorem 1, and we set $F_{m(r)}:=\nabla N_{m(r)}$. We shall restrict ourselves to the case $2 \le l \le d-1$ where l is the dimension of the space V; observe that necessarily $m^* \ge 2$ in this case. Using the fact that $F_{m(r)}$ is analytic (indeed, it is a polynomial map) and $F_{m(r)}(0)=\omega \in DC(\tau ,\gamma )$, we shall prove that the set of points $I \in B_{2r}$, with r small enough, for which $F_{m(r)}(I)$ is Diophantine has a relatively large Lebesgue measure. Such results are well known, see, for instance, [12], but we give a proof adapted to our context following [6].

Proposition 1

Assume that $2 \le l \le d-1$. There exists a constant C such that for r and $\bar{\gamma }$ small enough, if we set ${\bar{\tau }}:=(m^*-1) (d+1)+\tau +1$, then we have

$$\begin{aligned} \textrm{Leb}(\{ I\in B_{2r} \; |\; F_{m(r)}(I)\notin DC({\bar{\tau }}, {\bar{\gamma }})\})\le C {\bar{\gamma }}^{1/(m^*-1)}r^{d-1}. \end{aligned}$$

(4.1)

We first recall that by definition of V, there exist $\alpha _1, \dots , \alpha _l \in {\mathbb {N}}^d$ such that the vectors $\partial _I^{\alpha _1} F_{m^*}(0), \dots , \partial _I^{\alpha _l} F_{m^*}(0)$ are linearly independent, and in view of (2.3), we necessarily have $|\alpha _i| \le m^* -1$. For $F_m=(F_{m,1}, \dots , F_{m,d})$, we set $F_m^l=(F_{m,1}, \dots , F_{m,l})$; without loss of generality, we may assume that the square matrix

$$\begin{aligned} A^{l}_{m^*}(I)= \left( \partial _I^{\alpha _1}F_{m^*}^l(I)^{\top } \; | \ldots | \; \partial _I^{\alpha _l}F_{m^*}^l(I)^{\top } \right) \end{aligned}$$

has a nonzero determinant at $I=0$; hence, there exists a constant $\beta >0$ such that, denoting $S_l= \{\xi \in {\mathbb {R}}^l \; |\; |\xi |=1\}$, we have

$$\begin{aligned} \min _{\xi \in S_l}|\xi \cdot A^{l}_{m^*}(0)| \ge 3\beta . \end{aligned}$$

(4.2)

We have the following elementary lemma, where we consider the matrix

$$\begin{aligned} A^{l}_{r}(I)= \left( \partial _I^{\alpha _1}F_{m(r)}^l(I)^{\top } \; | \ldots | \; \partial _I^{\alpha _l}F_{m(r)}^l(I)^{\top } \right) . \end{aligned}$$

Lemma 1

For r small enough, we have

$$\begin{aligned} \min _{(I,\xi ) \in {\bar{B}}_{2r} \times S_l}|\xi \cdot A^{l}_{r}(I)| \ge \beta \end{aligned}$$

and as a consequence, for any $I \in {\bar{B}}_{2r}$,

$$\begin{aligned} \textrm{Vect}\left\{ \partial _I^{\alpha _1} F^l_{m(r)}(I), \dots , \partial _I^{\alpha _l} F^l_{m(r)}(I)\right\} =\textrm{Vect}\left\{ \partial _I^{\alpha } F^l_{m(r)}(I) \; | \; \alpha \in {\mathbb {N}}^d\right\} =V. \end{aligned}$$

Proof

First, in view of (4.2), for r small enough

$$\begin{aligned} \min _{(I,\xi ) \in {\bar{B}}_{2r} \times S_l}|\xi \cdot A_{m^*}^l(I)| \ge 2\beta . \end{aligned}$$

Then observe that (3.3) with $m=m^*$ implies, for all $I \in {\bar{B}}_{2r}$ and $\alpha \in {\mathbb {N}}^d$ with $|\alpha | \le m^*-1$, that

$$\begin{aligned} |\partial _I^\alpha F_{m(r)}(I)-\partial _I^\alpha F_{m^*}(I)| \le Cr \end{aligned}$$

for some positive constant C and consequently

$$\begin{aligned} \min _{(I,\xi ) \in {\bar{B}}_{2r} \times S_l}|\xi \cdot A_{r}^l(I)| \ge \beta \end{aligned}$$

for r small enough. This proves the first part of the statement. For the second part of the statement, we have the inclusions:

$$\begin{aligned} \textrm{Vect} \left\{ \partial _I^{\alpha _1} F_{m(r)}(I), \dots , \partial _I^{\alpha _l} F_{m(r)}(I)\} \subseteq \textrm{Vect}\{\partial _I^{\alpha } F_{m(r)}(I) \; | \; \alpha \in {\mathbb {N}}^d\right\} \subseteq V. \end{aligned}$$

Indeed, the first one is obvious, while the second one follows from the fact that $F_{m(r)}$ is analytic at $I=0$ together with the fact $V_{m(r)}=V$ since we are assuming r small enough. We have just shown that the vectors $\partial _I^{\alpha _1} F_{m(r)}(I), \dots , \partial _I^{\alpha _l} F_{m(r)}(I)$ are linearly independent for $I \in {\bar{B}}_{2r}$, and hence, they generate V and the subspaces above are all equal. $\square$

Proposition 1 will follow from the above lemma together with the following Pyartli-type inequality (the precise proposition below follows from Theorem 17.1 in [22]).

Proposition 2

Let $g: {\bar{B}}_{2r} \rightarrow {\mathbb {R}}$ be a function of class $C^{n+1}$ satisfying

$$\begin{aligned} \min _{I\in \bar{B}_{2r}} \max _{0\le j \le n} |D^{j}g(I)|\ge \beta \end{aligned}$$

for some integer $n \ge 1$ and $\beta >0$. Then, there exists $r'>0$ which depends only on d such that for any $0<r<r'$ and any $0< \varepsilon \le \beta (2n+2)^{-1}$, we have

$$\begin{aligned} \textrm{Leb}(\{I\in B_{2r}\; | \; |g(I)| \le \varepsilon \}) \le C |g|_{n+1}\varepsilon ^{1/n}r^{d-1}\ \end{aligned}$$

(4.3)

where $|g|_{n+1}$ is the $C^{n+1}$ norm of g and $C>0$ is a constant depending only on d, n and $\beta$.

Proof of Proposition 1

Recall that we are assuming $2 \le l \le d-1$. For r small enough, Lemma 1 applies and since $\{\partial _I^{\alpha _1} F^l_{m(r)}(I), \dots , \partial _I^{\alpha _l} F^l_{m(r)}(I)\}$ are linearly independent and generate V for all $I \in {\bar{B}}_{2r}$, there exist $b_{i,j}$ for $l+1 \le i \le d$ and $1 \le j \le l$ such that for all $I \in {\bar{B}}_{2r}$,

$$\begin{aligned} F_{m(r),l+1}(I)= \sum _{j=1}^{l}{b_{l+1, j} F_{m(r),j}(I)},\; \ldots , F_{m(r),d}(I)= \sum _{j=1}^{l}{b_{d,j} F_{m(r),j}(I)}.\nonumber \\ \end{aligned}$$

(4.4)

We can also write $\omega =(\omega _1, \ldots , \omega _l, \sum _{j=1}^{l}{b_{l+1, j}\omega _j}, \ldots , \sum _{j=1}^{l}{b_{d,j}\omega _j})$, since $\omega \in V$, and using the fact that $\omega \in DC(\tau , \gamma )$ with $|\omega |=1$, we obtain, for all $k \in {\mathbb {Z}}^d \setminus \{0\}$,

$$\begin{aligned} \sum _{j=1}^{l}\bigg |\sum _{i=l+1}^{d}{(b_{i,j}k_i+k_j)} \bigg | \ge \gamma |k|^{-\tau }. \end{aligned}$$

(4.5)

Now for any $k\in {\mathbb {Z}}^d \setminus \{0\}$, consider the vector $\xi _k:=(\xi _{k,1}, \ldots , \xi _{k,l}) \in S_l$ defined by

$$\begin{aligned} \xi _{k,j}:= \frac{\sum _{i=l+1}^{d}{b_{i,j}k_i+k_j}}{\left( \sum _{j=1}^{l}{|\sum _{i=l+1}^{d}{(b_{i,j}k_i+k_j)}|} \right) }, \quad 1 \le j \le l, \end{aligned}$$

and consider also the map $g_{r,k}: {\bar{B}}_{2r} \rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} g_{r,k}(I)=\xi _k \cdot F_{m(r)}^l(I)= \sum _{j=1}^l {\xi _{k,j} F_{m(r),j} (I)}. \end{aligned}$$

It follows from (4.4) and (4.5) that for all $I \in {\bar{B}}_{2r}$

$$\begin{aligned} |k \cdot F_{m(r)}(I)| \ge \gamma |k|^{-\tau } |g_{r,k}(I)| \end{aligned}$$

and thus, if we define, for all $k \in {\mathbb {Z}}^{d} \setminus \{0\}$ and some $\bar{\gamma }>0$ and ${\bar{\tau }} >0$,

$$\begin{aligned} U_k:=\left\{ I\in B_{2r} \; | \; |k \cdot F_{m(r)}(I)| < {\bar{\gamma }} |k|^{-{\bar{\tau }}} \right\} \end{aligned}$$

and

$$\begin{aligned} V_k:=\left\{ I\in B_{2r} \; |\; |g_{r,k}(I)|<\varepsilon _k:=\bar{\gamma }\gamma ^{-1} |k|^{-{\bar{\tau }}+\tau }\right\} \end{aligned}$$

we have the inclusion $U_k \subseteq V_k$ and consequently

$$\begin{aligned}&\textrm{Leb}(\{ I\in B_{2r} \; |\; F_{m(r)}(I)\notin DC({\overline{\tau }}, {\overline{\gamma }})\})\le \sum _{k \in {\mathbb {Z}}^{d} \setminus \{0\}} \textrm{Leb}(U_k) \nonumber \\&\qquad \le \sum _{k \in {\mathbb {Z}}^{d} \setminus \{0\}} \textrm{Leb}(V_k). \end{aligned}$$

(4.6)

It remains to estimate the Lebesgue measure of $V_k$. Clearly, the function $g_{r,k}$ is of class $C^{m^*}$ with a $C^{m^*}$-norm bounded due to the estimate in (3.3) with $m=m^*$, and from Lemma 1, we have

$$\begin{aligned}&\min _{I\in \bar{B}_{2r}} \max _{0\le j \le m^*-1} |D^{j}g_{r,k}(I)|\ge \min _{I \in \bar{B}_{2r}}\max _{j=1, \ldots , l}|\partial _I^{\alpha _j}g_{r,k}(I)| \\&\qquad \ge \min _{(I,\xi ) \in {\bar{B}}_{2r} \times S_l}|\xi \cdot A^{l}_{r}(I)| \ge \beta . \end{aligned}$$

For r small enough, and choosing ${\bar{\gamma }}$ small enough so that $\varepsilon _k=\bar{\gamma }\gamma ^{-1} |k|^{-{\bar{\tau }}+\tau } \le \beta (2\,m^*)^{-1}$ for all $k \in {\mathbb {Z}}^d {\setminus } \{0\}$, Proposition 2 applies to $g=g_{r,k}$ (and $n=m^*-1 \ge 1$) and yields the estimate

$$\begin{aligned} \textrm{Leb}(V_k) \le C\varepsilon _k^{1/(m^*-1)}r^{d-1}\le C\bar{\gamma }^{1/(m^*-1)} |k|^{(-{\bar{\tau }}+\tau )/(m^*-1)}r^{d-1} \end{aligned}$$

which, together with (4.6), yields the wanted estimate because of our choice of ${\bar{\tau }}=(m^*-1) (d+1)+\tau +1$.

5 Integrable Normal Forms Near a Set of Diophantine Points

In this section, we shall state the fact that a general $\mu$-perturbation of some integrable analytic Hamiltonian is restricted to some neighborhood of Diophantine points, conjugated (symplectically and analytically) to some integrable normal form up to a remainder, which is exponentially small with respect to $1/\mu$. Later on, this will be applied to the Hamiltonian $H \circ \Psi _r$ given by Theorem 1; thus, with $\mu$ exponentially small with respect to 1/r, on the set of Diophantine points given by Proposition 1 for some proper choice of ${\bar{\gamma }}$, eventually leading to a stability result which is doubly exponentially small with respect to 1/r.

To state this result precisely, we consider, for some positive parameters ${\bar{r}}$, ${\bar{\rho }}$, M and $\mu$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{H}(\theta , I)=N(I) + P(\theta , I) \in {\mathcal {A}}_{{\bar{\rho }},{\bar{r}}}, \\ |\nabla ^2 N|_{{\bar{r}}} \le M, \quad |P|_{{\bar{\rho }},{\bar{r}}} \le \mu \end{array}\right. } \end{aligned}$$

(5.1)

and given $0< {\bar{\gamma }}< {\bar{r}}$, ${\bar{\tau }} \ge d-1$, we consider the set

$$\begin{aligned} S=\{ I\in B_{{\bar{r}}-{\bar{\gamma }}} \; |\; \nabla N(I)\in DC({\bar{\tau }}, {\bar{\gamma }})\} \end{aligned}$$

(5.2)

which is assumed to be non-empty: this is the set of $(\bar{\tau },{\bar{\gamma }})$-Diophantine points in $B_{{\bar{r}}}$, which are at a distance ${\bar{\gamma }}$ from the boundary of $B_{{\bar{r}}}$. In the terminology of [20], the set S is completely $\alpha$, K-non-resonant, for any $K \ge 1$ and $\alpha ={\bar{\gamma }} K^{-{\bar{\tau }}}$. Given $\delta >0$, we let

$$\begin{aligned} V_\delta S:=\{I \in {\mathbb {C}}^d \; | \; d(I,S) < \delta \} \end{aligned}$$

be the complex $\delta$-neighborhood of S: we shall have $\delta <{\bar{\gamma }}$ below so that $V_\delta S \cap {\mathbb {R}}^d$ will be indeed included in $B_{{\bar{r}}}$. By a slight abuse of notation, we simply denote by $\Vert \cdot \Vert _{\rho , \delta }$ the uniform norm for functions, which are analytic and bounded on $\mathbb {T}^d_{\rho }\times V_\delta S$. The following statement follows from the normal form lemma of [20].

Theorem 2

Assume $\bar{H}$ is as in (5.1) with $S\ne \emptyset$ as in (5.2). Then, there exist positive constants ${\bar{c}}$ and ${\bar{C}}$, which depend only on d, ${\overline{\tau }}$, ${\overline{\rho }}$ and M such that setting

$$\begin{aligned} \delta :=\mu ^{1/2}, \quad \nu :=\left( \bar{c}^{-1} \bar{\gamma }^{-1} \delta \right) ^{{\bar{a}}}, \quad {\bar{a}}:=1/({\bar{\tau }}+1) \end{aligned}$$

and assuming that

$$\begin{aligned} \nu <1 \end{aligned}$$

(5.3)

there exists a symplectic embedding

$$\begin{aligned} \Phi : \mathbb {T}^d_{{\bar{\rho }}/6} \times V_{\delta /2} S \longrightarrow \mathbb {T}^d_{{\bar{\rho }}} \times V_{\delta }S \end{aligned}$$

with the estimates

$$\begin{aligned} \Vert \Pi _\theta \Phi -\textrm{Id}\Vert _{{\bar{\rho }}/6,\delta /2} \le \nu , \quad \Vert \Pi _I\Phi -\textrm{Id}\Vert _{{\bar{\rho }}/6,\delta /2} \le \nu \delta \end{aligned}$$

(5.4)

such that

$$\begin{aligned} \bar{H} \circ \Phi =N(I) +G(I)+ R(\theta , I) \end{aligned}$$

with the estimates

$$\begin{aligned} \Vert G\Vert _{\delta /2} \le {\overline{C}}\mu , \quad \Vert R\Vert _{\bar{\rho }/6,\delta /2} \le {\overline{C}}\mu \exp (-1/\nu ). \end{aligned}$$

(5.5)

6 Proofs of the Main Results

We are now ready to conclude the proof of Theorem A, as a consequence of Theorem 1, Proposition 1 and Theorem 2.

Proof of Theorem A

It is sufficient to prove the statement when the dimension l of the space V satisfies $2 \le l \le d-1$; the cases $l=1$ and $l=d$ will be consequences of, respectively, Theorem B and Theorem C. We shall assume r small enough finitely many times in the sequel, without explicitly mentioning it, and we shall denote by c and C positive constants, which may vary from line to line. First, Theorem 1 applies and yields a symplectic embedding $\Psi _r: \mathbb {T}^{d}_{\rho /2} \times {\mathcal {B}}_{3r} \longrightarrow \mathbb {T}^{d}_{\rho } \times {\mathcal {B}}_{4r}$ with the estimates (3.1) such that

$$\begin{aligned} H \circ \Psi _{r}(\theta , I)= N_{m(r)}(I)+ P_{r}(\theta , I) \end{aligned}$$

with the estimates (3.2) on $P_r$ and (3.3) on $N_{m(r)}$. We set

$$\begin{aligned}&{\bar{r}}:=2r, \quad {\bar{\rho }}:=\rho /2, \quad \mu :=\exp (-cr^{-a}), \\&{\bar{\gamma }}:=\mu ^{1/4}, \quad {\bar{\tau }}:=(m^*-1) (d+1)+\tau +1. \end{aligned}$$

Observe that any fixed positive power of $\mu$, even multiplied by a large positive constant or a fixed negative power of r, is bounded by $\exp (-cr^{-a})$ for some appropriate constant c, provided r is small enough. Then, Proposition 1 applies and gives the estimate

$$\begin{aligned} \textrm{Leb}(\{ I\in B_{{\bar{r}}}=B_{2r} \; |\; F_{m(r)}(I)\notin DC({\bar{\tau }}, {\bar{\gamma }})\})\le C {\bar{\gamma }}^{1/(m^*-1)}r^{d-1} \end{aligned}$$

and consequently, the set

$$\begin{aligned} S_r=\{ I\in B_{{\bar{r}}- {\bar{\gamma }}} \; |\; \nabla N_{m(r)}(I)=F_{m(r)}(I)\in DC({\bar{\tau }}, {\bar{\gamma }})\} \end{aligned}$$

is non-empty and we have the measure estimate

$$\begin{aligned} \textrm{Leb} (B_{2r} \setminus S_r) \le C \bar{\gamma }^{1/(m^*-1)}r^{d-1}+C{\bar{\gamma }} r^{d-1} \le C\exp (-cr^{-a})r^{d-1}. \end{aligned}$$

(6.1)

Next we want to apply Theorem 2 to

$$\begin{aligned} \bar{H}:=H \circ \Psi _r, \quad N:=N_{m(r)}, \quad P:=P_r \end{aligned}$$

and it follows from (3.3) with $m=2$ that $|\nabla ^2N_{m(r)}|_{{\bar{r}}}$ is indeed bounded by a constant, and so there are positive constants ${\bar{c}}$ and ${\bar{C}}$ such that setting

$$\begin{aligned} \delta =\mu ^{1/2}, \quad \nu =\left( \bar{c}^{-1} \bar{\gamma }^{-1} \delta \right) ^{{\bar{a}}}, \quad {\bar{a}}=1/({\bar{\tau }}+1) \end{aligned}$$

we do have

$$\begin{aligned} \nu =\left( \bar{c}^{-1} \mu ^{1/4}\right) ^{{\bar{a}}} \le \exp (-cr^{-a}) \end{aligned}$$

and since we have the inclusion $\mathbb {T}^{d}_{{\bar{\rho }}} \times V_\delta S_r \subseteq \mathbb {T}^{d}_{\rho /2} \times {\mathcal {B}}_{3r}$ and the condition (5.3) holds true, Theorem 2 applies and yields a symplectic embedding

$$\begin{aligned} \Phi =\Phi _r: \mathbb {T}^d_{{\bar{\rho }}/6} \times V_{\delta /2} S_r \longrightarrow \mathbb {T}^d_{{\bar{\rho }}} \times V_{\delta }S_r \end{aligned}$$

with the estimates (5.4) such that

$$\begin{aligned} {\tilde{H}}_r:=\bar{H} \circ \Phi _r=H \circ \Psi _r \circ \Phi _r=N_{m(r)}(I) +G_r(I)+ R_r(\theta , I) \end{aligned}$$

with the estimates

$$\begin{aligned} \Vert G_r\Vert _{\delta /2} \le {\overline{C}}\mu , \quad \Vert R_r\Vert _{\bar{\rho }/6,\delta /2} \le {\overline{C}}\mu \exp (-1/\nu ). \end{aligned}$$

(6.2)

From now on, we shall only consider real domains and the transformations restricted to these domains. We define

$$\begin{aligned} \tilde{{\mathcal {V}}}_r:=\mathbb {T}^d \times (V_{\delta /4}S_r \cap {\mathbb {R}}^d), \quad {\mathcal {V}}_r:=\Psi _r(\Phi _r(\tilde{{\mathcal {V}}}_r)) \end{aligned}$$

and we shall prove first that the stability estimates hold true for any solution $(\theta (t),I(t))$ of H with the initial condition $(\theta _0,I_0) \in {\mathcal {V}}_r$. To do so, we consider the corresponding solution $({\tilde{\theta }}(t),{\tilde{I}}(t))$ of ${\tilde{H}}_r=H \circ \Psi _r \circ \Phi _r$ with the initial condition $({\tilde{\theta }}_0,{\tilde{I}}_0) \in \tilde{{\mathcal {V}}}_r$, and we define

$$\begin{aligned} \omega (I_0):= \nabla N_{m(r)}({\tilde{I}}_0)+\nabla G_r({\tilde{I}}_0) \in {\mathbb {R}}^d. \end{aligned}$$

Since the transformations are symplectic, $\Psi _r(\Phi _r({\tilde{\theta }}(t),{\tilde{I}}(t)))=(\theta (t),I(t))$ as long as the solutions are defined, and from (3.1) and (5.4), we have

$$\begin{aligned} |{\tilde{I}}(t)-I(t)| \le Cr^2+\delta \nu \le Cr^2, \quad |{\tilde{\theta }}(t)-\theta (t)| \le Cr+\nu \le Cr. \end{aligned}$$

From the estimates (3.3) (again with $m=2$) and (6.2), together with Cauchy inequalities, we have

$$\begin{aligned} |\nabla ^2 N_{m(r)}|_{2r} \le C, \quad \Vert \nabla ^2 G_r\Vert _{\delta /3} \le C \end{aligned}$$

(6.3)

and if we set

$$\begin{aligned} T:=\exp (1/\nu ) \ge \exp \left( \exp (cr^{-a})\right) \end{aligned}$$

then

$$\begin{aligned} \Vert \partial _IR_r\Vert _{{\bar{\rho }}/6,\delta /3} \le T^{-1}, \quad \Vert \partial _\theta R_r\Vert _{{\bar{\rho }}/7,\delta /2} \le T^{-1}. \end{aligned}$$

(6.4)

From the Hamiltonian equations associated with ${\tilde{H}}$ and the second inequality of (6.4), we have

$$\begin{aligned} |{\tilde{I}}(t)-{\tilde{I}}_0| \le T^{-2/3} \quad \text {for} \quad |t| \le T^{1/3} \end{aligned}$$

(6.5)

and therefore

$$\begin{aligned} |I(t)-I_0| \le T^{-2/3} +2Cr^2 \le C r^2 \quad \text {for} \quad |t| \le T^{1/3}. \end{aligned}$$

Then, using (6.3), (6.5) and the definition $\omega (I_0)$, we have

$$\begin{aligned} |\nabla N_{m(r)}({\tilde{I}}(t))+\nabla G_r({\tilde{I}}(t))-\omega (I_0)| \le C T^{-2/3} \quad \text {for} \quad |t| \le T^{1/3}, \end{aligned}$$

and from the Hamiltonian equations and the first inequality of (6.4), we also have

$$\begin{aligned} |\dot{{\tilde{\theta }}}(t)-\nabla N_{m(r)}({\tilde{I}}(t))-\nabla G_r({\tilde{I}}(t))| \le T^{-2/3} \quad \text {for} \quad |t| \le T^{1/3}. \end{aligned}$$

Thus,

$$\begin{aligned} |\dot{{\tilde{\theta }}}(t)-\omega (I_0)| \le CT^{-2/3} \quad \text {for} \quad |t| \le T^{1/3}. \end{aligned}$$

This last inequality implies

$$\begin{aligned} |{\tilde{\theta }}(t)-{\tilde{\theta }}_0-t\omega (I_0)| \le CT^{-1/3} \quad \text {for} \quad |t| \le T^{1/3}, \end{aligned}$$

which gives

$$\begin{aligned} |\theta (t)-\theta _0-t\omega (I_0)| \le CT^{-1/3}+2Cr \le C r \quad \text {for} \quad |t| \le T^{1/3}. \end{aligned}$$

Since $T^{1/3} \ge \exp \left( \exp (c r^{-a})\right)$, this concludes the proof of the stability estimates, and now it remains to prove that ${\mathcal {V}}_r$ contains an open set ${\mathcal {U}}_r$ with the wanted relative measure estimate. To do so, we first observe that $\Phi _r(\tilde{{\mathcal {V}}}_r)$ is contained in $\mathbb {T}^d \times (V_{\delta }S_r \cap {\mathbb {R}}^d)$; hence, it is contained in $\mathbb {T}^d \times B_{2r}$ but also, in view of (5.4), $\Phi _r(\tilde{{\mathcal {V}}}_r)$ contains (for instance) $\mathbb {T}^d \times (V_{\delta /5}S_r \cap {\mathbb {R}}^d)$; hence, it contains $\mathbb {T}^d \times S_r$, and thus, from (6.1) we get

$$\begin{aligned} \textrm{Leb} (\mathbb {T}^d \times B_{2r} \setminus \Phi _r(\tilde{{\mathcal {V}}}_r)) \le \textrm{Leb} (\mathbb {T}^d \times B_{2r} \setminus \mathbb {T}^d \times S_r) \le C\exp (-cr^{-a})r^{d-1}. \end{aligned}$$

Then, from (3.1), $\Psi _r$ is a Lipeomorphism of $\mathbb {T}^d \times B_{2r}$ onto its image, which contains $\mathbb {T}^d \times B_{r}$, so that if we define

$$\begin{aligned} {\mathcal {U}}_r:={\mathcal {V}}_r \cap (\mathbb {T}^d \times B_{r})= \Psi _r(\Phi _r(\tilde{{\mathcal {V}}}_r)) \cap (\mathbb {T}^d \times B_{r}), \end{aligned}$$

we finally get

$$\begin{aligned} \textrm{Leb} (\mathbb {T}^d \times B_{r} \setminus {\mathcal {U}}_r) \le C\exp (-cr^{-a})r^{d-1} \le \exp (-cr^{-a}) \textrm{Leb} (\mathbb {T}^d \times B_{r}) \end{aligned}$$

and this concludes the proof.

Proof of Theorem B

The proof follows the same lines as in the proof of Theorem A, the only difference being that since we are assuming $V={\mathbb {R}}\omega$, then $F_{m(r)}(I)=\nabla N_{m(r)}(I)=\lambda _r(I)\omega$ with $\lambda _r(0)=1$, and from (3.3) with $m=2$, it follows that the real-valued function $\lambda _r$ is close to 1 for r small enough. We can therefore choose $\bar{\tau }=\tau$ and, for instance, $\bar{\gamma }=\gamma /2$ so that Proposition 1 becomes useless since in this case, one can choose $S_r=B_{2r}$ and consequently ${\mathcal {U}}_r=\mathbb {T}^d \times B_{r}$.

Proof of Theorem C

The proof follows directly from Theorem 1 and a general KAM theorem proved by Rüssmann. Indeed, as we already pointed out, the assumption that $V={\mathbb {R}}^d$ means that $N_{m^*}$, and consequently, $N_{m(r)}$ for r small enough, is Rüssmann non-degenerate; the main result of [22] applies to a perturbation of size $\mu =\exp (-cr^{-a})$, and the set not covered by DQP tori is estimated by a constant times $\mu ^{1/(2(m^*-1))}$, which is still bounded by a quantity of the form $\exp (-cr^{-a})$.