Abstract
The C*-algebraic formulation of generic interacting quantum field theories, recently presented by Detlev Buchholz and one of the authors (KF), is enriched by a unitary version of the Master Ward Identity, which was postulated some time ago by Franz Marc Boas, Ferdinand Brennecke and two of us (MD,KF). It is shown that the corresponding axiom implies the validity of the time slice axiom. Moreover, it opens the way for a new approach to Noether’s Theorem where it yields directly the unitaries implementing the symmetries. It also unravels interesting aspects of the role of anomalies in quantum field theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The C*-algebraic formulation of quantum physics is well known for its rather unique combination of conceptual clarity and mathematical precision [11]. In quantum field theory, the algebraic approach of Araki, Borchers, Haag and Kastler [1, 6, 38, 39] has led to deep insights into the structure of the theory. As particularly important examples, one may mention the theory of superselection sectors of Doplicher, Haag and Roberts (see e.g. [38]) which is at the basis of recent work in conformal field theory (see e.g. Rehren’s contribution in [11]), and Tomita–Takesaki modular theory [8, 64, 66] which is instrumental e.g. in Quantum Statistical Mechanics via the KMS conditions [9], in the reconstruction of symmetries via Wiesbrock’s half-sided modular condition/intersection [68, 69], in localization properties of field theories with their particle interpretation [17] and its mathematical ramifications [57], and which is fruitfully used nowadays to discuss entropy and entanglement in quantum field theories [25, 43, 52].
On the other hand, the axioms of algebraic quantum field theory have not yet been equally successful in fixing specific interacting theory models. As a bon mot, Rudolf Haag used to ask colleagues “What is the Lagrangian?” and no answer could satisfy him.
Recently, Detlev Buchholz and one of us (KF) succeeded in finding a framework where the classical Lagrangian determines a net of C*-algebras [20, 21]. It is a fully nonperturbative construction. It was formulated for the case of a scalar field with polynomial self-interaction (for the incorporation of fermions, see [13]). The algebras are generated by unitaries S(F) labeled by local functionals F of the (classical) scalar field configuration. F is interpreted as a local variation of the dynamics, and S(F) is the induced operation on the system (the scattering “S-matrix,” an interpretation as such is offered at the end of Sect.6). By definition, these unitaries satisfy a Causality Relation corresponding to the ordering in time when these operations are performed, and a relation which determines dynamics in terms of the classical Lagrangian and which is a unitary version of the Schwinger–Dyson equation known from perturbative quantum field theory [48]. In the case of the free Lagrangian, the canonical commutation relations in form of the Weyl relations are a consequence of the formalism [20, 22].
We discuss in this paper whether further relations can be added in order to enrich the structure and to bring the formalism nearer to standard quantum field theory. We thereby use inspiration from the path integral formulation and check whether the resulting relations are compatible e.g. with perturbation theory. An important relation is obtained by the field redefinition (see e.g. [2, 50, 53] and references therein). Its infinitesimal version appears in a somewhat different form in the quantum master equation of the BV formalism, and was precisely analyzed in renormalized perturbation theory under the name Master Ward Identity (MWI) in [10, 28, 29, 31, 36, 42]. We postulate in this paper a unitary version of this identity (Axiom “Symmetries” in Sect. 5)—including anomalies—and show that, in formal perturbation theory, it is essentially equivalent to the infinitesimal version (see Sect 10 and Appendix C).
The crucial ingredient for our formulation is an intrinsic nonperturbative concept of the renormalization group (Definition 4.2). It corresponds to the Stückelberg–Petermann renormalization group [12, 32, 61, 65] in formal perturbation theory. Here, it is used to characterize possible anomalies of the unitary Master Ward Identity.
We then prove that the new axiom implies the time slice axiom [40] (primitive causality in [39]), which states that each observable can be expressed in terms of observables in any neighborhood of a Cauchy surface. The remarkable stability of the algebra under a large class of time evolutions compares well to a similar property in non-relativistic quantum field theory [18] in the framework of Resolvent Algebras by Buchholz and Grundling [23].
Moreover, the axiom also characterizes symmetries of the theory. One of the deepest structural results of classical physics is the intimate relation between symmetries and conservation laws which were uncovered by Emmy Noether [58, 59] about 100 years ago. A similar connection also holds in quantum physics, but since the Lagrangian is not directly used in canonical quantization, it is less evident. In the path integral formulation, the situation looks better but mathematically rigorous results are rare in this formalism. Traditionally in quantum theory, one uses the classical form for the generators of symmetries and attempts finding the corresponding expressions in the quantized theory. There is no general unique procedure to do this and it might fail altogether. For example, in quantum field theory, one then has to rely on renormalized perturbation theory and has to check for anomalies.
We show that in the absence of anomalies, symmetries can be locally unitarily implemented (a unitary version of Noether’s TheoremFootnote 1). We also discuss the occurrence of anomalies and present two equivalent notions of the induced renormalization group flow; one related to anomalies of the Master Ward Identity (see formula (7.10) and the discussion below it), and the other (the standard one) expressed in terms of a flow of Lagrangians together with an associated field renormalization (Theorem 8.3). A new, unexpected, result is an anomalous version of Noether’s Theorem, Theorem 7.3, in which we prove the unitary implementation of symmetries, modulo renormalization group transformations.
It turns out to be useful to generalize the framework from theories on Minkowski space to theories on generic globally hyperbolic spacetimes and to make use of the locally covariant formulation [16, 44], extended in such a way that also interactions can be varied. As an immediate consequence, we find a closed expression for the algebraic adiabatic limit by which the net of algebras with an additional interaction can be constructed within the original net. A complication, not present in formal perturbation theory, consists in the possible change of the causal structure by interactions of kinetic type, i.e. quadratic functionals of first derivatives of the field (see e.g. [21]).
2 Lagrangians, Interactions and Dynamical Spacetimes
2.1 Local Functionals and Observables
We consider an n-component real scalar field \(\phi \). The classical configuration space \({{\mathscr {E}}}(M,{{\mathbb {R}}}^n)\) is the space of smooth functions on the manifold M with values in \({{\mathbb {R}}}^n\). Manifolds for us are topological spaces that are connected, Hausdorff and locally homeomorphic to a Euclidean space, together with a smooth differentiable structure (i.e. an atlas) and of generic dimension larger than 2.Footnote 2 We equip manifolds with Lagrangians \(L=L_0+V_0\), which are density-valued local functionals on the configuration space and are of the form
with a metric g for which the manifold is a globally hyperbolic spacetimeFootnote 3 and such that the linearized classical field equation is normally hyperbolic. Hence, specifying the kinetic part of the Lagrangian equips the manifold M with a metric that makes it into a globally hyperbolic spacetime. Signatures for the metrics are taken as \((+,-,\dots ,-)\), \(\mu _g\) denotes the density induced by g and \({\hat{V}}_0\) is of 1st order with respect to \(d\phi \) (see e.g. (2.9)). Globally hyperbolic manifolds are always time orientable, and we choose a fixed time orientation.
We label the fundamental observables by local functionals \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) on the configuration space, i.e. functionals of the form
with a smooth density-valued function \({\hat{F}}\) on the jet space of \({{\mathscr {E}}}(M,{{\mathbb {R}}}^n)\) with compact support in x. A particularly simple local functional is the basic field integrated with a test density \(h\in {{\mathscr {D}}}_{\mathrm {dens}}(M,{{\mathbb {R}}}^n)\):
We refer to Appendix A, where one finds definitions and properties of functionals, including, for instance, the important notion of their support. Next we want to add to a Lagrangian L the interaction given by a local functional F. In order to do this, we use the fact that a Lagrangian defines a family of local functionals L(f), \(f\in {{\mathscr {D}}}(M,[0,1])\), (named generalized Lagrangian in [12, 15]) by
Lagrangians \(L',L\) with
lead to the same equation of motion and are considered to be equivalent (notation \(L\sim L'\)). The map \(f\mapsto L(f)\) is a generalized field in the sense of [12, 15] (again, details are given in Appendix A). In the following, we shall always mean a Lagrangian L in the sense of a generalized field.
Given a local functional F, on the other hand, we can define a generalized field \(A_F\) by
In Appendix A, the support of a generalized field is defined and it is shown that \({\mathrm {supp} \, }A_F={\mathrm {supp} \, }F\). Therefore, a local functional F corresponds to a generalized field \(A_F\) with compact support. The addition of the interaction given by \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) to a Lagrangian L is now expressed by \(L+A_F\).
Next we construct the category \(\mathfrak {Loc}\). We first describe its objects: they are dynamical spacetimes i.e. pairs (M, L) where M is a manifold and L is a Lagrangian of the form (2.1), considered as a generalized field in the form of (2.4), together with a choice of time orientation. We consider local functionals F for which the generalized field \(A_F\) can be added to the Lagrangian L as an interaction, such that the linearized equation of motion remains normally hyperbolic with respect to a possibly changed metric \(g'\). This requires that F is of the form
with
where \(g'\) is a Lorentz metric for which M is globally hyperbolic with \({\mathrm {supp} \, }(g'-g)\) compact, and \(F_0\) is a local functional of the form
with \(h_0,h_1\) smooth functions on the bundle \(M\times {{\mathbb {R}}}^n\), with real values and values in the tangent bundle, respectively, and compactly supported on the base space M. We denote the set of these functionals by \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\). For later purposes, we denote by \(\mathrm {Q}(M,L)\) the subset of quadratic functionals.
For \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\), we have \(A_F(f)\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) if \(f\equiv 1\) on \({\mathrm {supp} \, }F\), hence the equivalence class of \(L+A_F\) and the associated metric are well defined. The time orientation is obtained from the time orientation of the unperturbed Lagrangian by continuity. Notice that \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) is not a linear space, but has the property that for any \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\)
Moreover, in case \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }G=\emptyset \), we have that with F and G also \(F+G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\), namely if \(g_1\) is the metric associated to \(L+A_F\) and \(g_2\) the metric associated to \(L+A_G\), then \(g_{12}\doteq g_1+g_2-g\) is the metric associated to \(L+A_{F+G}\) which is easily seen to be also globally hyperbolic.
Complications arise from the fact that the set of Lorentz metrics is, in general, not convex, hence \(A_F(f)\) for \(0\le f\le 1\) might not belong to \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\), for \(F_{g',g}\) of the form in (2.8) with \(g\ne g'\). In Appendix B, we solve this problem by introducing additional metrics \(g_i\), \(i=0,\dots ,4\), with \(g_0=g\), \(g_4=g'\) such that, for each pointwise convex combination
of \(g_{i-1}\) and \(g_i\), \(i=1,\dots ,4\), the manifold M is globally hyperbolic. We decompose
with \(F_0\) as above and \(F_i\doteq F_{g_{i},g_{i-1}}\) for \(i=1,\dots ,4\).
We thus get a quintuple of generalized fields \(A_{F_i}\), \(i=0,\dots ,4\) with \(A_{F_i}(f_i)\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+\sum _{j<i}A_{F_j})\) and \(\sum _i A_{F_i}(f_i)\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) provided \(f_i\in {{\mathscr {D}}}(M,[0,1])\), with \({\mathrm {supp} \, }f_k\subset (f_{k-1})^{-1}(1)\), \(k=1,\dots ,4\).
Let \({{\mathscr {D}}}_s(M)\) denote the set of finite sequences \(f=(f_1,\dots ,f_n)\) of test functions \(f_i\in {{\mathscr {D}}}(M,[0,1])\) subject to restrictions as above, and \(f\equiv 1\) on a set N means that \(f_i\equiv 1\) on N, \(i=1\dots ,n\).
Definition 2.1
(Interactions). The set of finite sequences \(V=(V_1,\dots ,V_n)\) of generalized fields \(V_i\) whose values, upon evaluation with test functions in \({{\mathscr {D}}}(M,[0,1])\), are local functionals in \({{\mathscr {F}}}_{\mathrm {loc}}(M,L+\sum _{j<i} V_j)\), shall be called interactions w.r.t the Lagrangian L and denoted by the symbol \(\mathrm {Int}(M,L)\). We use the notation \(V(f)=\sum _iV_i(f_i)\), \(f=(f_1,\dots ,f_n)\in {{\mathscr {D}}}_s(M)\) for the local functionals which approximate V for \(f\equiv 1\) on a sufficiently large region.
In the following, we always understand Lagrangians as generalized fields in the sense that they might depend on a finite sequence \(f\in {{\mathscr {D}}}_s(M)\). For example, for \(V=(V_1,\dots ,V_n)\in \mathrm {Int}(M,L)\), \(L+V\) is evaluated with an \((n+1)\)-tuple \((f_0,f_1,\ldots ,f_n)\in {{\mathscr {D}}}_s(M)\), and
We now turn to the morphisms. Morphisms of \(\mathfrak {Loc}\), \(\iota \in \mathrm {Hom}((M,L), (M',L'))\), are compositions of elementary morphisms of either of the following forms:
-
\(\iota _{\rho }\): Structure preserving embeddings, i.e. smooth embeddings \(\rho :M\rightarrow M'\) with \(\rho _{*}L=L'\) which preserve the time orientation and with causally convex image \(\rho (M)\).
Here \((\rho _{*}L)(f)\doteq \rho _{*}(L(f\circ \rho ))\), \(f\in {{\mathscr {D}}}_s(M')\) and \(\rho _{*}F[\phi ]\doteq F[\phi \circ \rho ]\), \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\).
-
\(\iota _{\Phi }\): Affine field redefinitions \(\Phi :\phi \mapsto \phi A+\phi _0\) with \((\phi A)_j(x)=\sum _{i=1}^n \phi _i(x)A_{ij}(x)\), \(A(x)\in \mathrm {GL}(n,{{\mathbb {R}}})\), where A and \(\phi _0\) are smooth functions of compact support, \(M'=M\), \(L'=\Phi _{*}L\).Footnote 4
Here, \((\Phi _{*}L)(f)\doteq \Phi _{*}(L(f))\), \(f\in {{\mathscr {D}}}_s(M)\) and \((\Phi _{*}F)[\phi ]\doteq F[\Phi (\phi )]\), \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\).
-
\(\iota _{V,+}\): Retarded interaction \(M'=M\), \(L'+V=L\), where \(V\in \mathrm {Int}(M',L')\) with past compact support [63].
-
\(\iota _{V,-}\): Advanced interaction \(M'=M\), \(L'+V=L\), where \(V\in \mathrm {Int}(M',L')\) with future compact support [63].
2.2 Dynamical Algebras
The associated quantum field theory is now a functor \({\mathfrak {A}}\) from \(\mathfrak {Loc}\) to the category \({\mathfrak {C}}^*\) of unital C*-algebras with unital homomorphisms as arrows. The dynamical algebra \({\mathfrak {A}}(M,L)\) is a C*-algebra freely generated by unitaries \(S_{(M,L)}(F)\), \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) with \(S_{(M,L)}(c)=e^{ic}1\) for constant functionals c, \(c\in {{\mathbb {R}}}\), modulo the following relations:
Axiom 1
(Causality Relation). Let \(G \in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) and \(F,H\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\). Then
when \({\mathrm {supp} \, }F\cap J_-^{L+A_G}({\mathrm {supp} \, }H)=\emptyset \) where \(J_-^{L+A_G}\) denotes the causal past with respect to the metric induced by \(L+A_G\), and
Axiom 2
(Dynamical Relation). For all \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\), we require
where
for any \(f\in {{\mathscr {D}}}_s(M)\) satisfying \(f \equiv 1\) on \({\mathrm {supp} \, }\psi \). This is the on-shell version of the Schwinger–Dyson relation in [20].
Remark 2.2
For the Dynamical Relation note that \(\delta L(\psi )\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\), and that with \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) also \(F^\psi \in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) and \(F^\psi +\delta L(\psi )\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\); we wish also to point out that \({\mathrm {supp} \, }\delta L(\psi )\subseteq {\mathrm {supp} \, }\psi \).
The “on-shell algebra” is distinguished from the “off-shell algebra” by the validity of the additional relation \(S_{(M,L)}(\delta L(\psi ))=1\) for all \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\); in perturbation theory this terminology agrees with the usual distinction between on-shell and off-shell time-ordered products, see [13, Sect. 7].
The morphisms \({{\mathfrak {A}}}\iota _{\bullet }\equiv \alpha _{\bullet }\) associated to the various elementary morphisms are monomorphisms \({{\mathfrak {A}}}(M,L)\rightarrow {{\mathfrak {A}}}(M',L')\) which act on the generators of the algebra as
In the last two equations \(f\in {{\mathscr {D}}}_s(M)\) with \(f\equiv 1\) on a neighborhood of \(J_-^L({\mathrm {supp} \, }F)\cap {\mathrm {supp} \, }V\) for (2.17) and of \(J_+^L({\mathrm {supp} \, }F)\cap {\mathrm {supp} \, }V\) for (2.18). Due to the Causality Relation, \(\alpha _{V,\pm }(S_{(M,L)}(F))\) do not depend on the remaining freedom in the choice of \(f=(f_1,\dots ,f_n)\). Namely, e.g. for the retarded case, let \(f_j'\in {{\mathscr {D}}}(M,[0,1])\) with \({\mathrm {supp} \, }f_j'\subset (f_{j-1})^{-1}(1)\) and \(f_j'\equiv 1\) on \({\mathrm {supp} \, }f_{j+1}\) where we put \(f_0\equiv 1\) and \(f_{n+1}=0\), and let \(f'\) denote the sequence f with \(f_j\) replaced by \(f_j'\). Then \({\mathrm {supp} \, }(V(f)-V(f'))\cap J_-^L({\mathrm {supp} \, }F)\cap {\mathrm {supp} \, }V=\emptyset \) and
We point out that \(\alpha _\Phi \) and \(\alpha _{V,\pm }\) are even surjective, that is, they are isomorphisms. For the latter two, there is a simple formula for the inverse, namely:
by using that \((-V)\in \mathrm {Int}(M,L)\).
Remark 2.3
We return to the Causality Relation (2.13): although it is a defining relation for \({{\mathfrak {A}}}(M,L)\), it has to be interpreted as “causality” in the dynamical spacetime \((M,L+A_G)\), i.e., it is required that \({\mathrm {supp} \, }F\) is later than \({\mathrm {supp} \, }H\) with respect to the metric given by \(L+A_G\); see [21].
In causal perturbation theory [14, 28, 35], the factorization (2.13) is required for the S-matrix (describing perturbations of the free theory) w.r.t. the causality structure of the free theory; actually, in that framework this factorization property is equivalent to its special case obtained by setting \(G=0\).
In the nonperturbative framework at hand, this equivalence does not hold. However, the Causality Relation (2.13) is equivalent to the just mentioned simpler causal factorization in dynamical spacetimes \((M,L+A_G)\), explicitly
if \({\mathrm {supp} \, }F\cap J_-^{L+A_G}({\mathrm {supp} \, }H)=\emptyset \), where \(F,H\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\). Namely, applying \(\alpha _{A_G,+}\) to (2.20), we indeed obtain (2.13).
We check that all these maps \(\alpha _{\bullet }\) preserve the defining algebraic relations. For \(\alpha _{\chi }\), this is the standard situation for local covariance. In detail, by using \((\rho _*F)^\psi =\rho _*(F^{\psi \circ \rho })\) (with \(\psi \in {{\mathscr {D}}}(M',{{\mathbb {R}}}^n)\)) we obtain
and for the Causality Relation the claim follows from the equivalence
The definition of \(\alpha _{V,\pm }\) is just the Bogoliubov formula; for the Dynamical Relation the claim relies on
and for the Causality Relation on
For \(\alpha _{\Phi }\) we only have to check the Dynamical Relation, since \({\mathrm {supp} \, }(\Phi _{*}F)={\mathrm {supp} \, }F\) and
We use the formula
with \(\psi = \psi 'A\), and the corresponding formula for L and \(L'=\Phi _{*}L\), and find
Due to the Dynamical Relation (2.14) in \({{\mathfrak {A}}}(M,L)\), the l.h.s. is equal to
so we see that \(\alpha _\Phi \) maps this relation in \({{\mathfrak {A}}}(M,L)\) to the same relation in \({{\mathfrak {A}}}(M',L')\).
Remark 2.4
(Net Structure). Given any dynamical spacetime (M, L), we can restrict the functor \({{\mathfrak {A}}}\) to relatively compact, causally convex subregions \({{\mathscr {O}}}\subset M\) and the arrows to inclusions \({{\mathscr {O}}}_1\subset {{\mathscr {O}}}_2\). This subfunctor is the Haag–Kastler net associated to (M, L) and will be denoted by \({{\mathfrak {A}}}_{(M,L)}\). An isomorphism \(\alpha :{{\mathfrak {A}}}(M,L)\rightarrow {{\mathfrak {A}}}(M',L')\) is called a net isomorphism if it extends to an equivalence between the corresponding functors, i.e. it extends to a bijective natural transformation. In detail, for \({{\mathscr {O}}}_1\subset {{\mathscr {O}}}_2\) as above, let \(\iota _{(M,L)}^{{{\mathscr {O}}}_2,{{\mathscr {O}}}_1}:{{\mathfrak {A}}}_{(M,L)}({{\mathscr {O}}}_1)\hookrightarrow {{\mathfrak {A}}}_{(M,L)}({{\mathscr {O}}}_2)\) be the pertinent embedding of algebras. That \(\alpha \) extends to a bijective natural transformation means that there exists a unique bijection \({{\tilde{\alpha }}}:M\rightarrow M'\) fulfilling \({{\mathfrak {A}}}_{(M',L')}\bigl ({{\tilde{\alpha }}}({{\mathscr {O}}})\bigr )=\alpha \bigl ({{\mathfrak {A}}}_{(M,L)}({{\mathscr {O}}})\bigr )\) for all causally convex \({{\mathscr {O}}}\subset M\) and that
3 Algebraic Adiabatic Limit
A problem with Bogoliubov’s formulae (2.17, 2.18) is that they do not apply to an interaction without support restriction. As remarked earlier [14, 47], this does not matter for the algebraic structure of the algebra of local observables for which it is sufficient to fix the interaction in a sufficiently large, however bounded, region (algebraic adiabatic limit), and it was also observed that the algebra of the interacting theory can be identified with the algebra of the free theory [20]. The formalism described above allows an elegant formula for this identification by writing the interaction as a sum of a past compact and a future compact part and composing the arrows for retarded and advanced interactions. Namely, we find:
Proposition 3.1
Let \(V_+\in \mathrm {Int}(M,L)\) have past compact support and \(V_-\in \mathrm {Int}(M,L+V_+)\) future compact support (for the respective causal structures). Given the isomorphisms \(\alpha _{V_-,-}:{{\mathfrak {A}}}(M,L+V)\rightarrow {{\mathfrak {A}}}(M,L+V_+)\) and \(\alpha _{V_+,+}:{{\mathfrak {A}}}(M,L+V_+)\rightarrow {{\mathfrak {A}}}(M,L)\), with \(V=V_++V_-\), then
defines an isomorphism from \({{\mathfrak {A}}}(M,L+V)\) to \({{\mathfrak {A}}}(M,L)\). It acts on the generators of the algebra as
where \(g,f\in {{\mathscr {D}}}_s(M)\) with \(g\equiv 1\) on a neighborhood of \(J^{L+V}_+({\mathrm {supp} \, }F)\cap {\mathrm {supp} \, }V_-\) and \(f\equiv 1\) on a neighborhood of \(J^{L+V_+}_-\bigl ({\mathrm {supp} \, }F\cup {\mathrm {supp} \, }V_-(g)\bigr )\cap {\mathrm {supp} \, }V_+\). The explicit expression (3.2) for \(\alpha _{V_+,V_-}(S(F))\) does not depend on the choices of f and g.
Proof
We shall use the abbreviation \(S=S_{(M,L)}\) for simplicity. The formula (3.2) is obtained straightforwardly by inserting the definitions (2.17) and (2.18) of \(\alpha _{V_+,+}\) and \(\alpha _{V_-,-}\), respectively. Also the independence of the choice of f and g under the given conditions derives from the corresponding facts about the retarded and advanced isomorphisms. Nevertheless, it is instructive to check the independence directly.
By iteration of the argument given before equation (2.19), let \(f'\) be the appropriate change for f satisfying the conditions above for fixed g. Then, we have that \({\mathrm {supp} \, }(V_+(f')-V_+(f))\) does not intersect \(J^{L+V_+}_-\bigl ({\mathrm {supp} \, }F\cup {\mathrm {supp} \, }V_-(g)\bigr )\), and by causal factorization we get
and
hence
Let now \(g'\) be another choice for g satisfying \(g'\equiv 1\) on a neighborhood of \(J^{L+V}_+({\mathrm {supp} \, }F)\cap V_-\). Then, \({\mathrm {supp} \, }(V_-(g')-V_-(g))\) does not intersect \(J^{L+V}_+({\mathrm {supp} \, }F)\) and we obtain
thus again \(\alpha _{V_+,V_-}(S_{(M,L+V)}(F))\) does not change.
To prove the joint independence of the choices, we use an intermediate choice \(f''\) for f which satisfies the conditions above for both g and \(g'\). Then, we first replace f by \(f''\), then g by \(g'\) and finally \(f''\) by \(f'\). \(\square \)
The isomorphism \(\alpha _{V_+,V_-}\) which embeds the original algebra (with Lagrangian \(L+V\)) into the algebra with Lagrangian L depends, however, on the split \(V=V_++V_-\).
This isomorphism changes the association of local subalgebras. But on the intersection \({\mathrm {supp} \, }V_+\cap {\mathrm {supp} \, }V_-\) the local subalgebras are only slightly deformed, as can be seen from the conditions on the test functions f and g in (3.2). In particular, if N is a globally hyperbolic neighborhood of \({\mathrm {supp} \, }V_+\cap {\mathrm {supp} \, }V_-\), then
where \(L\!\restriction _{N}\) denotes the restriction of \(f\mapsto L(f)\) to \({{\mathscr {D}}}_s(N)\). (To simplify the notation, this restriction is understood without mentioning at some places.)
This observation allows an easy proof of the validity of a weak form of the time slice axiom.
Definition 3.2
(Time slice in representation). We say that \({{\mathfrak {A}}}_{(M,L)}\) satisfies, in the representation \(\pi \), the time slice axiom for some Cauchy surface \(\Sigma \) of M whenever for any causally convex and globally hyperbolic neighborhood N of \(\Sigma \) we have
Then, it holds that
Theorem 3.3
Let \({{\mathfrak {A}}}_{(M,L)}\) satisfy, in the representation \(\pi \), the time slice axiom for some Cauchy surface \(\Sigma \) which is also a Cauchy surface for the metric associated to \(L+V\), and let \(\alpha \doteq \alpha _{V_+,V_-}: {{\mathfrak {A}}}(M,L+V)\rightarrow {{\mathfrak {A}}}(M,L)\) denote the isomorphism in (3.1) for some decomposition \(V=V_++V_-\). Then, \({{\mathfrak {A}}}_{(M,L+V)}\) satisfies, in the representation \(\pi \circ \alpha \), the time slice axiom for \(\Sigma \).
Proof
Let N be a neighborhood of \(\Sigma \). Choose a decomposition \(V=V_+'+V_-'\) with
Then, the induced isomorphism \(\alpha '\doteq \alpha _{V_+',V_-'}\) differs from \(\alpha \) by an inner automorphism \(\mathrm {Ad}(U)(\bullet )\doteq U\bullet U^{-1}\), \(\alpha =\alpha '\circ \mathrm {Ad}(U)\), with a unitary \(U\in {{\mathfrak {A}}}(M,L+V)\). From the above discussion, the following chain of identities holds true
by which the theorem is proven. \(\square \)
Remark 3.4
For the following particular case, Theorem 3.3 has already been proven in [24]. Looking at perturbation theory in the Fock representation, let \(L_0\) be the free Lagrangian (which may include a mass term). Then, \({{\mathfrak {A}}}(M,L_0)\) is the algebra consisting of Wick products of free fields; it is generated by the S-matrices \(S_{(M,L_0)}(F), \, F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L_0)\), where \(S_{(M,L_0)}(F)\) is the generating functional of the time-ordered products of the interaction F, fixed by suitable renormalization conditions. The time slice axiom holds in \({{\mathfrak {A}}}_{(M,L_0)}\), as shown in the first part of [24].
Given some Cauchy surface \(\Sigma \) of \((M,L_0)\), the interacting fields in the future of \(\Sigma \) depend only on the interaction in the future of \(\Sigma \), up to unitary equivalence (see the algebraic adiabatic limit in [14]). We consider therefore an interaction \(V\in \mathrm {Int}(M,L_0)\) with past compact support, hence \(\alpha _{V,+}\) (2.17) is an isomorphism from the interacting algebra \({{\mathfrak {A}}}(M,L_0+V)\) into the free algebra \({{\mathfrak {A}}}(M,L_0)\). For \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L_0+V)\), we introduce
\(G_V\) is the interacting field corresponding to G (i.e., it agrees with G for \(V=0\)), expressed in terms of the free theory. The relative S-matrix
(where still \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L_0+V)\)) is the generating functional of the time-ordered products of the interacting fields \(G_V\).
By means of the Causality Relation (2.13) for \(S_V\), it is proven in the same reference—in the second step—that the validity of the time slice axiom in \({{\mathfrak {A}}}(M,L_0)\) implies that this axiom holds also for the net of algebras
(where \([\cdots ]\) means the algebra generated by the elements of the indicated set). Actually, the proof of this second step in [24] is not limited to perturbation theory and agrees essentially with the proof of Theorem 3.3 given above. Finally, the time slice axiom holds then also for the net
i.e. , in \({{\mathfrak {A}}}_{(M,L_0+V)}\).
Due to possible changes of the causal structure by kinetic terms in the interaction, the splitting into the past and future compact part is not always possible. The isomorphy between algebras with different Lagrangians, however, holds in general.
Theorem 3.5
For every interaction \(V\in \mathrm {Int}(M,L)\), the algebras \({{\mathfrak {A}}}(M,L+V)\) and \({{\mathfrak {A}}}(M,L)\) are isomorphic.
Proof
By using the construction of Appendix B, we decompose \(V=\sum _{i=1}^5V_i\) such that \(V_i\in \mathrm {Int}(M,L+\sum _{j<i}V_j)\) and such that the spacetimes corresponding to \(L+\sum _{j<i}V_j\) and \(L+\sum _{j\le i}V_j\) possess a joint foliation by Cauchy surfaces. For each \(i=1,\dots ,5\), we then decompose \(V_i=V_i^++V_i^-\) with \(V_i^+\in \mathrm {Int}(M,L+\sum _{j<i}V_j)\) such that \({\mathrm {supp} \, }V_i^+\) is past compact (with respect to \(L+\sum _{j<i}V_j\)) and with \(V_i^-\in \mathrm {Int}(M,L+\sum _{j<i}V_j+V_i^+)\) such that \({\mathrm {supp} \, }V_i^-\) is future compact (with respect to \(L+\sum _{j<i}V_j+V_i^+\)). Then
is an isomorphism from \({{\mathfrak {A}}}(M,L+V)\) to \({{\mathfrak {A}}}(M,L)\). \(\square \)
Remark 3.6
The reader should not feel worried by this result that entails that the global algebras of free and interacting theories are isomorphic. What matters is the locality structure, i.e. the net structure, and the isomorphism does not extend to a net isomorphism, i.e. the sub-algebras related to bounded regions are not mapped bijectively to each other, thus the theories are not equivalent.
4 Renormalization group
In perturbation theory, the axiom Dynamical Relation is equivalent to the renormalization condition “Field Equation” [13, Sect. 7]. But in contrast to the classical theory, in perturbative quantum field theory the field equation alone does not in general completely fix the dynamical evolution. There remains some freedom which has to be fixed by additional conditions (“renormalization conditions”). They can be classified in terms of the Stückelberg–Petermann renormalization group, see [12, 32, 61, 65].
Example 4.1
We illustrate this problem on a simple example. We assume that the free real scalar field on 4-dimensional Minkowski space is perturbed by an interaction V with density \(\phi ^2(x)h(x)d^4x\) with \(h\in {{\mathscr {D}}}(M,{{\mathbb {R}}})\). We use the axioms for the time-ordered (or retarded) products given in [28]. Then, the Field Equation determines uniquely the time evolution of the interacting basic field (with derivatives), e.g. \((\square \phi )_V\), because only tree diagrams contribute. But in general, this does not hold for the interacting composite fields, e.g., \((\phi \square \phi )_V\), because of the contributions of divergent loop diagrams whose renormalization is unique only up to a real constant.
In this example, such indeterminacy can be removed by requiring the Master Ward Identity (MWI) as an additional renormalization conditionFootnote 5:
which has the same form as the identity in the classical theory.
In more complicated cases, the classical identities cannot always be preserved, and this is how the anomalies arise.
Similarly to the perturbative case, also in the nonperturbative framework of this paper, the axioms given so far do not yet fix completely the dynamics, that is, the time slice axiom does not hold for the algebra they define. There exists a large group of isomorphisms, which prevent the existence of a dynamical law. Actually, the axiom Dynamical Relation fixes the dynamics (for the free Lagrangian) only for the subalgebra generated by S-matrices S(F) with affine functionals F. For a given Lagrangian L, we consider the following group.
Definition 4.2
The renormalization group \({\mathscr {R}}(M,L)\) for a Lagrangian \(L=L_0+V\), with \(V\in \mathrm {Int}(M,L_0)\), is the set of all bijections Z of \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) which satisfy the following conditions:
-
(i)
(Compact support) The support of Z
$$\begin{aligned}&{\mathrm {supp} \, }Z\doteq \{x\in M\,|\, \text { for every neighborhood }U\ni x\,\text { there exist}\ G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L),\nonumber \\&\,F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\text { with }{\mathrm {supp} \, }F\subset U\text { such that } Z(F+G)\ne F+Z(G)\}, \end{aligned}$$(4.2)is compact.
-
(ii)
(Locality) Let \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) and \(F,H\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\) with the requirement that \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }H=\emptyset \). Then
$$\begin{aligned} Z(F+G+H)=Z(F+G)-Z(G)+Z(G+H)\ . \end{aligned}$$(4.3) -
(iii)
(Dynamics) Z preserves the dynamics, i.e.
$$\begin{aligned} Z(F^\psi +\delta L(\psi ))=Z(F)^{\psi }+\delta L(\psi )\ ,\ \psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\ . \end{aligned}$$(4.4) -
(iv)
(Field shift) Under shifts in configuration space, Z transforms as
$$\begin{aligned} Z(F^{\psi }-V(f))=Z(F-V(f))^{\psi }+\delta V(\psi ) \end{aligned}$$(4.5)with \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\), \(f\in {{\mathscr {D}}}_s(M)\), \(f\equiv 1\text { on }{\mathrm {supp} \, }\psi \), and \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L-V)\) .
-
(v)
(Causal Stability) Z does not change the causal structure, i.e.
$$\begin{aligned} J_{\pm }^{L+A_{Z(F)}}=J_{\pm }^{L+A_F}\ . \end{aligned}$$(4.6)
For the free Lagrangian (i.e. \(L=L_0\)), the condition (iv) takes the simpler form
Remark 4.3
For the free Lagrangian \(L_0\), the group \({{\mathscr {R}}}(M,L_0)\) can be compared with the Stückelberg–Petermann renormalization group \({{\mathscr {R}}}_0\) as defined in [12, 28, 32], see Appendix C. The conditions (ii)-(iv) given above appear also in the definition of \({{\mathscr {R}}}_0\), but there is a main difference: the elements \(Z_0\) of \({{\mathscr {R}}}_0\) may have non-compact support, which allows, e.g. , to impose translation invariance in Minkowski space as a renormalization condition.
Proposition 4.4
Let Z be in \({{\mathscr {R}}}(M,L)\), then it preserves the support of functionals in the sense that for all \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) and \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\) it holds
Proof
Let \(\psi \in {{\mathscr {D}}}\) with \({\mathrm {supp} \, }\psi \cap {\mathrm {supp} \, }F=\emptyset \). The assertion follows from
which can be verified as follows: let \(f\equiv 1\) on \({\mathrm {supp} \, }\psi \). Then by the conditions (ii) (Locality) and (iv) (Field shift)
\(\square \)
The renormalization group for a Lagrangian \(L+W\) is obtained from \({\mathscr {R}}(M,L)\) by the following definition:
Definition 4.5
Let \(Z\in {{\mathscr {R}}}(M,L)\) and let \(W\in \mathrm {Int}(M,L)\). Then, for \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+W)\) we define:
with \(f\in {{\mathscr {D}}}_s(M)\) and \(f\equiv 1\) on the supports of F and Z.
This definitionFootnote 6 is motivated by the following results:
Proposition 4.6
Let \(Z^W\) be defined in terms of \(Z\in {{\mathscr {R}}}(M,L)\) and \(W\in \mathrm {Int}(M,L)\) by (4.11). Then:
- (i):
-
\(Z^W(F)\) does not depend on the choice of the test function \(f\in {{\mathscr {D}}}_s(M)\),
- (ii):
-
\(Z^W\in {{\mathscr {R}}}(M,L+W)\).
Proof
(i) Let \(f_1,f_2\in {{\mathscr {D}}}_s(M)\) have the above-mentioned property. Since \({\mathrm {supp} \, }(W(f_1)-W(f_2))\cap ({\mathrm {supp} \, }F\cup {\mathrm {supp} \, }Z)=\emptyset \) we may use Locality (ii) and \(Z(W(f_1))=Z(W(f_2))+(W(f_1)-W(f_2))\) in the following way (by abuse of notation):
(ii) By (2.10), we see that \(Z^W\) maps \({{\mathscr {F}}}_{\mathrm {loc}}(M,L+W)\) into itself. \(Z^W\) is also invertible with (bilateral) inverse \((Z^W)^{-1}=(Z^{-1})^W\) as may be seen from the equation
We are now going to verify that each of the properties (i)-(v) in Definition 4.2 for \(Z^W\) follows from the corresponding property of \(Z\in {{\mathscr {R}}}(M,L)\). For Locality (ii), this is straightforward; for the other properties, we give the details.
To verify (i), let \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }Z=\emptyset \). Then, we obtain \(Z^W(F+G)-Z^W(G)=F\), hence \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }Z^W=\emptyset \). It follows that \({\mathrm {supp} \, }Z^W\subset {\mathrm {supp} \, }Z\).
The property (iii) can be checked as follows:
To verify (iv), we take into account that \(L+W=L_0+(V+W)\) and obtain
It remains to check (v). We have for \(f\in {{\mathscr {D}}}_s(M)\), \(f\equiv 1\) on some relatively compact region \({{\mathscr {O}}}\supset {\mathrm {supp} \, }Z\cup {\mathrm {supp} \, }F\)
But by assumption, \(L+A_{Z(F+W(f))}\) induces the same causal structure as \(L+A_{F+W(f)}\) which coincides on \({{\mathscr {O}}}\) with the causal structure of \(L+W+A_{Z(F)}\). Since \({{\mathscr {O}}}\) can be arbitrarily large, condition (v) is fulfilled. \(\square \)
Remark 4.7
The defining condition (iv) of \(Z\in {{\mathscr {R}}}(M,L_0+V)\) in Definition 4.2 can be obtained from its simpler formulation in the particular case of \({{\mathscr {R}}}(M,L_0)\) (given in (4.7)) in the following way: looking at \(Z^W\), we choose W such that it compensates the interaction, that is, \(W=-V\). Then, Proposition 4.6 states that \(Z^{-V}\in {{\mathscr {R}}}(M,L_0)\), hence we may apply (4.7):
Inserting the definition of \(Z^{-V}\), we precisely get the (general) formulation of (iv) in \({{\mathscr {R}}}(M,L_0+V)\) (given in (4.5)). Hence, (4.14) is an equivalent reformulation of (4.5).
We are now ready to prove that naming \({{\mathscr {R}}}(M,L)\) a renormalization group is sound:
Proposition 4.8
\({{\mathscr {R}}}(M,L)\) is a group.
Proof
We first show that \(Z_1Z_2\in {{\mathscr {R}}}(M,L)\) for \(Z_1,Z_2\in {{\mathscr {R}}}(M,L)\) by verifying that the conditions \((i)-(v)\) of Definition 4.2 hold.
- (ii):
-
(Locality) Let \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\), \(F,H\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\) and \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }H=\emptyset \). Then,
$$\begin{aligned}&Z_1Z_2(F+G+H)\nonumber \\&\quad =Z_1\bigl (Z_2(F+G)-Z_2(G)+Z_2(G+H)\bigr )\nonumber \\&\quad =Z_1\bigl (\underbrace{Z_2(F+G)-Z_2(G)}_{{\mathrm {supp} \, }F}+Z_2(G)+\underbrace{Z_2(G+H)-Z_2(G)}_{{\mathrm {supp} \, }H}\bigr )\nonumber \\&\quad =Z_1Z_2(F+G)-Z_1Z_2(G)+Z_1Z_2(G+H). \end{aligned}$$(4.15) - (iii):
-
(Dynamics)
$$\begin{aligned} Z_1Z_2\bigl (F^{\psi }+\delta L(\psi )\bigr )=Z_1\bigl (Z_2(F)^{\psi }+\delta L(\psi )\bigr ) =Z_1Z_2(F)^{\psi }+\delta L(\psi ).\nonumber \\ \end{aligned}$$(4.16) - (iv):
-
(Field shifts) This is evident for the massless Lagrangian \(L_0\). It remains true for the general case, since (iv) can equivalently be written as (4.14), and due to
$$\begin{aligned} Z_1^W Z_2^W(F)= & {} Z_1^W\bigl (Z_2(F+W(f))-W(f)\bigr )\nonumber \\= & {} Z_1\bigl (Z_2(F+W(f))-W(f)+W(g)\bigr )-W(g)\nonumber \\= & {} Z_1Z_2\bigl (F+W(f)\bigr )-W(f)+W(g)-W(g)\nonumber \\= & {} (Z_1Z_2)^W(F) \end{aligned}$$(4.17)where \(f\equiv 1\) on \({\mathrm {supp} \, }Z_1\cup {\mathrm {supp} \, }Z_2\cup {\mathrm {supp} \, }F\) and \(g\equiv 1\) on \({\mathrm {supp} \, }f\). In the third line, we have used that \({\mathrm {supp} \, }\bigl (W(g)-W(f)\bigr )\cap {\mathrm {supp} \, }Z_1=\emptyset \).
- (i):
-
(Compact support) Let \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }Z_i=\emptyset \), \(i=1,2\). Then,
$$\begin{aligned} Z_1Z_2(F+G)=Z_1\bigl (F+Z_2(G)\bigr ) =F+Z_1Z_2(G)\ , \end{aligned}$$(4.18)hence \({\mathrm {supp} \, }Z_1Z_2\subset {\mathrm {supp} \, }Z_1\cup {\mathrm {supp} \, }Z_2\).
- (v):
-
(Causal Stability) evident.
We now show that \(Z\in {{\mathscr {R}}}(M,L)\) implies \(Z^{-1}\in {{\mathscr {R}}}(M,L)\).
- (ii):
-
(Locality) Let \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) and \(F,H\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\) with \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }H=\emptyset \). Set \(G'\doteq Z^{-1}(G)\), \(F'\doteq Z^{-1}(F+G)-G'\) and \(H'\doteq Z^{-1}(G+H)-G'\). Then, \(F=Z(F'+G')-Z(G')\) and \(H=Z(G'+H')-Z(G')\); thus by (4.8), we have \({\mathrm {supp} \, }F'={\mathrm {supp} \, }F\) and \({\mathrm {supp} \, }H'={\mathrm {supp} \, }H\), hence
$$\begin{aligned} F+G+H=Z(F'+G')-Z(G')+Z(G'+H')=Z(F'+G'+H')\nonumber \\ \end{aligned}$$(4.19)by Locality of Z, and therefore
$$\begin{aligned} Z^{-1}(F+G+H)=Z^{-1}(F+G)-Z^{-1}(G)+Z^{-1}(G+H)\ . \end{aligned}$$(4.20) - (iii):
-
(Dynamics) We apply \(Z^{-1}\) to the equation
$$\begin{aligned} Z\bigl (Z^{-1}(F)^{\psi }+\delta L(\psi )\bigr )=F^{\psi }+\delta L(\psi ) \end{aligned}$$(4.21)and get the wanted relation.
- (iv):
-
(Field shifts) This is again evident for the Lagrangian \(L_0\). The general case follows from \(Z^{-V}\in {{\mathscr {R}}}(M,L_0)\) and the equality \((Z^W)^{-1}=(Z^{-1})^W\).
- (i):
-
(Compactness of support) It is easy to check that \(Z^{-1}\) verifies also (4.8). Indeed, let \(F'=Z^{-1}(F+G)-Z^{-1}(G)\), then
$$\begin{aligned} F=Z\bigl (F'+Z^{-1}(G)\bigr )-Z\bigl (Z^{-1}(G)\bigr ) \end{aligned}$$(4.22)hence \({\mathrm {supp} \, }F'={\mathrm {supp} \, }F\).
Now, let \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }Z=\emptyset \). Then from (4.22) with \({\mathrm {supp} \, }F'={\mathrm {supp} \, }F\), we get \(F=F'=Z^{-1}(F+G)-Z^{-1}(G)\). We conclude that \({\mathrm {supp} \, }Z^{-1}\subset {\mathrm {supp} \, }Z\), and therefore \({\mathrm {supp} \, }Z^{-1}={\mathrm {supp} \, }Z\).
- (v):
-
(Causal Stability) evident.
\(\square \)
Corollary 4.9
The map \({{\mathscr {R}}}(M,L)\rightarrow {{\mathscr {R}}}(M,L+W)\,;\,Z\mapsto Z^W\) (4.11) is a group isomorphism for any interaction \(W\in \mathrm {Int}(M,L)\).
Proof
The claim is evident from (4.12) and (4.17). \(\square \)
The nontriviality of the group \({{\mathscr {R}}}(M,L)\) gives rise to a group of automorphisms of \({{\mathfrak {A}}}(M,L)\) preventing the validity of the time slice axiom. In detail:
Proposition 4.10
The map
induces a representation \(\beta ^{\mathrm {ret}}\)(named retarded) of \({\mathscr {R}}(M,L)\) by automorphisms \(\beta _Z^{\mathrm {ret}}\) of \({{\mathfrak {A}}}(M,L)\). The analogous advanced representation \(\beta ^{\mathrm {adv}}\) of \({\mathscr {R}}(M,L)\) is obtained by reversing the order of the factors in (4.23).
Proof
We first check that \(\beta _Z\equiv \beta _Z^{\mathrm {ret}}\) preserves the defining relations of \({{\mathfrak {A}}}(M,L)\).
-
Causality Relation: Let \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) and \(F,H\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+A_G)\) for which it holds that \(J^{L+A_G}_+({\mathrm {supp} \, }F)\cap {\mathrm {supp} \, }H=\emptyset \). Then,
$$\begin{aligned}&S(Z(0))\,\beta _Z(S(F+G+H))\nonumber \\&\quad =S(Z(F+G+H))\nonumber \\&\quad =S(Z(F+G)-Z(G)+Z(G+H))\nonumber \\&\quad =S\bigl ((Z(F+G)-Z(G))+Z(G)+(Z(G+H)-Z(G))\bigr ). \end{aligned}$$(4.24)Since \({\mathrm {supp} \, }Z(F+G)-Z(G)={\mathrm {supp} \, }F\) and \({\mathrm {supp} \, }Z(G+H)-Z(G)={\mathrm {supp} \, }H\) and by Definition 4.2 (v) \(J^{L+A_{Z(G)}}_+=J^{L+A_G}_+\) we obtain
$$\begin{aligned}&S\bigl (((Z(F+G)-Z(G))+Z(G)+(Z(G+H)-Z(G)))\bigr )\nonumber \\&\quad =S(Z(F+G))S(Z(G))^{-1}S(Z(G+H))\nonumber \\&\quad =S(Z(0))\,\beta _Z(S(F+G))\,\beta _Z(S(G))^{-1}\,\beta _Z(S(G+H)). \end{aligned}$$(4.25) -
Dynamical Relation:
$$\begin{aligned}&S(Z(0))\,\beta _Z(S(F^{\psi }+\delta L(\psi )))\nonumber \\&\quad =S(Z(F^{\psi }+\delta L(\psi )))\nonumber \\&\quad =S(Z(F)^{\psi }+\delta L(\psi ))=S(Z(F))=S(Z(0))\,\beta _Z(S(F)). \end{aligned}$$(4.26)
We see that \(\beta _Z\) is an endomorphism. For \(Z_1,Z_2\in {\mathscr {R}}(M,L)\), we find
and with \(\beta _{\mathrm {id}_{{\mathscr {R}}(M,L)}}=\mathrm {id}_{{{\mathfrak {A}}}(M,L)}\) we conclude that \(Z\mapsto \beta _Z\) is a representation by automorphisms. \(\square \)
Remark 4.11
Compared with the perturbative S-matrix and the Stückelberg–Petermann renormalization group \({\mathscr {R}}_0\), Proposition 4.10 corresponds to the part of the Main Theorem of perturbative renormalization, stating that if S is an admissible S-matrix (i.e., satisfies the axioms for the time-ordered product) this holds also for \(S\circ Z\) for all \(Z\in {\mathscr {R}}_0\), see [12, 28, 32].
Remark 4.12
According to (4.8), the support of Z(F) does not necessarily coincide with the support of F but only the support of \(Z(F)-Z(0)\) does. Hence, the automorphism \(\beta ^{\mathrm {ret}}_Z\) does not in general preserve the local subalgebras, thus is not an automorphism of the net. Instead its image can be interpreted as a theory with an additional interaction Z(0) (in the sense of a generalized field) together with a field renormalization \(F\mapsto Z(F)-Z(0)\), see (8.8). This will be crucial in the discussion of the renormalization group flow in Sect. 8.
The automorphisms induced by the renormalization group transform under the addition of an interaction in the following way:
Proposition 4.13
Let \(V\in \mathrm {Int}(M,L)\) have past compact support and \(Z\in {{\mathscr {R}}}(M,L)\). Then
Analogously, if V is future compact, then it holds that \(\beta _Z^{\mathrm {adv}}\circ \alpha _{V,-}=\alpha _{V,-}\circ \beta _{Z^V}^{\mathrm {adv}}\).
Proof
Let \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+V)\). Then, if \(f\in {{\mathscr {D}}}_s(M)\) with \(f\equiv 1\) on a sufficiently large region and with the abbreviations \(S_{(M,L)}\equiv S\), \(S_{(M,L+V)}\equiv S'\), and \(\beta _{\bullet }\equiv \beta _{\bullet }^{\mathrm {ret}}\) the claim follows from
\(\square \)
We collect some properties of renormalization group elements.
Proposition 4.14
Let \(Z\in {\mathscr {R}}(M,L)\), \(L=L_0+V\) with the free massless Lagrangian \(L_0\) and \(V\in \mathrm {Int}(M,L_0)\).
- (i):
-
For an affine functional \(F=\langle \phi ,h\rangle +c\), \(c\in {{\mathbb {R}}}\), \(h\in {{\mathscr {D}}}_{\mathrm {dens}}(M,{{\mathbb {R}}}^n)\) the relation
$$\begin{aligned} Z(F+G)=F+Z(G),\ G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L) \end{aligned}$$(4.31)holds true. Therefore, the addition of a source term \(\langle \phi ,q\rangle \) to the Lagrangian, with a smooth density \(q\in {{\mathscr {E}}}_{\mathrm {dens}}(M,{{\mathbb {R}}}^n)\), does not change Z, i.e. \(Z^{\langle \phi ,q\rangle }=Z\), and \({{\mathscr {R}}}(M,L+\langle \phi ,q\rangle )={{\mathscr {R}}}(M,L)\).
- (ii):
-
We have
$$\begin{aligned} {\mathrm {supp} \, }Z(0)\subset {\mathrm {supp} \, }Z\cap {\mathrm {supp} \, }V\ \end{aligned}$$(4.32)and, more generally,
$$\begin{aligned} {\mathrm {supp} \, }Z(F)\subset {\mathrm {supp} \, }F\cup ({\mathrm {supp} \, }Z\cap {\mathrm {supp} \, }V). \end{aligned}$$(4.33)In addition, it holds that
$$\begin{aligned} {\mathrm {supp} \, }\bigl (Z(F)-F\bigr )\subset {\mathrm {supp} \, }Z\ ,\quad F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\ . \end{aligned}$$(4.34) - (iii):
-
Let \(V(f)\in \mathrm {Q}(M,L_0)\) for \(f\in {{\mathscr {D}}}_s(M)\). Then, Z is invariant under shifts,
$$\begin{aligned} Z(F^{\psi })=Z(F)^{\psi }\ ,\ \psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\ . \end{aligned}$$(4.35)Moreover, for \(F\in \mathrm {Q}(M,L)\) we find
$$\begin{aligned} Z(F)=F+c_F \end{aligned}$$(4.36)with a constant functional \(c_F\). In particular, Z(0) is a constant functional.
Proof
- (i):
-
Let \(h=h_0+K\psi \), \(h_0\in {{\mathscr {D}}}_{\mathrm {dens}}(M,{{\mathbb {R}}}^n)\), \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\) where \({\mathrm {supp} \, }h_0\cap {\mathrm {supp} \, }Z=\emptyset \) and K is minus the d’Alembertian, considered as a map from functions to densities. Then,
$$\begin{aligned} \langle \phi ,K\psi \rangle =\delta L(\psi )-\frac{1}{2}\langle \psi ,K\psi \rangle -V(f)^{\psi }+V(f) \end{aligned}$$(4.37)with \(f\in {{\mathscr {D}}}_s(M)\), \(f\equiv 1\) on \({\mathrm {supp} \, }\psi \). Since constant functionals have empty support, we obtain, from the definition of the support of Z,
$$\begin{aligned} \begin{aligned} Z(F+G)&=Z\bigl (G+\delta L(\psi )+V(f)-V(f)^{\psi }\bigr )+\langle \phi ,h_0\rangle -\frac{1}{2}\langle \psi ,K\psi \rangle +c\\&=Z\bigl ((G+V(f))^{-\psi }-V(f)\bigr )^{\psi }+\delta L(\psi )+\langle \phi ,h_0\rangle -\frac{1}{2}\langle \psi ,K\psi \rangle +c\\&=Z(G)-\delta V(\psi )+\delta L(\psi )+\langle \phi ,h_0\rangle -\frac{1}{2}\langle \psi ,K\psi \rangle +c\\&=Z(G)+F \end{aligned} \end{aligned}$$where the second equality follows from (iii) and the third one from (iv) in Definition 4.2.
- (ii):
-
Let \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\) with \({\mathrm {supp} \, }\psi \cap {\mathrm {supp} \, }Z\cap {\mathrm {supp} \, }V=\emptyset \). We decompose \(\psi =\psi _1+\psi _2\) with \({\mathrm {supp} \, }\psi _1\cap {\mathrm {supp} \, }Z=\emptyset \), \({\mathrm {supp} \, }\psi _2\cap {\mathrm {supp} \, }V=\emptyset \) and \({\mathrm {supp} \, }\psi _1\subset {\mathrm {supp} \, }\psi \). From Definition 4.2(iv), we have with \(f\equiv 1\) on \({\mathrm {supp} \, }\psi \), \(f\in {{\mathscr {D}}}_s(M)\)
$$\begin{aligned} Z(0)^{\psi }=Z(V(f)^{\psi }-V(f))-V(f)^{\psi }+V(f)=Z(\delta V(\psi ))-\delta V(\psi ). \end{aligned}$$(4.38)With \(\delta V(\psi _1+\psi _2)=\delta V(\psi _1)+\delta V(\psi _2)^{\psi _1}\) and \(\delta V(\psi _2)=0\) (Proposition A.5), we get
$$\begin{aligned} Z(0)^{\psi }=Z(\delta V(\psi _1))-\delta V(\psi _1)=Z(0) \end{aligned}$$(4.39)since \({\mathrm {supp} \, }\delta V(\psi _1)\cap {\mathrm {supp} \, }Z=\emptyset \). Hence, \({\mathrm {supp} \, }Z(0)\subset {\mathrm {supp} \, }Z\cap {\mathrm {supp} \, }V\) by definition of the support of functionals.
The statement (4.33) follows immediately from (4.8) and (4.32):
$$\begin{aligned} {\mathrm {supp} \, }Z(F)={\mathrm {supp} \, }\bigl ((Z(F)-Z(0))+Z(0)\bigr )\subset {\mathrm {supp} \, }F\cup {\mathrm {supp} \, }Z(0)\ . \end{aligned}$$To prove (4.34) we decompose \(F=F_1+F_2\) with \({\mathrm {supp} \, }F_2\cap {\mathrm {supp} \, }Z=\emptyset \). By the definition of \({\mathrm {supp} \, }Z\) we obtain
$$\begin{aligned} Z(F)&=Z(F_1)+F_2\ , \end{aligned}$$hence \(Z(F)-F=Z(F_1)-F_1\). Taking into account (4.33), we conclude that \({\mathrm {supp} \, }(Z(F_1)-F_1)\subset {\mathrm {supp} \, }F_1\cup {\mathrm {supp} \, }Z\). Since for any \(x\not \in {\mathrm {supp} \, }Z\) we can find a decomposition with \(x\not \in {\mathrm {supp} \, }F_1\) we arrive at the conclusion.
- (iii):
-
To prove (4.35) we use again Definition 4.2(iv) and get for \(f\equiv 1\) on \({\mathrm {supp} \, }\psi \), \(f\in {{\mathscr {D}}}_s(M)\)
$$\begin{aligned} Z(F^{\psi })= & {} Z((F+V(f)^{-\psi })^{\psi }-V(f))\nonumber \\= & {} Z(F+V(f)^{-\psi }-V(f))^{\psi }+\delta V(\psi )\nonumber \\= & {} Z(F)^{\psi }+(V(f)^{-\psi }-V(f))^{\psi }+\delta V(\psi )\nonumber \\= & {} Z(F)^{\psi } \end{aligned}$$(4.40)where we used (4.31) in the third equality.
In particular, for a quadratic functional \(F\in \mathrm {Q}(M,L)\) the difference \(F-F^\psi \) is affine, hence
$$\begin{aligned} Z(F)-F=Z(F^\psi +(F-F^\psi ))-F=Z(F^\psi )-F^\psi =(Z(F)-F)^\psi ,\nonumber \\ \end{aligned}$$(4.41)from which we conclude that \(Z(F)-F\) is a constant functional. \(\square \)
5 Master Ward Identity
In certain cases, several elementary morphisms exist between objects of \(\mathfrak {Loc}\). Namely let \(M'=M\), let \(\chi \) be a diffeomorphism of M with compact support, let \(L'=\chi _{*}L\) and assume that the time orientations coincide outside of the support of \(\chi \). Set
\(\delta _{\chi }L\) can be interpreted as a retarded or an advanced interaction.Footnote 7 Hence, we obtain the arrow \(\iota _\chi \) from \((M,L)\rightarrow (M,L')\) and the arrows \(\iota _{\delta _{\chi }L,+},\iota _{\delta _{\chi }L,-}\) from \((M,L')\rightarrow (M,L)\) and can build the automorphisms
of \({{\mathfrak {A}}}(M,L)\). We compute
and
If the support of \(\chi \) does not intersect the past (future) of \({\mathrm {supp} \, }F\), we have \(\chi _*F=F\) and from the Causality Relation we conclude that \(\alpha ^{\chi }_{\pm }\) acts trivially on \(S_{(M,L)}(F)\).
An analogous discussion can be performed for compactly supported affine field redefinitions \(\Phi \). Let again \(M'=M\), and let \(L'=\Phi _{*}L\). Set \(\delta _{\Phi }L=L'-L\) and define
In the case of a translation \(\Phi :\phi \rightarrow \phi +\psi \), we see that the Dynamical Relation fixes these automorphisms to the identity.
The diffeomorphisms \(\chi \) act on affine field redefinitions \(\Phi =(A,\phi _0)\) by
We find the following commutation relation
Motivated by this property, we define:
Definition 5.1
(Symmetry Transformations). The group of (compactly supported) symmetry transformations

is the semidirect product of the group of compactly supported diffeomorphisms of M, \(\mathrm {Diff}_c(M)\), with the group of compactly supported smooth and affine field redefinitions, \({\mathscr {C}}^{\infty }_c(M,\mathrm {Aff}({{\mathbb {R}}}^n))\), with respect to the action (5.6), i.e., the product in  is defined byFootnote 8
is defined byFootnote 8
The support of such a transformation  is
is
The group  acts on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) by
acts on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) by
By using (5.7), we verify that

We also see that the support of  is the smallest closed subset N of M such that \({\mathrm {supp} \, }F\cap N=\emptyset \) implies
is the smallest closed subset N of M such that \({\mathrm {supp} \, }F\cap N=\emptyset \) implies  . The diffeomorphism part
. The diffeomorphism part  of
of  can be recovered from
can be recovered from  by
by

We set  with \(f\in {{\mathscr {D}}}_s(M)\) and
with \(f\in {{\mathscr {D}}}_s(M)\) and  and observe the relation
and observe the relation

We also set
with  ; this can equivalently be written as
; this can equivalently be written as

and analogously for  ; finally we find
; finally we find

In a first step, we compute these automorphisms for the case of a linear field redefinition, a quadratic Lagrangian \(L=\frac{1}{2}\langle \phi ,K\phi \rangle \), with a normally hyperbolic formally self-adjoint differential operator K (again considered as a map from functions to densities), and affine functionals \(F_h=\langle \phi ,h\rangle +\frac{1}{2}\langle h,\Delta _{\mathrm {adv}} h\rangle = \langle \phi ,h\rangle +\frac{1}{2}\langle h,\Delta _{\mathrm {ret}} h\rangle \), \(h\in {{\mathscr {D}}}_{\mathrm {dens}}(M,{{\mathbb {R}}}^n)\) with the retarded (\(\Delta _{\mathrm {ret}}\)) and advanced (\(\Delta _{\mathrm {adv}}\)) inverses of K. Let
where A is a \(\mathrm {GL}(n,{{\mathbb {R}}})\)-valued smooth function with compact support and the upper index t denotes the transpose. Then
We use the formula
derived in [21] for test densities h and local functionals G. We have
and hence with \(h'\doteq K(A^t)^{-1}\Delta _{\mathrm {adv}} h\) we get
hence
Now, the elements \(W(h)\doteq S(F_h)\) satisfy the Weyl relations
where \(\Delta =\Delta _{\mathrm {ret}}-\Delta _{\mathrm {adv}}\), as derived in [20]. Since
we conclude that \(\alpha ^{\Phi }_+\) acts trivially on \(S_{(M,L)}(F_h)\). This remains true when we replace \(F_h\) by a general affine functional \(F=F_h+c,\,\,c\in {{\mathbb {R}}}\), due to \(S_{(M,L)}(G+c)=S_{(M,L)}(G)\,e^{ic}\). Analogously, we find \(\alpha ^{\Phi }_-(W(h))=W(h)\). This implies in particular that \(S_{(M,L)}(\delta _{\Phi }L)\) commutes with all Weyl operators and is thus a multiple of 1 in an irreducible representation of the Weyl algebra. Indeed, in a perturbative calculation only numerical terms can contribute to \(S_{(M,L)}(\delta _{\Phi }L)\).
An analogous calculation can be done for a generic element of  . To summarize, we have found cases in which
. To summarize, we have found cases in which  is equal to \(S_{(M,L)}(F)\) up to a constant phase factor
is equal to \(S_{(M,L)}(F)\) up to a constant phase factor  .
.
In a formal path integral calculation, the transformation  corresponds to a change of variables. There the time ordered exponential of some local functional F corresponds to the time ordered exponential of
corresponds to a change of variables. There the time ordered exponential of some local functional F corresponds to the time ordered exponential of  up to the Jacobian of the transformation. In renormalized perturbation theory this is taken into account in the BV-Laplacian, which is a term in the quantum master equation. Within causal perturbation theory, it results in the anomalous Master Ward Identity. See [36] for the detailed account of the BV formalism and its connection to the anomalous Master Ward Identity.
up to the Jacobian of the transformation. In renormalized perturbation theory this is taken into account in the BV-Laplacian, which is a term in the quantum master equation. Within causal perturbation theory, it results in the anomalous Master Ward Identity. See [36] for the detailed account of the BV formalism and its connection to the anomalous Master Ward Identity.
In our axiomatic framework, we incorporate it in the following axiom: We introduce an L-dependent action of  on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\)
on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\)

Obviously  for the unit
for the unit  and, since
and, since  , we easily verify that
, we easily verify that  . The possible deviation of the MWI is described in terms of a map
. The possible deviation of the MWI is described in terms of a map

from the group of symmetry transformations  (Def. 5.1) to the renormalization group of the Lagrangian L, \({{\mathscr {R}}}(M,L)\) (Def. 4.2), satisfying
(Def. 5.1) to the renormalization group of the Lagrangian L, \({{\mathscr {R}}}(M,L)\) (Def. 4.2), satisfying  ,
,  and the cocycle relation
and the cocycle relation

The set of these cocycles is denoted by \({\mathfrak {Z}}(M,L)\).
Axiom 3
(Symmetries). Let (M, L) be some dynamical spacetime. A representation \(\pi \) of \({{\mathfrak {A}}}(M,L)\) satisfies the unitary anomalous Master Ward Identity (unitary AMWI) if there exists some \(\zeta \in {\mathfrak {Z}}(M,L)\) such that

Let \(I_{\zeta }\) denote the intersection of all ideals annihilated by representations which satisfy the unitary AMWI for a specific \(\zeta \), and let \({{\mathfrak {A}}}(M,L,\zeta )\) denote the quotient \({{\mathfrak {A}}}(M,L)/I_{\zeta }\) and \({{\mathfrak {A}}}_{(M,L,\zeta )}\) the corresponding net. The C*-algebra \({{\mathfrak {A}}}(M,L,\zeta )\) is generated by the unitaries \(S_{(M,L,\zeta )}(F)=S_{(M,L)}(F)+I_{\zeta }\).
For any F with  , the identity (5.27) reads
, the identity (5.27) reads

by using Definition 4.2(i).
Remark 5.2
By (5.28), we see the reason why we do not require that the elements Z of the renormalization group \({{\mathscr {R}}}(M,L)\) satisfy \(Z(0)=\mathrm {constant}\) (as it is done for the Stückelberg–Petermann group \({{\mathscr {R}}}_0\), cf. Remark 4.3). Actually, terms like Z(0), besides Proposition 4.10, will play a prominent role later (see Sect. 8).
In Section 10, we show that in perturbation theory the unitary AMWI is essentially equivalent to the AMWI as established in [10]. If  , we call (5.27) the unitary Master Ward Identity (unitary MWI); in perturbation theory the latter is equivalent to the on-shell MWI introduced in [29, 31] and [28, Chap. 4].Footnote 9 The (on-shell) MWI is a universal formulation of symmetries valid in classical field theory [31]. For this reason, we call
, we call (5.27) the unitary Master Ward Identity (unitary MWI); in perturbation theory the latter is equivalent to the on-shell MWI introduced in [29, 31] and [28, Chap. 4].Footnote 9 The (on-shell) MWI is a universal formulation of symmetries valid in classical field theory [31]. For this reason, we call  the anomaly map.
the anomaly map.
The cocycle relation (5.26) is motivated by the following result:
Proposition 5.3
Let  and let \(\pi \) be a representation of \({{\mathfrak {A}}}(M,L)\) such that
and let \(\pi \) be a representation of \({{\mathfrak {A}}}(M,L)\) such that

Then, it holds that

Proof
We shall write \(S\equiv \pi \circ S_{(M,L)}\) for simplicity. A straightforward application of (5.29) and the definition of  gives
gives

\(\square \)
Note that in causal perturbation theory with S-matrices evaluated on off-shell field configurations [32], the relation (5.30) even implies the cocycle relation (5.26). In contrast, the S-matrices in Proposition 5.3 would correspond to perturbative S-matrices evaluated on on-shell configurations and are not injective maps on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\), so the cocycle relation does not automatically follow.
In the formulation of the cocycle condition, we used an action of the group  on renormalization group elements \(Z\in {\mathscr {R}}(M,L)\) by
on renormalization group elements \(Z\in {\mathscr {R}}(M,L)\) by

This is well defined due to the following result:
Lemma 5.4
Let \(Z\in {{\mathscr {R}}}(M,L)\) and  and let
and let  be defined by (5.32). Then,
be defined by (5.32). Then,  .
.
Proof
We have to check the defining conditions of \({{\mathscr {R}}}(M,L)\) (Definition 4.2) for  : Locality (ii) is obtained straightforwardly by using that \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }H=\emptyset \) implies
: Locality (ii) is obtained straightforwardly by using that \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }H=\emptyset \) implies  .
.
To verify (i) for  let
let  . Then, we obtain
. Then, we obtain

hence  , where
, where  is defined in (5.12).
is defined in (5.12).
To check (iii), we set \(\psi _*F\doteq F^{\psi }\) and \(\psi _L F\doteq \delta L(\psi )+\psi _*F\). With this, the condition (iii) says that \(\psi _L\) commutes with elements of the renormalization group. We have

and find

by using (iii) for Z in the third equality sign.
(iv) We first consider the case of a quadratic Lagrangian. Then,

where we used in the third line that  is an affine functional (hence we may apply Proposition 4.14(ii)) and that
is an affine functional (hence we may apply Proposition 4.14(ii)) and that  is an affine map, and in the 4th line the result (5.34).
is an affine map, and in the 4th line the result (5.34).
For the general case, we show that the transformation with  commutes with the addition of an interaction according to (4.11), namely we have
commutes with the addition of an interaction according to (4.11), namely we have

As explained in Remark 4.7, we have to show that  . From (5.35), we know that
. From (5.35), we know that  commutes with \(\psi _*\); therefore, this holds also for
commutes with \(\psi _*\); therefore, this holds also for  .
.
(v) With simplified notation, we have

But by assumption,  induces the same causal structure as
induces the same causal structure as  . Hence, also
. Hence, also  preserves the causal structure. \(\square \)
preserves the causal structure. \(\square \)
For later purpose, we prove the following results:
Proposition 5.5
Let \(\zeta \) be as introduced above. Then, the following properties hold:
- (i):
-
Let \(\zeta \in {\mathfrak {Z}}(M,L)\) and \(W\in \mathrm {Int}(M,L)\). Then,
 (Definition 4.5) is an element of \({\mathfrak {Z}}(M,L+W)\), i.e.,
(Definition 4.5) is an element of \({\mathfrak {Z}}(M,L+W)\), i.e.,  (5.38)
(5.38) - (ii):
-
The advanced and retarded maps \(\alpha _{V,\pm }\) (2.17) and (2.18) induce isomorphisms \({\overline{\alpha }}_{V,\pm }\) from \({{\mathfrak {A}}}(M,L+V,\zeta ^V)\) to \({{\mathfrak {A}}}(M,L,\zeta )\).
Proof
(i) According to Proposition 4.6, \(\zeta ^W\) takes values in \({{\mathscr {R}}}(M,L+W)\). To shorten the notations, we write W in place of W(f):

where the cocycle relation for \(\zeta \) is used in the last step.
(ii) The assertion follows from the observation that the unitary AMWI in \({{\mathfrak {A}}}(M,L+V,\zeta ^V)\) is mapped to the unitary AMWI in \({{\mathfrak {A}}}(M,L,\zeta )\). To wit, writing again V instead of V(f), we obtain

and

thus the ideal \(I_{\zeta ^V}\) is mapped onto the ideal \(I_\zeta \). The same applies for \(\alpha _{V,-}\). \(\square \)
Definition 5.6
(Cocycle Equivalence). Two cocycles \(\zeta ,\zeta '\in {\mathfrak {Z}}(M,L)\) are equivalent, if there exists some \(Z\in {{\mathscr {R}}}(M,L)\) with

One easily verifies that this is indeed an equivalence relation: symmetry follows from  and transitivity from
and transitivity from  . Equivalences between cocycles lead to the following relations:
. Equivalences between cocycles lead to the following relations:
Proposition 5.7
Let \(\zeta \in {\mathfrak {Z}}(M,L)\) be a cocycle and \(Z\in {{\mathscr {R}}}(M,L)\). Then,
- (i):
-
The map
 with
with  (5.43)
(5.43)is a cocycle, i.e., it satisfies the relation (5.26).
- (ii):
-
Both \(\beta _Z^{\mathrm {ret}}\) and \(\beta _Z^{\mathrm {adv}}\) (Proposition 4.10) induce isomorphisms \({\overline{\beta }}_Z^{\,\mathrm {ret/adv}}\) from \({{\mathfrak {A}}}(M,L,\zeta ')\) to \({{\mathfrak {A}}}(M,L,\zeta )\), where \(\zeta '\) is defined as in (i).
- (iii):
-
The isomorphism \(\epsilon _Z\doteq \alpha _{A_{Z(0)},+}^{-1}\circ \beta ^{\mathrm {ret}}_Z=\alpha _{A_{Z(0)},-}^{-1}\circ \beta ^{\mathrm {adv}}_Z\) extends to a net isomorphism
$$\begin{aligned} {{\mathfrak {A}}}_{(M,L,\zeta ')} \rightarrow {{\mathfrak {A}}}_{(M,L+A_{Z(0)},\zeta ^{A_{Z(0)}})}\ . \end{aligned}$$
Proof
- (i):
-
Inserting the definitions and the cocycle relation for \(\zeta \), we obtain

- (ii):
-
The automorphisms \(\beta _Z^{\mathrm {ret/adv}}\) map the ideals defined by the unitary AMWI into each other, as may be seen from the equation (denoting \(S_{(M,L)}=S\))
 (5.44)
(5.44)for the retarded case, the advanced case follows analogously.
- (iii):
-
Since \({\mathrm {supp} \, }(Z(F)-Z(0))={\mathrm {supp} \, }F\), the isomorphism \(\epsilon _Z\),
$$\begin{aligned} \epsilon _Z(S_{(M,L,\zeta ')}(F))=S_{(M,L+A_{Z(0)}, \zeta ^{A_{Z(0)}})}(Z(F)-Z(0))\ , \end{aligned}$$(5.45)preserves the local subalgebras.
\(\square \)
We can use the cocycle relation (5.26) for the map  to define a modified action of
to define a modified action of  on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) by
on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) by

namely

Remark 5.8
Note that the unitary AMWI can be written in terms of  as
as

We now consider the case that the cocycle  in the unitary AMWI is trivial for
in the unitary AMWI is trivial for  with
with  . We have the following result:
. We have the following result:
Proposition 5.9
The set  is a subgroup of
is a subgroup of  .
.
Proof
Let  then
then  , \(i=1,2\), hence
, \(i=1,2\), hence

thus  and
and  . Moreover, for
. Moreover, for 

so also  . \(\square \)
. \(\square \)
6 Time Slice Axiom and the Relative Cauchy Evolution
We now want to prove that the unitary AMWI implies the time slice axiom.
Theorem 6.1
(Time slice) Let \(N\subset M\) be a causally convex and globally hyperbolic neighborhood of a Cauchy surface of M with respect to the causal structure induced by the Lagrangian L and let \(\zeta \in {\mathfrak {Z}}(M,L)\) be a cocycle. Then,
Here,  is obtained by the restriction of
is obtained by the restriction of  .
.
Proof
We shall use the notation \(S\equiv S_{(M,L,\zeta )}\) for simplicity throughout the proof and do not display explicitly the restrictions as in (6.1). We first restrict ourselves to a stationary spacetime \({{\mathbb {R}}}\times \Sigma \) with time coordinate t and with a time independent quadratic Lagrangian L and a neighborhood N of the submanifold \(t=0\).
Let \(F\in {{\mathscr {F}}}_{\mathrm {loc}}({{\mathbb {R}}}\times \Sigma ,L)\). We show that S(F) can be written as a finite product of S-matrices whose arguments have supports in \(J_-(N)\cap {\mathrm {supp} \, }F\).
If \({\mathrm {supp} \, }F\subset J_-(N)\) this is trivial. If \({\mathrm {supp} \, }F\not \subset J_-(N)\), we argue as follows: Let \(a=\sup \{t|(t,x)\in {\mathrm {supp} \, }F\}\). Choose \(\tau \in (0,a/2)\) and a compactly supported diffeomorphism \(\chi \) with support in \(J_+(\Sigma )\) which acts on the set \(\{(t,x)\in J_-({\mathrm {supp} \, }F)|t\in [a/2,a]\}\) as a translation of the time variable by \(-\tau \) and maps the set \(\{(t,x)\in J_-({\mathrm {supp} \, }F)|t\in [0,a/2]\}\) into the set \(\{(t,x)\in J_-({\mathrm {supp} \, }F)|t\in [0,a/2-\tau ]\}\). An example for such a diffeomorphism is
with test functions \(\rho \in {{\mathscr {D}}}({{\mathbb {R}}}_+), \sigma \in {{\mathscr {D}}}(\Sigma )\) with \({\dot{\rho }}>-1\), \(\rho (t)=-\tau \), \(t\in [a/2,a]\) and \(0\le \sigma \le 1\), \(\sigma \equiv 1\) on \(\{x|(t,x)\in J_-({\mathrm {supp} \, }F)\text { for some }t\in [a/2,a]\}\); see Figure 1.
Illustration of the proof of Theorem 6.1: N is filled by a light gray, \({\mathrm {supp} \, }F\) and \(J_-({\mathrm {supp} \, }F)\cap \{t\ge a/2\}\) are sketched by a solid line, the remaining part of \(J_-({\mathrm {supp} \, }F)\) is sketched by a dotted line, \(\chi ({\mathrm {supp} \, }F)\) is filled by a dark gray, \(\chi \bigl (J_-({\mathrm {supp} \, }F)\bigr )=J_-^{L+\delta _{\chi }L}\bigl (\chi ({\mathrm {supp} \, }F)\bigr )\) and \(\chi \bigl (J_-({\mathrm {supp} \, }F)\cap \{t\ge a/2\}\bigr )\) are sketched by a dashed line. Note that the latter set is obtained from \(J_-({\mathrm {supp} \, }F)\cap \{t\ge a/2\}\) by a translation of the time variable by \((-\tau )\); however, \(J_-({\mathrm {supp} \, }F)\) and \(\chi (J_-({\mathrm {supp} \, }F))\) join at \(t=0\), since there they leave the support of \(\chi \)
Next we prove the following auxiliary result:
Lemma 6.2
Let (M, L) be a stationary dynamical spacetime. Let \(\chi \) be a compactly supported diffeomorphism of M with \(\chi (t,x)=(t+v,x)\) for all (t, x) in an open set U, where v is constant. Then, the variation \(\delta _\chi L\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) satisfies \({\mathrm {supp} \, }\delta _\chi L\cap \chi (U)=\emptyset \).
Proof
The thesis is equivalent to the condition
for any \(\phi \in {{\mathscr {E}}}(M)\) and any \(\psi \in {{\mathscr {E}}}_c(M)\) with \({\mathrm {supp} \, }\psi \subset \chi (U)\), where \(\delta _\chi L[\phi ]=L(f\circ \chi )[\phi \circ \chi ]-L(f)[\phi ]\) with \(f\in {{\mathscr {D}}}(M)\) and \(f\equiv 1\) on \({\mathrm {supp} \, }\chi \).
According to (2.4), we have \(L(f)[\phi ]=\int L(x)[f\phi ]\) where L(x) is a density which depends on the jet of \(f\phi \) at x. Thus
for any smooth function h with \(h\equiv 1\) on \({\mathrm {supp} \, }\psi \). We now choose an h with \({\mathrm {supp} \, }h\subset \chi (U)\). Then,
But since the functions \(hf,h\phi \) and \(\psi \) are supported in \(\chi (U)\), \(\chi \) acts on them as a time translation by v, and (6.3) follows from the stationarity of L. \(\square \)
Continuation of the proof of Theorem 6.1. From the unitary AMWI, we obtain
Since \(\zeta _{\chi }\in {{\mathscr {R}}}(M,L)\) and L is quadratic, \(\zeta _{\chi }^{-1}(0)\) is a constant (Proposition 4.14(ii)) and therefore \({\mathrm {supp} \, }\zeta _{\chi }^{-1}(F)={\mathrm {supp} \, }F\) (by using (4.8)).
Then, \({\mathrm {supp} \, }\chi _{*}\zeta _{\chi }^{-1}(F)=\chi ({\mathrm {supp} \, }F)\) and
and since by assumption L is stationary,
by using the Lemma. We decompose \(\delta _{\chi }L=H_++H_-\) such that
Since \(\chi (J_-({\mathrm {supp} \, }F))=J_-^{L+\delta _{\chi }L}(\chi ({\mathrm {supp} \, }F))\) and \(H_+\) does not change the metric in this region, we can replace \(\delta _{\chi }L\) by \(H_-\) and get \({\mathrm {supp} \, }H_+\cap J_-^{L+A_{H_-}} ({\mathrm {supp} \, }\chi _{*}\zeta _{\chi }^{-1}(F))=\emptyset \), thus we obtain the factorization
Again by the unitary AMWI, \(S(\delta _{\chi }L)=S(\zeta _{\chi }(0))\). \(\zeta _{\chi }(0)\) is a constant functional and thus has empty support. Hence, the arguments of all S-matrices on the right hand side have compact supports contained in \((J_+(N)\cap \{t\le a-\tau \})\cup (J_-(N)\cap {\mathrm {supp} \, }F)\).
We may now iterate the argument and find after a finite number of steps, that S(F) can always be written as a product of S-matrices whose arguments have support in \(J_-(N)\cap {\mathrm {supp} \, }F\).
We then repeat the procedure for the time reversed situation and arrive at the desired result for the special case of a free stationary Lagrangian.
For a generic choice of a dynamical spacetime (M, L), a cocycle \(\zeta \) and a neighborhood N of a Cauchy surface \(\Sigma \), we choose a foliation \(M={{\mathbb {R}}}\times \Sigma \) with \(\{0\}\times \Sigma \equiv \Sigma \) where the metric associated to L assumes the form
with a smooth positive function a and a smooth family \(h_t\) of Riemann metrics on \(\Sigma \). We then set
with
Let us define \(V\doteq L-L_0\in \mathrm {Int}(M,L_0)\), hence \(-V\in \mathrm {Int}(M,L)\). According to Proposition 5.5, \(\zeta ^{-V}\) is an \({{\mathscr {R}}}(M,L_0)\)-valued cocycle. We now use Theorem 3.3 for a faithful representation \(\pi _0\) of \({{\mathfrak {A}}}(M,L_0,\zeta ^{-V})\). Since \(L_0\) is stationary and quadratic, we know from the first part of the proof that the time slice axiom holds for \(\pi _0\). Since \(\Sigma \) is a Cauchy surface for both, g and \(g_0\), we conclude that, for any splitting \(V=V_++V_-\) into a past compact and a future compact part, the representation \(\pi \doteq \pi _0\circ \alpha _{V_+,V_-}\) has the property
Since with \(\pi _0\) also \(\pi \) is faithful, we conclude that
\(\square \)
Granted the time slice axiom, we can briefly discuss the relative Cauchy evolution that was defined and implemented in the more general framework of locally covariant quantum field theory [16], to which we refer for more details. The basic advanced and retarded maps in (2.17) and (2.18) interpolate between the algebra \({{\mathfrak {A}}}(M,L',\zeta )\) and the perturbed algebra \({{\mathfrak {A}}}(M,L,\zeta ^V)\), with \(L=L'+V\) (Proposition 5.5), where the interaction V changes also the metric g in a compact region of M, but the resulting transformed metric \(g+h\) remains globally hyperbolic. Let \(N_{\pm }\) be two neighborhoods of Cauchy surfaces in \((M,L')\), one in the past and the other in the future of the support of the perturbation V, w.r.t. the causal structure induced by \(L'\). Let \(\chi _{\pm }\) denote the isometric embeddings of \(N _{\pm }\) into M. We combine the basic retarded and advanced maps (2.17) and (2.18) with the monomorphisms \(\alpha _{\chi _{\pm }}\) induced by these embeddings. Since Theorem 6.1 holds, these combinations give rise to bijective maps. Let us call them as \({\tilde{\alpha }}_{V,-} \doteq \alpha _{\chi _-}\circ {\overline{\alpha }}_{V,-}^{-1}\) and \({\tilde{\alpha }}_{V,+} \doteq \alpha _{\chi _+}\circ {\overline{\alpha }}_{V,+}^{-1}\), where the extensions \({\overline{\alpha }}_{V,\pm }\) are the ones from Proposition 5.5(ii). We obtain:
Hence, it is straightforward to compute that the relative Cauchy evolution automorphism \(\beta _V\) of \({{\mathfrak {A}}}(M,L',\zeta )\) defined via these maps is given by
Remark 6.3
As expected, the relative Cauchy evolution i.e. scattering morphism as also called in [16], is indeed implemented by the scattering matrices. This also justifies, a posteriori, the interpretation of the symbols \(S_\bullet (F)\) as scattering matrices, inducing a perturbation of the theory by an intermediate change in the interaction and metric in a compact region.
Our new formulation of the relative Cauchy evolution also allows one to obtain the stress-energy tensor. If \(\delta _s L\) is the change in the Lagrangian induced by a change in the metric from g to \(g_s\), the S-matrix \(S_{(M,L,\zeta )}(\delta _s L)\) may be interpreted as the time-ordered exponentiated stress-energy tensor, so to obtain the stress-energy tensor, we need to be able to differentiate \(S_{(M,L,\zeta )}(\delta _s L)\) in an appropriately regular Hilbert space representation \(\pi \) for a smooth one-parameter family of metrics \(g_s\) with , \(g_0=g\), \(s\in [0,1]\) and \((g_s-g)\) compactly supported, satisfying the geometric assumptions as in Section 4.1 of [16]. Assume that \(\pi \) is such that \(\pi (S_{(M,L,\zeta )}(\delta _sL))\) is differentiable as a function of s in the sense of quadratic forms on a dense domain \({\mathscr {V}}\), i.e. we require that
with \(\theta \in {\mathscr {V}}\) and \(h_{\mu \nu }=\frac{d}{ds}(g_s)_{\mu \nu }\big \vert _{s=0}\), and that the right-hand side defines an operator-valued distribution \(T^{\mu \nu }\) with matrix elements \(t^{\mu \nu }\) and domain \({\mathscr {V}}\).
One should choose this domain according to the physical problem at hand, so that it remains invariant under some appropriate class of observables. Note that our current formulation is an improvement over the results of [16], since there one could only reconstruct the derivation given by the commutator with the stress-energy tensor, while here we obtained the stress-energy tensor itself.
Covariant conservation of the stress-energy tensor can be obtained as follows. Let \((\chi _s)\) be a 1-parameter group of compactly supported diffeomorphisms and consider the induced change \((g_s-g)\) of the metric and \(\delta _sL\) of the Lagrangian. We interpret the equation
for all \(\chi _s \in \mathrm {Diff}_c(M) \), as the finite version of the covariant conservation of the stress-energy tensor. Namely, differentiating this property in the representation \(\pi \) results in \(\nabla _\mu T^{\mu \nu }=0\), in the sense of operator-valued distributions (see, e.g., [41]).
To see when the stress energy tensor is covariantly conserved, note that by the unitary AMWI, we have that
so (6.16) holds if the cocycle \(\zeta \) is trivial for the subgroup \(\mathrm {Diff}_c(M)\) of  , i.e. in the absence of anomalies for diffeomorphisms.
, i.e. in the absence of anomalies for diffeomorphisms.
7 Symmetries of the Lagrangian and the Anomalous Noether Theorem
In this section, we will show how unbroken symmetries of the Lagrangian (those that survive quantization and do not lead to nontrivial anomalies) give rise to the unitary action on our algebras that can be interpreted as the quantum version of Noether’s theorem (Corollary 7.5), which follows from our main result: the Anomalous Noether Theorem (Theorem 7.3).
Let  denote the unit component of the semidirect product of the diffeomorphism group of M and the group of affine field redefinitions, as described in Definition 5.1, but without the restriction to compact support. Note that
denote the unit component of the semidirect product of the diffeomorphism group of M and the group of affine field redefinitions, as described in Definition 5.1, but without the restriction to compact support. Note that  is a normal subgroup of
is a normal subgroup of  . Each element
. Each element  has an action on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) that can be approximated locally by elements of
has an action on \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) that can be approximated locally by elements of  in the sense of the following definition.
in the sense of the following definition.
Definition 7.1
Let \({{\mathscr {O}}}\subset M\) be a relatively compact subset.  denotes the set of all
denotes the set of all  such that
such that  for all \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) with \({\mathrm {supp} \, }F\subset {{\mathscr {O}}}\).
for all \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) with \({\mathrm {supp} \, }F\subset {{\mathscr {O}}}\).
Note that this set is non-empty, since one can always use partitions of unity to construct these local approximations.
For a given Lagrangian L on M, we consider the subgroup of dynamical symmetries

The group of dynamical symmetries  is represented by automorphisms
is represented by automorphisms  of \({{\mathfrak {A}}}(M,L)\), induced by their action on the generators,
of \({{\mathfrak {A}}}(M,L)\), induced by their action on the generators,

The ideal \(I_{\zeta }\) of \({{\mathfrak {A}}}(M,L)\) induced by the cocycle \(\zeta \) is generated by the elements

We apply the automorphism  of \({{\mathfrak {A}}}(M,L)\) to these elements and obtain
of \({{\mathfrak {A}}}(M,L)\) to these elements and obtain

with the action

of  on \({\mathfrak {Z}}(M,L)\). Here, we used that
on \({\mathfrak {Z}}(M,L)\). Here, we used that  is a normal subgroup of
is a normal subgroup of  and that
and that

as well that  by assumption.
by assumption.
To verify the consistency of the definition (7.5), first note that  as one finds straightforwardly by checking the defining properties of \({{\mathscr {R}}}(M,L)\); in addition, one verifies that
as one finds straightforwardly by checking the defining properties of \({{\mathscr {R}}}(M,L)\); in addition, one verifies that  satisfies again the cocycle relation,
satisfies again the cocycle relation,

and associativity:

The latter is straightforward, while (7.7) is obtained by inserting the definitions and the cocycle relation for \(\zeta \) and by using

which relies on  .
.
From (7.4), we conclude that  and, therefore,
and, therefore,  induces an isomorphism
induces an isomorphism  of the quotient algebras
of the quotient algebras

Hence,  induces a flow on the space of theories with a given Lagrangian L, but possibly different cocycles \(\zeta \). This is quite analogous to the flow of the renormalization group under scalings for scale-invariant Lagrangians as we will discuss in the next section.
induces a flow on the space of theories with a given Lagrangian L, but possibly different cocycles \(\zeta \). This is quite analogous to the flow of the renormalization group under scalings for scale-invariant Lagrangians as we will discuss in the next section.
We want to understand better the action of  on cocycles. We use the fact that the symmetries of the Lagrangian can be locally approximated by compactly supported symmetries. We find the following relations:
on cocycles. We use the fact that the symmetries of the Lagrangian can be locally approximated by compactly supported symmetries. We find the following relations:
Proposition 7.2
Let \({{\mathscr {O}}}\subset M\) be an open relatively compact region and  . Then for
. Then for  , with
, with  defined as in (5.12) and
defined as in (5.12) and  as in Definition 7.1, we have:
as in Definition 7.1, we have:


where  is defined by the formula (7.5).
is defined by the formula (7.5).
Proof
 is equivalent to
is equivalent to  , hence
, hence  . Moreover,
. Moreover,  is a diffeomorphism of M which is the identity on
is a diffeomorphism of M which is the identity on  , hence due to
, hence due to 

and thus  . Now
. Now  , hence
, hence  . Inserting these relations into (7.5) yields the first equality.
. Inserting these relations into (7.5) yields the first equality.
We now use that  for
for  . Therefore,
. Therefore,  for
for  and with
and with

we get  . Hence
. Hence  . Then with
. Then with

and

for \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) (by using (4.2)) we get

Using the cocycle identity, we finally get the second equation

\(\square \)
We observe that, locally, the flow of  is induced by the anomaly map \(\zeta \) restricted to local approximations of
is induced by the anomaly map \(\zeta \) restricted to local approximations of  . We now study the consequences of the unitary AMWI.
. We now study the consequences of the unitary AMWI.
Theorem 7.3
(Anomalous Noether Theorem). Let (M, L) be a dynamical spacetime, equipped with a cocycle \(\zeta \in {\mathfrak {Z}}(M,L)\). For  and any choice of
and any choice of  , with \({{\mathscr {O}}}\subset M\) relatively compact and causally convex, there exists a unitary
, with \({{\mathscr {O}}}\subset M\) relatively compact and causally convex, there exists a unitary  such that
such that

for all \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\) for which \({\mathrm {supp} \, }F\subset {{\mathscr {O}}}\), with

and  if
if  .
.
Proof
The unitary AMWI yields for 

with  . We have
. We have  . Since \({{\mathscr {O}}}\) is causally convex, we decompose (see the corresponding procedure in Theorem 3.5)
. Since \({{\mathscr {O}}}\) is causally convex, we decompose (see the corresponding procedure in Theorem 3.5)

with \({\mathrm {supp} \, }Q_i^+\cap J_-^{L+A_{Q_{<i}}}({{\mathscr {O}}})=\emptyset \) and \({\mathrm {supp} \, }Q_i^-\cap J^{L+A_{Q_{<i}+Q_i^+}}_+({{\mathscr {O}}})=\emptyset \), \(Q_{<i}\doteq \sum _{j<i,\pm }Q_j^{\pm }\), in particular \(Q_{<1}=0\) and  . We then use stepwise causal factorization for \(S'(F+Q_{<6})\) with
. We then use stepwise causal factorization for \(S'(F+Q_{<6})\) with  (noticing that by Proposition 4.10 and 5.7, we have
(noticing that by Proposition 4.10 and 5.7, we have  ) starting with \(i=5\) and obtain
) starting with \(i=5\) and obtain

where we have also taken into account that

by the unitary AMWI for \(F=0\). We end up with (7.19), where
In the formula for U, one may replace \(S'\) by  .
.
The second equation in (7.20) is verified as follows

To prove the last statement, let  . We set
. We set  and use that
and use that  . Then
. Then  and
and  . We split
. We split

and use that  . Then,
. Then,

in the second step we have taken into account that  (see the proof of Proposition 7.2) and in the second last step that
(see the proof of Proposition 7.2) and in the second last step that  (4.34). This finishes the proof. \(\square \)
(4.34). This finishes the proof. \(\square \)
Remark 7.4
A simple example of implementation of the previous theorem can be found in Subsection 10.2.
We now turn to the group of unbroken symmetries,  . Elements of this group induce automorphisms
. Elements of this group induce automorphisms  of \({{\mathfrak {A}}}(M,L,\zeta )\), but may still have nontrivial anomaly. A group which has locally trivial anomalies can be defined by
of \({{\mathfrak {A}}}(M,L,\zeta )\), but may still have nontrivial anomaly. A group which has locally trivial anomalies can be defined by

Actually,  is a subgroup of
is a subgroup of  . Namely, let
. Namely, let  . By using Proposition 7.2, we obtain
. By using Proposition 7.2, we obtain

for a suitable choice of  ; in the last step we have taken into account that
; in the last step we have taken into account that  by using (4.33).
by using (4.33).
As a straightforward application of Theorem 7.3 to what just discussed, we find
Corollary 7.5
(Unitary Noether Theorem). For any  and a causally convex and relatively compact region \({{\mathscr {O}}}\), there exists a unitary \(U\in {{\mathfrak {A}}}(M,L,\zeta )\) such that
and a causally convex and relatively compact region \({{\mathscr {O}}}\), there exists a unitary \(U\in {{\mathfrak {A}}}(M,L,\zeta )\) such that

for all F with \({\mathrm {supp} \, }F\subset {{\mathscr {O}}}\).
This entails that symmetries  are locally implemented by unitaries, and the particular case of the unitary MWI
are locally implemented by unitaries, and the particular case of the unitary MWI

is a unitary version of a conservation law. This constitutes a unitary version of the Noether theorem. We see, however, that, dependent on the anomaly \(\zeta \), the Noether theorem applies only to a subgroup of unbroken symmetries.
Example 7.6
To give a concrete example for  in the case that
in the case that  , we look at scalar QED (for details see [34, Sect. 4.2]): for \(L=L_0\) the free Lagrangian (including the mass term for the complex scalar field \(\phi \)) and for the affine field redefinition
, we look at scalar QED (for details see [34, Sect. 4.2]): for \(L=L_0\) the free Lagrangian (including the mass term for the complex scalar field \(\phi \)) and for the affine field redefinition  given by
given by
where \(\alpha \in {{\mathscr {D}}}(M,{{\mathbb {R}}})\), one obtains

where j is the electromagnetic current of the free theory (i.e., the Noether current pertaining to the invariance of \(L_0\) under the global U(1)-transformation \(\phi (x)\mapsto \phi (x)\,e^{ia}\) with \(a\in {{\mathbb {R}}}\)).
8 Renormalization Group Flow
We have seen in the previous section that the presence of anomalies in form of a cocycle \(\zeta \) might induce a nontrivial action of the symmetry group  of the Lagrangian on the theory by the action of
of the Lagrangian on the theory by the action of  on \(\zeta \). We also observed that, locally, the action of
on \(\zeta \). We also observed that, locally, the action of  can be understood as an action of the renormalization group on the theory (Theorem 7.3) where the renormalization group element is given by
can be understood as an action of the renormalization group on the theory (Theorem 7.3) where the renormalization group element is given by  , for a local approximation
, for a local approximation  . We now want to see whether also a global interpretation is possible. For this purpose, we ask in which sense our cocycles can be extended to not necessarily compactly supported symmetry transformations
. We now want to see whether also a global interpretation is possible. For this purpose, we ask in which sense our cocycles can be extended to not necessarily compactly supported symmetry transformations  . A direct extension of \(\zeta \), however, might not map compactly supported functionals to compactly supported functionals.
. A direct extension of \(\zeta \), however, might not map compactly supported functionals to compactly supported functionals.
We therefore define for F with \({\mathrm {supp} \, }F\subset {{\mathscr {O}}}\), 

\(\theta \) is well defined in view of the following proposition:
Proposition 8.1
 does not depend on the choice of
does not depend on the choice of  .
.
Proof
Let  . Then,
. Then,  with
with  and
and  . The cocycle relation yields
. The cocycle relation yields

We have

Since  (by (4.34)) we get from Locality of
(by (4.34)) we get from Locality of  the relation
the relation

But the first term on the right hand side is equal to  . This yields the claim. \(\square \)
. This yields the claim. \(\square \)
In the next step, we show that the family  relatively compact, defines a generalized field
relatively compact, defines a generalized field  . Namely, given \(f\in {{\mathscr {D}}}(M)\), we choose \({{\mathscr {O}}}\) such that \({\mathrm {supp} \, }f\subset {{\mathscr {O}}}\) and set
. Namely, given \(f\in {{\mathscr {D}}}(M)\), we choose \({{\mathscr {O}}}\) such that \({\mathrm {supp} \, }f\subset {{\mathscr {O}}}\) and set

Analogously to (A.14), the defining properties of a generalized field (Definition A.1) are satisfied. Moreover, we prove that it is also well defined, namely
Proposition 8.2
 does not depend on the choice of
does not depend on the choice of  .
.
Proof
Choosing  as in the previous proposition, we have
as in the previous proposition, we have

The support of the first term on the right hand side is equal to  , hence its evaluation on configurations \(f\phi \) with \({\mathrm {supp} \, }f\subset {{\mathscr {O}}}\) is independent of \(\phi \), and we arrive at
, hence its evaluation on configurations \(f\phi \) with \({\mathrm {supp} \, }f\subset {{\mathscr {O}}}\) is independent of \(\phi \), and we arrive at

\(\square \)
We now can construct the flow of theories under the action of the symmetry group in terms of the renormalization group. By the Anomalous Noether Theorem, Theorem 7.3, we saw that, up to an inner automorphism, the action of  can locally be replaced by an isomorphism induced by a renormalization group transformation \({\overline{\beta }}^{\mathrm {ret}}_Z\).
can locally be replaced by an isomorphism induced by a renormalization group transformation \({\overline{\beta }}^{\mathrm {ret}}_Z\).
We recall that a renormalization group element \(Z\in {{\mathscr {R}}}(M,L)\) induces an isomorphism \(\beta ^{\mathrm {ret}}_Z\) and, from Remark 4.12 (see also (5.45)), that \(\beta ^{\mathrm {ret}}_Z\) can be interpreted as the composition of two actions: one adding an interaction Z(0) and the other transforming the local functionals by \(F\mapsto Z(F)-Z(0)\), i.e.
Passing to the quotient algebras depending on a cocycle \(\zeta \), notice that for both previous actions (extended to the quotients, with  , where
, where  is a constantFootnote 10) we give meaningful expressions, which depend only on
is a constantFootnote 10) we give meaningful expressions, which depend only on  , but neither on the choice of
, but neither on the choice of  nor of \({{\mathscr {O}}}\) (by Propositions 8.1 and 8.2). Hence, we interpret the
nor of \({{\mathscr {O}}}\) (by Propositions 8.1 and 8.2). Hence, we interpret the  -transformed theory as a theory with an additional interaction
-transformed theory as a theory with an additional interaction  and a field transformation
and a field transformation  . This corresponds nicely to the standard description of anomalies (as e.g. the scaling anomaly) by running coupling constants (i.e. addition of terms to the Lagrangian) and renormalizations of composite fields (i.e. field transformation). We formulate our findings in the following theorem:
. This corresponds nicely to the standard description of anomalies (as e.g. the scaling anomaly) by running coupling constants (i.e. addition of terms to the Lagrangian) and renormalizations of composite fields (i.e. field transformation). We formulate our findings in the following theorem:
Theorem 8.3
Symmetries  of a Lagrangian L induce, in the presence of a nontrivial anomaly \(\zeta \), a flow of the associated quantum field theory \({{\mathfrak {A}}}_{(M,L,\zeta )}\) which can be described in two equivalent ways: either as an action of
of a Lagrangian L induce, in the presence of a nontrivial anomaly \(\zeta \), a flow of the associated quantum field theory \({{\mathfrak {A}}}_{(M,L,\zeta )}\) which can be described in two equivalent ways: either as an action of  on the anomaly leading to the net \({{\mathfrak {A}}}_{(M,L,h^{-1}\zeta )}\) (see (7.10)) or as a change
on the anomaly leading to the net \({{\mathfrak {A}}}_{(M,L,h^{-1}\zeta )}\) (see (7.10)) or as a change  of the Lagrangian, followed by a transformation
of the Lagrangian, followed by a transformation  of the fields. The equivalence follows from the fact that the map
of the fields. The equivalence follows from the fact that the map

where  , induces a net isomorphism
, induces a net isomorphism  .
.
Remark 8.4
Note that if we restrict ourselves to scaling transformations, then Theorem 8.3 corresponds to the Theorem 6.2 of [12] (algebraic Callan–Symanzik equation). In the same paper, also the relations to other renormalization group flow equations (e.g., Polchinski) are discussed.
Remark 8.5
The map (8.9) corresponds to the net isomorphism \(\epsilon _Z\) (Proposition 5.7(iii)) with  , since (by Proposition 7.2) locally it holds that
, since (by Proposition 7.2) locally it holds that  . However, since
. However, since  has non-compact support, it does not suffice to refer to this result, instead we give a direct proof.
has non-compact support, it does not suffice to refer to this result, instead we give a direct proof.
Proof
Since  preserves the support due to condition (ii) for elements of the renormalization group, the map preserves the local subalgebras. We check whether it also maps the axioms for
preserves the support due to condition (ii) for elements of the renormalization group, the map preserves the local subalgebras. We check whether it also maps the axioms for  into the corresponding axioms for \({{\tilde{S}}}\doteq S_{(M,{{\tilde{L}}},{{\tilde{\zeta }}})}\) and vice versa.
into the corresponding axioms for \({{\tilde{S}}}\doteq S_{(M,{{\tilde{L}}},{{\tilde{\zeta }}})}\) and vice versa.
We use the fact that  interpolates between the respective Lagrangians, namely we have
interpolates between the respective Lagrangians, namely we have

as well as

where  , by using Proposition 7.2 in the second step.
, by using Proposition 7.2 in the second step.
Since  also satisfies the Locality condition of Definition 4.2 (ii), the Causality Relation (Axiom 1) for S is mapped into
also satisfies the Locality condition of Definition 4.2 (ii), the Causality Relation (Axiom 1) for S is mapped into

if \({\mathrm {supp} \, }G\cap J_-^{L+A_F}({\mathrm {supp} \, }H)=\emptyset \). This is the same axiom for \({{\tilde{S}}}\) due to  and since
and since  induces the same causal structure as \(L+A_F\). The Dynamical Relation (Axiom 2) for S is mapped into
induces the same causal structure as \(L+A_F\). The Dynamical Relation (Axiom 2) for S is mapped into  ; this follows straightforwardly from (8.10). Finally, the unitary AMWI for S is mapped into
; this follows straightforwardly from (8.10). Finally, the unitary AMWI for S is mapped into  , as a consequence of (8.11). This proves that the map is homomorphic. But since
, as a consequence of (8.11). This proves that the map is homomorphic. But since  is invertible, as a consequence of the invertibility of
is invertible, as a consequence of the invertibility of  for all
for all  , the map is also bijective. \(\square \)
, the map is also bijective. \(\square \)
9 Covariance
Up to now we did not impose any covariance conditions on the choice of the anomaly. In perturbative locally covariant quantum field theories, renormalization is restricted by the requirement that the quantities of interest (fields, time ordered products, etc.) can be understood as natural transformations between certain functors on the category of spacetimes. In our present paper, we enlarged this category. We will now consider several subcategories and natural transformations between functors on them and discuss the resulting restrictions for the anomaly.
We start with the space of local functionals. \({{\mathscr {F}}}_{\mathrm {loc}}\) associates to any dynamical spacetime (M, L) the space \({{\mathscr {F}}}_{\mathrm {loc}}(M,L)\). Arrows \(\iota _\rho :(M,L)\rightarrow (M',L')\) for diffeomorphisms \(\rho :M\rightarrow M'\) with \(\rho ^{*}L'=L\) induce maps \({{\mathscr {F}}}_{\mathrm {loc}}\iota _{\rho }\equiv \rho _{*}:{{\mathscr {F}}}_{\mathrm {loc}}(M,L)\rightarrow {{\mathscr {F}}}_{\mathrm {loc}}(M',L')\) with
Arrows  for symmetry transformations
for symmetry transformations  with \(M'=M\) and
with \(M'=M\) and  induce the maps
induce the maps  . We do not introduce the maps \({{\mathscr {F}}}_{\mathrm {loc}}\iota _{V,\pm }\) corresponding to interactions.
. We do not introduce the maps \({{\mathscr {F}}}_{\mathrm {loc}}\iota _{V,\pm }\) corresponding to interactions.
The functor of observable algebras \({{\mathfrak {A}}}:(M,L)\rightarrow {{\mathfrak {A}}}(M,L)\) is defined on the whole category. The S-matrix is a natural transformation
for the subcategory where the interaction arrows \(\iota _{W,\pm }\) are removed, as illustrated in Figure 2.
The interactions transform under symmetries and embeddings as

In order to include the arrows corresponding to interactions, we introduce a bundle over the space of past compactly supported interactions with fibers of associated local functionals,
In addition to the arrows for field redefinitions and embeddings which just act for both components as before, we also introduce the action of arrows \(\iota _{W,+}\) for interactions W with past compact support
where \(W\in \mathrm {Int}(M,L)\), \(V\in \mathrm {Int}(M,L+W)\) (hence \(V+W\in \mathrm {Int}(M,L)\)) and \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L+W+V)\). We then consider the relative S-matrices
and find that they define a natural transformation \(S^{\mathrm {rel}}:\mathrm {Int}_+^2\rightarrow {{\mathfrak {A}}}\), i.e.
if only the arrows for retarded interactions are considered, see Figure 3. An analogous construction can be done for the advanced case.
The functor \({{\mathscr {R}}}:(M,L)\mapsto {{\mathscr {R}}}(M,L)\) of renormalization groups maps the interaction arrows \(\iota _{V,\pm }\) to the maps \(Z\mapsto Z^{-V}\) (or equivalently: \(Z^V\mapsto Z\)). For symmetries, we get  . For embeddings \(\rho :(M,L)\rightarrow (M',L')\) there is the difficulty that (for \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M',L')\)) \(\rho ^{-1}_*F\) is only defined if \({\mathrm {supp} \, }F\subset \rho (M)\), hence we decompose \(F=F_0+F_1\) with \({\mathrm {supp} \, }F_0\subset \rho (M)\) and \({\mathrm {supp} \, }F_1\cap \rho ({\mathrm {supp} \, }Z)=\emptyset \) and set
. For embeddings \(\rho :(M,L)\rightarrow (M',L')\) there is the difficulty that (for \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M',L')\)) \(\rho ^{-1}_*F\) is only defined if \({\mathrm {supp} \, }F\subset \rho (M)\), hence we decompose \(F=F_0+F_1\) with \({\mathrm {supp} \, }F_0\subset \rho (M)\) and \({\mathrm {supp} \, }F_1\cap \rho ({\mathrm {supp} \, }Z)=\emptyset \) and set
The right hand side is independent of the split \(F=F_0+F_1\), since for another split \(F=F_0'+F_1'\) the functional \(G=F_0'-F_0=F_1-F_1'\) satisfies \({\mathrm {supp} \, }G\cap \rho ({\mathrm {supp} \, }Z)=\emptyset \), hence
We finally discuss the covariance properties of the cocycles \(\zeta \). The symmetry groups  do not depend on the Lagrangian and their elements
do not depend on the Lagrangian and their elements  do not transform under changes of the interaction. Under symmetry transformations
do not transform under changes of the interaction. Under symmetry transformations  , they transform by conjugation:
, they transform by conjugation:  . Under embeddings, we have to use that they are compactly supported. So we set
. Under embeddings, we have to use that they are compactly supported. So we set
with \(\rho \Phi \restriction _{\rho }\) as defined in (5.6) and extended to the identity outside of \(\rho (M)\), and with
The cocycles then transform by
under interactions \(\iota _{V;\pm }\), by  under symmetry transformations
under symmetry transformations  , (here we use the definition (7.5) for
, (here we use the definition (7.5) for  ), and by
), and by

under embeddings \(\iota _\rho \) by using (9.7). Note that \(\rho _{*}\zeta \) is defined only for symmetry transformations with support in the image of \(\rho \).
We can now discuss the appropriate naturality conditions on \(\zeta \). The covariance under adding interactions is already taking into account:  is a natural transformation with respect to \(\iota _{V,\pm }\), i.e.
is a natural transformation with respect to \(\iota _{V,\pm }\), i.e.  , as illustrated in Figure 4. As a consequence, it is sufficient to define the cocycle for a specific Lagrangian.
, as illustrated in Figure 4. As a consequence, it is sufficient to define the cocycle for a specific Lagrangian.
Actually, in perturbation theory one discusses the renormalization within the free theory (including its time ordered product) which determines then also the interacting theory. The covariance under embeddings is the crucial condition for local covariance. Due to the work of Hollands and Wald [44] (see also [49]), this condition is satisfied in perturbation theory; hence, we may impose it in our framework:  is a natural transformation with respect to \(\iota _\rho \), i.e.
is a natural transformation with respect to \(\iota _\rho \), i.e.  , see Figure 5.
, see Figure 5.
Analogously to the latter result, we can also impose the naturality condition for the arrows coming from symmetry transformations  , since due to the assumption on global hyperbolicity no compactly supported symmetry transformation leaves the Lagrangian invariant.
, since due to the assumption on global hyperbolicity no compactly supported symmetry transformation leaves the Lagrangian invariant.
There remains, however, the relation between the arrow corresponding to the application of a symmetry  and the arrow corresponding to the induced change of the Lagrangian:
and the arrow corresponding to the induced change of the Lagrangian:  , details are given in Figure 6.
, details are given in Figure 6.
Full naturality of \(\zeta \) would yield  , that is,
, that is,

But for such a \(\zeta \), the renormalization group flow would be trivial:
Proposition 9.1
Let \(\zeta \in {\mathfrak {Z}}(M,L)\).
- (i):
-
The cocycles
 and
and  are equivalent for every
are equivalent for every  ,
, 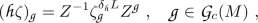 (9.14)
(9.14)with
 .
. - (ii):
-
If
 for all
for all  , then
, then  for all
for all  .
.
Proof
- (i):
-
We use the calculations in Section 7 leading to Proposition 7.2, but now for a generic element
 . The transformed cocycle
. The transformed cocycle  takes values in
takes values in  . The second equation in the proposition then assumes the form (9.14). This follows by the following chain of identities:
. The second equation in the proposition then assumes the form (9.14). This follows by the following chain of identities:  (9.15)
(9.15)where “(cr)” stands for the cocycle relation (5.26) in
 .
. - (ii):
-
For
 , the assumption (9.15) together with (9.13) implies
, the assumption (9.15) together with (9.13) implies  (9.16)
(9.16)Using that \(Z_1^VZ_2^V=(Z_1Z_2)^V\) (for \(Z_1,Z_2\in {{\mathscr {R}}}(M,L)\), \(V\in \mathrm {Int}(M,L)\)) we see that
 is a representation
is a representation  (9.17)
(9.17)Let now
 , and let
, and let  , \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\). Choose
, \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M,L)\). Choose  for some relatively compact, causally convex region \({{\mathscr {O}}}\subset M\) with
for some relatively compact, causally convex region \({{\mathscr {O}}}\subset M\) with  . Then according to Proposition 7.2, we have
. Then according to Proposition 7.2, we have  (9.18)
(9.18)The claim now follows from (9.17).
\(\square \)
The assumption of full naturality would exclude important examples of anomalies in perturbation theory. Instead we require that the equivalence class of \(\zeta \) is natural for the categorical structure described above.
Remark 9.2
The algebra \({{\mathfrak {A}}}(M,L,\zeta )\) is well defined for any choice of the cocycle \(\zeta \) satisfying the defining conditions given in formula (5.26) and directly before it. In particular, we may choose  for all
for all  . However, this would not be an optimal choice for a model (M, L) with a nontrivial anomaly (as one knows, e.g., from perturbative computations) since this might prevent the existence of physical states (as, e.g., the vacuum in Minkowski space) for \({{\mathfrak {A}}}(M,L,\zeta )\).
. However, this would not be an optimal choice for a model (M, L) with a nontrivial anomaly (as one knows, e.g., from perturbative computations) since this might prevent the existence of physical states (as, e.g., the vacuum in Minkowski space) for \({{\mathfrak {A}}}(M,L,\zeta )\).
10 The Unitary AMWI in Perturbation Theory
10.1 Perturbation Theory
The unitary anomalous MWI (see (5.27)) is an additional axiom. In this subsection, we show that an essentially equivalent condition holds in perturbation theory. In perturbation theory (in terms of formal power series in the coupling constant \(\lambda \)), for a free (i.e. quadratic) Lagrangian L, S-matrices are defined as time-ordered exponentials
Here \(\cdot _T\), the renormalized time-ordered product, is a binary, commutative and associative product [36] on a subspace (which contains the local functionals) of the space of all functionals on the configuration space (not restricted to solutions of the field equation, i.e. in the “off-shell formalism”Footnote 11). \(S(\lambda F)\) is realized as formal power series of functionals. \({{\mathscr {F}}}_{\mathrm {loc}}(M)\) is the vector space of polynomial local functionals on M. The formal parameter \(\lambda \) serves only as a bookkeeping device, so for the simplicity of notation we are going to omit it and write formal power series as infinite sums.
The perturbative S-matrix S is supposed to satisfy the causal factorization condition (2.13) (see Remark 2.3). It can be constructed by the Epstein–Glaser method [35], generalized to curved space times [14, 44, 45]. It is not uniquely determined by the condition (2.13), but according to Stora’s Main Theorem of Renormalization [32, 60, 61] any other solution \({\hat{S}}\) is of the form
where Z is a formal power series
of linear symmetric maps \(Z_n:{{\mathscr {F}}}_{\mathrm {loc}}(M)^{\otimes n}\rightarrow {{\mathscr {F}}}_{\mathrm {loc}}(M)\), and the composition has to be understood in the sense of insertions of a formal power series into another one. The formal power series Z are invertible (in the sense of formal power series) and generate a group, the renormalization group in the sense of Stúckelberg and Petermann [65], see also [32]. Applying (10.2) to the local functional \(F=0\), we immediately get \(Z(0)=Z_0=0\). However, for a better agreement with Definition 4.2 of \({{\mathscr {R}}}(M,L)\) and with Proposition 4.10, we may add a constant functional \(c\in {{\mathbb {R}}}\): in terms of \({{\tilde{Z}}}\doteq Z+c\) (hence \({{\tilde{Z}}}(0)=c\)) the Main Theorem formula (10.2) can equivalently be written as
with \(\beta _{{{\tilde{Z}}}}\doteq \beta _{{{\tilde{Z}}}}^{\mathrm {ret}}\) or \(\beta _{{{\tilde{Z}}}}\doteq \beta _{{{\tilde{Z}}}}^{\mathrm {adv}}\) (both choices coincide) and \(\beta _{{{\tilde{Z}}}}^{\mathrm {ret/adv}}\) defined in Proposition 4.10.
The ambiguity on the choice of S can be restricted by renormalization conditions which then also restrict the renormalization group to a subgroup. For our purposes, we need unitarity, field equation (FE) (i.e. the Schwinger–Dyson equation (2.14), see [13, Sect. 7]), Action Ward Identity and field independence and denote the corresponding subgroup of the renormalization group by \({{\mathscr {R}}}_0\). (For details see [32] or [28, Chap. 3.1].) We do not impose covariance conditions since we want to study the behavior of S under symmetry transformations  which would destroy these conditions. Since they are compactly supported we are interested in the subgroup \({{\mathscr {R}}}_c\) of \({{\mathscr {R}}}_0\) of renormalization group elements with compact support (in the sense of (4.2)). The explicit definition of \({{\mathscr {R}}}_c\) is given in Appendix C.
which would destroy these conditions. Since they are compactly supported we are interested in the subgroup \({{\mathscr {R}}}_c\) of \({{\mathscr {R}}}_0\) of renormalization group elements with compact support (in the sense of (4.2)). The explicit definition of \({{\mathscr {R}}}_c\) is given in Appendix C.
Note that (10.1) implies \(\frac{d}{d\lambda }\vert _{\lambda =0}S(\lambda F)=iF\) and hence \(Z_1=\mathrm {id}\). For a generally covariant formalism, however, this choice is too restrictive [45]. We take this generalization into account by admitting nontrivial, but still invertible \(Z_1\). For convenience, we continue to use the formulation for the S-matrix as in formula (10.1) and obtain the more general S-matrices by composition with the renormalization group map Z as in equation (10.2).
We use as an input the anomalous MWI from Brennecke and one of us [10, Thm. 7], see also [28, Chap. 4.3]. This identity is equivalent to a renormalized version of the Quantum Master Equation in the BV formalism (see [36]) and can be understood as an infinitesimal version of the unitary AMWI introduced in our paper, the latter turns out from Theorem 10.3 below.
 and \({{\mathscr {R}}}_c\) can be equipped with appropriate topologies and made into infinite-dimensional Lie groups modelled on locally convex topological vector spaces (for more details, see, e.g., [51, 55, 56] and [Rej16] for review in the context of perturbative AQFT). For
and \({{\mathscr {R}}}_c\) can be equipped with appropriate topologies and made into infinite-dimensional Lie groups modelled on locally convex topological vector spaces (for more details, see, e.g., [51, 55, 56] and [Rej16] for review in the context of perturbative AQFT). For  this is relatively easy, since \(\mathrm {Diff}_c(M)\) is a standard example of an infinite dimensional Lie group, while \({\mathscr {C}}^{\infty }_c(M,\mathrm {Aff}({{\mathbb {R}}}^n))\) is just the gauge group of point-wise affine transformations (smooth functions with values in the finite-dimensional Lie group of affine transformations on \({{\mathbb {R}}}^n\)), hence also standard. The action of diffeomorphisms on the group of affine transformations is smooth, so the Lie group structure on the semidirect product follows. As for \({{\mathscr {R}}}_c\), note that this is a subspace of the space of formal power series with values in multilinear maps from \({{\mathscr {F}}}_{\mathrm {loc}}(M)\) to \({{\mathscr {F}}}_{\mathrm {loc}}(M)\), which in itself is a topological vector space, so \({{\mathscr {R}}}_c\) can be equipped with the induced topology.
this is relatively easy, since \(\mathrm {Diff}_c(M)\) is a standard example of an infinite dimensional Lie group, while \({\mathscr {C}}^{\infty }_c(M,\mathrm {Aff}({{\mathbb {R}}}^n))\) is just the gauge group of point-wise affine transformations (smooth functions with values in the finite-dimensional Lie group of affine transformations on \({{\mathbb {R}}}^n\)), hence also standard. The action of diffeomorphisms on the group of affine transformations is smooth, so the Lie group structure on the semidirect product follows. As for \({{\mathscr {R}}}_c\), note that this is a subspace of the space of formal power series with values in multilinear maps from \({{\mathscr {F}}}_{\mathrm {loc}}(M)\) to \({{\mathscr {F}}}_{\mathrm {loc}}(M)\), which in itself is a topological vector space, so \({{\mathscr {R}}}_c\) can be equipped with the induced topology.
Note that we avoid the more subtle aspects of infinite dimensional differential geometry, since here we work with very explicit formulas and the precise choice of a setting for infinite dimensional calculus is not that relevant.
Let  denote the Lie algebra of
denote the Lie algebra of  (Definition 5.1) and \(\mathrm {Lie}\,{{\mathscr {R}}}_c\) the Lie algebra of \({{\mathscr {R}}}_c\). The anomalous MWI states that there exists a linear map
(Definition 5.1) and \(\mathrm {Lie}\,{{\mathscr {R}}}_c\) the Lie algebra of \({{\mathscr {R}}}_c\). The anomalous MWI states that there exists a linear map  such that
such that
for all \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\),  and with the action
and with the action
for \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\), and with \(\partial _X L\doteq \partial _X L(f)\) with \(f\equiv 1\) on \({\mathrm {supp} \, }X\), where the functional derivatives are considered as densities. This defines a map from  to \(\Gamma (T{{\mathscr {E}}}(M,{{\mathbb {R}}}^n))\), the space of vector fields on \({{\mathscr {E}}}(M,{{\mathbb {R}}}^n)\), by \(X\mapsto \partial _X\). The relation to the renormalized BV Laplacian \(\triangle \) of [36] is given by \(\triangle _F(\partial _X)\equiv \Delta X(F)\).
to \(\Gamma (T{{\mathscr {E}}}(M,{{\mathbb {R}}}^n))\), the space of vector fields on \({{\mathscr {E}}}(M,{{\mathbb {R}}}^n)\), by \(X\mapsto \partial _X\). The relation to the renormalized BV Laplacian \(\triangle \) of [36] is given by \(\triangle _F(\partial _X)\equiv \Delta X(F)\).
Remark 10.1
The statement that \(\Delta X\in \mathrm {Lie}\,{{\mathscr {R}}}_c\) is not given in the original formulation of the AMWI (in [10, Thm. 7] or [28, Chap. 4.3]), but apart from this the geometrical formulation of the AMWI (10.5) is equivalent to the original one, as one sees from the following translation (for illustration see [28, Example 4.2.1] and [34]). In the mentioned references the AMWI is formulated in terms of the local functional \(A\doteq \int d^4x\,\,h(x)Q(x)\,\frac{\delta L(f)}{\delta \phi (x)}\) (where \(h\in {{\mathscr {D}}}(M)\), Q is a polynomial in \(\phi \) and its partial derivatives and \(f\vert _{{\mathrm {supp} \, }h}=1\)), the pertinent derivationFootnote 12\(\delta _A\equiv \delta _{hQ}\doteq \int d^4x\,\,h(x)Q(x)\,\frac{\delta }{\delta \phi (x)}\) and the anomaly map \(F\mapsto \Delta _A(e_\otimes ^F)\equiv \Delta (e_\otimes ^F;hQ)\). Now, A and \(\delta _A\) can be obtained as follows: for a smooth curve  in
in  with
with  and with tangent vector
and with tangent vector  at \(\lambda =0\) we set
at \(\lambda =0\) we set

and consequently
for \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\), in particular \(A=\partial _X L\). In this paper, we write \(-\Delta X(F)\) for the anomaly map \(\Delta (e_\otimes ^F;hQ)\).
The statement that \(\Delta X\in \mathrm {Lie}\,{{\mathscr {R}}}_c\) for  is proved in Appendix C. It expresses that the Stückelberg–Petermann group has an additional purpose (besides describing the non-uniqueness of the perturbative S-matrix by the Main Theorem (10.2)): it also characterizes the anomalies of the MWI, restricted to fields Q which are of first order in \(\phi \). This is analogous to the two different purposes of the (nonperturbative) renormalization group \({{\mathscr {R}}}(M,L)\) (Definition 4.2) worked out in this paper: the automorphisms \(\beta _Z^{\mathrm {ret}/\mathrm {adv}}\) of \({{\mathfrak {A}}}(M,L)\) (with \(Z\in {\mathscr {R}}(M,L)\), see Proposition 4.10) and the characterization of the anomaly map
is proved in Appendix C. It expresses that the Stückelberg–Petermann group has an additional purpose (besides describing the non-uniqueness of the perturbative S-matrix by the Main Theorem (10.2)): it also characterizes the anomalies of the MWI, restricted to fields Q which are of first order in \(\phi \). This is analogous to the two different purposes of the (nonperturbative) renormalization group \({{\mathscr {R}}}(M,L)\) (Definition 4.2) worked out in this paper: the automorphisms \(\beta _Z^{\mathrm {ret}/\mathrm {adv}}\) of \({{\mathfrak {A}}}(M,L)\) (with \(Z\in {\mathscr {R}}(M,L)\), see Proposition 4.10) and the characterization of the anomaly map  (belonging to the unitary AMWI (5.27)) by
(belonging to the unitary AMWI (5.27)) by  .
.
For perturbative, scalar QED, the equivalence of the on-shell MWI and the unitary MWIFootnote 13 expressing global U(1)-symmetry is proved in [34, Thm. 4.1]. We now generalize this result in different ways, we prove it for the anomalous MWI and for arbitrary models and arbitrary symmetry transformations  .
.
Remark 10.2
In the following Theorem, we use the simple form of the S-matrix as in (10.1). Using instead a general S-matrix by composition with a renormalization group map Z would require in the result only a change to an equivalent cocycle, as explained in Definition 5.6 and Proposition 5.7. (The proofs of Lemma 5.4 and Proposition 5.7 apply also to the perturbative framework considered here, because the definition of \({{\mathscr {R}}}_c\) C.1 is analogous to the Definition of \({{\mathscr {R}}}(M,L)\) 4.2 reduced to the special case \(V=0\).)
Theorem 10.3
In formal perturbation theory (i.e. the equations hold in the sense of formal power series), the on-shell AMWI and the unitary AMWI are equivalent in the following sense:
- (i):
-
The on-shell AMWI (i.e., (10.5) \(\mathrm {mod}\ \frac{\delta L}{\delta \phi }\)) implies the unitary AMWI,
 (10.9)
(10.9)with a cocycle \(\zeta \) taking values in \({{\mathscr {R}}}_c\) and with
 .
. - (ii):
-
The unitary AMWI (10.9) implies the on-shell AMWI (10.5) where X is the tangent vector at \(\lambda =0\) of a smooth curve
 in
in  with
with  and the anomaly map \(\Delta X\) is given by
and the anomaly map \(\Delta X\) is given by 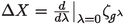 . It holds that \({\mathrm {supp} \, }\Delta X\subset {\mathrm {supp} \, }X\).
. It holds that \({\mathrm {supp} \, }\Delta X\subset {\mathrm {supp} \, }X\).
Proof
(i) Let  . We choose a smooth curve
. We choose a smooth curve  with
with  and
and  and let
and let  be defined by
be defined by  . In the spirit of Remark 5.8 we search for a smooth curve
. In the spirit of Remark 5.8 we search for a smooth curve  with
with  and
and

Inserting then \(\lambda =0\) and \(\lambda =1\) into  , we obtain the unitary AMWI (10.9).
, we obtain the unitary AMWI (10.9).
We get

(for \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\)); by using this result we perform the differentiation and obtain the condition

We insert the anomalous MWI (10.5) and find

We thus get the wanted family  as the unique solution of the differential equation
as the unique solution of the differential equation

with the initial condition  . Since
. Since

as explained in the next paragraph, it follows that  , in particular
, in particular  .
.
The claim (10.15) follows from \(\Delta X^{\lambda }\in \mathrm {Lie}\,{{\mathscr {R}}}_c\). In detail, let \(\mu \mapsto {\Upsilon }^\lambda _\mu \) be a smooth curve in \({{\mathscr {R}}}_c\) with \({\Upsilon }^\lambda _0=\mathrm {id}_{{{\mathscr {F}}}_{\mathrm {loc}}}\) and \(\Delta X^{\lambda }=\frac{d}{d\mu }\big \vert _{\mu =0}{\Upsilon }^\lambda _\mu \). Then, analogously to Lemma 5.4, using the formulas from Appendix C, also  lies in \({{\mathscr {R}}}_c\), and (10.15) follows by applying \(\frac{d}{d\mu }\vert _{\mu =0}\).
lies in \({{\mathscr {R}}}_c\), and (10.15) follows by applying \(\frac{d}{d\mu }\vert _{\mu =0}\).
To prove the statement on the support of  , we choose
, we choose  such that
such that  , \(0\le \lambda \le 1\) and thus
, \(0\le \lambda \le 1\) and thus  . Let \(F,G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) with
. Let \(F,G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) with  . We have \({\mathrm {supp} \, }(Z(F+G)-Z(G))\subset {\mathrm {supp} \, }F\) for \(Z\in {{\mathscr {R}}}_c\) (see [12, formula (6.3)] or Proposition 4.4) and hence
. We have \({\mathrm {supp} \, }(Z(F+G)-Z(G))\subset {\mathrm {supp} \, }F\) for \(Z\in {{\mathscr {R}}}_c\) (see [12, formula (6.3)] or Proposition 4.4) and hence

Thus with  , we find
, we find

and

i.e.  .
.
It remains to show that \(\zeta \) satisfies the cocycle identity. As shown in Proposition 5.3, the cocycle identity

holds after evaluation of both sides on on-shell configurations. However, \(G\mapsto S(G)\) is not injective as a map from local functionals to functionals on-shell. We solve this problem in the following way: we add a source term \(\langle \phi ,q\rangle \) to the free Lagrangian L. This does not change the time ordered product. From (10.5), we see that also the anomaly map \(\Delta X\) is not changed; hence, this holds also for the pertinent \(\zeta \) satisfying the unitary AMWI. By Proposition 5.3, we conclude

for all sources q, hence for all field configurations. Since the off-shell S-matrix is injective, we obtain the cocycle relation.
(ii) The assertion is obtained by applying \(\frac{d}{d\lambda }\vert _{\lambda =0}\) to the unitary AMWI (10.9) for  . The statement on the support follows from the fact that for any neighborhood U of \({\mathrm {supp} \, }X\) we can find a smooth curve
. The statement on the support follows from the fact that for any neighborhood U of \({\mathrm {supp} \, }X\) we can find a smooth curve  with
with  and
and  . Thus, \({\mathrm {supp} \, }\Delta X\subset U\) for all neighborhoods of \({\mathrm {supp} \, }X\) and hence \({\mathrm {supp} \, }\Delta X\subset {\mathrm {supp} \, }X\). \(\square \)
. Thus, \({\mathrm {supp} \, }\Delta X\subset U\) for all neighborhoods of \({\mathrm {supp} \, }X\) and hence \({\mathrm {supp} \, }\Delta X\subset {\mathrm {supp} \, }X\). \(\square \)
If the unitary AMWI (10.9) is anomaly free, then this holds also for the AMWI (10.5); explicitly, if  for a certain \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) and in a neighborhood of \(\lambda =0\), then \(\Delta X(F)=0\). From the proof, we see that the reversed statement holds in the following sense: if, for a certain \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) and a suitable choice of the curve
for a certain \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) and in a neighborhood of \(\lambda =0\), then \(\Delta X(F)=0\). From the proof, we see that the reversed statement holds in the following sense: if, for a certain \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) and a suitable choice of the curve  , it holds that
, it holds that  for all \(\lambda \in [0,1]\), then
for all \(\lambda \in [0,1]\), then  .
.
10.2 Scaling Anomaly
We determine the anomaly in a special case—the dilations in 4-dimensional Minkowski space \({{\mathbb {M}}}\), which are a combination of a structure preserving embedding \(\rho \) with an affine field redefinition \(\Phi \). We study the massless real scalar field case, i.e., \(L\doteq \frac{1}{2}\,(\partial \phi )^2\), and we work with the additional renormalization condition that the time-ordered product scales almost homogeneously (see [32]). Let  be a 1-parameter subgroup of
be a 1-parameter subgroup of  with generator
with generator  which acts on field configurations as
which acts on field configurations as

with \(\lambda \in {{\mathbb {R}}}\), \(\beta \in {{\mathscr {D}}}({{\mathbb {M}}},{{\mathbb {R}}})\). Let
for some open convex neighborhood U of the origin. Then for \(x\in e^{-|b|}U\), we have

In view of the AMWI, we compute
with the dilation current
We want to compute \(\Delta X(F)=\sum _{n=0}^\infty (\Delta X)^{(n)}(F^{\otimes n})/n!\) (understood as formal power series in F) for the particular local functional
Note that  for \(\lambda \in [-1,1]\). By using (10.6), we obtain
for \(\lambda \in [-1,1]\). By using (10.6), we obtain
The sequence \((\Delta X)^{(n)}(F^{\otimes n})\) can be computed by solving the unitary AMWI (10.5) by induction on n, see [10, formula (5.15)] or [28, formula (4.3.10)]. In 0th order, we use the conservation law for the dilation current in the massless theory and conclude that \(\Delta ^{(0)}=0\), in agreement with the general results of [10]. In first order, we obtain
and in second order
Since the MWI holds true in classical field theory, that is, for tree diagrams, the only potentially nonvanishing contributions come from local terms of the loops \(F\cdot _T \partial _XL[0]\), \(F\cdot _T\partial _XF[0]\) and \(F\cdot _T F\cdot _T \partial _XL[0]\). Integrating by parts, we note that
so due to our assumption on \(\beta \) and f given in (10.21) and (10.25), the only nonvanishing contribution to \(\Delta X(F)\) comes from \(F\cdot _T\partial _X F[0]\).
With \(D^2\) being the renormalized fish diagram,i.e.,
(where \(D_F\) is the Feynman propagator of the massless scalar field), and by using the Action Ward Identity, we compute
We may symmetrize, that is, we may replace \((1+\frac{1}{2}\,y^\mu \partial ^y_\mu )D^2(x-y)\) by
Using \(D_F(z)=\frac{-1}{4\pi ^2}\,\frac{1}{z^2-i0}\), we obtain
Moreover, since both sides have unique extensions from \({{\mathscr {D}}}'({{\mathbb {R}}}^4\setminus \{0\})\) to \({{\mathscr {D}}}'({{\mathbb {R}}}^4)\) which preserve almost homogeneous scaling, they agree everywhere. Inserting this result, we end up with
Here, we have taken into account that \((\Delta X)^{(n)}(F^{\otimes n})=0\) for all \(n\ge 3\). Proceeding by induction on n, this can be seen as follows (for details see [10, 32] and [28, Chaps. 3.1 and 4.3]): writing
the terms contributing to \(\Delta ^{(n)}(x_1,\ldots ,x_n;y)\) are (up to constant prefactors)
note that the last term is coming from
Now we use that
that is, on \({{\mathbb {M}}}^{n+1}\setminus \Delta _{n+1}\) the contributions to \(\Delta ^{(n)}(x_1,\ldots ,x_n;y)\) cancel out. This holds even on the whole manifold \({{\mathbb {M}}}^{n+1}\). To wit, looking at the causal Wick expansion of the terms given in (10.35), all coefficients (which are \({{\mathbb {C}}}\)-valued distributions depending on the relative coordinates) scale almost homogeneously with a degree smaller than 4n, as one verifies by power counting. Since we require that the extension of the time ordered products to the thin diagonal preserves almost homogeneous scaling, terms proportional to \(\partial ^a\delta (x_1-y,\ldots ,x_n-y)\) cannot be produced.
Proposition 10.4
The anomaly \(\zeta \) associated to the 1-parameter group  acts on
acts on
as

with constant functionals \(c(\lambda )\) not depending on F with \(c(0)=0\) and \(c'(0)=0\).
Moreover \(c(\lambda )\) can be removed by a suitable renormalization.
Proof
Obviously, the formula (10.37) for  satisfies the necessary condition
satisfies the necessary condition  . We have to show that there exist a \(c(\lambda )\) (with the mentioned properties) such that
. We have to show that there exist a \(c(\lambda )\) (with the mentioned properties) such that  satisfies the differential equation (10.14), that is,
satisfies the differential equation (10.14), that is,

by using that \(X^\lambda =X\).
First note that, since \(Z(G+a)=Z(G)+a\) for any \(Z\in {{\mathscr {R}}}_c\), \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) and \(a\in {{\mathbb {C}}}\), the assertion (10.37) can equivalently be written as

Now we insert (10.39) into the r.h.s. of (10.38) and use the facts that \(\Delta X(G+C)=\Delta X(G)\) for \(G\in {{\mathscr {F}}}_{\mathrm {loc}}({{\mathbb {M}}})\) and any constant functional C (as one easily sees from (10.5)), that  and that \(\Delta X\) is additive on functionals with disjoint support (property (iii) of \(z\in \mathrm {Lie}\,{{\mathscr {R}}}_c\) in Appendix C) and obtain
and that \(\Delta X\) is additive on functionals with disjoint support (property (iii) of \(z\in \mathrm {Lie}\,{{\mathscr {R}}}_c\) in Appendix C) and obtain

We have  , hence
, hence

Inserting (10.39) also into the l.h.s. of (10.38), we see that (10.39) satisfies (10.38) iff

taking also into account that \(c(0)=0\), \(c(\lambda )\) is uniquely fixed.
To remove c, we use a renormalization \(Z\in {{\mathscr {R}}}_0\) with

Since F is quadratic in \(\phi \), we may use the result of Proposition 5.7 that the cocycle belonging to the renormalized time ordered product is the equivalent cocycle  . For the latter, we find
. For the latter, we find

where we used

This concludes the proof. \(\square \)
We can also compute the action of global scaling transformations using the concepts of Section 8. Namely, let  act on configurations \(\phi \) as
act on configurations \(\phi \) as

Then, given f and \(\lambda \), we choose U such that \({\mathrm {supp} \, }f\subset e^{-|\lambda b|}U\) and find for all such U

The induced change of the Lagrangian vanishes, since for \(g\in {{\mathscr {D}}}({{\mathbb {M}}},{{\mathbb {R}}})\) we have

Finally, we may look at the anomalous Noether Theorem 7.3 which simplifies in our case since the transformation  does not change the causal structure. Following the proof of that theorem, we split
does not change the causal structure. Following the proof of that theorem, we split

such that \({\mathrm {supp} \, }Q_+\cap J_-(e^{|\lambda b|}U)=\emptyset \) and \({\mathrm {supp} \, }Q_-\cap J_+(e^{|\lambda b|}U)=\emptyset \) and find for \({\mathrm {supp} \, }f\subset U\) and \(\beta (x)=b\) for \(x\in e^{|\lambda b|}U\)

10.3 Axial Anomaly
Another famous example of an anomaly is the axial anomaly. For a massless Dirac field \(\psi \) in 4-dimensional Minkowski space, the axial current
is conserved as a consequence of the Dirac equation. It is the Noether current corresponding to the symmetry

namely with the free Lagrangian
we have

We compute the anomaly  on \(F=\int d^4x\,\, j_{\mu }(x)A^{\mu }(x)\) with the vector current \(j_{\mu }={\overline{\psi }}\gamma _{\mu }\psi \) and an external electromagnetic potential \(A^{\mu }\in {{\mathscr {D}}}({{\mathbb {M}}},{{\mathbb {R}}}^4)\). As shown in [13], the formalism of the present paper can be extended to Fermi fields by adding external Grassmann parameters in an appropriate way. For quadratic expressions in the basic Dirac field, these parameters are not needed.
on \(F=\int d^4x\,\, j_{\mu }(x)A^{\mu }(x)\) with the vector current \(j_{\mu }={\overline{\psi }}\gamma _{\mu }\psi \) and an external electromagnetic potential \(A^{\mu }\in {{\mathscr {D}}}({{\mathbb {M}}},{{\mathbb {R}}}^4)\). As shown in [13], the formalism of the present paper can be extended to Fermi fields by adding external Grassmann parameters in an appropriate way. For quadratic expressions in the basic Dirac field, these parameters are not needed.
As in the case of scaling we choose a 1-parameter group  with
with  . Its generator X acts on \(\psi \) and \({\overline{\psi }}\) as
. Its generator X acts on \(\psi \) and \({\overline{\psi }}\) as

Since  we obtain
we obtain  and, by using (10.54), we get
and, by using (10.54), we get  . Since
. Since  it holds that
it holds that

As in the case of scaling, only the divergent loop graphs contribute to the anomaly. We consider the distributions \(D_{\bullet }\in {{\mathscr {D}}}'({{\mathbb {R}}}^{4n})\)
the upper index “c” means that we select the contribution of all connected diagrams. By Furry’s theorem (which is a consequence of charge conjugation invariance of the time ordered product), \(D_{\mu _1,\dots ,\mu _n;\nu }\) vanishes for n odd. By using the inductive Epstein–Glaser construction of the time ordered product, one shows that the divergence of \(D_{\mu _1,\dots ,\mu _n;\nu }\) with respect to \(\nu \) and y vanishes outside of the origin and is therefore a derivative of the \(\delta \)-function
where \(p_{\bullet }\) is a family of homogeneous polynomials of the partial derivatives \(\partial ^{\nu _i}_{x_i}\) with degree \(3n+4-4n=4-n\). It is symmetric under permutations of the index i and odd under parity. The only nontrivial case is \(n=2\) where \(p_{\mu _1\mu _2}(\partial )=c\epsilon _{\mu _1\mu _2\rho \sigma }\partial ^{\rho }_{x_1}\partial ^\sigma _{x_2}\) with some constant \(c\in {{\mathbb {R}}}\). An explicit calculation yields \(c=\frac{1}{2\pi ^2}\) (for a derivation of this result based on the Epstein–Glaser method, see [33]), under the condition that the Ward identities for the vector current are satisfied, i.e., \(\partial ^{\mu _i}_{x_i}D_{\mu _1,\dots ,\mu _n;\nu }=0\) for all \(1\le i\le n\).
We compute \(\Delta X\) as in the previous section and find
with the 1-form \(A\doteq A_{\mu }dx^{\mu }\).
In order to compute  , we also have to determine
, we also have to determine  . We first study
. We first study  . Also here the only possible contribution comes from the triangle diagram
. Also here the only possible contribution comes from the triangle diagram

since for an even number of factors \(j^a\) the correlation functions can be renormalized to coincide with those of the vector current, and thus their divergences vanish, and for 5 factors the divergence of the correlation function with respect to one factor is of the form
with a tensor of 4th order which is symmetric with odd parity, hence \(a_{\bullet }=0\). The divergence of the triangle diagram does not vanish, actually it is of the form
(see, e.g. , [33]). Inserting it into (10.60) we see that also this term does not contribute, i.e.  .
.
Also mixed terms which possibly could contribute to the value of \(\Delta X\) on the sum  vanish. To explain this first note that
vanish. To explain this first note that  , since
, since  . In second order in G, the statement follows from \(\bigl (j\cdot _T j^a\cdot _T \partial j^a\bigr )^c[0]=\bigl (j\cdot _T j\cdot _T \partial j\bigr )^c[0]=0\) by Furry theorem. For \(n>2\), we obtain
. In second order in G, the statement follows from \(\bigl (j\cdot _T j^a\cdot _T \partial j^a\bigr )^c[0]=\bigl (j\cdot _T j\cdot _T \partial j\bigr )^c[0]=0\) by Furry theorem. For \(n>2\), we obtain
where we first use that \((\Delta X)^{(n)}\) is supported on the thin diagonal (see (10.36)) and then (10.5). In addition, we have taken into account that (since \((\Delta X)^{(2)} (F^{\otimes 2})\in {{\mathbb {R}}}\)) there is no connected diagram contributing to \(\bigl (G^{\cdot _T (n-2)}\cdot _T(\Delta X)^{(2)}(F^{\otimes 2})\bigr )=\bigl (G^{\cdot _T (n-2)}\bigr )\,(\Delta X)^{(2)}(F^{\otimes 2})\). By suitable renormalization (respecting the mentioned renormalization conditions), one can reach that
Hence,
So we obtain

Proceeding analogously to the scaling anomaly (Proposition 10.4), we can now solve the differential equation for  and obtain
and obtain

11 Conclusions and Outlook
In the program of constructing algebraic quantum field theories [20], we succeeded in incorporating both aspects of causality: the causal independence of spacelike separated regions as well as a dynamical law by which future and past in a region of causal dependence are fixed. We have proven the time-slice axiom and constructed the general expression for the relative Cauchy evolution. We have used the latter to obtain the stress-energy tensor as an unbounded operator, improving on the results of [16], where only the derivation obtained as the commutator with the stress-energy tensor could be reconstructed.
In addition to a classical Lagrangian which fixes the dynamics only in the case of the free theory and the subalgebra of Weyl operators, we introduced a cocycle on a group of classical symmetries with values in the renormalization group. Together with the Lagrangian this specifies the dynamics. Moreover, it describes whether classical symmetries of the Lagrangian are unbroken in the quantized theory, and allows a direct characterization of the renormalization group flow induced by anomalies. This means that anomalies appear when a classical symmetry is broken in the process of quantization and the departure from the classical expression is quantified in terms of a certain renormalization group cocycle. The transformation of the S-matrix obtained this way may be interpreted as a quantum symmetry arising from the classical symmetry modified by the cocycle. Such quantum symmetries can then be unitarily implemented, which is the content of our anomalous Noether theorem. We have also shown that in perturbation theory, the derivative of our cocycle is related to the BV Laplacian or the anomaly term in the perturbative anomalous Master Ward identity. This emphasizes the fact that our formulation indeed allows one to upgrade classical symmetries to quantum symmetries and their relative difference is reflected by the presence of anomalies.
There is one essential point missing in our construction, namely the implication of the spectrum condition, related to the existence of a vacuum, stability of states etc.[7]. There have been various attempts to understand this implication for the structure of the algebra, starting from Sergio Doplicher’s “algebraic spectrum condition” [26], including Rainer Verch’s approach to an algebraic concept of wave front sets [67], but it is fair to say that there is not yet a fully satisfactory answer. From our experience with perturbation theory, we know that the spectrum condition imposes constraints on the choice of cocycles which lead to the occurrence of anomalies. Ignoring the slight difference between \({{\mathscr {R}}}(M,L_0)\) and the Stückelberg–Petermann renormalization group (see Remarks 4.3 and 4.11), we strongly presume that, due to the main theorem of renormalization [12, 32, 61] and Proposition 5.7, the equivalence class of the cocycle is uniquely fixed. We may therefore formulate the remaining open problem in the algebraic construction of quantum field theories as the problem to determine this equivalence class.
In this paper, we treated only scalar theories, but we included also an example of computation of an anomaly for fermions along the line of [13]. It would be desirable to cover also gauge theories. We plan to return to this problem in future work.
Notes
The case of dimension 2 can be equally treated mutatis mutandis on some of the crucial results, e.g. those in Appendix B.
This entails that our manifolds are also paracompact, see [54].
More general field redefinitions could be considered [2, 50, 53]. We restrict ourselves here to affine field redefinitions, since they, together with their inverses, map polynomial functionals to polynomial functionals (this is important for the perturbative proof of the anomalous Master Ward Identity, see e.g. Section 10); moreover, they map the set of Lagrangians of 2nd order in the field into itself, thus allowing analytic control.
Note that there is no freedom of renormalization for the composite field \(\phi ^2_V\). Moreover, in classical field theory (4.1) is satisfied, as it is obtained by the pointwise product of \(\phi ^{\mathrm {class}}_{V}\) with the Field Equation \((\square +m^2)\phi ^{\mathrm {class}}_{V}(x) =-2f(x)\,\phi ^{\mathrm {class}}_{V}(x)\).
The notation \(Z^W\) should not be confused with the notation \(Z_W=Z(\bullet +W(f))-Z(W(f))\) used in [12]. The latter describes the renormalization of fields induced by a renormalization \(W(f)\mapsto Z(W(f))\) of the interaction W.
For the simplicity of notation, we will write \(\delta _{\chi }L\) instead of \(A_{\delta _{\chi }L}\).
Hence, we obtain the same commutation law as in (5.7): \((\mathrm {id}_\Phi ,\chi )\cdot (\Phi ,\mathrm {id}_\chi )=((\chi \Phi ),\mathrm {id}_\chi )\cdot (\mathrm {id}_\Phi ,\chi )\).
For perturbative, scalar QED a proof of the equivalence of the unitary MWI to the on-shell MWI is given in [34].
Here we use that for any \(Z\in {{\mathscr {R}}}(M,L)\) and any \(c\in {{\mathbb {R}}}\) it holds that also \(Z+c\in {{\mathscr {R}}}(M,L)\) and that \(\beta ^{\mathrm {ret}}_Z=\beta ^{\mathrm {ret}}_{(Z+c)}\). The latter relies on causal factorization: \(S_{(M,L)}((Z+c)(F))=S_{(M,L)}(Z(F))\,e^{ic}\).
This differs from the formalism often used in physics, where the time ordered products are identified with Fock space operators, corresponding to functionals which vanish on solutions of the free field equation (“on-shell formalism”). Since the functionals vanishing on solutions do not form an ideal for the off-shell time-ordered product, the on-shell time-ordered product is less well behaved.
The unitary MWI is also an on-shell statement.
References
Araki, H.: Mathematical theory of quantum fields. Oxford Science Publications, Oxford (2009)
Balduf, P.-H.: Propagator-cancelling scalar fields. arXiv:2102.04315
Bernal, A.N., Sanchez, M.: Smoothness of time functions and the metric splitting of globally hyperbolic spacetimes. Commun. Math. Phys. 257, 43–50 (2005)
Bogoliubov, N.N., Parasiuk, O.S.: Über die Multiplikation der Kausalfunktionen in der Quantentheorie der Felder. Acta Mathematica 97, 227–266 (1957)
Bogoliubov, N.N., Shirkov, D.V.: Introduction to the theory of quantized fields. Interscience Publishers, New York (1959)
Borchers, H.J.: Energy and momentum as observables in quantum field theory. Comm. Math. Phys. 2, 49–54 (1966)
Borchers, H.J.: Translation group and particle representations in quantum field theory. lecture notes in physics monographs, vol. 40. Springer-Verlag, Berlin Heidelberg (1996)
Borchers, H.-J.: On revolutionizing quantum field theory with Tomita’s modular theory. J. Math. Phys. 41(6), 3604–3673 (2000)
Bratteli, O., Robinson, D.W.: Operator algebras and quantum statistical mechanics 1 & 2, 2nd edn. Springer-Verlag, Berlin Heidelberg (1987)
Brennecke, F., Dütsch, M.: Removal of violations of the master ward identity in perturbative QFT. Rev. Math. Phys. 20, 119 (2008). https://doi.org/10.1142/S0129055X08003237
Brunetti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.): Advances in algebraic quantum field theories, mathematical physics studies. Springer, Berlin (2015)
Brunetti, R., Dütsch, M., Fredenhagen, K.: Perturbative algebraic quantum field theory and the renormalization groups. Adv. Theor. Math. Phys. 13, 1541–1599 (2009)
Brunetti, R., Dütsch, M., Fredenhagen, K., Rejzner, K.: C*-algebraic approach to interacting quantum field theory: Inclusion of Fermi fields. arXiv:2103.05740
Brunetti, R., Fredenhagen, K.: Microlocal analysis and interacting quantum field theories: Renormalization on physical backgrounds. Commun. Math. Phys. 208, 623–661 (2000)
Brunetti, R., Fredenhagen, K., Ribeiro, P.L.: Algebraic structure of classical field theory: Kinematics and linearized dynamics for real scalar fields. Commun. Math. Phys. 368, 519–584 (2019)
Brunetti, R., Fredenhagen, K., Verch, R.: The generally covariant locality principle: A new paradigm for local quantum field theory. Commun. Math. Phys. 237, 31–68 (2003)
Brunetti, R., Guido, D., Longo, R.: Modular localization and Wigner particles. Rev. Math. Phys. 14(7–8), 759–785 (2002)
Buchholz, D.: The resolvent algebra of non-relativistic bose fields: sectors, morphisms, fields and dynamics. Commun. Math. Phys. 362, 1159–1199 (2018)
Buchholz, D., Doplicher, S., Longo, R.: On Noether’s theorem in quantum field theory. Annals Phys. 170, 1 (1986). https://doi.org/10.1016/0003-4916(86)90086-2
Buchholz, D., Fredenhagen, K.: A C*-algebraic approach to interacting quantum field theories. Commun. Math. Phys. 377, 947–969 (2020). https://doi.org/10.1007/s00220-020-03700-9
Buchholz, D., Fredenhagen, K.: Dynamical C*-algebras and Kinetic Perturbations. Ann. Henri Poincaré 22, 1001–1033 (2021). https://doi.org/10.1007/s00023-020-01002-3
Buchholz, D., Fredenhagen, K.: Classical dynamics, arrow of time, and genesis of the Heisenberg commutation relations. Expo. Math. 28, 150–167 (2020)
Buchholz, D., Grundling, H.: The resolvent algebra: a new approach to canonical quantum systems. J. Funct. Anal. 254, 2725–2779 (2008)
Chilian, B., Fredenhagen, K.: The time slice axiom in perturbative quantum field theory on globally hyperbolic spacetimes. Commun. Math. Phys. 287, 513–522 (2009)
Ciolli, F., Longo, R., Ruzzi, G.: The information in a wave. Commun. Math. Phys. 379, 979–1000 (2020)
Doplicher, S.: An algebraic spectrum condition. Commun. Math. Phys. 1, 1–5 (1965)
Doplicher, S., Longo, R.: Standard and split inclusions of von Neumann algebras. Invent. math. 75, 493–536 (1984)
Dütsch, M.: From classical field theory to perturbative quantum field theory, Prog. Math. Phys., vol. 74. Birkhäuser (2019). https://doi.org/10.1007/978-3-030-04738-2
Dütsch, M., Boas, F.-M.: The master ward identity. Rev. Math. Phys. 14, 977–1049 (2002)
Dütsch, M., Fredenhagen, K.: Algbraic quantum field theory, perturbation theory and the loop expansion. Commun. Math. Phys. 219, 5–30 (2001)
Dütsch, M., Fredenhagen, K.: The master ward identity and generalized Schwinger-Dyson equation in classical field theory. Commun. Math. Phys. 243, 275–314 (2003)
Dütsch, M., Fredenhagen, K.: Causal perturbation theory in terms of retarded products, and a proof of the action ward identity. Rev. Math. Phys. 16, 1291–1348 (2004)
Dütsch, M., Krahe, F., Scharf, G.: Axial anomalies in massless finite QED. N. Cimento A 105(3), 399–422 (1992)
Dütsch, M., Peters, L., Rehren, K.H.: The master ward identity for scalar QED. Ann. Henri Poincaré (2021). https://doi.org/10.1007/s00023-021-01048-x
Epstein, H., Glaser, V.: The role of locality in perturbation theory. Annales Poincare Phys. Theor. A 19, 211–295 (1973)
Fredenhagen, K., Rejzner, K.: Batalin-Vilkoviski formalism in perturbative algebraic quantum field theory. Commun. Math. Phys. 317, 697–725 (2013)
Fredenhagen, K., Rejzner, K.: Perturbative Construction of Models of Algebraic Quantum Field Theory. In: Brunneti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.) Advances in algebraic quantum field theory. mathematical physics studies, pp. 31–74. Springer, Berlin (2015)
Haag, R.: Local quantum physics: Fields, particles, algebras. Springer, Berlin (1992)
Haag, R., Kastler, D.: An algebraic approach to quantum field theory. J. Math. Phys. 5, 848–861 (1964)
Haag, R., Schroer, B.: Postulates of quantum field theory. J. Math. Phys. 3, 248–256 (1962)
Hawking, S.W., Ellis, G.F.R.: The large scale structure of space-time. Cambridge University Press, Cambridge (1973)
Hollands, S.: Renormalized Quantum Yang-Mills Fields in curved spacetime. Rev. Math. Phys. 20, 1033–1172 (2008)
Hollands, S., Sanders, K.: Entanglement measures and their properties in quantum field theories, SpringerBriefs in mathematical physics, vol. 38. Springer, Cham (2018)
Hollands, S., Wald, R.M.: Local Wick polynomials and time ordered products of quantum fields in curved space-time. Commun. Math. Phys. 223, 289–326 (2001)
Hollands, S., Wald, R.M.: Existence of local covariant time-ordered products of quantum fields in curved spacetime. Commun. Math. Phys. 231, 309–345 (2002)
Hollands, S., Wald, R.M.: On the renormalization group in curved space-time. Commun. Math. Phys. 237, 123–160 (2003)
Il’in, V.A., Slavnov, D.S.: Observable algebras in the \(S\)-matrix approach. Theor. Math. Phys. 36, 32–41 (1978)
Itzykson, C., Zuber, J.-B.: Quantum field theory. McGraw-Hill, USA (1980)
Khavkine, I., Moretti, V.: Analytic dependence is an unnecessary requirement in renormalization of locally covariant QFT. Commun. Math. Phys. 344, 581–620 (2016)
Kreimer, D., Yeats, K.: Diffeomorphisms of quantum fields. Math. Phys. Anal. Geom. 20, 16 (2017)
Kriegl, A., Michor, P.W.: The convenient setting of global analysis, mathematical surveys and monographs, vol. 53. AMS, USA (1997)
Longo, R., Xu, F.: von Neumann entropy in QFT. arXiv:1911.09390
Mahmoud, A.A., Yeats, K.: Diffeomorphisms of scalar quantum fields via generating functions. arXiv:2007.12341
Marathe, K.B.: A condition for paracompactness of a manifold. J. Diff. Geometry 7, 571–573 (1972)
Neeb, K.H.: Monastir summer school. Infinite-dimensional Lie groups. TU Darmstadt preprint 2433 (2006). https://cel.archives-ouvertes.fr/cel-00391789/document
Neeb, K.H.: Towards a Lie theory for infinite-dimensional groups. Jap. J. Math. 3rd Series 1, 291–468 (2006)
Neeb, K.H., Ólafsson, G.: Nets of standard subspaces on Lie groups. Adv. Math. 384 (2021). Paper No. 107715, 69 pp
Noether, E.: Invarianten beliebiger Differentialausdrücke. Göttinger Nachrichten , 37–44 (1918)
Noether, E.: Invariante variationsprobleme. Göttinger Nachrichten 235–257 (1918)
Pinter, G.: Finite renormalizations in the Epstein-Glaser framework and renormalization of the \(S\)-Matrix of \(\phi ^4\)-Theory. Ann. Phys. (Leipzig) 10, 333 (2001)
Popineau, G., Stora, R.: A pedagogical remark on the main theorem of perturbative renormalization theory. Nucl. Phys. B 912, 70–78 (2016). (preprint: LAPP–TH, Lyon (1982))
Rejzner, K.: Locality and causality in perturbative algebraic quantum field theory. J. Math. Phys. 60(12), 122301 (2019). https://doi.org/10.1063/1.5111967
Sanders, K.: A note on spacelike and timelike compactness. Class. Quantum Gravity 30, 155014 (2013)
Stratila, S.V., Zsido, L.: Lectures on von Neumann algebras, 2nd edn. Cambridge University Press, Cambridge (2019)
Stückelberg, E.C.G., Petermann, A.: La normalisation des constantes dans la théorie des quanta. Helv. Phys. Acta 26, 499–520 (1953)
Takesaki, M.: Theory of operator algebras II. Springer, Berlin
Verch, R.: Wavefront sets in algebraic quantum field theory. Commun. Math. Phys. 205, 337–367 (2009)
Wiesbrock, H.-W.: Half-sided modular inclusions of von-Neumann-algebras. Comm. Math. Phys. 157(1), 83–92 (1993)
Wiesbrock, H.-W.: Modular intersections of von Neumann algebras in quantum field theory. Comm. Math. Phys. 193(2), 269–285 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Karl-Henning Rehren.
Dedicated to Detlev Buchholz on the occasion of his $$77^{\text {th}}$$ 77 th birthday.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Functionals and Generalized Fields
Definition A.1
The (functional) support of a map \(F:{{\mathscr {E}}}(M)\rightarrow {{\mathbb {C}}}\) is the smallest closed subset N of M such that \(F[\phi +\psi ]=F[\phi ]\) for all \(\phi ,\psi \in {{\mathscr {E}}}(M)\) with \({\mathrm {supp} \, }\psi \cap N=\emptyset \).
A local functional \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) is a map \(F:{{\mathscr {E}}}(M)\rightarrow {{\mathbb {R}}}\) with compact support which satisfies the Hammerstein relation
for \(\phi ,\chi ,\psi \in {{\mathscr {E}}}(M)\) with \({\mathrm {supp} \, }\phi \cap {\mathrm {supp} \, }\psi =\emptyset \).
A generalized field is a map \(A:{{\mathscr {D}}}(M)\rightarrow {{\mathscr {F}}}_{\mathrm {loc}}(M)\) with \({\mathrm {supp} \, }A(f)\subset {\mathrm {supp} \, }f\) such that
whenever \({\mathrm {supp} \, }f\cap {\mathrm {supp} \, }h=\emptyset \). Two generalized fields \(A, A'\) are equivalent if
The support of a generalized field A is defined by
Note that \(x\in {\mathrm {supp} \, }A(f)\) for every f with \(f\equiv 1\) near x if \(x\in {\mathrm {supp} \, }A(f')\) for some \(f'\) with \(f'\equiv 1 \) near x. Namely we can split \(f'=f_0+f_1+f_2\) with \(f=f_0+f_1\) and \(x\not \in {\mathrm {supp} \, }f_{1,2}\) and \({\mathrm {supp} \, }f_2\cap {\mathrm {supp} \, }f_0=\emptyset \). Then,
and
hence \(x\in {\mathrm {supp} \, }A(f)\) if \(x\in {\mathrm {supp} \, }A(f')\).
Obviously, for a generalized field A it holds that
Proposition A.2
Equivalent generalized fields have the same support.
Proof
Let \(A'\) be equivalent to A and \(x\not \in {\mathrm {supp} \, }A\). Then, there exists an \(f_0\equiv 1\) near x such that \(x\not \in {\mathrm {supp} \, }A(f_0)\). Since
we see that \(x\not \in {\mathrm {supp} \, }A'(f_0)\), hence \(x\not \in {\mathrm {supp} \, }A'\). \(\square \)
We can characterize equivalence classes of generalized fields by their relative action.
Definition A.3
Let A be a generalized field. The relative action of A is a map \(\delta A:{{\mathscr {D}}}(M)\rightarrow {{\mathscr {F}}}_{\mathrm {loc}}(M)\) defined by
To see that this definition does not depend on the choice of f, let \(f'\) be another choice. We split \(f'=f_0+f_1+f_2\) with \(f=f_0+f_1\) and \({\mathrm {supp} \, }\psi \cap {\mathrm {supp} \, }f_{1,2}=\emptyset \) and \({\mathrm {supp} \, }f_2\cap {\mathrm {supp} \, }f_0=\emptyset \). Then, the relation (A.5) holds true; and since \({\mathrm {supp} \, }A(f_1)\subset {\mathrm {supp} \, }f_1\) and \({\mathrm {supp} \, }A(f_1+f_2)\subset {\mathrm {supp} \, }f_1\cup {\mathrm {supp} \, }f_2\), we have \(A(f_1)[\phi +\psi ]=A(f_1)[\phi ]\) and \(A(f_1+f_2)[\phi +\psi ]=A(f_1+f_2)[\phi ]\). This yields the assertion.
Proposition A.4
Two generalized fields are equivalent iff their relative actions are equal.
Proof
Let \(A,A'\) be generalized fields. If they are equivalent, then \({\mathrm {supp} \, }(A-A')(f)\subset {\mathrm {supp} \, }(f-1)\) for all f. Let \(f\equiv 1\) on \({\mathrm {supp} \, }\psi \). We then have
since \({\mathrm {supp} \, }(f-1)\cap {\mathrm {supp} \, }\psi =\emptyset \).
Let on the other side \(\delta A=\delta A'\), \(f\in {{\mathscr {D}}}(M)\) arbitrary and \(x\not \in {\mathrm {supp} \, }(f-1)\). There exists a neighborhood V of x such that \(f\equiv 1\) on V. Then, for all \(\psi \) with \({\mathrm {supp} \, }\psi \subset V\)
hence \(x\not \in {\mathrm {supp} \, }(A-A')(f)\), i.e. A and \(A'\) are equivalent. \(\square \)
The proposition leads to a criterion for the support of a generalized field:
Proposition A.5
Let A be a generalized field and let \({\mathrm {supp} \, }\delta A\) be the smallest closed subset N of M such that \(\delta A(\psi )=0\) for all \(\psi \in {{\mathscr {D}}}(M\setminus N)\). Then, it holds that
Proof
Let \(x\in {\mathrm {supp} \, }A\). Then for any neighborhood V of x and any \(f\equiv 1\) on V, there exists some \(\psi \) with \({\mathrm {supp} \, }\psi \subset V\) such that
The opposite inclusion follows by essentially the same argument. \(\square \)
We now look at generalized fields with compact support and set
A(1) does not depend on \(\chi \), namely for \(\chi '\equiv 1\) on \({\mathrm {supp} \, }A\) we have
(where \(f\equiv 1\) on \({\mathrm {supp} \, }\chi \cup {\mathrm {supp} \, }\chi '\)) and \({\mathrm {supp} \, }(\chi '-\chi )\cap {\mathrm {supp} \, }A=\emptyset \), hence \(A(f)[\chi '\phi ]-A(f)[\chi \phi ]=\delta A((\chi '-\chi )\phi )[\chi \phi ]=0\). We also have \(A(1)=A'(1)\) for \(A,A'\) equivalent.
We have found a map \(A\mapsto A(1)\) from generalized fields with compact support to local functionals. On the other hand, we can also consider a map from local functionals to generalized fields
The associated relative action can be written as
by choosing \(f\equiv 1\) on \({\mathrm {supp} \, }F\); hence \({\mathrm {supp} \, }A_F={\mathrm {supp} \, }\delta A_F={\mathrm {supp} \, }F\). We also find
with \(\chi \equiv 1\) on \({\mathrm {supp} \, }F\). Moreover, the generalized field \(A_{A(1)}\) built from the local functional A(1) is equivalent to A, since \(\delta A_{A(1)}(\psi )=A(1)[\bullet +\psi ]-A(1)[\bullet ]=\delta A(\psi )\).
Appendix B. Interpolating Metrics
In this Appendix, we show that, given two Lorentz metrics \(g_0,g_1\) on the manifold M for which the manifold becomes globally hyperbolic, there exists a sequence of 5 metrics, starting with \(g_0\) and ending with \(g_1\), such that for each neighboring pair all pointwise convex combinations are Lorentz metrics for which M is globally hyperbolic, see (2.11).
We choose time functions \(t_i\) associated to \(g_i\), \(i=0,1\), with timelike differentials \(dt_i\) such that \({\mathrm {supp} \, }(t_1-t_0)\) is compact and such that the convex combinations \(\lambda dt_1+(1-\lambda ) dt_0\) nowhere vanish, \(0\le \lambda \le 1\) (always possible in more than 2 dimensions).
There exists a vector field X with \(\langle dt_i,X\rangle =1\), \(i=0,1\). In a first step, we define metrics \(g_i'\) with larger lightcones (i.e. \(g_i'\ge g_i\)) for which X is timelike. In the second step, we define a metric \(g_{01}\) whose lightcone contains X and is contained in the lightcones of both metrics. We obtain a sequence of 5 metrics,
such that for each neighboring pair all convex combinations are globally hyperbolic Lorentz metrics.
In detail, we construct the metrics \(g'_0,\,g'_1\) and \(g_{01}\) as follows: we define Riemannian metrics \(\gamma _{i}\) by
with \(a_i=(g_i^{-1}(dt_i,dt_i))^{-1}\). Let \(d_i=\gamma _i(X,X)\). We set
with \(k>1+d_0,1+d_1,2a_0,2a_1\) to be determined later, and find that X is timelike for \(g'_0\) as well as for \(g'_1\) and that \(g_i'\ge g_i\), \(i=0,1\). We then construct \(g_{01}\) by
where \(b,c>0\) are chosen such that X is timelike for \(g_{01}\) and such that each vector field Y which is timelike for \(g_{01}\) and future directed with respect to \(t_0+t_1\) is also timelike and future directed for \(g_i'\), \(i=0,1\).
The condition that X is timelike for \(g_{01}\) requires \(b>2c+d_0+d_1\). Let now Y be a future directed vector field with respect to \(g_{01}\) and \(t_0+t_1\). We see immediately that then \(\langle dt_i,Y\rangle >0\) for both values of i. We then use the inequality
with \(\lambda b=2c\) as well as with \(\lambda ^{-1}b=2c\). We obtain the inequalities
We therefore choose k such that
and get \(g_i'(Y,Y)>0\), \(i=0,1\).
Appendix C. Proof of \(\Delta X\in \mathrm {Lie}\,{{\mathscr {R}}}_c\)
In this appendix, we prove that the anomaly map \(\Delta X\) of the perturbative AMWI (10.5) lies in \(\mathrm {Lie}\,{{\mathscr {R}}}_c\). In a first step we list the defining properties of the subgroup \({{\mathscr {R}}}_c\) of the Stückelberg Petermann renormalization group \({{\mathscr {R}}}_0\) determined by the renormalization conditions given at the beginning of Sect. 10 and obtain the defining properties of \(\mathrm {Lie}\,{{\mathscr {R}}}_c\); we also give an explicit formula for the Lie bracket. In a second step we verify that the latter are satisfied by \(\Delta X(F)\equiv \Delta (e_\otimes ^F;hQ)\) by using the structural results for \(\Delta (e_\otimes ^F;hQ)\) derived in [10, Sect. 5.2] (see also [28, Chap. 4.3]).
Definition C.1
The compactly supported subgroup \({{\mathscr {R}}}_c\) of the Stückelberg–Petermann renormalization group is the set of formal power series \(Z=\sum _{n=0}^\infty \frac{1}{n!}Z_n\), with n-linear symmetric maps \(Z_n\) of local functionals to local functionals (cf. (10.3)), with the following properties:
-
(1)
\(Z_1\) is invertible,
-
(2)
\(Z(F+G)=Z(F)-Z(0)+Z(G)\) for \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }G=\emptyset \), \(F,G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\),
-
(3)
\(Z(F^{\psi }+\delta L(\psi ))=Z(F)^{\psi }+\delta L(\psi )\) for \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\),
-
(4)
\(Z(F)^{\psi }=Z(F^{\psi })\) for \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\),
-
(5)
\({\mathrm {supp} \, }Z\) is compact where the support is defined analogously to (4.2).
Mind the difference: the n-fold time ordered product \(F_1\cdot _T\,\,\cdots \,\,\cdot _T F_n\) is a \({{\mathbb {C}}}\)-valued functional, but Z(F) is an \({{\mathbb {R}}}\)-valued functional (by definition of \({{\mathscr {F}}}_{\mathrm {loc}}\)) —this is the reason why there is no defining property for \({{\mathscr {R}}}_c\) corresponding to the renormalization condition unitarity for the S-matrix. An immediate consequence of the property (4) is that \({\mathrm {supp} \, }Z(F)={\mathrm {supp} \, }F\) for all \(F\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) and thus \(Z(0)=Z_0=\mathrm {const}\). Note that condition (2) implies due to multilinearity of the coefficients of Z the general locality condition
-
(2’)
\(Z(F+G+H)=Z(F+H)-Z(H)+Z(G+H)\) with F, G as above and \(H\in {{\mathscr {F}}}_{\mathrm {loc}}\)
(see [12, Appendix B]); and, assuming the validity of (4), (3) can equivalently be written in the simpler form
-
(3’)
\(Z(F+\delta L(\psi ))=Z(F)+\delta L(\psi )\) for \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\).
We also point out that each \(Z_k\), \(k\in {{\mathbb {N}}}\), satisfies the properties (2)-(5) individually—this observation is crucial for the proof of the Main Theorem [32]. It is obvious for (2), (4) and (5); and (3’) can be verified as follows:
where \(c_\psi (\lambda )\) is a constant and we use that \(\delta L(\psi )=\langle \phi ,K\psi \rangle +\tfrac{1}{2}\langle \psi ,K\psi \rangle \) and that \(Z(F+c)=Z(F)+c\) (since \({\mathrm {supp} \, }c=\emptyset \)). In particular note that \(Z_1\bigl (\delta L(\psi )\bigr )=\delta L(\psi )\).
As mentioned in Subsection 10.1, we do not require that \(Z_1=\mathrm {id}\), in contrast to [12, 32], but in agreement with [46] . The reason is that the functional F as the argument of S has to be understood as related to a quantum observable \({\hat{F}}\) by normal ordering. A symmetry transformation then acts on F in two ways: via its action on field configurations and via its action on the normal ordering prescription. The latter action is incorporated in the action of the renormalization group in the unitary AMWI.
Usually, a normal ordering prescription is of the form
where H coincides up to smooth terms with an admissible 2-point function of the free theory (i.e. satisfying microlocal spectrum condition). We point out that the algebra of quantum observables \({{\hat{F}}}\) is abstractly defined and the formula (C.2) has to be understood in a formal sense, because \(\alpha _H^{-1} F\) does, in general, not exist as a functional, see [12] and [37]. If the normal ordering is changed one should keep \({\hat{F}}\) fixed and therefore has to admit changes of F. More explicitly, if the new normal ordering is characterized by \(H'\) we find
Note that \(Z_1\) is well defined on polynomial functionals, since \(H'-H\) is smooth. The set of admissible H is restricted by the above condition (5) on \(Z_1\). ((1)-(4) are obviously satisfied, because \(Z_1=\alpha _{H'-H}\) is invertible, linear, acts trivially on \(\delta L(\psi )=\langle \phi ,K\psi \rangle +\tfrac{1}{2}\langle \psi ,K\psi \rangle \) and commutes with functional derivatives.) Explicitly, since \(Z_1\) must have compact support, also \(H'-H\) and all its derivatives restricted to the diagonal must have compact support. Note that H appearing in (C.2) is a solution of the free field equation, but all further admissible \(H'\) do not necessarily have this property.
The associated Lie algebra \(\mathrm {Lie}\,{{\mathscr {R}}}_c\) is defined as follows: it is the set of formal power series \(z=\sum _{n=0}^\infty \frac{1}{n!}z_n\), with n-linear symmetric maps \(z_n\) of local functionals to local functionals, with the properties
- (i):
-
\(\mathrm {id}+\lambda z_1\) is invertible for \(\lambda \) sufficiently small,
- (ii):
-
\(z(F+G)=z(F)-z(0)+z(G)\) for \({\mathrm {supp} \, }F\cap {\mathrm {supp} \, }G=\emptyset \), \(F,G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\),
- (iii):
-
\(z(F^{\psi }+\delta L(\psi ))=z(F)^{\psi }\) for \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\),
- (iv):
-
\(z(F)^{\psi }=z(F^{\psi })\) for \(\psi \in {{\mathscr {D}}}(M,{{\mathbb {R}}}^n)\),
- (v):
-
the support of z,
$$\begin{aligned}&{\mathrm {supp} \, }z\doteq \{x\in M\,|\, \text { for every neighborhood }U\ni x\,\text { there exist}\ F,G\in {{\mathscr {F}}}_{\mathrm {loc}}(M),\nonumber \\&\text { with }{\mathrm {supp} \, }F\subset U\text { such that } z(F+G)\ne z(G)\}, \end{aligned}$$(C.4)is compact.
To obtain an explicit formula for \([z^a,z^b]_{\mathrm {Lie}\,{{\mathscr {R}}}_c}\), we use that it is connected to the product in the Lie group \({{\mathscr {R}}}_c\) by the expansion
where
By taking into account that
where
is linear in G, we obtain
By using (C.7) and (C.9), we see by a straightforward computation that \(Z^a(\lambda )Z^b(\lambda )Z^a(\lambda )^{-1}Z^b(\lambda )^{-1}\) is indeed of the form given in (C.5), and we can read off that
Remark C.2
The renormalization group \({{\mathscr {R}}}_c\) may be considered as a group of diffeomorphisms of the space of local functionals. Accordingly, the associated Lie algebra corresponds to a Lie algebra of vector fields equipped with the usual Lie bracket.
Finally, we are going to prove that \(\Delta X\in \mathrm {Lie}\,{{\mathscr {R}}}_c\). In first order, \(\Delta X\) is a second order differential operator, due to the two contractions in the time ordered product \(F\cdot _T \partial _XL\) (see (10.27)), terms with more contractions do not occur since \(\partial _XL\) is of second order in \(\phi \). Hence \(\mathrm {id}+\lambda (\Delta X)_1\) is invertible on polynomial local functionals, so condition (i) holds. \(\Delta X\) evidently also satisfies conditions (ii) and (v). Condition (iv) follows from the condition field independence (which implies formula (5.27) of [10]), due to the fact that  contains only affine field redefinitions, hence the term in equation (5.26) of [10] does not contribute.
contains only affine field redefinitions, hence the term in equation (5.26) of [10] does not contribute.
(iii) is not explicitly mentioned in [10]. It follows from the following calculation. We use the notation \(\psi _L\) and \(\psi _{*}\) introduced in the proof of Lemma 5.4, so that (iii) assumes the form \(z\psi _L=\psi _{*}z\), and find

We now use the fact that \(\Delta X(G+c)=\Delta X(G)\) for \(G\in {{\mathscr {F}}}_{\mathrm {loc}}(M)\) and a constant functional c and add a source term \(\langle \phi ,q\rangle \) to the Lagrangian, thus replacing L by \(L_q\doteq L+\langle \phi ,q\rangle \). Neither the time ordered product nor \(\Delta X\) nor \(\Delta X(\psi _{L_q}F)\) depend on q, and \(S(\psi _{L_q}F)=e^{i\langle \psi ,q\rangle }S(\psi _LF)\). Hence, the equation
holds everywhere. Since the off-shell S-matrix is invertible with respect to \(\cdot _T\), we arrive at condition (iii).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brunetti, R., Dütsch, M., Fredenhagen, K. et al. The Unitary Master Ward Identity: Time Slice Axiom, Noether’s Theorem and Anomalies. Ann. Henri Poincaré 24, 469–539 (2023). https://doi.org/10.1007/s00023-022-01218-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-022-01218-5





 (Definition
(Definition 
 with
with 




 (for the latter we assume
(for the latter we assume 



 and the induced change of the Lagrangian
and the induced change of the Lagrangian and
and  are equivalent for every
are equivalent for every  ,
, 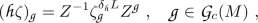
 .
. for all
for all  , then
, then  for all
for all  .
. . The transformed cocycle
. The transformed cocycle  takes values in
takes values in  . The second equation in the proposition then assumes the form (
. The second equation in the proposition then assumes the form (
 .
.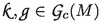 , the assumption (
, the assumption (
 is a representation
is a representation 
 , and let
, and let 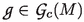 ,
,  for some relatively compact, causally convex region
for some relatively compact, causally convex region  . Then according to Proposition
. Then according to Proposition 

 .
. in
in  with
with  and the anomaly map
and the anomaly map 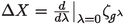 . It holds that
. It holds that