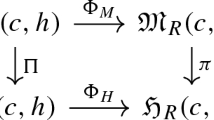Abstract
We provide new insight into the analysis of N-body problems by studying a compactification \(M_N\) of \({\mathbb {R}}^{3N}\) that is compatible with the analytic properties of the N-body Hamiltonian \(H_N\). We show that our compactification coincides with a compactification introduced by Vasy using blow-ups in order to study the scattering theory of N-body Hamiltonians and with a compactification introduced by Georgescu using \(C^*\)-algebras. In particular, the compactifications introduced by Georgescu and by Vasy coincide (up to a homeomorphism that is the identity on \({\mathbb {R}}^{3N}\)). Our result has applications to the spectral theory of N-body problems and to some related approximation properties. For instance, results about the essential spectrum, the resolvents, and the scattering matrices of \(H_N\) (when they exist) may be related to the behavior near \(M_N{\setminus } {\mathbb {R}}^{3N}\) (i.e., “at infinity”) of their distribution kernels, which can be efficiently studied using our methods. The compactification \(M_N\) is compatible with the action of the permutation group \(S_N\), which allows to implement bosonic and fermionic (anti-)symmetry relations. We also indicate how our results lead to a regularity result for the eigenfunctions of \(H_N\).


Similar content being viewed by others
References
Ammann, B., Carvalho, C., Nistor, V.: Regularity for eigenfunctions of Schrödinger operators. Lett. Math. Phys. 101(1), 49–84 (2012)
Ammann, B., Ionescu, A.D., Nistor, V.: Sobolev spaces on Lie manifolds and regularity for polyhedral domains. Doc. Math. 11, 161–206 (2006)
Ammann, B., Lauter, R., Nistor, V.: On the geometry of Riemannian manifolds with a Lie structure at infinity. Int. J. Math. Math. Sci. 2004(1–4), 161–193 (2004)
Ammann, B., Lauter, R., Nistor, V.: Pseudodifferential operators on manifolds with a Lie structure at infinity. Ann. Math. (2) 165(3), 717–747 (2007)
Ammann, B., Mougel, J., Nistor, V.: A regularity result for the bound states of \(N\)-body Schrödinger operators: blow-ups and Lie manifolds. arXiv:2012.13902 (2020)
Amrein, W., Boutet de Monvel, A., Georgescu, V.: \(C_0\)-Groups, Commutator Methods and Spectral Theory of \(N\)-Body Hamiltonians. Modern Birkhäuser Classics. Birkhäuser/Springer, Basel (1996). 2013, reprint of the 1996 edition
Bach, V., Breteaux, S., Petrat, S., Pickl, P., Tzaneteas, T.: Kinetic energy estimates for the accuracy of the time-dependent Hartree–Fock approximation with Coulomb interaction. J. Math. Pures Appl. (9) 105(1), 1–30 (2016)
Baldare, A., Côme, R., Lesch, M., Nistor, V.: Fredholm conditions and index for restrictions of invariant pseudodifferential to isotypical components. Max Planck Preprint and arXiv:2004.01543 (2020) to appear in Münster Math. J
Baldare, A., Côme, R., Lesch, M., Nistor, V.: Fredholm conditions for invariant operators: finite abelian groups and boundary value problems. J. Oper. Theory 85(1), 229–256 (2021)
Baldare, A., Côme, R., Nistor, V.: Fredholm conditions for operators invariant with respect to compact lie group actions. arXiv preprint arXiv:2012.03944 (December 2020) to appear in CR Acad. Sci, Paris
Bär, C.: Green-hyperbolic operators on globally hyperbolic spacetimes. Commun. Math. Phys. 333(3), 1585–1615 (2015)
Bär, C., Ginoux, N.: Classical and quantum fields on Lorentzian manifolds. In: Global Differential Geometry, Volume 17 of Springer Proceedings of Mathematics, pp. 359–400. Springer, Heidelberg (2012)
Benini, M., Dappiaggi, C., Hack, T.-P.: Quantum field theory on curved backgrounds—a primer. Int. J. Modern Phys. A 28(17), 1330023, 49 (2013)
Boutet de Monvel-Berthier, A., Georgescu, V.: Graded \(C^*\)-algebras and many-body perturbation theory. I. The \(N\)-body problem. C. R. Acad. Sci. Paris Sér. I Math. 312(6), 477–482 (1991)
Boutet de Monvel-Berthier, A., Georgescu, V.: Graded \(C^*\)-algebras and many-body perturbation theory. II. The Mourre estimate. 210, 6–7, 75–96 (1992). Méthodes semi-classiques, Vol. 2 (Nantes, 1991)
Carvalho, C., Côme, R., Qiao, Y.: Gluing action groupoids: Fredholm conditions and layer potentials. Rev. Roumaine Math. Pures Appl. 64(2–3), 113–156 (2019)
Carvalho, C., Nistor, V., Qiao, Y.: Fredholm conditions on non-compact manifolds: theory and examples. In: André, C., Bastos, M.A., Karlovich, A.Y., Silbermann, B., Zaballa, I. (eds.) Operator Theory, Operator Algebras, and Matrix Theory, Volume 267 of Operator Theory: Advances and Applications, pp. 79–122. Birkhäuser/Springer, Cham (2018)
Chruściel, P., Herzlich, M.: The mass of asymptotically hyperbolic Riemannian manifolds. Pac. J. Math. 212(2), 231–264 (2003)
Côme, R.: The Fredholm property for groupoids is a local property. Results Math. 74(4), 160 (2019)
Damak, M., Georgescu, V.: Self-adjoint operators affiliated to \(C^*\)-algebras. Rev. Math. Phys. 16(2), 257–280 (2004)
Dappiaggi, C., Finster, F., Murro, S., Radici, E.: The fermionic signature operator in de Sitter spacetime. J. Math. Anal. Appl. 485(2), 123808, 29 (2020)
Debord, C., Lescure, J.-M., Rochon, F.: Pseudodifferential operators on manifolds with fibred corners. Ann. Inst. Fourier (Grenoble) 65(4), 1799–1880 (2015)
Dereziński, J.: Asymptotic completeness of long-range \(N\)-body quantum systems. Ann. Math. (2) 138(2), 427–476 (1993)
Dereziński, J., Faupin, J., Nguyen, Q., Richard, S.: On radial Schrödinger operators with a Coulomb potential: general boundary conditions. Adv. Oper. Theory 5(3), 1132–1192 (2020)
Dereziński, J., Gérard, C.: Scattering Theory of Classical and Quantum \(N\)-Particle Systems. Texts and Monographs in Physics. Springer, Berlin (1997)
Dereziński, J., Gérard, C.: Mathematics of Quantization and Quantum Fields. Cambridge Monographs on Mathematical Physics. Cambridge University Press, Cambridge (2013)
Dereziński, J., Richard, S.: On Schrödinger operators with inverse square potentials on the half-line. Ann. Henri Poincaré 18(3), 869–928 (2017)
Dereziński, J., Wrochna, M.: Exactly solvable Schrödinger operators. Ann. Henri Poincaré 12(2), 397–418 (2011)
Dixmier, J.: \(C^*\)-algebras. North-Holland Publishing Co., Amsterdam-New York-Oxford (1977). Translated from the French by Francis Jellett, North-Holland Mathematical Library, vol. 15
Flad, H.-J., Harutyunyan, G., Schneider, R., Schulze, B.-W.: Explicit Green operators for quantum mechanical Hamiltonians. I. The hydrogen atom. Manuscr. Math. 135(3–4), 497–519 (2011)
Fulton, W., MacPherson, R.: A compactification of configuration spaces. Ann. Math. (2) 139(1), 183–225 (1994)
Georgescu, V.: On the essential spectrum of elliptic differential operators. J. Math. Anal. Appl. 468(2), 839–864 (2018)
Georgescu, V., Gérard, C., Häfner, D.: Resolvent and propagation estimates for Klein–Gordon equations with non-positive energy. J. Spectr. Theory 5(1), 113–192 (2015)
Georgescu, V., Iftimovici, A.: Localizations at infinity and essential spectrum of quantum Hamiltonians. I. General theory. Rev. Math. Phys. 18(4), 417–483 (2006)
Georgescu, V., Nistor, V.: On the essential spectrum of \(N\)-body Hamiltonians with asymptotically homogeneous interactions. J. Oper. Theory 77(2), 333–376 (2017)
Gérard, C.: An introduction to quantum field theory on curved spacetimes. In: Daudé, T., Häfner, D., Nicolas, J.P. (eds.) Asymptotic Analysis in General Relativity, Volume 443 of London Mathematical Society. Lecture Note Series, pp. 171–218. Cambridge University Press, Cambridge (2018)
Gérard, C., Stoskopf, T.: Hadamard states for quantized Dirac fields on Lorentzian manifolds of bounded geometry. arXiv:2108.11630
Griebel, M., Hamaekers, J.: Sparse grids for the Schrödinger equation. M2AN Math. Model. Numer. Anal. 41(2), 215–247 (2007)
Hörmander, L.: The Analysis of Linear Partial Differential Operators. III: Pseudo-differential Operators. Classics in Mathematics. Springer, Berlin (1994)
Hunsicker, E., Li, H., Nistor, V., Uski, V.: Analysis of Schrödinger operators with inverse square potentials II: FEM and approximation of eigenfunctions in the periodic case. Numer. Methods Partial Differ. Equ. 30(4), 1130–1151 (2014)
Hunziker, W., Sigal, I.M.: The quantum \(N\)-body problem. J. Math. Phys. 41(6), 3448–3510 (2000)
Jecko, T.: On the mathematical treatment of the Born–Oppenheimer approximation. J. Math. Phys. 55(5), 053504, 26 (2014)
Joyce, D.: A generalization of manifolds with corners. Adv. Math. 299, 760–862 (2016)
Junker, W., Schrohe, E.: Adiabatic vacuum states on general spacetime manifolds: definition, construction, and physical properties. Ann. Henri Poincaré 3(6), 1113–1181 (2002)
Klainerman, S., Rodnianski, I., Szeftel, J.: The bounded \(L^2\) curvature conjecture. Invent. Math. 202(1), 91–216 (2015)
Kondrat’ev, V.A.: Boundary value problems for elliptic equations in domains with conical or angular points. Transl. Moscow Math. Soc. 16, 227–313 (1967)
Kottke, C.: Blow-up in manifolds with generalized corners. Int. Math. Res. Not. 8, 2375–2415 (2018)
Kottke, C.: Functorial compactification of linear spaces. Proc. Am. Math. Soc. 147(9), 4067–4081 (2019)
Kottke, C., Melrose, R.: Generalized blow-up of corners and fiber products. Trans. Am. Math. Soc. 367(1), 651–705 (2015)
König, A.: Master thesis. University of Regensburg (2021). https://doi.org/10.5283/epub.47792
Lauter, R., Monthubert, B., Nistor, V.: Spectral invariance for certain algebras of pseudodifferential operators. J. Inst. Math. Jussieu 4(3), 405–442 (2005)
Lauter, R., Seiler, J.: Pseudodifferential analysis on manifolds with boundary—a comparison of b-calculus and cone algebra. In: Approaches to Singular Analysis (Berlin, 1999), Volume 125 of Operator Theory: Advances and Applications, pp. 131–166. Birkhäuser, Basel (2001)
Lee, J.: Introduction to Topological Manifolds, Volume 202 of Graduate Texts in Mathematics, 1st edn. Springer, New York (2000)
Lieb, E., Seiringer, R.: The Stability of Matter in Quantum Mechanics. Cambridge University Press, Cambridge (2010)
Mageira, A.: Some examples of graded \(C^*\)-algebras. Math. Phys. Anal. Geom. 11(3–4), 381–398 (2008)
Melrose, R.: Differential analysis on manifolds with coners. Book in preparation. Manuscript available at https://math.mit.edu/~rbm/book.html
Melrose, R.: Calculus of conormal distributions on manifolds with corners. Int. Math. Res. Not. 3, 51–61 (1992)
Melrose, R.: Spectral and scattering theory for the Laplacian on asymptotically Euclidian spaces. In: Spectral and Scattering Theory (Sanda, 1992), Volume 161 of Lecture Notes in Pure and Applied Mathematics, pp. 85–130. Dekker, New York (1994)
Melrose, R., Singer, M.: Scattering configuration spaces. arXiv:0808.2022
Mougel, J.: Essential spectrum, quasi-orbits and compactifications: application to the Heisenberg group. Rev. Roumaine Math. Pures Appl. 64, 325–343 (2019)
Mougel, J., Nistor, V., Prudhon, N.: A refined HVZ-theorem for asymptotically homogeneous interactions and finitely many collision planes. Rev. Roumaine Math. Pures Appl. 62(1), 287–308 (2017)
Mougel, J., Prudhon, N.: Exhaustive families of representations of \(C^\ast \)-algebras associated with \(N\)-body Hamiltonians with asymptotically homogeneous interactions. C. R. Math. Acad. Sci. Paris 357(2), 200–204 (2019)
Măntoiu, M., Nistor, V.: Spectral theory in a twisted groupoid setting: spectral decompositions, localization and Fredholmness. Münster J. Math. 13(1), 145–196 (2020)
Măntoiu, M., Purice, R., Richard, S.: Twisted crossed products and magnetic pseudodifferential operators. In: Advances in Operator Algebras and Mathematical Physics, Volume 5 of Theta Series in Advanced Mathematics, pp. 137–172. Theta, Bucharest (2005)
Mǎntoiu, M.: Essential spectrum and Fredholm properties for operators on locally compact groups. J. Oper. Theory 77(2), 481–501 (2017)
Nistor, V.: Desingularization of Lie groupoids and pseudodifferential operators on singular spaces. Commun. Anal. Geom. 27(1), 161–209 (2019)
Pedersen, G.: \(C^{\ast } \)-Algebras and Their Automorphism Groups, Volume 14 of London Mathematical Society Monographs. Academic Press, Inc., London (1979)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics. IV. Analysis of Operators. Academic Press, New York (1978)
Teschl, G.: Mathematical Methods in Quantum Mechanics, Volume 157 of Graduate Studies in Mathematics, 2nd edn. American Mathematical Society, Providence (2014). With applications to Schrödinger operators
Vasy, A.: Asymptotic behavior of generalized eigenfunctions in \(N\)-body scattering. J. Funct. Anal. 148(1), 170–184 (1997)
Vasy, A.: Propagation of singularities in many-body scattering. Ann. Sci. École Norm. Sup. (4) 34(3), 313–402 (2001)
Vasy, A.: Geometry and analysis in many-body scattering. In: Inside Out: Inverse Problems and Applications, Volume 47 of Mathematical Sciences Research Institute Publications, pp. 333–379. Cambridge University Press, Cambridge (2003)
Weyl, H.: The Theory of Groups and Quantum Mechanics. Dover Publications, Inc., New York (1950). Translated from the second (revised) German edition by H. P. Robertson, Reprint of the 1931 English translation
Yserentant, H.: Regularity and Approximability of Electronic Wave Functions, Volume 2000 of Lecture Notes in Mathematics. Springer, Berlin (2010)
Acknowledgements
We thank Vladimir Georgescu for useful discussions. We also thank anonymous referees and the handling editor for carefully reading our paper and for useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Stéphane Nonnenmacher.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
B.A. has been partially supported by SPP 2026 (Geometry at infinity) and the SFB 1085 (Higher Invariants), both funded by the DFG (German Science Foundation). J.M. and V.N. have been partially supported by ANR-14-CE25-0012-01 (SINGSTAR) funded by ANR (French Science Foundation).
Appendices
Appendix A: Proper Maps
We now provide a characterization of proper maps used in the main body of the paper. Let \(f : X \rightarrow Y\) be a continuous map between two Hausdorff spaces. Recall that f is called proper if \(f^{-1}(K)\) is compact for every compact subset \(K \subset Y\).
Lemma A.1
(Generalizes [53, Prop. 4.32]). Let \(f : X \rightarrow Y\) be a continuous map between two Hausdorff spaces with Y locally compact. If f is proper, then f is closed.
In [53, Prop. 4.32], the lemma is stated with the additional requirement that X be locally compact. However, in the proof the locally compactness of X is not needed. We omit the proof since we will apply the lemma only when X is locally compact.
Corollary A.2
Let \(f : X \rightarrow Y\) be a continuous injective map between two Hausdorff spaces with Y locally compact. If f is proper, then f is a homeomorphism onto its image.
Proof
The map \(f:X\rightarrow f(X)\) is bijective continuous and closed and thus a homeomorphism. \(\square \)
We shall say that f is locally proper if, for every \(y \in Y\), there exists an open neighborhood \(V_y\) of y in Y such that the map \(f^{-1}(V_y) \rightarrow V_y\) induced by f is proper.
Lemma A.3
Let \(f : X \rightarrow Y\) be a continuous map between two Hausdorff spaces with Y locally compact. Then f is proper if, and only if, it is locally proper.
Proof
Clearly, every proper map is locally proper, by definition. Let us assume that f is locally proper and let \(K \subset Y\) be a compact subset. For any \(y\in K\), we choose the open neighborhood \(V_y\) as in the definition of a locally proper map. As Y is locally compact, there is an open neighborhood \(W_y\) of y in \(V_y\) such that its closure \({\overline{W}}_y\) in Y is a compact subset of \(V_y\). The local properness of f together with the choice of \(V_y\) implies that \(f^{-1}({\overline{W}}_y\cap K)\) is compact. By the compactness of K, we can choose \(y_1,\ldots ,y_N\) such that K is covered by \(\left( W_{y_j}\right) _{1\le j\le N}\). Then \(K=\bigcup _{j=1}^N \left( {\overline{W}}_{y_j}\cap K\right) \). Hence,
is also compact. This completes the proof. \(\square \)
Appendix B: More on Submanifolds of Manifolds with Corners
We discuss here a few other notions of submanifolds and the relation to our concept of weak submanifold. While this is not needed for the proof of the main result, we hope the interested reader will find this material useful.
1.1 B.1 Submanifolds in Melrose’s Sense
We begin with Melrose’s concept of a submanifold in a manifold with corners, following [56, Definition 1.7.3].
Definition B.1
A subset S of a manifold with corners M of dimension n is a submanifold (in the sense of manifolds with corners) if, for every \(p \in S\), there exists \(0 \le k \le n\) and a (corner) chart \(\phi :U\rightarrow \Omega \subset {\mathbb {R}}_k^n := [0,\infty )^k \times {\mathbb {R}}^{n-k} \), numbers \(n'\le n\) and \(k'\le n'\), and a matrix \(G\in \mathop {\mathrm {GL}}(n,{\mathbb {R}})\) such that
-
(1)
\(p \in U\)
-
(2)
\(G \left( {\mathbb {R}}^{n'}_{k'}\times \{0\}\right) \subset {\mathbb {R}}^n_k.\)
-
(3)
\(\phi (S \cap U)\ =\ G \left( {\mathbb {R}}^{n'}_{k'}\times \{0\}\right) \cap \Omega .\)
Obviously, every submanifold in the sense of manifolds with corners is a weak submanifold, see Definition 2.10. In [56], all submanifolds are submanifolds in the sense of Definition 2.10, see e.g., Lemma 2.11. In Remarks 2.12 (a), we explained that any weak submanifold of a manifold with corners inherits an atlas, and thus this also applies to submanifolds in the above sense. However, it can be shown [50] that many submanifolds in our article are not submanifolds in the sense of manifolds with corners, but only weak submanifolds, as defined in Definition 2.10. In Example B.3, we provide an example of a weak submanifold of \({\mathbb {R}}^2_1\) that is not one in the sense of Definition B.1.
Example B.2
(Diagonal). Let N be a manifold with corners. Then \(M:=N\times N\) is also a manifold with corners. Consider the diagonal \(\Delta _N:=\{(p,p)\in M\mid p\in N\}\). Then \(\Delta _N\) is a submanifold of M in the sense of manifolds with corners.
The following provides examples of weak submanifolds that are not submanifolds in the sense of Definition B.1.
Examples B.3
-
(1)
The function \(f : {\mathbb {R}}^2_1 := [0, \infty ) \times {\mathbb {R}}\rightarrow {\mathbb {R}}^2_1\), \(f(x,y):=(x+y^2,y)\), is an injective immersion. It is a homeomorphism onto its image \(S:=f\bigl ({\mathbb {R}}^2_1\bigr )\). However, it can be easily seen that S is not a submanifold of \({\mathbb {R}}^2_1\) in the sense of manifolds with corners. On the other hand, S is a submanifold of \({\mathbb {R}}^2\) in the sense of manifolds with corners.
-
(2)
The function \(f(x):=(x,x^2)\) defines a injective immersion \({\mathbb {R}}^1_1\rightarrow {\mathbb {R}}^2_2\). It is a homeomorphism onto its image \(S:=f\bigl ({\mathbb {R}}^1_1\bigr )\). However, S is not a submanifold \({\mathbb {R}}^2_2\) in the sense of manifolds with corners. On the other hand, S is a submanifold of \({\mathbb {R}}^2_1\) and of \({\mathbb {R}}^2\) in the sense of manifolds with corners.
In our article, injective immersions that are homeomorphisms onto their images play an important role. Recall the following classical fact for manifolds N and M without boundary and without corners:
Examples B.3 show that \((*)\) does no longer hold if M and N are manifolds with corners and if we understand the word “submanifold” in the sense of Definition B.1. On the other, we proved in Proposition 2.13 that \((*)\) holds for manifolds with corners, if we replace “a submanifold” by “a weak submanifold.”
1.2 B.2 Other Classes of Submanifolds
For comparison and completeness, we recall now the definitions of some further classes of submanifolds. The reason the reader might be interested in these concepts is that the concept of a submanifold in the sense of Definition B.1 seems to be too unspecific and the concept of a p-submanifold (Definition 2.15) seems to be sometimes too restrictive. A first alternative is the concept of a “wib-submanifold”, where “wib” stands for a submanifold without an interior boundary.
Definition B.4
A submanifold \(S\subset M\) is called a wib-submanifold or a submanifold without interior boundary if it can be defined locally in suitable charts as the kernel of a linear function. More precisely: \(S\subset M\) is a wib-submanifold if, for every \(x \in S\), there exists a (corner) chart \(\phi :U\rightarrow \Omega \subset {\mathbb {R}}^n_k\), and a linear subspace L of \({\mathbb {R}}^n\), such that
-
(1)
\(x \in U\) and
-
(2)
\(\phi (S \cap U)\ =\ L \cap \Omega .\)
If \(G\in \mathop {\mathrm {GL}}(n,{\mathbb {R}})\) is as in Definition B.1, then we necessarily have \(L = G \left( {\mathbb {R}}^{n'}\times \{0\}\right) \). If \(x\in S\cap U\), then \(n':=\dim (L)\) is the dimension of S in x defined above. Obviously all p-submanifolds are wib-manifolds, which can be easily seen by defining the L in the definition above as the linear extension of \(L_I\) in Definition 2.15.
Remark B.5
In the above definition, we explicitly required S to be a submanifold. To justify this requirement, we will give an example of a closed subset \(S\subset M\) that is not a submanifold, but fulfills all other requirements of the definition of a wib-submanifold. Indeed, let
which is a cone over a square. The map \(f:{\mathbb {R}}^3\rightarrow {\mathbb {R}}^4\), \(f(x_1,x_2,x_3)= (x_1,x_2,x_3-x_1,x_3-x_2)\) has the property \(f^{-1}({\mathbb {R}}^4_4)=K\). Then for \(\phi ={\text {id}}\), \(x=0\), and \(L:=f({\mathbb {R}}^3)\) all requirements of the definition are satisfied, but \(S:=f(K)\) is not a submanifold of \({\mathbb {R}}^4_4\). It it were a submanifold, then its dimension would have to be 3, and then any boundary point of S is in at most 3 closed boundary hyperfaces. But \(0\in S\) is in 4 closed boundary hyperfaces of S.
Remark B.6
Note that Melrose also introduces the notions d-submanifold [56, Def. 1.7.4] and b-submanifold [56, Def. 1.12.9], whose definitions will not be recalled here. They satisfy
However, there are wib-manifolds that are not b-submanifolds, such as Melrose’s example of the submanifold \(\{x_3=x_1+x_2\}\in {\mathbb {R}}^3_3\). There are d-manifolds that are no wib-manifolds, for instance, \({\mathbb {R}}^1_1=[0,\infty )\subset {\mathbb {R}}\) or any surface with boundary in \({\mathbb {R}}^3\). However, all p-submanifolds introduced below are d-submanifolds and wib-submanifolds. Melrose shows that the diagonal \(\Delta _N\) is a b-submanifold of \(N\times N\), but in general not a d-submanifold. It follows that \(\Delta _N\) is not a p-submanifold.
Remark B.7
Let us remark that the concept of a tame submanifold considered in [2, Sect. 2.3] is a concept of a submanifold in an essentially different sense, it is actually a more restrictive notion of submanifold than the ones encountered in this paper. All notions of submanifolds discussed so far involve properties that may or may not hold for a subset N of a manifold with corners M. In contrast to this, tame submanifolds in [2, Sect. 2.3] are submanifolds of a Lie manifold (M, A), where M is a manifold with corners and A is a Lie algebroid on M with some compatibility conditions. Whether a subset N of M is a tame submanifold of (M, A) or not depends also on the Lie algebroid A. In any case, a tame submanifold will have a tubular neighborhood in the strongest sense. Similar remarks apply to the \(A({\mathcal {G}})\)-tame submanifolds considered in [66].
Rights and permissions
About this article
Cite this article
Ammann, B., Mougel, J. & Nistor, V. A Comparison of the Georgescu and Vasy Spaces Associated to the N-Body Problems and Applications. Ann. Henri Poincaré 23, 1141–1203 (2022). https://doi.org/10.1007/s00023-021-01109-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-021-01109-1