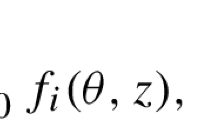Abstract
For a quasi-periodically forced differential equation, response solutions are quasi-periodic ones whose frequency vector coincides with that of the forcing function and they are known to play a fundamental role in the harmonic and synchronizing behaviors of quasi-periodically forced oscillators. These solutions are well-understood in quasi-periodically perturbed nonlinear oscillators either in the presence of large damping or in the non-degenerate cases with small or free damping. In this paper, we consider the existence of response solutions in quasi-periodically perturbed, second order differential equations, including nonlinear oscillators, of the form
where \(\lambda \) is a constant, \(0<\epsilon \ll 1\) is a small parameter, \(l>1\) is an integer, \(\omega \in \mathbb {R}^d\) is a frequency vector, and \(f: \mathbb {T}^d\times \mathbb {R}^2\rightarrow \mathbb {R}^1\) is real analytic and non-degenerate in x up to a given order \(p\ge 0\), i.e., \([f(\cdot ,0,0)]=[\frac{\partial f(\cdot ,0,0)}{\partial x}]=[\frac{\partial ^2 f(\cdot ,0,0)}{\partial x^2}]=\cdots =[\frac{\partial ^{p-1} f(\cdot ,0,0)}{\partial x^{p-1}}]=0\) and \([\frac{\partial ^{p} f(\cdot ,0,0)}{\partial x^{p}}]\ne 0\), where \([\ \ ]\) denotes the average value of a continuous function on \(\mathbb {T}^d\). In the case that \(\lambda =0\) and f is independent of \(\dot{x}\), the existence of response solutions was first shown by Gentile (Ergod Theory Dyn Syst 27:427–457, 2007) when \(p=1\). This result was later generalized by Corsi and Gentile (Commun Math Phys 316:489–529, 2012; Ergod Theory Dyn Syst 35:1079–1140, 2015; Nonlinear Differ Equ Appl 24(1):article 3, 2017) to the case that \(p>1\) is odd. In the case \(\lambda \ne 0\), the existence of response solutions is studied by the authors Si and Yi (Nonlinearity 33(11):6072–6099, 2020) when \(p=0\). The present paper is devoted to the study of response solutions of the above quasi-periodically perturbed differential equations for the case \(\lambda \ne 0\) by allowing \(p>0\). Under the conditions that \(0\le p<l/2\) and \(\lambda [\frac{\partial ^{p} f(\cdot ,0,0)}{\partial x^{p}}]> 0\) when \(l-p\) is even, we obtain a general result which particularly implies the following: (1) If either l is odd and \(\lambda <0\) or l is even and \([\frac{\partial ^{p} f(\cdot ,0,0)}{\partial x^{p}}]>0\), then as \(\epsilon \) sufficiently small response solutions exist for each \(\omega \) satisfying a Brjuno-like non-resonant condition; (2) If either l is odd and \(\lambda >0\) or l is even and \([\frac{\partial ^{p} f(\cdot ,0,0)}{\partial x^{p}}]<0\), then there exists an \(\epsilon _*>0\) sufficiently small and a Cantor set \(\mathcal {E}\in (0,\epsilon _*)\) with almost full Lebesgue measure such that response solutions exist for each \(\epsilon \in \mathcal {E}\) and \(\omega \) satisfying a Diophantine condition. Similar results are also obtained in the case \(\lambda =\pm \epsilon \) which particularly concern the existence of large amplitude response solutions.
Similar content being viewed by others
References
Braaksma, B., Broer, H.: On a quasi-periodic Hopf bifurcation. Ann. Inst. H. Poincaré Anal. Non Linéaire 4(2), 115–168 (1987)
Broer, H.W., Hanßmann, H., You, J.: Bifurcations of normally parabolic tori in Hamiltonian systems. Nonlinearity 18, 1735–1769 (2005)
Broer, H.W., Hanßmann, H., You, J.: Umbilical torus bifurcations in Hamiltonian systems. J. Differ. Equ. 222, 233–262 (2006)
Broer, H.W., Hanßmann, H., You, J.: On the destruction of resonant Lagrangean tori in Hamiltonian systems. In: Johann, A., Kruse, H.P., Ruppen, F., Schmitz, F. (eds.) Recent Trends in Dynamical Systems. Proceedings of a Conference in Honor of Jürgen Scheurle, Ch. 13, Springer, Berlin (2013)
Broer, H.W., Huitema, G.B., Sevryuk, M.B.: Quasi-periodic Tori in Families of Dynamical Systems: Order Amidst Chaos. Springer, Berlin (1996)
Cheng, H., Si, W., Si, J.: Whiskered tori for forced beam equations with multi-dimensional Liouvillean. J. Dyn. Differ. Equ. 32, 705–739 (2020)
Cheng, H., De la Llave, R., Wang, F.: Response solutions to the quasi-periodically forced systems with degenerate equilibrium: a simple proof of a result of W. Si and J. Si and extensions. Nonlinearity 34(1), 372–393 (2021)
Corsi, L., Gentile, G.: Oscillator synchronisation under arbitrary quasi-periodic forcing. Commun. Math. Phys. 316, 489–529 (2012)
Corsi, L., Gentile, G.: Resonant motions in the presence of degeneracies for quasi-periodically perturbed systems. Ergod. Theory Dyn. Syst. 35, 1079–1140 (2015)
Corsi, L., Gentile, G.: Resonant tori of arbitrary codimension for quasi-periodically forced systems. Nonlinear Differ. Equ. Appl. 24(1), article 3 (2017)
Friedman, M.: Quasi-periodic solutions of nonlinear ordinary differential equations with small damping. Bull. Am. Math. Soc. 73, 460–464 (1967)
Gentile, G.: Degenerate lower-dimensional tori under the Bryuno condition. Ergod. Theory Dyn. Syst. 27, 427–457 (2007)
Gentile, G.: Quasi-periodic motions in strongly dissipative forced systems. Ergod. Theory Dyn. Syst. 30(5), 1457–1469 (2010)
Gentile, G.: Construction of quasi-periodic responsive solutions in forced strongly dissipative systems. Forum Math. 24(4), 791–808 (2012)
Han, Y., Li, Y., Yi, Y.: Degenerate lower-dimensional tori in Hamiltonian systems. J. Differ. Equ. 227, 670–691 (2006)
Hanßmann, H.: The quasi-periodic center saddle bifurcation. J. Differ. Equ. 142(2), 305–370 (1998)
Hanßmann, H.: Hamiltonian torus bifurcations related to simple singularities. In: Laude, G.S., Medhin, N.G., Sambandham, M. (eds.) Dynamic Systems and Applications, pp. 679–685. Dynamics Publishers, Atlanta (2004)
Hanßmann, H.: Local and Semi-local Bifurcations in Hamiltonian Systems. Springer LNM, vol. 1893. Springer, Berlin (2007)
Hu, S., Liu, B.: Degenerate lower dimensional invariant tori in reversible system. Discrete Contin. Dyn. Syst. 38(8), 3735–3763 (2018)
Hu, S., Liu, B.: Completely degenerate lower-dimensional invariant tori for Hamiltonian system. J. Differ. Equ. 266(11), 7459–7480 (2019)
Lou, Z., Geng, J.: Quasi-periodic response solutions in forced reversible systems with Liouvillean frequencies. J. Differ. Equ. 263, 3894–3927 (2017)
Moser, J.: Combination tones for Duffings equation. Commun. Pure Appl. Math. 18, 167–181 (1965)
Si, W., Si, J.: Response solutions and quasi-periodic degenerate bifurcations for quasi-periodically forced systems. Nonlinearity 31(6), 2361–2418 (2018)
Si, W., Yi, Y.: Completely degenerate responsive tori in Hamiltonian systems. Nonlinearity 33(11), 6072–6099 (2020)
Stoker, J.J.: Nonlinear Vibrations in Mechanical and Electrical Systems. Interscience Publisher, New York (1950)
Wang, J., You, J., Zhou, Q.: Response solutions for quasi-periodically forced harmonic oscillators. Trans. Am. Math. Soc. 369(6), 4251–4274 (2017)
Xu, X., Si, W., Si, J.: Stoker’s problem for quasi-periodically forced reversible systems with multidimensional Liouvillean frequency. SIAM J. Appl. Dyn. Syst. 19, 2286–2321 (2020)
Yi, Y.: On almost automorphic oscillations. Fields Inst. Commun. 42, 75–99 (2004)
You, J.: A KAM theorem for hyperbolic-type degenerate lower dimensional tori in Hamiltonian systems. Commun. Math. Phys. 192, 145–168 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Dmitry Dolgopyat.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author was partially supported by the National Natural Science Foundation of China (Grant Nos. 12001315, 11971261, 11571201, 12071255), Shandong Provincial Natural Science Foundation, China (Grant No. ZR2020MA015), China Postdoctoral Science Foundation (Grant No. 2020M680089) and the Fundamental Research Funds of Shandong University (Grant No. 2019GN077). The second author was partially supported by NSERC discovery Grants 1257749 and RGPIN-2020-04451, a faculty development grant from the University of Alberta, and a Scholarship from Jilin University.
Rights and permissions
About this article
Cite this article
Si, W., Yi, Y. Response Solutions in Degenerate Oscillators Under Degenerate Perturbations. Ann. Henri Poincaré 23, 333–360 (2022). https://doi.org/10.1007/s00023-021-01093-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-021-01093-6