A direct proof of the non-existence of a MOL(6)

Abstract

It is well known that a Latin Square of order 6 has no orthogonal mate. Many proofs are known, some of which are very short, see for instance (Betten in Unterricht 36:449–453, 1983; Beth et al. in Design theory, Bibliographisches Institut Mannheim Wien, Zürich, 1985; Tarry in Comptes Rendus Ass Franc Sci Nat 1900(2), 170–203, 1901; Stinson in J Comb Theory A 36:373–376, 1984). This paper provides a short proof of this fact which avoids a case distinction on the isomorphism types of the Latin Square. We observe that any Latin Square of order 6 falls within exactly one of three categories. Either it has two rows which form a permutation whose cycle type is three transpositions. Or it has no subsquare of order 2, or it is a single Latin Square with symmetry group the rotation group of the cube of order 24. In each case, the nonexistence of an orthogonal mate can be seen quickly.

1 Introduction

Recall Euler’s problem of the 36 officers [16]: Can 36 officers, drawn from 6 different ranks and also from 6 different regiments, be arranged in a $6\times 6$-grid so that in each row (both horizontal and vertical) there are 6 officers of different rank and different regiments? The first proof of the impossibility was by Tarry [19], so it became known as the Euler/Tarry problem. It is equivalent to the existence of a pair of orthogonal Latin Squares of order 6. Further proofs for the non-existence were given, also very short ones, [4, 10, 18]. A computer proof with the program Orbiter [2] is instantaneous but does not give insight.

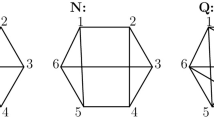
Besides the proof of the non-existence we are also interested in the structure of the Latin Squares of order 6 and the structure of a (hypothetical) MOL(6), see [6,7,8]. For notions as Latin Squares, orthogonal Latin Squares, pairs of mutual orthogonal Latin Squares (MOL), we refer the reader to [11, 13,14,15]. We will view a Latin Square and a (hypothetical) MOL as an incidence structure called a linear space. Therefore, in Sect. 2, we recall the notion of linear spaces. Our approach uses partitions into subsquares. In [6,7,8] we considered partitions of type $6=3+3$. Here, we look at partitions of type $6=2+2+2$. For a fixed partition we denote by $Q_{ij}$ the subsquare arising at the intersection of the $i^{th}$ row class and the $j^{th}$ column class. In the following figure we show the two partition types:

Theorem 1 describes how the 6 elements of a digit are distributed to the 9 subsquares.

A pair of rows in a Latin Square gives rise to a permutation of degree six. Since there can be no fixed points, the possible cycle types are

$$\begin{aligned} (2,2,2), (6), (4,2), (3,3) \end{aligned}$$

We will concentrate on the cycle type (2, 2, 2). Three cases arise:

A: There is a pair of type (2, 2, 2),

B: There is no pair of type (2, 2, 2) and no sub-LSQ(2) exists,

C: There is no pair of type (2, 2, 2) and there exists a sub-LSQ(2).

The non-existence of an orthogonal square in Case A is proved in Theorem 4, for Case B in Theorem 5, and C is ruled out in Theorems 7 and 8 together. We get the non-existence of a MOL(6) without relying on the classification of the Latin Squares.

In an Appendix we collect some properties of the Latin Squares. This is for illustration purposes only. It is not part of the proof.

2 Linear spaces

Definition 1

A (combinatorial) linear space $(V,{{\mathcal {B}}})$ consists of a set V of points (or variables), and a collection ${{\mathcal {B}}}$ of subsets (called blocks) such that each pair of different points lies on exactly one block and each block has at least two points.

We will show

Proposition 1

A Latin Square LSQ(6) is equivalent to a linear space on 18 points with 3 blocks of lenght 6 (called 6-blocks) and 36 blocks of lenght 3 (3-blocks).

Proof

Let the Latin Square be given as an $(6 \times 6)$-array, where on each position there is a digit $\in \{1,2,...,6\}$, such that in each row and each column there are 6 different digits. We define the corresponding linear space: Take as point set the set $V = R \cup C \cup D$ with $R = \{r_1,r_2,...,r_6\}$ (the 6 rows), $C=\{c_1,c_2,...,c_6\}$, (the 6 columns), and $D = \{d_1,d_2,...,d_6\}$, (the 6 digits). Now we define ${{\mathcal {B}}}$: We take the 3 6-blocks R, C and D. For each position $(r_i,c_j)$ of the array there is exactly one digit $d_k$, and we define these 36 triples $(r_i,c_j,d_k)$ as 3-blocks. Given a row $r_i$ and a digit $d_k$ then on row i there is exactly one column number j having digit i. So $r_i$ and $d_k$ are on exactly one of the distinguished 3-blocks. Similarly for a given pair $c_j$, $d_k$ there is exactly one row number and therefore the pair is on exactly one distinguished 3-block. If the two points are on R, on C, or on D, then the joining block ist the 6-block R, C, D, respectively. $\square$.

Definition 2

An isomorphism $\varphi : (V_1,{{{\mathcal {B}}}}_1) \rightarrow (V_2, {{{\mathcal {B}}}}_2)$ is a bijection $\varphi : V_1 \rightarrow V_2$ which maps blocks to blocks. An automorphism of a linear space is an isomorphism to itself.

This notion carries over to Latin Squares. Note, however, that $\varphi$ needs not map rows to rows, columns to colums and digits to digits, but may permute these point types.

Let $T =\{1,2,...,6\}$ and let a second Latin Square be given on the point set $R \cup C \cup T$. It has the same $(6 \times 6)$-array $R \times C$ as the first one und 36 3-blocks (r, c, t) with $t \in T$. Then each pair $(r,c) \in R \times C$ defines a pair $(d,t) \in D \times T$, d coming from the first and t from the second square.

Definition 3

The Latin Square $R \cup C \cup T$ is orthogonal to the Latin square $R \cup C \cup D$ if the 36 pairs (d, t) are pairwise different.

If $R\cup C \cup T$ is orthogonal to $R \cup C \cup D$, then also $R\cup C \cup D$ is orthogonal to $R \cup C \cup T$: the two Latin Squares are called a mutually orthogonal pair, abbreviated MOL(6).

Proposition 2

A (hypothetical) MOL(6) is equivalent to a linear space on 24 points with 4 6-blocks and 36 4-blocks.

Proof

Take as point set the set $V = R \cup C \cup D \cup T$, define the 4 6-blocks R, C, D, T and the 36 4-blocks (r, c, d, t), where (d, t) is the pair on position (r, c). $\Box$

Remark: We speak of a hypothetical MOL(6) since it turns out that no MOL(6) exists.

Definition 4

A transversal of a Latin Square LSQ(6) consists of 6 elements with 6 different rows, 6 different columns and 6 different digits.

In the following example of a transversal the six elements are encircled. We give the transversal a number, say 1, and write this number at the right side of the corresponding digit:

Suppose there are 6 disjoint transversals with numbers 1, 2, ..., 6,  then we set $T=\{1,2,...,6\}$, and get a second Latin Square with point set $V= R \cup C\cup T$. Each transversal number is combined with each digital number and therefore each of the 36 pairs $(d,t), d,t\in \{1,2,...,6\}$ occurs exactly once in the $(6 \times 6)$-array. Therefore $V =R \cup C \cup D$ is orthogonal to $V = R \cup C \cup T$, and the two Latin Squares are a pair of mutually orthogonal squares: MOL(6).

A nearexample:

In the last row we had to put two question marks since a MOL(6) does not exist. The existence of a MOL(6) would give a solution of Euler’s Problem: take the digits as ranks and the transversals as regiments.

Definition 5

A linear space $(V,{{\mathcal {B}}})$ is called regular if the partitions of $V \setminus \{p\}$ by the blocks incident with p are similar for all points $p \in V$.

Example: A Latin Square LSQ(6) is a regular linear space: each point is incident with one 6-block and 6 3-blocks. Also a MOL(6) is regular: each point is incident with one 6-block and 6 4-blocks.

Regular spaces were studied in [3].

3 Parity considerations

Consider a Latin Square LSQ(6) with a decomposition of type (2, 2, 2). For each of the nine $2\times 2$-squares, we call the two positions on the main diagonal positive, and the two positions on the opposite diagonal negative. So, altogether we get 18 positive and 18 negative positions:

Theorem 1

Each digit of a Latin Square LSQ(6) occurs in an even number of positive positions.

Proof

Each digit appears once in every row and also once in every column. Denote by $Q_{i,j}$ the $2\times 2$-subsquare in row i and column j ($i,j=1,2,3$) of the decomposition. Up to permutation of the blocks, there are 3 possibilities for how a digit, say 1, appears in the subsquares:

We claim that it is possible to rearrange rows and columns of the LSQ within the decompositions in such a way that all digits lie in positive positions.

To see that we consider the possible types, one-by-one. In case $\{2,2,2\}$ we interchange columns 1 and 2, columns 3 and 4, columns 5 and 6, if necessary. In the second case $\{2,1,1,1,1\}$ we consider the four quadrangles $Q_{22},Q_{23},Q_{32},Q_{33}$. If the element in $Q_{22}$ has a negative position, we may interchange the two rows or two columns to get

In row 2 there is either the element a (negative) or b (positive). If there is the negative element a we interchange column 3 and 4. If in column 2 there is a negative element c we interchange row 3 and row 4. The unique positive element in $Q_{44}$ follows.

For the type $\{1,1,1,1,1,1\}$ we apply a permutation if necessary to take the unique element in $Q_{11}$ to a positive position. After this we interchange (if necessary) row 5 and row 6, then (if necessary) columns 3 and 4, then rows 3 and 4, and after this columns 5 and 6. This takes all six elements to positive positions and proves the claim in this case.

Each interchanging of rows or columns changes the signs of the two elements in these two rows or two columns: $\{++\} \mapsto \{--\}, \{+-\} \mapsto \{-+\},\{-+\} \mapsto \{+-\}, \{--\} \mapsto \{++\}$. Therefore in each step the number of all positive positions is changed by $+2$, 0 or by $-2$. Going back from the final situation with 6 positive positions to the original situation, the theorem follows. $\square$

4 Assuming a pair of permutation type (2, 2, 2)

If there is a pair of rows (or of columns or of digits) with permutation type (2, 2, 2) then we may assume by isomorphism (Sect. 2) that the pair is in the Latin Square $R \cup C \cup T$, and the pair consists of two transversals of type (2, 2, 2). We then try to find an orthogonal mate $R \cup C \cup D$.

Proposition 3

Assume there exist two transversals a and b in $R \cup C \cup T$ with permutation type (2, 2, 2):

Then the corresponding digits in $R \cup C \cup D$ are

with

Case $A_1$: $e_1=3, e_2=4, (f_1,f_2)= \{5,6\}, (g_1,g_2)= \{1,2\}$,

Case $A_2$: $e_1=3,e_2=5, (f_1,f_2)= \{1,6\}, (g_1,g_2)= \{2,4\}$.

Proof

We first take the case that the pair $(e_1,e_2)$ is either $\{3,4\}$ or $\{5,6\}$, up to isomorphism $\{3,4\}$. Then it follows uniquely $(f_1,f_2)= \{5,6\}$ and $(g_1,g_2)= \{1,2\}$ what is $A_1$. Otherwise one element of $(e_1,e_2)$ is from (3, 4) and the other element from (5, 6), up to isomorphism $(e_1,e_2)=\{3,5\}$.

We show that up to isomorphism we can choose $1 \in \{{f_1,f_2}\}$: Suppose $1\in \{{g_1,g_2}\}$. We take a reflection with respect the diagonal, then we interchange the $2 \times 2$-squares $Q_{22}$ and $Q_{33}$ and after this we interchange digits 3 and 5, and digits 4 and 6. Then we get $1 \in \{{f_1,f_2}\}$ and therefore $(f_1,f_2)= \{1,6\}, (g_1,g_2)= \{2,4\}$ which is case $A_2$. $\square$

We call a tripel of $2 \times 2$-squares tactical if they arise in the shape of a permutation matrix.

Proposition 4

If for a tactical tripel of $2 \times 2$-squares two squares contain one element of the six elements of a digit, and the third square none of them, then the distribution is the cyclic distribution $\{1,1,1,1,1,1\}$.

Proof

Up to permutation of rows or columns the tactical tripel has the form

If one of the 6 empty squares contains at least two digits, then they must lie diagonally. This gives two digits 1 in a row or in a column, a contradiction. Therefore each square contains at most one digit and we get the type $\{1,1,1,1,1,1\}$.

Theorem 2

The partial structure $A_1$ in Proposition 3 is impossible.

Proof

The partial structure is up to isomorphism

All 6 digits fulfill the condition of Proposition 4 and have type $\{1,1,1,1,1,1\}$. Therefore we know for each digit the distribution to the $2\times 2$-subsquares $Q_{i,j}$:

We now determine for each $Q_{i,j}$ the exact positions of the 4 digits it contains. We begin with the square $Q_{12}$: Since in $Q_{22}$ the digits 5 and 6 are on a diagonal they have to be in different columns in $Q_{12}$, and since the digits 1 and 2 in $Q_{11}$ are on a diagonal, they have to be in $Q_{12}$ in different rows. It follows that the pairs $\{5,6\}$ and $\{1,2\}$ are diagonals in $Q_{12}$. The pair $\{5,6\}$ may be the main diagonal and $\{1,2\}$ the opposite diagonal or vice versa, furthermore for each pair there are two permutations possible. Therefore we get for the two pairs $\{5,6\}$ and $\{1,2\}$ in $Q_{12}$ 8 possiblities:

We abbreviate these 8 cases by the notation

Similarly one finds that in all nine $2 \times 2$-squares the two diagonals are made of two of the pairs $\{1,2\}$, $\{3,4\}$ or $\{5,6\}$ (next figure):

For each $2 \times 2$-square we call the main diagonal positive and the opposite diagonal negative. By Theorem 1, the number of positive positions of the 6 digits 1 is even, therefore the number of the positive diagonals $\{1,2\}$ is even as well. Similarly, the number of positive diagonals $\{3,4\}$ and $\{5,6\}$ is even and the sum of these three even numbers is also even. But there are 9 $2 \times 2$-squares which have 9 positive diagonals, and these 9 positive diagonals cannot be covered by an even number of positive diagonals, a contradiction.

This means that the Latin Square in $R \cup C \cup T$ with pair (2, 2, 2), we started with has no orthogonal mate. $\square$

Definition 6

We define the two Latin Squares LQS(6):

The first square is the multiplication table of the group $C_2 \times C_3$ (isomorphic to the cyclic group $C_6$) hence the name. Switching the digits in one of the subsquares of order two yields the Latin Square $(C_2 \times C_3)^{\sigma }$ on the right.

Theorem 3

The partial structure $A_2$ in Proposition 3 extends to the Latin Square $(C_2 \times C_3)$ or $(C_2 \times C_3)^{\sigma }$.

Proof

The partial structure is

We first show that it extends to

The notation $2\leftrightarrow 5$ means $2\;\;\;5$ or $5\;\;\;2$.

To prove this we use Proposition 4 and get the distributions of the 6 digits to the subsquares $Q_{ij}$:

We determine for each $Q_{i,j}$ the exact positions of the 4 digits it contains. We begin with the square $Q_{12}$: Since in $Q_{11}$ there are the digits 2 and 5 in the second row, the digits 2 and 5 in $Q_{12}$ have to be in the first row, either as 2 5 or as 5 2, which we indicate by the notation $2\leftrightarrow 5$. Since on position 44 (i. e. row 4, column 4) there is a digit 4, the digit 4 in $Q_{12}$ has to be in column 3, and the positions of the four digits in the square $Q_{12}$ follow. Similarly we find the positions of digits in the other $2 \times 2$-squares and it also follows $f_1=1$, $f_2=6$, $g_1=2$ and $g_2=4$.

After a suitable permutation of rows we obtain

Here we consider the $6 \times 6$-array as an array of $2 \times 2$-squares with parities

An inversion of a row (interchanging + and - there) means an interchanging of the two corresponding rows of the original Latin Square, similarly for the columns of the array. Each interchange of the digit pairs $\{1,3\},\{2,5\}$ or $\{4,6\}$ induces an automorphism of the Latin Square.

By suitable inversions of columns and rows we may assume that the array becomes

We assume 4, 3, or 2 minus signs at the remaining positions. Then we take suitable inversions and get

In all cases we can reach 8 or 9 positive signs. It follows that the Latin Square is isomorphic to $(C_2 \times C_3)$ or $(C_2 \times C_3)^{\sigma }$. $\square$

Proposition 5

The Latin Square $C_2 \times C_3$ has no orthogonal mate.

Proof

The digits 1,3,5 have 6 positive positions, each, and 2,4,6 have 6 negative positions, each. A transversal meets each of the digit numbers 1,2,3,4,5,6 exactly once and has therefore 3 positive and three negative positions. This is a contradiction to Theorem 1. $\square$

Proposition 6

The Latin Square $(C_2 \times C_3)^{\sigma }$ has no orthogonal mate.

Proof

This Latin Square has 2 digits with 6 positive positions, 2 digits with 6 negative positions, one digit with 4+, 2- and one digit with 2+ and 4-. It follows that two transversals have 3 positive and 3 negative positions, a contradiction to Theorem 1. $\square$

Theorem 4

A Latin Square LSQ(6) with a pair of rows (or columns or digits) of cycle type (2, 2, 2) has no orthogonal square.

Proof

We started with a Latin Square in $R\cup C \cup T$ having a pair of type (2, 2, 2) and tried to find an orthogonal square in $R \cup C \cup D$. In case $A_1$ there existed no such square (Theorem 2). In case $A_2$ there exist two orthogonal mates, the squares $(C_2 \times C_3)$ and $(C_2 \times C_3)^{\sigma }$ (Theorem 3). The starting Latin Square in $R \cup C \cup T$ and its orthogonal square in $R \cup C \cup D$ are a pair of mutually orthogonal latin squares. But by Propositions 5 and 6 the Latin Squares $(C_2 \times C_3)$ and $(C_2 \times C_3)^{\sigma }$ have no orthogonal mate, a contradiction. $\square$

5 Assuming the non-existence of a sub-LSQ(2)

Proposition 7

If a Latin Square LSQ(6) has no sub-LSQ(2) then it has a triple of rows

Proof

From the assumption follows that that each pair of rows has either the cycle type (3, 3) or (6). Take an arbitrary triple of rows. Then not all three pairs can have the type (6) since the permutation (6) is odd. It follows that there is at least one pair of rows having type (3, 3).

Start with this pair of rows:

If on row 3 and columns 1 to 3 there are three low digits, i.e. digits in $\{1,2,3\}$, then this gives case a). If there are two low digits then we have one high digit ($\in \{4,5,6\}$), up to isomorphism on row 3 and column 1 the digit 4 (we write this as 31:4). It follows that

and the pair of rows 1,3 is not of type (3, 3), a contradiction.

Next we assume that on row 3, columns 1 to 3 there is one low digit, up to isomorphism 31:3. We may choose 33:4 and get 34:1 since the row pair 1,3 is of type (3, 3). The positions of 5 and 6 are then unique what is b).

If on row 3, columns 1 to 3 there are digits 4,5,6, then the resulting pairs have type (2, 2, 2), (2, 4) or (6), a contradiction. $\Box$

Proposition 8

If a Latin Square LSQ(6) has no subsquare of order two then it has a subsquare of order 3.

Proof

It suffices to prove that the triple b) in Proposition 7 has no extension to an LSQ(6) without a sub-LSQ(2). Then the first three columns of a) are a Latin Square of order 3.

We start with b): In the fourth row and column 1 we may take the digit 4. Then 43:5 or 43:6 since we avoid an LSQ(2) in the column pair 1,3. In both cases we get a unique fourth row:

To prove this we find in the first case uniquely 42:1, then 45:3, then 46:2 and 44:6. In the second case there is 46:1, since digits 2 or 3 would give an LSQ(2). Row 4 is then detgermined uniquely.

In case $b_1)$ there is an LSQ(2) in rows 2,4 and columns 1,6. In case $b_2)$ there will be an LSQ(2) in rows 5,6 and columns 2,5. $\square$

Proposition 9

If an LSQ(6) has a subsquare LSQ(3), then it has no orthogonal mate.

In the squares right above and left down there are digits 4,5,6 and in the square right side down there are digits 1,2,3. Such a LSQ(6) has no transversal at all: A transversal has in one of the four squares at least two elements, say in the square left above. Then it has also two elements right side down, and therefore the transversal has four elements paired with digits from $\{1,2,3\}$, a contradiction. It follows that there exists no orthogonal mate. $\square$

Combining Propositions 8 and 9 gives

Theorem 5

A Latin Square LSQ(6) which has no sub-LSQ(2) has no orthogonal mate.

6 Parallel classes on an 8-point set

We consider a set $\{1,2,3,4,5,6,7,8\}$ of 8 elements. A partition into 4 disjoint subsets of size two is called a parallel class, for instance

$$\begin{aligned} \{1,2\},\{3,4\},\{5,6\},\{7,8\}. \end{aligned}$$

Up to isomorphism there are two pairs of disjoint parallel classes:

The first has two 2-cycles, the second one has one 4-cycle.

In order to study triples of disjoint parallel classes we recall from [3]: A regular linear space (12|3, 8, 24) is defined on 12 points and has 3 disjoint 4-blocks (i. e., subsets with 4 points), 8 3-blocks and 24 2-blocks with the condition: each pair of points is on exactly one block.

Proposition 10

The regular linear spaces (12|3, 8, 24) correspond bijectively to the disjoint triples of parallel classes on 8 points.

Proof

In the following figure a regular linear space is given by means of its incidence matrix (the 24 2-blocks deleted).

There are 12 rows (the 12 points) and 11 columns (3 4-blocks and 8 3-blocks). Taking the set of 3-blocks as 8-set, then we have on this 8-set three parallel classes (the rows of the incidence structure). If, conversely, a triple of parallel classes on an 8-point set is given, then we extend each 2-block to a 3-block (horizontally). We get 3 disjoint 4-blocks (vertically) and therefore a regular linear space on 12 points.

Each tripel has a row number r, a column number c and a digit number d. If we insert in an $4\times 4$-array at row r and column c the digit d then we get the figure at the right hand side.This presents the triple as a substructure of an LSQ(6). $\square$

Theorem 6

Up to isomorphism, there are 8 triples of parallel classes on an 8-point set, two of them have all three pairs of type (4).

Proof: We cite [3, p.114] and display these 8 geometries as $4\times 4$-arrays. We give for each space the automorphism group order and the cycle types of the three pairs rows/columns, rows/digits, columns/digits.

The last two spaces have three pairs of type (4). $\square$

7 The remaining case

So far, we have treated all LSQ(6) which have a pair of cycle type (2, 2, 2). We have also shown that the Latin Square without a sub-LSQ(2) has no orthogonal mate. The remaining case is treated next.

Theorem 7

Assume there is at least one sub-LSQ(2), but no pair with permutation type (2, 2, 2), then there is exactly one LSQ(6) with this property.

Proof

We start with an LSQ(2), say in rows 1,2, columns 1,2 and digits 1 and 2. We have to put in the digits $\{3,4,5,6\}$ in row 1,2 and columns 3,4,5,6. In order to avoid a pair (2, 2, 2) we need there a 4-cycle. Similarly the digits $\{3,4,5,6\}$ in column 1,2 and rows $\{3,4,5,6\}$ have to form a 4-cycle. Then we have to insert the 4 digits 1 and 4 digits 2 into the square Q of rows 3 to 6 and columns 3 to 6. Also here we need a 4-cycle, say

Then in Q there remain 8 empty positions which have to be filled with the digits 3, 3, 4, 4, 5, 5, 6, 6. All pairs rows/columns, rows/digits, columns/digits have the type (4) and by Theorem 6 there are up to isomorphism exactly two possibilities and we get for the subsquare Q the two cases

We now try to extend these partial structures to a latin square of order 6. We fill in rows 1,2 and columns 3 to 6 (unique up to interchanging the two rows). Also columns 1,2 and rows 3 to 6 follow uniquely (up to interchanging column 1 and 2).

In the first case (left figure) there exists a unique extension and we get the latin square of the theorem. The second case (right figure) has no extension: for position 21 we have digit 1 or digit 2. Then the pair of rows 2,3 resp. 2,6 has type (2, 2, 2), a contradiction.

We apply to this Latin Square the isomorphism:

This latin square has 4 sub-LSQ(2) shown in the following left figure

The encircled elements of the right figure define the 8 vertices of a 3-dimensional cube Z. The edges are: the 4 pairs within the same row (x-direction), the 4 pairs within the same column (y-direction) and the 4 pairs of digits having the same value (z-direction).

Theorem 8

The Latin Square of Theorem 7 has as automorphism group the orientation preserving motion group of the cube and the square has no orthogonal mate.

The cyclic rotation group around the z-axis ((a, b, c, d), (A, B, C, D)) defines a cyclic group $C_4$ around the center of the LSQ(6): (4,3,5,2)(1,6). In order to see the rotation groups around the x-axis and y-axis we apply an isomorphism to the LSQ(6) which maps each triple (r, c, d) to the triple (r, d, c), and interchange then rows 2 and 3. This gives the left square of the next figure. If we apply to the LSQ(6) the isomorphism $(r,c,d) \mapsto (d,c,r)$ and interchange rows 4 and 5, we get the right square:

These figures show the rotation group around the y-axis (left) and around the x-axis (right). It follows that the direct motion group of the cube acts as automorphism group of the LSQ(6). Assume that the orientation changing map of the cube, say $a\leftrightarrow A, b\leftrightarrow B, c\leftrightarrow C, d\leftrightarrow D$, is an isomorphism, then from the two subsquares

follows $6\mapsto 5$ and $6\mapsto 4$, a contradiction. Therefore $S_4$ is the full automorphism group of the latin square.

Next we show that this latin square has no orthogonal mate: the group is transitive on the set Z of 8 central (encircled) elements. No transversal is contained in the set of 28 outer elements (the elements in the complement of Z). Such a transversal would have at least two elements in, say, the square left above (rows 1 to 3, columns 1 to 3) and therefore also in the square right down. This would give a transversal with at least 4 elements from $\{1,2,3\}$, a contradiction. It follows that each transversal intersects the set Z in at least one element. Each automorphism maps transversals to transversals and pairs of disjoint transversals to pairs of disjoint transversals. Since the group is transitive on the set Z, all 6 transversals of an orthogonal square intersect Z in the same number $a>0$. But $a \times 6 \ne 8$, a contradiction.

Remark: This Latin Square has 8 transversals. One of them is given by (*) in the following figure, the other transversals follow by applying the automorphism group:

The transversal (*) intersects the cube Z in 3 elements. Description: for the fixed vertex (2) in the figure take the three neighboring vertices $4^*,2^*,5^*$ on the cube. Since the cube has 8 vertices this gives 8 triples (which extend to 8 transversals of the Latin Square).

8 Appendix

In this appendix we give descriptions of some latin squares occuring before.

8.1 List of the 12 LSQ(6)

In this computer printout of the 12 isomorphism types of latin squares LSQ(6) the order of the automorphism group is listed on top. Three of them have the same order 24. For these we also give the number l of subsquares LSQ(2), namely $l=15, l=11, l=4$.

8.2 A pair of permutation type (2, 2, 2)

In the list we see 10 squares which have a substructure

and they belong to the first case (2, 2, 2) we considered.

The first two squares (with order 432 resp. 144) are the Latin Squares $S_2 \times S_3$ resp. $(S_2 \times S_3)^{\sigma }$.

The two cases A1 and A2 in Theorems 2 and 3 can be described by the tactical decompositions:

A1:

Generating with a computer program [2] we get no geometry in case A1 and the two geometries in case A2. So, the computer confirms Theorem 4.

8.3 No subsquare LSQ(2) of order two

In the list there is exactly one square (the last one) with this property, the latin square with automorphism group order 648. It has the following TDA (tactical decomposition induced by the automorphism group):

The TDA of an incidence structure is defined by the orbits of the automorphism group on the point set and on the block set, see [9].

For the incidence matrix of the latin square

this means that there are two orbits, and this gives a flag transitive configuration $18_6 36_3$.

Remark: There are two other latin squares LSQ(6) with this property, the squares with $aut= 1296$ and $aut = 432$.

8.4 The remaining case

There are 229 symmetric configurations $12_3$, see for instance [1]. There is a unique configuration which has the largest automorphism group order, the order 72. We call this D88, since it is number 88 in Daublebsky’s paper, [12]. The following model of the configuration is taken from [1, fig. 5.1]. There are 3 parallel classes which can be seen in the corresponding incidence matrix.

Proposition 11

The LSQ(6) of Theorem 7 contains the configuration D88 as a substructure.

Proof

We choose the following substructure and apply an isomorphism.Then we describe it by its incidence matrix:

Here we see a cube (3-blocks 1 to 8) which is extended by a parallel class (4 pairwise disjoint 3-blocks), denoted by $9^*,...,12^*$.

The 8 triples 1, 2, ..., 8 are the 8 vertices of the cube. These 8 elements have a natural partition into 2 quadruples by the two inscribed tetrahedra: $1^-,4^-,6^-,7^-$ and $2^+,3^+,5^+,8^+$. With this partition we get:

This presentation shows D88 as a substructure of LSQ(6). There are three subcubes: the 8 blocks + and -, the 8 blocks + and * and the 8 blocks - and *. The automorphism group of D88 has order 72: the stabilizer of one of the cubes has order 24 (the orientation preserving group of symmetries) and the three cubes may be permuted cyclically. As a substructure of LSQ(6) we get only the group order 24 since the class * is fixed. $\square$