1 Introduction

In [1, ch. IX §8] Bottema and Roth devote a short section to the subject of plane symmetric rigid-body motions. The theoretical kinematics literature contains very little else on this subject. By contrast, in the theory of mechanisms and robotics plane symmetric mechanism are well known. Both single loop mechanisms and parallel robots with this type of symmetry are well represented in the literature. In this work we look in some detail at the properties of these rigid-body motions and their relationships with the geometry of curves in space.

We begin with generalities: the definition of plane symmetric motions and a proof that the axodes of these motions are always developable ruled surfaces. The next three sections deal with plane symmetric motions generated by reflections in the osculating, normal and rectifying planes of a space curve. It is shown that any ruled surface that is a tangent developable surface is the fixed axode for some plane symmetric motion. So, in some sense, the case of the motion based on the osculating planes to a curve is the general case. A connection is shown between the plane symmetric motion based on the normal planes to a curve and the Bishop motion for the same curve. The fixed axodes of the motions are the same, however the motions are different. This demonstrates that the fixed axode is not sufficient to determine a rigid-body motion. As well as looking at the motion based on the rectifying planes to a curve a fourth case, given by the reflection in the normal planes to the curve’s Darboux vector, is studied.

Section 6 deals with the acceleration properties of these plane symmetric motions. It is shown that the acceleration centre of a motion based on the osculating planes to a curve is the current point on the curve. The next section deals with particular types of curves that have partner curves. In these cases there are relations between the motions determined by the curve and the motion determined by its partner curve.

The final section looks at what might be thought of as an application of the results and methods developed in the rest of the article. The idea here is to study line-symmetric motions by thinking of a reflection in a line as a composite of reflections in orthogonal planes meeting at the line in question. In this way we are able to find the twist velocity and fixed axodes of line symmetric motions generated by reflections in the normal and binormal lines of a space curve.

2 General plane symmetric motions

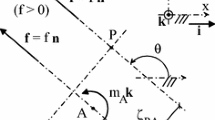
Reflection in a plane with unit normal vector \(\varvec{u}\) can be represented by a \(4\times 4\) homogeneous matrix partitioned as,

$$\begin{aligned} M=\begin{pmatrix} I-2\varvec{u}\varvec{u}^T&{}2d\varvec{u}\\ 0&{}1 \end{pmatrix} \end{aligned}$$

where d is the perpendicular distance from the plane to the origin, see Fig. 1. Notice that an arbitrary point \(\varvec{p}\), will be transformed to the point, \(\varvec{p} +2(d-\varvec{u}\cdot \varvec{p})\varvec{u}\) by such a reflection and this can be represented by the matrix product,

$$\begin{aligned} M\tilde{p}=\begin{pmatrix} I-2\varvec{u}\varvec{u}^T&{}2d\varvec{u}\\ 0&{}1 \end{pmatrix}\begin{pmatrix}\varvec{p}\\ 1\end{pmatrix}. \end{aligned}$$

The notation \(\tilde{p}\) here is intended to indicate an “extended vector”; \(\tilde{p}=(\varvec{p},\,1)^T\).

Fig. 1
figure 1

Reflection in a plane

Full size image

A plane symmetric motion can be thought of as the result of successive reflections in a continuous one-parameter family of planes. If a rigid body is being reflected then clearly the reflection in planes will change the orientation of the body. So, as an alternative description of a plane-symmetric motion an initial plane can be fixed, the motion is then given by first reflecting in the fixed plane and then reflecting in the successive planes in the family as before. If the fixed plane is the plane in the family associated with parameter value 0, then the rigid-body motion passes through the identity in the group of rigid-body displacements. It is also simple to see that subsequent displacements are pure rotations about lines in the fixed plane, or possibly translations parallel to the fixed plane.

In terms of \(4\times 4\) homogeneous matrices representing rigid-body displacements a plane symmetric motion can then be written as,

$$\begin{aligned} G(\mu )=\begin{pmatrix} I-2\varvec{u}(\mu )\varvec{u}(\mu )^T&{}2d(\mu )\varvec{u}(\mu )\\ 0&{}1 \end{pmatrix} \begin{pmatrix} I-2\varvec{u}_0\varvec{u}_0^T&{}2d_0\varvec{u}_0\\ 0&{}1 \end{pmatrix}, \end{aligned}$$

where \(\varvec{u}_0\) and \(d_0\) are the unit normal and perpendicular distance to the origin for the initial, fixed plane. Also \(\mu \) is the parameter of the motion, this will be suppressed in the following for brevity.

The twist velocity of such a motion can be computed as follows,

$$\begin{aligned} S_d=\dot{G}G^{-1}=2 \begin{pmatrix} \dot{\varvec{u}}\varvec{u}^T-\varvec{u}\dot{\varvec{u}}^T&{}\dot{d}\varvec{u}-d\dot{\varvec{u}}\\ 0&{}0 \end{pmatrix}, \end{aligned}$$

where the dot denotes differentiation with respect to the parameter \(\mu \). It is often more convenient to use a 6-vector representation of these Lie algebra elements, see [6]. Note that since \(\varvec{u}\) is a unit vector, \(\varvec{u} \cdot \varvec{u}=1\) and hence \(\varvec{u}\cdot \dot{\varvec{u}}=0\). In partitioned form the velocity twist of a general plane symmetric motion is given by,

$$\begin{aligned} \mathbf {s}_d= 2\begin{pmatrix} \varvec{u}\times \dot{\varvec{u}}\\ \varvec{r}\times (\varvec{u}\times \dot{\varvec{u}}) \end{pmatrix}, \end{aligned}$$
(2.1)

where, \(\varvec{r}=d\varvec{u}+\frac{\dot{d}}{|\dot{\varvec{u}}|^2}\dot{\varvec{u}}\). More generally, the point on the line can be written as \(\varvec{r}=d\varvec{u}+\frac{\dot{d}}{|\dot{\varvec{u}}|^2}\dot{\varvec{u}}+\lambda \varvec{u}\times \dot{\varvec{u}}\), where \(\lambda \) is arbitrary. This shows,

Theorem 2.1

The velocity twist of a plane symmetric motion always has pitch 0, and is hence what Study described as a Ribaucour motion, [10], see also [9].

The result above immediately gives the fixed axode of the motion, but also it can be shown that,

Theorem 2.2

The fixed axode of a plane-symmetric motion is a developable ruled surface.

Proof

The condition for a ruled surface to be developable is that its distribution parameter vanishes.

If a ruled surface is given in the form,

$$\begin{aligned} \varvec{r}+\lambda (\varvec{u}\times \dot{\varvec{u}}) \end{aligned}$$

then the distribution parameter of the surface is given by,

$$\begin{aligned} \delta =\frac{\det \big ( \dot{\varvec{r}},\,(\varvec{u}\times \dot{\varvec{u}}),\,(\varvec{u}\times \ddot{\varvec{u}}) \big )}{|\varvec{u}\times \ddot{\varvec{u}}|^2}, \end{aligned}$$

see for example [11, ch. III]. Expanding the determinant as a scalar triple product and remembering that \(\varvec{u}\cdot \dot{\varvec{u}}=0\), gives

$$\begin{aligned} \delta =\frac{(\dot{\varvec{r}}\cdot \varvec{u})(\varvec{u}\times \dot{\varvec{u}})\cdot \ddot{\varvec{u}}}{|\varvec{u}\times \ddot{\varvec{u}}|^2}. \end{aligned}$$

Developing \(\dot{\varvec{r}}\) finally gives,

$$\begin{aligned} \delta =\frac{\dot{d}}{|\varvec{u}\times \ddot{\varvec{u}}|^2}\big (\varvec{u}\times (\dot{\varvec{u}}\times \ddot{\varvec{u}})\big )\left( 1+\frac{\varvec{u}\cdot \ddot{\varvec{u}}}{|\dot{\varvec{u}}|^2}\right) . \end{aligned}$$

But since \(\varvec{u}\cdot \dot{\varvec{u}}=0\), differentiating again gives \(\dot{\varvec{u}}\cdot \dot{\varvec{u}}+\varvec{u}\cdot \ddot{\varvec{u}}=0\) and hence \(\delta =0\). \(\square \)

It is well known that there are just three possibilities,[2, Chap. 1]:

  1. 1.

    The planes are tangent to a cone.

  2. 2.

    The planes are tangent to a cylinder.

  3. 3.

    The fixed axode is the tangent developable to some curve.

If the planes are tangent to a cone all the planes will contain the vertex of the cone. The successive displacements will be rotations about lines in the initial plane passing through the vertex of the cone. So in this case the rigid-body motion will be a sequence of rotations about a fixed point, the vertex of the cone. That is, a spherical motion.

When the planes generating the motion are tangent to a general cylinder, the motion is clearly a planar motion.

The moving axode of a general plane-symmetric motion can be found in a similar fashion. The twist velocity of the motion in the moving coordinate frame is given by,

$$\begin{aligned} S_b=G^{-1}\dot{G}=G^{-1}S_dG. \end{aligned}$$

This is a conjugation in the group of the fixed-frame velocity twist, hence the body-fixed velocity twist will have the same pitch as the frame-fixed velocity. That is, the body-fixed velocity twist will also consist of pure rotations and the body-fixed velocity twists can be thought as the lines generating the moving axode of the motion. As short computation shows that,

$$\begin{aligned} S_b=2F_0\begin{pmatrix} \varvec{u}\dot{\varvec{u}}^T-\dot{\varvec{u}}\varvec{u}^T&{}d\dot{\varvec{u}}-\dot{d}\varvec{u}\\ 0&{}0 \end{pmatrix}F_0, \end{aligned}$$

where

$$\begin{aligned}F_0=\begin{pmatrix} I-2\varvec{u}_0\varvec{u}_0^T&{}2d_0\varvec{u}_0\\ 0&{}1 \end{pmatrix}, \end{aligned}$$

is the reflection in the initial plane. As for the fixed-frame velocity, this can be cast into a 6-vector form,

$$\begin{aligned} \mathbf {s}_b=2 \begin{pmatrix} \mathcal {U}_0&{}0\\ 2d_0U_0&{}-\mathcal {U}_0 \end{pmatrix} \begin{pmatrix} \varvec{u}\times \dot{\varvec{u}}\\ \varvec{r}\times (\varvec{u}\times \dot{\varvec{u}}) \end{pmatrix}. \end{aligned}$$
(2.2)

Here \(\mathcal {U}_0=I-2\varvec{u}_0\varvec{u}_0^T\) and the matrix \(U_0\) is the \(3\times 3\) anti-symmetric matrix corresponding to \(\varvec{u}_0\), that is \(U_0\varvec{x}=\varvec{u}_0\times \varvec{x}\) for any vector \(\varvec{x}\). As above, \(\varvec{r}=d\varvec{u}+\frac{\dot{d}}{|\dot{\varvec{u}}|^2}\dot{\varvec{u}}\). From this we see that:

Theorem 2.3

The moving axode of a plane-symmetric motion is the reflection of its fixed axode in the initial plane of the motion.

Proof

Equation (2.2) can clearly be written as,

$$\begin{aligned}\mathbf {s}_b= \begin{pmatrix} \mathcal {U}_0&{}\quad 0\\ 2d_0U_0&{}\quad -\mathcal {U}_0 \end{pmatrix} \mathbf {s}_d. \end{aligned}$$

Now, by considering the effect of the reflection \(F_0\), on a pair of points it is simple but tedious to compute that the effect of a reflection on the Plücker coordinates of the line joining the pair of point is given by the \(6\times 6\) matrix,

$$\begin{aligned} \begin{pmatrix} \mathcal {U}_0&{}\quad 0\\ 2d_0U_0&{}\quad -\mathcal {U}_0 \end{pmatrix}. \end{aligned}$$

\(\square \)

This means that the moving axode has the same type as the fixed axode; if the family of planes has a fixed point then the axodes consist of a pair of cones. When the family of planes are parallel to a fixed direction, the axodes consist of a pair of cylinders. Otherwise the axodes are a pair of tangent developable ruled surfaces.

These results appear in [1, ch. IX §8], the proofs above serve as an introduction to the notation and methods used in the rest of the article.

3 Reflections in the osculating planes of a space curve

Given a curve in space there are many ways to use this to define a rigid-body motion, the best known perhaps being the Frenet-Serret motion, [1, ch. IX §2]. It is well known that at each point on a regular curve, three planes can be found; the normal plane, osculating plane and rectifying plane. So as the parameter of the curve changes there are three 1-parameter families of planes determined by the curve. Each of these three families of planes can be taken as the continuous one-parameter family of planes determining a plane-symmetric motion.

To make it simpler to refer to these constructions the following definitions will be adopted.

Definition 3.1

The plane symmetric motion based on the osculating planes of a curve \(\varvec{\gamma }\) will be called the osculating planes motion of \(\varvec{\gamma }\). Likewise, the normal planes motion and the rectifying planes motion of \(\varvec{\gamma }\) will denote the plane-symmetric motions based on the normal planes and rectifying planes of \(\varvec{\gamma }\) respectively.

For the osculating planes motion, the instantaneous twist velocity is given by the intersection of consecutive planes, hence instantaneous rotations about the tangent lines to the original curve. The fixed axode is clearly the developable ruled surface generated by the tangent lines to the curve.

Consider a curve \(\varvec{\gamma }(\mu )\). For the osculating planes to this curve \(\varvec{u}=\varvec{b}\) is the unit binormal vector of the curve. The perpendicular distance to the origin can be found from any point on the plane, for example the point \(\varvec{\gamma }\), so \(d=\varvec{\gamma }\cdot \varvec{b}\). Substituting this into Eq. (2.1) gives the twist velocity as,

$$\begin{aligned} \mathbf {s}_d=-2\nu \tau \begin{pmatrix}\varvec{b}\times \varvec{n}\\ \varvec{r}\times (\varvec{b}\times \varvec{n}) \end{pmatrix}=2\nu \tau \begin{pmatrix}\varvec{t}\\ \varvec{r}\times \varvec{t} \end{pmatrix}, \end{aligned}$$

where \(\nu \) and \(\tau \) are the speed and torsion of the curve respectively. As usual \(\varvec{t}\) and \(\varvec{n}\) denote the unit tangent and principal normal vector to the curve. The point \(\varvec{r}\) is a point on the axis of the instantaneous twist. From above we have that,

$$\begin{aligned} \varvec{r}=d\varvec{u}+\frac{\dot{d}}{|\dot{\varvec{u}}|^2}\dot{\varvec{u}}= (\varvec{\gamma }\cdot \varvec{b})\varvec{b}+(\varvec{\gamma }\cdot \varvec{n})\varvec{n} \end{aligned}$$

A general point on the axis of the instantaneous twist is given by,

$$\begin{aligned} \varvec{r}\,'=(\varvec{\gamma }\cdot \varvec{b})\varvec{b}+(\varvec{\gamma }\cdot \varvec{n})\varvec{n}+\lambda \varvec{t}, \end{aligned}$$

where \(\lambda \) is arbitrary. But choosing \(\lambda =(\varvec{\gamma }\cdot \varvec{t})\) shows that \(\varvec{\gamma }\) lies on this axis, since,

$$\begin{aligned} (\varvec{\gamma }\cdot \varvec{b})\varvec{b}+(\varvec{\gamma }\cdot \varvec{n})\varvec{n}+(\varvec{\gamma }\cdot \varvec{t})\varvec{t}=\varvec{\gamma }, \end{aligned}$$

as \(\varvec{t},\,\varvec{n}\) and \(\varvec{b}\) form and orthonormal system of unit vectors. This shows that the fixed axode consists of the tangent lines to the curve \(\varvec{\gamma }\). This confirms the general argument given at the beginning of this section, however the computation gives more information since it is clear that at each instant the magnitude of the instantaneous twist is \(2\nu \tau \).

Note that this is really the general case for a tangent developable axode.

Theorem 3.2

Any tangent developable ruled surface is the fixed axode of some plane-symmetric motion.

Proof

For the planes generating a plane-symmetric motion it is sufficient to take the tangent planes of the ruled surfaces as generating planes of the plane-symmetric motion. Note that these are the osculating planes to the cuspidal edge of the tangent developable ruled surface. \(\square \)

4 Reflections in the normal planes of a curve

It is well known that the envelope of the normal planes to a curve form a developable ruled surface. The cuspidal edge of this developable is known as the pole curve, see [3]. Hence, the fixed axode of a plane-symmetric motion based on the normal planes to a curve \(\varvec{\gamma }\), will be the tangent lines to the pole curve of \(\varvec{\gamma }\).

In [9] it was shown that a Bishop motion (or RMF motion) based on a curve \(\varvec{\gamma }\) has as its fixed axode the tangent lines to the pole curve of \(\varvec{\gamma }\). However, the normal planes symmetric motion and the Bishop motion are not the same. To understand this, the velocity twists of the two motions will be computed.

For the normal planes the relations \(\varvec{u}=\varvec{t}\) and \(d=\varvec{\gamma }\cdot \varvec{t}\) can be substituted into Eq. (2.1) to give,

$$\begin{aligned} \mathbf {s}_d=2\begin{pmatrix} \varvec{t}\times (\nu \kappa )\varvec{n}\\ \varvec{r}\times \big (\varvec{t}\times (\nu \kappa )\varvec{n}\big ) \end{pmatrix}= 2\nu \kappa \begin{pmatrix} \varvec{b}\\ \varvec{r}\times \varvec{b} \end{pmatrix}. \end{aligned}$$

Here, the point \(\varvec{r}\) is given by,

$$\begin{aligned} \varvec{r}=(\varvec{\gamma }\cdot \varvec{t})\varvec{t}+(\frac{1}{\kappa }+\varvec{\gamma }\cdot \varvec{n})\varvec{n}. \end{aligned}$$

Arguing as in the previous section, this can be written as,

$$\begin{aligned} \mathbf {s}_d=2\nu \kappa \begin{pmatrix} \varvec{b}\\ (\varvec{\gamma }+\frac{1}{\kappa }\varvec{n})\times \varvec{b} \end{pmatrix}. \end{aligned}$$
(4.1)

The Bishop motion based on the curve \(\varvec{\gamma }\) will be given by a curve in the group SE(3),

$$\begin{aligned} G=\begin{pmatrix}R&{}\quad \varvec{\gamma }\\ 0&{}\quad 1\end{pmatrix} \end{aligned}$$

where the rotation matrix R has columns given by the tangent and normal vectors of the Bishop frame,

$$\begin{aligned} R=\Big (\varvec{t}\,\Big |\,\varvec{n}_1\,\Big |\,\varvec{n}_2\Big ). \end{aligned}$$

To find the velocity twist the Bishop frame equations can be written as,

$$\begin{aligned}&\dot{\varvec{t}}=\nu (-k_2\varvec{n}_1+k_1\varvec{n}_2)\times \varvec{t},\\&\dot{\varvec{n}}_1=\nu (-k_2\varvec{n}_1+k_1\varvec{n}_2)\times \varvec{n}_1,\\&\dot{\varvec{n}}_2=\nu (-k_2\varvec{n}_1+k_1\varvec{n}_2)\times \varvec{n}_2. \end{aligned}$$

where the vector \(-k_2\varvec{n}_1+k_1\varvec{n}_2=\kappa \varvec{b}\) is the the binormal vector multiplied by the curvature, see [9].

The velocity twist of this motion will be given by,

$$\begin{aligned}\dot{G}G^{-1}=\nu \begin{pmatrix}\kappa BR&{}\varvec{t}\\ 0&{}0\end{pmatrix} \begin{pmatrix}R^T&{}-R^T\varvec{\gamma }\\ 0&{}1\end{pmatrix} = \nu \begin{pmatrix}\kappa B&{}\varvec{t}-\kappa \varvec{b}\times \varvec{\gamma }\\ 0&{}0\end{pmatrix}, \end{aligned}$$

where B is the \(3\times 3\) anti-symmetric matrix corresponding to the binormal vector \(\varvec{b}\). The twist can be written as a partitioned 6-vector,

$$\begin{aligned} \mathbf {s}_d=\nu \kappa \begin{pmatrix}\varvec{b}\\ (\varvec{\gamma }+\frac{1}{\kappa }\varvec{n})\times \varvec{b} \end{pmatrix}. \end{aligned}$$

This proves the following,

Theorem 4.1

Given a curve \(\varvec{\gamma }\) the Bishop motion based on the curve and the normal planes symmetric motion based on the curve have the same fixed axode, but the magnitude of the twist velocity of the normal planes motion is twice that of the Bishop motion.

Notice also, that the moving axodes of the two motions are different. In Theorem 2.3 it was shown that the moving axode of a plane symmetric motion is a reflection of its fixed axode in the initial plane of the motion. For a Bishop motion it is known that the moving axode is a sequence of lines lying in a plane, [9].

5 Reflections in the rectifying planes of a curve

The rectifying planes of a curve have normal vector \(\varvec{u}=\varvec{n}\) and the distance to the origin of a rectifying plane is \(d=\varvec{\gamma }\cdot \varvec{n}\). The velocity twist of a plane-symmetric motion based on such a family of planes is then,

$$\begin{aligned}\mathbf {s}_d=2\begin{pmatrix} \varvec{n}\times \dot{\varvec{n}}\\ \varvec{r}\times (\varvec{n}\times \dot{\varvec{n}}) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \varvec{n}\times \dot{\varvec{n}}=\nu \varvec{n}\times (-\kappa \varvec{t}+\tau \varvec{b}) =\nu (\tau \varvec{t}+\kappa \varvec{b}), \end{aligned}$$

and points on the line are given by,

$$\begin{aligned} \varvec{r}=d\varvec{u}+\frac{\dot{d}}{|\dot{\varvec{u}}|^2}\dot{\varvec{u}}+\lambda \varvec{u}\times \dot{\varvec{u}}= (\varvec{\gamma }\cdot \varvec{n})\varvec{n}+(\varvec{\gamma }\cdot \dot{\varvec{n}})\frac{\dot{\varvec{n}}}{|\dot{\varvec{n}}|^2}+ \lambda \varvec{n}\times \dot{\varvec{n}}. \end{aligned}$$

Notice that, \(\varvec{n}\) and \(\dot{\varvec{n}}\) are orthogonal, so if we choose the parameter \(\lambda \) to be,

$$\begin{aligned} \lambda =\big (\varvec{\gamma }\cdot (\varvec{n}\times \dot{\varvec{n}})\big )\frac{\varvec{n}\times \dot{\varvec{n}}}{|\varvec{n}\times \dot{\varvec{n}}|^2} \end{aligned}$$

then we can see that the curve \(\varvec{\gamma }\) lies on the fixed axode, that is, the velocity twist is given by,

$$\begin{aligned} \mathbf {s}_d=2\nu \begin{pmatrix} \tau \varvec{t}+\kappa \varvec{b}\\ \varvec{\gamma }\times (\tau \varvec{t}+\kappa \varvec{b}) \end{pmatrix}. \end{aligned}$$

The cuspidal edge of the rectifying planes to a curve is known as the rectifying curve and it is well known that the original curve is a geodesic on the tangent developable to the rectifying curve, see [3, ch. I]. Here, of course, the tangent developable is the fixed axode of the rectifying planes motion.

Suppose we let \(\varvec{\delta }=\frac{1}{\sqrt{\kappa ^2+\tau ^2}}(\tau \varvec{t}+\kappa \varvec{b})\). This is a unit vector in the direction of the Darboux vector to the curve. The velocity twist of a rectifying planes motion can be written,

$$\begin{aligned} \mathbf {s}_d=2\nu \sqrt{\kappa ^2+\tau ^2}\begin{pmatrix} \varvec{\delta }\\ \varvec{\gamma }\times \varvec{\delta } \end{pmatrix}. \end{aligned}$$

This shows that, the velocity twist of a rectifying planes motion is a line in the direction of the Darboux vector of the curve, passing through the curve. A Frenet-Serret motion, based on the same curve would have a velocity twist in the same direction but here the pitch of the twist is not zero and the axis of the twist does not meet the curve, see [9].

This suggests another plane symmetric motion based on a curve. Imagine reflecting in the family of planes normal to the Darboux vector of the curve and passing through the curve at the current point on the curve. The fixed axode for this motion is then,

$$\begin{aligned} \mathbf {s}_d= 2\begin{pmatrix} \varvec{\delta }\times \dot{\varvec{\delta }}\\ \varvec{r}\times (\varvec{\delta }\times \dot{\varvec{\delta }}) \end{pmatrix}, \end{aligned}$$

see Eq. (2.1). Computations show that,

$$\begin{aligned} \dot{\varvec{\delta }}=\left( \frac{\kappa \dot{\tau }-\tau \dot{\kappa }}{\kappa ^2+\tau ^2}\right) \varvec{n}\times \varvec{\delta },\qquad \varvec{\delta }\times \dot{\varvec{\delta }}=\left( \frac{\kappa \dot{\tau }-\tau \dot{\kappa }}{\kappa ^2+\tau ^2}\right) \varvec{n} \end{aligned}$$

and

$$\begin{aligned} \varvec{r}=(\varvec{\gamma }\cdot \varvec{\delta })\varvec{\delta }+\frac{1}{|\dot{\varvec{\delta }}|^2}\frac{d(\varvec{\gamma }\cdot \varvec{\delta })}{d\mu }\dot{\varvec{\delta }}+\lambda \varvec{n}= \varvec{\gamma }+\frac{\nu \tau }{\sqrt{\kappa ^2+\tau ^2}}\dot{\varvec{\delta }}+\lambda '\varvec{n}, \end{aligned}$$

where \(\lambda '\) is arbitrary. This demonstrates the following:

Theorem 5.1

Given a curve \(\varvec{\gamma }\), the twist velocity of the plane symmetric motion generated by the normal planes to the curve’s Darboux vector \(\varvec{\delta }\), is given by,

$$\begin{aligned} \mathbf {s}_d=2\left( \frac{\kappa \dot{\tau }-\tau \dot{\kappa }}{\kappa ^2+\tau ^2}\right) \begin{pmatrix} \varvec{n}\\ (\varvec{\gamma }+\varvec{\zeta })\times \varvec{n} \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} \varvec{\zeta }=\frac{\nu \tau (\kappa \dot{\tau }-\tau \dot{\kappa })}{(\kappa ^2+\tau ^2)^{\frac{3}{2}}}\varvec{n}\times \varvec{\delta } \end{aligned}$$

and, as usual, \(\nu ,\,\kappa \) and \(\tau \) are the speed, curvature and torsion of the curve. So the lines of the fixed axode of this motion are parallel to the normals of the curve, but through a point displaced from the curve by \(\varvec{\zeta }\).

6 Acceleration

Let \(\varvec{p}_0\) be a point in the rigid-body when the value of the parameter is \(\mu =0\). Now, at subsequent values of the parameter the location of the point will be given by,

$$\begin{aligned}\begin{pmatrix} \varvec{p}(\mu )\\ 1 \end{pmatrix}=G(\mu ) \begin{pmatrix} \varvec{p}_0\\ 1 \end{pmatrix}. \end{aligned}$$

Differentiating gives the velocity of the point,

$$\begin{aligned}\begin{pmatrix} \dot{\varvec{p}}(\mu )\\ 0 \end{pmatrix}=\dot{G}(\mu ) \begin{pmatrix} \varvec{p}_0\\ 1 \end{pmatrix}= \dot{G}(\mu )G^{-1}(\mu ) \begin{pmatrix} \varvec{p}(\mu )\\ 1 \end{pmatrix}=S_d\begin{pmatrix} \varvec{p}(\mu )\\ 1 \end{pmatrix}. \end{aligned}$$

The acceleration of the point can be found by differentiating again,

$$\begin{aligned}\begin{pmatrix} \ddot{\varvec{p}}(\mu )\\ 0 \end{pmatrix}= (\dot{S}_d+S_d^2)\begin{pmatrix} \varvec{p}(\mu )\\ 1 \end{pmatrix}. \end{aligned}$$

Now, suppose that the motion that the rigid-body is subject to is a plane-symmetric motion given by reflection in the osculating planes to some curve \(\varvec{\gamma }\). Using the results above, and the Frenet-Serret relations for \(\varvec{\gamma }\), the velocity and acceleration of the arbitrary point \(\varvec{p}\) can be written as,

$$\begin{aligned} \dot{\varvec{p}}=2\nu \tau \varvec{t}\times (\varvec{p}-\varvec{\gamma })=2\nu \tau T(\varvec{p}-\varvec{\gamma }) \end{aligned}$$

and

$$\begin{aligned} \ddot{\varvec{p}}=2\Big (\frac{d(\nu \tau )}{d\mu }T+\nu ^2\tau \kappa N+\nu ^2\tau ^2 T^2 \Big )(\varvec{p}-\varvec{\gamma }). \end{aligned}$$

In the above pair of equations \(\nu ,\,\kappa \) and \(\tau \) are the speed, curvature and torsion of \(\varvec{\gamma }\); \(\varvec{t}\) and \(\varvec{n}\) are the tangent and normal vectors to \(\varvec{\gamma }\) at \(\mu \) and T and N are the \(3\times 3\) anti-symmetric matrices corresponding to \(\varvec{t}\) and \(\varvec{n}\) respectively.

From this we can find the acceleration centre of the motion:

Theorem 6.1

At any instant of an osculating planes motion based on a space curve \(\varvec{\gamma }\) the acceleration centre of the motion is located at the current point on the curve \(\varvec{\gamma }\).

Proof

The acceleration centre is the point whose acceleration is instantaneously zero. Clearly when \(\varvec{p}=\varvec{\gamma }\) the acceleration \(\ddot{\varvec{p}}\) vanishes. It remains to check that the matrix,

$$\begin{aligned} W=\Big (\frac{d(\nu \tau )}{d\mu }T+\nu ^2\tau \kappa N+\nu ^2\tau ^2 T^2 \Big ) \end{aligned}$$

is full rank so that the solution is unique. The determinant of W can be evaluated using the results in the appendix to reference [7], the computations give,

$$\begin{aligned} \det (W)=8\nu ^4\tau ^3\kappa \end{aligned}$$

which, in general, is non-zero. \(\square \)

It is clear from this that the acceleration centre of a plane-symmetric motion based on the normal planes to a curve \(\varvec{\gamma }\), must lie on the polar curve of \(\varvec{\gamma }\). Similarly, if the motion is based on the rectifying planes of \(\varvec{\gamma }\) the acceleration centre will lie on the rectifying curve of \(\varvec{\gamma }\).

For planes tangent to a cone, the vertex of the cone is the acceleration centre, in fact it is a fixed point for all of the motion. For a motion based on the tangent planes to a cylinder there is no acceleration centre.

From [7], it is to be expected that the inflection points of the motion do not lie on a cubic curve but on a conic since the motion is always an instantaneous pure rotation. In fact, it can be shown that:

Theorem 6.2

At any instant of an osculating planes motion based on a space curve \(\varvec{\gamma }\) the only point of inflection is the current point on the curve \(\varvec{\gamma }\).

Proof

Without loss of generality we can write a point on the rigid body as,

$$\begin{aligned} \varvec{p}=\varvec{\gamma }+x\varvec{t}+y\varvec{n}+z\varvec{b} \end{aligned}$$

where \(x,\,y\) and z are variables and \(\varvec{t},\,\varvec{n}\) and \(\varvec{b}\) are the tangent, normal and binormal vectors to \(\varvec{\gamma }\). Substituting this into the equations above for the velocity and acceleration of the point gives,

$$\begin{aligned} \dot{\varvec{p}}=2\nu \tau (y\varvec{b}-z\varvec{n}) \end{aligned}$$

and

$$\begin{aligned} \ddot{\varvec{p}}=2\left( \nu ^2\tau \kappa z\varvec{t}-\left( 2\nu ^2\tau ^2 y+\frac{d(\nu \tau )}{d\mu }z\right) \varvec{n}+\left( \frac{d(\nu \tau )}{d\mu } y-\nu ^2\tau \kappa x -2\nu ^2\tau ^2 y\right) \varvec{b}\right) . \end{aligned}$$

Comparing the coefficients of the mutually orthogonal vectors \(\varvec{t},\,\varvec{n}\) and \(\varvec{b}\) it can be immediately seen that \(z=0\) since \(\varvec{t}\) only appears in the expression for \(\ddot{\varvec{p}}\). Similarly, from the coefficient of \(\varvec{n}\), \(y=0\). Then finally, looking at the coefficients of \(\varvec{b}\) it can be seen that \(x=0\). \(\square \)

Finally, in this section the Bresse hyperboloid for these motions in studied. The points on this surface are points in the moving body where, instantaneously the velocity and acceleration are perpendicular. The result obtained is:

Theorem 6.3

At any instant of an osculating planes motion based on a space curve \(\varvec{\gamma }\), the points with perpendicular velocity and acceleration lie on an elliptical cone whose vertex is the current point on the curve \(\varvec{\gamma }\).

Proof

As in the proof of theorem 6.2, write an arbitrary point on the rigid body as,

$$\begin{aligned} \varvec{p}=\varvec{\gamma }+x\varvec{t}+y\varvec{n}+z\varvec{b} \end{aligned}$$

so that,

$$\begin{aligned} \dot{\varvec{p}}=2\nu \tau (y\varvec{b}-z\varvec{n}) \end{aligned}$$

and

$$\begin{aligned} \ddot{\varvec{p}}=2\left( \nu ^2\tau \kappa z\varvec{t}-\left( 2\nu ^2\tau ^2 y+\frac{d(\nu \tau )}{d\mu }z\right) \varvec{n}+\left( \frac{d(\nu \tau )}{d\mu } y-\nu ^2\tau \kappa x -2\nu ^2\tau ^2 y\right) \varvec{b}\right) . \end{aligned}$$

Now

$$\begin{aligned} \dot{\varvec{p}}\cdot \ddot{\varvec{p}}=4\nu \tau \Big (\frac{d(\nu \tau )}{d\mu }(y^2+z^2)-\nu ^2\tau \kappa xy\Big ). \end{aligned}$$

Setting the above to zero gives a homogeneous degree 2 equation in \(x,\,y\) and z. This can be written as,

$$\begin{aligned} y^2+z^2-\alpha xy=0 \end{aligned}$$

where \(\alpha = \nu ^2\tau \kappa /\frac{d(\nu \tau )}{d\mu }\). This can be rearranged to read,

$$\begin{aligned} (y-\frac{\alpha x}{2})^2+z^2=\left( \frac{\alpha x}{2}\right) ^2. \end{aligned}$$

Clearly \(x=y=z=0\) is a solution corresponding to the point \(\varvec{\gamma }\) on the curve. Because the equation is homogenous, every point on a line joining this point to another solution is also a solution. So the solutions form a cone with vertex \(\varvec{\gamma }\). Intersecting the cone with a plane parallel to the normal plane to the curve at \(\gamma \) means fixing the value of x. The intersection is a circle with centre located at \(\varvec{\gamma }+x\varvec{t}+\frac{\alpha x}{2}\varvec{n}\). \(\square \)

7 Motions based on curves with mates

Many special types of curves have been defined in the literature by the property that they can be used to define another curve, sometimes called a partner curve, mate, offset or parallel curve. In this section some relations between plane symmetric motions based on such curves and their mates are investigated.

Bertrand curves are curves such that at any point the principal normals to the curve and its partner curve coincide, [11, p. 29]. Notice that this means that the rectifying planes to the two curves are parallel. This leads to the following theorem,

Theorem 7.1

Let \(G_r(\mu )\) and \(\tilde{G}_r(\mu )\) be the rectifying planes motion based on a Bertrand curve and its mate respectively, then the product, \(G_r(\mu )\tilde{G}_r^{-1}(\mu )\), is always a pure translation.

Proof

Write,

$$\begin{aligned}G_r= \begin{pmatrix} I-2\varvec{n}\varvec{n}^T&{}2d\varvec{n}\\ 0&{}1 \end{pmatrix} \begin{pmatrix} I-2\varvec{n}_0\varvec{n}_0^T&{}2d_0\varvec{n}_0\\ 0&{}1 \end{pmatrix} \end{aligned}$$

for the motion associated with the Bertrand curve and

$$\begin{aligned}\tilde{G}_r= \begin{pmatrix} I-2\varvec{n}\varvec{n}^T&{}2\tilde{d}\varvec{n}\\ 0&{}1 \end{pmatrix} \begin{pmatrix} I-2\varvec{n}_0\varvec{n}_0^T&{}2\tilde{d}_0\varvec{n}_0\\ 0&{}1 \end{pmatrix}\end{aligned}$$

for the partner curve. The dependence on the parameter \(\mu \) has been suppressed for brevity. Inverting the second matrix and multiplying then gives,

$$\begin{aligned}G_r\tilde{G}_r^{-1} = \begin{pmatrix} I-2\varvec{n}\varvec{n}^T&{}2d\varvec{n}\\ 0&{}1 \end{pmatrix} \begin{pmatrix} I&{}2(d_0-\tilde{d}_0)\varvec{n}_0\\ 0&{}1 \end{pmatrix} \begin{pmatrix} I-2\varvec{n}\varvec{n}^T&{}2\tilde{d}\varvec{n}\\ 0&{}1 \end{pmatrix} =\begin{pmatrix} I&{}\quad \varvec{q}\\ 0&{}\quad 1 \end{pmatrix} \end{aligned}$$

where,

$$\begin{aligned} \varvec{q}=2(d-\tilde{d})\varvec{n}+2(d_0-\tilde{d}_0)(I-2\varvec{n}\varvec{n}^T)\varvec{n}_0.\end{aligned}$$

\(\square \)

Mannheim curves, are also partner curves. Here the principal normal line of the Mannheim curve coincides with the binormal line to the partner curve at the corresponding parameter value, see [4]. The computations above, proving theorem 7.1 will also show the following,

Theorem 7.2

Let \(G_r(\mu )\) and \(\tilde{G}_o(\mu )\) be the rectifying planes motion based on a Mannheim curve and the osculating planes motion based on its mate respectively, then the product, \(G_r(\mu )\tilde{G}_o^{-1}(\mu )\), is always a pure translation.

In [5], Menninger describes a pair of transformations from one curve to another. These are named the successor transformation and the predecessor transformation, one is the inverse of the other. The tangent vector to a curve is the normal vector to its successor curve and so the normal vector to a curve is the tangent vector to its predecessor. This gives another theorem in the same vein as the previous two, and with an almost identical proof:

Theorem 7.3

Let \(G_n(\mu )\) and \(\tilde{G}_r(\mu )\) be the normal planes motion based on a curve and the osculating planes motion based on its successor curve respectively, then the product, \(G_n(\mu )\tilde{G}_r^{-1}(\mu )\), is always a pure translation.

Note that we could also describe \(\tilde{G}_r(\mu )\) as the rectifying planes motion of a curve and \(G_n(\mu )\) as the normal planes motion of its predecessor curve. Clearly, composing these plane symmetric motion as in the theorems of this section will produce a motion that is composed of pure translations. Such motions are well known in robotics, but under several different names. In [8], it was shown that such motions are represented by curves in the Study quadric which lie entirely in the B-plane \(a_1=a_2=a_3=c_0=0\). These motions can also be described as point-symmetric motions, that is motions consisting of successive reflections in the points of a curve in space.

8 Line symmetric motions

Some of the ideas introduced above can be used to look at line symmetric motions. These are rigid-body motions generated by reflecting a rigid body in successive lines of a ruled surface, see [1] for example. A reflection in a line is simply a rotation of \(\pi \) radians about the line. Such a rotation can be generated by reflecting in a pair of orthogonal planes that intersect along the line. So for example, we can reflect in the normal and osculating planes of a space curve to get the line symmetric motion generated by the normal lines to the curve.

Consider a curve \(\varvec{\gamma }\) and let,

$$\begin{aligned}M=\begin{pmatrix} I-2\varvec{b}\varvec{b}^T&{}2(\varvec{\gamma }\cdot \varvec{b})\varvec{b}\\ 0&{}1 \end{pmatrix} \end{aligned}$$

represent reflection in the osculating planes of the curve and

$$\begin{aligned}N=\begin{pmatrix} I-2\varvec{t}\varvec{t}^T&{}2(\varvec{\gamma }\cdot \varvec{t})\varvec{t}\\ 0&{}1 \end{pmatrix} \end{aligned}$$

represent reflection in the normal planes to the curve. Reflection in both planes gives a \(\pi \)-rotation about the normal line to the curve given by MN. In [8] a line symmetric motion generated by a ruled surface was defined as a \(\pi \)-rotation about the initial generator of the surface, at the parameter value \(\mu =0\), followed by \(\pi \)-rotations about successive generators of the ruled surface. This was done to ensure that the curve in the SE(3) representing the motion passes through the identity of the group. In the following, omitting or including this initial \(\pi \)-rotation makes no difference.

Theorem 8.1

The twist velocity of the line symmetric motion generated by the normal lines to a curve \(\varvec{\gamma }\) is the sum of the twist velocities of the osculating planes motion and the normal planes motion associated with the curve.

Proof

The line symmetric motion is given by,

$$\begin{aligned} G=MNM_0N_0 \end{aligned}$$

where M and N are the reflections in the osculating planes and normal planes, as above; and \(M_0\) and \(N_0\) are the reflections in the initial osculating and normal planes to the motion. The twist velocity is given, as usual, by \(\dot{G}G^{-1}\), where the dot denotes differentiation with respect to the parameter \(\mu \). Substituting for G and remembering that reflections are self-inverse gives,

$$\begin{aligned} \dot{G}G^{-1}=(\dot{M}NM_0N_0+M\dot{N}M_0N_0)N_0M_0NM=\dot{M}M+M\dot{N}NM. \end{aligned}$$

Now \(\dot{N}N\) is the twist velocity of the normal planes motion so is represented by a pitch zero twist about a line normal to the osculating plane of the curve at the current point. The conjugation \(M\dot{N}NM\), reflects the line \(\dot{N}N\) in the osculating plane and hence doesn’t change \(\dot{N}N\). That is, \(M\dot{N}NM=\dot{N}N\). Hence we have the result,

$$\begin{aligned} \dot{G}G^{-1}=\dot{M}M+\dot{N}N. \end{aligned}$$

\(\square \)

From this and the results of Sects. 3 and 4 it can be seen that the twist velocity of the line symmetric motion generated by the normal lines to a curve \(\varvec{\gamma }\) are given, as a 6-vector, by,

$$\begin{aligned}\mathbf {s}_d=2\nu \tau \begin{pmatrix}\varvec{t}\\ \varvec{\gamma }\times \varvec{t} \end{pmatrix}+2\nu \kappa \begin{pmatrix} \varvec{b}\\ (\varvec{\gamma }+\frac{1}{\kappa }\varvec{n})\times \varvec{b} \end{pmatrix}= 2\nu \begin{pmatrix} \tau \varvec{t}+\kappa \varvec{b}\\ \varvec{\gamma }\times (\tau \varvec{t}+\kappa \varvec{b})+\varvec{t} \end{pmatrix}. \end{aligned}$$

The pitch h, of this twist is easily found to be,

$$\begin{aligned} h=\frac{(\tau \varvec{t}+\kappa \varvec{b})\cdot (\varvec{\gamma }\times (\tau \varvec{t}+\kappa \varvec{b})+\varvec{t})}{(\tau \varvec{t}+\kappa \varvec{b})\cdot (\tau \varvec{t}+\kappa \varvec{b})}= \frac{\tau }{\kappa ^2+\tau ^2}. \end{aligned}$$

To find the axis of this twist \(\ell \), that is, the generator line of the fixed axode, we subtract h times the first three components of the twist from the last three components, this gives,

$$\begin{aligned}\ell =\begin{pmatrix} \tau \varvec{t}+\kappa \varvec{b}\\ \varvec{\gamma }\times (\tau \varvec{t}+\kappa \varvec{b})+\frac{\kappa }{\kappa ^2+\tau ^2}(\kappa \varvec{t}-\tau \varvec{b}) \end{pmatrix} = \begin{pmatrix} \tau \varvec{t}+\kappa \varvec{b}\\ (\varvec{\gamma } +\frac{\kappa }{\kappa ^2+\tau ^2}\varvec{n})\times (\tau \varvec{t}+\kappa \varvec{b}) \end{pmatrix} \end{aligned}$$

Note, that we are now treating the components of this 6-vector as Plücker coordinates. Since these are homogeneous coordinates we may ignore overall multiplicative factors. Hence, we have shown the following:

Theorem 8.2

The Plücker coordinates of the fixed axode of the line symmetric motion generated by the normal lines to a curve \(\varvec{\gamma }\) are given by,

$$\begin{aligned}\ell = \begin{pmatrix} \varvec{\delta }\\ (\varvec{\gamma } +\frac{\kappa }{\kappa ^2+\tau ^2}\varvec{n})\times \varvec{\delta } \end{pmatrix}. \end{aligned}$$

This shows that the fixed axode consists of lines parallel to the Darboux vector \(\varvec{\delta }\) of the curve passing through a point displaced from the current point on the curve by \(\frac{\kappa }{\kappa ^2+\tau ^2}\) along the normal to the curve.

This method can also be used to investigate the line symmetric motion generated by reflections about the binormal lines to a curve. In this case the two plane symmetric motions which combine to produce this motion are reflections in the normal and rectifying planes. Let N be as above, the \(4\times 4\) matrix representing a reflection in the normal plane to the curve \(\varvec{\gamma }\), and let,

$$\begin{aligned}C=\begin{pmatrix} I-2\varvec{n}\varvec{n}^T&{}2(\varvec{\gamma }\cdot \varvec{n})\varvec{n}\\ 0&{}1 \end{pmatrix} \end{aligned}$$

be the matrix representing a reflection in the rectifying plane of \(\varvec{\gamma }\). Writing the line symmetric motion as,

$$\begin{aligned} G=CNC_0N_0 \end{aligned}$$

it is clear from the proof of Theorem 8.1, that the twist velocity of the motion is,

$$\begin{aligned} \dot{G}G^{-1}=\dot{C}C+C\dot{N}NC. \end{aligned}$$

This time however, the twist \(\dot{N}N\) must be reflected in the rectifying plane of the curve. A straightforward computation reveals that the 6-vector representation of the twist \(C\dot{N}NC\) is,

$$\begin{aligned}2\nu \kappa \begin{pmatrix} -\varvec{b}\\ (\varvec{-\gamma }+\frac{1}{\kappa }\varvec{n})\times \varvec{b} \end{pmatrix}. \end{aligned}$$

Hence the velocity twist of the line symmetric motion generated by the binormal lines to a curve \(\varvec{\gamma }\) is given by,

$$\begin{aligned} \mathbf {s}_d= 2\nu \begin{pmatrix} \tau \varvec{t}+\kappa \varvec{b}\\ \varvec{\gamma }\times (\tau \varvec{t}+\kappa \varvec{b}) \end{pmatrix}+ 2\nu \kappa \begin{pmatrix} -\varvec{b}\\ (\varvec{-\gamma }+\frac{1}{\kappa }\varvec{n})\times \varvec{b} \end{pmatrix}= 2\nu \tau \begin{pmatrix} \varvec{t}\\ \varvec{\gamma }\times \varvec{t}+\frac{1}{\tau }\varvec{t} \end{pmatrix}. \end{aligned}$$

From this have the following:

Theorem 8.3

The pitch of the twist velocity of a line symmetric motion generated by the binormal lines to a curve \(\varvec{\gamma }\) is \(h=1/\tau \) and the fixed axode of the motion is generated by the tangent lines to the curve.

9 Concluding remarks

The differential geometry of curves and surfaces is a classical subject with little recent attention from mainstream mathematics. This applies even more to theoretical kinematics which has been neglected for several decades. The advent of modern robotics has, to some extent, rekindled an interest in kinematics and this work can certainly be considered a product of that theme.

This work was prompted by the striking relation between the normal planes motion and the Bishop motion for any curve. It would be useful if there was a simple way to construct a Bishop motion from a plane symmetric motion. The difficulty seems to be that it is difficult to tell when a plane symmetric motion is the normal planes motion for some curve. This problem would appear to be similar to the classical problem of determining when a curve is the pole curve to some other curve.

Although most of the results in this article refer to the axodes and twist velocities of motions we have been able to say a little about the acceleration properties of plane symmetric motions. It would be useful to extend this to higher order properties of these motions and to other special motions.

Finally, the work on curves with partners, although rudimentary, suggests possible new connections between the classical differential geometry of curves and theoretical kinematics.