Global Regular Axially-Symmetric Solutions to the Navier–Stokes Equations with Small Swirl

Abstract

Axially symmetric solutions to the Navier–Stokes equations in a bounded cylinder are considered. On the boundary the normal component of the velocity and the angular components of the velocity and vorticity are assumed to vanish. If the norm of the initial swirl is sufficiently small, then the regularity of axially symmetric, weak solutions is shown. The key tool is a new estimate for the stream function in certain weighted Sobolev spaces.

1 Introduction

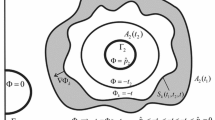
In this work we consider axially-symmetric solutions to the Navier–Stokes equations in bounded cylindrical domains $\Omega \subset {\mathbb {R}}^{3}$ with the boundary $S:=\partial \Omega$.

To describe the problem we transform the Cartesian coordinates $x=(x_1,x_2,x_3)$ into cylindrical coordinates by the relation

$$\begin{aligned} x_1 = r\cos \varphi ,\quad x_2=r\sin \varphi ,\quad x_3=z. \end{aligned}$$

This relation determines the orthonormal basis $({\bar{e}}_r, \bar{e}_\varphi , {\bar{e}}_z)$, where

$$\begin{aligned} {\bar{e}}_r=(\cos \varphi ,\sin \varphi ,0),\quad \bar{e}_\varphi =(-\sin \varphi ,\cos \varphi ,0),\quad {\bar{e}}_z=(0,0,1) \end{aligned}$$

are unit vectors along the radial-, the angular-, and the z-axes, respectively.

Using this orthonormal basis we can decompose the velocity vector $\textbf{v}$ as follows

$$\begin{aligned} {\textbf {v}} = v_r(r,z,t){\bar{e}}_r + v_\varphi (r,z,t){\bar{e}}_\varphi + v_z(r,z,t){\bar{e}}_z. \end{aligned}$$

For the vorticity vector $\varvec{\omega }=\textrm{rot}\,\textbf{v}$ we have the expression

$$\begin{aligned} \varvec{\omega }=-v_{\varphi ,z}(r,z,t)\bar{e}_r+\omega _\varphi (r,z,t)\bar{e}_\varphi +\frac{1}{r}(rv_\varphi )_{,r}(r,z,t){\bar{e}}_z. \end{aligned}$$

Here $\omega _\varphi$ can be computed explicitly, i.e. $\omega _\varphi =v_{r,z}-v_{z,r}$.

Let $R, a > 0$. Then, we define

$$\begin{aligned} \Omega =\{x\in {\mathbb {R}}^{3}:r<R,\ |z|<a\} \end{aligned}$$

and by $\partial \Omega = S_1\cup S_2$ we denote the boundary of $\Omega$, where

$$\begin{aligned} \begin{aligned} S_1&= \left\{ x\in {\mathbb {R}}^{3}:r=R,\ |z|<a\right\} ,\\ S_2&= \left\{ x\in {\mathbb {R}}^{3}:r<R,\ z\in \{-a,a\}\right\} . \end{aligned} \end{aligned}$$

The system of equations we investigate reads

$$\begin{aligned} \left\{ \begin{aligned}&\textbf{v}_t + (\textbf{v}\cdot \nabla )\textbf{v} - \nu \Delta \textbf{v} + \nabla p = \textbf{f}{} & {} \text {in }\Omega ^T = \Omega \times (0,T),\\&{{\,\textrm{div}\,}}\textbf{v} = 0{} & {} \text {in }\Omega ^T,\\&\textbf{v}\cdot {\bar{n}} = 0{} & {} \text {on }S^T = S\times (0,T),\\&\omega _\varphi =0{} & {} \text {on }S^T,\\&v_\varphi =0{} & {} \text {on }S^T,\\&\textbf{v}\big \vert _{t=0} = \textbf{v}_0{} & {} \text {in }\Omega \times \{t = 0\} \end{aligned} \right. \end{aligned}$$

(1.1)

where ${\bar{n}}$ is the unit outward normal to S vector.

To present our main result we need to introduce the quantity

$$\begin{aligned} u=rv_\varphi . \end{aligned}$$

(1.2)

It is called the swirl and is a solution to the problem

$$\begin{aligned} \left\{ \begin{aligned}&u_{,t} + \textbf{v}\cdot \nabla u-\nu \Delta u+{2\nu \over r}u_{,r}=rf_\varphi \equiv f_0{} & {} \text {in }\Omega , \\&u = 0{} & {} \text {on }S^T,\\&u\big \vert _{t=0} = rv_\varphi (0)\equiv u(0){} & {} \text {in }\Omega \times \{t = 0\}. \end{aligned} \right. \end{aligned}$$

(1.3)

We have to emphasize that the boundary conditions (1.1)$_{3,4}$ were introduced by Ladyžhenskaya in [1]. Condition (1.1)$_4$ is necessary for solvability of some initial-boundary value problems for $\omega _\varphi$ (see (1.15)$_2$).

Theorem 1

(Main result). Fix $0< r_0 < R$. Let

$$\begin{aligned} \begin{aligned} D_1^2&\equiv 3\left\Vert \textbf{f}\right\Vert _{L_{1(0,t;L_2(\Omega ))}(\Omega ^t)}^2 + 2\left\Vert \textbf{v}(0)\right\Vert _{L_2(\Omega )}^2< \infty ,\\ D_2&\equiv \left\Vert f_0\right\Vert _{L_1(0,t;L_{\infty }(\Omega ))}+\left\Vert u(0)\right\Vert _{L_\infty (\Omega )} < \infty . \end{aligned} \end{aligned}$$

Let us introduce

$$\begin{aligned} M(t)= & {} c\left( \left\Vert \frac{f_\varphi }{r}\right\Vert _{L_2(0,t;L_{\frac{6}{5}}(\Omega ))}^2 + \left\Vert f_{\varphi }\right\Vert _{L_4(\Omega ^t)}^4 + \left\Vert \frac{\omega _\varphi (0)}{r}\right\Vert _{L_2(\Omega )}^2 \right. \nonumber \\{} & {} \left. + \int _\Omega {v_\varphi ^4(0)\over r^2}\textrm{d}x\right) + c{D_1^{10}D_2^8\over r_0^{16}} \equiv M'(t)+c{D_1^{10}D_2^8\over r_0^{16}}. \end{aligned}$$

(1.4)

Let

$$\begin{aligned} \begin{aligned} \alpha (t,r_0)&= \left\Vert u\right\Vert _{L_{\infty }(\Omega _{r_0}^t)}^2, \qquad \text {where }\Omega _{r_0}=\{x\in \Omega :r\le r_0\},\\ M&= M(T),\\ M'&= M'(T). \end{aligned} \end{aligned}$$

Assume that $\gamma > 1$ and $\alpha (t, r_0)$ is so small that

$$\begin{aligned} \alpha (t,r_0)\le & {} c(\gamma - 1)M \\{} & {} \cdot \left( \gamma M D_2^2 + D_1^2 (\gamma M)^2 + (\gamma M)^2\exp \left( c(\gamma M)^2\right) \left( \left\Vert \frac{v_\varphi (0)}{r}\right\Vert _{L_3(\Omega )}^2 + \left\Vert \frac{f_\varphi }{r}\right\Vert _{L_1(0,t;L_3(\Omega ))}^2\right) \right) ^{-1} \\\equiv & {} \Phi (M). \end{aligned}$$

Then

$$\begin{aligned} \left\Vert \frac{\omega _\varphi }{r}\right\Vert _{L_{\infty }(0,t;L_2(\Omega ))}^2 + \left\Vert \frac{\omega _\varphi }{r}\right\Vert _{L_2(0,t;H^1(\Omega ))}^2 \le \gamma M. \end{aligned}$$

(1.5)

Consider now the case $r_0=R$, thus $\Omega _R=\Omega$. Suppose that

$$\begin{aligned} \alpha (t,R)\le \left\Vert f_0\right\Vert _{L_1(0,t;L_{\infty }(\Omega ))} + \left\Vert u(0)\right\Vert _{L_{\infty }(\Omega )} \equiv \Phi (M'). \end{aligned}$$

Then

$$\begin{aligned} \left\Vert \frac{\omega _\varphi }{r}\right\Vert _{L_{\infty }(0,t;L_2(\Omega ))}^2 + \left\Vert \frac{\omega _\varphi }{r}\right\Vert _{L_2(0,t;H^1(\Omega ))}^2 \le \gamma M'. \end{aligned}$$

(1.6)

One may wonder what is the difference between (1.5) and (1.6). Careful comparison shows that (1.5) is obtained provided that $\alpha (t,r_0) = \left\Vert u\right\Vert ^2_{L_\infty (\Omega _{r_0}^t)}$ is sufficiently small in the neighborhood of $r = 0$. In (1.6) we do not need any smallness restrictions. This might suggest that we can take $r_0 = R$ and without any restrictions show the regularity of weak, axially symmetric solutions with non-vanishing $v_\varphi (0)$. Unsurprisingly, this is not true: (1.6) does not exist without obtaining (1.5) first. We will see later in the proof that we approach certain integral differently when r is close to 0 and when $0< r_0 < r$, where $r_0$ is fixed. Unfortunately, as (1.4) shows, passing with $r_0 \rightarrow 0^+$ is not possible.

We should emphasize that Theorem 1 does not directly imply the regularity of weak solutions but we may quickly deduce it following the reasoning from Lemma 2.9. Instead, we utilize one of many Serrin-type regularity criteria, e.g. [2, Theorem 3.(ii)], which states that if $\omega _\varphi \in L_\infty (0,t;L_2(\Omega ))$, then a weak solution $\textbf{v}$ to (1.1) is regular. Inequality (1.6) yields exactly

$$\begin{aligned} \left\Vert \omega _\varphi \right\Vert _{L_{\infty }(0,t;L_2(\Omega ))} \le cM', \end{aligned}$$

which for $\textbf{v}'=(v_r,v_z)$ yields

$$\begin{aligned} \left\Vert \textbf{v}'\right\Vert _{L_\infty (0,t;H^1(\Omega ))}\le cM', \end{aligned}$$

(1.7)

and eventually

$$\begin{aligned} \left\Vert v_r\right\Vert _{L_\infty (0,t;L_6(\Omega ))} + \left\Vert v_z\right\Vert _{L_\infty (0,t;L_6(\Omega ))} \le cM'. \end{aligned}$$

(1.8)

In light of [3, Theorem 1] the above inequality also implies the regularity of a weak solution $\textbf{v}$ to (1.1). In fact, there are many auxiliary results that could be utilized here. For a brief summary of Serrin-type regularity criteria for axially symmetric solutions to the Navier–Stokes equations we refer the reader to the introductions in e.g. [4, 5] and [6]. Lots of regularity criteria in terms of angular component of the velocity or of the swirl were established in e.g. [7,8,9,10,11,12,13].

In general, the problem of regularity of weak solutions to the Navier–Stokes equations in ${\mathbb {R}}^{3}$ has a long history. In 1968 it was shown independently by Ladyzhenskaya [1] and Ukhovskii et al. [14] that in class of axially symmetric solutions any weak solution is regular provided that $v_\varphi (0) = 0$. Shortly after Ladyzhenskaya wrote a book [15] which laid foundations for intensive research on regularity of weak solutions.

Before describing the steps of the proof of Theorem 1 let us briefly discuss recent results. In [16] the case $\Omega = {\mathbb {R}}^{3}$ is studied. Lei et al. show that if $\sup _{t \ge 0} \left|u(r,z,t)\right| \sim O\left( \ln ^{-2} r\right)$ (see Corollary 1.3), then $\textbf{v}$ is global and regular axially symmetric solution to (1.1)$_{1,2,6}$. This is an improvement over Wei’s result (see [17]), where $O\left( \ln ^{-\frac{3}{2}} r\right)$ is needed. These two results were recently improved in [18], where the condition

$$\begin{aligned} \left|u(r,z,t)\right| \le N e^{-c\left|\ln r\right|^\tau } \end{aligned}$$

implies the regularity of weak solutions. Here $0 < r \le \frac{1}{4}$ and $\tau$ is any number from (0, 1), c, N are some constants. Our result is somehow comparable—(1.4) suggests that $\left|u(r,z,t)\right| \sim e^{-\frac{1}{r^{16}}}$.

We have to emphasize that in papers [8, 10, 13] smallness condition looks very complicated and depends not only on the swirl but also on e.g. vorticity. In [19] to prove the regularity of weak, axially symmetric solutions we assume either $v_r \in L_\infty (0,t;L_3(\Omega ))$ or $\frac{v_r}{r} \in L_\infty (0,t; L_{\frac{3}{2}}(\Omega ))$. In both cases some smallness conditions are needed but they depend explicitly on the constant from the Poincaré inequality.

To the best of our knowledge that are not that many results concerning the regularity of weak, axially symmetric solutions to the Navier–Stokes equations in bounded cylinders (see e.g. [20]). Our main result is not only new but it also uses non-trivial weighted estimates for the stream functions. To explain this technique, we go back to (1.1) and following e.g. Ladyzhenskaya [1] or How et al. (see [21]) we rewrite it in the form

$$\begin{aligned} \left\{ \begin{aligned}&v_{\varphi ,t} + \textbf{v}\cdot \nabla v_\varphi -\nu \bigg (\Delta -\frac{1}{r^2}\bigg )v_\varphi +\frac{1}{r}v_rv_\varphi =f_\varphi{} & {} \text {in }\Omega ^T, \\&\begin{aligned}\omega _{\varphi ,t} + \textbf{v}\cdot \nabla \omega _\varphi -\nu \left( \Delta -\frac{1}{r^2}\right) \omega _\varphi +\frac{1}{r}\left( v_\varphi ^2\right) _{,z} \\ + \frac{1}{r}v_r\omega _\varphi =F_\varphi \end{aligned}{} & {} \text {in }\Omega ^T, \\&-\left( \Delta -\frac{1}{r^2}\right) \psi =\omega _\varphi{} & {} \text {in }\Omega ^T, \\&v_\varphi = \omega _\varphi = \psi = 0{} & {} \text {on }S^T, \\&v_\varphi \big \vert _{t=0}=v_\varphi (0){} & {} \text {in }\Omega \times \{t = 0\}, \\&\omega _\varphi \big \vert _{t=0}=\omega _\varphi (0){} & {} \text {in }\Omega \times \{t = 0\}, \\ \end{aligned} \right. \end{aligned}$$

(1.9)

where $F_\varphi =\textrm{rot}\,\textbf{f}\cdot {\bar{e}}_\varphi$ and $\psi$ is the stream function such that

$$\begin{aligned} v_r=-\psi _{,z},\quad v_z=\frac{1}{r}(r\psi )_{,r}. \end{aligned}$$

(1.10)

We recall that in (1.9) and whenever cylindrical coordinates in this manuscript are used we have

$$\begin{aligned} \nabla = {\bar{e}}_r \partial _r + {\bar{e}}_z \partial _z \qquad \text {and} \qquad \Delta =\partial _r^2+\frac{1}{r}\partial _r+\partial _z^2. \end{aligned}$$

(1.11)

To derive energy type estimates for the velocity we prefer (1.1)$_{1,2}$ in the form

$$\begin{aligned} \begin{aligned} \begin{aligned}&v_{r,t} + {\textbf {v}}\cdot \nabla v_r - \nu \left( \Delta v_r - \frac{1}{r^2}v_r\right) - \frac{1}{r}v_\varphi ^2 + p_{,r} = f_r,\\&v_{\varphi ,t} + {\textbf {v}}\cdot \nabla v_\varphi - \nu \left( \Delta v_\varphi - \frac{1}{r^2}v_\varphi \right) + \frac{1}{r}v_rv_\varphi = f_\varphi ,\\&v_{z,t} + {\textbf {v}}\cdot \nabla v_z - \nu \Delta v_z + p_{,z} = f_z,\\ {}&(rv_r)_{,r} + (rv_z)_{,z} = 0. \end{aligned} \end{aligned} \end{aligned}$$

(1.12)

Moreover, we have the following boundary

$$\begin{aligned} v_r\big \vert _{S_1} = 0, \quad v_z\big \vert _{S_2} = 0,\quad v_\varphi \big \vert _S=0, \quad v_{r,z}-v_{z,r}\big \vert _S=0 \end{aligned}$$

(1.13)

and initial conditions

$$\begin{aligned} v_r\big \vert _{t=0} = v_r(0),\qquad v_\varphi \big \vert _{t=0}=v_\varphi (0),\qquad v_z\big \vert _{t=0}=v_z(0). \end{aligned}$$

It is also convenient to introduce the quantities

$$\begin{aligned} u_1 = \frac{v_{\varphi }}{r},\quad \omega _1= \frac{\omega _{\varphi }}{r},\quad \psi _1 = \frac{\psi }{r},\quad f_1 = \frac{f_{\varphi }}{r},\quad F_1 = \frac{F_{\varphi }}{r}. \end{aligned}$$

(1.14)

Then, system (1.9) finally reads

$$\begin{aligned} \left\{ \begin{aligned}&u_{1,t} + {\textbf {v}}\cdot \nabla u_1 - \nu \left( \Delta u_1+\frac{2}{r}u_{1,r}\right) = 2u_1\psi _{1,z} + f_1{}&{} \text{ in } \Omega ^T,\\&\omega _{1,t} + {\textbf {v}}\cdot \nabla \omega _1-\nu \bigg (\Delta \omega _1+\frac{2}{r}\omega _{1,r}\bigg )=2u_1u_{1,z}+F_1{}&{} \text{ on } \Omega ^T, \\&-\Delta \psi _1-\frac{2}{r}\psi _{1,r}=\omega _1{}&{} \text{ in } \Omega ^T, \\&u_1 = \omega _1 = \psi _1 = 0{}&{} \text{ on } S^T, \\&u_1\big \vert _{t=0} = u_1(0){}&{} \text{ in } \Omega \times \{t = 0\}, \\&\omega _1\big \vert _{t=0} = \omega _1(0){}&{} \text{ in } \Omega \times \{t = 0\}. \\ \end{aligned} \right. \end{aligned}$$

(1.15)

Systems (1.15) and (1.9) are similar. Our main focus will be concentrated on $\int _{\Omega ^t} \frac{v_r}{r} \frac{v_\varphi ^4}{r^2}\, \textrm{d}x\textrm{d}t'$. To handle this integral we need estimates for solutions to both (1.15) and (1.9). These estimates are presented in Sects. 2, 3 and 4. Finally, in Sect. 5 we eventually combine them. Apart from various energy estimates we also need two non-trivial estimates in weighted Sobolev spaces for solutions to (1.14)$_3$ (see Corollaries 2.10 and 2.11). Due to the order of the weight, we need to adjust the order of singularity of $\psi _1$ near $r = 0$. In Lemma 2.8 we will see that $\psi _1 \sim O(1)$, thus $\psi _1 \notin H^3_0(\Omega )$ (see Sect. 2). Therefore, we subtract from $\psi _1$ as much as it is needed for this difference to belong to $H^3_0(\Omega )$. This idea is motivated by Kondratev’s work (see [22]) and discussed in a separate manuscript (see [23]).

2 Notation and Auxiliary Results

First we introduce the function spaces

Definition 2.1

Let $\Omega$ be a cylindrical axially symmetric domain with axis of symmetry inside. We use the following notation for Lebesgue and Sobolev spaces:

$$\begin{aligned} \begin{aligned}&\left\Vert u\right\Vert _{L_p(Q)}=\left|u\right|_{p,Q},\quad \left\Vert u\right\Vert _{L_p(Q^t)}=\left|u\right|_{p,Q^t},\\&\left\Vert u\right\Vert _{L_{p,q}(Q^t)}=\left\Vert u\right\Vert _{L_q(0,t;L_p(Q))}=\left|u\right|_{p,q,Q^t}, \end{aligned} \end{aligned}$$

where $p,q\in [1,\infty ]$, Q replaces either $\Omega$ or S.

$$\begin{aligned} \begin{aligned}&\left\Vert u\right\Vert _{H^s(Q)}=\left\Vert u\right\Vert _{s,Q},\qquad \text {where }H^s(Q)=W_2^s(Q),\\&\left\Vert u\right\Vert _{W_p^s(Q)}=\left\Vert u\right\Vert _{s,p,Q},\\&\left\Vert u\right\Vert _{L_q(0,t;W_p^k(Q))}=\left\Vert u\right\Vert _{k,p,q,Q^t},\qquad \left\Vert u\right\Vert _{k,p,p,Q^t}=\left\Vert u\right\Vert _{k,p,Q^t}, \end{aligned} \end{aligned}$$

where $s,k\in {\mathbb {R}}^{1}_+$.

Finally, similarly to Definition 2.1 in [23] we introduce weighted spaces $L_{p,\mu }(\Omega )$, $\mu \in {\mathbb {R}}^{1}$, $p\in [1,\infty ]$, with the norm

$$\begin{aligned} \left\Vert u\right\Vert _{L_{p,\mu }(\Omega )}=\left( \int _\Omega |u|^pr^{p\mu }\textrm{d}x\right) ^{\frac{1}{p}} \end{aligned}$$

and

$$\begin{aligned} \left\Vert u\right\Vert _{H^k_\mu (\Omega )} = \left( \sum _{\left|\alpha \right| \le k} \int _\Omega \left|\textrm{D}^\alpha _{r,z} u(r,z)\right|^2r^{2(\mu + \left|\alpha \right| - k)}\, r\textrm{d}r\textrm{d}z\right) ^{\frac{1}{2}}, \end{aligned}$$

where $\textrm{D}^\alpha _{r,z} = \partial _r^{\alpha _1}\partial _z^{\alpha _2}$, $\left|\alpha \right| = \alpha _1 + \alpha _2$, $\left|\alpha \right| \le k$, $\alpha _i \in {\mathbb {N}}_0 \equiv \{0,1,2,\ldots \}$, $i=1,2$, $k\in {\mathbb {N}}_0$ and $\mu \in {\mathbb {R}}$. In fact, we only use $H^3_0(\Omega )$ and $H^2_0(\Omega )$ and these symbols should not be mixed with Sobolev spaces with zero trace.

We use notation: r.h.s—right-hand side, l.h.s.—left-hand side.

By c we denote generic constants. They are time-independent but they may depend on R. If a constant depends on a quantity l and this dependence needs to be tracked we write c(l). This means that $c(l) \sim c \cdot l$. Similarly $c\left( \frac{1}{l}\right) \sim \frac{c}{l}$.

Lemma 2.2

(Hardy’s inequality). Suppose that $f\ge 0$, $p\ge 1$ and $r\ne 0$. Then

$$\begin{aligned} \bigg (\int _0^\infty \left( \int _0^xf(y)\, \textrm{d}y\right) ^px^{-r-1}\textrm{d}x\bigg )^{1/p}\le \frac{p}{r}\left( \int _0^\infty |yf(y)|^py^{-r-1}\,\textrm{d}y\right) ^{1/p}. \end{aligned}$$

Lemma 2.3

Let $\textbf{f}\in L_{2,1}(\Omega ^t)$, $\textbf{v}(0)\in L_2(\Omega )$. Assume that $v_\varphi \big \vert _S=0$, ${\bar{n}}\cdot \textbf{v}\big \vert _S=0$, $\omega _\varphi \big \vert _S=0$. Then, solutions to (1.1) satisfy the estimate

$$\begin{aligned} {}&{} \left\| {\textbf{v}}(t)\right\| _{L_2(\Omega )}^2 + \nu \int _{\Omega ^t}\left( |\nabla v_r|^2+|\nabla v_\varphi |^2+|\nabla v_z|^2\right) \,\textrm{d}x\textrm{d}t' \nonumber \\ {}&{} \quad +\nu \int _{\Omega ^t}\left( {v_r^2\over r^2}+{v_\varphi ^2\over r^2}\right) \,\textrm{d}x\textrm{d}t'\le D_1^2. \end{aligned}$$

(2.1)

Proof

Multiplying (1.12)$_1$ by $v_r$, (1.12)$_2$ by $v_\varphi$, (1.12)$_3$ by $v_z$, adding the results, integrating over $\Omega$ and using (1.13) yields

$$\begin{aligned}{} & {} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int _\Omega \left( v_r^2+v_\varphi ^2+v_z^2\right) \,\textrm{d}x-\nu \int _{S_1} v_{z,r}v_zdS_1-\nu \int _{S_2}v_{r,z}v_rdS_2 \nonumber \\{} & {} \qquad + \nu \int _\Omega \left( |\nabla v_r|^2+|\nabla v_\varphi |^2+|\nabla v_z|^2\right) \,\textrm{d}x+ \nu \int _\Omega \bigg ({v_r^2\over r^2}+{v_\varphi ^2\over r^2}\bigg )\,\textrm{d}x \nonumber \\{} & {} \qquad + \int _\Omega \left( -\frac{1}{r}v_\varphi ^2v_r+\frac{1}{r}v_rv_\varphi ^2\right) \,\textrm{d}x +\int _\Omega \left( p_{,r}v_r+p_{,z}v_z\right) \,\textrm{d}x \nonumber \\{} & {} \quad = \int _\Omega \left( f_rv_r+f_\varphi v_\varphi +f_zv_z\right) \,\textrm{d}x. \end{aligned}$$

(2.2)

In view (1.13) the boundary terms in (2.2) vanish. The last term on the l.h.s. of (2.2) vanishes in virtue of (1.13) and the equation of continuity (1.12)$_4$.

Using that $\left|\textbf{v}\right|^2=v_r^2+v_\varphi ^2+v_z^2$, we rewrite (2.2) the form

$$\begin{aligned}{} & {} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\left\Vert \textbf{v}\right\Vert _{L_2(\Omega )}^2+\nu \int _\Omega \left( |\nabla v_r|^2 + |\nabla v_\varphi |^2+|\nabla v_z|^2\right) \,\textrm{d}x + \nu \int _\Omega \bigg ({v_r^2\over r^2}+{v_\varphi ^2\over r^2}\bigg )\,\textrm{d}x \nonumber \\{} & {} \quad =\int _\Omega \left( f_rv_r+f_\varphi v_\varphi +f_zv_z\right) \,\textrm{d}x. \end{aligned}$$

(2.3)

Applying the Hölder inequality to the r.h.s. of (2.3) yields

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left\Vert \textbf{v}\right\Vert _{L_2(\Omega )}\le \left\Vert \textbf{f}\right\Vert _{L_2(\Omega )}, \end{aligned}$$

(2.4)

where we used that $\left|\textbf{f}\right|^2=f_r^2+f_\varphi ^2+f_z^2$.

Integrating (2.4) with respect to time implies

$$\begin{aligned} \left\Vert \textbf{v}(t)\right\Vert _{L_2(\Omega )}\le \left\Vert \textbf{f}\right\Vert _{L_{2,1}(\Omega ^t)}+\left\Vert \textbf{v}(0)\right\Vert _{L_2(\Omega )}. \end{aligned}$$

(2.5)

Integrating (2.3) with respect to time, using the Hölder inequality in the r.h.s. of (2.3) and using (2.5) we obtain

$$\begin{aligned}{} & {} \frac{1}{2}\left\Vert \textbf{v}(t)\right\Vert _{L_2(\Omega )}^2 + \nu \int _{\Omega ^t}\left( |\nabla v_r|^2+|\nabla v_\varphi |^2+|\nabla v_z|^2\right) \,\textrm{d}x\textrm{d}t' +\nu \int _{\Omega ^t}\bigg ({v_r^2\over r^2}+{v_z^2\over r^2}\bigg )\,\textrm{d}x\textrm{d}t' \\{} & {} \quad \le \left\Vert \textbf{f}\right\Vert _{L_{2,1(\Omega ^t)}}\left( \left\Vert \textbf{f}\right\Vert _{L_{2,1}(\Omega ^t)} +\left\Vert \textbf{v}(0)\right\Vert _{L_2(\Omega )}\right) +\frac{1}{2}\left\Vert \textbf{v}(0)\right\Vert _{L_2(\Omega )}^2. \end{aligned}$$

The above inequality implies (2.1) and concludes the proof. $\square$

Lemma 2.4

Consider problem (1.3). Assume that $f_0\in L_{\infty ,1}(\Omega ^t)$, $u(0)\in L_\infty (\Omega )$. Then

$$\begin{aligned} \left\| u(t)\right\| _{L_\infty (\Omega )}\le D_2. \end{aligned}$$

(2.6)

Proof

Multiplying (1.3)$_1$ by $u|u|^{s-2}$, $s>2$ integrating over $\Omega$ and by parts and using that $u\big \vert _S=0$, we obtain

$$\begin{aligned} \frac{1}{s}\frac{\textrm{d}}{\textrm{d}t}\left\Vert u\right\Vert _{L_s(\Omega )}^s+{4\nu (s-1)\over s^2}\left\Vert \nabla |u|^{s/2}\right\Vert _{L_2(\Omega )}^2 + {\nu \over s}\int _\Omega \left( |u|^s\right) _{,r}\, \textrm{d}r \textrm{d}z =\int _\Omega f_0u|u|^{s-2}\textrm{d}x, \end{aligned}$$

(2.7)

where the last term of (2.7) equals $I \equiv \frac{\nu }{s} \int _{-a}^a \left|u\right|^s\big \vert _{r=0}^{r=R}\, \textrm{d}z$. From [24] it follows that $u\big \vert _{r=0}=0$. Since $u\big \vert _{r=R}=0$ and using the boundary condition $v_\varphi \big \vert _{S} = 0$ we conclude that $I = 0$. Then, we derive from (2.7) the inequality

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left\Vert u\right\Vert _{L_s(\Omega )}\le \left\Vert f_0\right\Vert _{L_s(\Omega )}. \end{aligned}$$

(2.8)

Integrating (2.8) with respect to time and passing with $s\rightarrow \infty$ we derive (2.6) from (2.8). This ends the proof. $\square$

Lemma 2.5

Let estimates (2.1) and (2.6) hold. Then

$$\begin{aligned} \left\Vert v_\varphi \right\Vert _{L_4(\Omega ^t)}\le D_1^{1/2}D_2^{1/2}. \end{aligned}$$

(2.9)

Proof

We have

$$\begin{aligned} \int _{\Omega ^t}|v_\varphi |^4\,\textrm{d}x\textrm{d}t'=\int _{\Omega ^t}r^2v_\varphi ^2{v_\varphi ^2\over r^2}\,\textrm{d}x\textrm{d}t' \le \left\Vert rv_\varphi \right\Vert _{L_\infty (\Omega ^t)}^2\int _{\Omega ^t}{v_\varphi ^2\over r^2}\,\textrm{d}x\textrm{d}t'\le D_2^2D_1^2. \end{aligned}$$

This implies (2.9) and concludes the proof. $\square$

Lemma 2.6

Let $\omega _1\in L_2(\Omega )$. Then solutions to (1.15)$_3$ satisfy

$$\begin{aligned} \left\Vert \psi _1\right\Vert _{H^1(\Omega )}^2+\int _{-a}^a\psi _1^2(0)\,\textrm{d}z\le c\left\Vert \omega _1\right\Vert _{L_2(\Omega )}^2, \end{aligned}$$

(2.10)

where $\psi _1(0)=\psi _1|_{r=0}$. In addition, if $\omega _1\in L_{2,\mu }(\Omega )$, $\mu \in (0,1)$ then

$$\begin{aligned} \left\Vert \psi _1\right\Vert _{L_{2,-\mu }(\Omega )}^2+\left\Vert \psi _1\right\Vert _{H^1(\Omega )}^2+\int _{-a}^a \psi _1^2(0)\,\textrm{d}z\le c\left\Vert \omega _1\right\Vert _{L_{2,\mu }(\Omega )}^2, \end{aligned}$$

(2.11)

where $\psi _1(0)=\psi _1|_{r=0}$.

Proof

Multiply (1.15)$_3$ by $\psi _1$, integrate over $\Omega$ and use boundary condition (1.15)$_4$. Then we obtain

$$\begin{aligned} \left\Vert \nabla \psi _1\right\Vert _{L_2(\Omega )}^2-\int _\Omega \partial _r\psi _1^2\, \textrm{d}r\textrm{d}z= \int _\Omega \omega _1\psi _1\, \textrm{d}x. \end{aligned}$$

(2.12)

Applying the Hölder inequality to the r.h.s. of (2.12), using the Poincaré inequality and boundary condition (1.3)$_4$ we obtain (2.10).

Using weighted spaces we can estimate the r.h.s. of (2.12) by

$$\begin{aligned} \left\Vert \omega _1\right\Vert _{L_{2,\mu }(\Omega )}\left\Vert \psi _1\right\Vert _{L_{2,-\mu }(\Omega )}. \end{aligned}$$

By the Hardy inequality (see Lemma 2.2) and $\mu \in (0,1)$, $r\le R$, we get

$$\begin{aligned} \int _\Omega |\psi _1|^2r^{-2\mu }\textrm{d}x\le c\int _\Omega |\psi _{1,r}|^2r^{2-2\mu }\textrm{d}x\le cR^{2-2\mu }\int _\Omega |\nabla \psi _1|^2\,\textrm{d}x. \end{aligned}$$

Since $\mu \in (0,1)$ the bound $\int _\Omega \left|\psi _1\right|^2 r^{-2\mu }\, \textrm{d}x < \infty$ does not imply $\psi _1\big \vert _{r=0} = 0$. Then (2.11) holds. This concludes the proof. $\square$

Lemma 2.7

Assume that $u_1(0)\in L_\infty (\Omega )$, $f_1, \psi _{1,z}\in L_1(0,t;L_\infty (\Omega ))$. Then for solutions to (1.15) the following inequality

$$\begin{aligned} \left\| u_1(t)\right\| _{L_\infty (\Omega )} \le \exp \left( \int _0^t\left\| \psi _{1,z}(t')\right\| _{L_\infty (\Omega )}\, \textrm{d}t'\right) D_2 \end{aligned}$$

(2.13)

holds.

Proof

Multiply (1.15)$_1$ by $u_1|u_1|^{s-2}$ and integrate over $\Omega$. Then we have

$$\begin{aligned} \frac{1}{s}\frac{\textrm{d}}{\textrm{d}t}\left\Vert u_1\right\Vert _{L_s(\Omega )}^s+{4\nu (s-1)\over s^2}\left\Vert \nabla u_1^{s/2}\right\Vert _{L_2(\Omega )}^2 =\int _\Omega \psi _{1,z}u_1^s\textrm{d}x+\int _\Omega f_1u_1^{s-1}\textrm{d}x. \end{aligned}$$

(2.14)

Applying the Hölder inequality to the r.h.s. of (2.14) and simplifying we get

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left\Vert u_1\right\Vert _{L_s(\Omega )}\le \left\Vert \psi _{1,z}\right\Vert _{L_\infty (\Omega )}\left\Vert u_1\right\Vert _{L_s(\Omega )} + \left\Vert f_1\right\Vert _{L_s(\Omega )}. \end{aligned}$$

(2.15)

Integrating with respect to time yields

$$\begin{aligned}{} & {} \left\Vert u_1(t)\right\Vert _{L_s(\Omega )} \le \exp \bigg (\int _0^t\left\Vert \psi _{1,z}(t')\right\Vert _{L_\infty (\Omega )} \,\textrm{d}t'\bigg )\left( \left\Vert f_1\right\Vert _{L_1(0,t;L_s(\Omega ))}+\left\Vert u_1(0)\right\Vert _{L_s(\Omega )}\right) . \end{aligned}$$

(2.16)

Passing with $s\rightarrow \infty$ we derive (2.13). This concludes the proof. $\square$

Lemma 2.8

Let $\psi _1$ be a solution to

$$\begin{aligned} \left\{ \begin{aligned} -&\Delta \psi _1 - \frac{2}{r}\psi _{1,r} = \omega _1{} & {} \text {in }\Omega ,\\&\psi _1 = 0{} & {} \text {on }S. \end{aligned} \right. \end{aligned}$$

(2.17)

Suppose that $\omega _1 \in L_2(\Omega )$. Then, any solution $\psi _1$ to (2.17) satisfies

$$\begin{aligned} \left\Vert \psi _1\right\Vert _{2,\Omega } \le c \left|\omega _1\right|_{2,\Omega }. \end{aligned}$$

(2.18)

Proof

We start with rewriting (2.17)$_1$ in the form

$$\begin{aligned} -\psi _{1,rr} - \psi _{1,zz} - \frac{3}{r}\psi _{1,r} = \omega _1. \end{aligned}$$

Multiplying this equality by $\frac{1}{r}\psi _{1,r}$ and integrating over $\Omega$ yields

$$\begin{aligned} 3\int _\Omega \left|\frac{1}{r}\psi _{1,r}\right|^2\, \textrm{d}x = -\int _\Omega \psi _{1,rr} \frac{1}{r} \psi _{1,r}\, \textrm{d}x - \int _\Omega \psi _{1,zz} \frac{1}{r} \psi _{1,r}\, \textrm{d}x - \int _\Omega \omega _1 \frac{1}{r} \psi _{1,r}\, \textrm{d}x. \end{aligned}$$

(2.19)

The first term on the r.h.s. of (2.19) equals

$$\begin{aligned} -\int _\Omega \psi _{1,rr}\psi _{1,r}\, \textrm{d}r \textrm{d}z = -\frac{1}{2} \int _\Omega \partial _r \psi _{1,r}^2\, \textrm{d}r \textrm{d}z = -\frac{1}{2} \int _{-a}^a \psi _{1,r}^2\big \vert _{r = 0}^{r = R}\, \textrm{d}z \equiv I_1. \end{aligned}$$

Integrating with respect to z in the second term on the r.h.s. of (2.19) yields

$$\begin{aligned} -\int _\Omega \left( \psi _{1,z}\psi _{1,r}\right) _{,z}\, \text {d}r \text {d}z + \int _\Omega \psi _{1,z}\psi _{1,rz}\, \text {d}r \text {d}z, \end{aligned}$$

where the first term vanishes because $\psi _{1,r}\vert _{z \in \{-a,a\}} = 0$ and the second equals

$$\begin{aligned} I_2 \equiv \frac{1}{2} \int _{-a}^a \psi _{1,z}^2\big \vert _{r = 0}^{r = R}\, \textrm{d}z. \end{aligned}$$

Using the boundary condition (2.17)$_2$ we obtain

$$\begin{aligned} I_2 = -\frac{1}{2} \int _{-a}^a \psi _{1,z}^2\big \vert _{r = 0}\, \textrm{d}z. \end{aligned}$$

From [25, Remark 4] we have

$$\begin{aligned} \begin{aligned} \psi&= a_1(r,z,t)\big \vert _{r = 0} r + a_3(r,z,t)\big \vert _{r = 0}r^3 + o(r^4),\\ \psi _1&= a_1(r,z,t)\big \vert _{r = 0} + a_3(r,z,t)\big \vert _{r = 0}r^2 + o(r^3),\\ \end{aligned} \end{aligned}$$

thus

$$\begin{aligned} \psi _{1,r}\big \vert _{r = 0} = 0. \end{aligned}$$

(2.20)

Using (2.20) in $I_1$ yields

$$\begin{aligned} I_1 = -\frac{1}{2} \int _{-a}^a \psi _{1,r}^2\big \vert _{r = R}\, \textrm{d}z. \end{aligned}$$

Applying the Hölder and Young inequalities to the last term on the r.h.s in (2.19) and combining it with $I_1$ and $I_2$ we obtain

$$\begin{aligned} \frac{1}{2}\int _\Omega \frac{1}{r^2}\psi _{1,r}^2\, \textrm{d}x + \frac{1}{2}\int _{-a}^a \psi _{1,r}^2\big \vert _{r = R}\, \textrm{d}z + \frac{1}{2} \int _{-a}^a \psi _{1,z}^2\big \vert _{r = 0}\, \textrm{d}z \le c \left|\omega _1\right|_{2,\Omega }^2. \end{aligned}$$

(2.21)

Since the last two termns on the l.h.s. are positive we conclude that

$$\begin{aligned} \int _\Omega \frac{1}{r^2} \psi _{1,r}^2\, \textrm{d}x \le c \left|\omega _1\right|_{2,\Omega }^2. \end{aligned}$$

(2.22)

Now we can rewrite (2.17) in the form

$$\begin{aligned} \left\{ \begin{aligned} -&\Delta \psi _1 = \omega _1 + \frac{2}{r}\psi _{1,r}{} & {} \text {in }\Omega ,\\&\psi _1 = 0{} & {} \text {on }S \end{aligned} \right. \end{aligned}$$

(2.23)

and consider it as the Dirichlet problem for the Poisson equation. Thus

$$\begin{aligned} \left\Vert \psi _1\right\Vert _{2,\Omega } \le c \left|\omega _1\right|_{2,\Omega }, \end{aligned}$$

(2.24)

where (2.22) was used. This ends the proof. $\square$

Lemma 2.9

Assume that $s \in (1,\infty )$. Suppose that $f\in L_1(0,t;L_s(\Omega ))$ and $u_1(0) \in L_s(\Omega )$. Then

$$\begin{aligned} \left|u_1\right|_{s, \Omega } \le \exp \left( cs\int _0^t \left|\omega _1(t')\right|^2_{2,\Omega }\, \textrm{d}t'\right) \left( s\left\Vert f_1\right\Vert _{L_1(0,t;L_s(\Omega ))} + \left\Vert u_1(0)\right\Vert _{L_s(\Omega )}\right) . \end{aligned}$$

Proof

In (2.14) we integrate by parts, use the boundary conditions (1.3)$_4$ and apply the Hölder and Young inequalities

$$\begin{aligned}{} & {} \frac{1}{s}\frac{\textrm{d}}{\textrm{d}t}\left|u_1\right|_{s,\Omega }^s+{4(s-1)\nu \over s^2}\int _\Omega \left|\nabla |u_1|^{s/2}\right|^2\,\textrm{d}x \nonumber \\{} & {} \quad \le \epsilon \left|\partial _zu_1^{s/2}\right|_{2,\Omega }^2 + \frac{c}{\varepsilon } \left|\psi _1\right|_{\infty ,\Omega }^2\left|u_1\right|_{s,\Omega }^s + \left|f_1\right|_{s,\Omega }\left|u_1\right|_{s,\Omega }^{s-1}. \end{aligned}$$

(2.25)

For sufficiently small $\varepsilon$ we get

$$\begin{aligned} \frac{1}{s}\frac{\textrm{d}}{\textrm{d}t}\left|u_1\right|_{s,\Omega }^s\le cs\left|\psi _1\right|_{\infty ,\Omega }^2\left|u_1\right|_{s,\Omega }^s + \left|f_1\right|_{s,\Omega }\left|u_1\right|_{s,\Omega }^{s-1}. \end{aligned}$$

(2.26)

Hence, we have

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left|u_1\right|_{s,\Omega }\le cs \left|\psi _1\right|_{\infty ,\Omega }^2\left|u_1\right|_{s,\Omega } + \left|f_1\right|_{s,\Omega }. \end{aligned}$$

Since $\epsilon = \frac{2(s-1)\nu }{s^2}$, then $\frac{c}{\epsilon } = \frac{cs^2}{2(s-1)\nu } \le cs$. Integrating with respect to time yields

$$\begin{aligned} \left|u_1\right|_{s,\Omega }\le \exp \left( cs\int _0^t\left|\psi _1(t')\right|_{\infty ,\Omega }^2\,\textrm{d}t'\right) \left( \left|u_1(0)\right|_{s,\Omega } + \left|f_1\right|_{s,1,\Omega ^t}\right) . \end{aligned}$$

(2.27)

Using Lemma 2.8

$$\begin{aligned} \left|\psi _1\right|_{\infty ,\Omega }\le c\left\Vert \psi _1\right\Vert _{2,\Omega }\le c\left|\omega _1\right|_{2,\Omega } \end{aligned}$$

we obtain

$$\begin{aligned} \left|u_1\right|_{s,\Omega }\le \exp \left( cs\int _0^t\left|\omega _1(t')\right|_{2,\Omega }^2\,\textrm{d}t'\right) \left( \left|u_1(0)\right|_{s,\Omega } + \left|f_1\right|_{s,1,\Omega ^t}\right) . \end{aligned}$$

(2.28)

This concludes the proof. $\square$

Corollary 2.10

(Theorem 1.3 in [23]). Suppose that $\psi _1$ is a weak solution to (1.15)$_{3,4}$. Let $\omega _1\in L_2(\Omega )$ and introduce

$$\begin{aligned} \chi (r,z) = \int _0^r\psi _{1,\tau }(1+K(\tau ))\,\textrm{d}\tau , \end{aligned}$$

where $K(\tau )$ is any smooth function with a compact support such that

$$\begin{aligned} \lim _{r\rightarrow 0^+} \frac{K(r)}{r^2} = c_0<\infty . \end{aligned}$$

Then

$$\begin{aligned} \left\Vert \psi _1 - \psi _1(0) - \chi \right\Vert _{L_2(-a,a;H_0^2(0,R))}^2 + \left\Vert \psi _{1,zr}\right\Vert _{L_2(\Omega )}^2 \\ +\left\Vert \psi _{1,zz}\right\Vert _{L_2(\Omega )}^2 \le c\left\Vert \omega _1\right\Vert _{L_2(\Omega )}^2, \end{aligned}$$

Corollary 2.11

(Theorem 1.4 in [23]). Let $\psi _1$ be a weak solution to (1.3)$_{3,4}$. Let $\omega _1\in H^1(\Omega )$. Then

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}}\left\Vert \psi _1 - \psi _1(0) - \eta \right\Vert _{H_0^3({\mathbb {R}}_+)}^2\, \textrm{d}z + \int _{{\mathbb {R}}}\int _{{\mathbb {R}}_+} \left( \left|\psi _{1,zzz}\right|^2 + \left|\psi _{1,zzr}\right|^2 + \left|\psi _{1,zz}\right|^2\right) \, r\textrm{d}r \textrm{d}z \\{} & {} \quad \le c\left\Vert \omega _1\right\Vert _{H^1(\Omega )}^2, \end{aligned}$$

where

$$\begin{aligned} \eta (r,z) = - \int _0^r(r-\tau )\bigg ({3\over r}\psi _{1,\tau }+\psi _{1,zz}+\omega _1\bigg ) (1+K(\tau ))\,\textrm{d}\tau \end{aligned}$$

and K is the same as in Corollary 2.10.

3 Estimate for $\omega _1$

Lemma 3.1

Assume that $\omega _1(0)\in L_2(\Omega )$, $u_1\in L_4(\Omega ^t)$, $F\in L_{6/5,2}(\Omega ^t)$, $t\le T$. Then the following inequality holds

$$\begin{aligned}{} & {} \frac{1}{2}\int _\Omega \omega _1^2\,\textrm{d}x + \frac{\nu }{2}\int _{\Omega ^t}\left|\nabla \omega _1\right|^2\,\textrm{d}x\textrm{d}t' + \nu \int _0^t\int _{-a}^a\omega _1^2\big \vert _{r=0}\, \textrm{d}z \textrm{d}t'\nonumber \\{} & {} \quad \le \frac{1}{\nu }\int _{\Omega ^t}u_1^4\,\textrm{d}x\textrm{d}t'+c\left|F_1\right|_{6/5,2,\Omega ^t}^2+\int _\Omega \omega _1^2(0)\,\textrm{d}x. \end{aligned}$$

(3.1)

Proof

Multiply (1.15)$_2$ by $\omega _1$, integrate over $\Omega$, integrate by parts. Next, integration with respect to time implies (3.1). This ends the proof. $\square$

4 Estimate for the Angular Component of Velocity

Consider problem (1.9)

Lemma 4.1

Assume that $f_\varphi \in L_2(\Omega ^t)$, $v_\varphi (0)\in L_{4,-1/2}(\Omega )$,

$$\begin{aligned} \left|\int _{\Omega ^t}{v_r\over r}{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t'\right|<\infty . \end{aligned}$$

(4.1)

Then, any solution to (1.9) satisfy

$$\begin{aligned}{} & {} \frac{1}{4}\int _\Omega \frac{v_\varphi ^4}{r^2}\, \textrm{d}x + \frac{3\nu }{4}\int _{\Omega ^t}\left|\nabla {\frac{v_\varphi ^2}{r}}\right|^2\,\textrm{d}x \textrm{d}t' + \frac{\nu }{2}\int _{\Omega ^t}\left|\frac{v_\varphi }{r}\right|^4\, \textrm{d}x \textrm{d}t' \nonumber \\{} & {} \quad \le \frac{3}{2}\int _{\Omega ^t}\frac{v_r}{r}\frac{v_\varphi ^4}{r^2}\, \textrm{d}x \textrm{d}t' + \frac{27}{4\nu ^3}\int _{\Omega ^t}f_\varphi ^4r^4\, \textrm{d}x \textrm{d}t' + \frac{1}{4}\int _\Omega \frac{v_\varphi ^4(0)}{r^2}\, \textrm{d}x. \end{aligned}$$

(4.2)

Proof

Multiply (1.9)$_1$ by ${v_\varphi ^3\over r^2}$ (see expansion (4.4) of $v_\varphi$ near the axis of symmetry) and integrate over $\Omega$. Then we have

$$\begin{aligned}&{} \displaystyle \frac{1}{4}\frac{\text {d}}{\text {d}t}\int _\Omega {v_\varphi ^4\over r^2}\text {d}x + \int _\Omega {\textbf {v}}\cdot \nabla v_\varphi \frac{v_\varphi ^3}{r^2}\text {d}x - \nu \int _\Omega \Delta v_\varphi \frac{v_\varphi ^3}{r^2}\text {d}x + \nu \int _\Omega \frac{v_\varphi ^4}{r^4}\text {d}x + \int _\Omega \frac{v_r}{r}\frac{v_\varphi ^4}{r^2}\text {d}x = \int _\Omega f_\varphi \frac{v_\varphi ^3}{r^2}\text {d}x. \end{aligned}$$

(4.3)

The second term in (4.3) equals

$$\begin{aligned} \frac{1}{4}\int _\Omega \textbf{v}\cdot \nabla v_\varphi ^4r^{-2}\textrm{d}x = \frac{1}{4}\int _\Omega \textbf{v}\cdot \nabla \left( v_\varphi ^4r^{-2}\right) \,\textrm{d}x + \frac{1}{2}\int _\Omega v_rv_\varphi ^4r^{-3}\textrm{d}x =\frac{1}{2}\int _\Omega {v_r\over r}{v_\varphi ^4\over r^2}\textrm{d}x, \end{aligned}$$

where we used that $\textbf{v}\cdot {\bar{n}}\big \vert _S=0$ and ${{\,\textrm{div}\,}}\textbf{v} = 0$.

Integrating by parts in the third term on the l.h.s. of (4.3) yields

$$\begin{aligned}{} & {} \int _\Omega \nabla v_\varphi \nabla v_\varphi ^3r^{-2}\textrm{d}x+\int _\Omega \nabla v_\varphi v_\varphi ^3\nabla r^{-2}\textrm{d}x = 3\int _\Omega v_\varphi ^2|\nabla v_\varphi |^2r^{-2}\textrm{d}x-2\int _\Omega v_{\varphi ,r}v_\varphi ^3r^{-3}\textrm{d}x\\{} & {} \quad =\frac{3}{4}\int _\Omega |\nabla v_\varphi ^2|^2r^{-2}\textrm{d}x-\frac{1}{2}\int _\Omega \partial _rv_\varphi ^4r^{-2}\, \textrm{d}r \textrm{d}z\\{} & {} \quad =\frac{3}{4}\int _\Omega \left|\frac{\nabla v_\varphi ^2}{r}\right|^2\,\textrm{d}x-\frac{1}{2}\int _\Omega \partial _r\left( v_\varphi ^4r^{-2}\right) \, \textrm{d}r\textrm{d}z-\int _\Omega v_\varphi ^4r^{-3}\, \textrm{d}r \textrm{d}z\equiv I. \end{aligned}$$

The first term in I equals

$$\begin{aligned}{} & {} \frac{3}{4}\int _\Omega \left|\nabla {v_\varphi ^2\over r}-v_\varphi ^2\nabla \frac{1}{r}\right|^2\,\textrm{d}x=\frac{3}{4}\int _\Omega \left|\nabla {v_\varphi ^2\over r}\right|^2\,\textrm{d}x -\frac{3}{2}\int _\Omega \nabla {v_\varphi ^2\over r}\cdot v_\varphi ^2\nabla \frac{1}{r}\textrm{d}x \\{} & {} \quad + \frac{3}{4}\int _\Omega \left|v_\varphi ^2\nabla \frac{1}{r}\right|^2\,\textrm{d}x =\frac{3}{4}\int _\Omega \left|\nabla {v_\varphi ^2\over r}\right|^2\,\textrm{d}x + \frac{3}{2}\int _\Omega \partial _r{v_\varphi ^2\over r}{v_\varphi ^2\over r^2}\textrm{d}x+\frac{3}{4} \int _\Omega \left|{v_\varphi \over r}\right|^4\,\textrm{d}x \equiv J. \end{aligned}$$

The middle term in J can be written in the form

$$\begin{aligned} \frac{3}{4}\int _\Omega \partial _r{v_\varphi ^4\over r^2}\,\textrm{d}r \textrm{d}z = \frac{3}{4}\int _{-a}^a{v_\varphi ^4\over r^2}\bigg \vert _{r=0}^{r=R}\, \textrm{d}z\equiv L. \end{aligned}$$

From [25, Remark 4] it follows that $v_\varphi$ behaves as

$$\begin{aligned} v_\varphi = a_1(r,z,t)\big \vert _{r = 0}r + a_3(r,z,t)\big \vert _{r = 0} r^3 + o(r^4), \qquad r \approx 0, \end{aligned}$$

(4.4)

for some functions $a_1$ and $a_3$. Since $v_\varphi \big \vert _{r=R}=0$ the second terms in I and L vanish.

Using the above calculations in (4.3) yields

$$\begin{aligned}{} & {} \frac{1}{4}\frac{\textrm{d}}{\textrm{d}t}\int _\Omega {v_\varphi ^4\over r^2}\textrm{d}x+\frac{3}{4}\nu \int _\Omega \left|\nabla {v_\varphi ^2\over r}\right|^2\, \textrm{d}x + \frac{3}{4}\nu \int _\Omega {v_\varphi ^4\over r^4}\textrm{d}x + \frac{3}{2}\int _\Omega {v_r\over r}{v_\varphi ^4\over r^2}\textrm{d}x =\int _\Omega f_\varphi {v_\varphi ^3\over r^2}\textrm{d}x. \end{aligned}$$

(4.5)

Applying the Hölder and Young inequalities to the r.h.s. of (4.5) and integrating the result with respect to time imply (4.2). This concludes the proof. $\square$

5 Global Estimate

Multiplying (3.1) by $\frac{\nu ^2}{4}$ and adding (4.2) we obtain

$$\begin{aligned}{} & {} {\nu ^2\over 8}\int _\Omega \omega _1^2(t)\,\textrm{d}x + \frac{\nu ^3}{8}\int _{\Omega ^t}|\nabla \omega _1|^2\,\textrm{d}x\textrm{d}t'+ \frac{1}{2}\int _\Omega {v_\varphi ^4(t)\over r^2}\textrm{d}x \nonumber \\{} & {} \quad + \frac{3\nu }{4}\int _{\Omega ^t}\bigg |\nabla {v_\varphi ^2\over r}\bigg |^2\,\textrm{d}x\textrm{d}t' + \frac{\nu }{4}\int _{\Omega ^t}\bigg |{v_\varphi \over r}\bigg |^4\, \textrm{d}x \,\textrm{d}t' \le \frac{3}{2}\bigg |\int _{\Omega ^t}{v_r\over r}{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t'\bigg | \nonumber \\{} & {} \quad + c\bigg (\left|F_1\right|_{6/5,2,\Omega ^t}^2+\left|\omega _1(0)\right|_{2,\Omega }^2 +\int _{\Omega ^t}r^4f_\varphi ^4\,\textrm{d}x\textrm{d}t'+\int _\Omega {v_\varphi ^4(0)\over r^2}\textrm{d}x\bigg ). \end{aligned}$$

(5.1)

Therefore, we have to estimate the first term on the r.h.s. of (5.1). To examine it we introduce the sets

$$\begin{aligned} \Omega _{r_0}=\{x\in \Omega :r\le r_0\}, \qquad \bar{\Omega }_{r_0}=\{x\in \Omega :r\ge r_0\}, \end{aligned}$$

(5.2)

where $r_0>0$ is given.

We write the first term on the r.h.s. of (5.1) in the form

$$\begin{aligned} \int _{\Omega ^t}{v_r\over r}{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t' = \int _{\Omega _{r_0}^t}{v_r\over r}{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t' + \int _{\bar{\Omega }_{r_0}^t}{v_r\over r}{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t' \equiv I+J. \end{aligned}$$

(5.3)

Lemma 5.1

Under the assumptions of Lemmas 2.3 and 2.5 we have

$$\begin{aligned} \left|J\right|\le \varepsilon _1\int _{\bar{\Omega }_{r_0}^t}\left|\partial _z\frac{v_\varphi ^2}{r}\right|^2\,\textrm{d}x\textrm{d}t' + \epsilon _2\sup _t\left|\psi _{,xx}\right|_{2,\Omega }^2 + c\left( \frac{1}{\epsilon _1},\frac{1}{\epsilon _2}\right) {D_1^{10}D_2^8\over r_0^{16}}. \end{aligned}$$

(5.4)

Proof

Since ${v_r\over r}=-\psi _{1,z}$ we have

$$\begin{aligned}{} & {} |J| = \bigg |\int _{\bar{\Omega }_{r_0}^t}\psi _{1,z}{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t'\bigg | \le \varepsilon _1\int _{\bar{\Omega }_{r_0}^t}\bigg |\partial _z{v_\varphi ^2\over r}\bigg |^2\,\textrm{d}x\textrm{d}t'+c\left( \frac{1}{\epsilon _1}\right) \int _{\bar{\Omega }_{r_0}^t}\psi _1^2{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t'\equiv J_1. \end{aligned}$$

In view of Lemma 2.5 the second term in $J_1$ is bounded by

$$\begin{aligned} \frac{1}{r_0^4}\int _{\bar{\Omega }_{r_0}^t}\psi ^2v_\varphi ^4\,\textrm{d}x\textrm{d}t'\le {D_1^2D_2^2\over r_0^4}\sup _{\bar{\Omega }_{r_0}^t}\psi ^2\le c{D_1^2D_2^2\over r_0^4}\sup _t\left|\psi _{,xx}\right|_{2,\Omega }^{\frac{3}{2}}\left|\psi \right|_{2,\Omega }^{\frac{1}{2}}\equiv J_2. \end{aligned}$$

Note that all consideration are either a priori or performed for regular, local solutions. Then, derivation of regular, global solutions can be achieved by extension with respect to time. Since $\psi$ is a solution to the problem

$$\begin{aligned} \left\{ \begin{aligned}&-\Delta \psi +{\psi \over r^2}=\omega{} & {} \text {in }\Omega ^T, \\&\psi = 0{} & {} \text { on }S^T, \end{aligned} \right. \end{aligned}$$

we have

$$\begin{aligned} \int _\Omega |\nabla \psi |^2\, \textrm{d}x + \int _\Omega {\psi ^2\over r^2}\, \textrm{d}x \le \int _\Omega \textbf{v}'^2\, \textrm{d}x \le cD_1^2. \end{aligned}$$

Then $J_2$ is bounded by

$$\begin{aligned} J_2\le \varepsilon _2\sup _t\left|\psi _{,xx}\right|_{2,\Omega }^2 + c\left( \frac{1}{\epsilon _2}\right) \frac{D_1^8D_2^8}{r_0^{16}}D_1^2. \end{aligned}$$

Using estimates for $J_1$ and $J_2$ we derive (5.4). This ends the proof. $\square$

Lemma 5.2

Let the assumptions of Lemma 2.3 hold. Additionally, assume that $v_\varphi (0)\in L_4(\Omega )$, $u\in L_\infty (\Omega ^t)$, $\left|u\right|_{\infty ,\Omega ^t}\le D_2$. Then I from (5.3) satisfies

$$\begin{aligned} \left|I\right|\le & {} \epsilon _3\left|\partial _z\frac{v_\varphi ^2}{r}\right|_{2,\Omega _{r_0}^t}^2 + c\left( \frac{1}{\epsilon _3}\right) \left|u\right|_{\infty ,\Omega _{r_0}^t}^2\left( D_2^2\left|\nabla \omega _1\right|_{2,\Omega ^t}^2 \right. \nonumber \\{} & {} + \left. \left|\omega _1\right|_{2,\infty ,\Omega ^t}^4D_1^2 + \left( \left|u_1(0)\right|_{3,\Omega _{r_0}}^2 + \left|f_1\right|_{3,1,\Omega ^t}^2\right) \left|\omega _1\right|_{2,\Omega ^t}^2\exp \left( c\left|\omega _1\right|_{2,\Omega ^t}^2\right) \right) . \end{aligned}$$

(5.5)

Proof

We have

$$\begin{aligned} |I|\le \varepsilon _3\int _{\Omega _{r_0}^t}\bigg |\partial _z{v_\varphi ^2\over r}\bigg |^2\,\textrm{d}x\textrm{d}t'+c(1/\varepsilon _3)\int _{\Omega _{r_0}^t}\psi _1^2{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t'\equiv I_1+I_2. \end{aligned}$$

We estimate $I_2$ by

$$\begin{aligned}{} & {} I_2 \le \int _{\Omega _{r_0}^t}|\psi _1-\psi _1(0) - \eta |^2{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t'+ \int _{\Omega _{r_0}^t}|\eta |^2{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t' +\int _{\Omega _{r_0}^t}|\psi _1(0)|^2{v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t'\\{} & {} \quad \equiv I_2^1+I_2^2+I_2^3, \end{aligned}$$

where $\psi _1(0)=\psi _1\big \vert _{r=0}$ and $\eta$ is defined in Corollary 2.11. Using this Corollary we have

$$\begin{aligned}{} & {} I_2^1 =\int _{\Omega _{r_0}^t}{|\psi _1-\psi _1(0) - \eta |^2\over r^6}{r^6v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t' \\{} & {} \quad \le c\sup _{\Omega _{r_0}^t}\left|u\right|^4\int _{\Omega _{r_0}^t}{|\psi _1-\psi _1(0) - \eta |^2\over r^6}\,\textrm{d}x\textrm{d}t'\le c\sup _{\Omega _{r_0}^t}|u|^4\left|\nabla \omega _1\right|_{2,\Omega ^t}^2. \end{aligned}$$

Consider $I_2^3$,

$$\begin{aligned}{} & {} I_2^3 \le \sup _{\Omega _{r_0}}|\psi _1(0)|^2\sup _{\Omega _{r_0}^t}|u| \int _{\Omega _{r_0}^t}\bigg |{v_\varphi \over r}\bigg |^3\,\textrm{d}x\textrm{d}t'\\{} & {} \quad =\sup _{\Omega _{r_0}}|\psi _1(0)|^2\sup _{\Omega _{r_0}^t}|u|\int _{\Omega _{r_0}^t} {v_\varphi ^2\over r^2}\bigg |{v_\varphi \over r}\bigg |\,\textrm{d}x\textrm{d}t' \\{} & {} \quad \le \sup _{\Omega _{r_0}^t}\left|\psi _1\right|^2\sup _{\Omega _{r_0}^t}|u| \left|\frac{v_\varphi }{r}\right|_{4,\Omega _{r_0}^t}^2\left|{v_\varphi \over r}\right|_{2,\Omega _{r_0}^t} \\{} & {} \quad \le \varepsilon \left|{v_\varphi \over r}\right|_{4,\Omega _{r_0}^t}^4 + c\left( \frac{1}{\epsilon }\right) \sup _t\left|\omega _1\right|_{2,\Omega }^4 \sup _{\Omega _{r_0}^t}|u|^2D_1^2, \end{aligned}$$

where we used Lemmas 2.3 and 2.8.

Consider $I_2^2$. To simplify presentation we express $\eta$ in the short form

$$\begin{aligned} \eta = \int _0^r(r-\tau )f(\tau )d\tau , \end{aligned}$$

where f replaces $\left( \frac{3}{r}\psi _{1,r} + \psi _{1,zz} + \omega _1\right) \left( 1 + K(r)\right)$.

Then

$$\begin{aligned}{} & {} I_2^2 =\int _{\Omega _{r_0}^t}\bigg |\int _0^r(r-\tau )f(\tau )d\tau \bigg |^2 {v_\varphi ^4\over r^2}\,\textrm{d}x\textrm{d}t' =\int _{\Omega _{r_0}^t}\bigg |\frac{1}{r}\int _0^r(r-\tau )f(\tau )d\tau \bigg |^2r^2v_\varphi ^2{v_\varphi ^2\over r^2}\,\textrm{d}x\textrm{d}t' \\{} & {} \quad \le \sup _{\Omega _{r_0}^t}|u|^2\int _{\Omega _{r_0}^t}\bigg |\frac{1}{r}\int _0^t(r-\tau )f(\tau ) d\tau \bigg |^2{v_\varphi ^2\over r^2}\,\textrm{d}x\textrm{d}t'\equiv L_1. \end{aligned}$$

Using the Hölder inequality in $L_1$ implies

$$\begin{aligned} L_1\le \left|u\right|_{\infty ,\Omega _{r_0}^t}^2\int _0^t\left( \int _{\Omega _{r_0}}\left|\frac{1}{r}\int _0^r(r-\tau )f(\tau )\, \textrm{d}\tau \right|^{2p}\textrm{d}x\right) ^{2/2p}\, \textrm{d}t \sup _t \left|u_1\right|_{2p',\Omega _{r_0}^T}^2\equiv L_2, \end{aligned}$$

where $1/p+1/p'=1$.

Applying the Hardy inequality for the middle term in $L_2$, gives

$$\begin{aligned}{} & {} \int _0^t\left( \int _{\Omega _{r_0}}\bigg |\frac{1}{r}\int _0^r(r-\tau )f(\tau )d\tau \bigg |^{2p}\textrm{d}x\right) ^{\frac{2}{2p}}\, \textrm{d}t' \\{} & {} \quad \le c\int _0^t\left( \int _{\Omega _{r_0}}\bigg |\int _0^rf(\tau )d\tau \bigg |^{2p}\textrm{d}x\right) ^{\frac{2}{2p}}\, \textrm{d}t' \\{} & {} \quad \le c\int _0^t\left( \int _{\Omega _0}\bigg |\int _0^r(\psi _{1,\tau \tau }+ \psi _{1,\tau \tau }K(\tau ))\, \textrm{d}\tau \bigg |^{2p}\textrm{d}x\right) ^{\frac{2}{2p}}\, \textrm{d}t'\equiv L_3, \end{aligned}$$

where we used that

$$\begin{aligned} f=-\psi _{1,rr}\left( 1 + K(r)\right) . \end{aligned}$$

To apply the Hardy inequality we use the formula

$$\begin{aligned} \int _0^r (r - \tau )f(\tau )\, \textrm{d}\tau = \int _0^r \int _0^\sigma f(\tau )\, \textrm{d}\tau \, \textrm{d}\sigma . \end{aligned}$$

Then, we use the following Hardy inequality (see e.g. [26, Ch. 1, Sec. 2.16])

$$\begin{aligned} \left( \int _0^{r_0}\left| \frac{1}{r}\int _0^r\int _0^\sigma f(\tau )\, \text {d}\tau \, \text {d}\sigma \right| ^{2p}\, r\text {d}r\right) ^{\frac{1}{2p}} \le c \left( \int _0^{r_0}\left| \int _0^r f(\tau )\, \text {d}\tau \right| ^{2p}\, r\text {d}r\right) ^{\frac{1}{2p}}. \end{aligned}$$

Integrating the result with respect to z we derive the first inequality in $L_3$. Continuing,

$$\begin{aligned} L_3\le c\int _0^t\bigg (\int _{\Omega _{r_0}}\bigg (|\psi _{1,r}|^{2p}+ \bigg |\int _0^r\psi _{1,\tau \tau }K(\tau )d\tau \bigg |^{2p}\bigg )\,\textrm{d}x\bigg )^{2/2p}\,\textrm{d}t'\equiv L_4. \end{aligned}$$

Using

$$\begin{aligned} \int _0^r\psi _{1,\tau \tau }K(\tau )d\tau =\psi _{1,r}K(r)-\int _0^r\psi _{1,\tau }K_{,\tau }d\tau \end{aligned}$$

in $L_4$ implies

$$\begin{aligned} L_4\le & {} c\int _0^t\left\Vert \psi _{1,r}\right\Vert _{2p,\Omega _{r_0}}^2\, \textrm{d}t' \\{} & {} + \int _0^t\! \left( \int _{\Omega _{r_0}}\!\left( |\psi _{1,r}K(r)|^{2p} + \left|\int _0^r\psi _{1,\tau } K_{,\tau }d\tau \right|^{2p}\right) \,\textrm{d}x\right) ^{\frac{1}{p}} \\\le & {} c\int _0^t\left\Vert \psi _{1,r}\right\Vert _{2p,\Omega _{r_0}}^2\, \textrm{d}t'\equiv L_5, \end{aligned}$$

where the properties of K are used. Finally, for $p\le 3$ and Lemma 2.8

$$\begin{aligned} L_5\le c\left| \omega _1\right| _{2,\Omega _{r_0}^t}^2. \end{aligned}$$

Summarizing

$$\begin{aligned} I_2^2\le & {} c\left|u\right|_{\infty ,\Omega _{r_0}^t}^2\left( \left|u_1(0)\right|_{2p',\Omega _{r_0}}^2 + \left|f_1\right|_{2p',1,\Omega _{r_0}^t}^2\right) \\{} & {} \cdot \exp \left( c\int _0^t\left|\omega _1(t')\right|_{2,\Omega _{r_0}}^2 \,\textrm{d}t'\right) \left|\omega _1\right|_{2,\Omega _{r_0}^t}^2, \end{aligned}$$

where $p'\ge \frac{3}{2}$ and Lemma 2.8 was used.

Using estimates of $I_2^1$, $I_2^2$, $I_2^3$, we obtain

$$\begin{aligned}{} & {} I_2 \le c\left|u\right|_{\infty ,\Omega _{r_0}^t}^2 \left( \left|u\right|_{\infty ,\Omega _{r_0}^t}^2 \left|\nabla \omega _1\right|_{2,\Omega ^t}^2 + \left|\omega _1\right|_{2,\infty ,\Omega ^t}^4D_1^2 \right. \\{} & {} \quad + \left. \left( \left|u_1(0)\right|_{3,\Omega _{r_0}}^2 + \left|f_1\right|_{3,1,\Omega _{r_0}^t}^2\right) \left|\omega _1\right|_{2,\Omega ^t}^2\exp \left( c\left|\omega _1\right|_{2,\Omega ^t} ^2\right) \right) . \end{aligned}$$

Exploiting the estimate in the bound of I we obtain (5.5). This concludes the proof. $\square$

Proof

(r) Using (5.3) and estimates (5.4) and (5.5) in (5.1) and assuming that $\varepsilon _1$ and $\varepsilon _3$ are sufficiently small we obtain the inequality

$$\begin{aligned}{} & {} \left|\omega _1\right|_{2,\infty ,\Omega ^t}^2+\left\Vert \omega _1\right\Vert _{L_2(0,t;H^1(\Omega )}^2\le c\left|u\right|_{\infty ,\Omega _{r_0}^t}^2 \left( D_2^2\left|\nabla \omega _1\right|_{2,\Omega ^t}^2 + D_1^2\left|\omega _1\right|_{2,\infty ,\Omega ^t}^4 \right. \nonumber \\{} & {} \quad + \left. \left( \left|u_1(0)\right|_{3,\Omega _{r_0}}^2 + \left|f_1\right|_{3,1,\Omega _{r_0}^t}^2\right) \left|\omega _1\right|_{2,\Omega ^t}^2\exp \left( c\left|\omega _1\right|_{2,\Omega ^t}^2\right) \right) + M(t), \end{aligned}$$

(5.6)

where M(t) is introduced in (1.4).

Let

$$\begin{aligned} X(t)=\left|\omega _1\right|_{2,\infty ,\Omega ^t}^2+\left\Vert \omega _1\right\Vert _{L_2(0,t;H^1(\Omega ))}^2. \end{aligned}$$

(5.7)

In view of this notation, (5.6) takes the form

$$\begin{aligned} X(t)\le & {} c\left|u\right|_{\infty ,\Omega _{r_0}^t}^2\left( D_2^2X + D_1^2X^2 \right. \nonumber \\{} & {} + \left. X^2\exp \left( cX^2\right) \left( \left|u_1(0)\right|_{3,\Omega }^2 + \left|f_1\right|_{3,1,\Omega _{r_0}^t}^2\right) \right) + M(t) \equiv \epsilon F(X(t)) + M(t). \end{aligned}$$

(5.8)

Consider the equality

$$\begin{aligned} X'(t) = \epsilon F\left( X'(t)\right) + M(t). \end{aligned}$$

(5.9)

Using the method of successive approximations we will show that there exists a solution $X'(t)$ and determine the magnitude of $\epsilon$ which ensures the existence of this solutions.

Suppose that

$$\begin{aligned} X'_{n+1}(t) = \epsilon F\left( X_n(t)\right) + M(t). \end{aligned}$$

(5.10)

Let $\gamma > 1$. Recall that $M = M(T)$ and assume that

$$\begin{aligned} \left|X'_n(t)\right| \le \gamma M. \end{aligned}$$

(5.11)

Then from (5.10) and (5.8) we obtain

$$\begin{aligned} \left|X'_{n+1}(t)\right|\le & {} c \left|u\right|_{\infty ,\Omega ^t} \left( D_2^2(\gamma M) + D_1^2(\gamma M)^2 \right. \nonumber \\{} & {} \left. + (\gamma M)^2 \exp \left( c(\gamma M)^2\right) \left( \left|u_1(0)\right|^2_{3,\Omega } + \left|f_1\right|^2_{3,1,\Omega _{r_0}^t}\right) \right) + M. \end{aligned}$$

(5.12)

Assume that

$$\begin{aligned}{} & {} \left|u\right|_{\infty ,\Omega ^t)} \le c(\gamma - 1)M \cdot \left( \gamma M D_2^2 + D_1^2 (\gamma M)^2 + (\gamma M)^2\exp \left( c(\gamma M)^2\right) \left( \left|u_1(0)\right|^2_{3,\Omega } + \left|f_1\right|^2_{3,1,\Omega _{r_0}^t}\right) \right) ^{-1}. \end{aligned}$$

Then

$$\begin{aligned} \left|X'_{n+1}(t)\right| \le \gamma M. \end{aligned}$$

(5.13)

Let now $\omega _1(0)$ be given. Let $\tilde{\omega }_1$ be an extension of $\omega _1(0)$ such that $\left|\tilde{\omega }_1\right|_{2,\infty (\Omega ^t)}^2 + \left\Vert \tilde{\omega }_1\right\Vert _{1,2,\Omega ^t}^2 < \infty$ and $\tilde{\omega }_1\big \vert _{t = 0} = \omega _1(0)$. Let

$$\begin{aligned} X_0' = \left| \tilde{\omega }_1\right| _{2,\infty (\Omega ^t)}^2 + \left\| \tilde{\omega }_1\right\| _{1,2,\Omega ^t}^2 < \gamma M. \end{aligned}$$

(5.14)

Then, (5.11), (5.13) and (5.14) imply that

$$\begin{aligned} \left|X'_n\right| \le \gamma M \qquad \text {for all }n \in {\mathbb {N}}_0. \end{aligned}$$

It remains to check the convergence of $X_n'$. Let

$$\begin{aligned} Y_n' = X_n' - X_{n-1}'. \end{aligned}$$

Then, (5.10) implies

$$\begin{aligned} \quad Y_{n+1}'= & {} c \left|u\right|_{\infty ,\Omega ^t} \left( D_2^2 Y_n' + D_1^2\left( X_n'^2 - X_{n-1}'^2\right) ^2 \right. \nonumber \\{} & {} \left. + \left( X_n'^2\exp \left( cX_n'^2\right) - X_{n+1}'^2 \exp \left( cX_{n-1}'^2\right) \right) \left( \left|u_1(0)\right|^2_{3,\Omega } + \left|f_1\right|^2_{3,1,\Omega _{r_0}^t}\right) \right) . \end{aligned}$$

(5.15)

Continuing, we have

$$\begin{aligned} \left| Y_{n+1}'\right|{} & {} \le {} c \left| u\right| _{\infty ,\Omega ^t} \left( D_2^2 \left| Y_n'\right| + D_1^2\left| Y_n'\right| \left( \left| X_n'\right| + \left| X_{n-1}'\right| \right) + \left( \left( X_n'^2 - X_{n-1}'^2\right) \exp \left( cX_n'^2\right) \right. \right. \\{} & {} \quad \left. + \left( X_n'^2 - X_{n-1}'^2\right) \exp \left( cX_{n-1}'^2\right) + X_{n-1}'^2\left( \exp \left( cX_n'^2\right) - \exp \left( cX_{n-1}'^2\right) \right) \right) \\{} & {} \quad \cdot \left. \left( \left| u_1(0)\right| ^2_{3,\Omega } + \left| f_1\right| ^2_{3,1,\Omega _{r_0}^t}\right) \right) \\{} & {} \le c \left| u\right| _{\infty ,\Omega ^t} \left( D_2^2 \left| Y_n'\right| + 2\gamma M D_1^2\left| Y_n'\right| + \left( \left| Y_n'\right| 2\gamma M \exp \left( c\left( \gamma M\right) ^2\right) \right. \right. \\{} & {} \quad + \left. \left. \left( \gamma M\right) ^2 \exp \left( c\left( \gamma M\right) ^2\right) \left| Y_n'\right| 2\gamma M\right) \left( \left| u_1(0)\right| ^2_{3,\Omega } + \left| f_1\right| ^2_{3,1,\Omega _{r_0}^t}\right) \right) \\{} & {} = {} c \left| u\right| _{\infty ,\Omega ^t} \left( D_2^2 + D_1^22\gamma M + 2\gamma M \left( \exp \left( c\left( \gamma M\right) ^2\right) \right) + 2(\gamma M)^3\exp \left( c(\gamma M)^2\right) \right) \\{} & {} \quad \cdot \left( \left| u_1(0)\right| ^2_{3,\Omega } + \left| f_1\right| ^2_{3,1,\Omega _{r_0}^t}\right) \left| Y_n'\right| . \end{aligned}$$

Hence, the sequence converges if

$$\begin{aligned}{} & {} \left|u\right|_{\infty ,\Omega ^t} \left( D_2^2 + D_1^2(2\gamma M) + \left( 2\gamma M \exp (c(\gamma M)^2)\right. \right. \\{} & {} \quad + \left. \left. 2(\gamma M)^3 \exp (c(\gamma M)^2)\right) \left( \left|u_1(0)\right|^2_{3,\Omega } + \left|f_1\right|^2_{3,1,\Omega _{r_0}^t}\right) \right) < 1. \end{aligned}$$

This ends the proof. $\square$

As explained after Theorem 1 we have to emphasize that (1.6) is crucial for deducing the regularity of weak solutions to problem (1.1).