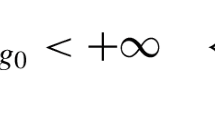1 Introduction

Suppose \(\Sigma \) is a smooth, compact, connected, embedded hypersurface in \({\mathbb R}^{d+1}\) without boundary. We then consider the motion of an incompressible viscous fluid that completely covers \(\Sigma \) and flows along \(\Sigma \). The motion can be modeled by the surface Navier–Stokes equations for an incompressible viscous fluid

$$\begin{aligned} \begin{aligned} \varrho \big (\partial _t u + {{\mathcal {P}}}_\Sigma (u\cdot \nabla _\Sigma u)\big ) - {{\mathcal {P}}}_\Sigma \, \textrm{div}_\Sigma \, {{\mathcal {T}}}_\Sigma&=0{} & {} \text {on}\;\;\Sigma \\ \textrm{div}_\Sigma u&=0{} & {} \text {on} \;\; \Sigma \\ u(0)&= u_0{} & {} \text {on}\;\; \Sigma . \end{aligned} \end{aligned}$$
(1.1)

Here, the density \(\varrho \) is a positive constant, \({{\mathcal {T}}}_\Sigma =2\mu _s {{\mathcal {D}}}_\Sigma (u) -\pi {{\mathcal {P}}}_\Sigma \), and

$$\begin{aligned} {{\mathcal {D}}}_\Sigma (u):=\frac{1}{2}{{\mathcal {P}}}_\Sigma \left( \nabla _\Sigma u + [\nabla _\Sigma u]^\textsf{T}\right) {{\mathcal {P}}}_\Sigma \end{aligned}$$

is the surface rate-of-strain tensor, with u the fluid velocity and \(\pi \) the pressure. Moreover, \({{\mathcal {P}}}_\Sigma \) denotes the orthogonal projection onto the tangent bundle \(\textsf{T}\Sigma \) of \(\Sigma \), \(\textrm{div}_\Sigma \) the surface divergence, and \(\nabla _\Sigma \) the surface gradient. We refer to Chapter 2 in [22] and the Appendix in [24] for more information concerning these objects.

The formulation (1.1) coincides with [12, formula (3.2)]. In that paper, the equations were derived from fundamental continuum mechanical principles. The same equations were also derived in [14, formula (4.4)], based on global energy principles. We mention that the authors of [12, 14] also consider material surfaces that may evolve in time.

Existence and uniqueness of solutions to the surface Navier–Stokes equations (1.1) was established in [24]. It was shown that the set of equilibria consists of all Killing vector fields on \(\Sigma \), and that all of these are normally stable. Moreover, it was shown that (1.1) can be reformulated as

$$\begin{aligned} \begin{aligned} \varrho \big (\partial _t u + {{\mathcal {P}}}_\Sigma (u\cdot \nabla _\Sigma u)\big ) - \mu _s( \Delta _\Sigma + \textsf{Ric}_\Sigma )u + \nabla _\Sigma \pi&=0{} & {} \text {on}\;\;\Sigma \\ \textrm{div}_\Sigma u&=0{} & {} \text {on} \;\; \Sigma \\ u(0)&= u_0{} & {} \text {on}\;\; \Sigma , \end{aligned} \end{aligned}$$
(1.2)

where \(\Delta _\Sigma \) is the (negative) Bochner-Laplacian and \(\textsf{Ric}_\Sigma \) the Ricci tensor. To be more precise, in slight abuse of the usual convention, we interpret \(\textsf{Ric}_\Sigma \) here as the (1, 1)-tensor given in local coordinates by \(\textsf{Ric}^\ell _k= g^{i\ell }R_{ik}\). We remind that in case \(d=2\), \(\textsf{Ric}_\Sigma u=K_\Sigma u\), with \(K_\Sigma \) being the Gaussian curvature of \(\Sigma \).

The formulation (1.2) shows that the surface Navier–Stokes equations can be formulated by intrinsic quantities that only depend on the geometry of the surface \(\Sigma \), but not on the ambient space. In an intrinsic formulation, the surface Navier Stokes equations (1.2) can be stated as

$$\begin{aligned} \begin{aligned} \varrho \big (\partial _t u + \nabla _u u) - \mu _s \Delta _\Sigma u- \mu _s\textsf{Ric}_\Sigma \, u + \textsf{grad }\,\pi&=0{} & {} \text {on}\;\;\Sigma \\ \textrm{div} u&=0{} & {} \text {on} \;\; \Sigma \\ u(0)&= u_0{} & {} \text {on}\;\; \Sigma , \end{aligned} \end{aligned}$$
(1.3)

where \(\nabla \) is the covariant derivative (induced by the Levi-Civita connection of \(\Sigma \)), and \(\textsf{grad}\,\pi =\nabla _\Sigma \pi \). An inspection of the proofs then shows that all the results in [24], and the results of this paper, are also valid for (1.3) for any smooth Riemannian manifold \(\Sigma \) without boundary. We remind that the Bochner Laplacian \(\Delta _\Sigma \) is related to the Hodge Laplacian by the formula \(\Delta _\Sigma = \Delta _H +\textsf{Ric}_\Sigma ,\) with the usual identification of vector fields and one-forms by means of lowering or rising indices.

We would like to point out that several formulations for the surface Navier–Stokes equations have been considered in the literature, see [6] for a comprehensive discussion, and also [12, Section 3.2]. It has been advocated in [8, Note added to Proof], and also in the more recent publications [6, 30], that the surface Navier–Stokes equations on a Riemannian manifold ought to be modeled by the system (1.3).

In Theorem 3.1, we show that the surface Stokes operator

$$\begin{aligned} A_{S,\Sigma }u:=-2 \mu _sP_{H,\Sigma } \mathcal {P}_\Sigma \textrm{div}_\Sigma \mathcal {D}_\Sigma (u) = -\mu _sP_{H,\Sigma }\big (\Delta _\Sigma +\textsf{Ric}_\Sigma \big ), \end{aligned}$$

with \(P_{\Sigma , H}\) being the surface Helmholtz projection, has the property that \((\omega + A_{S,\Sigma }) \) admits a bounded \(H^\infty \)-calculus in \(L_{q,\sigma }(\Sigma , \textsf{T}\Sigma )\) with \(H^\infty \)-angle \(\phi _{A_{S,\Sigma }}^\infty <\pi /2\), provided \(\omega \) is larger than the spectral bound of \(-A_{S,\Sigma }\) and \(1<q<\infty \).

For the Stokes operator on domains in Euclidean space under various boundary conditions, the existence of an \(H^\infty \)-calculus (or the related property of bounded imaginary powers) has been obtained by Giga [10], Abels [1], Noll and Saal [17], Saal [29], Prüss and Wilke [26], and Prüss [20]. We also refer to the survey article by Hieber and Saal [11] for additional references and information concerning the Stokes operator on domains in Euclidean space.

Having established the existence of a bounded \(H^\infty \)-calculus allows us to employ the results in Prüss, Simonett, and Wilke [23, 25] to establish existence and uniqueness of solutions to the system (1.1), or (1.3), for initial values \(u_0\) in the critical spaces \(B^{d/q-1}_{qp,\sigma }(\Sigma , \textsf{T}\Sigma )\), see Theorem 4.1 and Theorem 4.3.

In particular, our results imply existence and uniqueness of solutions for initial values \(u_0\in L_{q,\sigma }(\Sigma , \textsf{T}\Sigma )\) for \(q=d\), see Corollary 4.4. Hence, the celebrated result of Kato [13] is also valid for the surface Navier–Stokes equations.

For \(d=2\), we show in Theorem 4.9 that any solution to (1.1) with initial value \(u_0\in L_{2,\sigma }(\Sigma , \textsf{T}\Sigma )\) exists globally and converges exponentially fast to an equilibrium, that is, to a Killing field. The proof is based on an abstract result in [23], Korn’s inequality (established in Theorem A.3), and an energy estimate. Moreover, in Remark 4.10 we show that in case \(d\ge 3\), any global solution converges to an equilibrium.

We refer to [23, 26] for background information on critical spaces and for a discussion of the existing literature concerning critical spaces for the Navier–Stokes equations (and other equations) for domains in Euclidean space.

We would now like to briefly compare the results of this paper with previous results by other authors. Existence and uniqueness of solutions for the Navier–Stokes equations (1.3) for initial data in Morrey and Besov-Morrey spaces was established by Taylor [32] and Mazzucato [16], respectively; see also [6] for a comprehensive list of references. The authors in [16, 32] employ techniques of pseudo-differential operators and they make use of the property that the Hodge Laplacian commutes with the Helmholtz projection. In case \(d=2\), global existence is proved in [32, Proposition 6.5], but that result does not establish convergence of solutions.

The Boussinesq-Scriven surface stress tensor \({{\mathcal {T}}}_\Sigma \) has also been employed in the situation where two incompressible fluids which are separated by a free surface, where surface viscosity (accounting for internal friction within the interface) is included in the model, see for instance [5, 22]. Finally, we mention [12, 18, 27, 28] and the references contained therein for interesting numerical investigations.

Notation: We now introduce some notation and some auxiliary results that will be used in the sequel. It follows from the considerations in [24, Lemma A.1 and Remarks A.3] that

$$\begin{aligned} ({{\mathcal {P}}}_\Sigma \nabla _\Sigma u)^\textsf{T}=\nabla u\quad \text {and}\quad {{\mathcal {P}}}_\Sigma (u\cdot \nabla _\Sigma v)= \nabla _u v \end{aligned}$$
(1.4)

for tangential vector fields u, v, where \(\nabla \) denotes the covariant derivative (or the Levi-Civita connection) on \(\Sigma \). In the following, we will occasionally take the liberty to use the shorter notation \(\nabla _u v\) and \(\nabla u\) mentioned in (1.4). We recall that for sufficiently smooth vectors fields u, say \(u \in C^1(\Sigma ,\textsf{T}\Sigma )\), one has \(\nabla u\in C(\Sigma , \textsf{T}^1_1\Sigma )\), the space of all (1, 1)-tensors on \(\Sigma \). As the Levi-Civita connection \(\nabla \) is a metric connection, we have

$$\begin{aligned} \nabla _w(u|v)= (\nabla _wu|v) + (u| \nabla _w u) \end{aligned}$$
(1.5)

for tangential vector fields u, v, w on \(\Sigma \), where \((u|v):=g(u,v)\) is the Riemannian metric (induced by the Euclidean inner product of \({\mathbb R}^{d+1}\) in case \(\Sigma \) is embedded in \({\mathbb R}^{d+1}\)). Occasionally, we also write \(\textsf{grad}\,\varphi \) in lieu of \(\nabla _\Sigma \varphi \) for scalar functions \(\varphi \).

We use the notation

$$\begin{aligned} (u|v)_\Sigma = \int _\Sigma (u|v)\,d\Sigma , \end{aligned}$$

whenever the right hand side exists, say for \(u\in L_q(\Sigma , \textsf{T}\Sigma )\) and \(v\in L_{q'}(\Sigma , \textsf{T}\Sigma )\), where \(1/q+1/q'=1\). For \(k\in {\mathbb N}\) and \(q\in (1,\infty )\), the space \(H^k_q(\Sigma , \textsf{T}\Sigma )\) is defined as the completion of \( C^\infty (\Sigma , \textsf{T}\Sigma )\), the space of all smooth vector fields, in \(L_{1,\textrm{loc}}(\Sigma , \textsf{T}\Sigma )\) with respect to the norm

$$\begin{aligned} |u|_{H^k_q(\Sigma )}= \left( \sum _{i=0}^k |\nabla ^i u|^q_{L_q(\Sigma )}\right) ^{1/q}. \end{aligned}$$

The Bessel potential spaces \(H^s_q(\Sigma , \textsf{T}\Sigma )\) and the Besov spaces \(B^s_{qp}(\Sigma , \textsf{T}\Sigma )\) can then be defined through interpolation, see for instance [3, Section 7]. It is well-known that these spaces can be given equivalent norms by means of local coordinates, see for instance [3, Theorem 7.3] (for the more general context of singular and uniformly regular manifolds).

2 The Surface Stokes Operator

In [24, Corollary 3.4] we showed that there exists a number \(\omega _0>0\) such that for \(\omega >\omega _0\), the system

$$\begin{aligned} \begin{aligned} \partial _t u+\omega u - 2\mu _s \mathcal {P}_\Sigma \textrm{div}_\Sigma \mathcal {D}_\Sigma (u) + \nabla _\Sigma \pi&=f{} & {} \text {on}\;\;\Sigma \\ \textrm{div}_\Sigma u&=0{} & {} \text {on} \;\; \Sigma \\ u(0)&= u_0{} & {} \text {on}\;\; \Sigma \end{aligned} \end{aligned}$$
(2.1)

admits a unique solution

$$\begin{aligned} u\in H_{p,\mu }^1({\mathbb R}_+;L_q(\Sigma ,\textsf{T}\Sigma ))\cap L_{p,\mu }({\mathbb R}_+;H_q^2(\Sigma ,\textsf{T}\Sigma )),\quad \pi \in L_{p,\mu }({\mathbb R}_+;\dot{H}_q^1(\Sigma )), \end{aligned}$$

if and only if

$$\begin{aligned} f\in L_{p,\mu }({\mathbb R}_+;L_q(\Sigma ,\textsf{T}\Sigma )),\ u_0\in B_{qp}^{2\mu -2/p}(\Sigma ,\textsf{T}\Sigma )\quad \text {and}\quad \textrm{div}_\Sigma u_0=0. \end{aligned}$$

Moreover, the solution \((u,\pi )\) depends continuously on the given data \((f,u_0)\) in the corresponding spaces.

Let \(P_{H,\Sigma }\) denote the surface Helmholtz projection, defined by

$$\begin{aligned} P_{H,\Sigma } v:=v-\nabla _\Sigma \psi _v,\quad v\in L_q(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

where \(\nabla _\Sigma \psi _v\in L_q(\Sigma ,\textsf{T}\Sigma )\) is the unique solution of

$$\begin{aligned} (\nabla _\Sigma \psi _v|\nabla _\Sigma \phi )_\Sigma =(v|\nabla _\Sigma \phi )_\Sigma ,\quad \phi \in \dot{H}_{q'}^1(\Sigma ), \end{aligned}$$

see Lemma A.1. We note that \((P_{H,\Sigma }u|v)_\Sigma =(u|P_{H,\Sigma } v)_\Sigma \) for all \(u\in L_q(\Sigma ,\textsf{T}\Sigma )\), \(v\in L_{q'}(\Sigma ,\textsf{T}\Sigma )\), which follows directly from the definition of \(P_{H,\Sigma }\) (and for smooth functions from the surface divergence theorem). Indeed,

$$\begin{aligned} (P_{H,\Sigma } u|v)_\Sigma&=(u-\nabla _\Sigma \psi _u|v)_\Sigma =(u|v)_\Sigma -(\nabla _\Sigma \psi _u|v)_\Sigma \\&=(u|v)_\Sigma -(\nabla _\Sigma \psi _v|\nabla _\Sigma \psi _u)_\Sigma \\&=(u|v)_\Sigma -(u|\nabla _\Sigma \psi _v)_\Sigma \\&=(u|v-\nabla _\Sigma \psi _v)_\Sigma =(u|P_{H,\Sigma }v)_\Sigma , \end{aligned}$$

as \(\psi _u\in \dot{H}_q^1(\Sigma )\), \(\psi _v\in \dot{H}_{q'}^1(\Sigma )\). Let

$$\begin{aligned} X_0:=L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ):=P_{H,\Sigma }L_q(\Sigma ,\textsf{T}\Sigma ),\quad X_1:=H_{q,\sigma }^2(\Sigma ,\textsf{T}\Sigma ):=H_{q}^2(\Sigma ,\textsf{T}\Sigma )\cap X_0. \end{aligned}$$

The surface Stokes operator is defined by

$$\begin{aligned} A_{S,\Sigma }u:=-2 \mu _sP_{H,\Sigma } \mathcal {P}_\Sigma \textrm{div}_\Sigma \mathcal {D}_\Sigma (u),\quad u\in D(A_{S,\Sigma }):=X_1. \end{aligned}$$
(2.2)

Making use of the projection \(P_{H,\Sigma }\), (2.1) with \(\textrm{div}_\Sigma f=0\) is equivalent to the equation

$$\begin{aligned} \partial _t u+\omega u+A_{S,\Sigma }u=f,\quad t>0,\quad u(0)=u_0. \end{aligned}$$
(2.3)

Indeed, if \((u,\pi )\) is a solution to (2.1), then \(u=P_{H,\Sigma }u\) solves (2.3) as can be seen by applying \(P_{H,\Sigma }\) to the first equation in (2.1). Conversely, let u be a solution of (2.3). Then, by definition of \(P_{H,\Sigma }\),

$$\begin{aligned} A_{S,\Sigma }u=-2 \mu _sP_{H,\Sigma } \mathcal {P}_\Sigma \textrm{div}_\Sigma \mathcal {D}_\Sigma (u)=-2 \mu _s\mathcal {P}_\Sigma \textrm{div}_\Sigma \mathcal {D}_\Sigma (u)+2\mu _s\nabla _\Sigma \psi _v, \end{aligned}$$

where \(\psi _v\in \dot{H}_q^1(\Sigma )\) solves

$$\begin{aligned} (\nabla _\Sigma \psi _v|\nabla _\Sigma \phi )_\Sigma =(v|\nabla _\Sigma \phi )_\Sigma ,\quad \phi \in \dot{H}_{q'}^1(\Sigma ), \end{aligned}$$

with \(v:= \mathcal {P}_\Sigma \textrm{div}_\Sigma \mathcal {D}_\Sigma (u)\in L_q(\Sigma )\). Defining \(\pi :=2\mu _s\psi _v\), we see that \((u,\pi )\) is a solution of (2.1).

In particular, the operator \(A_{S,\Sigma }\) has \(L_{p}\)-maximal regularity, hence \(-(\omega +A_{S,\Sigma })\) generates an analytic \(C_0\)-semigroup in \(X_0\) (see for instance [22, Proposition 3.5.2]) which is exponentially stable provided \(\omega >s(-A_{S,\Sigma })\), where \(s(\cdot )\) denotes the spectral bound of \(-A_{S,\Sigma }\). This readily implies that the operator \(\omega +A_{S,\Sigma }\) is sectorial with spectral angle \(\phi _{\omega +A_{S,\Sigma }}<\pi /2\).

3 \(H^\infty \)-calculus

In this section, we are going to prove the following result.

Theorem 3.1

Let \(q\in (1,\infty )\) and \(\Sigma \) be a smooth, compact, connected, embedded hypersurface in \({\mathbb R}^{d+1}\) without boundary. Let \(A_{S,\Sigma }\) be the surface Stokes operator in \(L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\) defined in (2.2).

Then \(\omega +A_{S,\Sigma }\) admits a bounded \(H^\infty \)-calculus with \(H^\infty \)-angle \(\phi _{A_{S,\Sigma }}^\infty <\pi /2\) for each \(\omega >s(-A_{S,\Sigma })\), the spectral bound of \(-A_{S,\Sigma }\).

Remark 3.2

Let \({{\mathcal {E}}}\) denote the set of equilibria. We have shown in [24], Proposition 4.1, that \(s(-A_{S,\Sigma })=0\) provided \({{\mathcal {E}}}\ne \{0\}\) und \(s(-A_{S,\Sigma })<0\) if \({{\mathcal {E}}}=\{0\}\).

Therefore, it follows from Theorem 3.1 that for each \(\omega >0\) the operator \(\omega +A_{S,\Sigma }\) admits a bounded \(H^\infty \)-calculus with \(H^\infty \)-angle \(\phi _{A_{S,\Sigma }}^\infty <\pi /2\). In case \({{\mathcal {E}}}=\{0\}\) one may set \(\omega =0\).

3.1 Resolvent and Pressure Estimates

We consider the following resolvent problem

$$\begin{aligned} \begin{aligned} \lambda u+(\omega - 2\mu _s \mathcal {P}_\Sigma \textrm{div}_\Sigma \mathcal {D}_\Sigma )u + \nabla _\Sigma \pi&=f{} & {} \text {on}\;\;\Sigma \\ \textrm{div}_\Sigma u&=0{} & {} \text {on} \;\; \Sigma , \end{aligned} \end{aligned}$$
(3.1)

where \(\omega >s(-A_{S,\Sigma })\) and \(\lambda \in \Sigma _{\pi -\phi }\), \(\phi >\phi _{\omega +A_{S,\Sigma }}\). By sectoriality of the operator \(\omega +A_{S,\Sigma }\) (and since \(0\in \rho (\omega +A_{S,\Sigma })\)), it follows that for given \(f\in L_q(\Sigma ,\textsf{T}\Sigma )\) there exists a unique solution

$$\begin{aligned} u\in H_q^2(\Sigma ,\textsf{T}\Sigma ),\quad \pi \in \dot{H}_q^1(\Sigma ) \end{aligned}$$

of (3.1) and there is a constant \(C>0\) such that

$$\begin{aligned} (|\lambda |+1)|u|_{L_q(\Sigma )}+|u|_{H_q^2(\Sigma )}+|\nabla \pi |_{L_q(\Sigma )}\le C|f|_{L_q(\Sigma )}, \end{aligned}$$
(3.2)

for all \(\lambda \in \Sigma _{\pi -\phi }\). Note that without loss of generality, we may assume that \(P_0\pi =\pi \), where

$$\begin{aligned} P_0v:=v-\frac{1}{|\Sigma |}\int _\Sigma v \,d\Sigma \end{aligned}$$

for \(v\in L_1(\Sigma )\). Furthermore, if \({\text {div}}_\Sigma f=0\), the pressure \(\pi \) satisfies the estimate

$$\begin{aligned} |\pi |_{L_q(\Sigma )}\le C|u|_{H_q^1(\Sigma )} \end{aligned}$$
(3.3)

for some constant \(C>0\). The proof of estimate (3.3) follows exactly the lines of the proof of [24, Proposition 3.3].

3.2 Localization

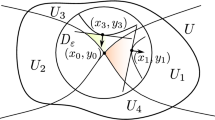
By compactness of \(\Sigma \), there exists a family of charts \(\{(U_k,\varphi _k):k\in \{1,\ldots ,N\}\}\) such that \(\{U_k\}_{k=1}^N\) is an open covering of \(\Sigma \). Let \(\{\psi _k^2\}_{k=1}^N\subset C^\infty (\Sigma )\) be a partition of unity subordinate to the open covering \(\{U_k\}_{k=1}^N\). Note that without loss of generality, we may assume that \(\varphi _k(U_k)=B_{\mathbb {R}^d}(0,r)\). We call \(\{(U_k,\varphi _k,\psi _k):k\in \{1,\ldots ,N\}\}\) a localization system for \(\Sigma \).

Let \(\{\tau _{(k)j}(p)\}_{j=1}^d\) denote a local basis of the tangent space \(\textsf{T}_p\Sigma \) of \(\Sigma \) at \(p\in U_k\) and denote by \(\{\tau _{(k)}^j(p)\}_{j=1}^d\) the corresponding dual basis of the cotangent space \(\textsf{T}^*_p\Sigma \) at \(p\in U_k\). Accordingly, we define \(g_{(k)}^{ij}=(\tau _{(k)}^i|\tau _{(k)}^j)\) and \(g_{(k)ij}\) is defined in a very similar way, see the Appendix in [24]. Then, with \(\bar{u}=u\circ \varphi _k^{-1}\), \(\bar{\pi }=\pi \circ \varphi _k^{-1}\) and so on, the system (3.1) with respect to the local charts \((U_k,\varphi _k)\), \(k\in \{1,\ldots ,N\}\), reads as follows.

$$\begin{aligned} \begin{aligned} \lambda \bar{u}_{(k)}^\ell + (\omega - \mu _s \bar{g}_{(k)}^{ij}\partial _i\partial _j)\bar{u}_{(k)}^\ell + \bar{g}_{(k)}^{i\ell }\partial _i\bar{\pi }_{(k)}&=\bar{f}_{(k)}^\ell +F_{(k)}^\ell (\bar{u},\bar{\pi }){} & {} \text {in}\;\;\mathbb {R}^d \\ \partial _i \bar{u}_{(k)}^i&=H_{(k)}(\bar{u}){} & {} \text {in} \;\; \mathbb {R}^d, \end{aligned} \end{aligned}$$
(3.4)

where

$$\begin{aligned} \bar{u}_{(k)}^\ell= & {} (\bar{u}\bar{\psi }_k|\bar{\tau }_{(k)}^\ell ),\ \bar{\pi }_{(k)}=\bar{\pi }\bar{\psi }_k, \\ \bar{f}_{(k)}^\ell= & {} (\bar{f}\bar{\psi }_k|\bar{\tau }_{(k)}^\ell ),\quad F_{(k)}^\ell (\bar{u},\bar{\pi })=\bar{\pi } \bar{g}_{(k)}^{i\ell }\partial _i\bar{\psi }_k+(B_{(k)}\bar{u}|\bar{\tau }_{(k)}^\ell ), \end{aligned}$$

\(\ell \in \{1,\ldots ,d\}\), \(B_{(k)}\) collects all terms of order at most one and

$$\begin{aligned} H_{(k)}(\bar{u})=\bar{u}^i\partial _i\bar{\psi }_k-\bar{u}_{(k)}^j (\bar{\tau }_{(k)}^i|\partial _i\bar{\tau }_{(k)j}). \end{aligned}$$

Here, upon translation and rotation, \(\bar{g}_{(k)}^{ij}(0)=\delta _j^i\) and the coefficients have been extended in such a way that \(\bar{g}_{(k)}^{ij}\in W_\infty ^2({\mathbb R}^d)\) and \(|\bar{g}_{(k)}^{ij}-\delta _j^i|_{L_\infty (\mathbb {R}^d)}\le \eta \), where \(\eta >0\) can be made as small as we wish, by decreasing the radius \(r>0\) of the ball \(B_{\mathbb {R}^d}(0,r)\).

In order to handle system (3.4), we define vectors in \({\mathbb R}^d\) as follows:

$$\begin{aligned} \bar{u}_{(k)}:=(\bar{u}_{(k)}^1,\ldots ,\bar{u}_{(k)}^d),\quad \bar{f}_{(k)}:=(\bar{f}_{(k)}^1,\ldots ,\bar{f}_{(k)}^d) \end{aligned}$$

and

$$\begin{aligned} {F}_{(k)}(\bar{u},\bar{\pi }):=({F}_{(k)}^1(\bar{u},\bar{\pi }),\ldots ,{F}_{(k)}^d(\bar{u},\bar{\pi })). \end{aligned}$$

Moreover, we define the matrix \(G_{(k)}=(\bar{g}_{(k)}^{ij})_{i,j=1}^d\in {\mathbb R}^{d\times d}\). With these notations, system (3.4) reads as

$$\begin{aligned} \begin{aligned} \lambda \bar{u}_{(k)}+(\omega - \mu _s (G_{(k)}\nabla |\nabla ))\bar{u}_{(k)} + G_{(k)}\nabla \bar{\pi }_{(k)}&=\bar{f}_{(k)}+F_{(k)}(\bar{u},\bar{\pi }){} & {} \text {in}\;\;\mathbb {R}^d \\ \textrm{div}\ \bar{u}_{(k)}&=H_{(k)}(\bar{u}){} & {} \text {in} \;\; \mathbb {R}^d. \end{aligned} \end{aligned}$$
(3.5)

Let us remove the term \(H_{(k)}(\bar{u})\), since it is not of lower order. For that purpose, we solve the equation \(\textrm{div}( G_{(k)}\nabla \phi _k)=H_{(k)}(\bar{u})\) by Lemma A.2 to obtain a unique solution \(\nabla \phi _k\in H_q^2({\mathbb R}^d)^d\) with

$$\begin{aligned} |\nabla \phi _k|_{H_q^2({\mathbb R}^d)}\le C|H_{(k)}(\bar{u})|_{H_q^1({\mathbb R}^d)}, \end{aligned}$$
(3.6)

where C is a positive constant. For this, observe that \(H_{(k)}(\bar{u})\) is compactly supported and we have \(\int _{{\mathbb R}^d}H_{(k)}(\bar{u})dx=0\). Therefore, \(H_{(k)}(\bar{u})\) induces a functional on \(\dot{H}_{q'}^1({\mathbb R}^d)\) with norm bounded by \(C|H_{(k)}(\bar{u})|_{L_q({\mathbb R}^d)}.\) To see this, choose \(R>0\) such that \(\textrm{supp}(H_{(k)}(\bar{u}))\subset B(0,R)\) and let \(\phi \in \dot{H}^1_{q'}({\mathbb R}^d).\) Then we have

$$\begin{aligned} \int _{{\mathbb R}^d} H_{(k)}(\bar{u})\phi \,dx =\int _{B(0,R)} H_{(k)}(\bar{u})(\phi -\hat{\phi })\,dx , \end{aligned}$$

where \(\hat{\phi }= |B(0,R)|^{-1} \int _{B(0,R)} \phi \,dx\). By the Poincaré-Wirtinger inequality,

$$\begin{aligned} \begin{aligned} |\int _{B(0,R)} H_{(k)}(\bar{u})(\phi -\hat{\phi })\,dx |&\le C |H_{(k)}(\bar{u})|_{L_q} |\nabla \phi |_{L_{q'}(B(0,R))} \\&\le C |H_{(k)}(\bar{u})|_{L_q} |\nabla \phi |_{L_{q'}({\mathbb R}^d)}. \end{aligned} \end{aligned}$$

Let

$$\begin{aligned} \tilde{u}_{(k)}=\bar{u}_{(k)}-G_{(k)}\nabla \phi _k\quad \text {and}\quad \tilde{\pi }_{(k)}=\bar{\pi }_{(k)}+(\lambda +\omega )\phi _k. \end{aligned}$$

It follows from (3.5) that the functions \((\tilde{u}_{(k)}, \tilde{\pi }_{(k)})\) then solve the system

$$\begin{aligned} \begin{aligned} \lambda \tilde{u}_{(k)}+(\omega - \mu _s (G_{(k)}\nabla |\nabla ))\tilde{u}_{(k)}+ G_{(k)}\nabla \tilde{\pi }_{(k)}&=\bar{f}_{(k)}+\tilde{F}_{(k)}(\bar{u},\bar{\pi }){} & {} \text {in}\;\;\mathbb {R}^d \\ \textrm{div}\ \tilde{u}_{(k)}&=0{} & {} \text {in} \;\; \mathbb {R}^d, \end{aligned} \end{aligned}$$
(3.7)

where \(\tilde{F}_{(k)}(\bar{u},\bar{\pi }):=F_{(k)}(\bar{u},\bar{\pi })+\mu _s (G_{(k)}\nabla |\nabla )(G_{(k)}\nabla \phi _k).\) In order to remove the pressure term in (3.7) we introduce the projections \(P_k^G\), defined by

$$\begin{aligned} P_k^Gv:=v-G_{(k)}\nabla \Phi _k,\quad v\in L_q({\mathbb R}^d). \end{aligned}$$

Here, \(\nabla \Phi _k\in L_q({\mathbb R}^d)\) is the unique solution of \(\textrm{div}(G_{(k)}\nabla \Phi _k)=\textrm{div}\, v\) in \(\dot{H}_q^{-1}({\mathbb R}^d)\), established in Lemma A.2. It is readily seen that \(P_k^Gv=v\) if \(\textrm{div}\, v=0\) and \(P_k^G(G_{(k)}\nabla \tilde{\pi }_{(k)})=0\). Applying the projection \(P_k^G\) to equation (3.7) leads to

$$\begin{aligned} \begin{aligned} \lambda \tilde{u}_{(k)}+(\omega - \mu _s P_k^G(G_{(k)}\nabla |\nabla ))\tilde{u}_{(k)}&=P_k^G(\bar{f}_{(k)}+\tilde{F}_{(k)}(\bar{u},\bar{\pi })){} & {} \text {in}\;\;\mathbb {R}^d. \\ \end{aligned} \end{aligned}$$
(3.8)

We claim that each of the operators \(\omega +A_{S,k}^G:=\omega -\mu _sP_k^G(G_{(k)}\nabla |\nabla )\) in (3.8) admits a bounded \(H^\infty \)-calculus in \(P_k^GL_q({\mathbb R}^d)=L_{q,\sigma }({\mathbb R}^d)\), provided \(\omega \) is sufficiently large. To see this, we write

$$\begin{aligned} -A_{S,k}^Gu=-A_S u+\mu _s((G_{(k)}-I)\nabla |\nabla )u-\mu _sG_{(k)}\nabla \Phi _k, \end{aligned}$$

where \(A_S=-\mu _sP_H\Delta u=-\mu _s\Delta u\) is the Stokes operator in \(L_{q,\sigma }({\mathbb R}^d)\) and \(P_H\) is the Helmholtz projection in \({\mathbb R}^d\).

Recall that each matrix \(G_{(k)}\) is a perturbation of the identity in \({\mathbb R}^{d\times d}\). Therefore,

$$\begin{aligned} |\mu _s((G_{(k)}-I)\nabla |\nabla )u|_{L_q({\mathbb R}^d)}\le \eta |u|_{H_q^2({\mathbb R}^d)}, \end{aligned}$$

where we may choose \(\eta >0\) as small as we wish. Furthermore,

$$\begin{aligned} |G_{(k)}\nabla \Phi _k|_{L_q({\mathbb R}^d)}\le C|(G_{(k)}\nabla |\nabla )u-\Delta u|_{{L}_q({\mathbb R}^d)}\le \eta |u|_{H_q^2({\mathbb R}^d)}, \end{aligned}$$

by Lemma A.2, since

$$\begin{aligned} \textrm{div}(G_{(k)}\nabla \Phi _k)=\textrm{div}\, (G_{(k)}\nabla |\nabla )u=\textrm{div}\, (G_{(k)}\nabla |\nabla )u-{\text {div}}\Delta u \end{aligned}$$

as \({\text {div}}\Delta u=\Delta {\text {div}} u=0\) in \({\mathbb R}^d\). As before, we may choose \(\eta >0\) as small as we wish.

Note that the shifted Stokes operator \(\omega +A_S\) admits a bounded \(H^\infty \)-calculus in \(L_{q,\sigma }({\mathbb R}^d)\) with angle \(\phi _{A_S}^\infty <\pi /2\), see e.g. [22, Theorem 7.1.2]. By the abstract perturbation result [7, Theorem 3.2] (see also [20, Section 3]), there exists \(\omega _0>0\) such that each of the operators \(\omega + A_{S,k}^G\) admits a bounded \(H^\infty \)-calculus in \(L_{q,\sigma }({\mathbb R}^d)\) if \(\omega \ge \omega _0\). Moreover, for any given \(\phi _0>\phi _{A_S}^\infty \) we may assume \(\phi _{A_{S,k}^G}^\infty \le \phi _0\), provided that \(|G_{(k)}-I|_\infty \) is sufficiently small.

This yields the following representation of the resolvent \(u=(\lambda +\omega +A_{S,\Sigma })^{-1} f\).

$$\begin{aligned} u&=P_{H,\Sigma }\sum _{k=1}^N\psi _k^2 u=P_{H,\Sigma }\sum _{k=1}^N\psi _k(\bar{u}_{(k)}^\ell \bar{\tau }_{(k)\ell })\circ \varphi _k\\&=P_{H,\Sigma }\sum _{k=1}^N\psi _k((\tilde{u}_{(k)}|e_\ell )\bar{\tau }_{(k)\ell })\circ \varphi _k+P_{H,\Sigma }\sum _{k=1}^N\psi _k((G_{(k)}\nabla \phi _k|e_\ell )\bar{\tau }_{(k)\ell })\circ \varphi _k\\&=Tu+{S(\lambda )f}+R(\lambda )f, \end{aligned}$$

where \(\{e_\ell \}_{\ell =1}^d\) is the standard basis in \({\mathbb R}^d\) and

$$\begin{aligned} \begin{aligned} Tu:&=P_{H,\Sigma }\sum _{k=1}^N\psi _k((G_{(k)}\nabla \phi _k |e_\ell )\bar{\tau }_{(k)\ell })\circ \varphi _k, \\ S(\lambda )f:&=P_{H,\Sigma }\sum _{k=1}^N\psi _k(((\lambda +\omega +A_{S,k}^G)^{-1}P_k^G\bar{f}_{(k)}|e_\ell )\bar{\tau }_{(k)\ell })\circ \varphi _k \\ R(\lambda )f:&=P_{H,\Sigma }\sum _{k=1}^N\psi _k(((\lambda +\omega +A_{S,k}^G)^{-1}P_k^G\tilde{F}_{(k)}(\bar{u}(f),\bar{\pi }(f))|e_\ell )\bar{\tau }_{(k)\ell })\circ \varphi _k. \end{aligned} \end{aligned}$$

In a next step, we will estimate the term \(R(\lambda )f\) in \(L_{q}(\Sigma ,\textsf{T}\Sigma )\). To this end, observe that the operators \(P_{H,\Sigma }\) and \(P_k^G\) are bounded in \(L_{q}(\Sigma ,\textsf{T}\Sigma )\) and \(L_{q}({\mathbb R}^d)\), respectively. This, together with (3.2), (3.3), (3.6) and the fact that each of the operators \(\omega +A_{S,k}^G\) is sectorial in \(L_{q,\sigma }({\mathbb R}^d)\) for \(\omega \) sufficiently large, yields the estimate

$$\begin{aligned} |R(\lambda )f|_{L_q(\Sigma )}\le \frac{C}{(|\lambda |+1)^{3/2}}|f|_{L_q(\Sigma )} \end{aligned}$$
(3.9)

for some constant \(C>0\). Indeed, by (3.2), (3.3), (3.6), we obtain

$$\begin{aligned} |\tilde{F}_{(k)}(\bar{u},\bar{\pi })|_{L_q({\mathbb R}^d)}&\le C\left( |{F}_{(k)}(\bar{u},\bar{\pi })|_{L_q({\mathbb R}^d)}+|\nabla \phi _k|_{H_q^2({\mathbb R}^d)}\right) \\&\le C\left( |{\pi }|_{L_q(\Sigma )}+|{u}|_{H_q^1(\Sigma )}\right) \\&\le C|{u}|_{H_q^1(\Sigma )}\\&\le C(1+|\lambda |)^{-1/2}((1+|\lambda |)|{u}|_{L_q(\Sigma )}+|{u}|_{H_q^2(\Sigma )})\\&\le C(1+|\lambda |)^{-1/2}|f|_{L_q(\Sigma )}. \end{aligned}$$

Here we have also used complex interpolation \(H_q^1(\Sigma )=[L_q(\Sigma ),H_q^2(\Sigma ))]_{1/2}\).

Next, observe that \(T:L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\rightarrow H_q^1(\Sigma ,\textsf{T}\Sigma )\cap L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\), since \(G_{(k)}\in W_\infty ^2({\mathbb R}^d)^{d\times d}\) and \(\nabla \phi _{k}\in H_q^1({\mathbb R}^d)^d\) for each \(k\in \{1,\ldots ,N\}\), hence T is compact in \(L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\). Consequently, \(I-T\) is a Fredholm operator with index 0. In particular, \(\ker (I-T)\) is finite dimensional and the range \(\textrm{ran}(I-T)\) is closed in \(L_q(\Sigma )\). Let \(\{v_1,\ldots ,v_m\}\) be an orthonormal basis of \(\ker (I-T)\) and define

$$\begin{aligned} Q:L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\rightarrow \ker (I-T) \end{aligned}$$

by

$$\begin{aligned} Qu=\sum _{k=1}^m(u|v_k)_\Sigma v_k. \end{aligned}$$

Then it can be readily checked that Q is a projection onto \(\ker (I-T)\) and it is continuous in \(L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\) for any \(q\in (1,\infty )\), since \(v_k\in H_q^1(\Sigma ,\textsf{T}\Sigma )\) for any \(q\in (1,\infty )\) (using a bootstrap argument). Consequently, the operator

$$\begin{aligned} I-T:\textrm{ran}(I-Q)\rightarrow \textrm{ran}(I-T) \end{aligned}$$

is invertible with bounded inverse.

We use the resolvent representation

$$\begin{aligned} (I-T)u={S(\lambda )f}+R(\lambda )f, \end{aligned}$$

to conclude that the right hand side belongs to \(\textrm{ran}(I-T)\), hence

$$\begin{aligned} (I-Q)u =(I-T)^{-1}\left( {S(\lambda )f}+R(\lambda )f\right) . \end{aligned}$$

Let \(\phi _0\in (\phi _{A_S}^\infty ,\pi /2)\) such that \(\phi _{A_{S,k}^G}^\infty \le \phi _0\) for each \(k\in \{1,\ldots ,N\}\). For \(h\in H_0(\Sigma _{\phi })\), \(\phi \in (\phi _0,\pi /2)\), we then obtain

$$\begin{aligned} (I-Q)h(\omega +A_{S,\Sigma })f= & {} (I-T)^{-1}\left( P_{H,\Sigma }\sum _{k=1}^N\psi _k((h(\omega +A_{S,k}^G)P_k^G\bar{f}_{(k)}|e_\ell )\bar{\tau }_{(k)\ell })\circ \varphi _k\right. \\{} & {} \left. \quad +\frac{1}{2\pi i}\int _\Gamma h(-\lambda )R(\lambda )fd\lambda \right) , \end{aligned}$$

with \(\Gamma =(\infty ,0]e^{-i(\pi -\theta )}\cup [0,\infty )e^{i(\pi -\theta )}\), \(\theta \in (\phi _0,\phi )\). Estimate (3.9) then yields

$$\begin{aligned} |(I-Q)h(\omega +A_{S,\Sigma })|_{\mathcal {B}(L_q(\Sigma ))}\le C|h|_\infty , \end{aligned}$$

since each of the operators \(\omega +A_{S,k}^G\) has a bounded \(H^\infty \)-calculus. The remaining part \(Qh(\omega +A_{S,\Sigma })\) may be treated as follows.

$$\begin{aligned} Qh(\omega +A_{S,\Sigma })f&=Q\frac{1}{2\pi i}\int _\Gamma h(-\lambda )(\lambda +\omega )(\lambda +\omega +A_{S,\Sigma })^{-1}f\frac{d\lambda }{\lambda +\omega }\\&=Q\frac{1}{2\pi i}\int _\Gamma h(-\lambda )(I-A_{S,\Sigma }(\lambda +\omega +A_{S,\Sigma })^{-1})f\frac{d\lambda }{\lambda +\omega }\\&=Qh(\omega ) f-Q\frac{1}{2\pi i}\int _\Gamma h(-\lambda )A_{S,\Sigma }(\lambda +\omega +A_{S,\Sigma })^{-1}f\frac{d\lambda }{\lambda +\omega }. \end{aligned}$$

For the last integral, we employ the definition of the projection Q from above to obtain

$$\begin{aligned} Q\frac{1}{2\pi i}&\int _\Gamma h(-\lambda )A_{S,\Sigma }(\lambda +\omega +A_{S,\Sigma })^{-1}f\frac{d\lambda }{\lambda +\omega }\\&=\frac{1}{2\pi i}\sum _{k=1}^mv_k\int _\Gamma h(-\lambda )(A_{S,\Sigma }(\lambda +\omega +A_{S,\Sigma })^{-1}f|v_k)_\Sigma \frac{d\lambda }{\lambda +\omega }\\&=2\mu _s\frac{1}{2\pi i}\sum _{k=1}^mv_k\int _\Gamma h(-\lambda )(\mathcal {D}_\Sigma (\lambda +\omega +A_{S,\Sigma })^{-1}f:\nabla _\Sigma v_k) \frac{d\lambda }{\lambda +\omega }. \end{aligned}$$

By (3.2), we therefore obtain

$$\begin{aligned} |Qh(\omega +A_{S,\Sigma })|_{\mathcal {B}(L_q(\Sigma ))}\le C|h|_\infty , \end{aligned}$$

for some constant \(C>0\). Consequently, the operator \(\omega +A_{S,\Sigma }\) admits a bounded \(H^\infty \)-calculus in \(L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\) with angle \(\phi _{A_{S,\Sigma }}^\infty <\pi /2\) provided \(\omega >0\) is large enough. An application of [22, Corollary 3.3.15] finally yields that it is enough to require \(\omega >s(-A_{S,\Sigma })\). This completes the proof of Theorem 3.1.

4 Critical Spaces

4.1 Strong Setting

We consider the abstract system

$$\begin{aligned} \partial _t u+A_{S,\Sigma }u=F_\Sigma (u),\quad t>0,\quad u(0)=u_0, \end{aligned}$$
(4.1)

where \(F_\Sigma (u):=-P_{H,\Sigma }\mathcal {P}_\Sigma (u\cdot \nabla _\Sigma u)= -P_{H,\Sigma }\nabla _u u\). Let \(q\in (1,\infty )\),

$$\begin{aligned} X_0:=L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\quad \text {and} \quad X_1:=D(A_{S,\Sigma })=H_{q,\sigma }^2(\Sigma ,\textsf{T}\Sigma ). \end{aligned}$$

Furthermore, let \(X_\beta =[X_0,X_1]_\beta \) for some \(\beta \in (0,1)\), where \([\cdot ,\cdot ]_\beta \) denotes the complex interpolation functor. Then, by Theorem 3.1, it holds that \(X_\beta =D((\omega +A_{S,\Sigma })^\beta )\) for \(\omega >s(-A_{S,\Sigma })\). In [24, Section 3.5], we determined the real and complex interpolation spaces \((X_0,X_1)_{\alpha ,p}\) and \([X_0,X_1]_\alpha \) as

$$\begin{aligned}{}[X_0,X_1]_\alpha&=H_{q,\sigma }^{2\alpha }(\Sigma ,\textsf{T}\Sigma ), \\ (X_0,X_1)_{\alpha ,p}&=B_{qp,\sigma }^{2\alpha }(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

for \(\alpha \in (0,1)\) and \(p\in (1,\infty ),\) where \(H_{q,\sigma }^{s}(\Sigma ,\textsf{T}\Sigma ):= H_{q}^{s}(\Sigma ,\textsf{T}\Sigma )\cap L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\) and \(B_{qp,\sigma }^{s}(\Sigma ,\textsf{T}\Sigma ):= B_{qp}^{s}(\Sigma ,\textsf{T}\Sigma )\cap L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\) for \(s\in (0,2)\).

By Hölder’s inequality, the estimate

$$\begin{aligned} |F_\Sigma (u)|_{L_q(\Sigma )}\le C|u|_{L_{qr'}(\Sigma )}|u|_{H_{qr}^1(\Sigma )} \end{aligned}$$

holds. We choose \(r,r'\in (1,\infty )\), \(1/r+1/r'=1\), in such a way that

$$\begin{aligned} 1-\frac{d}{qr}=-\frac{d}{qr'},\quad \text {or equivalently,}\quad \frac{d}{qr}=\frac{1}{2}\left( 1+\frac{d}{q}\right) , \end{aligned}$$

which is feasible if \(q\in (1,d)\). Next, by Sobolev embedding, we have

$$\begin{aligned}{}[X_0,X_1]_{\beta }\subset H_{q}^{2\beta }(\Sigma ,\textsf{T}\Sigma )\hookrightarrow H_{qr}^1(\Sigma ,\textsf{T}\Sigma )\cap L_{qr'}(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

provided

$$\begin{aligned} 2\beta -\frac{d}{q}=1-\frac{d}{qr},\quad \text {or equivalently,}\quad \beta =\frac{1}{4}\left( \frac{d}{q}+1\right) . \end{aligned}$$

The condition \(\beta <1\) requires \(q>d/3\), hence \(q\in (d/3,d)\). For \(q\in (d/3,d)\) we define the critical weight by

$$\begin{aligned} \mu _c:=\frac{1}{2}\left( \frac{d}{q}-1\right) +\frac{1}{p}, \end{aligned}$$

with \(2/p+d/q\le 3\), so that \(\mu _c\in (1/p,1]\). We consider now the problem

$$\begin{aligned} \partial _t u+\omega u+A_{S,\Sigma }u=F_\Sigma (u)+\omega u,\quad t>0,\quad u(0)=u_0, \end{aligned}$$
(4.2)

where \(\omega >s(-A_{S,\Sigma })\). It is clear that u is a solution of (4.1) if and only if u is a solution to (4.2). Note that for each \(\omega >s(-A_{S,\Sigma })\), the operator \(\omega +A_{S,\Sigma }\) admits a bounded \(H^\infty \)-calculus in \(X_0\) with \(H^\infty \)-angle \(\phi _{A_{S,\Sigma }}^\infty <\pi /2\). We may therefore apply [23, Theorem 1.2] to (4.2) which yields the following result.

Theorem 4.1

Let \(p\in (1,\infty )\), \(q\in (d/3,d)\) such that \(\frac{2}{p}+\frac{d}{q}\le 3\). Then for any initial value \(u_0\in B_{qp,\sigma }^{d/q-1}(\Sigma ,\textsf{T}\Sigma )\) there exists a unique strong solution

$$\begin{aligned} u\in H_{p,\mu _c}^1((0,a);L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ))\cap L_{p,\mu _c}((0,a);H_{q,\sigma }^2(\Sigma ,\textsf{T}\Sigma )) \end{aligned}$$

of (4.1) for some \(a=a(u_0)>0\), with \(\mu _c=1/p+d/(2q)-1/2\). The solution exists on a maximal time interval \([0,t_+(u_0))\) and depends continuously on \(u_0\). In addition, we have

$$\begin{aligned} u\in C([0,t_+);B_{qp,\sigma }^{d/q-1}(\Sigma ,\textsf{T}\Sigma ))\cap C((0,t_+);B_{qp,\sigma }^{2-2/p}(\Sigma ,\textsf{T}\Sigma )) \end{aligned}$$

which means that the solution regularizes instantaneously if \(2/p+d/q<3\).

Remark 4.2

Note that in case \(d=3\) and \(p=q=2\), the initial value belongs to

$$\begin{aligned} B_{22,\sigma }^{1/2}(\Sigma ,\textsf{T}\Sigma )=H_{2,\sigma }^{1/2}(\Sigma ,\textsf{T}\Sigma ). \end{aligned}$$

Hence, the celebrated result of Fujita & Kato [9] holds true for the surface Navier–Stokes equations.

4.2 Weak Setting

In order to cover the case \(q\ge d\), we proceed as follows. Let \(A_0=\omega +A_{S,\Sigma }\), \(\omega >s(-A_{S,\Sigma })\) and recall that \(X_0=L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )\). By [2, Theorems V.1.5.1 & V.1.5.4], the pair \((X_0,A_0)\) generates an interpolation-extrapolation scale \((X_\alpha ,A_\alpha )\), \(\alpha \in \mathbb {R}\), with respect to the complex interpolation functor. Note that for \(\alpha \in (0,1)\), \(A_\alpha \) is the \(X_\alpha \)-realization of \(A_0\) (the restriction of \(A_0\) to \(X_\alpha \)) and

$$\begin{aligned} X_\alpha = D(A_0^\alpha )=[X_0,X_1]_\alpha =H_{q,\sigma }^{2\alpha }(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

since \(A_0\) admits a bounded \(H^\infty \)-calculus.

Let \(X_0^\sharp :=(X_0)'\) and \(A_0^\sharp :=(A_0)'\) with \(D(A_0^\sharp )=:X_1^\sharp \). Then \((X_0^\sharp ,A_0^\sharp )\) generates an interpolation-extrapolation scale \((X_\alpha ^\sharp ,A_\alpha ^\sharp )\), the dual scale, and by [2, Theorem V.1.5.12], it holds that

$$\begin{aligned} (X_\alpha )'=X^\sharp _{-\alpha }\quad \text {and}\quad (A_\alpha )'=A^\sharp _{-\alpha } \end{aligned}$$

for \(\alpha \in \mathbb {R}\). Choosing \(\alpha =1/2\) in the scale \((X_\alpha ,A_\alpha )\), we obtain an operator

$$\begin{aligned} A_{-1/2}:X_{1/2}\rightarrow X_{-1/2}, \end{aligned}$$

where \(X_{-1/2}=(X_{1/2}^\sharp )'\) (by reflexivity) and, since also \(A_0^\sharp \) has a bounded \(H^\infty \)-calculus,

$$\begin{aligned} X_{1/2}^\sharp = D((A_0^\sharp )^{1/2})=[X_0^\sharp ,X_1^\sharp ]_{1/2} =H_{q',\sigma }^1(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

with \(p'=p/(p-1)\) being the conjugate exponent to \(p\in (1,\infty )\). Moreover, we have \(A_{-1/2}=(A_{1/2}^\sharp )'\) and \(A_{1/2}^\sharp \) is the restriction of \(A_0^\sharp \) to \(X_{1/2}^\sharp \). Thus, the operator \(A_{-1/2}:X_{1/2}\rightarrow X_{-1/2}\) inherits the property of a bounded \(H^\infty \)-calculus with \(H^\infty \)-angle \(\phi _{A_{-1/2}}^\infty <\pi /2\) from the operator \(A_0\).

Since \(A_{-1/2}\) is the closure of \(A_0\) in \(X_{-1/2}\) it follows that \(A_{-1/2}u=A_0u\) for \(u\in X_1=D(A_0)=H_{q,\sigma }^2(\Sigma ,\textsf{T}\Sigma )\) and thus, for all \(v\in X_{1/2}^\sharp \), it holds that

$$\begin{aligned} \langle A_{-1/2}u,v\rangle =(A_0u|v)_{\Sigma }=2\mu _s\int _\Sigma {{\mathcal {D}}}_\Sigma (u):{{\mathcal {D}}}_\Sigma (v)\, d\Sigma +{\omega (u|v)_\Sigma }, \end{aligned}$$

where we made use of the surface divergence theorem. Using that \(X_1\) is dense in \(X_{1/2}\), we obtain the identity

$$\begin{aligned} \langle A_{-1/2}u,v\rangle =2\mu _s\int _\Sigma {{\mathcal {D}}}_\Sigma (u):{{\mathcal {D}}}_\Sigma (v)\, d\Sigma +{\omega (u|v)_\Sigma }, \end{aligned}$$

valid for all \((u,v)\in X_{1/2}\times X_{1/2}^\sharp \). We call the operator \(A_{S,\Sigma }^\textsf{w}:=A_{-1/2}-\omega \) the weak surface Stokes operator, given by its representation

$$\begin{aligned} \langle A_{S,\Sigma }^\textsf{w}u,v\rangle =2\mu _s\int _\Sigma {{\mathcal {D}}}_\Sigma (u):{{\mathcal {D}}}_\Sigma (v)\, d\Sigma ,\quad (u,v)\in X_{1/2}\times X_{1/2}^\sharp . \end{aligned}$$

Multiplying (4.1) by a function \(\phi \in X_{1/2}^\sharp = H_{q',\sigma }^1(\Sigma ,\textsf{T}\Sigma )\) and using the surface divergence theorem, we obtain the weak formulation

$$\begin{aligned} \partial _t u+A_{S,\Sigma }^\textsf{w}u=F_\Sigma ^\textsf{w}(u),\quad u(0)=u_0, \end{aligned}$$
(4.3)

in \(X_{-1/2}\), where

$$\begin{aligned} \langle F_\Sigma ^\textsf{w}(u),\phi \rangle :=(\nabla _u\phi |u)_\Sigma . \end{aligned}$$

Note that u is a solution of (4.3) if and only if u solves

$$\begin{aligned} \partial _t u+\omega u+A_{S,\Sigma }^\textsf{w}u=F_\Sigma ^\textsf{w}(u)+\omega u,\quad u(0)=u_0, \end{aligned}$$
(4.4)

in \(X_{-1/2}\). We will apply Theorem 1.2 in [23] to (4.4) with the choice

$$\begin{aligned} X_0^\textsf{w}=X_{-1/2}\quad \text {and}\quad X_1^\textsf{w}=X_{1/2}. \end{aligned}$$

For that purpose, we will first characterize some relevant interpolation spaces. Let

$$\begin{aligned} \begin{aligned}&H^s_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ):= \left\{ \begin{aligned}&H^s_q(\Sigma ,\textsf{T}\Sigma )\cap L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ),&\qquad 0\le s \le 1,\\&\big (H^{-s}_{q',\sigma }(\Sigma ,\textsf{T}\Sigma )\big )',&\ \ \qquad -1\le s<0, \end{aligned} \right. \\{} & {} \\&B^s_{qp,\sigma }(\Sigma ,\textsf{T}\Sigma ):= \left\{ \begin{aligned}&B^s_{qp}(\Sigma ,\textsf{T}\Sigma )\cap L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ),&\quad 0< s \le 1,\\&(X_0^\textsf{w},X_1^\textsf{w})_{1/2,p},&\quad s=0,\\&\big (B^{-s}_{q'p',\sigma }(\Sigma ,\textsf{T}\Sigma )\big )',&\quad -1\le s<0. \end{aligned} \right. \end{aligned} \end{aligned}$$
(4.5)

By similar arguments as in [26, Section 2.3] we obtain

$$\begin{aligned} \begin{aligned}&[X_{-1/2}, X_{1/2}]_\theta \ \, =\ H^{2\theta -1}_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ),\quad{} & {} \theta \in (0,1), \\&(X_{-1/2}, X_{1/2})_{\theta ,p} = B^{2\theta -1}_{qp,\sigma }(\Sigma ,\textsf{T}\Sigma ),\quad{} & {} \theta \in (0,1) . \\ \end{aligned} \end{aligned}$$
(4.6)

Next we show that the nonlinearity \(F_\Sigma ^\textsf{w}:X_\beta ^\textsf{w} \rightarrow X_{0}^\textsf{w} \) is well defined, where \(X_\beta ^\textsf{w}\) denotes the complex interpolation space, that is, \(X^\textsf{w}_\beta :=[X_0^\textsf{w},X_1^\textsf{w}]_{\beta } \) for \(\beta \in (1/2,1).\) By (4.5), (4.6) and Sobolev embedding, we have

$$\begin{aligned} X_\beta ^\textsf{w} \hookrightarrow H_q^{2\beta -1}(\Sigma ,\textsf{T}\Sigma ) \hookrightarrow L_{2q}(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$
(4.7)

provided that \(2\beta -1\ge \frac{d}{2q}\). From now on, we assume \(2\beta -1=\frac{d}{2q}\), which means \(q>d/2\) as \(\beta <1\). Then, by Hölder’s inequality and (4.7), we obtain

$$\begin{aligned} |\langle F_\Sigma ^\textsf{w}(u),\phi \rangle |\le |u|_{L_{2q}(\Sigma )}^2 |\phi |_{H^1_{q'}(\Sigma )} \le C |u|^2_{X_\beta ^\textsf{w}}\,|\phi |_{H^1_{q'}(\Sigma )}, \end{aligned}$$

showing that

$$\begin{aligned} F_\Sigma ^\textsf{w}: X_\beta ^\textsf{w} \rightarrow X^\textsf{w}_0\quad \text {with}\quad |F_\Sigma ^\textsf{w}(u)|_{X_0^\textsf{w}}\le C |u|^2_{X^\textsf{w}_\beta }. \end{aligned}$$

For \(2\beta -1=d/2q\), the critical weight \(\mu _c\in (1/p,1]\) is given by \(\mu _c:=\mu ^\textsf{w}_c=1/p+d/2q\) and the corresponding critical trace space in the weak setting reads

$$\begin{aligned} X_{\gamma ,\mu _c}^\textsf{w}=(X_0^\textsf{w},X_1^\textsf{w})_{\mu _c-1/p,p}= B_{qp,\sigma }^{d/q-1}(\Sigma ,\textsf{T}\Sigma ). \end{aligned}$$

Note that in case \(q\in (d/2,d)\), the critical spaces in the weak and strong setting coincide.

The existence and uniqueness result for (4.3) in critical spaces reads as follows.

Theorem 4.3

Let \(p\in (1,\infty )\) and \(q\in (d/2,\infty )\) such that \(\frac{2}{p}+\frac{d}{q}\le 2\). Then for any initial value \(u_0\in B_{qp,\sigma }^{d/q-1}(\Sigma ,\textsf{T}\Sigma )\) there exists a unique solution

$$\begin{aligned} u\in H_{p,\mu _c}^1((0,a); H^{-1}_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ) )\cap L_{p,\mu _c}((0,a); H^1_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )) \end{aligned}$$

of (4.3) for some \(a=a(u_0)>0\), with \(\mu _c =1/p+d/2q\). The solution exists on a maximal time interval \([0,t_+(u_0))\) and depends continuously on \(u_0\). Moreover,

$$\begin{aligned} u\in C([0,t_+); B_{qp,\sigma }^{d/q-1}(\Sigma ,\textsf{T}\Sigma )). \end{aligned}$$

Suppose \(p>2\) and \(q\ge d\). Then each solution with \(u_0\in B_{qp,\sigma }^{d/q-1}(\Sigma ,\textsf{T}\Sigma )\) satisfies in addition

$$\begin{aligned} u\in H^1_{p,\textrm{loc}}((0,t^+); L_{q,\sigma }(\Sigma , \textsf{T}\Sigma ))\cap L_{p,\textrm{loc}}((0, t^+); H^2_{q,\sigma }(\Sigma , \textsf{T}\Sigma )). \end{aligned}$$

Hence, in this case, each solution regularizes instantaneously and becomes a strong solution.

Proof

Since \(A_{-1/2}=\omega +A_{S,\Sigma }^\textsf{w}\) admits a bounded \(H^\infty \)-calculus in \(X_{-1/2}\) with \(H^\infty \)-angle \(\phi _{A_{-1/2}}^\infty <\pi /2\), the first assertion follows readily from [23, Theorem 1.2].

Suppose that \(p>2\) and \(q\ge d\). Then \(\mu _c=1/p + d/2q<1\) and [23, Theorem 1.2] yields \(u\in C((0,t_+); B^{1-2/p}_{qp,\sigma } (\Sigma ,\textsf{T}\Sigma )).\) Therefore,

$$\begin{aligned} u(t)\in X_{\gamma ,1}^\textsf{w}=(X_{-1/2},X_{1/2})_{1-1/p,p}=B_{qp,\sigma }^{1-2/p}(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

for \(t\in (0,t_+(u_0))\). Noting that for \(\mu \in (1/p,1/2]\) we have the embedding

$$\begin{aligned} B_{qp,\sigma }^{1-2/p}(\Sigma ,\textsf{T}\Sigma )\hookrightarrow B_{qp,\sigma }^{2\mu -2/p}(\Sigma ,\textsf{T}\Sigma ) \end{aligned}$$

at our disposal, we may now solve (4.1) by [24, Theorem 3.5] with initial value \(u(t_0)\), \(t_0\in (0,t_+(u_0))\), to obtain a strong solution. The assertion of the theorem follows now from uniqueness, see [15, Theorem 3.4(c)]. \(\square \)

Corollary 4.4

Suppose \(d\ge 2\). Then equation (4.3) has for each initial value \(u_0\in L_{d,\sigma }(\Sigma , \textsf{T}\Sigma )\) a unique solution which enjoys the regularity properties of Theorem 4.3 with \(q=d\) for each fixed p with \(p>2\) and \(p\ge d\).

Proof

Suppose \(p>2\) and \(p\ge d\). Then the embedding \( L_{d,\sigma }(\Sigma , \textsf{T}\Sigma )\hookrightarrow B^0_{dp,\sigma }(\Sigma , \textsf{T}\Sigma ) \) holds, see for instance [4, Theorem 6.2.4 and Theorem 6.4.4]. The assertion follows now from Theorem 4.3 with \(q=d\). \(\square \)

We now consider the limiting case \(p=q=d=2\). In this case, we have \(\mu _c =1\) and the corresponding critical trace space is given by

$$\begin{aligned} X_{\gamma ,\mu _c}^\textsf{w}=(X_{-1/2},X_{1/2})_{1/2,2}= [X_{-1/2},X_{1/2}]_{1/2}=L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

see for example [33, Remark 1.18.10.3].

We may now also extend each weak solution to a strong solution. To this end, observe that

$$\begin{aligned} X_{\gamma ,\mu _c}^\textsf{w}=(X_{-1/2},X_{1/2})_{1/2,2}\hookrightarrow (X_{-1/2},X_{1/2})_{1/2,r} \end{aligned}$$

for any \(r\in (2,\infty )\). Then we solve (4.3) by Theorem 4.3 with \(u_0\in (X_{-1/2},X_{1/2})_{1/2,r}\) and \(\mu _c=1/r+1/2\) (choosing \(p=r\) and \(q=d=2\)). This yields

$$\begin{aligned} u\in H_{r,\mu _c}^1((0,a);X_0^\textsf{w})\cap L_{r,\mu _c}((0,a);X_1^\textsf{w}) \end{aligned}$$

with \(X_1^\textsf{w}=H_{2,\sigma }^1(\Sigma ,\textsf{T}\Sigma )\) and \(X_0^\textsf{w}=H^{-1}_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )\). Since now \(u(t)\in B_{2r,\sigma }^{1-2/r}(\Sigma ,\textsf{T}\Sigma )\) for \(t\in (0,a)\), we may argue as above to conclude that the weak solution regularizes to a strong solution

$$\begin{aligned} u\in H^1_{r,\textrm{loc}}((0,a); L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ))\cap L_{r,\textrm{loc}}((0,a); H^2_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )). \end{aligned}$$

Moreover,

$$\begin{aligned} u(t)\in (L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ), H^2_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ))_{1-1/r ,r}=B^{2-2/r}_{2r,\sigma }(\Sigma ,\textsf{T}\Sigma ) \hookrightarrow B^{2\mu -2/p}_{qp,\sigma }(\Sigma ,\textsf{T}\Sigma ) \end{aligned}$$

for \(t\in (0,a)\), provided \(q\ge 2\), \(p\ge r\) and \(2-2/r-d/2 \ge 2\mu -2/p\ - d/q\). For \(d=2\) this means

$$\begin{aligned} \mu \le 1/2 + 1/p + 1/q -1/r. \end{aligned}$$

We now solve (4.1) with initial value \(u(t_0)\in B^{2\mu -2/p}_{qp,\sigma }(\Sigma ,\textsf{T}\Sigma )\) by [24, Theorem 3.5] to obtain a solution

$$\begin{aligned} v \in H^1_{p,\mu }((0,a); L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ))\cap L_{p,\mu }((0,a); H^2_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )). \end{aligned}$$

As in the proof of [15, Theorem 3.4(c)] we conclude that uniqueness holds, that is, \(v(t)=u(t_0 +t)\). As \(t_0\) can be chosen arbitrarily small, this implies that u shares the regularity properties of v for \( t>0\). We have shown the following result.

Theorem 4.5

Let \(d=2\). Then for any \(u_0\in L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )\), problem (4.3) admits a unique solution

$$\begin{aligned} u\in H^1_{2}((0, a), H^{-1}_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ))\cap L_{2}((0, a);H^1_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )) \end{aligned}$$

for some \(a=a(u_0)>0\). The solution exists on a maximal time interval \([0,t^+(u_0))\). In addition, we have

$$\begin{aligned} u\in C([0,t^+); L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )). \end{aligned}$$
(4.8)

Furthermore, each solution satisfies

$$\begin{aligned} u\in H^1_{p,\textrm{loc}}((0, t^+); L_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ))\cap L_{p,\textrm{loc}}((0, t^+) ; H^2_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )) \end{aligned}$$

for any fixed \(q\in (1,\infty )\) and any fixed \(p\in (2,\infty )\). Therefore, any solution with initial value \(u_0\in L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )\) regularizes instantaneously and becomes a strong \(L_p\)-\(L_q\) solution.

Proof

According to the considerations preceding the Theorem, the assertions hold true for a fixed \(q\ge 2\) and \(p\in (2, \infty ).\) The case \(q\in (1,2)\) follows readily from the result in the \(L_2\)-case and the embedding \(L_2(\Sigma ,\textsf{T}\Sigma )\hookrightarrow L_q(\Sigma ,\textsf{T}\Sigma )\). \(\square \)

4.3 Energy Estimates and Global Existence

In [24] we showed that the set of equilibria \({\mathcal {E}}\) for (1.1), respectively (4.1), consists exactly of the Killing vector fields on \(\Sigma \), that is,

$$\begin{aligned} {\mathcal {E}}=\{u\in C^\infty (\Sigma ,\textsf{T}\Sigma )\mid {\mathcal {D}}_\Sigma (u)=0\}. \end{aligned}$$

We recall that the condition \({\mathcal {D}}_\Sigma (u)=0\) implies that u is divergence free (which follows from the relation \(\textrm{div}_\Sigma \,u = \textsf{tr}\,{\mathcal {D}}_\Sigma (u)\)). Moreover, one can show that any vector field \(u\in H^1_q(\Sigma ,\textsf{T}\Sigma )\) satisfying \({\mathcal {D}}_\Sigma (u)=0\) is already smooth, see for instance [19, Lemma 3]. Lastly, we recall that \({\mathcal {E}}\) is a finite dimensional vector space. If fact, \(\textrm{dim}\,{\mathcal {E}}\le d(d+1)/2\), with equal sign for the case where \(\Sigma \) is isometric to a Euclidean sphere, see for instance the remarks in Section 4.1 of [24].

Let us define the space

$$\begin{aligned} V^j_2(\Sigma ):=\{v\in H^j_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ) \mid (v|z)_\Sigma =0\ \text {for all}\ z\in {\mathcal {E}}\},\quad j\in \{0,1\}. \end{aligned}$$
(4.9)

Note that \(V^j_2(\Sigma )\) is a closed subspace of \( H^j_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )\), and hence is a Banach space. Moreover, \(H^j_{2,\sigma }(\Sigma , \textsf{T}\Sigma )={\mathcal {E}} \oplus V^j_2(\Sigma )\), see Remark 4.10(a).

From now on we assume that \(d=2\), and we show that any solution of (4.3) with initial value \(v_0\in L_{2,\sigma }(\Sigma )\) being orthogonal to \({\mathcal {E}}\) will remain orthogonal for all later times. Moreover, we establish an energy estimate for such solutions.

Proposition 4.6

Let \(d=2\). Suppose \(v_0\in V^0_2(\Sigma )\) and let v be the solution of (4.3) established in Theorem 4.5. Then

  1. (a)

    \(v(t)\in V^0_2(\Sigma )\) for \(t\in [0,t^+(v_0))\) and \(v(t)\in V^1_2(\Sigma )\) for \(t\in (0, t^+(v_0)).\)

  2. (b)

    There exists a universal constant \(M>0\) such that

    $$\begin{aligned} |v(t)|^2_{L_2(\Sigma )}+ \int _0^t |v(s)|^2_{H^1_2(\Sigma )}\, ds \le M |v_0|^2_{L_2(\Sigma )}, \quad t\in (0,t^+(v_0)). \end{aligned}$$

Proof

(a) According to Theorem 4.5, we know that

$$\begin{aligned} v\in H^1_{p,\textrm{loc}}((0, t^+); L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ))\cap L_{p,\textrm{loc}}((0, t^+) ; H^2_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )) \end{aligned}$$

for \(p>2\). Pick any \(z\in {\mathcal {E}}\). Then

$$\begin{aligned} \frac{d}{dt} (v(t) | z)_\Sigma =- (\nabla _{v(t)}v(t) | z)_\Sigma - (A_{S,\Sigma } v(t) | z )_\Sigma = -(\nabla _{v(t)}v(t) | z)_\Sigma , \end{aligned}$$

where the time derivative exists for almost all \(t\in (0, t^+(v_0))\). For the last equal sign we employed the property that \(A_{S,\Sigma }\) is symmetric on \(L_{2,\sigma }(\Sigma )\) and \(N(A_{S,\Sigma })={\mathcal {E}}\), see [24, Proposition 4.1]. In a next step we show that

$$\begin{aligned} (\nabla _v v | z )_\Sigma =0\quad \text {for all}\quad v\in H^1_{2,\sigma }(\Sigma ). \end{aligned}$$

Indeed, this follows from

$$\begin{aligned} \begin{aligned} (\nabla _v v | z)_\Sigma&= \int _\Sigma (\nabla _v v | z)\,d\Sigma = \int _\Sigma \big (\nabla _v (v | z)- (v| \nabla _v z)\big )\,d\Sigma \\&= \int _\Sigma \Big ( (v| \textrm{grad}(v | z))- (v| \nabla _v z)\Big )\,d\Sigma = 0, \end{aligned} \end{aligned}$$

where we used (1.5), the surface divergence theorem and the property that z is a Killing vector field, (which implies \((\nabla _v z| v) + (v | \nabla _v z)=0)\). Hence, we have shown that \(\frac{d}{dt} ( v(t)|z )_\Sigma =0\) for almost all \(t\in (0, t^+(v_0))\). (4.8) now implies

$$\begin{aligned} (v(t)| z)_\Sigma =(v_0 | z)_\Sigma =0\quad \text {for all}\quad t\in [0,t^+(v_0)). \end{aligned}$$

(b) Similarly as in part (a), one shows (suppressing the variable t) that

$$\begin{aligned} \begin{aligned} \frac{d}{dt} \frac{1}{2} |v(t)|^2_{L_2(\Sigma )}&=-\int _{\Sigma } \big ( (\nabla _v v|v) + (A_{S,\Sigma } v |v)\big )\,d\Sigma = -2\mu _s\int _{\Sigma } |{\mathcal {D}}_\Sigma (v)|^2\,d\Sigma . \end{aligned} \end{aligned}$$

The assertion in part (a) and Korn’s inequality (A. 2) readily imply

$$\begin{aligned} \frac{d}{dt} |v(t)|^2_{L_2(\Sigma )} + \alpha \, |v(t)|^2_{H^1_2(\Sigma )}\le 0,\quad t\in (0, t^+(v_0)), \end{aligned}$$
(4.10)

with an appropriate constant \(\alpha >0\). Integration yields the assertion in (b), as \(|v|^2_{L_2(\Sigma )}\) is absolutely continuous on \([0,t^+(v_0))\). \(\square \)

Proposition 4.7

Suppose that \(d=2\) and \(v_0\in V^0_2(\Sigma )\).

Then problem (4.3) admits a unique global solution v enjoying the regularity properties stated in Theorem (4.5), with \(t^+(v_0)=\infty \).

Moreover, there exists a constant \(\alpha >0\) such that

$$\begin{aligned} |v(t)|_{L_2(\Sigma )} \le e^{-\alpha t} |v_0|_{L_2(\Sigma )}, \quad t\ge 0. \end{aligned}$$
(4.11)

Proof

By the abstract result [23, Theorem 2.4] on global-in-time existence, the maximal time of existence \(t_+(u_0)\) satisfies the following property:

$$\begin{aligned} t_+(u_0)<\infty \Longrightarrow u\notin L_p((0,t_+);[X_0^\textsf{w},X_1^\textsf{w}]_{\mu _c}). \end{aligned}$$

Observe that in case \(p=q=d=2\), it holds \(\mu _c=1/p+d/(2q)=1\), hence if

$$\begin{aligned} u\in L_2((0,t_+);H_2^1(\Sigma ,\textsf{T}\Sigma )), \end{aligned}$$

then the weak solution exists globally in time. Proposition 4.6 guarantees that any solution v with initial value \(v_0\in V^0_2(\Sigma )\) satisfies

$$\begin{aligned} v\in L_2((0,t^+(v_0)), H^1_2(\Sigma ,\textsf{T}\Sigma )) \end{aligned}$$

and, hence, global existence of the weak solution follows. Since we know that the weak solution in this case regularizes to a strong solution, we obtain global in time existence of strong solutions for \(q=d=2\) as well.

Finally, we conclude from (4.10) that \( \frac{d}{dt} |v(t)|^2_{L_2(\Sigma )} + \alpha \, |v(t)|^2_{L_2(\Sigma )}\le 0\) for any \(t>0\) and this implies the estimate in (4.11). \(\square \)

Remark 4.8

Suppose \(u_*\in {\mathcal {E}}\) and \(v_0\in V^0_2(\Sigma )\). Then the assertions of Theorem 4.1, Theorem 4.5 as well as Propositions 4.6 and 4.7 hold true for solutions of

$$\begin{aligned} \partial _t v + A_{S,\Sigma }v = -P_{H,\Sigma }(\nabla _v v + \nabla _{u_*}v + \nabla _v u_*),\quad v(0)=v_0, \end{aligned}$$
(4.12)

respectively its weak formulation

$$\begin{aligned} \partial _t v + A^\textsf{w}_{S,\Sigma }v = F^\textsf{w}_\Sigma (v), \quad v(0)=v_0, \end{aligned}$$
(4.13)

where \(\langle F^\textsf{w}_\Sigma (v),\phi \rangle = ( v | \nabla _v \phi )_\Sigma + (v| \nabla _{u_*}\phi )_\Sigma + (u_* | \nabla _v \phi )_\Sigma \) for \(\phi \in H^1_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )\).

In particular, each solution of(4.13) with initial value \(v_0\in V^0_2(\Sigma )\) exists globally and there exists a positive constant \(\alpha \) such that

$$\begin{aligned} |v(t)|_{L_2(\Sigma )} \le e^{-\alpha t} |v_0|_{L_2(\Sigma )}, \quad t\ge 0. \end{aligned}$$

Proof

One readily verifies that the assertions of Theorems 4.1 and 4.5 remain valid for problem (4.12) and (4.13), respectively. In fact, one only needs to verify that the terms on the right hand side can be estimated in the same way as in the proof of Theorems 4.1 and 4.5.

Next we show that \(v(t)\in V^0_2(\Sigma )\) for \(t\in [0,t^+(v_0))\). Let \(z\in {\mathcal {E}}\). Following the proof of Proposition 4.6(a), we obtain

$$\begin{aligned} \frac{d}{dt} (v(t) | z)_\Sigma = -(\nabla _{v(t)}v(t)+\nabla _{u_*}v(t) + \nabla _{v(t)}u_* | z)_\Sigma , \quad t\in (0,t^+(v_0)). \end{aligned}$$

According to the proof of Proposition 4.6(a), \((\nabla _v v|z)=0\) and it remains to show that \((\nabla _{u_*}v+ \nabla _{v}u_* | z)_\Sigma =0\) for any \(v\in H^1_{2,\sigma }(\Sigma , \textsf{T}\Sigma ).\) This follows from

$$\begin{aligned} \begin{aligned} (\nabla _{u_*} v + \nabla _v u_*| z)_\Sigma&= \int _\Sigma \big (\nabla _{u_*} (v | z)+\nabla _v(u_*|z)- (u_*| \nabla _v z)-(v| \nabla _{u_*} z)\big )=0 \end{aligned} \end{aligned}$$

where we used (1.5), the surface divergence theorem and the property that z is a Killing vector field. The same arguments as in the proof of Propositions 4.6 and 4.7 yield the remaining assertions. \(\square \)

Theorem 4.9

(Global existence). Suppose \(d=2\).

Then any solution of (4.3) with initial value \(u_0\in L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )\) exists globally, has the regularity properties listed in Theorem 4.5, and converges at an exponential rate to the equilibrium \(u_* = P_{{{\mathcal {E}}}} u_0\) in the topology of \(H_q^{2}(\Sigma ,\textsf{T}\Sigma )\) for any fixed \(q\in (1,\infty )\), where \(P_{{{\mathcal {E}}}}\) is the orthogonal projection of \(u_0\) onto \({{\mathcal {E}}}\) with respect to the \(L_2(\Sigma , \textsf{T}\Sigma )\) inner product.

Proof

Let \(u_0\in L_{2,\sigma }(\Sigma ,\textsf{T}\Sigma )\) be given. Then there exist unique elements \(u_*\in {\mathcal {E}}\) and \(v_0\in V^0_2(\Sigma )\) such that \(u_0=u_*+v_0 \). Let v be the unique (global) solution of problem  (4.13), respectively (4.12), whose existence has been asserted in Remark 4.8 Then

$$\begin{aligned} u(t):=u_* + v(t),\quad t>0, \end{aligned}$$

yields a (unique) global solution of (4.1), respectively (4.3), with initial value \(u_0\). For this, we just need to observe that

$$\begin{aligned} \partial _t u_* + A_{S,\Sigma } u_* = - P_{H,\Sigma } \nabla _{u_*} u_*. \end{aligned}$$

Indeed, this follows from the relations \(N(A_{S,\Sigma })={\mathcal {E}}\) and \(\nabla _{u_*}u_*=\frac{1}{2} \textrm{grad}(u_* | u_*)\), with the latter assertion implying \(P_{H,\Sigma } \nabla _{u_*} u_*=0\). It follows readily that \(u(t)\rightarrow u_*\) as \(t\rightarrow \infty \) at an exponential rate in \(L_2(\Sigma ,\textsf{T}\Sigma )\). To prove convergence in the stronger topology \(H_q^{2}(\Sigma ,\textsf{T}\Sigma )\), we proceed as follows.

(i) First, we note that \(L_2(\Sigma ,\textsf{T}\Sigma )\hookrightarrow B_{2r}^0(\Sigma ,\textsf{T}\Sigma )\) for any fixed \(r\ge 2\). For fixed, but arbitrary \(t_1>0\), we solve (4.3) with initial value \(u_1:=u(t_1)\in B_{2r,\sigma }^0(\Sigma ,\textsf{T}\Sigma )\). Choosing \(\mu _c=1/r+1/2\), it follows from [23, Theorem 1.2] that there exist positive numbers \(\tau =\tau (u_*)\), \(\varepsilon =\varepsilon (u_*)\) and \(C_1=C_1(u_*)\) such that

$$\begin{aligned} |u(\cdot , {\hat{u}}_1) - u(\cdot , u_*)|_{{\mathbb E}_{1,\mu _c}(0,2\tau )}\le C_1 |{\hat{u}}_1-u_*|_{B_{2r,\sigma }^0(\Sigma )} \end{aligned}$$
(4.14)

for all \({\hat{u}}_1\in B_{2r,\sigma }^0(\Sigma ,\textsf{T}\Sigma )\) with \(|{\hat{u}}_1-u_*|_{B_{2r,\sigma }^0(\Sigma )}<\varepsilon ,\) where

$$\begin{aligned} {\mathbb E}_{1,\mu _c}(0,2\tau ) =H_{r,\mu _c}^1((0,2\tau );H_{2,\sigma }^{-1}(\Sigma ,\textsf{T}\Sigma ))\cap L_{r,\mu _c}((0,2\tau );H_{2,\sigma }^{1}(\Sigma ,\textsf{T}\Sigma )). \end{aligned}$$

It should be observed here that \(u(t, u_*)=u_*\), as \(u_*\) is an equilibrium.

By following the arguments in [22, page 228] and employing

$$\begin{aligned} X^\textsf{w}_\gamma = (X^\textsf{w}_0, X^\textsf{w}_1)_{1-1/r,r}= (H^{-1}_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ), H^{1}_{2,\sigma }(\Sigma ,\textsf{T}\Sigma ))_{1-1/r, r}=B^{1-2/r}_{2r,\sigma }(\Sigma , \textsf{T}\Sigma ), \end{aligned}$$

see (4.6), we conclude with (4.14) that there is a constant \(C_2=C_2(u_*)\) such that

$$\begin{aligned} |u(\cdot , {\hat{u}}_1) - u(\cdot , u_*)|_{C([\tau ,2\tau ], B^{1-2/r}_{2r,\sigma }(\Sigma ))}\le C_2 |{\hat{u}}_1 -u_*|_{B_{2r}^0(\Sigma )}. \end{aligned}$$

Letting \(C_3\) be the embedding constant of \(L_2(\Sigma ,\textsf{T}\Sigma )\hookrightarrow B^0_{2r}(\Sigma ,\textsf{T}\Sigma )\) we choose \(t_1\) large enough such that \(|u(t_1)-u_*|_{L_2(\Sigma )}<\varepsilon /C_3\). Setting \(t_2=\tau \), we may deduce from the estimates above that

$$\begin{aligned} |u(t_2,u_1)-u_*|_{B_{2r}^{1-2/r}(\Sigma )}\le C|u_1-u_*|_{L_{2}(\Sigma )}, \end{aligned}$$
(4.15)

with \(C=C(u_*)=C_2C_3 \). Here we have also used the uniqueness of solutions, cf. [15, Theorem 3.4(c)].

(ii) For fixed, but arbitrary \(r>2\), we now choose a weight \(\mu \in (\frac{1}{r},\frac{1}{2}]\) so that

$$\begin{aligned} B_{2r}^{1-2/r}(\Sigma ,\textsf{T}\Sigma )\hookrightarrow B_{2r}^{2\mu -2/r}(\Sigma ,\textsf{T}\Sigma ). \end{aligned}$$

Solving (4.1) with initial value \(u_2:=u(t_2,u_1)\in B_{2r,\sigma }^{2\mu -2/r}(\Sigma ,\textsf{T}\Sigma )\) and repeating the above procedure in the ‘strong’ spaces \((X_0,X_1)\), we obtain the estimate

$$\begin{aligned} |u(t_3,u_2)-u_*|_{B_{2r}^{2-2/r}(\Sigma )}\le C|u_2-u_*|_{B_{2r}^{1-2/r}(\Sigma )}, \end{aligned}$$
(4.16)

for some \(t_3=t_3(u_*)>0\).

(iii) Next, we use the Sobolev embedding

$$\begin{aligned} B_{2r}^{2-2/r}(\Sigma ,\textsf{T}\Sigma )\hookrightarrow B_{sr}^{2\mu -2/r}(\Sigma ,\textsf{T}\Sigma ), \end{aligned}$$

valid for \(s\ge 2\) and \(\mu \in (\frac{1}{r},\frac{1}{2}+\frac{1}{s}]\). Choosing \(t_1>0\) from above sufficiently large, we infer from (4.16) that \(u(t_3,u_2)\) is close to \(u_*\) in the topology of \(B_{sr}^{2\mu -2/r}(\Sigma ,\textsf{T}\Sigma )\). Solving (4.1) with initial value \(u_3:=u(t_3,u_2)\in B_{sr,\sigma }^{2\mu -2/r}(\Sigma ,\textsf{T}\Sigma )\) and repeating the above procedure in the ‘strong’ spaces \((X_0,X_1)\), we obtain the estimate

$$\begin{aligned} |u(t_4,u_3)-u_*|_{B_{sr}^{2-2/r}(\Sigma )}\le C|u_3-u_*|_{B_{2r}^{2-2/r}(\Sigma )}, \end{aligned}$$
(4.17)

for some \(t_4=t_4(u_*)>0\).

(iv) We will now consider (4.1) in the spaces

$$\begin{aligned} (X_{1/2}, X_{1+1/2})= (H^1_{s,\sigma }(\Sigma , \textsf{T} \Sigma ), H^3_{s,\sigma }(\Sigma , \textsf{T} \Sigma )), \end{aligned}$$

where \((X_\alpha , A_\alpha )\) is the interpolation-extrapolation scale with respect to the complex interpolation functor, based on \(X_0=L_{s,\sigma }(\Sigma , \textsf{T}\Sigma )\), \(s\in (1,\infty )\), introduced at the beginning of Section 4.2. We note that \(A_{1/2}\), the realization of \(A_0=\omega + A_{S,\Sigma }\) in \(X_{1/2}\), has exactly the same properties as \(A_0\). For \(\beta =1/2\) we obtain

$$\begin{aligned}{}[X_{1/2}, X_{1+1/2}]_{\beta }=[H^1_{s,\sigma }(\Sigma , \textsf{T} \Sigma ), H^3_{s,\sigma }(\Sigma , \textsf{T} \Sigma )]_{1/2}=H^2_{s,\sigma }(\Sigma , \textsf{T} \Sigma ). \end{aligned}$$

It is easy to see that the nonlinearity

$$\begin{aligned} F_\Sigma : H^2_{s,\sigma }(\Sigma , \textsf{T}\Sigma )\times H^2_{s,\sigma }(\Sigma , \textsf{T}\Sigma ) \rightarrow H^1_{s,\sigma }(\Sigma , \textsf{T}\Sigma ) \end{aligned}$$

is bilinear and bounded. We can employ [23, Theorem 1.2 or 2.1] for problem (4.1) to obtain a solution \(u(\cdot , u_4)\) with initial value \(u_4=u(t_4,u_3)\in B_{sr}^{2-2/r}(\Sigma ,\textsf{T}\Sigma ).\) To do so, we choose \(\mu =1/2\) and verify that

$$\begin{aligned} \begin{aligned} X_{\gamma ,\mu }:&=(X_{1/2}, X_{1+1/2})_{1/2-1/r,r}=B^{2-2/r}_{sr,\sigma }(\Sigma , \textsf{T}\Sigma ), \\ X_{\gamma ,1}:&=(X_{1/2}, X_{1+1/2})_{1-1/r,r}=B^{3-2/r}_{sr,\sigma }(\Sigma , \textsf{T}\Sigma ). \end{aligned} \end{aligned}$$

Noting that the numbers \(\mu =1/2\) and \(\beta =1/2\) satisfy the assumptions of [23] Theorem 1.2 or 2.1, we can once more repeat the procedure outlined in step (i) to obtain

$$\begin{aligned} |u(t_5,u_4)-u_*|_{B_{sr}^{3-2/r}(\Sigma )}\le C|u_4-u_*|_{B_{sr}^{2-2/r}(\Sigma )}, \end{aligned}$$
(4.18)

for some \(t_5=t_5(u_*)>0\), provided \(t_1\) is chosen sufficiently large. Combining the estimates (4.15)–(4.18) and using the semiflow property, we obtain the estimate

$$\begin{aligned} |u(t_5+t_4+ t_3+t_2+t_1,u_0)-u_*|_{B_{sr}^{3-2/r}(\Sigma )}\le C|u(t_1,u_0)-u_*|_{L_2(\Sigma )}. \end{aligned}$$

Since \(|u(t_1,u_0)-u_*|_{L_2(\Sigma )}\rightarrow 0\) at an exponential rate as \(t_1\rightarrow \infty \), we conclude that \(u(t,u_0)\) converges to \(u_*\) at an exponential rate in the topology of \(B^{3-2/r}_{sr,\sigma }(\Sigma , \textsf{T} \Sigma )\) as well, as \(t\rightarrow \infty \).

(iv) Finally, given \(q\in (1,\infty )\), the embedding \(B_{sr,\sigma }^{3-2/r}(\Sigma ,\textsf{T}\Sigma )\hookrightarrow H_{q,\sigma }^{2}(\Sigma ,\textsf{T}\Sigma ),\) being valid for sufficiently large parameters s and r, yields the last assertion of the theorem. \(\square \)

Remarks 4.10

(a) Let \(d\ge 2\) and let \({{\mathfrak {F}}}^s(\Sigma )\) denote any of the spaces

$$\begin{aligned} H^s_{q,\sigma }(\Sigma , \textsf{T}\Sigma ),\ B^s_{qp,\sigma }(\Sigma ,\textsf{T}\Sigma ), \quad \text {where }s\in {\mathbb R},\ 1<p,q<\infty . \end{aligned}$$

Then we have

$$\begin{aligned} {{\mathfrak {F}}}^s(\Sigma ) = {{\mathcal {E}}}\oplus \{v\in {{\mathfrak {F}}}^s(\Sigma ): \langle v, z\rangle _\Sigma =0, \ z\in {{\mathcal {E}}}\}. \end{aligned}$$
(4.19)

Here, \(\langle v, z \rangle _\Sigma : = (v|z)_\Sigma \) if \(s>0\). In case \(s\le 0\),

$$\begin{aligned} \langle \cdot , \cdot \rangle _\Sigma : {{\mathfrak {F}}}^{s} (\Sigma ) \times ({{\mathfrak {F}}}^\prime )^{-s}(\Sigma ) \rightarrow {\mathbb R}\end{aligned}$$

denotes the duality pairing, induced by \((\cdot | \cdot )_\Sigma \), where

$$\begin{aligned} ({{\mathfrak {F}}}^\prime )^s(\Sigma )\in \{H^s_{q',\sigma }(\Sigma ,\textsf{T}\Sigma ), B^s_{q'p',\sigma }(\Sigma ,\textsf{T}\Sigma )\}. \end{aligned}$$

Since we can identify \({{\mathcal {E}}}\subset C^\infty (\Sigma , \textsf{T}\Sigma )\) as a subspace of \({{\mathfrak {F}}}^s(\Sigma )\), the expression \(\langle v, z \rangle _\Sigma \) is defined for every \((v,z)\in {{\mathfrak {F}}}^s(\Sigma )\times {{\mathcal {E}}}\) and (4.19) is, therefore, meaningful.

Proof

We will provide a proof of (4.19). As \({{\mathcal {E}}}\) is finite dimensional, we can find a basis \(\{z_1,\ldots , z_m\}\) for \({{\mathcal {E}}}\) which has the property that \((z_i | z_j)_\Sigma =\delta _{ij}\). With this at hand, we define the projection

$$\begin{aligned} P^s_{{\mathcal {E}}}: {{\mathfrak {F}}}^s(\Sigma ) \rightarrow {{\mathcal {E}}}, \quad P^s_{{\mathcal {E}}}v:= \sum _{j=1}^m \langle v , z_j \rangle z_j, \end{aligned}$$
(4.20)

onto \({{\mathcal {E}}}\). This yields the direct topological decomposition \({{\mathfrak {F}}}^s(\Sigma )= {{\mathcal {E}}}\oplus V^s(\Sigma )\), where \( V^s(\Sigma )= (I-P^s_{{\mathcal {E}}}) {{\mathfrak {F}}}^s(\Sigma ).\) In order to justify (4.19), it suffices to show that

$$\begin{aligned} V^s(\Sigma ) ={\hat{V}}^s(\Sigma ):=\{v\in {{\mathfrak {F}}}^s(\Sigma ) \mid \langle v, z\rangle _\Sigma =0, \ z\in {{\mathcal {E}}}\}. \end{aligned}$$

Suppose \(v\in V^s(\Sigma )\). Then \(v=(I-P^s_{{\mathcal {E}}})v\) and we obtain

$$\begin{aligned} \langle v, z_j \rangle _\Sigma = \langle (I-P^s_{{\mathcal {E}}})v, z_j \rangle _\Sigma = \langle v, z_j \rangle _\Sigma -\langle P^s_{{\mathcal {E}}}v, z_j \rangle _\Sigma =0,\quad j=1,\ldots , m, \end{aligned}$$

showing that \(v\in {\hat{V}}^s(\Sigma ).\) Suppose now that \(v \in {\hat{V}}^s(\Sigma )\). Since \({{\mathfrak {F}}}^s(\Sigma )= {{\mathcal {E}}}\oplus V^s(\Sigma )\), there are unique elements \((z,w)\in {{\mathcal {E}}}\times V^s(\Sigma )\) such that \(v=z+w\). Then, by the first step,

$$\begin{aligned} 0=\langle v, z \rangle _\Sigma = \langle z+w, z \rangle _\Sigma =\langle z,z \rangle _\Sigma = |z|^2_{L_2(\Sigma )}, \end{aligned}$$

hence \(z=0\) and therefore \(v=w\in V^s(\Sigma )\). \(\square \)

(b) It is interesting to note that the assertions of Propositions 4.6 and 4.7 remain valid in case \(d>2\), with the following modifications:

Let \(p>2\) and \(q\ge d > 2\). Suppose \(v_0\in B^{d/q-1}_{qp,\sigma }(\Sigma , \textsf{T}\Sigma ) \) satisfies \(\langle v_0, z\rangle _\Sigma =0\) for every \(z\in {\mathcal {E}}\), where \(\langle v_0, z\rangle _\Sigma \) has the same meaning as in (a). Let v be the unique solution of (4.3) with initial value \(v_0\).

Then there exists a constant \(\alpha >0\) such that

$$\begin{aligned} |v(t)|_{L_2(\Sigma )}\le e^{-\alpha (t-\tau )} |v(\tau )|_{L_2(\Sigma )},\quad t\in [\tau ,t^+(v_0)), \end{aligned}$$
(4.21)

for fixed \(\tau \in [0,t^+(v_0))\), where \(\tau \in (0 ,t^+(v_0))\) in case \(v_0\notin L_{2,\sigma }(\Sigma , \textsf{T}\Sigma )\).

Proof

According to Theorem 4.3, there exists a unique solution v to problem (4.3) with regularity

$$\begin{aligned} \begin{aligned} v&\in H_{p,\mu _c}^1((0,a); H^{-1}_{q,\sigma }(\Sigma ,\textsf{T}\Sigma ))\cap L_{p,\mu _c}((0,a); H^1_{q,\sigma }(\Sigma ,\textsf{T}\Sigma )) \\&\cap H^1_{p,\textrm{loc}}((0,t^+); L_{q,\sigma }(\Sigma , \textsf{T}\Sigma ))\cap L_{p,\textrm{loc}}((0, t^+); H^2_{q,\sigma }(\Sigma , \textsf{T}\Sigma )) \end{aligned} \end{aligned}$$
(4.22)

for each fixed \(a\in (0, t^+)\). For \(z\in {{\mathcal {E}}}\) we obtain, as in the proof of Theorem 4.6,

$$\begin{aligned} \frac{d}{dt} \langle v(t) , z\rangle _\Sigma =- (\nabla _{v(t)}v(t)| z)_\Sigma - (A_{S,\Sigma } v(t) | z )_\Sigma = -(\nabla _{v(t)}v(t) | z)_\Sigma =0, \end{aligned}$$

for all \(t\in (0 ,t^+(v_0))\). Therefore, \(\langle v(\cdot ), z\rangle _\Sigma \in H^1_{p,\mu _c}(0, a)\) and \(\frac{d}{dt} \langle v(t) | z\rangle _\Sigma =0\) for \(t\in (0,t^+(v_0))\). By [21, Lemma 2.1(b)], or [22, Lemma 3.2.5(b)], we infer that \(\langle v(\cdot ), z\rangle _\Sigma \in H^1_{1,\textrm{loc}}([0, a])\) for any fixed \(a\in (0, t^+(v_0))\). We can now conclude from the fundamental theorem that

$$\begin{aligned} \langle v(t), z\rangle _\Sigma =0,\quad t\in [0, t^+(v_0)). \end{aligned}$$
(4.23)

Let \(\tau \in (0,t^+(v_0))\) be fixed. As \(p,q>2\), we conclude from (4.22) and (4.23) that \(v(t)\in V^1_2(\Sigma )=\{u\in H^1_2(\Sigma , \textsf{T}\Sigma )\mid (u |z)_\Sigma =0,\ z\in {{\mathcal {E}}}\}\) for any \(t\in [\tau ,t^+(v_0))\). Hence, Korn’s inequality (A. 2) holds true for v(t) with \(t\in [\tau , t^+(v_0))\), and we can now follow the proof of Propositions 4.6(b) and 4.7 to obtain the assertion in (4.21). \(\square \)

(c) Suppose \(d>2\) and \(q\ge d\). Then (4.21) holds true with \(\tau =0\) for initial values \(v_0\in B^{2\mu -2/p}_{qp,\sigma }(\Sigma , \textsf{T}\Sigma )\) satisfying the assumptions of [24, Theorem 3.5(b)] and \((v_0 | z)_\Sigma =0\) for all \(z\in {{\mathcal {E}}}\).

(d) Suppose \(p>2\) and \(q\ge d>2\). Then every global solution of (4.3), respectively (4.1), converges exponentially fast to an equilibrium, namely to \(P_{{\mathcal {E}}}u_0\) (where \(P_{{\mathcal {E}}}\) is the projection defined in (4.20)), provided the initial value \(u_0\) satisfies the assumptions of Theorem 4.3 or [24, Theorem 3.5(b)].

Proof

This follows by similar arguments as in the proof of Remark 4.8 and Theorem 4.9. \(\square \)

(e) According to Theorem 4.3 in [24], any solution with initial value \(u_0\) sufficiently close to an equilibrium exists globally and, hence, converges to \(P_{{\mathcal {E}}}u_0\) at an exponential rate.