Skip to main content
SpringerLink
Log in

Denjoy–Wolff Points on the Bidisk via Models

  • Published:
Integral Equations and Operator Theory Aims and scope Submit manuscript

Abstract

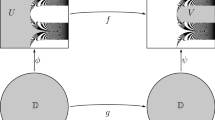
Let \(F=(\phi , \psi ):\mathbb {D}^2\rightarrow \mathbb {D}^2\) denote a holomorphic self-map of the bidisk without interior fixed points. It is well-known that, unlike the case with self-maps of the disk, the sequence of iterates

$$\begin{aligned} \{F^n:=F\circ F\circ \cdots \circ F\} \end{aligned}$$

needn’t converge. The cluster set of \(\{F^n\}\) was described in a classical 1954 paper of Hervé. Motivated by Hervé’s work and the Hilbert space perspective of Agler, McCarthy and Young on boundary regularity, we propose a new approach to boundary points of Denjoy–Wolff type for the coordinate maps \(\phi , \psi .\) We establish several equivalent descriptions of our Denjoy–Wolff points, some of which only involve checking specific directional derivatives and are particularly convenient for applications. Using these tools, we are able to refine Hervé’s theorem and show that, under the extra assumption of \(\phi \) and \(\psi \) possessing Denjoy–Wolff points with certain regularity properties, one can draw much stronger conclusions regarding the behavior of \(\{F^n\}.\)

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abate, M.: Horospheres and iterates of holomorphic maps. Math. Z. 198(2), 225–238 (1988)

    Article  MathSciNet  Google Scholar 

  2. Abate, M.: Iteration theory of holomorphic maps on taut manifolds. Research and Lecture Notes in Mathematics. Complex Analysis and Geometry. Mediterranean Press, Rende, pp. xvii+417 (1989)

  3. Abate, M.: The Julia–Wolff–Carathéodory theorem in polydisks. J. Anal. Math. 74, 275–306 (1998)

    Article  MathSciNet  Google Scholar 

  4. Abate, M., Raissy, J.: Wolff-Denjoy theorems in nonsmooth convex domains. Ann. Mat. Pura Appl. (4) 193(5), 1503–1518 (2014)

    Article  MathSciNet  Google Scholar 

  5. Agler, J., Tully-Doyle, R., Young, N.J.: Boundary behavior of analytic functions of two variables via generalized models. Indag. Math. (N.S.) 23(4), 995–1027 (2012)

    Article  MathSciNet  Google Scholar 

  6. Agler, J., McCarthy, J.E.: Pick interpolation and Hilbert function spaces. Vol. 44. Graduate Studies in Mathematics, pp. xx+308. American Mathematical Society, Providence (2002)

  7. Agler, J., McCarthy, J.E., Young, N.J.: A Carathéodory theorem for the bidisk via Hilbert space methods. Math. Ann. 352(3), 581–624 (2012)

    Article  MathSciNet  Google Scholar 

  8. Agler, J., McCarthy, J.E., Young, N.J.: Facial behaviour of analytic functions on the bidisc. Bull. Lond. Math. Soc. 43(3), 478–494 (2011)

    Article  MathSciNet  Google Scholar 

  9. Agler, J., McCarthy, J.E., Young, N.: Operator analysis—Hilbert space methods in complex analysis. Vol. 219. Cambridge Tracts in Mathematics, pp. xv+375. Cambridge University Press, Cambridge (2020)

  10. Arosio, L., Gumenyuk, P.: Valiron and Abel equations for holomorphic self-maps of the polydisc. Int. J. Math. 27(4), 1650034 (2016)

    Article  MathSciNet  Google Scholar 

  11. Budzyńska, M.: The Denjoy–Wolff theorem for condensing mappings in a bounded and strictly convex domain in a complex Banach space. Ann. Acad. Sci. Fenn. Math. 39(2), 919–940 (2014)

    Article  MathSciNet  Google Scholar 

  12. Budzyńska, M.: The Denjoy–Wolff theorem in Cn. Nonlinear Anal. 75(1), 22–29 (2012)

    Article  MathSciNet  Google Scholar 

  13. Budzyńska, M., Kuczumow, T., Reich, S.: Theorems of Denjoy–Wolff type. Ann. Mat. Pura Appl. (4) 192(4), 621–648 (2013)

    Article  MathSciNet  Google Scholar 

  14. Burckel, R.B.: Iterating analytic self-maps of discs. Am. Math. Mon. 88(6), 396–407 (1981)

    Article  MathSciNet  Google Scholar 

  15. Caratheodory, C.: Theory of functions of a complex variable, vol. 2, p. 220. Translated by F. Steinhardt. Chelsea Publishing Co., New York (1954)

  16. Chu, C.-H., Rigby, M.: Horoballs and iteration of holomorphic maps on bounded symmetric domains. Adv. Math. 311, 338–377 (2017)

    Article  MathSciNet  Google Scholar 

  17. Chu, C.-H., Rigby, M.: Iteration of self-maps on a product of Hilbert balls. J. Math. Anal. Appl. 411(2), 773–786 (2014)

    Article  MathSciNet  Google Scholar 

  18. Denjoy, A.: Sur l’itération des fonctions analytiques. C. R. Acad. Sci. Paris 182, 255–257 (1926)

    Google Scholar 

  19. Earle, C.J., Hamilton, R.S.: A fixed point theorem for holomorphic mappings. Global Analysis (Proc. Sympos. Pure Math., Vols. XIV, XV, XVI, Berkeley, Calif., 1968), pp. 61–65. Amer. Math. Soc., Providence (1970)

  20. Frosini, C.: Busemann functions and the Julia–Wolff–Carathéodory theorem for polydiscs. Adv. Geom. 10(3), 435–463 (2010)

    Article  MathSciNet  Google Scholar 

  21. Frosini, C.: Dynamics in the complex bidisc (2004). arXiv:math/04020

  22. Frosini, C.: Dynamics on bounded domains. The p-harmonic equa- tion and recent advances in analysis. Vol. 370. Contemp. Math., pp. 99–117. Amer. Math. Soc., Providence (2005)

  23. Hervé, M.: Itération des transformations analytiques dans le bicercleunit é. Ann. Sci. Ecole Norm. Sup. (3) 71 (1954)

  24. Hervé, M.: Quelques propriétés des applications analytiques d’une boule à m dimensions dan elle-même. J. Math. Pures Appl. (9) 42, 117–147 (1963)

    MathSciNet  Google Scholar 

  25. Julia, G.: Extension nouvelle d’un lemme de Schwarz. Acta Math. 42(1), 349–355 (1920)

    Article  MathSciNet  Google Scholar 

  26. Khanh, T.V., Thu, N.V.: Iterates of holomorphic self-maps on pseudoconvex domains of finite and infinite type in Cn. Proc. Am. Math. Soc. 144(12), 5197–5206 (2016)

    Article  Google Scholar 

  27. MacCluer, B.D.: Iterates of holomorphic self-maps of the unit ball in CN. Mich. Math. J. 30(1), 97–106 (1983)

    Article  MathSciNet  Google Scholar 

  28. McCarthy, J.E., Pascoe, J.E.: The Julia–Carathéodory theorem on the bidisk revisited. Acta Sci. Math. (Szeged) 83(1–2), 165–175 (2017)

    Article  MathSciNet  Google Scholar 

  29. Mellon, P.: A Wolff theorem for finite rank bounded symmetric domains. J. Math. Anal. Appl. 456(1), 57–68 (2017)

    Article  MathSciNet  Google Scholar 

  30. Mellon, P.: Denjoy–Wolff theory for finite-dimensional bounded symmetric domains. Ann. Mat. Pura Appl. (4) 195(3), 845–855 (2016)

    Article  MathSciNet  Google Scholar 

  31. Nowell, J.: Denjoy–Wolff sets for analytic maps on the polydisk. Ph.D. Thesis, University of Florida (2019)

  32. Sarason, D.: Sub-Hardy Hilbert spaces in the unit disk. Vol. 10. University of Arkansas Lecture Notes in the Mathematical Sciences. AWiley-Interscience Publication, pp. xvi+95. Wiley, New York (1994)

  33. Shapiro, J.H.: Composition Operators and Classical Function Theory. Universitext: Tracts in Mathematics, pp. xvi+223. Springer, New York (1993)

  34. Sola, A., Tully-Doyle, R.: Dynamics of low-degree rational inner skew-products on T2. Ann. Polon. Math. 128(3), 249–273 (2022)

    Article  MathSciNet  Google Scholar 

  35. Wlodarczyk, K.: Julia’s lemma and Wolff’s theorem for J-algebras. Proc. Am. Math. Soc. 99(3), 472–476 (1987)

    MathSciNet  Google Scholar 

  36. Wolff, J.: Sur l’itération des fonctions bornées. C. R. Acad. Sci. Paris 182, 200–201 (1926)

    Google Scholar 

  37. Wolff, J.: Sur l’itération des fonctions holomorphes dans une région, et dont les valeurs appartiennent à cette r égion. C. R. Acad. Sci. Paris 182, 42–43 (1926)

    Google Scholar 

  38. Wolff, J.: Sur une généralisation d’un théorème de Schwarz. C. R. Acad. Sci. Paris 182, 918–920 (1926)

    Google Scholar 

Download references

Acknowledgements

The second author would like to thank John McCarthy and Greg Knese for helpful suggestions.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Florida, Gainesville, FL, USA

    Michael T. Jury

  2. Department of Mathematics and Statistics, Washington University in St. Louis, St. Louis, MO, USA

    Georgios Tsikalas

Authors
  1. Michael T. Jury
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Georgios Tsikalas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Georgios Tsikalas.

Ethics declarations

Conflict of interest

The authors have no competing interests to declare that are relevant to the content of this article. Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Jury partially supported by National Science Foundation Grant DMS 2154494. Tsikalas partially supported by National Science Foundation Grant DMS 2054199 and by Onassis Foundation—Scholarship ID: F ZR 061-1/2022-2023.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jury, M.T., Tsikalas, G. Denjoy–Wolff Points on the Bidisk via Models. Integr. Equ. Oper. Theory 95, 30 (2023). https://doi.org/10.1007/s00020-023-02751-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00020-023-02751-6

Keywords

Mathematics Subject Classification

Search

Navigation