Achromatic arboricity on complete graphs

Abstract

In this paper we study the achromatic arboricity of the complete graph. This parameter arises from the arboricity of a graph as the achromatic index arises from the chromatic index. The achromatic arboricity of a graph G, denoted by $A_{\alpha }(G)$, is the maximum number of colors that can be used to color the edges of G such that every color class induces a forest but any two color classes contain a cycle. In particular, if G is a complete graph we prove that

$$\begin{aligned} \frac{1}{4}n^{\frac{3}{2}}-c_1n \le A_{\alpha }(G)\le \frac{1}{\sqrt{2}}n^{\frac{3}{2}}-c_2n \end{aligned}$$

where $c_1$ and $c_2$ are constants such that $0<c_1,c_2<\frac{1}{2}$.

1 Introduction

Let G be a finite simple graph. A k-coloring of G is a surjective function $\varsigma$ that assigns a number from the set $\{1,2,\dots ,k\}$ to each vertex of G such that any two adjacent vertices have different colors. A k-coloring $\varsigma$ is called complete if for each pair of different colors $i,j\in \{1,2,\dots ,k\}$ there exists an edge $xy\in E(G)$ such that $\varsigma (x)=i$ and $\varsigma (y)=j$.

While the chromatic number $\chi (G)$ of G is defined as the smallest number k for which there exists a k-coloring of G, the achromatic number $\alpha (G)$ of G is defined as the largest number k for which there exists a complete k-coloring of G (see [10]). Note that any $\chi (G)$-coloring of G is also complete. Therefore, for any graph G

$$\begin{aligned} \chi (G)\le \alpha (G). \end{aligned}$$

In [8] the authors introduce the parameter called a-vertex arboricity of a graph G, denoted as ava(G), defined as the largest number of colors that can be used to color the vertices of G such that every color induces a forest but merging any two yields a monochromatic cycle, this parameter arises from the vertex arboricity parameter, denoted by va(G), which is defined as the minimal number of induced forests which cover all the vertices (see [7]), and clearly as a minimal decomposition of trees is complete, we have that

$$\begin{aligned} va(G)\le ava(G). \end{aligned}$$

Inspired by these parameters and by our previous work, related to edge complete colorings, most specifically with the achromatic (proper colorings), the pseudoachromatic (non-proper colorings), and pseudoconnected (connected and no proper colorings) indices of the complete graphs [1,2,3,4]; we will say that an edge-coloring of a graph G is acyclic if any chromatic class forms an acyclic graph and it is ${\mathcal {C}}$-complete if any pair of chromatic classes contain at least a cycle. Moreover, we define the achromatic arboricity parameter for a graph G, denoted by $A_{\alpha }(G)$, as the largest number of colors of an acyclic and ${{\mathcal {C}}}$-complete coloring.

This parameter arises from the well-known arboricity parameter of a graph G, defined by Nash-William [12, 13], and denoted for A(G), that is the minimum number of acyclic subgraphs into which E(G) can be partitioned. Note that the union of two parts forms a subgraph with at least a cycle. In consequence, we have that

$$\begin{aligned} A(G)\le A_{\alpha (G)}. \end{aligned}$$

In this paper, we give a lower and an upper bound for the achromatic arboricity parameter with a small gap between them, more precisely, we prove that $A_{\alpha }(K_n)\approx \frac{1}{c}n^{\frac{3}{2}}$ for $\sqrt{2}\le c \le 4$.

This paper is organized as follows. In Sect. 2 we give a general upper bound. In Sect. 3 we give a lower bound using the properties and the structure of the finite projective planes. In Sect. 4, we prove our main theorem as a consequence of the previous results. Finally, in Sect. 5 we give the exact values of the achromatic arboricity for $K_n$ when $2\le n \le 7$.

2 The upper bound for the achromatic arboricity of $K_n$

In this section, we prove an upper bound for $A_{\alpha }(K_{n})$. The technique has been used previously by different authors in different papers cited in the introduction of this paper.

Remark 1

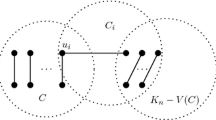
Let H be an acyclic subgraph of $K_n$ such that $|E(H)|\le \frac{n}{2}$. If H is incident to r edges of $K_n{\setminus } E(H)$ then there exists a matching M of at most |E(H)| edges incident to s edges of $K_n{\setminus } E(M)$ such that $r\le s$.

Proof

Suppose that $|V(H)|=2x$. Take a matching M of $K_n$ such that $V(M)=V(H)$. Then M has size x and it is incident to $s=r+|V(H)|-x$ edges.

If $|V(H)|=2x+1=n$, a maximum matching of $K_n$ has x edges and it is incident to $s=r+|V(H)|-x$ edges, because if v is the unique vertex in $V(H)\setminus V(M)$, the edges incident to v, they also are incident to any other vertex of the matching, consequently in M inside the r edges of $K_n{\setminus } E(H)$ that inside in H.

Finally, if $|V(H)|=2x+1<n$, let v be a vertex of $V(K_n){\setminus } V(H)$ and take a matching M of $K_n$ such that $V(M)=V(H)\setminus \{u\}$ where $u\in V(H)$. The matching $M\cup \{uv\}$ has $x+1$ edges and it is incident to $s=r+|V(H)|-(x+1)+t$ where t is the number of edges between $V(H)\cup \{v\}$ and $V(K_n)\setminus (V(H)\cup \{v\})$ and the result follows. $\square$

Lemma 1

If $n\ge 5$ then

$$\begin{aligned} A_{\alpha }(K_{n})\le \left\lfloor \max \left\{ \min \{f_n(x),g_n(x)\} :x\in {\mathbb {N}}\right\} \right\rfloor \end{aligned}$$

where $f_n(x)=n(n-1)/2x$ and $g_n(x)=x(n-x-1)+1$.

Proof

Let $\varsigma :E(K_n) \rightarrow [k]$ be a k-edge-coloring of $K_n$, acyclic and ${{\mathcal {C}}}$-complete, with $k=A_{\alpha }(K_n)$. Let $x= min\{ \left| \varsigma ^{-1}(i)\right| : i\in \left[ k\right] \}$ be, i.e., x is the cardinality of the smallest color class of $\varsigma$. Without loss of generality, let $x= \left| \varsigma ^{-1}(k)\right|$ be. Since $\varsigma$ defines a partition of the edges of $K_n$ it follows that $k\le f_n(x):=n(n-1)/2x$.

Since $\varsigma$ is acyclic, by Remark 1, we can suppose that $\varsigma ^{-1}(k)$ forms a matching of size x, we will call this matching as X; notice that the graph generated by X has order equal or greater to any other subgraph of size x of $K_n$, consequently the number of colors incident with the color assigned to X is maximum where X is a matching; by the same reason, x is at most $\frac{n}{2}$. The number of pair of edges in the subgraph edge-induced by $E(K_{2x})\setminus \varsigma ^{-1}(k)$ is at most $\frac{\left( {\begin{array}{c}2x\\ 2\end{array}}\right) -x}{2}=x(x-1)$. On the other hand, there is $2x(n-2x)$ edges incident to some vertex of $\varsigma ^{-1}(k)$ exactly once, we denote this set of edges by $X_I$. Since every two color classes of $\varsigma$ have at least two incidences, there are at least two edges that have a vertex in common with some edge in $\varsigma ^{-1}(k)$, hence, the number of color classes incident to $\varsigma ^{-1}(k)$ containing some edge in $X_I$ is at most $x(n-2x)$ and the number of color classes incident to $\varsigma ^{-1}(k)$ containing no edge in $X_I$ is at most $x(x-1)$ since two edges are required to obtain a cycle. Hence, there are at most $g_n(x)-1$ color classes incident with some edge in $\varsigma ^{-1}(k)$ where

$$\begin{aligned} g_n(x)-1:=x(n-2x)+x(x-1), \end{aligned}$$

therefore

$$\begin{aligned} g_n(x)-1=xn-x^2-x, \end{aligned}$$

it follows that $k\le g_n(x)=xn-x^2-x+1$. In consequence, we have

$$\begin{aligned} A_{\alpha }(K_{n})\le \min \{f_n(x),g_n(x)\}. \end{aligned}$$

And we conclude that

$$\begin{aligned} A_{\alpha }(K_{n})\le \left\lfloor \max \left\{ \min \{f_n(x),g_n(x)\} :x\in {\mathbb {N}}\right\} \right\rfloor . \end{aligned}$$

$\square$

The function $f_n$ is a hyperbola and the function $g_n$ is a parabola, see Fig. 1. Then we have the following lemma.

Fig. 1

The functions $g_n$ and $f_n$ for a fixed value n

Lemma 2

Let $x_0,x_1\in {\mathbb {R}}^{+}$, such that $f_n(x_0)=g_n(x_0)$, and $f_n(x_1)=g_n(x_1)$. If $x_0<x_1$ then

$$\begin{aligned} g_n(x_0)=f_n(x_0)=\max \left\{ \min \{f_n(x),g_n(x)\} :x\in {\mathbb {R}}^{+}\right\} \end{aligned}$$

where $x_0=\sqrt{(n+5/8)/2+\epsilon }+1/4$ and $\epsilon >0$.

Proof

Note that $f_n(x) \le g_n(x)$ for $x_0 \le x \le x_1$ and $g_n(x)<f_n(x)$ in any other case for $x \in {\mathbb {R}}^{+}$. Since $f_n(x_0)>f_n(x_1)$ it follows that $g_n(x_0)=f_n(x_0)=\max \left\{ \min \{f_n(x),g_n(x)\} :x\in {\mathbb {R}}^{+}\right\} .$

The equation $f_n(x_0)=g_n(x_0)$ is reduced to $n^2-(2x_0^2+1)n+2x_0(x^2_0+x_0-1)=0$. Since the discriminant $D=4x_0^4-8x_0^3-4x_0^2+8x_0+1$, $\sqrt{D}=2x_0^2-2x_0-2-\epsilon$, for some $\epsilon >0$. Then the positive solution for n is $n=2x_0^2-x_0-\frac{1}{2}-\frac{\epsilon }{2}$ and the lemma holds true because $x_0=\sqrt{(n+5/8)/2+\frac{\epsilon }{4}}+1/4$ provides the positive solution. $\square$

Now, we can prove the upper bound in the following theorem.

Theorem 1

Let $n\ge 5$ be an integer then the achromatic arboricity of the complete graph of order n is upper bounding by:

$$\begin{aligned} A_{\alpha }(K_{n})\le \frac{1}{\sqrt{2}}n^{\frac{3}{2}}-c_2n \end{aligned}$$

where $c_2$ is a constant such that $0<c_2<\frac{1}{2}$.

Proof

By Lemma 2, $g_n(x_0)=nx_0-x_0^2-x_0+1$ and $x_0=\sqrt{n/2}+\epsilon$, for a small $\epsilon >0$. We obtain:

$$\begin{aligned} g_n(x_0)=n(\sqrt{n/2}+\epsilon )-(\sqrt{n/2}+\epsilon )^2-(\sqrt{n/2}+\epsilon )+1, \end{aligned}$$

and then $g_n(x_0)= \frac{1}{\sqrt{2}}n^{\frac{3}{2}}- \frac{n}{2}-(2\epsilon +1)\sqrt{\frac{n}{2}}+n\epsilon -\epsilon ^2-\epsilon +1$ and the result follows. $\square$

3 A lower bound for the achromatic arboricity of $K_n$ for some values of n

In this section, we provide a lower bound for the achromatic arboricity of $K_n$, for some values n greater than 13. We use the technique of identifying the structure of the finite projective plane of order q, for q an odd prime and $n=q^2+q+1$, with the complete graph $K_n$ to take advantage of its properties (see also [1,2,3,4]) to find an acyclic and ${\mathcal {C}}$-complete coloring of $K_n$ to give a lower bound of its achromatic arboricity.

First of all, we recall some definitions and properties of the projective planes that we will use along with the proof of the lower bound.

A projective plane is a set of n points and a set of n lines, with the following properties.

• 1. For any two distinct points there is exactly one line incident to both.

• 2. For any two distinct lines there is exactly one point incident to both.

• 3. There exists four points such that no line is incident to three of them or more.

A projective plane has the same number of points and lines, that is $n=q^2+q+1$ points and lines, for a suitable q. Each line has $q+1$ points and each point belongs to $q+1$ lines; we say that q is the order of such plane, and a projective plane of order q is denoted by $\Pi _q$.

Let $\mathrm{I\!P}$ be the set of points of $\Pi _q$ and let $\mathrm{I\!L}= \{\mathrm{I\!l}_1,\dots , \mathrm{I\!l}_n\}$ the set of lines of $\Pi _q$. We identify the points of $\Pi _q$ with the set of vertices of the complete graph $K_n$. Then, the set of points of each line of $\Pi _q$ induces a subgraph $K_{q+1}$ in $K_n$. Given a line $\mathrm{I\!l}_i\in \mathrm{I\!L}$, let $l_i=(V(l_i),E(l_i))$ be the subgraph of $K_n$ induced by the set of $q+1$ points of $\mathrm{I\!l}_i$. By the properties of the projective plane, for each pair $i,j\in [n]$, $|V(l_i)\cap V(l_j)| =1$ and $\{E(l_1), \dots , E(l_n)\}$ is a partition of the edges of $K_n$. Therefore, when we say that a graph G isomorphic to $K_n$ is a representation of the projective plane $\Pi _q$ means that V(G) is identified with the points of $\Pi _q$ and that there is a set of subgraphs (lines) $\{l_1, \dots , l_n\}$ of G, for which a line $\mathrm{I\!l}_i$ of $\Pi _q$, $l_i$ is the induced subgraph by the set of points of $\mathrm{I\!l}_i$.

Let us recall that any complete graph of even order $q+1$ admits a factorization by $\frac{q+1}{2}$ Hamiltonian paths, see [6]. This factorization of the complete graph $K_{q+1}$ can be used as edge-coloring for the lines of $K_n$.

In particular, if q is a prime power there exists a $\Pi _q$, that arises from finite fields ${\mathbb {Z}}_q$ for q prime, and from GF(q), the Galois Field of order q, when q is a prime power. It is called the algebraic projective plane, and it is denoted by PG(2, q) (see [11]). Since the proof of Theorem 3 only requires projective planes of order prime, we will use the algebraic projective plane PG(2, q) for q a prime number (the field that we will use is ${\mathbb {Z}}_q$).

Now we give a useful description PG(2, q): Let $p_{\infty }$ and $l_{\infty }$ a pair of incident point and line in the projective plane, and we call them the infinity point and the line, respectively. Since each line have $q+1$ points and each point is incident with $q+1$ lines, let $\{p_0,p_1,\ldots ,p_{q-1}\}$ be the set of points incident to $l_{\infty }$ different to $p_{\infty }$ and let $\{l_0,l_1,\ldots ,l_{q-1}\}$ be the set of lines incident to $p_{\infty }$ different to $l_{\infty }$.

For each $i\in {\mathbb {Z}}_q$, let $\{(i,0),(i,1),\ldots ,(i,q-1)\}$ be the set of points different from $p_{\infty }$ incident to $l_i$ and let $\{[i,0],[i,1],\ldots ,[i,q-1]\}$ be the set of lines different from $p_{\infty }$ incident to $p_i$.

To finish with the projective plane description we have that, for $a,b\in {\mathbb {Z}}_q$, the line [a, b] is incident or contains the set of points: $p_a \cup \{(x,y) | y=ax+b$ for $x,y\in {\mathbb {Z}}_q\}$.

Theorem 2

If q is an odd prime number and $n=q^2+q+1$ then

$$\begin{aligned} \frac{q+1}{4}(n+1)\le A(K_n). \end{aligned}$$

Proof

Let q be an odd prime number and G (isomorphic to $K_n$) be a representation of the algebraic projective plane PG(2, q).

We proceed to give a partition of the lines of the projective plane taking a single line and distributing the rest of $q^2+q$ lines in $\frac{q^2+q}{2}$ sets of two lines each one, with the property that, as the pair of lines of any set intersecting in one and only one point, we describe any of these sets as a triplet (p, m, l) such that $p=m\cap l$. Notice that, by properties of the projective plane, the points of the triplets are unique and different. Only as a remark, notice that these triplets do not form a partition of the points of PG(2, q), because we are given only $\frac{q^2+q}{2}$ of them. Our objective is to assign an acyclic and ${\mathcal {C}}$-complete coloring to the lines of PG(2, q), and to achieve it should be necessary to have the properties given in the triplets. Then, first, we will give the single line and the collection of triplets, and, second, we will give an acyclic ${\mathcal {C}}$-complete edge-coloring of G that attain the given lower bound.

• (1) The single line is $l_0$, and the first triplet is $(p_0,[0,0],l_{\infty })$.

• (2) Take the set $X=\{p_1,\ldots ,p_{\frac{q-1}{2}}\}$, a subset of $\frac{q-1}{2}$ points of $l_{\infty }$, and call A the set of lines between the point (0, 0) and X, that is $A=\{[i,0]: i\in \{1,\ldots , \frac{q-1}{2}\}\}$, and let B a set of lines between the points of X and the point $(0,2i-1)$, that is $B=\{[i,2i-1]: i\in \{1,\ldots , \frac{q-1}{2}\}\}.$ Then, we have a set $T_1$ of $\frac{q-1}{2}$ triplets of two lines and one intersection point between them:

  $$\begin{aligned} T_1=\{(p_i,[i,0],[i,2i-1]):i\in \{1,\ldots , \frac{q-1}{2}\}\}. \end{aligned}$$

• (3) Take the intersection points between the lines $[i,2i-1]$ and $l_i$, such that:

  $$\begin{aligned} (i,i^2+2i-1)=[i,2i-1]\cap l_i, \ \text {for} \ i\in \{1,\ldots , \frac{q-1}{2}\}. \end{aligned}$$

  And the set of lines between these points $(i,i^2+2i-1)$ and (0, 2i), they are the lines $C=\{[\frac{i^2-1}{i},2i]: i\in \{1,\ldots , \frac{q-1}{2}\}\}.$ Then, we have another set of $\frac{q-1}{2}$ triplets of two lines and one intersection point between them:

  $$\begin{aligned} T_2=\{(i,i^2+2i-1),l_i,[\frac{i^2-1}{i},2i]:i\in \{1,\ldots , \frac{q-1}{2}\}\}. \end{aligned}$$

  Note that we have covered all the lines $[i,2i-1]$ (containing the points $(0,2i-1)$ and $(i,i^2+2i-1)$) and all the lines $[\frac{i^2-1}{i},2i]$ (containing the points (0, 2i) and $(i,i^2+2i-1)$) for $1\le i \le \frac{q-1}{2}$.

• (4) For any vertex $(i,i^2+2i-t)\in l_i$ with $t\in {\mathbb {Z}}_q-\{1\}$, we have the lines $\{[\frac{i^2-t+1}{i},2i-1]\}$ between $(i,i^2+2i-t)$ and $(0,2i-1)$, and the lines $\{[\frac{i^2-t}{i},2i]\}$ between $(i,i^2+2i-t)$ and (0, 2i) with $t\in {\mathbb {Z}}_q-\{1\}$. Now we define $(q-1)\frac{q-1}{2}$ triplets as follows:

  $$\begin{aligned} T_3= & {} \{((i,i^2+2i-t),[\frac{i^2-t+1}{i},2i-1],[\frac{i^2-t}{i},2i]):\ t\ \in {\mathbb {Z}}_q-\{1\},\\{} & {} \text {and}\ i\in \{1,\ldots , \frac{q-1}{2}\}\}. \end{aligned}$$

• (5) The last set of triplets is defined by:

  $$\begin{aligned} T_4=\{((i,i^2),[i,0],l_i):i\in \{\frac{q+1}{2}, \dots , q-1\}\}. \end{aligned}$$

• (6) Hence, we have: $1+|T_1|+|T_2|+|T_3|+|T_4|=1+\frac{q-1}{2}+\frac{q-1}{2}+(q-1)\frac{q-1}{2}+\frac{q-1}{2}$ triplets that cover a set of $2+2(q-1)+(q-1)^2+q-1=q^2+q$ lines. Then, all the lines of PG(2, q) are covered except for the line $l_0$. The left side of Fig. 2 shows a decomposition of the lines of PG(2, 3) while the right side shows $K_{13}$.

Fig. 2

Descomposition of PG(2, 3) by triplets and the complete coloring for $K_{13}$

Now, we proceed to color the complete graph G.

To begin with, we color the complete subgraph $K_{q+1}$ associated with the line L by Hamiltonian paths, therefore we use $\frac{q+1}{2}$ colors. The remaining lines are colored by pairs, according to the triplets (p, l, m).

For each triplet (p, l, m), we color the complete subgraph $K_{q+1}$ associated with the line l by Hamiltonian paths and we copy the coloring to the complete subgraph associated with the line m.

Therefore, we use $\frac{q+1}{2}(\frac{n-1}{2}+1)=\frac{q+1}{4}(n+1)$ colors.

The coloring is acyclic because the color classes of the line $l_{\infty }$ are paths, and each color class of a triplet is the identification of two paths by a vertex. In the sequel, we will prove that it is ${\mathcal {C}}$-complete:

If two color classes are at the edges of a line, clearly they contain a cycle since they are the union of two Hamiltonian paths. If a color class is the edges of $l_{\infty }$ and another color class is in the edges of the lines of a triplet (p, l, m), the triangle formed by l, m and $l_{\infty }$ produces a cycle.

Finally, if two color classes are in the edges of the lines of the triplets (p, l, m) and $(p',l',m')$, since $p\not = p'$, the triangle formed by l, m and $l'$ produces a cycle, and then the union of any two color classes contains at least a cycle.

The right side of Fig. 2 shows the part of $K_{13}$ where the line $l_0$ and the two lines of the triplet $(p_1,[1,0],[1,1])$ are colored. $\square$

4 Main Result

Before proving Theorem 3 we state the following lemma.

Lemma 3

For any graph G, if H is a subgraph of G, then $A_{\alpha }(G)\ge A_{\alpha }(H)$.

Proof

Given a coloring $\varsigma$ of H which performs $A_{\alpha }(H)$, we extend this to an acyclic coloring of G such that the coloring is ${\mathcal {C}}$-complete in a greedy way. That is if the new edge can be colored in an already used color, do it; otherwise, assign a new color, which henceforth forms a cycle with any of the other colors. Thus, the obtained coloring si acyclic, and ${\mathcal {C}}$-complete. $\square$

Now we have our main result.

Theorem 3

Let $n\ge 13$ be an integer then the achromatic arboricity of the complete graph of order n is bounding by:

$$\begin{aligned} \frac{1}{4}n^{\frac{3}{2}}-c_1n \le A_{\alpha }(K_{n})\le \frac{1}{\sqrt{2}}n^{\frac{3}{2}}-c_2n, \end{aligned}$$

where $c_1$ and $c_2$ are constants such that $0<c_1,c_2<\frac{1}{2}$.

Proof

The upper bound is given in Theorem 1. To prove the lower bound, we use a strengthened version of Bertrand’s Postulate, which follows from the Prime Number Theorem, see [5, 9]: For $\epsilon >0$, there exists an $N_\epsilon$, such that for all real $x\ge N_\epsilon$ there exists a prime q between x and $(1+\epsilon )x$. Let $\epsilon >0$ be given, and suppose $n>(N_\epsilon +1)^2(1+\epsilon )^2$. Let $x=\sqrt{n}/(1+\epsilon ) -1$, so $x\ge N_\epsilon$. We now select a prime q with $x\le q \le (1+\epsilon )x$. Then $q^2+q+1\le (x+1)^2(1+\epsilon )^2=n$. Since projective planes of all prime orders exist it follows from Theorem 2 and Lemma 3 that:

$$\begin{aligned} A(K_n)\ge A(K_{q^2+q+1})\ge \frac{q+1}{4}(q^2+q+2)\ge \frac{n^{3/2}}{4(1+\epsilon )^3}-\frac{n}{4(1+\epsilon )^2}+\frac{\sqrt{n}}{2(1+\epsilon )}. \end{aligned}$$

Since $\epsilon$ was arbitrarily small the result follows. $\square$

5 The achromatic arboricity of $K_n$ for small values of n.

In this section, we study the achromatic arboricity of $K_n$ for small values of n. Table 1 shows the exact values for $2\le n\le 7$, Fig. 3 displays colorations that attain lower bounds for $2\le n\le 7$ and Table 2 shows upper and lower bounds for $8\le n\le 12$.

Table 1 Exact values for $A_{\alpha }(K_n)$, $2\le n\le 7.$

It is easy to see that the upper bounds for $n=2,3$ equal the values of Table 1.

Fig. 3

Colorings that give lower bounds of $A_\alpha (K_n)$ for $2\le n\le 7$

For the case $n=4$, if we suppose $A_{\alpha }(K_4)\ge 4$, then there are at least two color classes of size one, whose union does not contain a cycle, a contradiction, then $A_{\alpha }(K_4)=3$.

For the case of $n=5$, Lemma 1 says that $A_{\alpha }(K_5)\le 5$ and the smallest color class has two edges. We suppose $A_{\alpha }(K_5)= 5$ and then each color class has exactly two edges. If the edges of a color class contain a $P_3$, say abc, the edge ac is in the cycle with vertices a, b, and c, so, the other six edges incident to $P_3$ generate 3 different color classes necessarily (each on this color classes has to be connected). Hence, the edge ac is in a color class that is a matching, say ac and de. Take the color class containing the edge bd. On one hand, the color class is the set of two edges bd and bc (or bd and ab) making a cycle with abd. On the other hand, the color class is the set of two edges bd and be making a cycle with ac and be, a contradiction. Therefore, each color class is a matching size two. Then the union of two color classes is a $C_4$ and the union of three color classes is a $K_4$ necessarily. The remaining edges generate a $K_{1,4}$ which does not contain matchings of size two. In consequence, $A_{\alpha }(K_5)= 4$.

For the case of $n=6$, Lemma 1 says that $A_{\alpha }(K_6)\le 7$ and the smallest color class has two edges. If we suppose $A_{\alpha }(K_6)= 7$, then there are six color classes of size two and one color class of size three. If the edges of a color class of size two produce a $P_3$, it would be incident to at most 5 more color classes, then each color class of size two has to be a matching. Then the union of two color classes of size two is a $C_4$ and the union of three color classes of size two is a $K_4$ necessarily, a contradiction because there are at least six color classes of size two. Therefore, $A_{\alpha }(K_6)= 6$.

For the case of $n=7$, Lemma 1 says that $A_\alpha (K_7)\le 9$ and the smallest color class has two edges. If we suppose $A_\alpha (K_7)= 9$, there are at least six color classes of size two, however, a $P_3$ is incident to at most six color classes, hence, the color classes of size two are matchings but only there are at most three of them (on a $K_4$), a contradiction. If we suppose $A_\alpha (K_7)= 8$, there are three color classes of size two which are matching in a $K_4$ subgraph and there are five color classes of size three. On one hand, each color class of three vertices must be incident to three vertices of the $K_4$. On the other hand, there are at most four color classes of size three incident to three vertices of the $K_4$, a contradiction, and then $A_\alpha (K_7)= 7$.

To end, we calculate the upper bounds given in Lemma 1 for $A_\alpha (K_n)$ for $8 \le n \le 12$ in Table 2, and the lower bounds perform their values as follows: to obtain a coloring of $K_8$, take the colored graph $K_7$ with 7 colors and add a new v vertex and all edges between $K_7$ and v color them with a new color, such edges form a star. Repeat this process to obtain a lower bound for $n=9,10,11,12$.

Table 2 Bounds for $A_{\alpha }(K_n)$, $8\le n\le 12.$