Abstract
In this article we prove that all squares with sides of lengths \(\frac{1}{m+1}, \frac{1}{m+2}, \dots \) can be packed in a rectangle with a one side fixed and a relatively small area. We give a similar result for all of three Moser’s Packing Problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Amram Meir and Leo Moser [7] formulated the following problem. What is the smallest area of a rectangle into which we can pack squares with sides of lengths \(\frac{1}{2}, \frac{1}{3}, \dots \)? Attempts to find an answer to the above question went in two directions.
One was checking for what values of \(t>\frac{1}{2}\) we can pack squares with sides \(\frac{1}{2^t}, \frac{1}{3^t}, \dots \) into a rectangle with area \(\sum _{n=2}^{\infty } \frac{1}{n^{2t}}\). The best answer was found by Terence Tao [9], who proved that for any real number  and for any sufficiently large natural number m, squares with side lengths of \(\frac{1}{m^t}, \frac{1}{(m+1)^t}, \dots \) can be packed into a square of area \(\sum _{n=m}^{\infty } \frac{1}{n^{2t}}\). Unfortunately, his arguments did not seem to extend to the critical case \(t=1\).
and for any sufficiently large natural number m, squares with side lengths of \(\frac{1}{m^t}, \frac{1}{(m+1)^t}, \dots \) can be packed into a square of area \(\sum _{n=m}^{\infty } \frac{1}{n^{2t}}\). Unfortunately, his arguments did not seem to extend to the critical case \(t=1\).
On the other hand, considerations have been reduced to packing some finite number of initial squares into a rectangle with area \({\sum _{n=2}^{\infty } \frac{1}{n^2}=\frac{\pi ^2}{6}-1}\) and proving that the remaining squares can be packed into a rectangle with a relatively small area. The best known estimate was found by Marc Paulhus [8], who showed that squares with side lengths of \(\frac{1}{2}, \dots , \frac{1}{m}\) for \(m=10^9\) could be packed into a rectangle with one side equal to \(\frac{1}{2}\) and area equal to \(\frac{\pi ^2}{6}-1\). Next, he gave (as it later turned out) an incorrect proof from which it was concluded that the remaining squares could be packed into a certain rectangle.
Antal Joós [5] found a mistake in Paulhus’ proof, and Paulina Grzegorek and Janusz Januszewski [2] gave the correct proof in the special case when \(m=10^9\) and one of the sides of the rectangle is equal to \(\frac{1}{2}\).
Many authors have considered packaging problems of a similar nature (see also [1, 3, 4, 6]). The main goal of this article is to provide them with a mathematical basis for a such considerations. We formulate and prove a general version of the result proven by Paulina Grzegorek and Janusz Januszewski. The main result of the paper is Theorem 5.1 giving a formal proof that for each m we can pack all squares with sides of lengths \(\frac{1}{m+1}, \frac{1}{m+2}, \dots \) into a rectangle of a relatively small area.
Amram Meir and Leo Moser [7] also formulated two analogous and similar problems using the identities \({\sum _{n=1}^{\infty } \frac{1}{(2n+1)^2}=\frac{\pi ^2}{8}-1}\) and \({\sum _{n=1}^{\infty } \frac{1}{n(n+1)} =1}\). The main result of this paper also applies to the above two problems.
For the problem related with last identity \({\sum _{n=1}^{\infty } \frac{1}{n(n+1)} =1}\), the best known estimate was found Mingliang Zhu and Antal Joós [10]. They showed that the first \(1.35*10^{11}\) rectangles with dimensions \(\frac{1}{1} \times \frac{1}{2}\), \(\frac{1}{2} \times \frac{1}{3} \dots \) can be packed into the unit square, and as a consequence that all of these rectangles can be packed into a square with side of length \(1+\epsilon \) for \(\epsilon < 1.49 * 10^{-11}\).
2 Approximation of harmonic numbers
2.1 Simple inequalities
To begin with, we will give four simple inequalities, which we will use later in this article.
-
The function \(\ln (x)+\frac{1}{2x}\) is increasing on the interval
 because its derivative $$\begin{aligned} \left( \ln (x)+\frac{1}{2x}\right) '=\frac{x-\frac{1}{2}}{x^2}>0 \end{aligned}$$
because its derivative $$\begin{aligned} \left( \ln (x)+\frac{1}{2x}\right) '=\frac{x-\frac{1}{2}}{x^2}>0 \end{aligned}$$for every real number
 . In particular, if \(\alpha \ge 0\) is a real number, then $$\begin{aligned} \ln ( \left\lfloor e^{\alpha } n \right\rfloor )+ \frac{1}{2 \left\lfloor e^{\alpha } n \right\rfloor } \le \ln ( e^{\alpha } n)+ \frac{1}{2 e^{\alpha } n} \end{aligned}$$(2.1)
. In particular, if \(\alpha \ge 0\) is a real number, then $$\begin{aligned} \ln ( \left\lfloor e^{\alpha } n \right\rfloor )+ \frac{1}{2 \left\lfloor e^{\alpha } n \right\rfloor } \le \ln ( e^{\alpha } n)+ \frac{1}{2 e^{\alpha } n} \end{aligned}$$(2.1)for each positive integer number n because \(\left\lfloor e^{\alpha } n \right\rfloor \le e^{\alpha }n\).
-
For each real number
 , there is an inequality $$\begin{aligned} y+\ln (1-y)<-\frac{y^2}{2} \end{aligned}$$(2.2)
, there is an inequality $$\begin{aligned} y+\ln (1-y)<-\frac{y^2}{2} \end{aligned}$$(2.2)because the expression \(x+\ln (1-x)+\frac{x^2}{2}\) is equal to 0 for \(x=0\), and its derivative
$$\begin{aligned} \left( x+\ln (1-x)+\frac{x^2}{2}\right) '=\frac{-x^2}{1-x} < 0 \end{aligned}$$for any real number
 .
. -
For each real number
 , there is an inequality $$\begin{aligned} y+\ln (1-y) > - \frac{y^2}{2} - \frac{y^3}{2} \end{aligned}$$(2.3)
, there is an inequality $$\begin{aligned} y+\ln (1-y) > - \frac{y^2}{2} - \frac{y^3}{2} \end{aligned}$$(2.3)because the expression \(x+\ln (1-x) + \frac{x^2}{2} + \frac{x^3}{2}\) is equal to 0 for \(x=0\) , and its derivative
$$\begin{aligned} \left( x+\ln (1-x) + \frac{x^2}{2} + \frac{x^3}{2}\right) ' = \frac{3x^2\left( \frac{1}{3}-x\right) }{2(1-x)} > 0 \end{aligned}$$for any real number
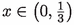 .
. -
Let \(\alpha >0\) be a real number and n be a natural number such that \({n \ge \frac{4}{e^{\alpha }-1}}\). Then
$$\begin{aligned} \left\lfloor e^{\alpha } n \right\rfloor = \left\lfloor n+(e^{\alpha } -1)n \right\rfloor \ge n+4. \end{aligned}$$Furthermore, using the above inequality twice, we obtain
$$\begin{aligned} \left\lfloor e^{\alpha } \left\lfloor e^{\alpha }n \right\rfloor \right\rfloor \ge n+8. \end{aligned}$$(2.4)
2.2 Classical harmonic number inequalities
For any natural number n let \(H_{n}=\sum \limits _{j=1}^{n} \frac{1}{j}\) denote the \(n-th\) harmonic number, and \({\gamma =\lim _{n\rightarrow \infty } \left( H_{n}-\ln \left( n\right) \right) }\) be the Euler–Mascheroni constant gamma. As we see, harmonic numbers can be approximated by the natural logarithm. The following two facts give the precision of this approximation.
Fact 2.1
For each positive integer number \(n\), there are inequalities
Proof
We define two sequences \(( a_{n})_{n=1}^{\infty }\), \(( b_{n} )_{n=1}^{\infty }\) as follows. Let
for any natural number \(n\). Obviously, by the definition of the constant \(\gamma \), each of these two sequences tends to \(\gamma \) when \(n\) goes to infinity, i.e.,
We will prove that the sequence \(( a_{n} )_{n=1}^{\infty }\) is decreasing, and the sequence \(( b_{n} )_{n=1}^{\infty }\) is increasing.
Now we will prove that the difference \(a_{n+1}-a_{n}\) is negative. By the definition of the sequence \(( a_{n} )_{n=1}^{\infty }\) in 2.5, we have
Then, using 2.2, we obtain
because \(n+1 < n+2\). Therefore, since the sequence \((b_{n})_{n=1}^{\infty }\) is decreasing and goes to \(\gamma \), each element of this sequence is larger than \(\gamma \), i.e.
for any natural number \(n\). Thus, we have proved the first inequality.
Similarly, we prove the second inequality. By the definition of the sequence \(( b_{n} )_{n=1}^{\infty }\) in 2.5, we have
In the special case when \(n=1\), we obtain \({b_2-b_1=\frac{1}{2}+\frac{1}{4}-\ln (2)>0}\) because \(\ln (2) \approx 0.69\). Otherwise, when \(n+1 \ge 3\), then using (2.3), we obtain
Therefore, since the sequence \((b_{n})_{n=1}^{\infty }\) is increasing and goes to \(\gamma \), each element of this sequence is less than \(\gamma \), i.e.
for any natural number \(n\). Thus, we have proved the second inequality. \(\square \)
Fact 2.1 can be weakened to a more popular and friendly form.
Fact 2.2
Let \(n\) be a positive integer number. Then, there are inequalities
Proof
Let \(n\) be a positive integer number. Using Fact 2.1, we obtain
and
Thus, by using 2.2 we arrive at
\(\square \)
3 Some convex function
Let n, N be fixed positive integer numbers. We define the function \(G: {\mathbb {R}}_{+} \rightarrow {\mathbb {R}}\) by
The following three lemmas will be useful in approximating the value of the function G on the interval  . The first lemma gives the upper bound of \(G(n+2)\) as follows.
. The first lemma gives the upper bound of \(G(n+2)\) as follows.
Lemma 3.1
Let n, N be fixed natural numbers such that \(n \ge 17\) and \(N \ge n + 7\). Then, there is an inequality
Proof
Let n, N be fixed natural numbers such that \(n \ge 17\) and \(N \ge n + 7\). The following inequalities are satisfied.
Multiplying the inequalities by sides and canceling the common factor \({(n-2)(n+7)}\), we obtain
We divide both sides by \( N n (n^2+n-3) (n+1)(n+2)\). Hence
and thus
Next, we decompose each fraction into the difference of two fractions and then we move its subtrahend to the other side
which concludes the proof. \(\square \)
The second lemma shows that the largest value of the function G on the interval  is \(G(n+2)\).
is \(G(n+2)\).
Lemma 3.2
Let n, N be fixed natural numbers such that \({n \ge 14}\) and \({N \ge n + 6}\). For each  , there is an inequality
, there is an inequality
Proof
Let n, N be fixed natural numbers such that \({n \ge 14}\) and \({N \ge n + 6}\). The following inequalities are satisfied:
Multiplying the inequalities by sides and canceling the common factor \({(n-2)(n+3)(n+6)}\), we obtain
We divide both sides by \(2N(n^2+n-3)(n+2)(n+N)\) and multiply by \({(N+n)-2(n+2)=N-(n+4) >0}\). Then
Next, we decompose each fraction into the difference of two fractions and then we move its subtrahend to the other side
Thus
We put \(C=\frac{(n+1)}{N(n^2+n-3)}\). The function G (see (3.1) for definition) has a second derivative
for \(x>0\). Therefore, the function G is convex on the set of positive real numbers, and then for  , the largest value of the function G(x) is taken at either of the two ends of the interval. By 3.2, we obtain that
, the largest value of the function G(x) is taken at either of the two ends of the interval. By 3.2, we obtain that
for each real number  . \(\square \)
. \(\square \)
The third lemma, with some additional assumptions, shows that the upper bound of a sum \(\frac{1}{A}+\frac{1}{B}\) is G(A).
Lemma 3.3
Let n, A, B, N be positive integer numbers such that \({n<A<B \le N}\) and \(A+B \le N+n\) and \(H_{n}+H_{N} < H_{A}+H_{B}\). Then, there is an inequality
Proof
Let n, A, B, N be positive integer numbers such that \(n<A<B\le N\) and
and
By applying the above condition and both inequalities of Fact 2.2, we obtain
Thus
Both sides of the inequality are natural numbers, so
Therefore from 3.3 we obtain
Obviously there are three inequalities
-
\(1 > \frac{A+B}{2B}\) because \(B>A\),
-
\(1 > \frac{n+N}{2N}\) because \(N>n\),
-
\(\frac{2}{n(n+1)} \ge \frac{2}{n A}\) because \(A \ge n+1\).
Multiplying these three inequalities by sides, we obtain
Therefore, by 3.5 we have
Recall that \(A+B \le n+N\) (see 3.3). Thereby
Since \(n<N\), we obtain
Obviously \(\ln (1-y)<-y\) for any real number  (see 2.2). Then
(see 2.2). Then
Finally by applying both inequalities of Fact 2.1 and the initial condition \(H_{n}+H_{N} < H_{A}+H_{B}\)(see 3.4), we obtain
Hence, by 3.6 we obtain
and thus
In the end, we will give an upper estimate of the sum \(\frac{1}{A}+\frac{1}{B}\). From 3.7 we obtain
what was there to prove. \(\square \)
4 Tools
The basic tool of this article will be the following two propositions.
Proposition 4.1
Let \(\alpha >0\) be a real number. For any natural number \({n\ge \frac{1}{e^{\alpha }-1}}\), there is an inequality
Proof
Let \(\alpha >0\) be a real number and \(n\) be a natural number such that \(n\left( e^{\alpha }-1 \right) \ge 1\). Using both inequalities of Fact 2.1 we obtain
and since the function \(\ln (x)+\frac{1}{2x}\) is increasing for \(x \ge \frac{1}{2}\) (see 2.1), then
because \(n\left( e^{\alpha } -1 \right) \ge 1\). \(\square \)
The second proposition is as follows.
Proposition 4.2
Let n, N be natural numbers such that \({n \ge 17}\) and \({N \ge n+7}\). For each natural numbers A, B such that \(n< A < B \le N\) and
there is an inequality
Remark. For \(N>2n\), the constant \(\frac{n+1}{nN}\) can be improved to \(\frac{1}{\left\lfloor N \left( 1-\frac{1}{n+1}\right) \right\rfloor +1}\), but it is not asymptotically more useful.
Proof
Since for any number A it holds that \(\frac{1}{A}<\frac{1}{A-1}\), it is sufficient to prove Proposition 4.2 for the minimum value of A, i.e. for \(A=n+1\) and for \(A>n+1\) such that A is the smallest number satisfying the condition 4.2.
First, we prove Proposition 4.2 in the special case when \({A=n+1}\). Let n, N be natural numbers. Let A, B be natural numbers such that \(A=n+1\) and \(A < B \le N\) and the condition 4.2 holds. Using 4.2 we obtain
Thus
because \(j \le N\). Therefore,
Thereby
Now we will prove Proposition 4.2 in the second case. Let n, N be natural numbers such that \({n \ge 17}\) and \({N \ge n+7}\). Let A, B be natural numbers such that \(n< A < B \le N\) and such that A is the smallest number satisfying the condition 4.2, i.e.,
Using the above inequality we obtain
because \(A < B\). Therefore
Both sides of the above equation are natural numbers. Thus
In particular, since \(A < B\), we obtain
Thus

Recall that \(n<A<B \le N\) are natural numbers such that \(n \ge 17\), \(N\ge n+7\), and  . Then using Lemmas 3.3, 3.2 and 3.1 ends the proof of Proposition 4.2. (See 4.3 and 4.2 to check the assumptions of Lemma 3.3.) Thus
. Then using Lemmas 3.3, 3.2 and 3.1 ends the proof of Proposition 4.2. (See 4.3 and 4.2 to check the assumptions of Lemma 3.3.) Thus
\(\square \)
5 Main results
Theorem 5.1
Let \(\alpha >0\) be a real number and \(m \ge 17\) be a natural number such that \(m \ge \frac{4}{(e^{\alpha }-1)}\). All squares with side lengths \(\frac{1}{m+1}, \frac{1}{m+2}, \dots \) can be packed into the rectangle with dimensions \(\alpha \times \epsilon \), where
Proof
Let \(\alpha >0\) be a real number and \(m \ge 17\) be a natural number such that \(m \ge \frac{4}{(e^{\alpha }-1)}\). We define the sequence \((n_j)_{j=0}^{\infty }\) by the recursion
with the initial condition \(n_0=m\). The sequence \((n_j)_{j=0}^{\infty }\) is obviously non-decreasing. Moreover, from (2.4) we obtain that for each non-negative integer number j it holds that \(n_{j+1} \ge n_j + 8.\) In addition, by the definition of the floor function, for each index j we obtain
Thus
Let t be a natural number. We use (5.1) t times
Thus, since \(n_0=m\), we obtain
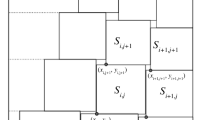
Let \(\alpha >0\) be a real number and m be a natural number. Let \(t=0\). We put \(n=n_t\) and \(N=n_{t+1}\), and \(h_t= \frac{1}{n+1}+\frac{n+1}{n N}\). Take a rectangle of size \(\alpha \times h_t\), i.e., with side length \(\alpha \) and height length \(h_t\). Using Proposition 4.1, we can inscribe squares with side lengths \(\frac{1}{n+1}, \dots , \frac{1}{\left\lfloor e^{\alpha }n \right\rfloor }\) into the bottom row, i.e., we inscribe the first square into the bottom left corner of the rectangle, and each successive square is inscribed as a tangent to the previous square and to the bottom side of length \(\alpha \). Similarly, starting from the upper left corner, we can inscribe squares with side lengths \(\frac{1}{N}, \dots , \frac{1}{\left\lfloor e^{\alpha }n \right\rfloor +1}\) into the upper row as tangents to the upper side of length \(\alpha \). An example of such packing for \(\alpha =\frac{1}{5}\) and \(n=23\) is shown in Fig. 1.
We claim that the squares of the bottom row do not overlap the squares of the top row. Otherwise, if a certain square of the lower row with side length \(\frac{1}{A}\) overlapped a certain square of the lower row with side length \(\frac{1}{B}\), then the inequality \(\frac{1}{A}+\frac{1}{B} > h_t\) would be satisfied. Of course, then \(n<A<B \le N\) and the sum of the lengths of the sides of the squares from \(\frac{1}{N}\) to \(\frac{1}{B+1}\) would be less than that of those from \(\frac{1}{n+1}\) to \(\frac{1}{A}\), i.e., \(H_{A}-H_{n} >H_{N}-H_{B}\) would also be satisfied. Thus we would get a contradiction to Proposition 4.2.
We repeat the reasoning for \(t=0, 1, \dots \) and then we merge all the rectangles into one large rectangle. Therefore, we can inscribe all squares with sides of length \(\frac{1}{m+1}, \frac{1}{m+2}, \dots \) into a rectangle with dimensions \(\alpha \times \epsilon \), where
Thus since \(n_{j+1} > n_{j}+1\), we obtain
Thereby, we conclude from (5.2) that
\(\square \)
Let \(\alpha >0\) be a real number. For a given natural number \(m \ge 17\) such that \(m \ge \frac{4}{(e^{\alpha }-1)}\), let S denote the sum of the areas of all squares with sides of lengths \(\frac{1}{m+1}, \frac{1}{m+2}, \dots \), and let R denote the area of the rectangle with dimensions \(\alpha \times \epsilon \) obtained from Theorem 5.1.
Corollary 5.2
The ratio \(\frac{R}{S}\) is upper bounded by a constant that does not depend on m but depends solely on \(\alpha \).
Proof
Since \(j<j+1\) for any natural number j, we obtain
Using the above observation and Theorem 5.1, we conclude that
Obviously \(2 \le m\) and \(\frac{4}{e^{\alpha }-1} \le m\). Therefore, 5.3 can be weakened to
Remark. For large values of m, the fraction \(\frac{m+1}{m-\frac{1}{e^{\alpha }-1}}\) in 5.3 is approximately equal to 1. \(\square \)
The main implication of Corollary 5.2 is that if we want to improve some result on packaging in an asymptotically observable way, we need to pack more initial squares into a rectangle.
Since for any natural number j, a rectangle with dimensions \(\frac{1}{j} \times \frac{1}{j+1}\) is contained in a square with side \(\frac{1}{j}\), and a square with side \(\frac{1}{2j+1}\) is contained in a square with side \(\frac{1}{2j}\), then the following two corollaries can be concluded from Theorem 5.1.
Corollary 5.3
Let \(\alpha >0\) be a real number and \(m \ge 17\) be a natural number such that \(m \ge \frac{4}{(e^{\alpha }-1)}\). All rectangles with dimensions \(\frac{1}{m+1} \times \frac{1}{m+2}, \frac{1}{m+2} \times \frac{1}{m+3} \dots \) can be packed into the rectangle with dimensions \(\alpha \times \epsilon \), where
Corollary 5.4
Let \(\alpha >0\) be a real number and \(m-1 \ge 17\) be a natural number such that \(m-1 \ge \frac{4}{(e^{\alpha }-1)}\). All squares with side lengths \(\frac{1}{2m+1}, \frac{1}{2m+3}, \dots \) can be packed into the rectangle with dimensions \(\frac{\alpha }{2} \times \frac{\epsilon }{2}\), where
Availability of data and materials
Not applicable.
References
Ball, K.: On packing unequal squares. J. Combin. Theory Ser. A 75(2), 353–357 (1996)
Grzegorek, P., Januszewski, J.: A note on three Moser’s problems and two Paulhus’ lemmas. J. Combin. Theory Ser. A 162(02), 222–230 (2019)
Hougardy, S.: On packing squares into a rectangle. Comput. Geom. 44(10), 456–463 (2011)
Jennings, D.: On packing unequal rectangles in the unit square. J. Combin. Theory Ser. A 68, 465–469 (1994)
Joós, A.: On packing of rectangles in a rectangle. Discrete Math. 341(09), 2544–2552 (2018)
Joós, A.: On packing of unequal squares in a rectangle. Acta Polytech. Hung. 19(01), 51–62 (2022)
Meir, A., Moser, L.: On packing of squares and cubes. J. Combin. Theory Ser. A 5, 126–134 (1968)
Paulhus, M.M.: An algorithm for packing squares. J. Combin. Theory Ser. A 82, 147–157 (1998)
Tao, T.: Perfectly packing a square by squares of nearly harmonic sidelength. arXiv:2202.03594 (2022)
Zhu, M., Joós, A.: Packing \(1.35\cdot 10^{11}\) rectangles into a unit square. arXiv:2211.10356 (2022)
Acknowledgements
We thank Liao Zhang for the comments given during the writing of this text.
Funding
Mikołaj Marciniak was supported by Narodowe Centrum Badań i Rozwoju, Grant Number POWR.03.05.00-00-Z302/17-00.
Author information
Authors and Affiliations
Contributions
The main, lead and correspondent author is Mikołaj Marciniak. The percentage contributions of authors to this paper is as follows: Mikołaj Marciniak—40%, Mariola Marciniak—30%, Katarzyna Chmielewska—30%.
Corresponding author
Ethics declarations
Conflict of interest
A potential conflict of interest is that the first author Katarzyna Chmielewska and Attila Gilányi collaborate and have joint publications. However, the topics of their joint articles are not relevant to the topic of this paper.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chmielewska, K., Marciniak, M. & Marciniak, M. Packing squares into a rectangle with a relatively small area. Aequat. Math. 97, 805–821 (2023). https://doi.org/10.1007/s00010-023-00939-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00010-023-00939-0




 because its derivative
because its derivative  . In particular, if
. In particular, if  , there is an inequality
, there is an inequality  .
. , there is an inequality
, there is an inequality 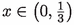 .
.