Uniform Convergent Expansions of the Error Function in Terms of Elementary Functions

Abstract

We derive a new analytic representation of the error function ${\text {erf}}\,\, z$ in the form of a convergent series whose terms are exponential and rational functions. The expansion holds uniformly in z in the double sector $\vert \arg (\pm z)\vert <\pi /4$. The expansion is accompanied by realistic error bounds.

1 Introduction

The error function ${\text {erf}}\,\,z$ is defined in the form [11, Section 7.2, Equation 7.2.1]

$$\begin{aligned} {\text {erf}}\,\, z:=\frac{2}{\sqrt{\pi }}\int _0^z e^{-t^2}\mathrm{{d}}t=\frac{2z}{\sqrt{\pi }}\int _0^1 e^{-z^2t^2}\mathrm{{d}}t. \end{aligned}$$

(1)

It is a special function that plays a fundamental role in statistics, since it is related to the normal Gaussian distribution. It has also important applications in uniform asymptotic expansions of integrals and also in the so-called Stokes phenomenon [1]. For other mathematical and physical applications the reader is referred to [11, Section 7.20].

Different expansions of this function can be found in the literature. The power series expansion of the error function is given by [11, Section 7.6, Equation 7.6.1]

$$\begin{aligned} {\text {erf}}\,\,z=\frac{2}{\sqrt{\pi }}\sum _{n=0}^{\infty }\frac{(-1)^{n}z^{2n +1}}{n!(2n+1)},\quad z\in {\mathbb {C}}. \end{aligned}$$

(2)

This expansion converges absolutely for $z\in {\mathbb {C}}$. It may be derived from the second integral representation in (1) by replacing the factor $e^{-z^2t^2}$ by its Taylor series at the origin and interchanging sum and integral. This Taylor series expansion converges for $z\in {\mathbb {C}}$, but the convergence is not uniform in |z|, since the error term grows with $\vert z\vert$. Therefore, the expansion (2) is not uniform in |z| as the remainder is unbounded in |z|. A different power series expansion of ${\text {erf}}\,z$ is given by [11, Section 7.6, Equation 7.6.2]

$$\begin{aligned} {\text {erf}}\,z=\frac{2}{\sqrt{\pi }}e^{-z^{2}}\sum _{n=0}^{\infty }\frac{2^{ n}z^{2n+1}}{1\cdot 3\cdots (2n+1)},\quad z\in {\mathbb {C}}. \end{aligned}$$

(3)

As the previous series, it converges for $z\in {\mathbb {C}}$, but the convergence is not uniform in |z|. An asymptotic expansion of ${\text {erf}}\,z$ for large |z| and $|\arg z|<\frac{3\pi }{4}$ is given by [11, Section 7.12, Equation 7.12.1]

$$\begin{aligned} {\text {erf}}\,z\sim 1-\frac{e^{-z^{2}}}{\sqrt{\pi }}\sum _{m=0}^{\infty }(-1)^{ m}\frac{{\left( {1/2}\right) _{m}}}{z^{2m+1}} \end{aligned}$$

(4)

and

$$\begin{aligned} {\text {erf}}\,(-z)\sim -1+\frac{e^{-z^{2}}}{\sqrt{\pi }}\sum _{m=0}^{\infty }(-1)^{ m}\frac{{\left( {1/2}\right) _{m}}}{z^{2m+1}}. \end{aligned}$$

(5)

Simple error bounds for these two asymptotic expansions are indicated in [11, Section 7.12]; they are not uniform in $\vert z\vert$, as they blow up when $z\rightarrow 0$. Other expansions in series of Bessel functions and spherical Bessel functions can be found in [9, pp. 57–58] and [11, Section 7.6] respectively. We do not give details here since, in contrast to the above expansions, these expansions are not given in terms of elementary functions.

In this paper we derive a convergent expansion of ${\text {erf}}\,z$ in terms of elementary functions that holds uniformly in z in the double sector $\vert \arg (\pm z)\vert <\pi /4$. To this end, we apply the method introduced in [8]. This technique provides a general theory of analytic expansions of integral transforms with the following properties: (i) it is uniform in a selected variable z in an unbounded subset of the complex plane that includes the point $z=0$; (ii) it is convergent; (iii) it is given in terms of elementary functions of z. This method was previously applied successfully to a selection of different special functions (see [2,3,4,5,6,7]).

For the application of this method to the error function, the starting point is an integral representation different from (1) that we specify below. As an illustration of the approximations that we are going to obtain, we anticipate the following ones, valid for $\vert \arg (\pm z)\vert <\pi /4$

$$\begin{aligned} {\text {erf}}\,z=\frac{4 z e^{-z^2} \left( \pi e^{2 z^2} z^4+3\right) }{\sqrt{\pi } \left( 4 z^4-2 z^2+3+\sqrt{16 \pi e^{2 z^2} z^{10}+16 z^8+32 z^6+28 z^4-12 z^2+9}\right) } +\theta _2(z), \end{aligned}$$

with $|\theta _2(z)|\le 0.0517371$ for $z>0$ or

$$\begin{aligned} {\text {erf}}\,z=\frac{4 z e^{-z^2} \left( 4 \pi e^{2 z^2} z^8+20 z^4+40 z^2+105\right) }{\sqrt{\pi } \left[ 16 z^8- 8 z^6+ 12 z^4 - 30 z^2 +105 + \sqrt{s(z})\right] }+\theta _3(z), \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} s(z):=&\,256 z^{16}+1024 z^{14}+3008 z^{12}+5568 z^{10}+3984 z^8-2400 z^6+3420 z^4\\ {}&-6300 z^2 +256 \pi e^{2 z^2} z^{18}+11025, \end{aligned} \end{aligned}$$

(6)

and $|\theta _3(z)|\le 0.031527$ for $z>0$. For complex z in the double sector $\vert \arg (\pm z)\vert <\pi /4$ the error bounds $\theta _2(z)$ and $\theta _3(z)$ are less sharp (we specify them below).

Because of the symmetry ${\text {erf}}\,(-z)=-{\text {erf}}\,z$, in the following, we only consider without loss of generality, $\Re z>0$. Also, through all the paper we use the principal argument $\arg z\in (-\pi ,\pi ]$ for any complex number z, and square roots assume their principal value. Section 2 contains the main result of the paper and Section 3 some numerical experiments showing the accuracy and some properties of the expansion.

2 A Uniform Convergent Expansion of ${\text {erf}}\,z$

We first consider the following lemma that will be useful in the proof of the main result of the paper.

Lemma 1

For $z\in {\mathbb {C}}$, $\vert \arg z\vert \le \pi$, we have that $|1+\sqrt{1+z}|\ge |\sqrt{z}|$.

Proof

We define $w:=\sqrt{z+1}$. We have that $|\arg (z+1)|\le \pi$, and then $\Re w\ge 0$, and it is clear that

$$\begin{aligned} |w+1|\ge |w-1|\; \Rightarrow \; |\sqrt{w+1}|\ge |\sqrt{w-1}|\; \Rightarrow \;|w+1|\ge |\sqrt{w^2-1}|. \end{aligned}$$

The result follows by replacing w by $\sqrt{z+1}$. $\square$

Theorem 1

Consider $z\in {\mathbb {C}}$ with $\vert \arg z\vert <\pi /4$. Then, for $n=1,3,5,\ldots$,

$$\begin{aligned} {\text {erf}}\,z=\frac{2e^{-z^2}}{\sqrt{\pi }}\frac{\frac{\pi }{4}z^{2n-1}e^{2z^2} +{\mathcal {B}}_n(z^2)}{{\mathcal {A}}_n(z^2)+\sqrt{{\mathcal {A}}_n^2(z^2) +\frac{\pi }{4}z^{4n-2}e^{2z^2}+z^{2n-1}{\mathcal {B}}_n(z^2)}} +R_n(z), \end{aligned}$$

(7)

where ${\mathcal {A}}_n(z^2)$ and ${\mathcal {B}}_n(z^2)$ are polynomials that, for convenience, we write in the form

$$\begin{aligned} {\mathcal {A}}_n(z):=z^{n-1/2}A_n(z), \quad A_n(z):=\sum _{k=0}^{n-1}(-1)^k(1/2)_k\frac{1}{2 z^{k+1/2}}, \end{aligned}$$

(8)

$$\begin{aligned} {\mathcal {B}}_n(z):=z^{n-1/2}B_n(z), \quad B_n(z):=\sum _{k=0}^{n-1}(-1)^k\sum _{j=0}^{k-1}\frac{(k-j+1/2)_j}{2 z^{j+1}}. \end{aligned}$$

(9)

The remainder term $R_n(z)$ is bounded in either of the following forms

$$\begin{aligned} |R_n(z)| \le \sqrt{\frac{4}{\pi }\sum _{k=0}^{n-1}\frac{(-1)^{n-k+1}}{2k+1}-1}, \qquad |R_n(z)|\le \frac{2}{\sqrt{\pi (2n+1)}}. \end{aligned}$$

(10)

For $z>0$ we have the sharper bounds

$$\begin{aligned} |R_n(z)|\le \frac{2}{\pi }\sum _{k=0}^{n-1}\frac{(-1)^{n-k+1}}{2k+1}-\frac{1}{2}, \qquad |R_n(z)|\le \frac{2}{\pi (2n+1)}. \end{aligned}$$

(11)

Proof

We consider the alternative integral representation of the error function [11, Section 7.7, Equation 7.7.5]

$$\begin{aligned} F(a):=\frac{\pi }{4}e^a(1-({\text {erf}}\,\sqrt{a})^2)=\int _0^1\frac{e^{-at^2}}{1+t^2}\,\mathrm{{d}}t, \quad \Re a>0, \end{aligned}$$

(12)

and the Taylor expansion of the factor $1/(1+t^2)$ in (12) at the end point $t=0$ of the integration interval (0, 1),

$$\begin{aligned} \frac{1}{1+t^2}=\sum _{k=0}^{n-1}(-1)^k t^{2k}+r_n(t), \end{aligned}$$

(13)

where $r_n(t)$ is the remainder term

$$\begin{aligned} r_n(t):=\sum _{k=n}^{\infty }(-1)^k t^{2k}=\frac{(-t^2)^n}{1+t^2}. \end{aligned}$$

(14)

Replacing expansion (13) into (12) and interchanging sum and integral we obtain, for any $n=1,2,3,\ldots$,

$$\begin{aligned} F(a)=\sum _{k=0}^{n-1}(-1)^k\gamma _k(a)+{\tilde{R}}_n(a), \end{aligned}$$

(15)

with

$$\begin{aligned} \gamma _k(a):=\int _0^1e^{-at^2}t^{2k}\mathrm{{d}}t, \qquad {\tilde{R}}_n(a):=(-1)^n\int _0^1 e^{-at^2}\frac{t^{2n}}{1+t^2}\,\mathrm{{d}}t. \end{aligned}$$

(16)

After the change of variable $t^2\rightarrow s$ in the integral definition of $\gamma _k(a)$ in (16) we obtain

$$\begin{aligned} \gamma _k(a)=\frac{1}{2}\int _0^1e^{-at}t^{k-1/2}\mathrm{{d}}t. \end{aligned}$$

(17)

Integrating by parts $k-2$ times in (17), we obtain

$$\begin{aligned} \gamma _k(a)=-\frac{e^{-a}}{2a}\sum _{j=0}^{k-1}\frac{(k-j+1/2)_j}{a^j} +\frac{\sqrt{\pi }}{2a^{k+1/2}}\left( \frac{1}{2}\right) _k {\text {erf}}\,\sqrt{a}. \end{aligned}$$

(18)

Before we complete the derivation of formula (7), we need to obtain some error bounds for the remainder term ${\tilde{R}}_n(a)$ in (16). We have that

$$\begin{aligned} |{\tilde{R}}_n(a)|\le \int _0^1 e^{-t^2\Re a}\frac{t^{2n}}{1+t^2}\,\mathrm{{d}}t\le \int _0^1 \frac{t^{2n}}{1+t^2}\,\mathrm{{d}}t= (-1)^n \frac{\pi }{4}+\sum _{k=0}^{n-1}\frac{(-1)^{n-k+1}}{2k+1}.\nonumber \\ \end{aligned}$$

(19)

A different bound of the remainder term in (16) can be found from

$$\begin{aligned} |{\tilde{R}}_n(a)|\le \int _0^1 e^{-t^2\Re a}\frac{t^{2n}}{1+t^2}\,\mathrm{{d}}t\le \int _0^1 \frac{t^{2n}}{1+t^2}\,\mathrm{{d}}t\le \int _0^1 t^{2n}\,\mathrm{{d}}t=\frac{1}{2n+1}. \end{aligned}$$

(20)

We complete now the derivation of formula (7). From (12), (15) and (18), and using the definitions (15) of $A_n$ and $B_n$, we get the following algebraic equation of the second order for the unknown $x:={\text {erf}}\,\sqrt{a}$

$$\begin{aligned} x^2+\frac{4}{\sqrt{\pi }}e^{-a}A_n(a)x-\left[ 1+\frac{4}{\pi }e^{-2a}B_n(a)-\frac{4}{\pi }e^{-a}{\tilde{R}}_n(a)\right] =0, \end{aligned}$$

(21)

where ${\tilde{R}}_n(a)$ has been defined in (16).

Solving equation (21) for x we obtain the two possible solutions

$$\begin{aligned} x_\pm =\frac{2}{\sqrt{\pi }}e^{-a}\left( -A_n(a)\pm \sqrt{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)-e^a{\tilde{R}}_n(a)}\right) . \end{aligned}$$

(22)

To decide which one of these solutions corresponds to ${\text {erf}}\,\sqrt{a}$, we consider the following properties of the error function and $A_n(a)$, $B_n(a)$ and ${\tilde{R}}_n(a)$ for positive a: $A_n(a)>0$ if n is odd; $B_n(a)<0$ if n is even and $B_n(a)>0$ if n is odd; ${\tilde{R}}_n(a)>0$ if n is even and ${\tilde{R}}_n(a)<0$ if n is odd.

• We have that $\lim _{a\rightarrow +\infty }{\text {erf}}\,\sqrt{a}=1$, and only the solution $x_+$ satisfies this condition.

• We have that $\lim _{a\rightarrow 0^+}{\text {erf}}\,\sqrt{a}=0$, and only the solution $x_+$ with n odd satisfies this condition.

Therefore, for odd n, the correct solution is

$$\begin{aligned} {\text {erf}}\,\sqrt{a}=x_+=\frac{2}{\sqrt{\pi }}e^{-a}\left( -A_n(a)+\sqrt{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)}\right) +R_n(a), \end{aligned}$$

(23)

where we have defined

$$\begin{aligned} R_n(a):={} & {} \frac{2}{\sqrt{\pi }}e^{-a}\sqrt{A_n^2(a)+\frac{\pi }{4}e^{2a} +B_n(a)}\nonumber \\{} & {} \left( \sqrt{1-\frac{e^a{\tilde{R}}_n(a)}{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)}}-1\right) . \end{aligned}$$

(24)

Or equivalently

$$\begin{aligned} {\text {erf}}\,\sqrt{a}=\frac{2}{\sqrt{\pi }}e^{-a}\frac{\frac{\pi }{4}e^{2a} +B_n(a)}{A_n(a)+\sqrt{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)}}+R_n(a), \end{aligned}$$

(25)

with n odd. Setting $a=z^2$ and multiplying numerator and denominator of the fraction on the right hand side above by $z^{2n-1}$ we obtain (7) with $R_n(a)$ given above.¹

In the remaining of this proof we derive the error bounds for the remainder term $R_n(a)$ given in the statement of the theorem.

When $a>0$ it is possible to get more accurate bounds for the remainder term $R_n(a)$ in (24). Therefore, we analyze first the particular case $a>0$ and then the general case $\Re a>0$.

• Case $a>0$. We use that $\sqrt{1+x}-1\le x/2$ for all $x>0$, and that, for odd n,

  $$\begin{aligned} \begin{aligned} A_n(a)&=\frac{e^a}{2\sqrt{\pi }}\left[ \pi {\text {erfc}}(\sqrt{a})-(-1)^n\Gamma \left( n+\frac{1}{2}\right) \Gamma \left( \frac{1}{2}-n,a\right) \right] \\&\ge \frac{e^a}{2\sqrt{\pi }}\Gamma \left( n+\frac{1}{2}\right) \Gamma \left( \frac{1}{2}-n,a\right) . \end{aligned}\nonumber \\ \end{aligned}$$

  (26)

  Then

  $$\begin{aligned} \begin{aligned} |R_n(a)|&\le \frac{1}{\sqrt{\pi }}\frac{|{\tilde{R}}_n(a)|}{\sqrt{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)}} \le \frac{1}{\sqrt{\pi }}\frac{|{\tilde{R}}_n(a)|}{\sqrt{A_n^2(a)+\frac{\pi }{4}e^{2a}}}\\&\le \frac{2e^{-a}}{\pi }\frac{|{\tilde{R}}_n(a)|}{\sqrt{1+\frac{1}{\pi ^2}\Gamma ^2 \left( n+\frac{1}{2}\right) \Gamma ^2\left( \frac{1}{2}-n,a\right) }}. \end{aligned}\nonumber \\ \end{aligned}$$

  (27)

  Since $\Gamma (n+1/2)\ge \Gamma (n)=(n-1)!$ and from [10, Section 8.10, Equation 8.10.5],

  $$\begin{aligned} \vert \Gamma (1/2-n,a)\vert>{a^{1/2-n}e^{-a}\over a+n+1/2}, a>0, \end{aligned}$$

  we find that

  $$\begin{aligned} |R_n(a)|\le \frac{2e^{-a}}{\pi }\frac{\left| {\tilde{R}}_n(a)\right| }{\sqrt{1+\frac{1}{\pi ^2}[(n-1)!]^2\frac{a^{1-2n}e^{-2a}}{(n+a+1/2)^2}}}. \end{aligned}$$

  (28)

  Using the bound (19) we find

  $$\begin{aligned} |R_n(a)|\le \frac{2e^{-a}}{\pi }\frac{\left[ (-1)^n \frac{\pi }{4}+\sum _{k=0}^{n-1}\frac{(-1)^{n-k+1}}{2k+1}\right] }{\sqrt{1+\frac{1}{\pi ^2}[(n-1)!]^2 \frac{a^{1-2n}e^{-2a}}{(n+a+1/2)^2}}}, \end{aligned}$$

  (29)

  from where we deduce the first bound in (11) for odd n. On the other hand, using (20) we find

  $$\begin{aligned} |R_n(a)|\le \frac{2e^{-a}}{\pi (2n+1)}\frac{1}{\sqrt{1+\frac{1}{\pi ^2}[(n-1)!]^2\frac{a^{1-2n}e^{-2a}}{(n+a+1/2)^2}}}, \end{aligned}$$

  (30)

  from where we deduce the second bound in (11). From either of the bounds in (11) we see that (7) is a uniform convergent expansion of ${\text {erf}}\,z$ for $z>0$.

• Case $\Re a>0$. We rewrite the remainder (24) in the form

  $$\begin{aligned} \begin{aligned} R_n(a)&=-\frac{2}{\sqrt{\pi }\sqrt{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)}}\frac{{\tilde{R}}_n(a)}{\left( \sqrt{1-e^a\frac{{\tilde{R}}_n(a)}{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)}}+1\right) }. \end{aligned} \end{aligned}$$

  (31)

  Using Lemma 1 with

  $$\begin{aligned} z=-e^a\frac{{\tilde{R}}_n(a)}{A_n^2(a)+\frac{\pi }{4}e^{2a}+B_n(a)} \end{aligned}$$

  we find

  $$\begin{aligned} |R_n(a)|\le \frac{2e^{-\frac{\Re a}{2}}}{\sqrt{\pi }}\sqrt{{\tilde{R}}_n(a)}. \end{aligned}$$

  From bound (19) we have

  $$\begin{aligned} |R_n(a)|\le \frac{2e^{-\frac{\Re a}{2}}}{\sqrt{\pi }}\sqrt{(-1)^n \frac{\pi }{4}+\sum _{k=0}^{n-1}\frac{(-1)^{n-k+1}}{2k+1}}, \end{aligned}$$

  (32)

  and the first bound in (10) follows for odd n. On the other hand, from bound (20),

  $$\begin{aligned} |R_n(a)|\le \frac{2e^{-\frac{\Re a}{2}}}{\sqrt{\pi (2n+1)}}\le \frac{2}{\sqrt{\pi (2n+1)}}, \end{aligned}$$

  (33)

  and the second bound in (10) follows. From any of these bounds we conclude that (7) is a uniform convergent expansion of ${\text {erf}}\,z$ with $z\in {\mathbb {C}}$ and $\vert \arg z\vert <\pi /4$.

$\square$

Fig. 1

Graphics of ${\text {erf}}\, z$ (dashed) and the approximations (2) ( ), (3) ( ), (4)-(5) ( ) and (7) ( ), for $n=1$ (left) and $n=3$ (right) with $z\in [-2,2]$

Fig. 2

Absolute value of the relative errors in the approximation of the real part (left) and the imaginary part (right) of ${\text {erf}}\, (ze^{i\pi /100})$ for $n=3$ ( ), $n=5$ ( ), $n=7$ ( ) and $z\in [0,3]$

Fig. 3

Absolute value of the relative errors (r.e.) in the approximation of ${\text {erf}}\, z$ using the approximations (2) ( ), (3) ( ), (4) ( ) and (7) (dashed). The first graph corresponds to $n=1$ in the interval [0, 2], and the second one to $n=5$ in the interval [1, 2.5]

Table 1 Absolute value of the relative errors in the approximation of ${\text {erf}}\, (z)$ using (2), (3), (4) and (7) with the series truncated after n terms for $z=2.5$

Table 2 Absolute value of the relative errors in the approximation of ${\text {erf}}\, (2\,e^{i\arg z})$ using (7) with the series truncated after n terms and different values of $\arg z\in [0,\pi /4)$

3 Numerical Experiments

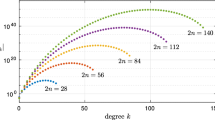
In the following pictures we compare ${\text {erf}}\, z$ to the approximations provided by the Taylor expansions (2) and (3), the asymptotic expansion (4), and the uniform expansion (7) for different (odd) values of n. All the computations were carried out with the symbolic manipulator Wolfram Mathematica 11.3; in particular, the command Erf was used to compute the “exact” value of the error function (Figs. 1, 2, 3). Expansions (2) and (3) are more competitive for small |z|, whereas expansion (4) is more competitive for large |z|. However, expansion (7) is more competitive for intermediate values of |z| and moreover, it is more competitive globally, in $L_1$ norm say (Tables 1, 2).