1 Introduction

Until the selection of the Advanced Encryption Standard [13], Feistel Networks (FN) have undoubtedly been the most popular design framework for iterated block ciphers, whose popularity is today shared with those of Substitution Permutation Networks (SPN). Feistel Networks are characterized by the idea of splitting the message into two halves, say left part and right part, and applying in each round a key-dependent non-linear transformation, called F-function, to the right part, which is successively mixed with the left part, just before the two halves are swapped [14]. As a notable feature, FNs do not require the F-function to be invertible to perform decryption. The framework of SPNs is instead characterized by a sequence of carefully designed key-dependent round functions made by invertible layers acting on the whole block, whose composition provides increasing global complexity. If, on the one hand, SPNs’ minimalistic design allows a simple description and consequently a more careful security assessment, on the other hand, the structure of FNs gives the designers more freedom in the choice of the layers intervening during the encryption, although keeping the transformation confined only in typically half of the block in a single round.

The Lai–Massey scheme (LM) [27], born from the design strategy of IDEA [18, 19], combines the advantages of both frameworks, splitting the message into two halves but mixing the left and right part of the state and consequently getting the entire message involved in the round transformation. In terms of security, its pseudo-randomness behavior, its resistance to impossible differential cryptanalysis and other generic attacks has been addressed in recent years [16, 22, 23, 29]. Little is known,Footnote 1 instead, on the group-theoretical security of such a design strategy, whereas the one of SPNs and FNs has been generally addressed in several works in the last decades.

The contribution of this paper is a group-theoretical analysis of the LM scheme aimed at detecting invariant subspaces, i.e. subspaces of the message space which are invariant under the encryption functions and whose knowledge can be exploited by the cryptanalysts, which are studied by looking at the group generated by the round functions of the cipher. Such a group, probably already investigated in the Cold War context, was first defined in 1975 by Coppersmith and Grossman [11]. In 1999, Paterson introduced the imprimitivity attack showing, in a DES-like cipher, that the group \(\Gamma \) generated by the encryption functions may be imprimitive, i.e. it may exist a partition of the message space which is invariant under the action of \(\Gamma \) and whose knowledge can be exploited to significantly reduce the complexity of a brute-force attack. Later, a similar methodology called invariant subspace attack has been introduced for the cryptanalysis of PRINTcipher [20]. Today, the resistance to the imprimitivity attack of many known constructions has been proved [1, 2, 10, 25, 26], and primitivity conditions have been established also for large families of ciphers. For example, Aragona et al. [3, Theorem 4.5] have shown that the primitivity of the group generated by the rounds of an FN can be reduced to the primitivity of the group generated by the rounds of an SPN whose round functions are the ones implemented as F-functions within each round of the FN. In other words, they prove that the primitivity of structure of an FN, in spite of its complexity, can be inherited from a simpler design.

Using a similar approach, we prove here that the primitivity of the group generated by the rounds of an SPN implies the one of a group containing the group generated by the rounds of an LM which features in its structure the same key-dependent transformation acting in the SPN. The cryptographic implication of the result is twofold: on one hand we show, as in the case of FN, that the primitivity of LM schemes can be inherited from simpler designs; on the other hand, we show that in a LM scheme with 2n bits, it is enough to search for invariant subspaces in an n-dimensional space.

1.1 Organization of the Paper

In Sect. 2, we introduce the notation and the preliminary results, and present our algebraic model of Lai–Massey scheme which is the subject of the study. In Sect. 3, we prove the primitivity reduction from the LM to the SPN. Some results on the existence of invariant subspaces in the classical LM scheme are presented in Sect. 4. The paper is concluded with final considerations and open problems in Sect. 5.

2 Preliminaries and the Lai–Massey Scheme

Let us introduce some notation and preliminary results.

2.1 Spaces

Let n be a non-negative integer and \(V \mathrel {{\mathop {=}\limits ^{{{\tiny {\mathrm{def}}}}}}}{{\,\mathrm{\mathbb {F}}\,}}_2^n\) be the n-dimensional vector space over \({{\,\mathrm{\mathbb {F}}\,}}_2\). We denote by \({{\,\mathrm{Sym}\,}}(V)\) the symmetric group acting on V and by \({\mathbb {1}}\) its identity. The map \({\mathbb {0}} : V \rightarrow V\) denotes the null function. The group of the translations on V, i.e. the group of the maps \(\sigma _v: V \rightarrow V\), such that \(x\mapsto x+v\), is denoted by \(T_n\), whereas the group of translations on \(V \times V\) is denoted by \(T_{2n}\), where the translation \(\sigma _{(v,w)}\) acts on (x, y) as \((x,y)\mapsto (x+v, y+w)\). Let us also denote by \({{\,\mathrm{AGL}\,}}(V)\) the group of all affine permutations of V and by \({{\,\mathrm{GL}\,}}(V)\) the group of the linear ones.

2.1.1 Groups

Let G be a group acting on a set \(M\). For each \(g \in G\) and \(v \in M\) we denote the action of g on v as vg. The group G is said to be transitive on \(M\) if for each \(v,w \in M\) there exists \(g \in G\) such that \(vg=w\). A partition \({\mathcal {B}}\) of \(M\) is trivial if \({\mathcal {B}}=\{M\}\) or \({\mathcal {B}}=\{\{v\} \mid v \in M\}\), and G-invariant if for any \(B \in {\mathcal {B}}\) and \(g \in G\) it holds \(Bg \in {\mathcal {B}}\). Any non-trivial and G-invariant partition \({\mathcal {B}}\) of \(M\) is called a block system for G. In particular any \(B \in {\mathcal {B}}\) is called an imprimitivity block. The group G is primitive in its action on \(M\) (or G acts primitively on \(M\)) if G is transitive and there exists no block system. Otherwise, the group G is imprimitive in its action on \(M\) (or G acts imprimitively on \(M\)). We recall here some well-known results that will be useful in the remainder of this paper [8].

Lemma 2.1

If T is a transitive subgroup of G, then a block system for G is also a block system for T.

Lemma 2.2

Let \(M\) be a finite vector space over \({\mathbb {F}}_2\) and T its translation group. Then T is transitive and imprimitive on \(M\). A block system \({\mathcal {U}}\) for T is composed by the cosets of a non-trivial and proper subgroup \( U < (M,+)\), i.e.

$$\begin{aligned} {\mathcal {U}} = \{ U + v \mid v \in M \}. \end{aligned}$$

2.1.2 Ciphers

A block cipher \(\Phi \) is a family of key-dependent permutations

$$\begin{aligned} \{E_K \mid E_K: \ M \rightarrow M, \, K \in {\mathcal {K}} \}, \end{aligned}$$

where \(M\) denotes the message space and \({\mathcal {K}}\) is called the key space. The permutation \(E_K\) is called the encryption function induced by the user-provided key K. The block cipher \(\Phi \) is called an iterated block cipher if there exists \(r \in {\mathbb {N}}\) such that for each \(K \in {\mathcal {K}}\) the encryption function \(E_K\) is obtained as the composition of r round functions, i.e. \(E_K = \varepsilon _{1,K}\,\varepsilon _{2,K}\ldots \varepsilon _{r,K}\). To provide efficiency, each round function is the composition of a public component provided by the designers, and a private component derived from the user-provided key by means of the public procedure known as key-schedule. The group

$$\begin{aligned} \Gamma _{\infty }(\Phi )\mathrel {{\mathop {=}\limits ^{{{\tiny {\mathrm{def}}}}}}}\langle \varepsilon _{i,K} \mid K \in {\mathcal {K}}, 1 \le i \le r\rangle \end{aligned}$$

called the group generated by the round functions of \(\Phi \), is studied to prevent group-theoretical attacks [7, 17, 24].

An iterated block cipher \(\Phi \) is called an r-round Substitution Permutation Network (SPN) if \(M = V\) and for each \(1 \le i \le r\) we have

$$\begin{aligned} \varepsilon _{i,K} \mathrel {{\mathop {=}\limits ^{{{\tiny {\mathrm{def}}}}}}}\rho \sigma _{k_i}, \end{aligned}$$

where \(\rho \in {{\,\mathrm{Sym}\,}}(V)\setminus {{\,\mathrm{AGL}\,}}(V)\), and \(\rho = \gamma \lambda \) is the composition of a brick-layer transformation \(\gamma \) and a linear layer \(\lambda \). If \(\Phi \) is an SPN, then it is easy to check that \(\Gamma _{\infty }(\Phi ) = \left\langle \rho , T_n\right\rangle \).

2.2 A Model for the Lai–Massey Scheme

We introduce here our algebraic description of the Lai–Massey scheme [18] as presented by Vaudenay [27] and our further generalization studied in this paper. We assume that the function acting inside the LM transformation is bijective.

Fig. 1
figure 1

The ith round function of a Lai–Massey cipher

Full size image

Definition 2.3

Let r be a non-negative integer, \(\rho \in {{\,\mathrm{Sym}\,}}(V){\setminus } {{\,\mathrm{AGL}\,}}(V)\) and \(\pi \in {{\,\mathrm{GL}\,}}(V)\). An r-round Lai–Massey cipher \({{\mathrm {LM}}}(\rho ,\pi )\) is a set of encryption functions

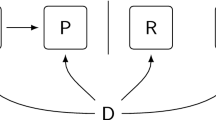
$$\begin{aligned} \{E_K \mid K \in {\mathcal {K}}\} \subseteq {{\,\mathrm{Sym}\,}}(V\times V), \end{aligned}$$

such that for each \(K \in {\mathcal {K}}\) the map \(E_K\) is the composition of r functions, i.e. \(E_K =\overline{\varepsilon _{1,K}}\,\overline{\varepsilon _{2,K}}\ldots \overline{\varepsilon _{r,K}}\). The ith round function \(\overline{\varepsilon _{i,K}}\), displayed in Fig. 1, is defined as

$$\begin{aligned} \overline{\varepsilon _{i,K}} \mathrel {{\mathop {=}\limits ^{{{\tiny {\mathrm{def}}}}}}}\overline{\rho }\, \overline{\pi }\sigma _{({k_i}\pi ,k_i)}, \end{aligned}$$
(2.1)

where

  • \(\overline{\rho }\) denotes the formal operator \( \begin{pmatrix} {\mathbb {1}} &{} {\mathbb {1}}\\ {\mathbb {1}} &{} {\mathbb {0}} \end{pmatrix} \begin{pmatrix} {\mathbb {1}}&{} {\mathbb {1}}+\rho \\ {\mathbb {0}} &{} {\mathbb {1}} \end{pmatrix} \in {{\,\mathrm{Sym}\,}}(V\times V)\);

  • \(\overline{\pi }\) denotes the formal operator \(\begin{pmatrix} \pi &{} {\mathbb {0}}\\ \pi &{} {\mathbb {1}} \end{pmatrix} \in {{\,\mathrm{Sym}\,}}(V\times V)\);

  • the key-schedule \({\mathcal {K}} \rightarrow V^{r}\), \(K \mapsto (k_1,k_2,\ldots ,k_r)\) is surjective with respect to any round.

The same construction is an r-round generalized Lai–Massey cipher when the key addiction in the round function of Eq. (2.1) is replaced by the more general \(\sigma _{({k_i},k_j)}\), for \((k_i,k_j) \in V\times V\).

Remark 2.4

Notice that, by the assumption on the key-schedule, we can always assume without loss of generality that \(0\rho = 0\), provided that, in each round, the value \((0\rho \pi ,0\rho )\) is added to the round key of the previous iteration. Moreover, it is well known that, for security concerns, the permutation \(\pi \) is required to be an orthomorphism [27], i.e. \({\mathbb {1}} + \pi \) is a permutation. However, we do not make use of this hypothesis in our analysis. We strongly use, instead, the assumption that such a function is linear.

The previous formal definition coincides with the classical definition given by Vaudenay [27] of LM schemes where \(\rho \) is bijective. Indeed, given \((x,y) \in V\times V\), we have

$$\begin{aligned} (x,y)\overline{\varepsilon _{i,K}} = \big ((x+(x+y)\rho +k_i)\pi , y+(x+y)\rho +k_i\big ). \end{aligned}$$

Moreover, it is easy to check that \(\overline{\varepsilon _{i,K}}\) is invertible with the following inverse

$$\begin{aligned} \overline{\varepsilon _{i,K}}^{\,-1} = \overline{\pi }^{-1}\overline{\rho }^{-1}\sigma _{(k_i,k_i)}, \end{aligned}$$

where \(\overline{\rho }^{-1} = \begin{pmatrix} {\mathbb {1}}+\rho &{} \rho \\ {\mathbb {1}} &{} {\mathbb {1}} \end{pmatrix} \) and \(\overline{\pi }^{-1} = \begin{pmatrix} \pi ^{-1} &{} {\mathbb {0}}\\ {\mathbb {1}} &{} {\mathbb {1}} \end{pmatrix} \).

Note that, as in the Feistel Network case, the inverse \(\overline{\varepsilon _{i,K}}^{\, -1}\) of the round function \(\overline{\varepsilon _{i,K}}\) of a Lai–Massey cipher does not involve the inverse of \(\rho \). We have nonetheless assumed that \(\rho \) is bijective since in our result it is used as generator of a group.

It is worth mentioning that even if IDEA was the starting point for the definition of the LM framework, it does not fit in the presentation of Definition 2.3 since, e.g. in IDEA the round key is mixed to the state using operations different from the XOR.

Let us now define the group generated by the permutations as in Eq. (2.1), keeping the classical notation with the infinity symbol, and a larger group.

Definition 2.5

Given \(\rho \in {{\,\mathrm{Sym}\,}}(V)\setminus {{\,\mathrm{AGL}\,}}(V)\) and \(\pi \in {{\,\mathrm{GL}\,}}(V)\), let us define

$$\begin{aligned} \Gamma _\infty ({{\mathrm {LM}}}(\rho ,\pi ))&\mathrel {{\mathop {=}\limits ^{{{\tiny {\mathrm{def}}}}}}}&\left\langle \overline{\rho }\,\overline{\pi }\sigma _{({k_i}\pi ,k_i)}\mid k_i \in V\right\rangle , \end{aligned}$$
(2.2)
$$\begin{aligned} \Gamma _{\infty }({{\mathrm {GLM}}}(\rho ,\pi ))&\mathrel {{\mathop {=}\limits ^{{{\tiny {\mathrm{def}}}}}}}&\left\langle \overline{\rho }\overline{\pi }, T_{2n}\right\rangle . \end{aligned}$$
(2.3)

Notice that the former is the group generated by the round functions of the LM scheme; the latter is the group of the rounds of a generalized LM scheme, containing all the round functions of the LM scheme as well as the entire translation group on 2n bits. The group of Eq. (2.3), in fact, corresponds to a generalized key action in the LM scheme, since in each round the key \(({k_i}\pi ,k_i)\) is replaced by the more general \(({k_i},k_j)\).

Since, as anticipated, we aim at proving a primitivity reduction from the generalized LM scheme to a suitable SPN, we need the definition of a third group, which contains \(\Gamma _{\infty }({{\mathrm {GLM}}}(\rho ,\pi ))\) and which is better linked to the SPN, as we will prove below.

Definition 2.6

Given \(\rho \in {{\,\mathrm{Sym}\,}}(V)\setminus {{\,\mathrm{AGL}\,}}(V)\) and \(\pi \in {{\,\mathrm{GL}\,}}(V)\), let us define

$$\begin{aligned} \Gamma ({{\mathrm {GLM}}}(\rho ,\pi )) \mathrel {{\mathop {=}\limits ^{{{\tiny {\mathrm{def}}}}}}}\left\langle \overline{\rho }, \overline{\pi }, T_{2n}\right\rangle . \end{aligned}$$
(2.4)

Notice that \( \Gamma _\infty ({{\mathrm {LM}}}(\rho ,\pi )) \le \Gamma _\infty ({{\mathrm {GLM}}}(\rho ,\pi )) \le \Gamma ({{\mathrm {GLM}}}(\rho ,\pi )). \)

Remark 2.7

On the one hand, considering a generalized key action and larger groups is a necessary technical detail because, to prove the primitivity, we need to make sure that the group under consideration is transitive and in particular that it contains the whole translation group (see Lemma 2.2). On the other hand the imprimitivity of \(\Gamma ({\mathrm {GLM}}(\rho ,\pi ))\) implies that both \(\Gamma _\infty ({\mathrm {GLM}}(\rho ,\pi ))\) and \(\Gamma _\infty ({\mathrm {LM}}(\rho ,\pi ))\) are imprimitive. Therefore, once invariant subspaces for \(\Gamma ({\mathrm {GLM}}(\rho ,\pi ))\) are found, they are invariant subspaces also for \(\Gamma _\infty ({\mathrm {LM}}(\rho ,\pi ))\). Notice that considering every possible translation in \(T_{2n}\) in Eqs. (2.3) and (2.4) also means that, even in the generalized case, the study is carried out without considering the role of the particular choice of the key-schedule. This is however a common practice in the study of the primitivity of the groups generated by the rounds of a cipher, except for some recent results [4, 6].

In the following section, we will prove our main contribution, i.e. that \(\Gamma ({\mathrm {GLM}}(\rho ,\pi ))\) is primitive provided that \(\left\langle \rho , T_n\right\rangle \) is primitive. It is worth mentioning again that \(\left\langle \rho , T_n\right\rangle \) is the group generated by the round functions of the SPN whose function \(\rho \) is the same that composes the building block for the round functions of the LM. In this sense, the primitivity of a generalized Lai–Massey scheme is reduced to the one of the corresponding SPN with half of the block size.

3 The Primitivity Reduction

To prove our results, we need to determine a block system for \(V \times V\). To do so, we use the following characterization of subgroups of the direct product of two groups in terms of suitable sections of the direct factors [15].

Theorem 3.1

(Goursat’s Lemma) Let \(G_1\) and \(G_2\) be two groups. There exists a bijection between

  1. 1.

    the set of all subgroups of the direct product \(G_1\times G_2\), and

  2. 2.

    the set of all triples \((A/B,C/D,\psi )\), where

    • A is a subgroup of \(G_{1}\);

    • C is a subgroup of \(G_{2}\);

    • B is a normal subgroup of A;

    • D is a normal subgroup of C;

    • \(\psi : A/B\rightarrow C/D\) is a group isomorphism.

Then each subgroup of \(G_1\times G_2\) can be uniquely written as

$$\begin{aligned} U_{\psi }= \{ (a,c) \in A \times C : (a + B) \psi =c + D \}. \end{aligned}$$

Note that the isomorphism \(\psi : A/B\rightarrow C/D\) induces a homomorphism \(\varphi : A \rightarrow C\) such that \((a+B)\psi =a\varphi + D\) for any \(a\in A\), and \(B\varphi \le D\). Such homomorphism is not unique.

Corollary 3.2

([3]) Using notation of Theorem 3.1, given any homomorphism \(\varphi \) induced by \(\psi \), we have

$$\begin{aligned} U_{\psi } = \{ (a, a \varphi + d) \mid a \in A, d \in D \}. \end{aligned}$$
(3.1)

Definition 3.3

A subgroup \( U \le V\times V\) is a linear block for \(f \in {{\,\mathrm{Sym}\,}}(V\times V)\) if for each \((v,w) \in V\times V\) there exists \((v',w') \in V \times V\) such that

$$\begin{aligned} (U +(v,w))f = U+(v',w'). \end{aligned}$$
(3.2)

Notice that we can always assume \((v',w') = (v,w)f.\)

In the following result, we assume the existence of a linear block U for \(\overline{\rho }\). In this case, we have

$$\begin{aligned}(v',w') = (v+w, w+(v+w)\rho ).\end{aligned}$$

Moreover, it is easy to check that U is a linear block also for \(\overline{\rho }^{-1}\), from which we obtain

$$\begin{aligned}(U +(v,w))\overline{\rho }^{-1} = U +(v+w+v\rho ,w+v\rho ).\end{aligned}$$

We use Theorem 3.1 and Corollary 3.2 to provide an useful decomposition of U. The explicit dependence of all the groups from \(\rho \) is here omitted.

Lemma 3.4

Let \(U \le V \times V\), and let \(A,B,C,D \le V\) and \(\varphi : A \rightarrow C\) an homomorphism such that \(U = \{ (a, a \varphi + d) \mid a \in A, d \in D\}\). Let us assume that U is a linear block for \(\overline{\rho }\). Then the following conditions hold:

  1. 1.

    \(D \le A\);

  2. 2.

    \(A \varphi \le A\);

  3. 3.

    \(D \varphi \le D\).

Proof

Since U is a linear block for \(\overline{\rho }\), taking \(u=v=0\) in Eq. (3.2) we have that for each \(a \in A\) and \(d \in D\) there exist \(x \in A\) and \(y \in D\) such that

$$\begin{aligned} (a,a\varphi +d)\overline{\rho }= & {} (a,a\varphi +d) \begin{pmatrix} {\mathbb {1}} &{} {\mathbb {1}}\\ {\mathbb {1}} &{} {\mathbb {0}} \end{pmatrix} \begin{pmatrix} {\mathbb {1}}&{} {\mathbb {1}}+\rho \\ {\mathbb {0}} &{} {\mathbb {1}} \end{pmatrix} \\= & {} (a+a\varphi +d,a\varphi +d + (a+a\varphi +d)\rho )\\= & {} (x,x\varphi +y). \end{aligned}$$

If \(a=0\), then \(x=d\) and, therefore, \(D \le A\), so (1) is proved. If \(d=0\), then \(x = a + a\varphi \) and, therefore, \(A\varphi \le A\), which is (2). As noticed, U is also a linear block for \(\overline{\rho }^{-1}\), hence for each \(a \in A\) and \(d \in D\) there exist \(x \in A\) and \(y \in D\) such that

$$\begin{aligned} (a,a\varphi +d) \overline{\rho }^{-1}= & {} (a,a\varphi +d) \begin{pmatrix} {\mathbb {1}}+\rho &{} \rho \\ {\mathbb {1}} &{} {\mathbb {1}} \end{pmatrix} \\= & {} (a+a\varphi +d+a\rho , a\varphi +d+a\rho )\\= & {} (x,x\varphi + y). \end{aligned}$$

If \(a=0\), then \(y=d\varphi +d\), and consequently \(d\varphi \in D\), which proves (3). \(\square \)

We now use the previous lemma to show our main result on the primitivity of the Lai–Massey scheme. Notice that the result is valid for any choice of \(\pi \).

Theorem 3.5

If \(\left\langle \rho , T_n\right\rangle \) is primitive, then \(\Gamma ({\mathrm {GLM}}(\rho ,\pi ))\) is primitive.

Proof

It is enough to prove that \(\left\langle \overline{\rho }, T_{2n}\right\rangle \) is primitive. Let us assume that it is imprimitive, i.e. that there exists a block system \({\mathcal {U}}\) for \(\left\langle \overline{\rho }, T_{2n}\right\rangle \). Then, from Lemma 2.2, the block system is \({\mathcal {U}} = \{U + (v,w) \mid (v,w) \in V\times V\}\) for a non-trivial proper subspace U of \(V\times V\). Since U is a linear block for \(\overline{\rho }\), we have that for each \((v,w) \in V\times V\) and for each \(a \in A\) and \(d \in D\) there exist \(x \in A\) and \(y \in D\) such that

$$\begin{aligned}&(a+v, a\varphi + d+ w)\overline{\rho }\\&\quad = (a+a\varphi +d+v+w, (a+a\varphi +d+v+w)\rho + a\varphi +d+w) \\&\quad = (x+v+w, x\varphi +y+w+(v+w)\rho ). \end{aligned}$$

If \(a=0\), then \(x=d\) and

$$\begin{aligned} y+ d\varphi +d+(v+w)\rho = (d+v+w)\rho . \end{aligned}$$

From Lemma 3.4 we have \(d\varphi \in D\), and therefore, since \(\rho \) is bijective, we obtain the equality

$$\begin{aligned} (D+v+w) \rho = D+(v+w) \rho . \end{aligned}$$

If D is a non-trivial proper subgroup of V, then \(\{D+v \mid v \in V\}\) is a block system for \(\left\langle \rho , T_n\right\rangle \), which proves our claim. To conclude the proof, let us prove that both the assumptions \(D=\{0\}\) and \(D={{\,\mathrm{\mathbb {F}}\,}}_2^n\) lead to contradictions.

\([\mathbf {D} = {{\,\mathrm{\mathbb {F}}\,}}_\mathbf {2}^\mathbf {n}]\) Since \(D \le A\), then \(A= {{\,\mathrm{\mathbb {F}}\,}}_2^n\), and therefore \(B=C = {{\,\mathrm{\mathbb {F}}\,}}_2^n\), since from the hypothesis \(A/B \cong C/D\). This proves that U is not proper, a contradiction.

\([\mathbf {D} = \{\mathbf {0}\}]\) In this case we have \(U = \{(a,a\varphi ) \mid a \in A\}\), and so, for each \((v,w) \in V\times V\) and for each \(a \in A\) there exists \(x \in A\) such that

$$\begin{aligned} (a+v,a\varphi +w)\overline{\rho }= & {} (a+a\varphi +v+w, (a+a\varphi +v+w)\rho + a\varphi +w)\\= & {} (x+v+w, x\varphi +w+(v+w)\rho ), \end{aligned}$$

then \(x= a+a\varphi \) and

$$\begin{aligned} (a+a\varphi +v+w)\rho = a\varphi ^2+(v+w)\rho . \end{aligned}$$
(3.3)

Since \(B\varphi \le D\), then \(B\varphi = \{0\}\) and so, if \(a \in B\) from Eq. (3.3) we obtain

$$\begin{aligned} (a+v+w)\rho =(v+w)\rho , \end{aligned}$$

which implies \(a= 0\), i.e. \(B=\{0\}\). This proves that \(\varphi = \psi : A \rightarrow C\) is an isomorphism. But \(A\varphi \le A\), from Lemma 3.4, therefore \( \varphi \) is an automorphism of A and, from Eq. (3.3), we obtain

$$\begin{aligned} (A+v+w)\rho = A + (v+w)\rho . \end{aligned}$$

In the case under consideration, i.e. when \(D = \{0\}\), the claim is proved by showing that \(\{A+v \mid v \in V\}\) is a block system. This is addressed in the remainder of the proof. Let us prove that A is non-trivial and proper. If \(A = \{0\}\), then \(C = D = \{0\}\), and so also \(B = \{0\}\); therefore, U is trivial, a contradiction. To conclude, let us assume \(A = {{\,\mathrm{\mathbb {F}}\,}}_2^n\). From Eq. (3.3), setting \(v=w=0\), we obtain that \(a\varphi ^2=(a+a\varphi )\rho \). If \(a \in A\) is a fixed point of \(\varphi \), i.e. \(a = a\varphi \), then \((a+a\varphi )\rho = 0\), and so \(a\varphi ^2 = 0\). Therefore \(a = 0\), since \(\varphi \) is an automorphism. We have proved that \(\varphi \) is fixed-point free, except for the trivial one \(a=0\), from which it follows that \({\mathbb {1}} + \varphi \) is injective and, since \(A \varphi \le A\), we have \(\{a+a\varphi \mid a \in A\} = A = {{\,\mathrm{\mathbb {F}}\,}}_2^n\). Therefore \(\rho \) is linear on \({{\,\mathrm{\mathbb {F}}\,}}_2^n\), a contradiction. \(\square \)

We have already observed that \(\left\langle \rho , T_n\right\rangle \) is the group \(\Gamma _{\infty }(\Phi )\) generated by the rounds of the Substitution Permutation Network \(\Phi \) whose ith round function is \(\varepsilon _{i,K} = \rho \sigma _{k_i}\) for some \(\rho = \gamma \lambda \in {{\,\mathrm{Sym}\,}}(V)\setminus {{\,\mathrm{AGL}\,}}(V)\). The conditions which prove \(\Gamma _{\infty }(\Phi )\) primitive in the case of the SPNs has been extensively studied, due to the popularity of the design framework. It has been proved that the primitivity is granted for example when \(\rho \) features a non-linear layer \(\gamma \) which satisfies some well-established conditions of non-linearity, provided that it is followed by a diffusion map \(\lambda \) providing sufficient diffusion. The interested reader may refer to Caranti et al. [10], where the primitivity of SPNs is studied in the larger context of translation-based ciphers, or to Aragona et al. [2].

3.1 Different Rounds

In our analysis, we have assumed that, for sake of simplicity, in both the cases of SPNs and of LMs, the same round function is applied to each round, with the only exception of the round key. It is worth being mentioned here that almost no real cipher can exactly fit this model, due to the natural need to differentiate the encryption routine for both security and efficiency reasons (see, e.g. the first and last round of AES [13]). However, this does not represent an actual limitation when it comes to evaluate the security of a design from the point of view of the group generated by the round functions. If we assume, indeed, that our targets SPN and LM feature different round functions for each round, then the primitivity of \(\left\langle \overline{\rho }_i, \overline{\pi }_i, T_{2n}\right\rangle \) can be reduced to that of \(\left\langle \rho _i, T\right\rangle \), proceeding as in Theorem 3.5. When this is true for one round i, then the full group

$$\begin{aligned} \left\langle \left\langle \overline{\rho }_i, \overline{\pi }_i, T_{2n}\right\rangle \mid 1 \le i \le r\right\rangle \end{aligned}$$
(3.4)

is primitive.

Assuming that the definition of SPN and Definition 2.3 allow different round functions for each round, then the following consequence of Theorem 3.5 can be derived.

Corollary 3.6

If a given round of an SPN generates a primitive group, then the group defined as in Eq. (3.4) generated by the rounds of the corresponding generalized LM is primitive.

4 Invariant Subspaces in the LM Scheme

Our main result of Sect. 3, i.e. Theorem 3.5, shows a 2n-to-n primitivity reduction from the generalized 2n-bit LM scheme to the corresponding n-bit SPN. The result has a counterpart. Let us assume, indeed, that \(U \le V\) is an invariant subspace for \(\rho \) and for \(\pi \), or in other words, for each \(u\in U\), \(u\rho \) and \(u\pi \) belong to U. Then \(U \times U \le V \times V\) is an invariant subspace for \(\overline{\rho }\) and \(\overline{\pi }\). Indeed, for \((u_1,u_2) \in U \times U\),

$$\begin{aligned} (u_1,u_2)\overline{\rho }= & {} (u_1,u_2) \begin{pmatrix} {\mathbb {1}} &{} {\mathbb {1}}\\ {\mathbb {1}} &{} {\mathbb {0}} \end{pmatrix} \begin{pmatrix} {\mathbb {1}}&{} {\mathbb {1}}+\rho \\ {\mathbb {0}} &{} {\mathbb {1}} \end{pmatrix} \\= & {} (u_1+u_2 ,u_2+(u_1+u_2)\rho ) \in U \times U, \end{aligned}$$

and analogously

$$\begin{aligned} (u_1,u_2)\overline{\pi }=(u_1,u_2) \begin{pmatrix} \pi &{} {\mathbb {0}}\\ \pi &{} {\mathbb {1}} \end{pmatrix} = ((u_1+u_2)\pi ,u_2) \in U \times U. \end{aligned}$$

This proves that when the n-bit SPN-related group \(\left\langle \rho , T_n\right\rangle \) is imprimitive, with the addition of the easily verified condition that the imprimitivity block is also fixed by \(\pi \), then the group of the rounds of the generalized 2n-bit LM scheme \(\Gamma ({\mathrm {GLM}}(\rho ,\pi ))\) is imprimitive. From this straightforward consideration, when \(\left\langle \rho , T_n\right\rangle \) is imprimitive two implications are obtained:

  • the imprimitivity blocks of \(\Gamma ({\mathrm {GLM}}(\rho ,\pi ))\) for the generalized LM scheme are all and only those coming from imprimitivity blocks of the SPN;

  • the actual group \(\Gamma _\infty ({\mathrm {LM}}(\rho ,\pi ))\) of the classical LM scheme is imprimitive, since it is contained in an imprimitive group, i.e. it is vulnerable to the invariant subspace attack.

With the aim of attacking the classical LM scheme, the cryptanalysts can run on the SPN an exhaustive search for detecting invariant subspaces, or an algorithm of Leander et al. [21]. If the search fails, nothing can be concluded on the existence of invariant subspaces for the classical LM scheme. If the search succeeds, an invariant subspace for classical LM scheme has been obtained.

Remark 4.1

Notice that, as already mentioned, our results on the primitivity of \(\Gamma ({\mathrm {GLM}}(\rho ,\pi ))\) do not depend on \(\pi \), since such a group has been chosen because it is easily linked to the SPN, which features no \(\pi \). In particular, we prove the primitivity even when \(\pi =1\). However, it is known that \(\pi \) is required be a non-trivial function in the classical LM scheme. When this is not the case, then the partition

$$\begin{aligned} \left\{ \{ (x,y) \mid x+y = a \} \mid a \in V \right\} , \end{aligned}$$

is invariant for \(\Gamma _\infty ({\mathrm {LM}}(\rho ,\pi ))\), which then is imprimitive for each choice of \(\rho \).

5 Final Considerations and Open Problems

In this paper we have addressed the primitivity of the group generated by the round functions of a generalized Lai–Massey scheme, when bijective functions are considered in each round function, and we have determined conditions for the existence of invariant subspaces in the classical scheme. It is worth mentioning here that, like other security notions, the primitivity itself is not sufficient to ensure that the cipher is widely covered against general attacks. As a matter of fact, a cipher whose round functions generate a primitive group could still be extremely weak: consider for example a modified version of the AES, where the diffusion layer is replaced by a circulant brick-wise permutation.Footnote 2 The obtained cipher features almost no diffusion in its round functions, nonetheless they generate a primitive group [10]. This remains true also when a cipher can generate the symmetric group [12]. On the other side though, the imprimitivity of the group denotes the presence of invariance subspaces, which can lead, with a high probability, to a fatal attack against the cipher. For this reason, we believe that is important to provide the designers with a structure method to avoid the imprimitivity attack, which, together with other tools [5], may be used to prove a cipher invariant-subspace free.

The technical approach used in this paper required to impose some limitations on the setting:

  1. 1.

    since the primitivity of the generalized LM scheme is obtained as a reduction to the SPN case, we needed to assume the bijectivity of \(\rho \), though the LM framework allows more general cases;

  2. 2.

    the function \(\pi \) is assumed to be linear.

The primitivity of the LM scheme and its generalization when the two previously listed assumptions are not met is still open, as well as the problem below.

5.1 2-Transitivity

It is well known that every 2-transitive group is primitive [8]. It may be natural to ask whether an alternative version of Theorem 3.5 could be obtained, where primitivity is replaced by 2-transitivity. In the case \(n=3\), we have exhaustively searched using Magma [9] for all the non-linear functions \(\rho \) such that \(\left\langle \rho , T_3\right\rangle \) is a 2-transitive group. For all of those, \(\left\langle \overline{\rho }, T_6\right\rangle \) is always 2-transitive. Setting \(n=4\), a partial search in the space led to no counterexamples. A brute-force search when \(n\ge 4\) is out of the scopes of this work since requires code optimization and a faster programming language. On the other side, it is well known that the 2-transitivity of \(\Gamma _{\infty }({\mathrm {LM}}(\rho ,\pi ))\) is equivalent to the transitivity of the stabilizer of (0, 0) on \(V \times V\setminus \{(0,0)\}\). However, a description of \(\Gamma _{\infty }({\mathrm {LM}}(\rho ,\pi ))_{(0,0)}\) is not easily obtained from \(\left\langle \rho , T_n\right\rangle _0\) due to the non-linear dependence introduced by the Lai–Massey formal operator. For these reasons, at the time of writing we are not able to conjecture that the 2-transitivity of \(\left\langle \rho , T_n\right\rangle \) implies that \(\Gamma _{\infty }({\mathrm {LM}}(\rho ,\pi ))\) is 2-transitive, and we leave this as an open problem.