Skip to main content
SpringerLink
Log in

Voronovskaja Type Theorems and High-Order Convergence Neural Network Operators with Sigmoidal Functions

  • Published:
Mediterranean Journal of Mathematics Aims and scope Submit manuscript

Abstract

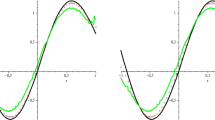
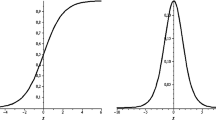
In the present paper, asymptotic expansion and Voronovskaja type theorem for the neural network operators have been proved. The above results are based on the computation of the algebraic truncated moments of the density functions generated by suitable sigmoidal functions, such as the logistic functions, sigmoidal functions generated by splines and other. Further, operators with high-order convergence are also studied by considering finite linear combination of the above neural network type operators and Voronovskaja type theorems are again proved. At the end of the paper, numerical results are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Alavi, J., Aminikhah, H.: Applying cubic B-Spline quasi-interpolation to solve 1D wave equations in polar coordinates. In: ISRN Computational Mathematics (2013)

  2. Austin, J., Hodge, V.J., O’Keefe, S.: Hadoop neural network for parallel and distributed feature selection. Neural Netw. 78, 24–35 (2016)

    Article  MATH  Google Scholar 

  3. Baldi, P., Sadowsky, P.: A theory of local learning, the learning channel, and the optimality of backpropagation. Neural Netw. 83, 51–74 (2016)

    Article  Google Scholar 

  4. Bardaro, C., Mantellini, I.: Approximation properties for linear combinations of moment type operators. Comput. Math. Appl. 62(5), 2304–2313 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bardaro, C., Mantellini, I.: Asymptotic formulae for linear combinations of generalized sampling operators. Zeitschrift fur Anal. ihre Anwendungen 32(3), 279–298 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Barron, A.R.: Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inform. Theory 39(3), 930–945 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  7. Barron, A.R., Klusowski, J.M.: Uniform approximation by neural networks activated by first and second order ridge splines (2016). arXiv:1607.07819

  8. Butzer, P.L., Nessel, R.J.: Fourier Analysis and Approximation I. Academic Press, New York, London (1971)

    Book  MATH  Google Scholar 

  9. Cao, F., Chen, Z.: The approximation operators with sigmoidal functions. Comput. Math. Appl. 58(4), 758–765 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cao, F., Chen, Z.: The construction and approximation of a class of neural networks operators with ramp functions. J. Comput. Anal. Appl. 14(1), 101–112 (2012)

    MathSciNet  MATH  Google Scholar 

  11. Cao, F., Chen, Z.: Scattered data approximation by neural networks operators. Neurocomputing 190, 237–242 (2016)

    Article  Google Scholar 

  12. Cao, F., Liu, B., Park, D.S.: Image classification based on effective extreme learning machine. Neurocomputing 102, 90–97 (2013)

    Article  Google Scholar 

  13. Cheang, G.H.L.: Approximation with neural networks activated by ramp sigmoids. J. Approx. Theory 162, 1450–1465 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  14. Chui, C.K., Mhaskar, H.N.: Deep nets for local manifold learning (2016). arXiv:1607.07110

  15. Coroianu, L., Gal, S.G.: Saturation results for the truncated max-product sampling operators based on sinc and Fejér-type kernels. Sampl. Theory Signal Image Process. 11(1), 113–132 (2012)

    MathSciNet  MATH  Google Scholar 

  16. Costarelli, D.: Interpolation by neural network operators activated by ramp functions. J. Math. Anal. Appl. 419(1), 574–582 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  17. Costarelli, D., Spigler, R.: Approximation results for neural network operators activated by sigmoidal functions. Neural Netw. 44, 101–106 (2013)

    Article  MATH  Google Scholar 

  18. Costarelli, D., Spigler, R.: Approximation by series of sigmoidal functions with applications to neural networks. Ann. di Mat. 194(1), 289–306 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Costarelli, D., Vinti, G.: Rate of approximation for multivariate sampling Kantorovich operators on some functions spaces. J. Int. Equations Appl. 26(4), 455–481 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  20. Costarelli, D., Vinti, G.: Pointwise and uniform approximation by multivariate neural network operators of the max-product type. Neural Netw. 81, 81–90 (2016)

    Article  MATH  Google Scholar 

  21. Costarelli, D., Vinti, G.: Convergence for a family of neural network operators in Orlicz spaces. Math. Nachr. 290(2–3), 226–235 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. Costarelli, D., Vinti, G.: Saturation classes for max-product neural network operators activated by sigmoidal functions. Results Math. 72(3), 1555–1569 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  23. Costarelli, D., Vinti, G.: Estimates for the neural network operators of the max-product type with continuous and p-integrable functions. Results Math. 73(1), 12 (2018). https://doi.org/10.1007/s00025-018-0790-0

    Article  MathSciNet  MATH  Google Scholar 

  24. Cybenko, G.: Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 2, 303–314 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  25. Di Marco, M., Forti, M., Grazzini, M., Pancioni, L.: Necessary and sufficient condition for multistability of neural networks evolving on a closed hypercube. Neural Netw. 54, 38–48 (2014)

    Article  MATH  Google Scholar 

  26. Di Marco, M., Forti, M., Nistri, P., Pancioni, L.: Discontinuous neural networks for finite-time solution of time-dependent linear equations. IEEE Trans. Cybern. (2015). https://doi.org/10.1109/TCYB.2015.2479118

  27. Fard, S.P., Zainuddin, Z.: The universal approximation capabilities of cylindrical approximate identity neural networks. Arab. J. Sci. Eng. 41, 3027 (2016)

  28. Fard, S.P., Zainuddin, Z.: Theoretical analyses of the universal approximation capability of a class of higher order neural networks based on approximate identity. In: Nature-inspired computing: concepts, methodologies, tools, and applications (2016). https://doi.org/10.4018/978-1-5225-0788-8.ch055(in print)

  29. Hahm, N., Hong, B.I.: A Note on neural network approximation with a sigmoidal function. Appl. Math. Sci. 10(42), 2075–2085 (2016)

    Google Scholar 

  30. Iliev, A., Kyurkchiev, N.: On the Hausdorff distance between the Heaviside function and some transmuted activation functions. Math. Model. Appl. 2(1), 1–5 (2016)

    Google Scholar 

  31. Iliev, A., Kyurkchiev, N., Markov, S.: On the approximation of the cut and step functions by logistic and Gompertz functions. Biomath 4(2), 1510101 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  32. Ismailov, V.E.: On the approximation by neural networks with bounded number of neurons in hidden layers. J. Math. Anal. Appl. 417(2), 963–969 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  33. Ito, Y.: Independence of unscaled basis functions and finite mappings by neural networks. Math. Sci. 26, 117–126 (2001)

    MathSciNet  MATH  Google Scholar 

  34. Kainen, P.C., Kurková, V.: An integral upper bound for neural network approximation. Neural Comput. 21, 2970–2989 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  35. Korovkin, P.P.: On convergence of linear positive operators in the space of continuous functions. Dokl. Akad. Nauk SSSR 90(953), 961–964 (1953)

    MathSciNet  Google Scholar 

  36. Kurková, V.: Lower bounds on complexity of shallow perceptron networks. Eng. Appl. Neural Netw. Commun. Comput. Inf. Sci. 629, 283–294 (2016)

    Google Scholar 

  37. Lin, S., Zeng, J., Zhang, X.: Constructive neural network learning (2016). arXiv:1605.00079

  38. Llanas, B., Sainz, F.J.: Constructive approximate interpolation by neural networks. J. Comput. Appl. Math. 188, 283–308 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  39. Maarten, J.: Non-equispaced B-spline wavelets. Int. J. Wavelets Multiresolution Inf. Process. 14(6), 35 (2016)

  40. Maiorov, V.: Approximation by neural networks and learning theory. J. Complex. 22(1), 102–117 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  41. Maiorov, V., Meir, R.: On the near optimality of the stochastic approximation of smooth functions by neural networks. Adv. Comput. Math. 13(1), 79–103 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  42. Makovoz, Y.: Uniform approximation by neural networks. J. Approx. Theory 95(2), 215–228 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  43. Marsden, M.J.: An identity for spline functions with applications to variation-diminishing spline approximation. J. Approx. Theory 3(1), 7–49 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  44. Mhaskar, H., Poggio, T.: Deep vs. shallow networks: an approximation theory perspective. Anal. Appl. 14(6), 829–848 (2016)

  45. Monaghan, J.J.: Extrapolating B splines for interpolation. J. Comput. Phys. 60(2), 253–262 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  46. Scardapane, S., Wang, D.: Randomness in neural network: an overview. In: Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, vol. 7, p. e1200 (2017). https://doi.org/10.1002/widm.1200

  47. Schmidhuber, J.: Deep learning in neural networks: An overview. Neural Netw. 61, 85–117 (2015)

    Article  Google Scholar 

Download references

Acknowledgements

The second and the third authors are members of the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). The second author has been partially supported within the 2019 GNAMPA-INdAM Project “Metodi di analisi reale per l’approssimazione attraverso operatori discreti e applicazioni”, while the third author within the projects: (1) Ricerca di Base 2017 dell’Università degli Studi di Perugia—“Metodi di teoria degli operatori e di Analisi Reale per problemi di approssimazione ed applicazioni” , (2) Ricerca di Base 2018 dell’Università degli Studi di Perugia—“Metodi di Teoria dell’Approssimazione, Analisi Reale, Analisi Nonlineare e loro Applicazioni”, (3) “Metodi e processi innovativi per lo sviluppo di una banca di immagini mediche per fini diagnostici” funded by the Fondazione Cassa di Risparmio di Perugia, 2018. This research has been accomplished within RITA (Research ITalian network on Approximation).

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, University of Perugia 1, Via Vanvitelli, 06123, Perugia, Italy

    Danilo Costarelli & Gianluca Vinti

Authors
  1. Danilo Costarelli
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gianluca Vinti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Danilo Costarelli.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Costarelli, D., Vinti, G. Voronovskaja Type Theorems and High-Order Convergence Neural Network Operators with Sigmoidal Functions. Mediterr. J. Math. 17, 77 (2020). https://doi.org/10.1007/s00009-020-01513-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00009-020-01513-7

Mathematics Subject Classification

Keywords

Search

Navigation