On Four-Dimensional Poincaré Duality Cobordism Groups

Abstract

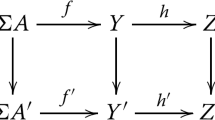
This paper continues the study of four-dimensional Poincaré duality cobordism theory from our previous work Cavicchioli et al. (Homol. Homotopy Appl. 18(2):267–281, 2016). Let P be an oriented finite Poincaré duality complex of dimension 4. Then, we calculate the Poincaré duality cobordism group $\Omega _{4}^{{\text {PD}}}(P)$. The main result states the existence of the exact sequence $0 \rightarrow L_4 (\pi _1 (P))/A_4 (H_2 (B\pi _1 (P), L_2)) \rightarrow {{\widetilde{\Omega }}}_{4}^{\mathrm{PD}}(P) \rightarrow \mathbb Z_8 \rightarrow 0$, where ${{\widetilde{\Omega }}}_{4}^{\mathrm{PD}}(P)$ is the kernel of the canonical map ${\Omega }_{4}^{\mathrm{PD}}(P) \rightarrow H_4 (P, \mathbb Z) \cong \mathbb Z$ and $A_4 : H_4 (B\pi _1, \mathbb L) \rightarrow L_4 (\pi _1 (P))$ is the assembly map. It turns out that ${\Omega }_{4}^{\mathrm{PD}}(P)$ depends only on $\pi _1 (P)$ and the assembly map $A_4$. This does not hold in higher dimensions. Then, we discuss several examples. The cases in which the canonical map $\Omega _{4}^{{\text {TOP}}}(P) \rightarrow \Omega _{4}^{{\text {PD}}}(P)$ is not surjective are of particular interest. Its image coincides with the kernel of the total surgery obstruction map. In fact, we establish an exact sequence

where s is Ranicki’s total surgery obtruction map. In the above cases, there are ${\text {PD}}_4$-complexes X which cannot be homotopy equivalent to manifolds.