Abstract
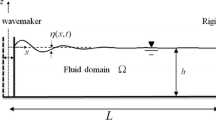
The problem of the impact of waves on the bottom, which can be deformed and changed, is considered. This task is an urgent problem of military-technical construction at the design stage in order to protect the supports of hydraulic structures from the possible force impact of the water element. Along with the theoretical study, an important applied aspect is the result of numerical simulation with possible further implementation through modern integrated software development environments.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Aleshkov YuZ (1990) Theory of interaction of waves with obstacles. L, 372 p
Aleshkov YuZ (2001) Waves on the surface of loose media caused by fluid flow. Vestn. St. Petersburg. university Ser. 1: Mathematics, mechanics, astronomy Issue. 4 (No. 25), pp 35–43
Frankl FI (1953) On the motion of sand waves. DAN SSSR 89(1):9–32
Ilyichev AT (2003) Solitary waves in hydromechanics models. M, 256 p 8; Peregudin SI, Kholodova SE (2011) On the features of the propagation of non-stationary waves in a rotating spherical layer of an ideal incompressible stratified electrically conductive fluid in the equatorial latitudinal belt. ApplMech Techn Phys 52(2):(306):44–51
Kholodova SE (2008) Dynamics of a rotating layer of an ideal electrically conductive incompressible fluid. Comput Math Mathem Phys 48(5):882–898
Peregudin SI (2003) Spatial wave motions on the surface of loose media. Proceedings of Srednevolzhsk. mat. about-va. V 5, No 1, pp 130–138
Peregudin S, Peregudina E, Kholodova S (2019) The Influence of dissipative effects on dynamic processes in a rotating electrically conductive liquid medium. J Phys Conf Series 1359(1):012118
Peregudin S, Peregudina E, Kholodova S (2021) Mathematical modeling of the dynamics of a rotating layer of an electrically conducting fluid with magnetic field diffusion effects. Springer Geology, pp 277–87
Shulyak BA (1971) Physics of waves on the surface of a loose medium and liquid, 400 p
Velikanov MA (1949) Dynamics of channel flows, 474 p
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Peregudin, S.I., Kholodova, S.E. (2023). The Problem of Propagation of Plane Long Waves in a Nonhomogeneous Liquid over a Deformable Bottom. In: Chaplina, T. (eds) Processes in GeoMedia—Volume VII. Springer Geology. Springer, Singapore. https://doi.org/10.1007/978-981-99-6575-5_17
Download citation
DOI: https://doi.org/10.1007/978-981-99-6575-5_17
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-99-6574-8
Online ISBN: 978-981-99-6575-5
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)