Keywords

1 Introduction

Wang [1] takes micro-topography as a main condition and directly introduces it into the theory of multilateral boundary rock blasting. Zhang et al. [2] analyzed and processed the blasting vibration signal by HHT method, and obtained that EMD can decompose the signal well according to different time scales, and the decomposed intrinsic mode function can reflect the intrinsic characteristics of the signal itself. Chen et al. [3] studied the control blasting design of rock mass structure, put forward the control theory of rock mass structure, and established the basic theory of rock mass blasting under geological boundary conditions. Guan et al. [4] uses the extreme point symmetric continuation method to eliminate the endpoint effect, which improves the computational efficiency and practicability of HHT. Zhang et al. [5] analyzed the empirical formula of blasting vibration prediction, and concluded that the nonlinear regression correction formula has the highest accuracy. Based on rock wave impedance and rock mass integrity coefficient, Hu et al. [6] constructs the expression of attenuation of peak vibration velocity of open pit bench blasting seismic wave with equivalent distance. Gao et al. [7] obtains the time-history relationship of seismic wave energy by wavelet transform, and deduces the calculation formula of vibration reduction delay of bench blasting interference. Zhang et al. [8] uses wavelet transform decomposition and response spectrum analysis to study the energy distribution characteristics of blasting vibration signal, and obtains that the main vibration frequency band of blasting vibration signal energy tends to low frequency band.

The above research results mainly focus on the horizontal boundary conditions, and it is not enough to consider the micro-topography change as an additional factor to the blasting theory and blasting method. Based on HHT analysis technique and multi-boundary rock comprehensive blasting theory, considering various terrain and geological conditions, a formula for calculating the charge of multi-boundary deep-hole blasting is put forward in this paper, which significantly improves the blasting effect.

2 Basic Principle of HHT Analysis Method

2.1 EMD Decomposition Principle

EMD decomposition is an important part of HHT transform, the core of which is to decompose vibration signal into a series of modal functions.

Assuming that the sampling sequence of slope blasting vibration signal is S(t), the EMD decomposition process can be expressed as:

$$ S\left( t \right) = \sum\limits_{i = 1}^{n} {c_{i} \left( t \right)} + R_{n} \left( t \right) $$
(1)

In Eq. (1), n is the order of signal decomposition. ci(t) is the i-order IMF component. Rn(t) is the residual component after n-order decomposition.

The remaining part R1(t) of the signal can be obtained by the first IMF component c1(t):

$$ R_{1} \left( t \right) = S\left( t \right) - c_{1} \left( t \right) $$
(2)

By analogy, the n-order IMF component cn(t) and residual component Rn(t) of the original signal can be obtained. When both cn(t) and Rn(t) are less than the threshold, the EMD decomposition process ends.

EMD decomposition is based on the local characteristics of the signal, and the operation process of the algorithm is adaptive. IMF component is stable, linear and symmetrical, and is suitable for processing blasting vibration signals.

2.2 Hilbert Transform and Spectrum

The combination of several IMF components of the original signal is obtained by EMD decomposition, and the Hilbert spectrum can be obtained by combining the instantaneous spectra of all IMF components by Hilbert transform. Hilbert transform is a kind of linear transformation, which has intuitive physical meaning and emphasizes the local properties of signals.

Hilbert transformation of IMF components:

$$ H\left[ {c\left( t \right)} \right] = \frac{1}{\pi }PV\int_{ - \infty }^{\infty } {\frac{{c\left( {t^{\prime}} \right)}}{{t - t^{\prime}}}} dt^{\prime} $$
(3)

In Eq. (3), PV is Cauchy principal value.

Constructing the analytic signal z(t):

$$ z\left( t \right) = c\left( t \right) + jH\left[ {c\left( t \right)} \right] = a\left( t \right){\text{e}}^{j\Phi \left( t \right)} $$
(4)

In Eq. (4), a(t) is the amplitude function.

$$ a\left( t \right) = \sqrt {c^{2} \left( t \right) + H^{2} \left[ {S\left( t \right)} \right]} $$
(5)

Φ(t) is the phase function:

$$ \Phi \left( t \right) = \arctan \frac{{H\left[ {c\left( t \right)} \right]}}{c\left( t \right)} $$
(6)

Define the instantaneous frequency as:

$$ f\left( t \right) = \frac{d\Phi \left( t \right)}{{dt}} $$
(7)

The expression for the Hilbert instantaneous energy spectrum is:

$$ H\left( {\omega ,t} \right) = {\text{Re}} \sum\limits_{i = 1}^{n} {a_{i} \left( t \right)} {\text{e}}^{{\int {\omega_{i} } \left( t \right)dt}} $$
(8)

H(ω,t) integrates time to get Hilbert marginal spectrum:

$$ h\left( \omega \right) = \int_{0}^{t} {H\left( {\omega ,t} \right)} dt $$
(9)

Hilbert marginal spectrum expresses the amplitude of each frequency in the whole world.

Hilbert energy spectrum expression:

$$ E\left( \omega \right) = \int_{0}^{t} {H^{2} \left( {\omega ,t} \right)} dt $$
(10)

Hilbert energy spectrum can express the energy accumulated at different frequencies in the whole time.

3 Calculation Principle of Multi-boundary Blasting Charge

3.1 Principle of Charge Layout for Multi-face Empty Blasting

  1. (1)

    The upper charge adopts small hill bag and short hill bag, while the lower charge adopts long hill bag and all kinds of empty blasting overlap each other. When the lower charge has favorable terrain of lateral throwing, throwing blasting should be adopted.

  2. (2)

    The upper cartridge is in favorable terrain, commanding and has large relative potential energy, so a larger cartridge should be arranged, and the design throwing rate can be relatively small.

  3. (3)

    The upper charge should be arranged on the side near the high slope in the middle line, and it is strictly forbidden to over explode or damage the slope.

  4. (4)

    At the foot of the low slope, in the section with poor or no accumulation conditions, the collapse of each layer of charge should be reduced as much as possible, and the charge should be arranged along the free surface in a plane charge-type multi-face empty blasting.

  5. (5)

    The initiation sequence of the upper and lower charge is that the upper charge is initiated first, and the lower charge is initiated again after the upper rock mass collapses. Secondly, the charges on both sides of the lower layer or the lowest layer are detonated, and finally the intermediate charges in the lower layer are detonated again.

3.2 Calculation Formula of Multi-boundary Blasting Charge

With the development and application of blasting technology, it is more and more important to study the relationship and interaction between boundary conditions and explosive explosion energy. Considering the interaction between blasting effect and topographic and geological boundary conditions, the formula for calculating the explosive charge of multi-boundary deep-hole blasting is obtained as follows:

$$ Q = KW^{3} F\left( {E,\alpha } \right) = KF\left( {E,\alpha } \right)aWh $$
(11)

In Eq. (11), a is the hole distance (m). h is the drilling depth (m).

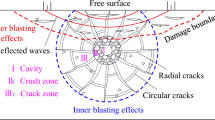
The multi-boundary blasting principle considers the stability and leakage of rock mass, the formation mechanism and development law of blasting cracks, and the formation mechanism of blasting engineering geological disasters. Combined with the classification of blasting rock mass, the classification of blasting rock mass structural plane and the design of controlled blasting of rock mass structure, the comprehensive blasting theory of medium potential energy and explosive blasting energy is put forward.

4 Project Example

4.1 Engineering Geological Conditions

Jinou Coal Mine is located in the west wing of Zhuozishan anticline, with scarce surface vegetation, fragile ecology, drought and little rain, and strong wind in winter and spring. The strata in the mining area and its vicinity are Carboniferous, Permian and Quaternary from old to new. Sinan, Cambrian and Ordovician limestone are distributed in turn from the axis of Zhuozishan anticline to the two wings, which constitute the sedimentary basement of coal-bearing strata and are in parallel and unintegrated contact with the overlying coal-bearing strata.

4.2 Design of Multi-boundary Deep Hole Blasting

Using hole packing or air interval charge to control explosive energy distribution. The millisecond delay reverse initiation technology in the hole is adopted to limit the maximum initiation charge in a single stage and control the blasting vibration and flying rocks. The anhydrous pore is made of ANFO explosive, and the water pore is made of emulsion explosive. Blasting design parameters are shown in Table 1.

Table 1 Table of blasting parameters
Full size table

4.3 Design of Accurate Delay Initiation Network

Based on the principle of stress wave superposition, free surface increase and rock block collision, the millisecond delay time is calculated by using the empirical formula of multi-boundary theory:

$$ \Delta t = K_{1} \cdot W(24 - f) $$
(12)

In Eq. (12), △t is the millisecond delay interval (ms). K1 is the fracture coefficient of rocks, which is 0.5 for rocks with few fractures, 0.75 for rocks with medium fractures and 0.9 for rocks with developed fractures. W is the chassis resistance line (m). f is the rock firmness coefficient.

After calculation, the delay time is designed as 25 ms between holes and 60 ms between rows (Fig. 1).

Fig. 1
A network diagram starts at the exploder and segments into 3 layers with nodes in meter second. In the first layer, 12 nodes range from 0 to 275. In the second layer, 10 nodes range from 60 to 285. In the third layer, 8 nodes range from 120 to 295.

Detonation network diagram of deep hole blasting

Full size image

5 Characteristic Analysis of Blasting Vibration Signal

5.1 Vibration Velocity Analysis

Measuring points are arranged at the horizontal distance of 110 m, 130 m, 150 m and 170 m from the blasting source to sample the blasting vibration velocity. In this paper, the blasting vibration velocity at a horizontal distance of 110 m from the blasting source is taken as an example to analyze the characteristics of blasting vibration signals, and the sampling time is 0.8 s.

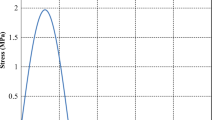
According to Fig. 2, the blasting vibration velocity increases first and then decreases, and reaches the maximum at 0.171 s. Then, with the passage of blasting load time, the particle vibration velocity decays continuously, and gradually approaches 0 at about 0.5 s.

Fig. 2
A line graph plots vibration velocity versus time with a fluctuating line. Some of the estimated values are as follows. (0, 0.45), (0.1, negative 0.46), (0.2, negative 0.2), (0.3, 0.1), and (0.8, 0).

Time history curve of vibration velocity

Full size image

5.2 HHT Analysis

As can be seen from Fig. 3, the frequency components contained in the original signal are very rich, but most of them are below 60 Hz. The dominant frequency of the signal is mainly between 0 and 40 Hz, and the main frequency of vibration is 24.43 Hz. The energy contained in the high frequency components gradually decays.

Fig. 3
A line graph plots amplitude versus frequency with a fluctuating line. Some of the estimated values are as follows. (0, 28), (10, 55), (20, 60), (40, 5), (100, 0), (160, 0), and (200, 0).

Hilbert marginal spectrum

Full size image

6 Conclusions

Multi-boundary blasting technology reduces the engineering cost, protects the rock mass outside the excavation boundary from damage as much as possible, accelerates the construction progress and improves the quality of blasting engineering.

  1. (1)

    Based on HHT analysis technique, the main frequency of blasting vibration signal energy is in 0–40 Hz, and it is mainly in the low frequency band, and the energy contained in the high frequency component gradually decays.

  2. (2)

    Multi-boundary deep-hole controlled blasting has uniform rock fragmentation, and all of them collapse within the design range, which has achieved good blasting effect.