Keywords

1 Introduction

Orthotropic steel decks (OSDs) are broadly used in steel bridges for its superior advantages, like light weight, reliable force and convenient construction [1]. However, various categories of fatigue cracks are found in orthotropic steel decks because of the repeated traffic loads, together with welding residual tensile stress and welding defects [2]. There are several typical fatigue details, such as the butt welds, arc notch, rib-deck welds [3,4]. Thereinto, the arc notch between U-rib and diaphragm has attracted wide attention due to its complex and special structure over recent years [5].

There are already extensive researches focus on evaluating the fatigue performance of the arc notch between diaphragm and U-rib. Cyclic vehicle loading causes the out-of-plane deformation of U-ribs and diaphragms, and large great out-of-plane bending stresses appear at the arc notch due to the relative constraint between U-rib and diaphragm [6, 7]. Fatigue tests show that out-of-plane stress could reach 20% to 35% of in-plane stress [8]. Based on large quantities of measured data, many fatigue cracks at arc notch mainly appear on U-rib weld toe, diaphragm weld toe and the fillet [9].

In this study, field monitoring in orthotropic steel deck of a real bridge was carried out and the strain data at arc notch between diaphragm and U-rib under vehicle loads were recorded. The fatigue performance of this typical fatigue detail was evaluated.

2 Field Monitoring

2.1 Measuring Points

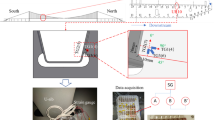
Inspection records of a cable-stayed steel bridge show that there are a large number of fatigue cracks grow at arc notch between diaphragm and U-rib in OSD, and more than half of cracks occur below overtaking lane. As the traffic volumes at the upstream side are much more, arc notch of 17# U-rib at the Diaphragm NJ22-3 below truck lane at the downstream side was chosen as the monitoring target, seen in Fig. 1.

Fig. 1
Two diagrams are labeled a and b. a. Longitudinal bridge has the following markings, N A 34, N J 18, mid-span, S J 18, Tower S T 0, and S A 34. b. Transverse bridge has the following markings, emergency, truck, express, and overtaking lanes on either sides.

Measuring points layout

Full size image

Tri-axial strain gauges were used and set at 10 mm away from the arc notch and the rib weld toe. And uniaxial strain gauges were arranged at the arc notch with a distance of 10 mm away from edge. The measuring points were named as G1-G3, G1 was arranged at diaphragm weld toe, G2 was arranged at U-rib weld toe, G3 was arranged at the fillet of arc notch, as shown in Fig. 2.

Fig. 2
Three illustrations are labeled a to c. They are measuring point G, G 2, and G 3 which are diaphragm weld toe, U rib weld toe, and the fillet. They mark diaphragm, strain gauge, and U rib.

Strain gauge arrangement

Full size image

The resistance of these gauges was 120Ω,and the sensitivity ratio is from 1.0% to 3.0%. The strain data were captured by a dynamic strain indicator with a frequency of 512 Hz to obtain the strain cycles caused by vehicle loads. The strain data were recorded for 24 h.

2.2 Stress Time History

The strain data were converted into stress data by Hooke’s Law σ = Eε. For the material of OSD in the studied bridge, the yield strength is about 345 MPa, Young’s modulus E is about 2.06 × 105 MPa, and the Poisson’s ratio is about 0.3.

Figure 3 plots part of stress time-history of G1. Under vehicle loads, the stress at 0°direction (i.e., parallel to the weld) is negative which means the structural detail is under compressive stress at 0°direction. The mean and maximum value of compressive stress at 0°direction are 6.5 and 20 MPa respectively. The mean/peak value of tensile stress and compressive stress at 45°direction are about 7/12 and 4/12 MPa respectively, which mean the stress at 45°direction of this detail is dominated by tensile stress. The mean/peak value of tensile stress and compressive stress at 90°direction (i.e., perpendicular to the weld) are about 5/13 and 10/20 MPa respectively, which mean the stress at 45°direction of this detail is dominated by compressive stress. The measuring point area is under tension–compression cyclic loading at 45°and 90°direction, which is the main reason for fatigue cracking. The maximum stresses occur at 90°direction,thus the fatigue cracks are more likely to propagate at 0° direction, which agrees well with the reality.

Fig. 3
Three graphs plot stress versus time in minutes for 0, 45, and 90 directions. The graph curves fluctuate and depict various peaks.

Part of stress time-history of G1

Full size image

Figure 4 plots part of stress time-history of G2. Under vehicle loads, the stress at 0°direction is compressive stress with the mean and maximum value are 20 and 37 MPa respectively. This measuring point area at 45°and 90°direction is under tension–compression cyclic loading. The peak value of tensile stress and compressive stress at 45°direction are 10 and 25 MPa. And the peak value of tensile stress and compressive stress at 90°direction are 16.5 and 10 MPa. The maximum compressive stress occurs at 0°direction among three directions, which indicates that cracks are more prone to grow at 90°direction, consistent with reality.

Fig. 4
Three graphs plot stress versus time in minutes for 0, 45, and 90 directions. The graph curves fluctuate with various peaks.

Stress time-history of G2

Full size image

Figure 5 plots part of stress time-history of G3. The fillet at arc notch is mainly under compressive stress with the peak value of 45 MPa, and tensile stress occurs less frequently with the peak value of 15 MPa. The measuring point area is prone to crack due to the combined action of cyclic compressive stress and welding residual tensile stress.

Fig. 5
A graph plots stress versus time in minutes. The graph curve fluctuates with positive and negative peaks.

Stress time-history of G3

Full size image

3 Analysis of Measurement Results

3.1 Fatigue Stress Amplitude

Based on the stress data in Sect. 2.2, the rain-flow counting method [10] was applied to get the stress range spectrum. The stress amplitude below 4 MPa was removed because the low-stress random amplitudes below 4 MPa had little contribution to the fatigue damage. The segment length of stress range is 2.0 MPa. The fatigue stress spectrums of measuring points are presented in Fig. 6.

Fig. 6
Three bar graphs plot cycle number versus stress for G 1, G 2, and G 3. The highest values of G 1, G 2, and G 3 are (5, 1100), (5, 2100), (5, 1500). The values are approximated.

Fatigue stress spectrums of measuring points

Full size image

As shown in Fig. 6, variation trends of stress spectrums are similar, appearing as the cycle numbers decrease gradually with the increase of stress amplitudes. More than 90% of stress amplitudes are below 10 MPa which means that the measuring points are under low cyclic stress for most of the time. Large stress amplitude could enlarge the initial defects of the components, thereby reduce the fatigue limit. Then, as time grows, fatigue damage increases under low stress amplitude.

3.2 Fatigue Damage

Fatigue damage degree refers to the damage accumulation of bridges under cyclic vehicle loading. Recommended in Chinese standard (JTG D64-2005), the value of design fatigue strength of arc notch between U-rib and diaphragm is 70 MPa, and of rib-to-diaphragm weld is 71 MPa. Miner’s linear cumulative rule is often used in practice projects [11]. In the light of Miner’s linear cumulative rule, fatigue damage caused by each stress amplitude can be expressed by \(\Delta \sigma_{i} /N\), and superimposed linearly. Hence, fatigue damage degree of any component under random stress amplitude (\(\Delta \sigma_{i}\), i = 1, 2, 3……) can be defined by Eq. (1).

$$ D = \sum\limits_{i = 1}^{\infty } {\Delta D_{i} } = \sum\limits_{i = 1}^{\infty } {\frac{{n_{i} }}{{N_{i} }}} $$
(1)

where D is the fatigue damage degree, \({\text{n}}_{{\text{i}}}\) is the cycle number of stress amplitude \(\Delta \sigma_{i}\). \({\text{N}}_{{\text{i}}}\) is the cycle number when fatigue failure occurs on the component under stress amplitude \(\Delta \sigma_{i}\) in fatigue tests. According to Chinese standard (JTG D64-2005), \({\text{N}}_{{\text{i}}}\) can be calculated by Eq. (2).

$$ N_{{\text{i}}} \;{ = }\;{2} \times {10}^{{6}} \times ({{\sigma_{{0}} } \mathord{\left/ {\vphantom {{\sigma_{{0}} } {\Delta \sigma_{{x,{\text{i}}}} }}} \right. \kern-0pt} {\Delta \sigma_{{x,{\text{i}}}} }})^{3} $$
(2)

Fatigue damage degrees of three measuring points are given in Table 1.

Table 1 Fatigue damage degrees of measuring points
Full size table

As shown in Table 1, fatigue damage degree of U-rib weld toe is the largest, which means that U-rib weld toe is more prone to crack. The damage degree of the fillet at arc notch is also at a high level, suggesting that this part is more vulnerable to fatigue loads.

3.3 Conclusions

  1. (1)

    Diaphragm weld toe and the fillet at arc notch subject mainly to cyclic compressive stress, while U-rib weld toe endures tension–compression cyclic stress, and residual welding stress also made contribution to fatigue cracking.

  2. (2)

    The stress peak amplitude of U-rib weld toe is higher than diaphragm weld toe and the fillet at arc notch, so is the fatigue damage degree. Fatigue cracking is more easily appear at U-rib weld toe, matches the actual inspection of the bridge well.