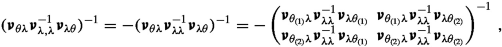Skip to main content
SpringerLink
Log in

Asymptotic Expansions for Several GEL-Based Test Statistics and Hybrid Bartlett-Type Correction with Bootstrap

  • Chapter
  • First Online:
Research Papers in Statistical Inference for Time Series and Related Models

  • 294 Accesses

Abstract

This paper mainly discusses two issues about asymptotic expansions for the distributions of \(\chi ^2\)-type test statistics. First, it is shown that the generalized empirical likelihood ratio, Wald-type, and score-type test statistics for a subvector hypothesis in the possibly over-identified moment restrictions are, in general, not Bartlett-correctable, except for the empirical likelihood ratio test statistic. Second, starting with the classical likelihood or the modern generalized empirical likelihood, the Bartlett-type corrected test statistics, with the bootstrap procedure, are proposed to achieve a higher-order accurate testing inference for the nonparametric setup as well as the parametric setup.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 189.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD 249.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    The idea of using “estimating equations” has a long history in the literature, at least since Karl Pearson’s introduction of the so-called method of moments. It seems that a motivation behind Qin and Lawless [62] is Godambe’s optimal estimating equations theory. In the econometric literature, Hansen’s [32] generalized method of moments is a basic inferential technique. We do not mention these two big methodologies anymore, to save space.

  2. 2.

    The finding was first announced by the author at The Mathematical Society of Japan (Spring Meeting 2012).

  3. 3.

    The bootstrap method was introduced by Efron [25], inspired by an earlier work on the jackknife. The methodology of the bootstrap is a computer-intensive technique that provides a basis for every field from modern statistical science. It is well recognized that its theoretical validity, as well as a deep understanding of the bootstrap procedure, is closely related to higher-order asymptotic statistical theory (e.g., Hall [30]); the details are omitted here.

  4. 4.

    A hybrid method of “the bootstrap-based Bartlett-type adjustment” from the ordinary parametric likelihood/GEL testing inference was reported by the author at Nara-Symposium (September 2014) that Professor Taniguchi organized, and also at the Japanese Joint Statistical Meeting (September 2014).

  5. 5.

    The following properties hold:

    • If \(Y^{(N)}=o_F^{(N)}(q_1,q_2)\), then,  (i) \(Y^{(N)}=o_F^{(N)}(q_1',q_2')\) for any \(q_1 \ge q_1'\)(\(\ge 0\)) and \(q_2' \ge q_2\); (ii) \(N^{-\tau } Y^{(N)}=o_F^{(N)}(q_1,q_2')\) for any \(\tau >0\) and \(q_2' \ge 0\).

    • If \(Y_\textrm{I}^{(N)}=o_F^{(N)}(q,q_2)\) and \(Y_\textrm{II}^{(N)}=o_F^{(N)}(q,q_2')\), then,

      $$Y_\textrm{I}^{(N)}+Y_\textrm{II}^{(N)}=o_F^{(N)}(q,\max (q_2,q_2')) \quad \text{ and } \quad Y_\textrm{I}^{(N)} Y_\textrm{II}^{(N)}=o_F^{(N)}(q,q_2+q_2')\,. $$
  6. 6.

    The GELR is a GEL counterpart of Wilks [76] from the parametric likelihood. As a special case of \(\rho (\cdot )=\rho _\textrm{EL}(\cdot )\), the ELR by Qin and Lawless [62] is most popular in the literature.

  7. 7.

    The Wald-type is a GEL counterpart of Wald [75] from the parametric likelihood.

  8. 8.

    The score-type (or Lagrange multiplier) is a GEL counterpart of [65] (see also [69]) from the parametric likelihood. For a history about Rao’s score test, we refer the readers to [5]. See also [8] for the score-type test statistic from the estimating equation models.

  9. 9.

    The gradient-type is a GEL counterpart of [73] from the parametric likelihood.

  10. 10.

    Newey and Smith [56] established that

    $$N^{1/2}(\widehat{\boldsymbol{{\eta }}}^{(N)\rho }-\boldsymbol{{\eta }}_0) {\mathop {\longrightarrow }\limits ^{d}}\textrm{N}\left( \textbf{0}_{p+M}\,,\, \left( \begin{array}{@{}c@{~}c@{}} ( \boldsymbol{{\nu }}_{\theta \lambda } \boldsymbol{{\nu }}_{\lambda ,\lambda }^{-1} \boldsymbol{{\nu }}_{\lambda \theta } )^{-1} &{} \textbf{O}_{p,M} \\ \textbf{O}_{M,p} &{} \textbf{P} \\ \end{array} \right) \right) \,, $$

    where \(\boldsymbol{{\nu }}_{\lambda ,\lambda }=-\boldsymbol{{\nu }}_{\lambda \lambda }\) and

    $$\textbf{P} =\boldsymbol{{\nu }}_{\lambda ,\lambda }^{-1} -\boldsymbol{{\nu }}_{\lambda ,\lambda }^{-1} \boldsymbol{{\nu }}_{\lambda \theta } ( \boldsymbol{{\nu }}_{\theta \lambda } \boldsymbol{{\nu }}_{\lambda ,\lambda }^{-1} \boldsymbol{{\nu }}_{\lambda \theta } )^{-1} \boldsymbol{{\nu }}_{\theta \lambda } \boldsymbol{{\nu }}_{\lambda ,\lambda }^{-1}\,. $$

    We can see that

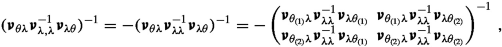
    which yields \(N^{1/2}(\widehat{\boldsymbol{{\theta }}}_{(1)}^{(N)\rho }-\boldsymbol{{\theta }}_{(1)0}) {\mathop {\longrightarrow }\limits ^{d}}\textrm{N}(\textbf{0}_{p_1},\boldsymbol{{\nu }}_{(11 \cdot 2)}^{-1}) \), since

    $$(\textbf{I}_{p_1}~ \textbf{O}_{p_1,p_2}) ( \boldsymbol{{\nu }}_{\theta \lambda } \boldsymbol{{\nu }}_{\lambda \lambda }^{-1} \boldsymbol{{\nu }}_{\lambda \theta } )^{-1} \left( \begin{array}{@{}c@{}} \textbf{I}_{p_1} \\ \textbf{O}_{p_2,p_1} \\ \end{array} \right) =-( \boldsymbol{{\nu }}_{\theta _{(1)}\lambda } \textbf{M}_{\lambda \lambda } \boldsymbol{{\nu }}_{\lambda \theta _{(1)}} )^{-1} =\boldsymbol{{\nu }}_{(11 \cdot 2)}^{-1}\,. $$

    It follows that \(\textrm{W}^{(N)\rho } {\mathop {\longrightarrow }\limits ^{d}}\chi ^2_{p_1}\) and \(\textrm{W}_\dagger ^{(N)\rho } {\mathop {\longrightarrow }\limits ^{d}}\chi ^2_{p_1}\).

  11. 11.

    By Proposition 10.2 of Sect. 10.6.3, we have, in principle,

    $$E_F^{(N)}[\textrm{ELR}^{(N)}] =p_1 +\frac{1}{N}\, (\kappa _{b_1,b_2}^{-2,-6,1/3,0,1/4,-1/12}+\kappa _{b_1}^{-2,1/3}\kappa _{b_2}^{-2,1/3}) \nu _{(11\cdot 2)}^{b_1b_2} +o(N^{-1})\,. $$
  12. 12.

    Some authors may use the terminology of the Bartlett correction in the sense that the expectation of the test statistic is closer to that of the original (uncorrected) test statistic.

  13. 13.

    We stress that the classical likelihood-based parametric case is also allowed here. See Kakizawa [45,46,47,48,49].

  14. 14.

    There were, at least for me, confusing expressions in Cordeiro and Ferrari [20, (1) and (2)]; indeed, using the relation \(2g_{\nu +2}(x)=G_\nu (x)-G_{\nu +2}(x)\), one can rearrange Harris’s [34, (3.2)] asymptotic expansion for the distribution of the Rao test statistic \(S_\textrm{R}\), as follows:

    $$\begin{aligned}{} & {} \Pr (S_\textrm{R} \le x) \\= & {} G_m(x) +\frac{1}{24n}\,[ A_3 G_{m+6}(x) +(A_2-3A_3) G_{m+4}(x) +(A_1-2A_2+3A_3) G_{m+2}(x) \\{} & {} \qquad \qquad \qquad +(-A_1+A_2-A_3) G_m(x) ] +o(n^{-1}) \\= & {} G_m(x) -\frac{1}{12n} \Bigl [ \frac{A_1-A_2+A_3}{m} +\frac{(A_2-2A_3)x}{m(m+2)} +\frac{A_3\,x^2}{m(m+2)(m+4)} \Bigr ] x g_m(x) +o(n^{-1})\,. \end{aligned}$$
  15. 15.

    A seminal work in this area is an unpublished working paper of Rothenberg [68], cited by Anderson’s book (see also Fujikoshi [27]); it would, however, not available almost anywhere from the world.

  16. 16.

    Similar conclusion holds for the modern GEL framework; indeed, Bravo [10] explicitly derived \(N^{-1/2}\)-asymptotic expansion for the distribution (under a sequence of contiguous alternatives) of a class of ECR test statistics for testing a simple full vector parameter hypothesis in the just-identified moment restrictions. To the best of our knowledge, the literature is, however, little.

  17. 17.

    Note that

    $$1-P_F^{(N)}(\mathcal{X}_0^{(N)}) \le P_F^{(N)} \Bigl [ \max _{i \in \{ 1,\ldots ,N \}} \sup _{\theta \in \Theta } ||\textbf{g}(\textbf{X}_i,\boldsymbol{{\theta }})|| > \frac{1}{2}\,N^{1/2-\xi _0} \Bigr ] =o(N^{-1}) $$

    (see Lemma 10.2).

  18. 18.

    There exists an integer \(N_{0,\rho }\) such that \(\pm N^{-\xi _0} \log N \in \mathcal{N}_\rho \)(\(\subset \mathcal{V}_\rho \)) for all \(N \ge N_{0,\rho }\).

  19. 19.

    Apply the fact (10.1) to get

    $$\begin{aligned} \rho _{M+1}^\uparrow (\boldsymbol{{\nu }}+\boldsymbol{{\Psi }}^{(N)\rho }(\boldsymbol{{\eta }}))\ge & {} \rho _{M+1}^\uparrow (\boldsymbol{{\nu }})-||\boldsymbol{{\Psi }}^{(N)\rho }(\boldsymbol{{\eta }})|| \ge \frac{1}{ ||\boldsymbol{{\nu }}^{-1}|| }-||\boldsymbol{{\Psi }}^{(N)\rho }(\boldsymbol{{\eta }})|| >\frac{1}{ 2||\boldsymbol{{\nu }}^{-1}|| }\,, \\ \rho _M^\uparrow (\boldsymbol{{\nu }}+\boldsymbol{{\Psi }}^{(N)\rho }(\boldsymbol{{\eta }}))\le & {} \rho _M^\uparrow (\boldsymbol{{\nu }})+||\boldsymbol{{\Psi }}^{(N)\rho }(\boldsymbol{{\eta }})|| \le -\frac{1}{ ||\boldsymbol{{\nu }}^{-1}|| }+||\boldsymbol{{\Psi }}^{(N)\rho }(\boldsymbol{{\eta }})|| <-\frac{1}{ 2||\boldsymbol{{\nu }}^{-1}|| }\,, \end{aligned}$$

    since \(\min \{ \rho _{M+1}^\uparrow (\boldsymbol{{\nu }}),-\rho _M^\uparrow (\boldsymbol{{\nu }}) \} =1/||\boldsymbol{{\nu }}^{-1}|| \) (see (10.6)).

  20. 20.

    Some straightforward but tedious calculations show that

    $$\begin{aligned} \kappa _{a_1}^{\rho _3,\tau _1}= & {} -\nu ^\mathcal{G}_{a_1r,r'} \nu _{(22)}^{rr'} +\frac{1}{2}\,{\nu ^\rho }^\mathcal{G}_{a_1r_1r_2} \nu _{(22)}^{r_1r_1'} \nu _{r_1',r_2'} \nu _{(22)}^{r_2r_2'} \\{} & {} +\frac{1}{2} \Bigl ( \tau _1 {\nu ^\rho }^\mathcal{G\,\,G\,\,G}_{a_1b\,b'} -\nu ^\mathcal{G\,\,G\,\,G}_{a_1b,b'} -\sum _{\beta '=1}^M \mathcal{G}_{[\beta ']b'} {\nu ^\rho }^\mathcal{G\,\,G}_{a_1b[\beta ']} \Bigr ) \nu _{(11 \cdot 2)}^{bb'}\,, \end{aligned}$$

    and that \(\kappa _{a_1,a_2,a_3}^{\rho _3,\tau _1}\) and \(\kappa _{a_1,a_2,a_3,a_4}^{-2,\rho _4,1/3,\tau _2,\tau _3,\tau _4}\) are explicitly given in the proof of Theorem 10.1; the lengthy general expression for \(\kappa _{a_1,a_2,a_3,a_4}^{\rho _3,\rho _4,\tau _1,\tau _2,\tau _3,\tau _4}\) is, however, omitted here. Although, in principle, we can write down \(\kappa _{a_1,a_2}^{\rho _3,\rho _4,\tau _1,\tau _2,\tau _3,\tau _4}\), we have not rearranged it, due to the rather lengthy algebra (the task would be no practical importance, in many cases).

References

  1. Anderson, T. W. (2003). An Introduction to Multivariate Statistical Analysis, 3rd ed. New York: Wiley.

    MATH  Google Scholar 

  2. Baggerly, K.A. (1998). Empirical likelihood as a goodness-of-fit measure. Biometrika 85 535–547.

    Article  MathSciNet  MATH  Google Scholar 

  3. Barndorff-Nielsen, O.E. and Cox, D.R. (1994). Inference and Asymptotics. London: Chapman and Hall.

    Book  MATH  Google Scholar 

  4. Bartlett, M.S. (1937). Properties of sufficiency and statistical tests. Proc.Roy.Soc.Lond. A 160 268–282.

    Article  MATH  Google Scholar 

  5. Bera, A.K. and Bilias, Y. (2001). Rao’s score, Neyman’s \(C(\alpha )\) and Silvey’s LM tests: an essay on historical developments and some new results. J.Statist.Plann.Inference 97 9–44.

    Article  MathSciNet  MATH  Google Scholar 

  6. Bhattacharya, R.N. and Ghosh, J.K. (1978). On the validity of the formal Edgeworth expansion. Ann.Statist. 6 434–451. Correction: (1980). 8 1399.

    Google Scholar 

  7. Bhattacharya, R.N. and Rao, R.R. (1976). Normal Approximation and Asymptotic Expansions. New York: Wiley.

    MATH  Google Scholar 

  8. Boos, D.D. (1992). On generalized score tests. Amer.Statist. 46 327–333.

    Google Scholar 

  9. Bravo, F. (2002). Testing linear restrictions in linear models with empirical likelihood. Econom.J. 5 104–130.

    Article  MathSciNet  MATH  Google Scholar 

  10. Bravo, F. (2003). Second-order power comparisons for a class of nonparametric likelihood-based tests. Biometrika 90 881–890.

    Article  MathSciNet  MATH  Google Scholar 

  11. Bravo, F. (2004). Empirical likelihood based inference with applications to some econometric models. Econometric Theory 20 231–264.

    Article  MathSciNet  MATH  Google Scholar 

  12. Bravo, F. (2006). Bartlett-type adjustments for empirical discrepancy test statistics. J.Statist.Plann.Inference 136 537–554.

    Article  MathSciNet  MATH  Google Scholar 

  13. Camponovo, L. and Otsu, T. (2014). On Bartlett correctability of empirical likelihood in generalized power divergence family. Statist.Probab.Lett. 86 38–43.

    Article  MathSciNet  MATH  Google Scholar 

  14. Chandra, T.K. and Mukerjee, R. (1991). Bartlett-type modification for Rao’s efficient score statistic. J.Multivariate Anal. 36 103–112.

    Article  MathSciNet  MATH  Google Scholar 

  15. Chen, S.X. (1993). On the accuracy of empirical likelihood confidence regions for linear regression model. Ann.Inst.Statist.Math. 45 621–637.

    Article  MathSciNet  MATH  Google Scholar 

  16. Chen, S.X. (1994). Empirical likelihood confidence intervals for linear regression coefficients. J.Multivariate Anal. 49 24–40.

    Article  MathSciNet  MATH  Google Scholar 

  17. Chen, S.X. and Cui, H. (2006). On Bartlett correction of empirical likelihood in the presence of nuisance parameters. Biometrika 93 215–220.

    Article  MathSciNet  MATH  Google Scholar 

  18. Chen, S.X. and Cui, H. (2007). On the second-order properties of empirical likelihood with moment restrictions. J.Econometrics 141 492–516.

    Article  MathSciNet  MATH  Google Scholar 

  19. Corcoran, S.A. (1998). Bartlett adjustment of empirical discrepancy statistics. Biometrika 85 967–972.

    Article  MATH  Google Scholar 

  20. Cordeiro, G.M. and Ferrari, S.L.P. (1991). A modified score test statistic having chi-squared distribution to order \(n^{-1}\). Biometrika 78 573–582.

    MathSciNet  MATH  Google Scholar 

  21. Cox, D.R. (1988). Some aspects of conditional and asymptotic inference: a review. Sankhyā A 50 314–337.

    MathSciNet  MATH  Google Scholar 

  22. Cressie, N. and Read, T. (1984). Multinomial goodness-of-fit tests. J.R.Stat.Soc.Ser. B 46 440–464.

    MathSciNet  MATH  Google Scholar 

  23. Cribari-Neto, F. and Cordeiro, G.M. (1996). On Bartlett and Bartlett-type corrections. Econometric Rev. 15 339–367.

    Article  MathSciNet  MATH  Google Scholar 

  24. DiCiccio, T., Hall, P. and Romano, J. (1991). Empirical likelihood is Bartlett-correctable. Ann.Statist. 19 1053–1061.

    Article  MathSciNet  MATH  Google Scholar 

  25. Efron, B. (1979). Bootstrap methods: another look at the jackknife. Ann.Statist. 7 1–26.

    Article  MathSciNet  MATH  Google Scholar 

  26. Fisher, R.A. (1922). On the mathematical foundations of theoretical statistics. Philos.Trans.R.Soc.Lond.Ser.A Math.Phys.Eng.Sci. 222 309–368.

    Google Scholar 

  27. Fujikoshi, Y. (1988). Comparison of powers of a class of tests for multivariate linear hypothesis and independence. J.Multivariate Anal. 26 48–58.

    Article  MathSciNet  MATH  Google Scholar 

  28. Fujikoshi, Y. (1997). A method for improving the large-sample chi-squared approximations to some multivariate test statistics. Amer.J.Math.Management Sci. 17 15–29.

    Google Scholar 

  29. Fujisawa, H. (1997). Improvement on chi-squared approximation by monotone transformation. J.Multivariate Anal. 60 84–89.

    Article  MathSciNet  MATH  Google Scholar 

  30. Hall, P. (1992). The Bootstrap and Edgeworth Expansion. New York: Springer.

    Book  MATH  Google Scholar 

  31. Hall, P. and La Scala, B. (1990). Methodology and algorithms of empirical likelihood. Internat.Statist.Rev. 58 109–127.

    Article  MATH  Google Scholar 

  32. Hansen, L.P. (1982). Large sample properties of generalized method of moments estimators. Econometrica 50 1029–1054.

    Article  MathSciNet  MATH  Google Scholar 

  33. Hansen, L.P., Heaton, J. and Yaron, A. (1996). Finite-sample properties of some alternative GMM estimators. J.Bus.Econom.Statist. 14 262–280.

    Google Scholar 

  34. Harris, P. (1985). An asymptotic expansion for the null distribution of the efficient score statistic. Biometrika 72 653–659.

    Article  MathSciNet  MATH  Google Scholar 

  35. Harris, P. and Peers, H.W. (1980). The local power of the efficient scores test statistic. Biometrika 67 525–529.

    Article  MathSciNet  MATH  Google Scholar 

  36. Hayakawa, T. (1975). The likelihood ratio criterion for a composite hypothesis under a local alternative. Biometrika 62 451–460.

    Article  MathSciNet  MATH  Google Scholar 

  37. Hayakawa, T. (1977). The likelihood ratio criterion and the asymptotic expansion of its distribution. Ann.Inst.Statist.Math. 29 359–378. Correction: (1987). 39 681.

    Google Scholar 

  38. Horn, R.A. and Johnson, C.R. (1985). Matrix Analysis. Cambridge: Cambridge University Press.

    Book  MATH  Google Scholar 

  39. Iwashita, T. (1997). Adjustment of Bartlett type to Hotelling’s \(T^2\)-statistic under elliptical distributions. Amer.J.Math.Management Sci. 17 91–96.

    Google Scholar 

  40. Jensen, J.L. (1993). A historical sketch and some new results on the improved log likelihood ratio statistic. Scand.J.Statist. 20 1–15.

    MathSciNet  MATH  Google Scholar 

  41. Jing, B.Y. and Wood, A.T.A. (1996). Exponential empirical likelihood is not Bartlett correctable. Ann.Statist. 24 365–369.

    Article  MathSciNet  MATH  Google Scholar 

  42. Kakizawa, Y. (1996). Higher order monotone Bartlett-type adjustment for some multivariate test statistics. Biometrika 83 923–927.

    Article  MathSciNet  MATH  Google Scholar 

  43. Kakizawa, Y. (1997). Higher-order Bartlett-type adjustment. J.Stat.Plan.Inference 65 269–280.

    Article  MathSciNet  MATH  Google Scholar 

  44. Kakizawa, Y. (2009). Third-order power comparisons for a class of tests for multivariate linear hypothesis under general distributions. J.Multivariate Anal. 100 473–496.

    Article  MathSciNet  MATH  Google Scholar 

  45. Kakizawa, Y. (2012a). Generalized Cordeiro–Ferrari Bartlett-type adjustment. Statist.Probab.Lett. 82 2008–2016.

    Article  MathSciNet  MATH  Google Scholar 

  46. Kakizawa, Y. (2012b). Improved chi-squared tests for a composite hypothesis. J.Multivariate Anal. 107 141–161.

    Article  MathSciNet  MATH  Google Scholar 

  47. Kakizawa, Y. (2013). Third-order local power properties of tests for a composite hypothesis. J.Multivariate Anal. 114 303–317.

    Article  MathSciNet  MATH  Google Scholar 

  48. Kakizawa, Y. (2015). Third-order local power properties of tests for a composite hypothesis, II. J.Multivariate Anal. 140 99–112.

    Article  MathSciNet  MATH  Google Scholar 

  49. Kakizawa, Y. (2017). Third-order average local powers of Bartlett-type adjusted tests: Ordinary versus adjusted profile likelihood. J.Multivariate Anal. 153 98–120.

    Article  MathSciNet  MATH  Google Scholar 

  50. Kitamura, Y. and Stutzer, M. (1997). An information-theoretic alternative to generalized method of moments estimation. Econometrica 65 861–874.

    Article  MathSciNet  MATH  Google Scholar 

  51. Kojima, M. and Kubokawa, T. (2013). Bartlett-type adjustments for hypothesis testing in linear models with general error covariance matrices. J.Multivariate Anal. 122 162–174.

    Article  MathSciNet  MATH  Google Scholar 

  52. Kolaczyk, E.D. (1994). Empirical likelihood for generalized linear models. Statist.Sinica 4 199–218.

    MathSciNet  MATH  Google Scholar 

  53. Lawley, D.N. (1956). A general method for approximating to the distribution of likelihood ratio criteria. Biometrika 43 295–303.

    Article  MathSciNet  MATH  Google Scholar 

  54. Magdalinos, M.A. (1992). Stochastic expansions and asymptotic approximations. Econometric Theory 8 343–367.

    Article  MathSciNet  Google Scholar 

  55. Mukerjee, R. (1993). Rao’s score test: Recent asymptotic results. In: Handbook of Statistics, Vol.11. Maddala, G.S., Rao, C.R. and Vinod, H.D. Eds. Amsterdam: North-Holland, pp.363–379.

    Google Scholar 

  56. Newey, W.K. and Smith, R.J. (2004). Higher order properties of GMM and generalized empirical likelihood estimators. Econometrica 72 219–255.

    Article  MathSciNet  MATH  Google Scholar 

  57. Owen, A.B. (1988). Empirical likelihood ratio confidence intervals for a single functional. Biometrika 75 237–249.

    Article  MathSciNet  MATH  Google Scholar 

  58. Owen, A.B. (1990). Empirical likelihood ratio confidence regions. Ann.Statist. 18 90–120.

    Article  MathSciNet  MATH  Google Scholar 

  59. Owen, A.B. (1991). Empirical likelihood for linear models. Ann.Statist. 19 1725–1747.

    Article  MathSciNet  MATH  Google Scholar 

  60. Owen, A.B. (2001). Empirical Likelihood. London: Chapman and Hall.

    MATH  Google Scholar 

  61. Peers, H.W. (1971). Likelihood ratio and associated test criteria. Biometrika 58 577–587.

    Article  MATH  Google Scholar 

  62. Qin, J. and Lawless, J. (1994). Empirical likelihood and general estimating equations. Ann.Statist. 22 300–325.

    Article  MathSciNet  MATH  Google Scholar 

  63. Qin, J. and Lawless, J. (1995). Estimating equations, empirical likelihood and constraints on parameters. Canad.J.Statist. 23 145–159.

    Article  MathSciNet  MATH  Google Scholar 

  64. Ragusa, G. (2011). Minimum divergence, generalized empirical likelihoods, and higher order expansions. Econometric Rev. 30 406–456.

    Article  MathSciNet  MATH  Google Scholar 

  65. Rao, C.R. (1948). Large sample tests of statistical hypotheses concerning several parameters with applications to problems of estimation. Math.Proc.Cambridge Philos.Soc. 44 50–57.

    Article  MathSciNet  MATH  Google Scholar 

  66. Rao, C.R. and Mukerjee, R. (1997). Comparison of LR, score, and Wald tests in a non-iid setting. J.Multivariate Anal. 60 99–110.

    Article  MathSciNet  MATH  Google Scholar 

  67. Rocke, D.M. (1989). Bootstrap Bartlett adjustment in seemingly unrelated regression. J.Amer.Statist.Assoc. 84 598–601.

    Google Scholar 

  68. Rothenberg, T.J. (1977). Edgeworth expansions for multivariate test statistics. IP–255, Center for Research in Management Science, University of California, Berkeley.

    Google Scholar 

  69. Silvey, S.D. (1959). The Lagrange multiplier test. Ann.Math.Statist. 30 389–407.

    Article  MathSciNet  MATH  Google Scholar 

  70. Siotani, M., Hayakawa, T. and Fujikoshi, Y. (1985). Modern Multivariate Analysis: A Graduate Course and Handbook. Ohio: American Sciences Press.

    MATH  Google Scholar 

  71. Taniguchi, M. (1991a). Higher Order Asymptotic Theory for Time Series Analysis. Berlin: Springer-Verlag.

    Book  MATH  Google Scholar 

  72. Taniguchi, M. (1991b). Third-order asymptotic properties of a class of test statistics under a local alternative. J.Multivariate Anal. 37 223–238.

    Article  MathSciNet  MATH  Google Scholar 

  73. Terrell, G.R. (2002). The gradient statistic. Comput.Sci.Statist. 34 206–215.

    Google Scholar 

  74. Thomas, D.R. and Grunkemeier, G.L. (1975). Confidence interval estimation of survival probabilities for censored data. J.Amer.Statist.Assoc. 70 865–871.

    Google Scholar 

  75. Wald, A. (1943). Tests of statistical hypothesis concerning several parameters when the number of observations is large. Trans.Amer.Math.Soc. 54 426–482.

    Google Scholar 

  76. Wilks, S.S. (1938). The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann.Math.Statist. 9 60–62.

    Article  MATH  Google Scholar 

  77. Zhang, B. (1996). On the accuracy of empirical likelihood confidence intervals for \(M\)-functionals. J.Nonparametr.Stat. 6 311–321.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Hokkaido University, Kita-ku, Sapporo, Hokkaido, 060-0809, Japan

    Yoshihide Kakizawa

Authors
  1. Yoshihide Kakizawa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yoshihide Kakizawa .

Editor information

Editors and Affiliations

  1. Faculty of Science and Engineering, Waseda University, Shinjuku-ku, Tokyo, Japan

    Yan Liu

  2. Faculty of Science, Niigata University, Nishi-ku, Niigata, Japan

    Junichi Hirukawa

  3. Faculty of Economics and Business, Hokkaido University, Kita-ku, Sapporo, Hokkaido, Japan

    Yoshihide Kakizawa

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Kakizawa, Y. (2023). Asymptotic Expansions for Several GEL-Based Test Statistics and Hybrid Bartlett-Type Correction with Bootstrap. In: Liu, Y., Hirukawa, J., Kakizawa, Y. (eds) Research Papers in Statistical Inference for Time Series and Related Models. Springer, Singapore. https://doi.org/10.1007/978-981-99-0803-5_10

Download citation

Publish with us

Policies and ethics

Search

Navigation