Keywords

20.1 Global Fallout

From the first atmospheric nuclear weapon test at Alamogordo, New Mexico, conducted by the USA in July 1945, to the last atmospheric weapon test at Lop Nor conducted by the People’s Republic of China in October 1980, several countries have conducted a series of nuclear weapons tests in the atmosphere. The large quantities of anthropogenic radioactive nuclides injected into the stratosphere originated from nuclear weapons tests that gradually migrated to the troposphere (0.5–1.7 years, Hirose et al. 1987) and fell as radioactive fallout on land and ocean surfaces throughout the globe, so-called global fallout. The total amount of radiation released from atmospheric nuclear weapons tests peaked in the 1950s and early 1960s. Global fallout included various radionuclides such as 90Sr, 137Cs, 239Pu, and 240Pu. Among them, 137Cs originated from the global fallout (hereafter, 137Cs-GFO) and has attracted significant social attention for its environmental impact due to its long half-life (30.2 years) and has been used in studies of soil erosion processes. Two regions of high 137Cs fallout characterize the global spatial distribution of 137Cs fallout; these areas are located on the eastern sides of the Eurasian continent and the North American continent in the Northern Hemisphere. The Japanese archipelago is in the high deposition region (Aoyama 2018); therefore, it had been exposed to radioactive contamination even before the Chernobyl and Fukushima nuclear accidents. We address the consequences of 137Cs-GFO over the Japanese archipelago.

This chapter was based on Ito et al. (2020), but with an additional discussion on the vertical distribution of 137Cs-GFO in forest soils and derived sediment migration on forested hillslopes over 50 years.

20.2 Cumulative Deposition of 137Cs-GFO (From Monthly Data Collected by Meteorological Observatories and Local Authorities)

Many stations across Japan have observed the 137Cs-GFO deposits since the late 1950s. The monthly deposit of 137Cs-GFO observed by the Meteorological Research Institute (MRI, located in Tokyo until March 1980 and at Tsukuba after April 1980) and its decay-corrected cumulative deposit was shown as time-series data (Fig. 20.1). The monthly deposit of 137Cs-GFO reached its maximum in the early 1960s (0.55 kBq m−2 month−1, June 1963). The decay-corrected cumulative 137Cs-GFO peaked in the late 1960s, with a maximum value of ~6.05 kBq m−2 (June–August 1966). This was 55–75% of the monthly 137Cs deposit in Tokyo immediately after the Fukushima Daiichi Nuclear Power Plant (FDNPP) accident (8.1–11.0 kBq m−2, March 2011, Shinjuku, Tokyo).

Fig. 20.1
Two graphs, a scatterplot and a line graph, of the decomposition of 137 Cs. a, the graph records the monthly deposition, the data starts with reconstructed value, observation in Tokyo, observation in Tsukuba, and F D N P P accident. b, the graph plots two lines, the increasing dotted line represents cumulative deposition, and the decreasing line represents decay-corrected cumulative deposition.

Deposition of 137Cs observed by the Meteorological Research Institute. (a) Monthly 137Cs deposition from July 1945 to March 2020. (b) Cumulative (thin black dashed line) and decay-corrected cumulative (thick gray line) deposition of 137Cs from July 1945 to July 2010. Data source: IGFD database, Aoyama (2019); Environmental Radiation Database, the Secretariat of the Nuclear Regulation Authority, https://search.kankyo-hoshano.go.jp/servlet/search.top. The MRI was located in Tokyo until March 1985 and at Tsukuba after April 1985. From July 1945 to March 1957, before the start of 137Cs observation, data were interpolated with reconstructed values (Katsuragi 1983; Aoyama 1999). From August 2010 to March 2011, the monthly 137Cs observation was missing due to contamination of the experimental and measurement environment caused by the FDNPP accident

Full size image

The decay-corrected cumulative deposit of 137Cs-GFO as of October 1, 2008 (hereafter, referred to as cumulative fallout), was estimated by adding up the decay-corrected monthly deposit of 137Cs-GFO (including reconstructed values before the start of 137Cs observation from July 1945 to March 1957, see also footnote in Fig. 20.1 for data source). The cumulative fallout in Tokyo from July 1945 to September 2008 was estimated to be 2.73 kBq m−2 as of October 1, 2008 (Ito et al. 2020), and the average elapsed time from 137Cs-GFO fallout, as of October 1, 2008, was 45.2 years. Thus, the theoretical value of the cumulative fallout was ~45% of the maximum in the late 1960s. This value for Tokyo is the most accurate estimate of the cumulative fallout in Japan, since the measurement in Tokyo was the most prolonged and uninterrupted in Japan. However, regional differences in global fallout within Japan were substantial, as will be shown later, and the estimated value for Tokyo does not necessarily give a representative cumulative fallout value for Japan.

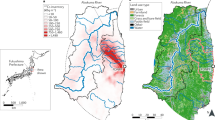
The cumulative fallout was reconstructed for 39 stations that started observations before 1980 (including MRI-Tsukuba, which started its observation in April 1980). The amount of 137Cs-GFO deposition during the no-observation period was determined by proportional calculation using other stations’ values as reference. Details of the reconstruction method are shown elsewhere (Ito et al. 2020). The average (±SD) cumulative fallout was 2.47 ± 0.95 kBq m−2 (n = 39), ranging from 1.23 to 5.00 kBq m−2 (Fig. 20.2a, revised from Ito et al. 2020). Figure 20.3 shows the spatial distribution of the reconstructed cumulative fallout (revised from Ito et al. 2020). It was more abundant on the Sea of Japan side of northern Japan (e.g., Akita and Fukui) and less abundant on the Pacific side of western Japan and the Seto Inland Sea coast (e.g., Osaka and Okayama). A numerical list of the reconstructed values has been provided elsewhere (Ito et al. 2020).

Fig. 20.2
Four graphs. a, histogram of cumulative fallout, the highest bar is between 1.5 and 2, and the error bar data are minimum 1, lower quartile 1.3, upper quartile 3, and maximum 5. b, histogram of inventory on a site basis, the highest bar is between 1.5 and 2, and the error bar data are as follows. Minimum 0, lower quartile 1, median, 1.5, upper quartile 3, and maximum 9.5. c, histogram plots inventory on a soil pit basis, the height of the bars decreases as the number increases, and the error bar data are minimum 0, lower quartile 1, median 1.5, upper quartile 3, and maximum 23. d, scatter plot of inventory on a site basis versus inventory on a soil pit basis.

Global fallout of radiocesium 137 (137Cs-GFO) in Japan (kBq m−2). (a) Frequency distribution of cumulative fallout: the decay-corrected cumulative depositions of 137Cs-GFO for fallout observatories. (b) Frequency distribution of inventory data on a plot basis: simple arithmetic mean of ≤4 soil pits in the NFSCI survey site of the 137Cs-GFO inventory in 0–30 cm deep forest soils. (c) Frequency distribution of inventory data on a soil pit basis: the 137Cs-GFO inventory in 0–30 deep forest soils for each soil pit. (d) Relations of the 137Cs-GFO inventory on a site basis against the 137Cs-GFO inventory on a soil pit basis. The value of 137Cs-GFO is shown as of October 1, 2008. The box–whisker plots mark the minimum and maximum and the 25th, 50th, and 75th percentile points. [Figures (a–c) were revised from Ito et al. (2020)]

Full size image
Fig. 20.3
A heat map of Japan highlights the spatial distribution of 137 Cs. Inventory and cumulative fallout are marked on the map with colors to indicate 137 Cs G F O. Inset map of Japan highlights annual precipitation, with a color spectrum of annual precipitation that ranges between 600 and 2500.

Spatial distribution of 137Cs-GFO and precipitation across Japan. Forest soil inventory on a plot basis (circle, 0–30 cm depth) and cumulative fallout (square) (kBq m−2). The value of 137Cs-GFO is shown as of October 1, 2008. Normal total annual precipitation was also shown in the lower right (mm). [Revised from Ito et al. (2020)]

Full size image

The 137Cs emitted from the Chernobyl nuclear power plant accident (April 26, 1986) also accumulated in the forest soil in Japan before the FDNPP accident. Most of the Chernobyl-generated 137Cs fallout at the MRI (Tsukuba, Japan) occurred during May 1986 (Aoyama et al. 1986, 1987; Higuchi et al. 1988, Fig. 20.1). The amount of 137Cs fallout from May 1986 to April 1987 (within a year after the Chernobyl accident) and the amount of 137Cs fallout from May 1986 to September 2008 correspond to less than 3% and 5%, respectively, of the decay-corrected cumulative fallout as of October 2008 (Fig. 20.1). Thus, most of the 137Cs detected in Japanese forests before the FDNPP accident came from the global fallout.

20.3 Residual 137Cs-GFO in Forest Soils in Japan Before the FDNPP Accident

The FDNPP accident (March 11, 2011) resulted in an additional 2.7 PBq of 137Cs deposition onto the terrestrial environment in Japan (Onda et al. 2020). Airborne monitoring survey reported that 137Cs deposit on the ground surface within the zone 80 km from the FDNPP ranged from 10 to >3000 kBq m−2 (Nuclear Regulation Authority, https://radioactivity.nsr.go.jp/en/list/307/list-1.html). This value ranged from 1.3 to >400 times higher than the simple (i.e., nondecay-corrected) cumulative amount of 137Cs-GFO in Tokyo mentioned above. The majority (approximately 70%) of the areas where the FDNPP-generated radioactive materials fell were forests. Among the contaminated radioactive cesium (137Cs and 134Cs), the consequence of 137Cs, which has a considerably long half-life of 30.2 years, in forested areas has been a significant concern for local inhabitants (Onda et al. 2020).

Many studies on the redistribution of 137Cs fallout, both 137Cs-GFO (Jagercikova et al. 2015) and the Chernobyl-generated 137Cs (Rafferty et al. 2000; Zhiyanski et al. 2008), have revealed the long-term persistence of 137Cs in soil upon its adsorption onto clays (Dyer et al. 2000). The FDNPP-generated 137Cs has also been expected and demonstrated to remain in the surface layer of the forest soil and decrease in the long-term due to radioactive decay. This prospect has been substantiated, although it was based on a fewer than 10-year study period (Onda et al. 2020). However, Japan is prone to sediment-related disasters (e.g., mass movements and soil erosion) due to a combination of various geographical factors (e.g., rainfall, snowmelt, earthquake, soil, geological structure, and topography) (Yoshimatsu and Abe 2006). Such disasters may result in a specific redistribution pattern of 137Cs (Fukuyama et al. 2005), which could lead to discharge from the forest watershed. Some of the FDNPP-generated 137Cs has been reported to be discharged from forests into rivers, owing to sediment runoff caused by the heavy rainfall and steep terrain (Ueda et al. 2013; Shinomiya et al. 2014; Tsuji et al. 2016; Iwagami et al. 2017). Although FDNPP-contaminated forest areas continue to represent more stable contaminant stores (Taniguchi et al. 2019), the residual status of 137Cs in Japan after a long period could be different from that of Chernobyl.

Therefore, we investigated the extent to which 137Cs-GFO, which fell into forests about half a century ago (around 1960), remained in forest soil in the late 2000s. This is an attempt to clarify the long-term persistence of 137Cs in Japan and to verify whether the prediction of the behavior of 137Cs based on the Chernobyl study (137Cs is retained in the surface layer of forest soil for a long time) is also applicable to the Japanese archipelago.

The Forestry and Forest Products Research Institute (FFPRI) has been storing soil samples from forests throughout Japan collected just before the FDNPP accident [the National Forest Soil Carbon Inventory (NFSCI) project, 2006–2010] (Ugawa et al. 2012; Nanko et al. 2017). We used the NFSCI soil samples to clarify how much 137Cs had accumulated in Japanese forests before the FDNPP accident (Ito et al. 2020). As mentioned in the previous section, this 137Cs was mainly a global fallout, with some (~3%) from the Chernobyl nuclear accident.

The 137Cs inventory in the surface layer of mineral soil (30 cm) at the forests was estimated at 316 spatially uniformly selected locations from the NFSCI survey sites across Japan. Repeated subsamplings with four soil pits were conducted at each site. The locations of the soil pits were systematically determined, where the four soil pits were made at four directions (N, E, W, and S) on a circle of 35.68 m in diameter centered on the NFSCI survey site reference point located on the latitude–longitude grid (Ugawa et al. 2012).

Mineral soil samples in each soil pit were collected from three layers: 0–5, 5–15, and 15–30 cm. From the 137Cs concentration in the soil samples and the soil bulk density, the inventory of 137Cs per square meter was estimated up to the surface soil layer of 30 cm. The activity concentration of 137Cs measurement was performed using an NaI well-type scintillation counter (2480 WIZARD2 Automatic Gamma Counter; PerkinElmer, Inc., Waltham, MA, USA). This NaI gamma counter system can perform measurements with an expanded uncertainty of 6.6% for certified materials. Details of the calibration, certification, and detection limit are shown elsewhere (Ito et al. 2020). The 137Cs-GFO inventory was calculated by multiplying the 137Cs activity concentration, which was decay-corrected to October 1, 2008 (i.e., the intermediate point in the soil-sampling period) data using a half-life of 30.2 years for 137Cs, a layer thickness of 30 cm, and the bulk density of the soil sample.

The 137Cs-GFO inventory in 0–30 cm deep forest soils (hereafter referred to as inventory) was estimated on-site. The average ± SD (±SE) of 316 sampling sites was 2.27 ± 1.73 (±0.10) kBq m−2 (ranging from 0.09 to 9.43 kBq m−2, n = 316) (Ito et al. 2020). A right-skewed distribution, peaking at ~1.5 kBq m−2, was observed (Fig. 20.2b). This skewness was somewhat similar to that of the cumulative fallout (Fig. 20.2a), but the distribution differed, because there were several values <1.0 kBq m−2 and a long-tail distribution in the range above 6.0 kBq m−2. A wider range and an L-shaped frequent distribution were presented on a soil pit basis, and the average ± SD (±SE) of 1171 soil pits was 2.29 ± 2.30 (±0.07) kBq m−2 (ranging from 0.00 to 22.89 kBq m−2, Fig. 20.2c). The more right-skewed distribution indicated a high frequency of sites (or pits) with inventories below the average and a low frequency but still a high number of sites (or pits) with values well above the average. Figure 20.2d shows the soil pit inventory versus the on-site inventory (i.e., an average of the inventory on a soil pit basis). A large variation in the inventory could be observed among the ~4 soil pits even within the same site. The forest redistribution of 137Cs-GFO implied by Fig. 20.2d will be discussed in detail later in Sect. 20.5.

The inventory was also characterized by its spatial distribution. The Pacific coast had low inventory, and the Japanese coast of northern Japan had high inventory (Fig. 20.3, revised from Ito et al. 2020). Comparing this with the spatial distribution of the total annual precipitation (lower right panel, Fig. 20.3), we found that the inventory did not precisely correspond to the total annual precipitation. The low correlation between fallout and precipitation amount is characteristic of Japan (Malakhov and Pudovkina 1970). Our study also confirmed a previous finding (Ito et al. 2020).

The air dose from 137Cs-GFO was sufficiently low compared to that from natural radiation sources. The monthly external exposure was 0.0021 (for adults) and 0.0027 mSv (for newborns) (Omori et al. 2020), corresponding to an average inventory value of 137Cs-GFO (2.27 kBq m−2) on October 1, 2008. Note that dose conversion coefficients for external exposure to 137Cs distributed in the soil of 1.28E−06 (adults) and 1.67E−06 mSv/h per kBq m−2 (newborns) were used in this calculation (Satoh et al. 2014), and it was assumed that the 137Cs radiation source was distributed as 0.5 g cm−2 at the soil surface. This is an extremely low value compared to the 0.07 mSv external exposure from cosmic and terrestrial radiation and a similar low value of 0.2 mSv/month from all natural radiation sources (UNSCEAR 2020).

20.4 Does 137Cs-GFO Remain in the Forest’s Surface Soil After 50 Years?

The average (±SD) cumulative 137Cs-GFO for fallout observatories was 2.47 (±0.95) kBq m−2 (n = 39) (see Sect. 20.2), whereas the average (±SD) inventory of 137Cs-GFO in forest soils on a sampling site basis was 2.27 (±1.73) kBq m−2 (n = 316) (see Sect. 20.3), as of October 1, 2008 (Ito et al. 2020). Statistically testing whether these values were the same is equivalent to determining whether 137Cs-GFO remained in the forest after ~50 years. The inventory (i.e., the inventory of 137Cs-GFO in 0–30-cm deep forest soils) and the cumulative fallout (i.e., the decay-corrected cumulative deposits of 137Cs-GFO for fallout observatories) were both corrected to the values, as of October 1, 2008. However, we determined that it would be inappropriate to compare inventory and cumulative fallout on that basis alone. The locations of meteorological stations and forest soil research sites did not coincide (Fig. 20.3). The forest soil survey sites were evenly spaced throughout Japan, but the spatial distribution of available meteorological stations was not uniform. To properly compare the inventory and cumulative fallout, which were data sets collected at different locations, the statistical analysis was processed to adjust for total annual precipitation and regional differences.

We used a general linear mixed-effect (GLM) model to estimate 137Cs-GFO using total annual precipitation, regions, and dataset categories (i.e., inventory or cumulative fallout) as fixed effects and sampling sites for NFSCI as a random effect. Post hoc comparisons between the dataset categories were examined using the Tukey-HSD test (p < 0.05). In other words, the GLM model determined the inventory’s least-squares means (LSM), and the cumulative fallout normalized the effects of total annual precipitation and region and tested whether there was a statistically significant difference between the inventory and the cumulative fallout. Details of the GLM analysis are shown elsewhere (Ito et al. 2020).

Note that the NFSCI forest soil survey sites were incorporated as a random effect in the model. This allowed us to adequately address the soil survey’s sampling design, which has four repeated soil pits at each NFSCI site, into the statistical analysis. Eventually, this random effect incorporation enabled us to reveal the 137Cs-GFO redistribution via 137Cs-GFO-contaminated sediment migration on the forested hillslopes.

The GLM analysis indicated that the inventory and the cumulative fallout were not significantly different (p = 0.34, Ito et al. 2020). It was empirically demonstrated that most of the 137Cs-GFO remained on the soil surface even half a century after the fallout. However, the inventory’s model-estimated LSM (2.08 kBq m−2) was maintained as 79.1% of the cumulative fallout (2.63 kBq m−2) (Ito et al. 2020). These results will be discussed in more detail at the end of the next section.

20.5 Vertical Distribution of 137Cs-GFO Reveals Sediment Redistribution Over 50 Years

20.5.1 Downward Infiltration in Soils Alone Cannot Explain the Various Vertical Distribution Patterns of 137Cs-GFO

The inventory varied considerably among the four soil pits in the same NFSCI site (see Fig. 20.2d and Sect. 20.3). This was demonstrated in a GLM analysis using the 137Cs-GFO inventory as an objective variable and the NFSCI sampling plots as a random effect term, where the ratio of the variance components of the site as a random effect to the total variance was estimated. It demonstrated that the variance component estimate within the site variability (58.8%) was greater than the variability among the site (41.2%). Why was the difference in 137Cs-GFO inventory within sites (i.e., between locations less than 30 m away) greater than the difference among sites (i.e., between locations at least 30 km away)? We thought that it would be implausible to explain this by the spatial variation in the amounts of 137Cs-GFO deposits alone.

We analyzed the soil’s vertical distribution pattern of 137Cs-GFO to determine the reason for this intra-site variability in the 137Cs-GFO inventory. As noted in Sect. 20.3, the soil samples used in this study were collected from three layers of each soil pit: 0–5, 5–15, and 15–30 cm. A comprehensive meta-analysis estimated that the 137Cs penetration velocities ranged from 0.05 to 0.76 cm year−1 (median of 0.28 cm year−1) over 25 years, in which velocities for Cambisols, corresponding to a typical forest soil in Japan (brown forest soils), averaged 0.11 cm year−1 (Jagercikova et al. 2015). Applying these penetration velocities to the monthly deposits of 137Cs in Tokyo, the vertical distribution of 137Cs-GFO as of October 1, 2008, was estimated as shown in Fig. 20.4. For Cambisols-average (0.11 cm year−1), the total inventory of 2.73 kBq m−2 was likely distributed in the 0–5 cm layer (1.43 kBq m−2, 52% of total) and the 5–15 cm layer (1.30 kBq m−2, 48%).

Fig. 20.4
A graph plots 137 Cs G F O penetration velocity. The x-axis represents soil depth ranges from 0 to 30 above.

Hypothetical vertical distribution of 137Cs-GFO as of October 1, 2008, estimated by assuming constant vertical penetration velocities for the monthly deposition of 137Cs in Tokyo. The penetration velocity was based on Jagercikova et al. (2015). The area of the black bar was proportional to the amount of inventory in each soil layer. Numbers in italics indicated the amount of the inventory. In assuming a penetration velocity of 0.76 cm year−1, 2.37 kBq m−2 of 137Cs was estimated to be present in the soil at more than 30 cm depth

Full size image

Here, we consider the intermediate velocity of the four vertical penetration velocities listed in the example (Fig. 20.4). Suppose we assume that 137Cs-GFO mitigates only vertically through the soil at a constant infiltration rate. In that case, there are five possible vertical distributions: only in the first layer (0–5 cm), in the first and second (5–15 cm) layers, mainly in the second layer, in the second and third (15–30 cm) layers, and mainly in the third layer.

However, the 137Cs-GFO vertical distribution patterns obtained from the actual data varied widely. We categorized 1136 soil pits with a complete three depth layer into a total of 15 patterns for the vertical distribution of 137Cs-GFO based on the relative magnitude of its accumulation in the three soil layers (Fig. 20.5, see the footnote for details of the classification criteria). Among these, four patterns contained some percentage (more than 0.5% of the total inventory) of 137Cs-GFO in all three layers (the fifth to eighth patterns from the left in Fig. 20.5). These four patterns accounted for 44% of the total soil pits. As mentioned in the previous paragraph, such patterns rarely appear under the assumption of vertical mitigation of 137Cs-GFO at a constant infiltration rate. Additionally, we found several soil pits, 16% of the total, showing patterns where the amount of 137Cs-GFO per unit depth was the smallest in the second layer (the four patterns noted on the right side of Fig. 20.5). The infiltration-driven assumption, or at least the assumption of a constant infiltration rate, can hardly explain the existence of these patterns. In the next subsection, we examine whether the 137Cs-GFO inventory in the soil pit showing each vertical distribution pattern is consistent with the expected magnitudes based on the infiltration-driven assumption.

Fig. 20.5
A graph plots the vertical distribution of 137 Cs in three layers of soil. The graph plots expected filtration, expected inventory, soil depth, frequency, mean, and types.

Vertical distribution patterns of 137Cs-GFO based on the relative magnitude of its accumulation in the three soil layers. Schematic diagram of the 15 patterns. To assess the relative accumulation of 137Cs-GFO in each soil layer, we introduced two indices (Ito et al. 2020): the percentage of 137Cs-GFO amount for each soil layer to the total of soil pit (Pn, %) for each nth soil layer, where n represents the order of the soil layer (1, 0–5 cm, 2, 5–15 cm; and 3, 15–30 cm depth), and the amount of 137Cs-GFO per unit depth for each soil layer (Qn, kBq m−2 cm−1). We set the threshold to Pn < 0.5% for a layer having “None” 137Cs-GFO accumulation. We extracted the layers for which the index Pn was determined to be “None.” The other soil layer was determined to be “More” and “Less,” or “Most,” “Mid,” and “Least,” in order of increasing index Qn. We categorized the vertical distribution pattern by combining these four statuses for the three layers of each soil pit. The bold gray curve is a hypothetical vertical distribution to intuitively understand the relative amounts of 137Cs-GFO in the three layers. In the upper part of the schematic diagram, relative magnitudes of infiltration rate and inventory of 137Cs-GFO are expected from the vertical distribution pattern, assuming that the vertical distribution of 137Cs-GFO in soil depends only on the vertical infiltration of 137Cs-GFO. The vertical distribution patterns were arranged based on the similarity of these expected relative magnitudes of expected infiltration and expected inventory. At the bottom of the schematic diagram, frequency (the number of occurrences and %) and mean value (±SD) of the 137Cs-GFO (kBq m−2) inventory were shown for each pattern. Mean values were simple arithmetic averages without normalization by GLM. The number of types (subtypes) presented in Ito et al. (2020) was shown in the lower-most column. In the original paper, the vertical distribution patterns were classified into nine types with three subtypes using the same two indices, but in this chapter, the patterns were subdivided into 15 patterns

Full size image

20.5.2 The 137Cs-GFO Inventory Predicted by Assuming Only Downward Infiltration in Soils Is Entirely Different from the Actual Value

We assume that the redistribution of 137Cs-GFO was determined only by downward migration at a constant infiltration rate. The upper part of the schematic diagram shows relative magnitudes of infiltration rate and 137Cs-GFO inventory expected from the vertical distribution pattern (Fig. 20.5).

In the four patterns on the far left (Fig. 20.5), the third layer and the second and third layers were “None.” Based on the infiltration-driven assumption, even the earliest fallout of 137Cs-GFO did not reach the second/third layer even after 63 years (i.e., even in 2008, 63 years after 1945) due to the very slow infiltration rate (“Very Late” to “Late” in expected infiltration, first line at the upper part of the schematic diagram, Fig. 20.5). Therefore, all the fallen 137Cs-GFO would have remained in the soil within 15 or 5 cm of the surface layer, and the total inventory should be “Very Large” (expected inventory, second line at the upper part of the schematic diagram, Fig. 20.5). However, contrary to this expectation, the inventory for these four patterns was much smaller than that for the other patterns (0.62–2.01 kBq m−2, the lower part of the schematic diagram, Fig. 20.5).

There were five patterns where the third layer was “All,” “Most,” or “More,” indicating that the third layer had the largest concentration of 137Cs-GFO (patterns of eighth, 10th, 11th, 14th, and 15th from the left, Fig. 20.5). In these five patterns, the infiltration rate must be so fast that a considerable amount of 137Cs-GFO has already reached the third layer (“Very Fast” to “Fast” in expected infiltration, Fig. 20.5). It could be assumed that some of the 137Cs-GFO has penetrated the soil below the third layer, deeper than 30 cm below the surface, and therefore the inventory of 137Cs-GFO should be “Small” or “Very Small” (expected inventory, Fig. 20.5). However, partly contrary to this expectation, the inventory trends were split between two extremes: 2 of the 5 patterns had fairly small inventories, as expected, whereas 3 patterns were quite large, even the largest inventory of the 15 patterns (the eighth pattern from the left, Fig. 20.5).

We have concluded that the infiltration-driven assumption could not reasonably explain the 137Cs-GFO-related combinations between the vertical distribution patterns and inventory quantities. In the next subsection, we will try to provide a consistent description of the 137Cs-GFO-related combinations with respect to horizontal sediment migration on forested hillslopes.

20.5.3 The Sediment Redistribution Is Consistent with the Correspondence Between the Vertical Distribution Pattern and the Inventory

The GLM model for estimating 137Cs-GFO constructed in Sect. 20.4 is mentioned again. The GLM model, which incorporated three fixed effects (total annual precipitation, region, and dataset category) and a random effect (NFSCI sampling sites), was significantly estimated 137Cs-GFO (p < 0.0001). Applying the GLM analysis, the 137Cs-GFO variability within the NFSCI sampling sites (58.8% of the total) was greater than that among the sites (41.2%). This considerable within-sites variation among ~4 soil pit repetitions within a 0.1 ha plot strongly indicated the large microscale heterogeneity of the 137Cs-GFO distribution within a catchment (Ito et al. 2020). We hypothesized that this spatially uneven 137Cs-GFO distribution was due to horizontal sediment migration within a forest catchment. Similarly, we hypothesized that the various vertical distribution patterns of 137Cs-GFO mentioned in the previous subsection (Fig. 20.5) were also caused by horizontal sediment migration. Therefore, we introduced the vertical distribution pattern as an explanatory variable in the GLM described above and examined whether the accuracy of 137Cs-GFO estimation could be improved.

We modified the GLM model by incorporating the vertical distribution pattern as an additional explanatory variable (hereafter, revised GLM model). The vertical distribution pattern had a significantly strong explanatory effect in the revised GLM model (p < 0.0001). In other words, under normalized conditions for the impact of the other explanatory variable, the 137Cs-GFO inventory differed significantly by vertical distribution pattern. Moreover, the 137Cs-GFO variability within the NFSCI sampling sites in the revised GLM model (25.8% of the total) was considerably less than that in the previous GLM model (58.8%). This indicates that the vertical distribution pattern effectively explained the within-forest variation in the 137Cs-GFO inventory.

We calculated the LSM of the 137Cs-GFO inventory for each vertical distribution pattern and examined the post hoc Tukey-HSD test using the revised GLM model. The 15 vertical distribution patterns were shown rearranged by the magnitude of the LSM value (Fig. 20.6). Generally, the pattern of high inventory was the accumulation of 137Cs-GFO in all three layers (right side of Fig. 20.6). Alternatively, the pattern of low inventory was the lack of 137Cs-GFO (i.e., “None”) in any layer (left side of Fig. 20.6). The following Sects. (20.5.3.1–20.5.3.6) discuss sediment transportations that can be assumed from the combinations of vertical distribution patterns and sediment migration.

Fig. 20.6
A bar graph and a chart. The former plots the frequency of the pattern, the inventory makes high erosion, erosion, replacement, stable, redeposition, and high deposition. The chart marks the movement of sediment particles in the vertical direction due to various physical or biological processes. The L S M represents the average value of 137 Cs G F O for each pattern, and the error bars indicate the variability around that mean.

Vertical distribution patterns of 137Cs-GFO were rearranged by the 137Cs-GFO inventory. Named pattern number, frequency (number of occurrences and %), the least-squares mean (LSM) of 137Cs-GFO (kBq m−2), and reclassified pattern (see Fig. 20.7) for each pattern were shown in the lower part of the schematic diagram. Bars and error bars show the LSM and standard error calculated by the GLM. The expected sediment migration (underlined text) was shown above or below the bar. The filled pattern in the bar indicates the frequency of occurrence. Post hoc comparisons between patterns (Tukey-HSD test) were indicated by letters above the bars showing the LSM of 137Cs-GFO

Full size image

20.5.3.1 Pattern of Stable

The pattern with the greatest frequency of occurrence among the 15 vertical distribution patterns was the one with 137Cs-GFO in all three layers and decreasing concentration from the surface layer to the bottom layer, accounting for 29% of the total (pattern 10, Fig. 20.6). We considered this pattern the most stable with respect to sediment migration, because it had the smallest difference in the amount of 137Cs-GFO from the cumulative fallout in the revised GLM model (data not shown).

Although we named the pattern “stable,” we cannot say for sure that there was no 137Cs transfer at all. Tracer studies using 137Cs have been accumulated as a method to clarify such long-term sediment transport (Ritchie and Ritchie 2005). This method is based on determining a reference site in the study area that can be assumed to have been stable without sediment disturbance, not only landslide and erosion but also rain splash transport and soil creep (Benda et al. 2005). This determination is performed with great care, because it determines the study’s accuracy (Mabit et al. 2013; Fulajtar et al. 2017). The location of the soil pits used in this study was systematically determined, and it is unlikely that they would have happened to match any of the reference sites. The soil pits classified as “stable” in this study were not stable enough to be reference sites. It is appropriate to regard this “stable” pattern as a spot where significant erosion or accumulation did not appear in the vertical distribution patterns or as a “neutral” spot where erosion and accumulation were almost balanced.

20.5.3.2 Pattern of Erosion

Vertical distribution patterns 2 and 7 can be regarded as high erosion and erosion spots, respectively (Fig. 20.6). Pattern 7, at 23.3% of the total, was the second most common pattern. In these patterns, 137Cs-GFO was distributed only in the surface layer or the surface and second layers, where the inventory was significantly smaller than that of pattern 10, considered “stable.” As described in Sect. 20.5.2, the hypothesis that this pattern was due to a slow penetration rate is inconsistent with a very small inventory. Therefore, this situation can be explained by the fact that some surface-soil-adsorbing 137Cs-GFO was eroded and transported elsewhere, and that the others remained in the spot. Forestry environments have been characterized by significant sediment redistribution in Japan (Gomi et al. 2008). This study also indicates that a large part of the forested area was subject to slow and mild erosion over a steep forested hillslope.

20.5.3.3 Pattern of Redeposition

The third most common pattern, pattern 13, 9.0% of the total, had 137Cs-GFO in all three layers, with the second layer having the largest concentration, followed by the first, and the third layer being the smallest (pattern 13, Fig. 20.6). We consider this pattern to be the result of sediment redeposition. In other words, the sediment that eroded from the upslope area remained within the forest catchment instead of fluvial discharge.

It might be hypothesized that pattern 13 suggests being “stable” with faster infiltration rates than pattern 10, but this hypothesis could be rejected due to the large inventory of pattern 13. If the fast infiltration rate caused less 137Cs-GFO in the first layer, it should also cause 137Cs-GFO to infiltrate deeper than the third layer, resulting in a smaller inventory for the soil pits. However, the data showed the exact opposite. It makes more sense to consider that the accumulation of 137Cs-GFO-rich soil (the most surface soils at the peak of fallout deposition) from the surrounding area led to a significantly large inventory for pattern 13.

Moreover, we consider patterns 14 and 15 to indicate high redeposition. These patterns represent extremely large inventories, although their frequency was low at 3.7% and 2.0% of the total. Comparing these three redeposition patterns (patterns 13–15), the inventory was larger for those with more 137Cs-GFO in deeper layers. This indicates that the greater redeposited soil over 50 years, the greater the accumulation of earlier eroded 137Cs-GFO-rich soil in the deeper layers. Thus, it would be reasonable to expect a larger inventory in such a pattern.

The small concentration of 137Cs-GFO in the top surface layer in patterns 14 and 15 can be reasonably explained by considering that the recently eroded soil from the surrounding area (i.e., soil redeposited in the top surface layer in patterns 14 and 15) did not contain much 137Cs-GFO, because it was subsoil at the time of maximum fallout.

These “redeposition” patterns occupied 34 out of 66 (52%) soil pits with relatively high inventory (>6 kBq m−2), which corresponded to a long-tail of a right-skewed frequency distribution of inventory on a soil pit basis (see Sect. 20.3, Fig. 20.2c). In particular, soil pits with outstandingly high inventory (top six soil pits with >14 kBq m−2, Fig. 20.2c) belonged to patterns 13–15 without exception.

In these “(High) Redeposition” patterns, the accumulation of 137Cs-GFO may not be limited to the surface layer of 30 cm but could be deeper. This situation can occur if the sediment redeposition over 50 years is more than 30 cm thick.

20.5.3.4 Pattern of Replacement

Pattern 9 had “Less” in the first layer, “More” in the second layer, and “None” in the third layer (Fig. 20.6). The frequency was relatively high, accounting for 6.2% of the total. The inventory (2.08 kBq m−2) was between “Stable” (pattern 10) and “Erosion” (pattern 7) and not significantly different from either of them. We considered this pattern as indicating sediment replacement along the slope transect. A relatively slow and prolonged sediment redistribution with downward transport of 137Cs-GFO-rich soil and redepositing 137Cs-GFO-poor soil upward could result in the less 137Cs-GFO in the top layer and the inventory being slightly smaller than the “stable” pattern. Repeated sheet wash erosion and soil creeping over the years may have contributed to this soil replacement.

20.5.3.5 Patterns of Subsoil Cover

Patterns 1, 4, 6, and 11 had the presence of the “None” layer in common, that is, soil layer containing very little 137Cs-GFO, on the surface (Fig. 20.6). The occurrence of these patterns was not very high, with a range of 0.9–1.2%. The total rate of occurrence of the four patterns was 4.3%. Due to the small number of occurrences, there was no significant difference in the inventory between these four patterns and any of patterns 2 (High Erosion), 7 (Erosion), 10 (Stable), and 13 (Redeposition), except for between patterns 1 and 13.

These patterns were considered spots where at least 5 cm of soil containing little 137Cs-GFO from the surrounding area was redeposited. It was assumed that the redeposited soil was a subsoil at the time of 137Cs-GFO deposition. It was impossible to determine whether this redeposition of subsoil occurred over a long period or was caused by a single event such as a landslide (or possibly anthropogenic events such as road construction). However, it can be considered a considerable mass movement.

The inventory of these patterns ranged from very small (0.64 kBq m−2, pattern 1) to larger than “Stable” (2.68 kBq m−2, pattern 11). This can be inferred as a difference in the conditions before the subsoil redeposition. Erosion may have occurred even before subsoil accumulation in pattern 1, and continuous redeposition of topsoils may have occurred in pattern 11.

20.5.3.6 Patterns of Multiple Covers

The remaining four patterns (3, 5, 8, and 12) had the second layer as “None” or “Least” in common (Fig. 20.6). 137Cs-poor soil was likely redeposited first, and then, 137Cs-rich soil was redeposited (but there may be other processes). This can be rephrased as patterns that experienced multiple sediment transport events with different sources of soils.

The inventory of these patterns was as widely ranged as the patterns of subsoil cover (Sect. 20.5.3.5). The occurrence rates of these patterns (3, 5, 8, and 12) were 5.1%, 1.0%, 8.4%, and 1.5%, respectively. The total occurrence of the four patterns was 16.0% of the total, much higher than the total of patterns of subsoil cover (4.3%).

20.5.4 Whole Picture of 137Cs-GFO-Containing Sediment Migration

We classified the vertical distribution patterns in the previous Sect. 20.5.3 into six categories with respect to sediment transport: stable (pattern 10, 29.0%), erosion (pattern 7, 23.3%), (high) redeposition (patterns 13–15, 14.7%), replacement (pattern 9, 6.2%), subsoil cover (patterns 1, 4, 6, 11, 4.3%), and multiple cover (patterns 3, 5, 8, and 12, 16.0%). In this section, we will aggregate the vertical distribution pattern with respect to gain and loss of 137Cs-GFO.

The stable pattern (pattern 10, 29.0%) was used as the standard. Patterns 1–9 with less 137Cs-GFO inventory were reclassified as patterns of erosion, and patterns 11–15 with more 137Cs-GFO inventory were reclassified as patterns of redeposition. We further revised the GLM model, incorporating the reclassified pattern (i.e., stable, erosion, and redeposition) as an explanatory variable instead of the 15 vertical distribution patterns (patterns 1–15, Fig. 20.6). This further revised GLM model (i.e., a GLM model with reclassified pattern, total annual precipitation, region, and dataset category as fixed effects and NFSCI sampling sites as a random effect) determined the LSM values for each reclassified pattern (Fig. 20.7). These LSM values were 137Cs-GFO inventory estimates in a hypothetical location normalized for other fixed and random effects associated with the total amount of the 137Cs-GFO deposition. The LSMs suggest that the difference between stable and redeposition was slightly less than twice the difference between stable and erosion (Fig. 20.7).

Fig. 20.7
A bar graph with error bars plots the least-square means of 137 Cs G F O. The erosion bar reaches 1.6 with the error bar extending to 1.8, the stable bar reaches 2.2 with the error bar extending to 2.5 and the redeposition bar reaches 3.4 with the error bar extending to 4.6. A pie chart in the graph plots the percentage of erosion, stability, and redeposition.

Vertical distribution patterns of 137Cs-GFO aggregated by the redistribution of 137Cs-GFO. Bars and error bars show the LSM and 95% confidence intervals, respectively. The pie chart shows the frequency of the pattern

Full size image

The frequency of occurrence of the three patterns is also shown in Fig. 20.7. It is suggested that more than 50% of the forest area was reduced in 137Cs-GFO due to sediment erosion, and that the area with enhanced 137Cs-GFO due to sediment accumulation was approximately 1/3 of the area of erosion. Thus, more than 70% of the total forested area (i.e., the sum of the erosion and redeposition patterns) was considered altered by these sediment migrations. This suggests the frequency of sediment transport in forests on the Japanese archipelago over the past 50 years. To summarize, a general pattern of sediment migration within a forest catchment became apparent, that is, thinly eroded sediment from a large area accumulates thickly in a narrow area.

20.6 Destination of 137Cs-GFO in Forested Areas Across Japan After Half a Century from Fallout Deposition

This study empirically demonstrated that most 137Cs-GFO in the forests remained in the surface soil after several decades of fallout. Precisely, we found no significant difference between the inventory and cumulative fallout in the GLM model (Sect. 20.4, Ito et al. 2020). However, the GLM analysis also showed that the estimated inventory was only 79% of the cumulative fallout. Where does the remaining 21% of the 137Cs-GFO reside other than in the 0–30 cm of the forest soil surface?

The first possibility is sediment discharges into stream water, that is, 137Cs-GFO loss via fluvial discharge from forest catchments. The reported annual 137Cs runoff of the total deposition of the forest catchment after the FDNPP accident was less than 0.3% (Onda et al. 2020). The yearly runoff rate of 0.3% year−1 was equivalent to 12.8% of the accumulated 137Cs-GFO discharge percentage over 50 years (provisionally calculated using MRI observation data, see Fig. 20.1). This may be an overestimate or an underestimate. First, the measurements based on the runoff rate immediately after the FDNPP accident are potentially overestimated, because the annual 137CS runoff rate decreases exponentially over time (Kato et al. 2017). However, as mentioned in the next section, there were many sediment-related disasters during the peak of the GFO fallout, so the runoff rate at that time might have been higher than the 0.3% year−1 used in the estimation.

The second possibility is that some 137Cs-GFO was pooled locally in the deep soil. As shown in Sect. 20.5.3.3, there were soil pits with a very large inventory, although the number of occurrences was small. In those high redeposition patterns (patterns 14–15, Fig. 20.6), more 137Cs-GFO was found in the deeper layers, suggesting a high possibility that 137Cs-GFO was also pooled in deeper layers than 30 cm.

The percentage of these two possible 137Cs-GFO destinations is unknown. Clarifying the 137Cs-GFO inventory in deeper soils at the high redeposition sites will provide more reliable estimates.

20.7 Sediment Migration and Past Forest Conditions: Suggestions for the Future

This study clearly showed that sediment migration within the forest catchment accompanied by spatial redistribution of 137Cs-GFO had frequently been occurring in the past half-century. Consequently, the 137Cs-GFO inventory becomes spatially heterogeneous in the forest. In the early 1960s, when global fallout peaked, Japanese forests were recovering from extensive deforestation during and after World War II. Overlogging of forests induces soil erosion (García-Ruiz et al. 2017), and the effects continue for ~20 years after the logging pressure decreases (Tada 2018). In Japan, sediment-related disasters frequently occurred from 1950 to 1985 (Tada 2018). During the same period, minor sediment migration that was not counted as landslides must have occurred frequently. The periods of the global fallout coincided with the frequent occurrence of sediment migration. In essence, the forest management history over the past half-century may be closely related to the 137Cs-GFO redistribution.

This study demonstrated that most 137Cs-GFO remained in the forest even after experiencing a period of poor-forested conditions. If forests can be appropriately managed in the future (in other words, without falling below past levels), the discharge of FDNPP-generated 137Cs into aquatic ecosystems could be suppressed.

Topsoil discharge is considerably influenced by the forest floor cover condition caused by the forest understory vegetation and litter layer. Forest management is necessary to prevent the forest floor from becoming bare of the mineral soil layer to reduce the discharge. Specifically, it is essential to conduct appropriate thinning in planted forest areas to create a light environment on the forest floor that allows forest floor vegetation to cover the ground surface (Fig. 20.8). Additionally, as the density of Japanese deer increases, the decline of forest floor vegetation has been a severe problem throughout Japan, and it is essential to address this issue (Fig. 20.9). Even clear-cutting, one of the most severe disturbances in forest management, has been shown to have only a temporary effect in promoting the discharge of FDNPP-generated 137Cs (Nishikiori et al. 2019). Implementing long-term proactive forest management in the affected areas is necessary to prevent sediment discharge from the forest watershed.

Fig. 20.8
Four photographs. a, trees on the slope. b, a collapsed tree and soil. c, trees on the slope and the roots of the trees are exposed. d, trees on the slope with fresh leaves on all the branches.

Forest floors of hinoki cypress (Chamaecyparis obtusa) forests. (a) A forest floor with exposed mineral soils under limited light environment without timely thinning. (b) Extreme soil erosion. (c) Soil pillars created with rain splash erosion on the forest floor (the lower-left bar is approximately 10 cm). (d) Vegetation-covered forest floor under improved light conditions due to thinning

Full size image
Fig. 20.9
Two photographs. a, the photo presents a birch tree in a forest, with ferns under it. b, the photo presents the cut-down trees on a slope.

Forest floor of forest areas with a high density of sika deer

(a) A birch forest floor dominated by unpalatable ferns. (b) A clear-cut evergreen oak forest floor with bare mineral soils and a few unpalatable shrubs. The evergreen oak forest details are shown elsewhere (Suzuki and Ito 2014)

Full size image

Finally, the study results were achieved using archived soil samples obtained from nationwide systematic sampling. The fallout observation data that the Japan Meteorological Agency and local authorities have maintained for many years also provided essential information for this study. There are many examples, not limited to this study, where the existence of scientifically reliable samples and specimens contributed to the resolution of issues that were not envisioned when they were collected. To meet future demands, we believe that it is essential to continue observations and sample management in various fields of science.