Keywords

1 Introduction

With the constantly increasing trend of our infrastructure construction, the world bridge center has been transferred gradually from developed countries like America, Japan to China. At the same time, since the bridge construction in our country is experiencing the process of large span, high technology along with high difficulties, more and more bridges start to apply the SHM (structural health monitoring) system in case of assuring the structure operation safety [1,2,3,4].

The sensors in SHM systems usually have a short-term limit of life scale because of the complex operation environment as well as the improper use, which also makes it difficult to match the sensors have short-term life with those built structures that can last hundreds of years. What’s worse, the data distortion caused by the failure of the sensors will also lead to the high false alarm rate, which can pose a certain threat to the operation of the expensive health monitoring system. In this case, it is urgent to carry out related researches on self-diagnosis of sensor faults.

Self-diagnosis of sensor faults can be divided into two types [5]. One is based on models, the other is focused on the data. The model-based type can estimate the system output by forming observers with precise mathematical models or finite element models and then compare the output data with actual measured values to obtain details of faults [6]. The model-based type takes the advantage of high efficiency and good effect, which also shows its terrific adaption to those sensor systems with accurate linear models. However, the development of model-based method has been restricted when considering the difficulties of establishing precise non-linear mathematical models on structural engineering with large complex nonlinear system [7, 8].

The data-based method is to process the output data obtained by the sensor measurement, and diagnose the sensor faults based on the analysis results [9, 10]. One outstanding advantage of this method over model-based method is that it does not require precise mathematical models and rich prior knowledge.

The neural network method is widely used in the field of fault diagnosis because of its fast response, good fault tolerance, strong learning ability, excellent adaptive performance, and high degree of nonlinear approximation. Deep learning has undergone structural changes based on neural networks, which not only overcomes the shortcomings of traditional neural networks, but also makes the new round of deep learning methods more widely used. The main feature of this method is that it can do adaptive feature learning and strengthen the extraction and combination of abstract fault features which realizes artificial intelligence in the true sense [11].

In the field of bridge SHM, research based on deep learning has initially realized structural damage identification and location, abnormal data diagnosis and classification [12,13,14,15]. It is shown that although deep learning method has already carried out some researches in the field of bridge SHM, they mainly focus on the detection and identification of bridge apparent disease, and the routine fault diagnosis of sensors. In another word, researches on sensor fault self-diagnosis are still in the initial stage, few theoretical results have been obtained and therefore it is necessary to study many basic problems systematically and deeply.

In this case, the FS-LSTM sensor fault diagnosis method is proposed when considering problems of sensor fault diagnosis in the bridge SHM system, with the law of data produced by sensors in abnormal working conditions and the principle of deep learning. Based on the traditional LSTM neural network, the prediction ability and robustness of the network are improved by constructing a new fully connected layer and state memory unit, thereby improving the recognition rate of sensor faults, and reducing the occurrence of false alarms.

2 Mathematical Model of Sensor Faults

Acceleration sensors with different test principles often have different failures, and acceleration sensors with the same test principle may also have different types of failures [16]. Therefore, difference can appear in sensors faults’ causes, locations, and forms. In a word, these faults can be generalized into the following five types according to the statistical law of the distorted data output by the fault sensor.

2.1 Constant

When internal coil of the sensor has been broken, its sensitivity will decrease and output constant, this kind of fault can be defined as the constant fault.

$$ x_{out} (t) \equiv c $$
(1)

As is shown in formula (1), where c stands for a constant, \(x_{out} (t)\) represents the output signal of sensor. Since noise is inevitably introduced in the process of data collection and transmission, when the sensor has a stuck fault, the collected signal closer to the true value can be expressed as

$$ x_{out} ({\text{t}}) \equiv c + \delta $$
(2)

where δ represents white noise.

2.2 Gain

When the internal spring of the sensor undergoes plastic deformation, the output signal of the sensor can be several times of the real signal. This type of fault is defined as the sensor gain fault, and the mathematical model is shown as follows

$$ x_{out} (t) = \beta x(t) + \delta $$
(3)

where \(x(t)\), β stands for real signal and gain coefficient respectively, the size of the gain is different at each moment and the gain coefficient is proportional to the signal variance.

2.3 Bias

When the sensor base is loose or the sensitive components creep, the sensor will appear as a deviation fault. Its mathematical model is expressed as follows:

$$ x_{out} = x(t) + d + \delta $$
(4)

where d represents the degree of Bias.

2.4 Gain and Linear Drift

When the transmission cable is artificially bent and rubbed on the ground, there exist a gain and linear drift change in the response of the fault sensor over time. The mathematical model can be expressed as

$$ x_{out} = \beta_{1} x(t) + a + b \cdot t + \delta $$
(5)

where β1, a, b, t represents constant term, linear offset monomial term and time variable respectively.

2.5 Noise

When the sensor is subject to external electromagnetic interference. Its mathematical model is expressed as follows:

$$ x_{{out}} = {\rm K} $$
(6)

where, K stands for a random signal with unknown mean and variance. However, in a lot of cases white noise is usually used to represent this kind of signal.

3 Fault Diagnosis Method of FS-LSTM

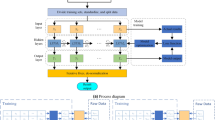
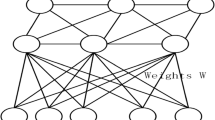
In order to deal with the long-term or short-term time dependence of the time series data in the bridge structure, while considering that the bridge structure is exposed to humidity, high temperature and complex external environment for a long time. The acceleration response of the bridge structure is determined by both time dependence and environmental factors. Two improvements have been made to the acceleration response characteristics of the bridge structure, which are carried out based on the neutral network basic architecture shown in literature [17] as well as lots of real bridge acceleration data. As is demonstrated in Fig. 1, the first improvement is to introduce a fully connected layer between the input layer and the LSTM layer and the second one is to add a full training sample (epoch) state memory unit to the LSTM layer, instead of only performing state memory on each training sample batch.

Fig. 1
A neural network is divided into layers. Input layer on the bottom, followed by a fully connected layer, S L T S M layer, hidden layer and output layer on top.

FS-LSTM neural network simple architecture

Full size image

The first improvement is considered because the acceleration response of the bridge structure is a time series output. The acceleration response at the current time point is similar to the data at the historical time point within a certain range, and will be affected by the temperature, air humidity, air humidity and external factors such as rain and snow. As is shown in Fig. 2, taking the 10 s’ data of the same sensor from a real bridge in different seasons and months, it can be found that the data amplitude of each season is obviously different. Therefore, in order to make a reasonable prediction of the acceleration response. It is necessary to fully consider the influence of external factors and the acceleration at all time.

Fig. 2
A wavelength graph for April, August, October and January. The highest wavelength for August is between 500 to 1200 data at negative 0.1 acceleration meter per second.

Four season data of a real bridge accelerometer

Full size image

The reason for proposing the second improvement is that considering the current network has poor robustness by setting the memory state on the grouped data, and the memory state unit is added through all training samples to improve its robustness. As is shown in Fig. 3, in the improved model, when constructing the LSTM layer, the inherent state parameter must be set to true. It is not necessary to specify the input size, and encoding the number of samples, along with the time step and the feature number in time step must through setting batch input shape. What’s more, by adding Stateful unit to LSTM layer under the Keras frame, the LSTM network can get more refined control. At the same time, the same batch size is used when evaluating the model and making predictions. Usually, after training a group each time, the state in the network is reset and the model is fitted, and the model is called to predict or evaluate the model each time. These all allow the new model to establish a state throughout the training sequence and even maintain that state when it needs to make predictions.

Fig. 3
A structural illustration of X 1 to X a . Batch 1 with iteration 1 followed by batch 2 with iteration 2 followed by batch 3 with iteration 3 to batch 4 with iteration m minus 1 to batch m.

Full training sample to add a structure diagram of the memory state unit

Full size image

3.1 Update and Forecasting Process

  1. (1)

    Network Update Process

FS-LSTM has two improvements in the network structure. Compared with the LSTM network, in the update process of network weights and deviations, there are extra weight and deviation vector Wout, bout and full training sample state vector output by the fully connected layer. The forward calculation is mainly reflected in the input gate, as is shown in formula (7), (8), and the other steps are the same as the forward calculation of LSTM in literature [17].

$$ f\left( {{\varvec{u}}_{l}^{t} } \right) = f\left[ {{\mathbf{W}}{\varvec{X}}^{t} \;\;{\mathbf{W}}^{n} {\varvec{r}}^{t} } \right] + \left[ {{\mathbf{b}}\;\;{\mathbf{b}}^{n} } \right] $$
(7)
$$ f\left( {{\varvec{u}}_{l,F}^{t} } \right) = f\left( {{\mathbf{W}}^{{{\text{out}}}} {\varvec{f}}u_{l}^{t} + {\mathbf{b}}^{{{\text{out}}}} } \right) $$
(8)

W and b represent the weight and deviation vector of the input samples, Wn and bn stand for weight and deviation vector of full training sample, \({\mathbf{W}}^{{{\text{out}}}}\) and \({\mathbf{b}}^{{{\text{out}}}}\) are weight and deviation vector of fully-connected layer, \({\varvec{u}}_{l}^{t} \;{\text{and}}\;{\varvec{u}}_{l,F}^{t}\) represent the output of the inactive layer input and the output of the fully connected layer.

Backpropagation is mainly to obtain the weight Wout, the deviation bout, and the update process of the triple gate weight and deviation parameters of the fully connected layer output after adding the full training sample state vector rt. The gradient calculation of the entire backpropagation process of the algorithm is shown as follows (9)–(19).

$$ {\varvec{\delta}}_{w,k}^{t} = \left( {{\mathbf{W}}^{{{\text{out}}}} \;{\mathbf{W}}} \right)^{{\text{T}}} {\varvec{\delta}}_{k}^{t} \user2{f^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right){\varvec{h}}\left( {S_{k}^{t} } \right)\user2{f^{\prime}}\left( {{\varvec{u}}_{w,k}^{t} } \right) $$
(9)
$$ {\varvec{\delta}}_{{\upphi ,k}}^{t} = \left( {{\mathbf{W}}^{{{\text{out}}}} \;{\mathbf{W}}} \right)^{{\text{T}}} {\varvec{\delta}}_{k}^{t} \user2{f^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right){\varvec{h}}\left( {S_{k}^{t} } \right)\user2{f^{\prime}}\left( {{\varvec{u}}_{w,k}^{t} } \right)S_{k - 1}^{t} {\varvec{f}}\left( {{\varvec{u}}_{w,k}^{t} } \right) $$
(10)
$$ {\varvec{\delta}}_{l,k}^{t} = \left( {{\mathbf{W}}^{{{\text{out}}}} \;{\mathbf{W}}} \right)^{{\text{T}}} {\varvec{\delta}}_{k}^{t} \user2{f^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right)\user2{h^{\prime}}\left( {S_{k}^{t} } \right)\user2{f^{\prime}}\left( {{\varvec{u}}_{l,k}^{t} } \right)S_{kc}^{t} {\varvec{f}}\left( {{\varvec{u}}_{w,k}^{t} } \right) $$
(11)
$$ {\varvec{\delta}}_{c,k}^{t} = \left( {{\mathbf{W}}^{{{\text{out}}}} \;{\mathbf{W}}} \right)^{{\text{T}}} {\varvec{\delta}}_{k}^{t} \user2{f^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right)\user2{h^{\prime}}\left( {{\varvec{S}}_{k}^{t} } \right)\user2{h^{\prime}}\left( {{\varvec{u}}_{c,k}^{t} } \right){ }b_{kl}^{t} { }{\varvec{f}}\left( {{\varvec{u}}_{w,k}^{t} } \right) $$
(12)
$$ \frac{{\partial L_{N} }}{{\partial {\varvec{W}}^{out} }} = \mathop \sum \limits_{t = 1}^{N} {\varvec{\delta}}_{k}^{t} \left( {{\varvec{f}}{ }\left( {{\varvec{u}}_{l}^{t} } \right)} \right)^{{\text{T}}} $$
(13)
$$ \frac{{\partial L_{N} }}{{\partial {\varvec{b}}^{out} }} = \mathop \sum \limits_{t = 1}^{N} {\varvec{\delta}}_{k}^{t} $$
(14)
$$ \frac{{\partial L_{N} }}{{\partial {\mathbf{W}}}} = \mathop \sum \limits_{t = 1}^{N} \left( {{\mathbf{W}}^{out} } \right)^{{\mathbf{T}}} {\varvec{\delta}}_{k}^{t} f{^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right)\left( {X^{t} } \right)^{{\text{T}}} $$
(15)
$$ \frac{{\partial L_{N} }}{{\partial {\mathbf{W}}^{n} }} = \mathop \sum \limits_{t = 1}^{N} \left( {{\mathbf{W}}^{out} } \right)^{{\mathbf{T}}} {\varvec{\delta}}_{k}^{t} {\varvec{f}}{^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right)\left( {{\varvec{r}}^{t} } \right)^{{\text{T}}} $$
(16)
$$ \frac{{\partial L_{N} }}{{\partial {\varvec{b}}}} = \mathop \sum \limits_{t = 1}^{N} \left( {{\mathbf{W}}^{out} } \right)^{{\mathbf{T}}} {\varvec{\delta}}_{k}^{t} \user2{f^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right) $$
(17)
$$ \frac{{\partial L_{N} }}{{\partial {\varvec{b}}^{n} }} = \mathop \sum \limits_{t = 1}^{N} \left( {{\mathbf{W}}^{out} } \right)^{{\mathbf{T}}} {\varvec{\delta}}_{k}^{t} \user2{f^{\prime}}\left( {{\varvec{u}}_{l}^{t} } \right) $$
(18)
$$ \left\{ {\begin{array}{*{20}c} { \frac{{\partial L_{N} }}{{\partial {\varvec{W}}^{x\tau } }} = \mathop \sum \limits_{t = 1}^{N} {\varvec{\delta}}_{\tau ,k}^{t} \left( {X^{t} } \right)^{T} } \\ { \frac{{\partial L_{N} }}{{\partial {\varvec{W}}^{h\tau } }} = \mathop \sum \limits_{t = 1}^{N} {\varvec{\delta}}_{\tau ,k}^{t} \left( {{\varvec{h}}_{k - 1}^{t} } \right)^{T} } \\ {\frac{{\partial L_{N} }}{{\partial {\varvec{b}}_{\tau } }} = \mathop \sum \limits_{t = 1}^{N} {\varvec{\delta}}_{\tau ,k}^{l} } \\ \end{array} } \right.,\tau \in \left\{ {c,l,\upphi ,w} \right\} $$
(19)

The above is all the gradient solving process in FS-LSTM, and all weights and deviation coefficients in the network can be updated by using the above gradients. from the back propagation process shown in formula (9)–(19), δ represents the reciprocal of the weight, N is the total time step, L represents the loss function, k represents the last time step, \({\mathbf{W}}^{x\tau }\) represents the state corresponding to the input value, the weight parameters of input gate, forget gate and output gate, \({\mathbf{W}}^{h\tau }\) represents the corresponding state, input gate, forget gate and output gate weight parameter of the output at the previous moment, \(\user2{ b}_{\tau }\) is the corresponding deviation with state, input gate, forget gate and output gate.

  1. (2)

    Network Forecasting Process

In the improved FS-LSTM network for fault diagnosis of the bridge structure acceleration sensor, suppose there are m samples, the i-th sample is the time series data of length t, where t represents the time step of the sequence, that is, use data from t time points to predict the data at the next time point.

The number of nodes in the input layer and output layer of the network is determined by the characteristics of the network task and the sample. In the prediction process, acceleration data with a specific time lag is grouped into input (represented by the dotted rectangle) and prediction (represented by the solid rectangle), as shown in Fig. 4.

Fig. 4
A network model with each input directly leading to output. Input, X t minus 4, X t minus 3, X t minus 2, X t minus 1, X t leads to X sub t + 1 and X sub t + 2 output.

Network prediction process

Full size image

The predicted value \(\hat{\user2{y}}^{{\left( {\varvec{i}} \right)}}\) is generated through the constructed FS-LSTM network model. The loss function is selected to minimize the sum of square errors and the L2 regularization of the model, as shown in formula (20). Subsequently, the mini-batch gradient descent optimization method is used for weight correction and model training to make it approach the target value. The bridge structure acceleration time series prediction model uses a small batch of samples to calculate the gradient loss in each iteration of the gradient descent.

$$ Loss\left( {\hat{y},y} \right) = \frac{1}{2}\mathop \sum \limits_{j = 1}^{m} (y^{\left( i \right)} - \hat{y}^{\left( i \right)} )^{2} + \frac{1}{2}\lambda \sum \theta^{2} $$
(20)

where, \({ }{\varvec{y}}^{{\left( {\varvec{i}} \right)}}\) stands for the true value of the i-th sample. λ represents the regularization parameter, and θ is the model parameter.

At the same time, in order to prevent the local explosion of gradient and the robustness of model training, the method of gradient truncation is introduced. The principle of gradient truncation is to determine whether the L2 norm of the gradient loss generated by the model during backpropagation exceeds the preset gradient threshold. If it exceeds, the gradient is truncated by using formula (21).

$$ \hat{g} = \frac{threshold}{{\left\| {\hat{g}} \right\|^{2} }}\hat{g} $$
(21)

where, \(\hat{\user2{g}}\) represents the gradient loss, \({ }\left\| {} \right\|^{2}\) represents the L2 norm, and threshold represents the threshold set in advance. At the same time, in order to prevent network overfitting, the dropout parameter is used to reduce the complexity of the model.

3.2 Determine Network Structure Hyper Parameters

In the FS-LSTM bridge acceleration time series model, the main hyper parameters include the number of output layer nodes, the number of input layer nodes, the time step of time series data, the number of neurons in the fully connected layer, the number of LSTM units in the hidden layer, the loss of the model threshold, number of sample training mini-batch, and initial learning rate. The K-fold cross-validation algorithm in literature [18] is used to determine the hyper parameters of the network in the improved LSTM bridge acceleration time series prediction model. FS-LSTM neural network structure network model parameter settings are shown in Table 1.

Table 1 FS-LSTM neural network parameter list
Full size table

3.3 Fault Threshold

When the sensor is healthy and the structure is intact, the established FS-LSTM NN is used to calculate its predicted value, and the residual Re of the true value and the predicted value is used as an indicator for diagnosing sensor faults. Residual error calculation is shown in formula (22).

$$ {\varvec{Re}} = \left\| {\hat{y} - y} \right\|^{2} $$
(22)

According to the parameter confidence interval setting in statistics, the mean and variance of the residual series are calculated by Eqs. (23) and (24).

$$ \mu ({\varvec{R}}_{{\varvec{e}}} ) = \frac{1}{n}\sum\limits_{i = 1}^{n} {{\text{R}}_{{{\text{ei}}}} } $$
(23)
$$ \sigma^{2} ({\varvec{R}}_{{\varvec{e}}} ) = \frac{1}{n - 1}\sum\limits_{i = 1}^{n} {\left[ {{\text{R}}_{{{\text{ei}}}} - \mu ({\varvec{R}}_{{\varvec{e}}} )} \right]^{2} } $$
(24)

where Rei is the residual value corresponding to different moments. The confidence interval with a confidence level of α can be expressed as:

$$ P(\mu - Z_{{\frac{\alpha }{2}}} \sigma ,\mu + Z_{{\frac{\alpha }{2}}} \sigma ) = 1 - \alpha^{{}} $$
(25)

where α is the confidence level; Z is the coefficient related to confidence level and it is set as 3, and the confidence level is 99.74%. Therefore, the threshold can be derived from the \(3\sigma\) criteria:

$$ \lambda = \mu ({\varvec{R}}_{{\varvec{e}}} ) + 3\sigma^{2} ({\varvec{R}}_{{\varvec{e}}} ) $$
(26)

The \(\lambda\) value is the fault threshold for judging whether the sensor is faulty or not. When \(R_{ei} > \lambda\) the sensor is faulty, and vice versa.

4 Numerical Example

Using ANSYS finite element software to build a three-span continuous beam model, elastic modulus E = 3 × 1010 N/m2, Poisson’s ratio μ = 0.3, density ρ = 2500 kg/m3. The beam length is 40 m, the rectangular section is 0.25 m × 0.6 m, and the beam is equally divided into 200 units, as shown in Fig. 5. Random white noise pulsation is selected to excite of the continuous beam, without considering the influence of damping, and the acceleration time history response is calculated by the Newmark-β method [19]. The placement position of the 10 acceleration sensors on the beam is shown in Fig. 5, and they are numbered S1–S10 sensors from left to right. Where the S1 sensor marked by the red solid circle is an analog fault sensor, and the S6 and S8 marked by the green dashed circle are randomly selected health sensors for each span, and they are supposed to verify whether there will be a second type of error in the fault diagnosis (the sensor health is misdiagnosed as a fault).

Fig. 5
An illustration of a ruler of 40 m is divided into S 1 to S 10. 40 meters divided into 3, 3, 3, 6, 3, 3, 4, 8, 2, 3, 2.

Three-span continuous beam model

Full size image

Randomly generate 400 pieces of white noise data, each piece of white noise data contains 120 data points, assuming that each data point has an interval of 0.01 s. Apply each piece of white noise data as ground pulsation excitation to the structure support, and calculate the acceleration response \(y_{i,j}^{*} \left( t \right)\) of the structure where the sensor is installed. The subscript i represents the sensor number, i = 1, 2…,10; j represents the number of white noise excitation, j = 1, 2,…400; t represents the time step, t = 1,2,…120. In order to avoid the non-stationary acceleration response of the structure at the initial stage of excitation, the first 20 data points of all the structure acceleration response records \(y_{i,j}^{*} \left( t \right)\) are discarded, that is, each acceleration response data contains only 100-time steps. Then, for each structural response record of each sensor, white noise with a signal-to-noise ratio (SNR) of 20 is added to obtain the test value \( y_{i,j}^{*} \left( t \right) \) of each sensor.

Assuming that the S1 sensor has constant fault, gain fault, bias fault, gain and linear drift fault, noise fault in sequence and these five operating conditions plus its own health conditions, a total of six operating conditions have been studied. Failure simulation can be found through formula (2)–(6), the fault parameters are selected by interpolation operation to obtain the optimal parameter combination. Each sensor response sample data consists of 40,000 time points. In order to study without loss of generality, randomly select a sensor from each remaining span as the research object (S6 and S8 sensors) to verify whether there will be a second type of fault diagnosis error (the intact sensor is misdiagnosed as a faulty sensor). The training set data (40,000 × 68%) and Eqs. (22)–(26) are used to calculate the fault thresholds of the three selected sensors. The calculation results are shown in Table 2.

Table 2 Sensor fault thresholds
Full size table

The fault diagnosis result of the S1 sensor is shown in Fig. 6. The diagnosis result shows that under the above five fault conditions when the sensor has stuck faults, gain faults, deviation faults, gain linear drift faults, and noise faults in sequence, its residual values will greatly exceed the failure threshold obtained when they are healthy. From this, it can be determined that when the above five types of faults occur in the sensor, the proposed methods can work effectively.

Fig. 6
5 graphs for residual and threshold illustrate different wavelengths that are detections. Faults, a, constant. b, gain. c, bias. d, gain linear drift. e, Noise. Highest wavelength in noise fault.

Five fault detection results of the S1 sensor

Full size image

In order to compare the diagnostic effects of the traditional LSTM and the improved FS-LSTM network, Figs. 7 and 8 show the fault diagnosis results of the S6 and S8 health sensors in different networks, as can be seen from Fig. 7a and b when the sensor does not fail, the residual values are all less than the set threshold. Although there are four test points in Fig. 7b (marked by the circle in Fig. 7b) that exceed the set threshold, they are in the allowable range (40,000 × 32% × 0.26%≈33) of the \(3\sigma\) Guidelines, so the sensor is considered healthy. Compared with the FS-LSTM network diagnosis result, the LSTM network diagnosis result shows that many test points exceed the threshold, far exceeding the number allowed by the \(3\sigma\) criteria. Therefore, if the traditional LSTM network is used to diagnose the fault of the sensor, its diagnosis result does not match the actual sensor fault condition, and a misdiagnosis will occur.

Fig. 7
2 graphs illustrate residual and threshold. Different wavelengths are given for residuals. The highest wavelength for the S 6 sensor diagnosis result. A residual is a horizontal straight line.

Fault detection results for health sensors under FS-LSTM

Full size image
Fig. 8
2 graphs illustrate residual and threshold. Different wavelengths given for residuals. The highest wavelength for S 6 sensor diagnosis. A residual is a horizontal straight line.

Fault detection results of health sensors under LSTM

Full size image

5 Conclusion

Based on the traditional long and short-term memory neural network, a new type of deep learning network is constructed by introducing fully connected layers and epoch state memory units. The parameter update, prediction process and the design of hyper parameters of the new network, have been described in detail. By setting a reasonable fault threshold, a new method of sensor fault diagnosis in the bridge health monitoring system is proposed. Numerical example studies show that when the sensor has stuck faults, gain faults, deviation faults, gain linear drift faults, and noise faults in sequence, the proposed FS-LSTM fault diagnosis method can correctly distinguish whether the faults in the bridge monitoring system are faulty or not.; At the same time, by randomly selecting the health sensor for each span, it is verified that the proposed method will not cause the second type of fault diagnosis error that misdiagnoses the health sensor as a fault sensor. The above research results are mainly based on the structural response of the finite element simulation for sensor fault diagnosis. In the future, the applicability of the proposed method can be further explored through the actual response of the real bridge.