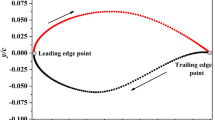
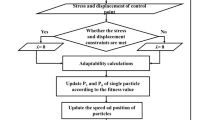
Abstract
A two-step optimization method is proposed for aerodynamic shape optimization (ASO), and the efficiency of the 2nd-step optimization is improved by proper orthogonal decomposition-based (POD-based) geometric parameterization. The two-step optimization method is constituted by particle swarm optimization (PSO) combined with Hicks-Henne shape functions and steepest descent algorithm (SDA) bonded with POD-based parameterization method. After the 1st-step optimization, superior data (SD) given with better values of objective functions which can satisfy all the constraints are filtered to extract POD bases. The POD bases only cover design space near the 1st-step optimized solution and can parameterize the geometric shape with fewer design variables (DVs). Fewer DVs and smaller design space can improve the efficiency of the 2nd-step optimization,. The two-step optimization method is validated by a case of NASA Rotor 37 aiming to increase peak adiabatic efficiency. The efficiency of the 2nd-step optimization is improved by using POD-based geometric parameterization, which is proved by comparing with SDA using the conventional parameterization method.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Vicini A, Quagliarella D (1999) Airfoil and wing design through hybrid optimization strategies. AIAA J 37(5):634–641
Duan YH, Cai JS, Li YZ (2012) Gappy proper orthogonal decomposition-based two-step optimization for airfoil design. AIAA J 50(4):968–971
Chernukhin O, Zingg DW (2013) Multimodality and global optimization in aerodynamic design. AIAA J 51(6):1342–1354
Cao CQ, Cai JS, Qu K et al (2017) An efficient multistep ROM method for prediction of flows over airfoils. In: 55th AIAA aerospace sciences meeting
Li JC, Cai JS, Qu K (2018) Adjoint-based two-step optimization method using proper orthogonal decomposition and domain decomposition. AIAA J 56(3):1133–1145
Han ZH, Zhang Y, Song CX et al (2017) Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization. AIAA J 55(12):4330–4346
Toal DJJ, Bressloff NW, Keane AJ (2010) Geometric filtration using proper orthogonal decomposition for aerodynamic design optimization. AIAA J 48(5):916–928
Ghoman S, Wang Z, Chen P et al (2012) A POD-based reduced order design scheme for shape optimization of air vehicles. In: 53rd AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics and materials conference 20th AIAA/ASME/AHS adaptive structures conference 14th AIAA.
Poole DJ, Allen CB, Rendall TCS (2015) Metric-based mathematical derivation of efficient airfoil design variables. AIAA J 53(5):1349–1361
Masters DA, Taylor NJ, Rendall TCS et al (2017) Geometric comparison of aerofoil shape parameterization methods. AIAA J 55(5):1575–1589
Cinquegrana D, Iuliano E (2018) Investigation of adaptive design variables bounds in dimensionality reduction for aerodynamic shape optimization. Comput Fluids 174:89–109
Lukaczyk TW, Constantine P, Palacios F et al (2014) Active subspaces for shape optimization. In: 10th AIAA multidisciplinary design optimization conference
Robinson GM, Keane AJ (2001) Concise orthogonal representation of supercritical airfoils. J Aircraft 38(3):580–583
D'Agostino D, Serani A, Campana EF et al (2018) Deep autoencoder for off-line design-space dimensionality reduction in shape optimization. In: 2018 AIAA/ASCE/AHS/ASC structures, structural dynamics, and materials conference
Holmes P, Lumley JL, Berkooz G et al (2012) Turbulence, coherent structures, dynamical systems and symmetry. Cambridge University Press
Sirovich L, Kirby M (1987) Turbulence and the dynamics of coherent structures. part 1: coherent structures. Q Appl Math 45(3):561–571
Duan YH, Wu WH, Fan ZL et al (2016) An introduction of aerodynamic shape optimization platform for compressor blade. Turbo expo: power for land, sea, and air. american society of mechanical engineers
Shi Y, Eberhart RC (1998) Parameter selection in particle swarm optimization. International conference on evolutionary programming. Springer, Berlin, Heidelberg.
Venter G, Sobieszczanski-Sobieski J (2003) Particle swarm optimization. AIAA J 41(8):1583–1589
Reuther J, Jameson A (1995) Aerodynamic shape optimization of wing and wing-body configurations using control theory. In: 33rd aerospace sciences meeting and exhibit
Duan YH, Wu WH, Zhang PH et al (2019) Performance improvement of optimization solutions by POD-based data mining. Chinese J Aeronaut 32(4):826–838
Wang DX, He L, Li YS et al (2010) Adjoint aerodynamic design optimization for blades in multistage turbomachines—part ii: validation and application. J Turbomach 132(2)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Zhang, C., Duan, Y., Wang, G., Chen, H. (2023). A Two-Step Optimization Method Using POD-Based Geometric Parameterization for Aerodynamic Shape Optimization. In: Lee, S., Han, C., Choi, JY., Kim, S., Kim, J.H. (eds) The Proceedings of the 2021 Asia-Pacific International Symposium on Aerospace Technology (APISAT 2021), Volume 1. APISAT 2021. Lecture Notes in Electrical Engineering, vol 912. Springer, Singapore. https://doi.org/10.1007/978-981-19-2689-1_11
Download citation
DOI: https://doi.org/10.1007/978-981-19-2689-1_11
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-19-2688-4
Online ISBN: 978-981-19-2689-1
eBook Packages: EngineeringEngineering (R0)