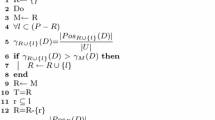Abstract
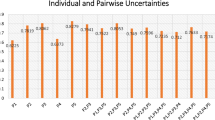
Dimensionality reduction is the most popular technique, which is used in data analytics for the optimal solution over high-dimensional data. Many times some inconsistency and uncertainty are presented in huge data so to deal with such a type of data soft set theory is being developed. Soft set theory handles the difficulties of older theories like fuzzy set, rough set using new property that is parameterization reduction. This paper presents different soft set based NPR algorithms for information systems that give optimal solutions for big data. The goal of this article is to focus on the dimensionality reduction approach of data mining using soft set theory which can be applied to machine learning field. Thus normal dimensionality reduction of soft set (NDRSS) algorithm is proposed for real-time data to give a better optimal solution than existing soft set algorithms. The result shows that how-high dimensional data is to be reduced using soft set theory in machine learning.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Molodtsov, D.: Soft set theory—first results. Comput. Math. Appl. 37(4–5), 19–31 (1999)
Maji, P.K., Roy, A.R., Biswas, R.: An application of soft sets in a decision making problem. Comput. Math. Appl. 44(8–9), 1077–1083 (2002)
Chen, D., Tsang, E.C.C., Yeung, D.S., Wang, X.: The parameterization reduction of soft sets and its applications. Int. J. Comput. Math. with Appl. 49, 757–763 (2005)
Kong, Z., Liqun, G., Lifu, W., Steven, L.: The normal parameter reduction of soft sets and its algorithm. Comput. Math. Appl. 56, 3029–3037 (2008)
Herawan, T., Rose, A.N.M., Deris, M.M.: Soft Set Theoretic Approach for Dimensionality, pp. 171–178 (2009)
Ma, X., Sulaiman, N., Qin, H., Herawan, T., Zain, J.M.: A new efficient normal parameter reduction algorithm of soft sets. Comput. Math. Appl. 62(2), 588–598 (2011)
Ma, X., Sulaiman, N., Qin, H.: Parameterization value reduction of soft Sets and its algorithm. In: 2011 IEEE Colloquium on Humanities, Science and Engineering. IEEE, pp. 261–264 (2011)
Kumar, D.A., Rengasamy, R.: Parameterization reduction using soft set theory for better decision making. In: 2013 International Conference on Pattern Recognition, Informatics and Mobile Engineering. IEEE, pp. 365–367 (2013)
Danjuma, S., Ismail, M.A., Herawan, T.: An alternative approach to normal parameter reduction algorithm for soft set theory. IEEE Access 5, 4732–4746 (2017)
Ma, X., Qin, H.: Weighted normal parameter reduction for soft set. In: 2018 14th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). IEEE, pp. 712–716 (2018)
Thangavel, K., Pethalakshmi, A.: Dimensionality Reduction Based on Rough Set Theory: A Review, vol. 9, pp. 1–12 (2009)
Zhe, D.: A Dimensionality reduction based on rough set theory for complex massive data. In: 2015 8th International Congress on Image and Signal Processing (CISP). IEEE, pp. 1520–1528 (2015)
UCI Machine Learning Repository. https://archive.ics.uci.edu/ml/datasets.php
Wang, S.Q., Gao, C.Y., Luo, C., Zheng, G.M., Zhou, Y.N.: Research on feature selection/attribute reduction method based on rough set theory. Procedia Comput. Sci. 154, 194–198 (2019)
Pant, J., Juyal, A., Bahuguna, S.: Soft set, a soft computing approach for dimensionality reduction. Int. J. Innov. Sci. Eng. Technol. 2(4), 728–735 (2015)
Sharma, O., Gupta, P., Sheoran, A.: Dimensionality reduction using fuzzy soft set theory. Int. J. Stat. Reliab. Eng. 154–158 (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Lanjewar, P.D., Momin, B.F. (2022). Application of Soft Set Theory for Dimensionality Reduction Approach in Machine Learning. In: Srivastava, P., Thakur, S.S., Oros, G.I., AlJarrah, A.A., Laohakosol, V. (eds) Mathematical, Computational Intelligence and Engineering Approaches for Tourism, Agriculture and Healthcare . Lecture Notes in Networks and Systems, vol 214. Springer, Singapore. https://doi.org/10.1007/978-981-16-3807-7_17
Download citation
DOI: https://doi.org/10.1007/978-981-16-3807-7_17
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-16-3806-0
Online ISBN: 978-981-16-3807-7
eBook Packages: EngineeringEngineering (R0)