Keywords

1 Introduction

Sediment transport in surface water bodies is a topic that is gaining increasing relevance and scientific interest. With a focus on sedimentation and resuspension, applied research has been performed concerning rivers (Sibetheros et al. 2013; Zavattero et al. 2016), channels (Visescu et al. 2016), coastal zones (Amoudry and Souza 2011; Aoki et al. 2015), reservoirs (Kondolf et al. 2014; Sumi and Hirose 2009), and floodwaters (Eaton and Lapointe 2001; Berghout and Meddi 2016). Here, the focus lies on the floodwaters, although the discussed methods can also be applied to other fields.

In reservoirs, the deposition of sediments is a general problem; the water storage capacity may be reduced drastically due to sediment deposition. Groundwater recharge can be reduced or completely inhibited due to the deposition of fine particles. This is a crucial issue at dams that are also designed for groundwater recharge, as shown by a case study in Oman (Prathapar an Bawain 2014). Additionally, in Oman, Saber et al. (2019) examined various aspects of reservoir sedimentation. Few studies have attempted to estimate the overall sediment budgets of reservoirs. From extensive observations on beach profiles along the Batinah coast in northern Oman, Kwarteng et al. (2016) estimated that approximately 960,000 m3 per year of sediments are supplied from the coastal plain, of which roughly half is currently trapped by numerous dams built in the area. While onshore withheld sediments cause problems for the long-term operation of dams, sediment deficits along coasts may lead to serious beach erosion problems.

The topics of suspended and bed-load transport have been investigated for a long time, and associated studies have mainly dealt with perennial flow channels and steady flows. There are far fewer studies on ephemeral streams and transient regimes, as these appear in connection with floods. There are a few case studies from the Negev Desert (Reid et al. 1998) and from Saudi Arabia (Nouh 1988a, b). In their review, Karimaee Tabarestani and Zarrati (2015) clearly stated that sediment transport under unsteady conditions is very different than that under steady flow.

Scott (2006) points to the fact that for high sediment loads appearing in ephemeral streams, the flow regime may become non-Newtonian. In sediment-laden water bodies, deposition causes problems if it occurs in incorrect places. Navigation may become hindered or even impossible, as shown by Ezzeldin et al. (2019). On the other hand, unwanted scouring may emerge due to sediment removal and cause problems concerning the stability of bridge piers and foundations (Pizarro et al. 2020).

Numerical models can play an important role in understanding these processes. The locations and amounts of erosion and sedimentation can be identified using numerical models. With validated numerical models, potential measures to mitigate flood damage can be simulated, examined, and evaluated on computers.

However, simulation techniques and tools for the implementation of such models are still in development and have not yet been well established. The physics of the situation in question is complex. Some water flow models are also extended to treat sediment transport processes. If there is erosion or deposition at the bottom of a channel, the depth of the water column changes, and thus, the flow regime is altered. This two-way coupling of flow and transport must be incorporated using a multiphysics approach; water flows and sediment transport must be simulated simultaneously.

2 Modeling

Here, we present a multiphysics approach in which the coupling between flow and transport is taken into account. As a first approach, we attempt to minimize complexity, and with it, the required computational resources. For flow modeling, we choose the shallow water equations (SWE), a system of two coupled differential equations. These equations constitute a minimalistic approach, as the vertical direction is not explicitly considered, and thus, the problem setting is reduced to 2D or even 1D in rivers and channels. The sediment transport is described by two equations: one for the suspended particle load in the water column and one for the bed load. The latter is formulated as an expression of the bottom elevation.

For an initial check of the ability of such an analytical system of minimal complexity to simulate flow and transport, a test case is simulated. The situation is simple, consisting of a circular obstacle placed into a uniform 2D flow field. It is shown that it is possible to capture both erosion and deposition at different locations along the obstacle wall by a multiphysics modeling approach.

Fluid flow modeling is based on the mathematical analytical formulations represented by differential equations. The Saint–Venant equations, also known as the shallow water equations for depth-averaged flow in one or two spatial dimensions, can be written as:

$$\frac{\partial }{{\partial t}}(H - d) + \nabla \cdot \left( {H{\mathbf{u}}} \right) = 0$$
(16.1)
$$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + g\nabla H - {\mathbf{F}} = 0$$
(16.2)

with total water depth H, water depth d below a reference level, velocity vector u, and acceleration due to gravity g (Takase et al. 2011). In vector F, the contributions of all other forces are gathered. The equations are derived from the volume and momentum conservation principles and are formulated using depth-averaged velocities. The system comprising Eqs. (16.1) and (16.2) is nonlinear. The derivation is based on several assumptions: (1) the fluid is incompressible, (2) in the vertical direction, there is a hydrostatic pressure distribution, (3) depth-averaged values can be used for all properties and velocities, (4) the bottom slopes are small, (5) there are no density effects from variable fluid density or fluid viscosity, (6) the eddy viscosity is much larger than the molecular viscosity, and (6) the atmospheric pressure gradient can be ignored. Despite these numerous assumptions, the validity of SWEs for many application cases is widely accepted.

Friction at the walls, i.e., the interfaces between fluids and solids, can be taken into account by an additional term in Eq. (16.2) (Brufau and García-Navarro 2000; Duran 2015):

$$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + g\nabla H + g\eta n^{2} \frac{{\left| {\mathbf{u}} \right|}}{{\eta ^{{4/3}} }}{\mathbf{u}} - {\mathbf{F}} = 0$$
(16.3)

with water height η above a reference height and Manning coefficient n. In 1D, i.e., for rivers, channels, and channel systems, Eqs. (16.1) and (16.3) constitute a coupled system for H and u. In 2D, the equations are used to determine three variables, H and two components of u.

For sediment transport, we choose the concentration of suspended material, c, as the dependent variable. Following the methods used in Li and Duffy (2011), the differential equation reads as follows:

$$\frac{{\partial Hc}}{{\partial t}} + \nabla \cdot \left( {Hc{\mathbf{u}}} \right) - E + D = 0$$
(16.4)

where E and D denote the erosion and deposition terms, which will be outlined below. Using the product rule, Eq. (16.4) can be rewritten as follows.

$$H\frac{{\partial c}}{{\partial t}} + c\frac{{\partial H}}{{\partial t}} + H\nabla \cdot \left( {c{\mathbf{u}}} \right) + c\nabla \cdot \left( {H{\mathbf{u}}} \right) - E + D = 0$$
(16.5)

Both terms with leading factor c cancel out because of Eq. (16.1). The remainder can be written as follows.

$$\frac{{\partial c}}{{\partial t}} + \nabla \cdot \left( {c{\mathbf{u}}} \right) - \frac{1}{H}\left( {E - D} \right) = 0$$
(16.6)

The corresponding conservative form is given as follows.

$$\frac{{\partial c}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right)c - \frac{1}{H}\left( {E - D} \right) = 0$$
(16.7)

Note that the sediment load is represented as a concentration with mass/volume units. In Eq. (16.7), diffusion is not considered. Analogous to mass transport, diffusive processes are taken into account by an additional term.

$$\frac{{\partial c}}{{\partial t}} - \nabla \left( {{\mathbf{D}}\nabla c} \right) + \left( {{\mathbf{u}} \cdot \nabla } \right)c - \frac{1}{H}\left( {E - D} \right) = 0$$
(16.8)

Here, D denotes the dispersion tensor, in which all types of diffusive processes are gathered (Rowinski and Kalinowska 2006). In the following equation, we consider turbulent diffusivity as the most relevant part, described as follows:

$${\mathbf{D}} = \frac{\upsilon }{{{\text{Sc}}}}{\mathbf{I}}$$
(16.9)

with turbulent viscosity υ and turbulent Schmidt number Sc. I denotes the 2D unit matrix.

Except for the consideration of diffusion, the presented approach is similar to those outlined in Cao et al. (2004), Li and Duffy (2011), and Rowan and Seaid (2017). Analogous to the cited references, the changes in the bed that occur due to settling and resuspension are thus governed by the formula:

$$\frac{{\partial d}}{{\partial t}} - \frac{1}{{1 - \theta }}\left( {E - D} \right) = 0$$
(16.10)

where θ denotes the bed-load porosity.

The system comprising Eqs. (16.1), (16.3), (16.7), and (16.10) is a coupled multiphysics approach. The terms H and u appear in Eq. (16.7), forming the link between the flow and transport processes. As the next section shows, there are further dependencies in the exchange terms D and E, constituting a coupling between Eqs. (16.7) and (16.10). The back-coupling is given as the depth, d, which appears in Eq. (16.1).

3 Sedimentation and Erosion Approaches

For the settling and resuspension terms, several approaches can be found in the current literature. For D, Li and Duffy (2011) propose the following equation:

$$D = \beta v_{{\text{s}}} c$$
(16.11)

with the settling velocity vs. The amount of settling material is proportional to the settling velocity and the concentration of suspended material. The β factor thus has the dimension of length−1 and is the mean travel length in the vertical direction. In our first approach, we use an expression in which β is set to H/2, the mean settling depth.

$$D/H = 2v_{{\text{s}}} c/H$$
(16.12)

The model allows working with a constant settling velocity, but more complex approaches can also be utilized. For example, the more general approach,

$$D = v_{{\text{s}}} c_{{\text{s}}} \left( {1 - c_{{\text{s}}} } \right)^{m}$$
(16.13)

proposed by Cao et al. (2004) can be included easily. The sediment concentration near-bed cs is proportional to the sediment concentration with a proportionality factor, α, greater than 1: \(c_{{\text{s}}} = \alpha c\). Rowan and Seaid (2017) suggested the use of Eq. (16.13) with power m = 1.4 for noncohesive materials. Also dealing with 1D settings in channels and channel networks, Zhang et al. (2014) made D dependent on the carrying capacity, \(c_{*}\):

$$D = v_{{\text{s}}} \alpha \left( {c - c_{ * } } \right)$$
(16.14)

with

$$c_{ * } = K\left( {{\raise0.7ex\hbox{${u^{3} }$} \!\mathord{\left/ {\vphantom {{u^{3} } {gRv_{{\text{s}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${gRv_{{\text{s}}} }$}}} \right)^{m}$$
(16.15)

depending on the hydraulic radius, R, and the parameters K and m. Li and Duffy (2011) extended the 1D approach for use in 2D systems, using the following expressions for β and vs:

$$\beta = \min \left\{ {2,(1 - \theta )/c} \right\}$$
(16.16)
$$v_{{\text{s}}} = \sqrt {\left( {13.95\nu /\delta } \right)^{2} + 1.09g\delta \left( {{{\rho _{{\text{s}}} } \mathord{\left/ {\vphantom {{\rho _{{\text{s}}} } {\rho _{f} - 1}}} \right. \kern-\nulldelimiterspace} {\rho _{f} - 1}}} \right) - 13.95\nu /\delta }$$
(16.17)

with particle diameter δ, kinematic viscosity ν, and particle and fluid densities ρs and ρf, respectively. For resuspension, Li and Duffy (2011) proposed the following equation:

$$E = \alpha \left( {\Theta - \Theta _{{\text{c}}} } \right)H\left| {\mathbf{u}} \right|$$
(16.18)

with coefficient α and Shields parameters Θ and Θc, defined by \(\Theta = {{u_{*}^{2} } \mathord{\left/ {\vphantom {{u_{*}^{2} } {sg\delta }}} \right. \kern-\nulldelimiterspace} {sg\delta }}\), and the following equations.

$$u_{*} = \sqrt {gh\left( {S_{{fx}}^{2} + S_{{fy}}^{2} } \right)}$$
(16.19)
$$S_{{fx}} = {{nu_{x} \left| {\mathbf{u}} \right|} \mathord{\left/ {\vphantom {{nu_{x} \left| {\mathbf{u}} \right|} {h^{{4/3}} }}} \right. \kern-\nulldelimiterspace} {h^{{4/3}} }}\quad S_{{fy}} = {{nu_{y} \left| {\mathbf{u}} \right|} \mathord{\left/ {\vphantom {{nu_{y} \left| {\mathbf{u}} \right|} {h^{{4/3}} }}} \right. \kern-\nulldelimiterspace} {h^{{4/3}} }}$$
(16.20)
$$s = \rho _{s} /\rho _{f} - 1$$
(16.21)

The term Θc denotes the critical Shields parameter, which must be exceeded by Θ for resuspension (erosion) to become active. In his classical paper, Shields (1936) demonstrated that Θc depends on the grain size Reynolds number. Cao et al. (2004) used a similar relation to that shown in Eq. (16.18) and considered the dependence of α on parameters δ, s, Θc, and fluid velocity.

In the presented approaches, the terms are dependent on particle size and density. For the general modeling approach, heterogeneous sediment must be partitioned into several classes of different sizes and weights, similar to the implementation in SISYPHE (TELEMAC 2020). The numerical calculation must then be performed for each different sediment class. In the presented numerical approach, this can be included easily. For each class, a differential equation, as formulated in Eq. (16.8), must be added. In Eq. (16.10), the contributions of the various sediment fractions must be added. For the first demonstration of the approach, we restrict our simulations to a single sediment type.

4 Demonstration Model

The capability of the modeling approach is demonstrated for the problem of scouring as a result of flooding. In their recent review on the science behind scours at bridge foundations, Pizzaro et al. (2020) identified scouring as an erosional process and characterized it as the interaction between any type of underwater structure and the water flowing in a river or wadi channel. According to Pizzaro et al. (2020), scouring is by far the leading cause of bridge failure worldwide and thus causes significant direct losses of infrastructure and disruption of road networks.

In Oman, it is reported that the 1996 cyclone washed away roads and 21 bridges. Resulting from Cyclone Gonu, which hit the Oman coast in 2007‚ “roads and bridges were washed out, and major sites in the capital area were totally isolated and inaccessible for days” (Al-Shaqsi 2010). Investigations of scours and their underlying processes are thus topics of high relevance. Figure 16.1 shows the early stage of an advancing flood at a bridge pier.

Fig. 16.1
figure 1

Sketch of a flood passing a bridge pier

Full size image

Measures that aim to avoid damage to bridges during flood events are considered during the design phase of bridge construction or when reinforcing the foundations of existing bridges. The calculations are usually based on a designed flood event with a specified magnitude and a return period of 100 or 200 years. The depth of the scour is then calculated under the assumption of a one-to-one relationship between the flood discharge and the steady-state scour depth (Pizarro et al. 2020). This approach leaves several processes out of consideration that acts simultaneously during the passing of a flood.

Using numerical models, it is possible to simulate the simultaneous actions of numerous processes. Sedimentation and erosion are processes that appear at different locations in rivers or wadis during flood events. In computer models, suspended loads of different sizes and bed loads can be treated in parallel. Concerning floods, it is crucial to examine transient development and not long-term equilibrium.

To demonstrate how the proposed numerical approach performs concerning scour development near an obstacle, we deal with a simple geometric setup. The model region is given by a square cavity that is open on two opposite sides and closed on the other sides. In the center, a circular obstacle is located, representing a bridge pier. The situation is sketched in Fig. 16.2.

Fig. 16.2
figure 2

Sketch of a flood domain with a cylindrical obstacle

Full size image

It is assumed that there is a sudden increase in the water column height at the inflow boundary. The inflowing water has a constant load of particulate matter. The initial values of the water table and depth are constants. The initial particulate load concentration is zero.

The numerical simulations are performed using the COMSOL Multiphysics (2020) program. This is a versatile and flexible software applicable for coupled partial differential equations solved by the finite element method. The program is currently used for all kinds of multiphysics applications in the fields of engineering, physics, chemistry, biology, medicine, hydraulics, etc. It is operated via a graphical user interface that allows comfortable handling and coupling of multiple physics modes.

The entire system can be implemented in COMSOL Multiphysics using pde-modes. We utilized a physics mode for the SWE (Schlegel 2012), i.e., Eqs. (16.1) and (16.2). The particulate load in the water column, following Eq. (16.7), is modeled by the solute transport mode. For simplicity, only one sediment class is considered. The settling velocity is considered in a loss term according to Eq. (16.12). Finally, the coefficient form pde of COMSOL Multiphysics is utilized to include the bed load represented by Eq. (16.10) in the model. All input parameters are gathered in Table 16.1.

Table 16.1 Parameters of the demonstrated model
Full size table

For extreme flood events, Lumbroso and Gaume (2012) examined common guidance documents to determine the distributions of the mean maximum velocity, Manning parameter, and Froude number. According to their presentation, the 50% threshold of the mean maximum velocity is 1 m/s; that of the Manning parameter is 0.04 s/m1/3; and that of the Froude number is approximately 0.5. The lower Froude numbers used in our simulation, calculated on the basis of the initial and inflow depths, are more representative of common flood events. Following the methods of Li and Duffy (2011), several parameter values were taken from Cao et al. (2004). To emphasize the flow and transport coupling, we increased the resuspension parameter from the value used by the authors of previous studies.

For the SWE and transport equation, linear elements are used, and for the bed equation, quadratic elements are used. The finite element mesh is refined at the obstacle boundaries. When constructing the mesh, maximum element side lengths of only 0.01 m at the upstream side and 0.005 m at the downstream side were allowed. The resulting mesh, consisting of 2476 elements, is shown in Fig. 16.3. The discretization of the entire system of coupled differential equations has 10,468 degrees of freedom.

Fig. 16.3
figure 3

Model finite element mesh

Full size image

It is well known that the numerical solution of the advection–diffusion transport equation may suffer from severe instabilities. Straightforward modeling, either using finite differences or finite element techniques, may produce spurious oscillations. The numerical solution of SWEs (16.1) and (16.2) may have the same problem, as examined by Holzbecher and Hadidi (2017). To suppress these instabilities, various stabilization schemes have been proposed.

For the transport equation, the most basic stabilization method is the introduction of artificial diffusivity (Quarteroni 2017). In CFD implementations, an artificial viscosity, ν, can be introduced, which appears in an additional term on the left side of Eq. (16.2) (Chen et al. 2013).

$$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + g\nabla H - \nu \nabla ^{2} {\mathbf{u}} - {\mathbf{F}} = 0$$
(16.22)

In straightforward implementations of numerical methods, stability problems are likely to occur. Using basic stabilization methods, nonphysical terms, such as artificial diffusivity and viscosity, are introduced, which may lead to increased smoothing of steep gradients (Margolin 2019). For this reason, more sophisticated schemes have been proposed. To avoid stabilization problems in our demonstration case, several of these schemes are utilized: streamline stabilization, shock wave capturing, and artificial kinematic viscosity for the SWEs and streamline and crosswind diffusion for the transport equation. COMSOL Multiphysics offers options to easily include these schemes in the finite element formulation.

5 Results

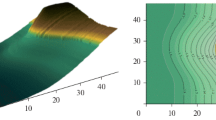
Figure 16.4 shows the outcome of the numerical model outlined above. The subfigures show the water table and bottom elevation at four different time instants. For better visualization, the water table is shifted by −0.6 m.

Fig. 16.4
figure 4

Water table (color) and ground surface (gray) at different time instants: t = 0.1 (top left), 0.3 (top right), 0.5 (bottom left), and 0.9 (bottom right) s; all units in m

Full size image

At time t = 0.1 s, the wave that is initiated by the elevated water table at the inlet is moving into the domain, with the wave front reaching the obstacle. The bottom of the domain is still almost flat as in the initial state. At time t = 0.3 s, the wave trough has passed the obstacle. The water depth is increased at the upstream edge of the obstacle and at the outlet and is decreased behind the obstacle. The bottom surface begins to show slight changes from the initial constant state.

At t = 0.5 s, the water depth distant from the obstacle fluctuates slightly around the same value; at the outlet, it is slightly higher than at the inlet, while a slight wave trough is seen in between the outlet and inlet. At the upstream edge of the obstacle, the water level is still higher, and the water level is lower behind the downstream edge of the obstacle. The changes at the bottom elevation have become more pronounced: at the flanks, the digging of scours can be observed, while the bottom of the domain is elevated in the wake of the obstacle.

In the subfigure for t = 0.9 s, the general observation is still the same. The water table deviations from a constant value decrease. Depth extremes are still present at the obstacle boundaries: The highest value appears upstream, and the lowest value appears downstream. The changes in the bottom elevation increase further: Trough-building is observed at the flanks and sedimentation is observed in the wake.

These findings are highlighted in Fig. 16.5, which depicts the water table and bottom elevation changes at two positions as functions of time. The flank position is located directly at the obstacle boundary at the most transverse point relative to the main flow axis. The downstream position is located slightly beyond the obstacle, downstream near the flow axis. The water depth increases from 1 m to approximately 1.65 m at both positions. The graphs clearly show the deepening of the bottom of the domain at the flanks, down to almost 10 cm, and these values nearly stabilize after 0.6 s. The increase in the wake amounts to only a few centimeters but is still increasing at the end of the simulated period.

Fig. 16.5
figure 5

Water table and bottom elevation changes at selected locations

Full size image

6 Conclusions

An ideal–typical situation of scour development near an obstacle was set up in order to examine the capability of the numerical 2D coupled multiphysics approach to simulate basic processes changing the bottom of the water body. Results in Fig. 16.4 identify scours at the flanks of the obstacle and sedimentation downstream. This coincides with field observations, shown in Fig. 16.6 showing an upstream view in a wadi with a stone obstacle. Water-filled scours at the sides of the stone can be identified, while in the backwater (front in the photograph) sediment is deposited.

Fig. 16.6
figure 6

Depression and sedimentation around an obstacle; view upstream in Wadi Abyad, Oman

Full size image

Further, experimental and numerical research is needed to examine the real capabilities and limits of the approach. In order to improve simulations with respect to field data, the proposed approach offers many options for the consideration of additional dependencies and processes. Sediment transport processes are complex. Even concerning the more specialized topic of scours at bridge foundations, a current review (Pizarro et al. 2020) sees no consensus between scientists of different disciplines (physicists, hydrologists, hydro-, structural, and geotechnical engineers). The cooperation between different scientific branches is thus a challenge. Theoretical and numerical efforts have to be synchronized with experimental studies, in the laboratory and in the field.