High Spatial Resolution Hyperspectral Imaging with Machine-Learning Techniques

Abstract

Recent advances in scanning transmission electron microscopy (STEM) techniques have enabled us to obtain spectroscopic datasets such as those generated by electron energy-loss (EELS)/energy-dispersive X-ray (EDX) spectroscopy measurements in a PC-controlled way from a specified region of interest (ROI) even at atomic scale resolution, also known as hyperspectral imaging (HSI). Instead of conventional analytical procedures, in which the potential constituent chemical components are manually identified and the chemical state of each spectral component is successively determined, a statistical machine-learning approach, which is known to be more effective and efficient for the automatic resolution and extraction of the underlying chemical components stored in a huge three-dimensional array of an observed HSI dataset, is used. Among the statistical approaches suitable for processing HSI datasets, methods based on matrix factorization such as principal component analysis (PCA), multivariate curve resolution (MCR), and nonnegative matrix factorization (NMF) are useful to find an essential low-dimensional data subspace hidden in the HSI dataset. This chapter describes our developed NMF method, which has two additional terms in the objective function, and which is particularly effective for analyzing STEM-EELS/EDX HSI datasets: (i) a soft orthogonal penalty, which clearly resolves partially overlapped spectral components in their spatial distributions and (ii) an automatic relevance determination (ARD) prior, which optimizes the number of components involved in the observed data. Our analysis of real STEM-EELS/EDX HSI datasets demonstrates that the soft orthogonal penalty is effective to obtain the correct decomposition and that the ARD prior successfully identifies the correct number of physically meaningful components.

1 Introduction

Current scientific analytical instruments are mostly computer-controlled and based on digital circuits. This facilitates automated measurements because the experimental procedures can be specified by using program code. For instance, recent advances in scanning transmission electron microscopy (STEM) techniques, including the development of brighter electron sources, digitally controlled operation, detectors with higher sensitivity, and sophisticated online signal processing, have enabled us to obtain comprehensive information not only on the local structures but also on the chemistry of solids by concurrently applying spectroscopic methods such as electron energy-loss (EELS) and energy-dispersive X-ray (EDX) spectroscopy to a specified region of interest (ROI). The spectrometers collect a set of spectra, each from the subnanometer area of the sample, using subnanometric incident electron probe scanning over the two-dimensional ROI with a subnanometric step width. This method is known as hyperspectral imaging (HSI). The typical data acquisition time is now reduced to several minutes for an entire EELS dataset with 2,000 energy channels over 10⁴ = 100 × 100 pixels (sampling points). Accordingly, the associated volume of data to be analyzed has been drastically increasing. In this context, statistical analysis methods could be more effective to thoroughly extract information embedded in massive amounts of data without any preconception, rather than relying on conventional spectral analysis of sampling points detected manually based on the insight of experts.

Among the various statistical approaches, principal component analysis (PCA) [1,2,3] is one of the most fundamental and popular methods. PCA successively casts mutually orthogonal eigenvectors (basis vectors) and associated score images (spatial intensity distributions of the corresponding basis vectors) in the order of significance, that is, in the order of the magnitude of eigenvalues, by way of the singular value decomposition of the HSI data matrix consisting of the experimental spectra as its row vectors. Trebbia and Bonnet [2] and Bosman et al. [3] applied PCA to EELS-HSI datasets, and not only detected exotic chemical bonding states in the samples, but also effectively filtered statistical noise from the HSI data matrix by reconstructing this matrix with a few essential basis spectra and their spatial intensity distributions. Parish and Brewer [4] studied the validity of PCA in a quantitative composition analysis of the constituent phases in their EDX-HSI data. Note that, in their treatment, the phase overlapping areas were masked for exclusion from the quantification process; otherwise, the derived phase compositions could be biased with respect to the actual ones. These reports on PCA assumed that each pixel contains a linear combination of principal components with the orthogonality condition intrinsic to PCA. Using simulated atomic resolution EELS-HSI data, Lichteret and Verbeeck [5] pointed out that, when the noise level exceeds the intensity of the signal of interest, the signal intensities are distributed over a number of principal components, and are thus usually considered as noise. This behavior seems statistically natural, but we would not notice this phenomenon in actual experimental data. On the other hand, Spiegelberg and Rusz recently reexamined the applicability of PCA to noisy EELS data [6]. In order to estimate the amount of bias present in each principal component, Lichtert and Verbeeck [5] proposed evaluation criteria which, however, do not exhibit the correct asymptotic behavior considering the size of the dataset. Spiegelberg and Rusz [6] proposed alternative evaluation criteria, taking the size of the dataset into account.

Dobigeon and Brun [7] compared the results obtained by applying PCA, independent component analysis (ICA) [8], vertex component analysis (VCA) [9], and Bayesian linear unmixing (BLU) [10] to experimental EELS-HSI data. They eventually found that BLU provided the most plausible spatial distributions for the constituent spectral components, presumably because of its more realistic modeling of the EELS-HSI data. Spiegelberg et al. [11] also discussed a set of such data decomposition methods. In particular, they established randomized VCA (RVCA), an extension of VCA for application to noisy data, and compared its efficiency with that of minimum volume simplex analysis (MVSA) and BLU.

Over a decade, our research group has been developing an alternative method to nonnegative matrix factorization (NMF), or multivariate curve resolution (MCR) for the analysis of EELS-HSI [12, 13]. We consider this approach to be successful because NMF naturally restricts both the spatial intensities and basis spectra to nonnegative values. Contrary to NMF, the methods mentioned above such as PCA allow the spatial intensities and spectra to have negative values, which hampers the direct physical interpretation of the resolved spectral profiles. We adopted the modified alternating least-square (MALS) fitting algorism of NMF [14] to map the different phases in the degradation of Li battery cathodes [15,16,17,18,19] and the chemical states of nitrogen in nitrogen-doped TiO₂ [20, 21]. We also successfully applied NMF to a series of EELS datasets for the extraction of atom site-specific core-loss spectra, where the relative excitation probabilities of the spectra varied with the diffraction condition because of the electron channeling effects [22,23,24,25]. In these applied data analyses, the nonnegative constraint of the elements of extracted basis spectra and spatial intensity distributions were effective, and the resulting spectra extracted by NMF were consistent with the computational results obtained by first principles calculations [15,16,17,18,19, 22,23,24,25].

In general, approaches such as PCA and NMF are known as matrix factorization because these methods factorize a HSI data matrix into the product of two thin matrices, i.e. matrices of the spatial intensity distribution and basis spectra, with some suitable constraints resulting from the designed model. The next section first briefly formalizes the problem setting of matrix factorization with HSI data [26, 27]. We then present our proposed NMF [26], which presents two advantages with respect to HSI analysis against conventional NMFs: (i) spatially clear decomposition of overlapping intensity distributions achieved by introducing a spatially orthogonal penalty term and (ii) automatic selection of a number of essential chemical components by introducing a penalty term of an automatic relevance determination (ARD) prior distribution. Our analysis of real STEM-EDX/EELS HSI datasets demonstrates that the spatial orthogonal penalty is effective to obtain the correct decomposition and the ARD prior can successfully select the correct number of physically meaningful components.

2 Methodology

2.1 Mathematical Formulation of HSI Data

The observed HSI data are stored in a three-dimensional array termed a data cube $\varvec{D}\left( {\varvec{x},\varvec{ y},\varvec{ E}} \right)$, which is a function of the two-dimensional spatial position $\left( {\varvec{x},\varvec{ y}} \right)$ on the specimen and the absorption/emission energy E. For the convenience of mathematical manipulation, the data cube is often transformed to a two-dimensional $\varvec{N}_{{\varvec{xy}}}$ × $\varvec{N}_{{\varvec{ch}}}$ matrix $\varvec{X}$, where $\varvec{N}_{{\varvec{xy}}} = \varvec{N}_{\varvec{x}} \varvec{ } \times \varvec{ N}_{\varvec{y}}$ is the number of pixels, i.e. the product of the number of scanning steps $\varvec{N}_{\varvec{x}}$ and $\varvec{N}_{\varvec{y}}$ along the spatial $\varvec{x}$- and $\varvec{y}$-axis, respectively, and $\varvec{N}_{{\varvec{ch}}}$ is the number of detector channels. After the transformation, the observed spectrum at position $\left( {\varvec{x},\varvec{ y}} \right)$ is stored in a row of matrix $\varvec{X}$. A basic statistical method to extract a few essential basis spectra and their spatial intensity distribution assumes that the spectral intensity at each sample pixel is represented by a linear combination of the basis spectra associated with the underlying chemical components (states or phases). Assuming that the number of essential chemical components in the observed spatial region is $\varvec{K}$, which is much smaller than the size of matrix $\varvec{X}$, this analysis can be formulated by matrix factorization, which factorizes HSI data matrix $\varvec{X}$ into low rank (or thin) matrices of the spatial intensity distribution $\varvec{C}$ and basis spectra $\varvec{S}$:

$$ \varvec{X} \approx \varvec{CS}^{{\mathbf{T}}} , $$

(9.1)

where the size of $\varvec{C}$ is $\varvec{N}_{{\varvec{xy}}} \times \varvec{ K}$ and the size of $\varvec{S}$ is $\varvec{N}_{{\varvec{ch}}} \times \varvec{ K}$, and superscript ${\mathbf{T}}$ denotes a matrix transpose. Each column vector of $\varvec{S}$ (referred to as loading in multivariate analysis) is a basis spectrum of a chemical component. On the other hand, each column vector of $\varvec{C}$ (referred to as score) is a spatial intensity distribution over the ROI positions. Hence, each row vector of $\varvec{C}$ is the intensities of $\varvec{K}$ chemical components at a spatial position. Using the i-th column of matrix $\varvec{C}$, a two-dimensional spatial distribution of the i-th chemical component can be reconstructed by rearranging the elements such that they are returned to the original two-dimensional position.

The matrix factorization can identify both spatial intensity matrix $\varvec{C}$ and spectral matrix $\varvec{S}$ by minimizing the reconstruction error, which is the distance between observation $\varvec{X }$ and the reconstruction, i.e. $\varvec{CS}^{{\mathbf{T}}}$. This identification is possible because matrix $\varvec{X}$, which consists of a huge number of elements with a relatively much smaller $\varvec{K}$, is highly redundant. Thus, the identification problem is equal to that intended to find the essential subspace where the original $\varvec{X}$ occurs. This approach can identify plausible $\varvec{C}$ and $\varvec{S}$ with much higher signal-to-noise ratios (SNRs) than those manually selected from the small number of representative observed spatial points, i.e. point-to-point analysis.

Matrix factorization needs to assume a suitable restriction of $\varvec{C}$ and $\varvec{S}$ because the optimization problem results in many local minima. Principal component analysis (PCA) identifies $\varvec{C}$ and $\varvec{S}$ by minimizing the squared error $\left\| {X - CS^{\rm{T}} } \right\|^{2}$ with the orthogonal constraints in both $\varvec{C}$ and $\varvec{S}.$ Owing to the orthogonal constraint, PCA can easily find the global solution using a singular value decomposition (SVD) algorithm. However, PCA can generate unnatural $\varvec{C}$ and $\varvec{S}$, in which the element can include negative spatial intensities and spectral values. Moreover, the strong orthogonal constraint cannot allow overlaps to exist among the chemical components in both spatial and spectral space. These problems require the outputs by PCA to be adjusted to obtain physically meaningful insights. We overcame these problems by using an approach involving non-negative matrix factorization, in which the elements of $\varvec{C}$ and $\varvec{S}$ are not allowed to be negative.

2.2 Non-negative Matrix Factorization with a Gaussian Noise Model

This section presents a formal mathematical description of our model and algorithms to provide the concept of our developed NMF. Let $\varvec{X} \in \varvec{R}_{ + }^{{N_{xy} \times N_{ch} }}$ be an HSI data matrix, where $\varvec{R}_{ + }$ is the set of all nonnegative real numbers. NMF factorizes $\varvec{X}$ into two thin matrices $\varvec{C} \in \varvec{R}_{ + }^{{N_{xy} \times K}}$ and $\varvec{S} \in \varvec{R}_{ + }^{{N_{ch} \times K}}$, where K is much smaller than both $N_{xy}$ and $N_{ch}$. Hence, the factorization model is given by

$$ \varvec{X} = \varvec{CS}^{\text{T}} +\varvec{\varepsilon} $$

(9.2)

where $\varvec{\varepsilon}\in \varvec{R}^{{N_{xy} \times N_{ch} }}$ is a noise matrix of which the elements are generated statistically independent of each other. In our problem setting, only $\varvec{X}$ is observed, whereas $\varvec{C}$ and $\varvec{S}$ are not observed. The goal of NMF is to identify the optimal $\varvec{C}$ and $\varvec{S}$ under a suitable noise model $\varvec{\varepsilon}$. One of the most common models is a Gaussian noise model, in which an element of a noise matrix is generated from a Gaussian distribution:

$$ p\left( {\varepsilon_{ij} |0,\sigma^{2} } \right) = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}{ \exp }\left\{ { - \frac{{\varepsilon_{ij}^{2} }}{{2\sigma^{2} }}} \right\}, $$

(9.3)

where $\sigma^{2}$ is the noise variance. Since the statistically independent assumption of $\varvec{\varepsilon}= \varvec{X} - \overline{\varvec{X}}$, where $\overline{\varvec{X}} = \varvec{CS}^{\varvec{T}}$ is the noiseless data matrix, the log-likelihood function of matrix $\varvec{X}$ is given by

$$ \log \,p\left( {\varvec{X} |\overline{\varvec{X}} ,\sigma^{2} } \right) = -\frac{1}{{2\sigma^{2} }}\mathop \sum \limits_{i = 1}^{{N_{xy} }} \mathop \sum \limits_{j = 1}^{{N_{ch} }} \left( {X_{ij} - \overline{X}_{ij} } \right)^{2} - \frac{{N_{xy} N_{ch} }}{2}{ \log }2\pi \sigma^{2} $$

(9.4)

Taking a common statistical estimation approach of the maximum likelihood estimation, i.e. maximizing $\log p\left( {\varvec{X}|\overline{\varvec{X}} ,\sigma^{2} } \right)$, C and S can be optimized using only data matrix $\varvec{X}$. By taking the negative value of the log-likelihood, i.e. $- \log p\left( {\varvec{X}|\overline{\varvec{X}} ,\sigma^{2} } \right)$, and neglecting $\sigma^{2}$ in the first term and the second term, the optimization problem is transformed into the minimization of the squared error function between observation X and reconstruction $\overline{\varvec{X}}$:

$$ D_{EU} \left( {\varvec{X}|\overline{\varvec{X}} } \right) = \frac{1}{2}\mathop \sum \limits_{i = 1}^{{N_{xy} }} \mathop \sum \limits_{j = 1}^{{N_{ch} }} \left( {X_{ij} - \overline{X}_{ij} } \right)^{2} . $$

(9.5)

Contrary to PCA, the minimization problem of Eq. (9.5) over both $\varvec{C}$ and $\varvec{S}$ is non-convex, and contains a number of local minima. The optimization algorithm for an NMF does not always converge to the global optimum of $\varvec{C}$ and $\varvec{S}$. Hence, it is necessary to run the optimization algorithm multiple times from different initializations, resulting in considerable computational cost. The computational efficiency has been improved by developing fast optimization algorithms such as matrix multiplication (MM) [28], alternating least-squares (ALS) [29], and hierarchical alternating least-squares (HALS) [30]. In general, MM is sensitive to the initial configuration, whereas the other algorithms are not. Among these approaches, HALS offers the best convergence to local minima. Hence, we adopted the HALS framework for the optimization of our new NMF model. Another problem presented by NMFs is that the number of chemical components needs to be manually selected in advance, which inevitably introduces a problem similar to that of PCA if the noise level is larger than the signal intensities. As the number of components increases, the reconstruction error naturally decreases. However, this decrease is not essential to identify $\varvec{C}$ and $\varvec{S}$ because it results in overfitting to observed data when the number of components is excessively large. Thus, relying on the reconstruction error only cannot be useful to identify the essential number of physically meaningful components.

To overcome the above difficulties in STEM-EELS/EDX HSI data analysis, we developed a new NMF model that imposes the following penalty terms on the spatial intensity matrix $\varvec{C}$: (i) a spatial orthogonal penalty [31] and (ii) a sparse penalty to optimize the number of components, termed an automatic relevance determination (ARD) prior [32]. For the optimization of low-rank matrices $\varvec{C}$ and $\varvec{S}$, we further developed an algorithm based on hierarchical alternating least-squares (HALS) [30], which is more efficient than the matrix multiplication (MM) [28] used before [32]. The following section describes these extended models and their optimization algorithms.

2.3 Optimization Algorithms with Soft Spatial Orthogonal Constraint

A goal of HSI data analysis is to identify the pure spectra and spatial intensity distributions of each chemical component from the spectra and distribution of a mixture of chemical components, i.e. observed matrix $\varvec{X}$. The basic NMF model, e.g. the minimization of Eq. (9.5), often generates unresolved spectra and spatial distributions that still contain spatially overlapped or unnaturally unresolved spectra because the basic NMF induces sparse decomposition of $\varvec{C}$ and $\varvec{S}$. However, the EELS spectrum of a pure chemical component is not sparse, meaning that the intensities of an EELS spectrum are more than zero over all energy bands, whereas the intensities of an EDX spectrum are almost zero except for the peak positions. Hence, poor resolution is more problematic in STEM-EELS analysis than in EDX analysis.

Our approach to solve the above problem entails introducing the spatial orthogonal constraint [31]. This constraint ensures that spectral matrix $\varvec{S}$ is relatively more relaxed than $\varvec{C}$ and then $\varvec{S}$ can be non-sparse. Because the exact orthogonal constraint is too strict, we used weight parameter $w$ to relax this constraint, which is known as a soft spatial orthogonal constraint. Then our objective function of $\varvec{C}_{ \cdot k}$ to be minimized is formulated as follows:

$$ \frac{1}{2}\mathop \sum \limits_{i = 1}^{{N_{xy} }} \mathop \sum \limits_{j = 1}^{{N_{ch} }} \left( {\left[ {\varvec{X}^{{\left( \varvec{k} \right)}} } \right]_{ij} - \left[ {\varvec{C}_{ \cdot k} \varvec{S}_{ \cdot k}^{\text{T}} } \right]_{ij} } \right)^{2} + w\, \cdot \xi_{k} \varvec{C}_{ \cdot k}^{\text{T}} \varvec{c}^{\left( k \right)} \quad {\text{s}}.{\text{t}}. \quad \left\| {\varvec{C}_{ \cdot k} } \right\|_{2} = 1, $$

(9.6)

where

$$ \varvec{X}^{\left( k \right)} = \varvec{X} - \varvec{CS} + \varvec{C}_{ \cdot k} \varvec{S}_{ \cdot k}^{\text{T}} ,\quad {\text{k}} = 1, \ldots ,{\text{K}}, $$

(9.7)

$$ \varvec{c}^{\left( k \right)} = \mathop \sum \limits_{m \ne k} \varvec{C}_{ \cdot m} ,\quad {\text{k}} = 1, \ldots ,{\text{K}}. $$

(9.8)

Parameter $w, 0 \le w \le 1$, is important to adjust the orthogonal penalty and $\xi_{k}$ is the Lagrange multiplier for the exact orthogonal constraint of $\varvec{C}$. When $w = 1$ the optimized $\varvec{C}$ is an exact orthogonal matrix in which any chemical components do NOT overlap. When $w = 0$, among all the components, the optimized components in $\varvec{C}$ may extensively overlap. The optimal value of $w$ depends on the situation, such as the spatial resolution of the data (step width of STEM-HSI) and localization of chemical components. Thus, the optimal value of $w$ must be chosen according to the measurement level.

Applying some algebra to Eq. (9.6) enables us to obtain an analytical solution in terms of the Lagrange multiplier $\xi_{k}$. Substituting the obtained $\xi_{k}$, the update rule of $\varvec{C}_{ \cdot k}$ is given by

$$ \varvec{C}_{ \cdot k} = \left[ {\varvec{X}^{\left( k \right)} \varvec{S}_{ \cdot k} - w\frac{{\varvec{c}^{{\left( k \right){\text{T}}}} \varvec{X}^{\left( k \right)} \varvec{S}_{ \cdot k} }}{{\varvec{c}^{{\left( k \right){\text{T}}}} \varvec{c}^{\left( k \right)} }}\varvec{C}_{ \cdot k} } \right]_{ + } ,\quad k = 1, \ldots ,K $$

(9.9)

where the operator $\left[ \varvec{A} \right]_{ + }$ replaces all negative values in matrix $\varvec{A}$ with zeros. Hence, it can be calculated by $\left[ \varvec{A} \right]_{ + } = \left\{ {\varvec{A} + {\text{abs}}\left( \varvec{A} \right)} \right\}/2$, where function abs outputs a matrix consisting of the absolute value of the elements in $\varvec{A}$. The second term weighted by $w$ is due to the orthogonal penalty term. After applying Eq. (9.9), each column of $\varvec{C}$ should be normalized by

$$ \varvec{C}_{ \cdot k} \leftarrow \varvec{C}_{ \cdot k} /\left\| {\varvec{C}_{ \cdot k} } \right\|_{2} ,\quad k = 1, \ldots ,K. $$

(9.10)

Thus, we omit the normalization of $\varvec{S}$, and the update is given by

$$ \varvec{S}_{ \cdot k} = \left[ {\left( {\varvec{X}^{\left( k \right)} } \right)^{\text{T}} \varvec{C}_{ \cdot k} } \right]_{ + } ,\quad k\, = \,1, \ldots ,K. $$

(9.11)

Figure 9.1 provides the pseudo-code of this NMF, which we named SO-NMF.

Fig. 9.1

Pseudocode of our NMF with the soft orthogonal constraint (SO-NMF)

2.4 Probabilistic View of a NMF Model with an Automatic Relevance Determination Prior

Optimizing the number of components using only the observed HSI data is practically important. Maximum likelihood estimation (or an estimation based on minimizing errors) cannot be effective for the optimization because it causes overfitting of the HSI data when the number of components is large. This overfitting problem is avoided by using a Bayes estimation (or a maximum a posteriori (MAP) estimation) with a prior distribution of scale parameters (relevance weights) [32]. The process of choosing only the important components is known as automatic relevance determination (ARD).

To perform ARD in NMF, we assume a prior distribution for $\varvec{C}$ using an exponential distribution with a scale parameter $\lambda_{k}$ for the probability density of column $k$ of $\varvec{C}$, i.e. $\varvec{C}_{ \cdot k}$:

$$ p\left( {C_{nk} |\lambda_{k} } \right) = \frac{1}{{\lambda_{k} }}{ \exp }\left( { - \frac{{C_{nk} }}{{\lambda_{k} }}} \right), \quad n = 1, \ldots ,N_{xy} , \quad k = 1, \ldots ,K. $$

(9.12)

The above density distribution generates nonnegative random values with a large probability density around zero, resulting in a sparse matrix of $\varvec{C}$. For the prior distribution of $\lambda_{k}$, we assume an inverse-Gamma distribution:

$$ p\left( {\lambda_{k} |a,b} \right) = \frac{{b^{a} }}{{\Gamma \left( a \right)}}\lambda_{k}^{{ - \left( {a + 1} \right)}} { \exp }\left( { - \frac{b}{{\lambda_{k} }}} \right),\quad k = 1, \ldots ,K, $$

(9.13)

where $a$ and $b$ are hyper-parameters to adjust the sparseness of $\lambda_{k}$. On the other hand, the probability density distribution of column $k$ of S, i.e. $p\left( {\varvec{S}_{{ \cdot \varvec{k}}} } \right)$, is assumed to be uniformly distributed on the unit hyper-sphere in ${\mathbf{R}}_{ + }^{{N_{ch} }}$. Using Eqs. (9.4), (9.12), and (9.13), the negative log-likelihood function of an NMF model with ARD priors is given by

$$ \begin{aligned} L\left( {\varvec{C},\varvec{S},\varvec{\lambda},\sigma^{2} } \right) & = - \log p\left( {\varvec{X}|\overline{\varvec{X}} ,\sigma^{2} } \right) - \mathop \sum \limits_{i = 1}^{{N_{xy} }} \mathop \sum \limits_{k = 1}^{K} \log p\left( {C_{ik} |\lambda_{k} } \right) \\ & \quad - \mathop \sum \limits_{k = 1}^{K} \log p\left( {\varvec{S}_{{ \cdot \varvec{k}}} } \right) - \mathop \sum \limits_{k = 1}^{K} \log p\left( {\lambda_{k} |a,b} \right) \\ & \quad = \frac{{N_{xy} N_{ch} }}{2}{ \log }2\pi \sigma^{2} + \frac{1}{{2\sigma^{2} }}\mathop \sum \limits_{i = 1}^{{N_{xy} }} \mathop \sum \limits_{j = 1}^{{N_{ch} }} \left( {X_{ij} - \overline{X}_{ij} } \right)^{2} \\ & \quad + \mathop \sum \limits_{k = 1}^{K} \frac{1}{{\lambda_{k} }}\left( {b + \mathop \sum \limits_{i = 1}^{{N_{xy} }} C_{ik} } \right) + \left( {N_{xy} + a + 1} \right)\mathop \sum \limits_{k = 1}^{K} { \log }\lambda_{k} \\ & \quad + {\text{K}}\left( {a{ \log }b - { \log }\,\Gamma \left( a \right)} \right), \\ \end{aligned} $$

(9.14)

With regard to the optimization of $\varvec{C}$, $L\left( {\varvec{C},\varvec{S},\varvec{\lambda},\sigma^{2} } \right)$ is a penalized likelihood function with the L₁ norm of C, resulting in a sparse matrix C. The NMF minimizing $L\left( {\varvec{C},\varvec{S},\varvec{\lambda},\sigma^{2} } \right)$ is referred to as ARD–NMF.

Because the simultaneous optimization of $L\left( {\varvec{C}, \varvec{S},\varvec{\lambda},\sigma^{2} } \right)$ over all $\varvec{C}, \varvec{S},\varvec{\lambda},\,{\text{and}}\,\sigma^{2}$ is non-convex, multiple optimizations from different initial configurations are required. To update $\varvec{C}$ and $\varvec{S}$, we use HALS [30], which updates each column $\varvec{C}_{ \cdot k}$ and $\varvec{S}_{ \cdot k}$ alternately. Applying some algebra to the minimization of $L\left( {\varvec{C}, \varvec{S},\varvec{\lambda},\sigma^{2} } \right)$, we obtain the following update rule for $\varvec{C}_{ \cdot k}$:

$$ \varvec{ C}_{ \cdot k} = \left[ {\varvec{X}^{\left( k \right)} \varvec{S}_{ \cdot k} - \frac{{\sigma^{2} }}{{\lambda_{k} }}} \right]_{ + } ,\quad k = 1, \ldots ,K $$

(9.15)

The second term in Eq. (9.15) is attributable to the ARD prior, which induces the sparse matrix of $\varvec{C}$. The update rule for $\varvec{S}_{ \cdot k}$ by HALS is given by

$$ \varvec{S}_{ \cdot k} = \frac{{\widetilde{\varvec{s}}_{k} }}{||{\widetilde{{\varvec{s}}}_{k} ||}}_{2} ,\quad k = 1, \ldots ,K $$

(9.16)

where $\left\| x \right\|_{2}$ is the L ₂ norm of vector $\varvec{x}$ and

$$ \widetilde{\varvec{s}}_{k} = \left[ {\left( {\varvec{X}^{\left( k \right)} } \right)^{\text{T}} \varvec{C}_{ \cdot k} } \right]_{ + } ,\quad k = 1, \ldots ,K $$

(9.17)

Similarly, the update rules for the relevance weight $\varvec{\lambda}$ and $\sigma^{2}$ to minimize $L\left( {\varvec{C}, \varvec{S},\varvec{\lambda},\sigma^{2} } \right)$ with all other quantities fixed are given by

$$ \lambda_{k} = \frac{{b + \mathop \sum \nolimits_{i = 1}^{{N_{xy} }} C_{ik} }}{{N_{xy} + a + 1}},\quad k = 1, \ldots ,K $$

(9.18)

$$ \sigma^{2} = \frac{1}{{N_{xy} N_{ch} }}\mathop \sum \limits_{i = 1}^{{N_{xy} }} \mathop \sum \limits_{j = 1}^{{N_{ch} }} \left( {X_{ij} - \overline{X}_{ij} } \right)^{2} $$

(9.19)

The hyper-parameter $b$ can be set using an approximate empirical estimator [32] as follows:

$$ b = \frac{{\left( {a - 1} \right)\sqrt {N_{ch} } }}{K}\frac{1}{{N_{xy} N_{ch} }}\mathop \sum \limits_{i = 1}^{{N_{xy} }} \mathop \sum \limits_{j = 1}^{{N_{ch} }} X_{ij} , $$

(9.20)

In our experiments, the hyper-parameter $a$ was set to $a = 1 + \delta$, where $\delta = 10^{ - 16}$, to choose the minimum number of components with the minimum $L\left( {\varvec{C}, \varvec{S},\varvec{\lambda},\sigma^{2} } \right)$. After the optimization of ARD-NMF, the relevance (or importance) values of components are given by $\lambda_{k} , k = 1, \ldots ,K$. Because the values of redundant components cannot be exactly zero, we empirically set a threshold value to remove such components.

2.5 Optimization Algorithm for C with Both ARD and Spatial Orthogonal Constraint

When we simply combine the soft orthogonal constraint and the ARD effect using both penalty terms, then the update rule of $\varvec{C}_{ \cdot k} \varvec{ }$ can be obtained as follows:

$$ \varvec{C}_{ \cdot k} = \left[ {\varvec{X}^{\left( k \right)} \varvec{S}_{ \cdot k} - \frac{{\sigma^{2} }}{{\lambda_{k} }} - w\frac{{\varvec{c}^{\left( k \right)T} \left( {\varvec{X}^{\left( k \right)} \varvec{S}_{ \cdot k} - \sigma^{2} /\lambda_{k} } \right)}}{{\varvec{c}^{{\left( k \right){\text{T}}}} \varvec{c}^{\left( k \right)} }}\varvec{C}_{ \cdot k} } \right]_{ + } ,\quad k = 1, \ldots ,K $$

(9.21)

In this update, $\varvec{C}_{ \cdot k}$ should not be renormalized to reduce the effect of the orthogonal constraint for irrelevant components. We propose Eq. (9.21) as an update rule for $\varvec{C}_{ \cdot k}$ when the orthogonal constraint is necessary. Figure 9.2 shows the pseudo-code of our proposed NMF algorithm, which we named ARD-SO-NMF. In the special case without the orthogonal constraint, i.e. $w = 0$, the algorithm is simply ARD-NMF. Line 12–20 has the purpose of merging the components when the spectra are similar. In this procedure, the similarity is evaluated by using the cosine similarity and the spectra are considered to be the same when the value exceeds 0.99. This operation is necessary to choose the correct number of components because the orthogonality condition with w > 0 enforces splitting of the components even when the spectra are exactly the same. Our MATLAB and Python codes are available at https://github.com/MotokiShiga.

Fig. 9.2

Pseudocode of our NMF with ARD and the soft orthogonal constraint (ARD-SO-NMF)

3 Application

3.1 Experimental Procedures

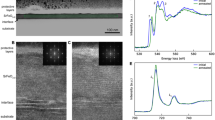
A real dataset was acquired from a cross-sectional TEM (XTEM) sample of a Si diode, prepared by a focused ion beam (FIB) technique. We recorded the HSI data for Si-L _2,3 including zero-loss peak (ZLP) using a JEOL JEM-1000 K RS ultra-high voltage S/TEM of Nagoya University, operated at 1000 kV, with a Gatan Quantum equivalent EEL spectrometer of which the energy dispersion was set to 0.2 eV/channel. The sample thickness of the measured area was estimated at 0.1 μm from the low-loss spectrum. The energy drift of the spectra during the acquisition was corrected by ZLP alignment and calibration. After the energy calibration, the pre-edge background modeled by a power law was subtracted to isolate the Si-L _2,3 spectrum. Figure 9.3 shows an annular dark-field STEM (ADF-STEM) image of the ROI of the Si diode, a manually validated component map and spectra.

Fig. 9.3

a Cross-sectional ADF-STEM image, b spatial distribution of three components, and c their reference Si-L _2,3 spectra of silicon diode test sample

Another experimental STEM-EELS HSI dataset was prepared by measuring the atomic resolution EELS-HSI of Mn₃O₄. Polycrystalline Mn₃O₄ with a spinel crystal structure was obtained, and a TEM sample was prepared by conventional ion milling as previously described [24]. We measured the Mn-L _2,3 HSI using a JEOL ARM-200F aberration-corrected STEM, operated at 200 kV, with the Gatan Quantum EELS having an energy dispersion of 0.5 eV/channel. The average full width at half maximum (FWHM) of ZLP collected simultaneously (Dual EELS mode) with Mn L _2,3 was approximately 2 eV. The thickness of the measured area was approximately 40 nm, estimated from the low-loss spectra. Prior to applying NMF to the data, the energy drift of the spectra during the acquisition was corrected using the dual EELS mode synchronized with the ZLP alignment and calibration. After the energy calibration, the pre-edge background intensities were subtracted by modeling them with a power law.

Figure 9.4a–c show the ADF-STEM image, schematic projected structure of the Mn_Tet (divalent Mn occupying the tetrahedral site, Mn_Oct (trivalent Mn at the octahedral site) and O (oxygen) columns along the present incident beam direction and the extracted site-specific spectra, respectively. In (a) the heavier element (Mn) alone appears bright. These data are more difficult to analyze, because the inner shell excitation is delocalized by a certain distance and the neighboring atomic columns simultaneously contribute to the spectrum intensity at a sampling point due to electron channeling effects [25] and orbital hybridization between the elements.

Fig. 9.4

a ADF-STEM image, b corresponding atom-site positions in the framed area of (a), and c Mn-L _2,3 reference spectra for STEM-EELS-HSI data from Mn₃O₄

For all datasets, even after the above pre-processing, a few elements in X had small negative values due to background removal. Thus, we replaced these values with zeros. To normalize the scale of X, all elements were divided by the average of the elements in X.

An STEM-EDX-HSI dataset was acquired from a sintered ceramic composite of Y-doped ZrO₂–LaSrMnO₃ (supplied by courtesy of Dr. T. Mori of the National Institute of Materials Science), which exhibits a distinct composition variation across the electron transparent sample area. A thin film was prepared for TEM by using an FIB technique. We measured the EDX-HSI using a JEOL 2100F S/TEM operated at 200 kV, equipped with a JEOL EDX silicon drift detector, Dry SD60GV. Figure 9.5 shows the ADF-STEM image and typical counts (spectra) in representative points, corresponding to the two different phases, where the maximum net peak counts per pixel do not exceed 10 counts, and have a typical sparse feature that is suitable for testing the relevance of the proposed method.

Fig. 9.5

ADF-STEM image of LaSrMnO₃-Y doped ZrO₂ ceramic composite sample (a) and typical EDX counts per pixel from framed areas (b)

3.2 Spatial Orthogonal Constraint on STEM-EELS Data

We evaluated the effect of the orthogonal constraint by changing the value of w with a fixed number of components, i.e. SO-NMF. We used the two STEM-EELS-HSI datasets described in Sect. 9.3.1. Because neither the spatial distribution maps nor the spectra in the datasets are sparse, the conventional NMF optimization has multiple local minima. Thus, reaching the global minima (or a good local minimum) is difficult. Our aim in this experiment was to verify that the orthogonal constraint reduces the search space and that SO-NMF generates a reasonable decomposition of NMF.

3.2.1 XSTEM-EELS Data from a Silicon Device

The method was first applied to the dataset from the Si diode sample, as shown in Fig. 9.3 in Sect. 9.3.1. The number of components in SO-NMF was set to K = 3, which is the number of reference components. In the result with w = 0 (no orthogonal constraint: first row in Fig. 9.6), the third spectral components exhibit unnatural intensity decreases at 110 eV, where a sharp peak from the first spectral component is overlaid. This can happen in EELS-HSI under certain conditions [17]. This sudden lowering in intensity disappears when spatial orthogonality (w ≥ 0.01) is included, as seen in Fig. 9.6. Slight cross-talk between the second and third components remains in both the spatial distribution maps and spectra for w = 0.01. The resolved spectral profiles and their spatial distributions are almost the same for w ≥ 0.05, which effectively reproduces the spectra and expected spatial distributions, although the spatial phase separation seems (unnaturally) overly emphasized for w = 1.0.

Fig. 9.6

Results of SO-NMF with various weights of spatial orthogonality constraint for Si-L _2,3 STEM-EELS-HSI data

3.2.2 Atomic Resolution STEM-EELS of Mn₃O₄

Next, we validated the method using the atomic resolution Mn-L _2,3 SI data from the Mn₃O₄ spinel sample (cf. Fig. 9.4 in Sect. 9.3.1). The number of components in SO-NMF was set to K = 3, which is the number of components determined by ARD-SO-NMF in Sect. 9.3.3.3. The SO-NMF results for 0 ≤ w ≤ 1 are shown in Fig. 9.7, with the score images in the first, second, and third columns and the resolved spectral profiles in the fourth column. In the case without spatial orthogonality (w = 0), the resolved spectral profiles are inconsistent with the expected reference profiles (Fig. 9.4c), the peak at around 640 eV of component 2 shifted to the left. Further, component 3 exhibits a physically unnatural intensity drop at the distinct peak positions of component 1, as for the case of no orthogonality (Fig. 9.7, top-right figure). With a small spatial orthogonality (w = 0.01) included, the spectral shapes converged to those consistent with the reference spectra and the additional component localized on the oxygen columns. It can be seen that there is an optimum value of w for reproducing good spectral profiles and plausible spatial distributions. As w increases, the spatial distributions become more orthogonal to each other, whereas the resolved spectral shapes converge to one form. For w ≥ 0.5 the spatial distributions are far from the actual projected structures, even though the resolved spectral shapes are essentially identical.

Fig. 9.7

Results of SO-NMF with various weights of the spatial orthogonality constraint for Mn-L _2,3 STEM-EELS-HSI data

We subsequently focus on the additional third component, the spatial distribution of which was found to be localized on the projected oxygen atom positions. This localization was attributed to the electron channeling effect [25], which is responsible for propagating the incident electron wave function along the neighboring Mn columns for a sample exceeding a certain thickness when the electron probe is placed on the oxygen column. The resolved spectrum of the third component actually exhibits a spectral profile characteristic of the weighted average of the other two components, because each oxygen atom is coordinated with trivalent Mn_Oct and divalent Mn_Tet atoms.

3.3 Results of Optimizing the Number of Components by ARD-NMF

3.3.1 STEM-EDX Data

To examine whether ARD can select the correct number of components, our ARD-NMF (i.e. without the orthogonal constraint imposed, w = 0) was applied to the STEM-EDX-HSI data of a Y-doped ZrO₂(YSZ)–LaSrMnO₃(LSM) ceramic composite material. The conventional elemental distributions are shown in Fig. 9.8 for reference purposes. Starting with 10 components, only two survived after the optimization algorithm terminated, as shown in Fig. 9.9. The distribution of each identified component shown in Fig. 9.9a is consistent with the elemental distributions of: (1) the union of La, Mn, and Sr and (2) the union of Zr and Y in Figs. 9.5 and 9.8. The identified spectra shown in Fig. 9.9c consist of sets of peaks, each reflecting the correct composition of YSZ or LSM in Fig. 9.5. This indicates that our ARD-NMF identified the constituent phases correctly for this STEM-EDX data.

Fig. 9.8

EDX elemental maps of LaSrMnO₃-Y-doped ZrO₂ ceramic composite sample

Fig. 9.9

Result of ARD-NMF for STEM-EDX-HSI data

These results indicate that the present method effectively removed the statistical noise in the resolved spectra (Fig. 9.9c), and the score images (Fig. 9.9a) exhibit no artificial mixing of the two spectral components. Note that a 10-nm layer of LSM (Fig. 9.9a: Comp.#1) covers the YSZ substrate surface; this can be seen more clearly here than in the elemental maps.

3.3.2 XSTEM-EELS Data from a Silicon Device

We then applied both ARD-NMF and ARD-SO-NMF with K = 10 to the EELS-HSI data of Si-L _2,3 energy-loss near edge structure (ELNES) obtained from a cross-sectional Si diode sample. The reference component spectra (Fig. 9.3c) are not sparse, that is, nonzero values range over the energy-loss axis. We compared the results of ARD-NMF with those from ARD-SO-NMF to verify that the orthogonal constraint produces a clearer decomposition for non-sparse data. The results are shown in Figs. 9.10 and 9.11.

Fig. 9.10

Result of ARF-NMF (w = 0) for Si-L _2,3 STEM-EELS-HSI data from silicon diode sample

Fig. 9.11

Result of ARF-SO-NMF (w = 0.01) for Si-L _2,3 STEM-EELS-HSI data from silicon diode sample

Figure 9.10b shows that ARD-NMF selected four components whereas the reference contains three. In Fig. 9.10a, the generated component distribution of components 1 and 3 exhibit extensive overlap, whereas the actual spectra of these components are not overlapped, as also seen in the case of w = 0 in Fig. 9.6. This result was attributed to a property of basic NMF, which induces a sparse decomposition on both spatial and spectra matrices.

The ARD-SO-NMF results (with w = 0.1) are shown in Fig. 9.11b. Figure 9.11c shows that the identified spectra are consistent with the reference spectra shown in Fig. 9.3c. The spatial distributions of components obtained by ARD-SO-NMF (Fig. 9.11a) are clearly separated, whereas those resulting from ARD-NMF (Fig. 9.10a) overlap extensively. This difference demonstrates the effect of the orthogonal constraint. In this case, ARD-SO-NMF selected three components and their spectra are consistent with their reference spectra, whereas the spectra by ARD-NMF (w = 0) display unnatural reductions in intensity. Thus, these results suggest that the method can effectively detect subtle spectral differences by introducing the orthogonal constraint.

3.3.3 Atomic Resolution STEM-EELS of Mn₃O₄

The ARD-NMF technique was also applied to the experimental atomic resolution Mn-L _2,3 SI data from the Mn₃O₄ spinel sample. Figures 9.12a–c show the ARD-NMF results with K = 10. As shown in Fig. 9.12b, ARD-NMF selected three components and eliminated the other seven components during the optimization. Thus, ARD-NMF detected an additional component other than those related to the two Mn sites, as discussed in Sect. 9.3.2.2. The spatial distributions of the resolved components shown in Fig. 9.12a and c are basically consistent with the projected Mn_Oct and a Mn_Tet atom positions in Figs. 9.4b and 9.4c, respectively, the relative chemical shifts of which are also consistent with their valence states. However, the boundary between the components is less clear because of the delocalization of the chemical bonding states, and the resolved spectral profiles (Fig. 9.12c) are inconsistent with the expected theoretical profiles, with component 2 exhibiting physically unnatural intensity decreases at the distinct peak positions of component 1. Because an ARD prior induces sparseness, this problem often occurs when ARD-NMF is applied to EELS in which different spectral profiles largely overlap.

Fig. 9.12

Result of ARF-NMF (w = 0) for Mn-L _2,3 STEM-EELS-HSI data from Mn₃O₄

We overcame this problem by applying ARD-SO-NMF with w = 0.01. Figure 9.13a demonstrates that, because of the orthogonal condition, the components are separated more clearly. Especially, overlaps between the first component and the others are resolved with greater clarity, as shown in Fig. 9.13a, and detection of the third component was improved.

Fig. 9.13

Result of ARF-SO = NMF (w = 0.01) for Mn-L _2,3 STEM-EELS-HSI data from Mn₃O₄

4 Discussion

The ARD-SO-NMF and ARD-NMF algorithms proposed in this study were able to optimize the number of spectral components for both the EDX and EELS datasets. An additional orthogonal constraint was required when neither the spatial distribution nor the spectra were sparse. Such a constraint is offered by the proposed ARD-SO-NMF. Our NMF realistically extracts spectral components from the EELS-HSI data when the spatial orthogonality penalty is appropriate, implying that different spectral features are spatially well separated.

Because of the differing complexities intrinsic to EELS and EDX spectra, NMF processes these datasets differently. An EDX spectrum can be characterized by a set of Gaussian-like peaks, generally separated in energy, whereas an elemental core EELS includes various spectral components overlapped in the same energy range, where the corresponding electronic energy levels in solids are approximately continuously distributed. Furthermore, the spectral components of EDX are mostly sparse and orthogonal along the energy axis, contrary to those in EELS. NMF with only an error function as the objective function prefers the orthogonal basis spectra in the energy axis because of their completeness. On the other hand, NMF with spatial orthogonality models the practical situation, in which an EELS-HSI dataset is assumed to be more orthogonal in space than in energy, more accurately.

There are several local minima in the likelihood functions. The type of NMF algorithm appears to eventually achieve a more appropriate minimum, although it is not mathematically possible to prove the dependence. Moreover, because of the computational cost, it is difficult to obtain all of the local minima, even when we apply the spatial orthogonality constraint and sparse priors for the ARD effect, i.e. by using a small value of K, in the data matrix. The present NMF method is capable of minimizing and extracting the objective function of particular solutions by systematically varying the weight of the spatial orthogonality in the object function. In both of the EELS examples presented herein, an increase in w caused the resolved components to be distributed more widely over the sample space and their spectral shapes to become less sparse (or orthogonal). This change in spectral shape, which is prone to be sparse under the basic NMF, is clearly resolved and exhibits the composition more accurately when the orthogonal constraint is applied. Hence, the proposed NMF can identify chemical states from the resolved spectra more accurately than existing methods that do not use spatial orthogonality. In the case of the atomic resolution HSI of Mn₃O₄, the method resulted in physically meaningless solutions when we overestimated the spatial orthogonality. In general, we can reach solutions that are physically more realistic/interpretable, comparable to the theoretical spectra predicted by first principles calculations or reference experimental spectra, by changing the value of w systematically and understanding the extent to which the spectral shapes and spatial distributions of the resolved components vary. This scheme seems much more effective and pragmatic than estimating the solution bounds by repeating the decomposition routines with many different initial random numbers in the loading or score matrices.

In this respect the proposed SO constraint may fail when the spatial distributions of the component states strongly overlap with each other. Spiegelberg et al. proposed an alternative scheme to extract nonnegative source signals of strongly mixed data [33], instead of imposing the present SO constraint. By randomly drawing samples from the space of positive spectra in the signal subspace spanned by the prominent principal components, a sampled dataset of which the spectral components can be conveniently extracted using, e.g., VCA or NMF, is obtained with a large probability. These components typically correspond well to the pure spectra of the original data assuming that the spectral components are orthogonal to each other in at least one channel.

Existing processing schemes can produce controversial results should the spectral background be subtracted in advance before the statistical processing, and this probably depends on the type of spectral data being processed. Although background subtraction is generally considered to lose important spectral information, we believe background subtraction to be necessary in the present framework because our NMF assumes that no background structure is incorporated. As demonstrated in the supplementary material in a previous paper [26], our proposed NMF was unable to provide the expected correct results for STEM-EELS SI without background subtraction, which thus presents further work for the future, i.e. incorporating a background structure in our model.

5 Summary

We proposed a new multivariate curve resolution method based on NMF with two penalty terms: (i) a soft orthogonal constraint to effectively resolve overlapping spectra, and (ii) an ARD prior to optimize the number of components. Validations using experimental STEM-EDX/EELS SI data demonstrated that the ARD prior successfully resolved the correct number of physically interpretable spectral components. The soft orthogonal constraint was effective for STEM-EELS HSI data that were neither sparse in the spatial nor the spectral regions. The proposed SO-NMF and ARD-SO-NMF schemes can successfully resolve physically meaningful components by reducing the search space for low-rank matrices, even in cases where conventional NMF is unable to correctly resolve the components. These advantages reduce the costs of HSI data analysis and of extracting hidden spectral information from experimental data using objective and statistical measures rather than empirical knowledge. The proposed method is applicable to any type of HSI dataset, such as that generated by Raman spectroscopy, infrared absorption, and time-of-flight mass spectroscopy. Future prospects would include investigating the ability of the present ARD-NMF scheme to correctly detect small amounts of significant phases.