Skip to main content
SpringerLink
Log in

Quantum from Principles

  • Chapter
  • First Online:
Quantum Theory: Informational Foundations and Foils

Part of the book series: Fundamental Theories of Physics ((FTPH,volume 181))

Abstract

Quantum theory was discovered in an adventurous way, under the urge to solve puzzles—like the spectrum of the blackbody radiation—that haunted the physics community at the beginning of the 20th century. It soon became clear, though, that quantum theory was not just a theory of specific physical systems, but rather a new language of universal applicability. Can this language be reconstructed from first principles? Can we arrive at it from logical reasoning, instead of ad hoc guesswork? A positive answer was provided in Phys Rev A, 81:062348, 2010 [34], Phys Rev A, 84:012311, 2011 [26], where we put forward six principles that identify quantum theory uniquely in a broad class of theories. We first defined a class of “theories of information”, constructed as extensions of probability theory in which events can be connected into networks. In this framework, we formulated the six principles as rules governing the control and the accessibility of information. Directly from these rules, we reconstructed a number of quantum information features, and eventually, the whole Hilbert space framework. In short, our principles characterize quantum theory as the theory of information that allows for maximal control of randomness.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 119.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 159.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 159.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    This was also the title of one influential conference, held in May 2000 at the Université de Montréal [22], which kickstarted the new wave of quantum axiomatizations.

  2. 2.

    More precisely, “nothing that the theory cares to describe”.

  3. 3.

    Per se, the mathematical formalism does not force us to interpret the order of sequential composition as an order in time. Nevertheless, composition in time is the reference situation that we will have in mind when phrasing our axioms.

  4. 4.

    Note that the summation is well-defined thanks to the vector space structure of \(\mathsf {Transf}_{\mathbb R}(\mathrm {A}\rightarrow \mathrm{B})\).

  5. 5.

    In previous works, we used different names for transformations that do not allow for side information: in Refs. [26, 34] they were called atomic, while in the popularized version of Ref. [49] they were called fine-grained. We apologize with our readers for the changes of terminology, due to an ongoing search for the word that best captures this operational concept. In this chapter, we adopted the word pure, because (i) this term is the standard one in the case of states and (ii) using the same term for transformations should hopefully ease the reading. Still, a warning is in order: when the set of transformations \(\mathsf {Transf}(\mathrm {A}\rightarrow \mathrm{B})\) is convex, the pure transformations \(\mathsf {Pur}\mathsf {Transf}(\mathrm {A}\rightarrow \mathrm{B})\) may not coincide with the extreme points of \(\mathsf {Transf}(\mathrm {A}\rightarrow \mathrm{B})\). For example, in quantum theory the identity effect \( I_\mathrm {A}\) is an extreme point of the set of effects, but is not pure in the sense of our definition because it can be decomposed e.g. as \(I_\mathrm {A}= \sum _{n=1}^{d_\mathrm {A}} \, P_n\), where the effects \( \{P_n = |n\rangle \langle n|~|~ n=1,\dots , \, d_\mathrm {A}\}\) represent a projective measurement on some orthonormal basis \(\{ |n\rangle ~|~ n= 1,\dots \, , d_\mathrm {A}\}\).

  6. 6.

    Note that, in principle, our definition of “internal transformations” may not include all the transformations in the interior of the cone, because the \(\lambda \, \mathcal {F}\) and \(\mathcal {G}\) may fail to coexist in a test. However, this annoying discrepancy disappears under the mild assumption that the set of transformations is convex. Later, we will justify this assumption on the basis of the Causality axiom.

  7. 7.

    It turns out that the second condition is automatically satisfied if the theory satisfies the Causality axiom—see the next section.

  8. 8.

    We differentiate the names in order to highlight the different roles of these principles in our reconstruction. Mathematically, there is no difference between axioms, postulates, background assumptions, and requirements in the OPT framework (all of them are “axioms”). The point of using different names is just to provide a more intuitive picture.

  9. 9.

    Recall that we are assuming that the state spaces are finite-dimensional.

  10. 10.

    The expression is due to John Smolin, see e.g. the lecture notes [58].

  11. 11.

    It is worth stressing that Schrödinger’s paper was not just about the existence of entangled states, but also about how entanglement interacted with the reversible dynamics and with the process of measurement (cf. the notion of steering, which made its first appearance in the very same paper).

  12. 12.

    We recall that a face of a convex set C is a convex subset \(F\subseteq C\) satisfying the condition that, for every \(x \in F\), if x is a non-trivial convex combination of \(x_1\) and \(x_2\) with \(x_1,x_2 \in C\), then \(x_1\) and \(x_2\) belong to F.

  13. 13.

    We call an effect of system \(\mathrm {A}\) normalized iff there exists an effect a state \(\rho \) such that \((a|\rho ) =1\).

  14. 14.

    In the original work [26], we also required that projections be pure. However, in the context of our axioms, purity is implied by the two conditions in the present definition. This follows from the fact that i) one can construct a pure projection, and ii) it is possible to prove that projections are unique. A sketch of proof is the following: First, one can prove that for every pure state \(\alpha \in F\) one must have \((\alpha ^\dag | \, \Pi _F = (\alpha ^\dag |\) (this follows from the definition and from Proposition 14). As a consequence, one also has \((a_F | \, \Pi _F = (a_F|\). This implies that, for every state \(\rho \in \mathsf {St}(\mathrm {A})\), the unnormalized state \(\Pi _F \, | \rho )\) is proportional to a state in F. Now, for two projections \(\Pi _F\) and \(\Pi _F'\) one must have

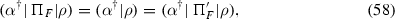
    figure a

    for every pure state \(\alpha \in F\). Since the states \(\Pi _F\, |\rho )\) and \(\Pi _F' \, |\rho )\) are proportional to states in F and \(\alpha \in F\) is a generic pure state, Ideal Compression implies \(\Pi _F\, |\rho ) = \Pi _F' \, |\rho )\), or equivalently, \(\Pi _F = \Pi _F'\), because the state \(\rho \) is generic.

  15. 15.

    In general, the dimension of the convex set \(C_\mathrm {A}\) is given by \(D_\mathrm {A}-1\).

References

  1. A. Einstein, B. Podolsky, N. Rosen, Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935). doi:10.1103/PhysRev.47.777

    Article  ADS  MATH  Google Scholar 

  2. E. Schrödinger, Discussion of probability relations between separated systems, in Mathematical Proceedings of the Cambridge Philosophical Society, vol. 31 (Cambridge University Press, Cambridge, 1935), pp. 555–563

    Google Scholar 

  3. G. Birkhoff, J.V. Neumann, The logic of quantum mechanics. Ann. Math. 37(4), 823–843 (1936). http://www.jstor.org/stable/1968621

    Google Scholar 

  4. G.W. Mackey, Quantum mechanics and Hilbert space. Am. Math. Mon. 64, 45–57 (1957)

    Article  MathSciNet  MATH  Google Scholar 

  5. G. Ludwig, Versuch einer axiomatischen grundlegung der quantenmechanik und allgemeinerer physikalischer theorien. Zeitschrift für Physik 181(3), 233–260 (1964)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. C. Piron, Axiomatique quantique. Helvetica Physica Acta 37(4–5), 439 (1964)

    MathSciNet  MATH  Google Scholar 

  7. J. Jauch, C. Piron, On the structure of quantal proposition systems, in The Logico-Algebraic Approach to Quantum Mechanics (Springer, Berlin, 1975), pp. 427–436

    Google Scholar 

  8. E.G. Beltrametti, G. Cassinelli, The Logic of Quantum Mechanics, vol. 15 (Cambridge University Press, Cambridge, 2010)

    MATH  Google Scholar 

  9. B. Coecke, D. Moore, A. Wilce, Current Research in Operational Quantum Logic: Algebras, Categories, Languages, vol. 111 (Springer, Berlin, 2000)

    Google Scholar 

  10. Quantum logic, http://en.wikipedia.org/wiki/Quantum_logic. Accessed: 2015-04-30

  11. C.H. Bennett, G. Brassard, Quantum cryptography: public key distribution and coin tossing, in Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (1984), pp. 175–179

    Google Scholar 

  12. A.K. Ekert, Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67(6), 661 (1991)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. P.W. Shor, Algorithms for quantum computation: discrete logarithms and factoring, in IEEE 35th Annual Symposium on Foundations of Computer Science, 1994 Proceedings (1994), pp. 124–134

    Google Scholar 

  14. L.K. Grover, A fast quantum mechanical algorithm for database search, in Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing, STOC’96 (ACM, New York, 1996), pp. 212–219. doi:10.1145/237814.237866

  15. W. Wootters, W. Zurek, A single quantum cannot be cloned. Nature 299(5886), 802–803 (1982)

    Article  ADS  Google Scholar 

  16. D. Dieks, Communication by EPR devices. Phys. Lett. A 92(6), 271–272 (1982)

    Article  ADS  Google Scholar 

  17. C.H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W.K. Wootters, Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70(13), 1895 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. C.H. Bennett, S.J. Wiesner, Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 69(20), 2881 (1992)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. C.A. Fuchs, Quantum mechanics as quantum information, mostly. J. Mod. Opt. 50(6–7), 987–1023 (2003)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. G. Brassard, Is information the key? Nat. Phys. 1(1), 2–4 (2005)

    Article  Google Scholar 

  21. C.A. Fuchs et al., Quantum foundations in the light of quantum information. NATO Sci. Ser. Sub Ser. III Comput. Syst. Sci. 182, 38–82 (2001)

    Google Scholar 

  22. C.A. Fuchs (ed.), Coming of Age With Quantum Information (Cambridge University Press, Cambridge, 2011)

    Google Scholar 

  23. L. Hardy, Quantum theory from five reasonable axioms, arXiv preprint arXiv:quant-ph/0101012

  24. G.M. D’Ariano, How to derive the Hilbert-space formulation of quantum mechanics from purely operational axioms. AIP Conf. Proc. 844, 101 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. G.M. D’Ariano, Probabilistic theories: what is special about quantum mechanics, in Philosophy of Quantum Information and Entanglement, ed. by A. Bokulich, G. Jaeger (Cambridge University Press, Cambridge, 2010), pp. 85–126. doi:10.1017/CBO9780511676550.007

    Chapter  Google Scholar 

  26. G. Chiribella, G.M. D’Ariano, P. Perinotti, Informational derivation of quantum theory. Phys. Rev. A 84, 012311 (2011). doi:10.1103/PhysRevA.84.012311

    Article  ADS  Google Scholar 

  27. L. Hardy, Reformulating and reconstructing quantum theory, arXiv:1104.2066

  28. L. Masanes, M.P. Müller, A derivation of quantum theory from physical requirements. New J. Phys. 13(6), 063001 (2011)

    Article  ADS  Google Scholar 

  29. B. Dakic, C. Brukner, Quantum theory and beyond: is entanglement special?, in Deep Beauty: Understanding the Quantum World Through Mathematical Innovation, ed. by H. Halvorson (Cambridge University Press, Cambridge, 2011), pp. 365–392

    Chapter  Google Scholar 

  30. P. Goyal, K.H. Knuth, J. Skilling, Origin of complex quantum amplitudes and Feynman’s rules. Phys. Rev. A 81, 022109 (2010). doi:10.1103/PhysRevA.81.022109

    Article  ADS  Google Scholar 

  31. L. Masanes, M.P. Müller, R. Augusiak, D. Pérez-García, Existence of an information unit as a postulate of quantum theory. Proc. Natl. Acad. Sci. 110(41), 16373–16377 (2013)

    Article  ADS  Google Scholar 

  32. A. Wilce, Conjugates, correlation and quantum mechanics, arXiv:1206.2897

  33. H. Barnum, M.P. Mueller, C. Ududec, Higher-order interference and single-system postulates characterizing quantum theory, arXiv:1403.4147

  34. G. Chiribella, G.M. D’Ariano, P. Perinotti, Probabilistic theories with purification. Phys. Rev. A 81, 062348 (2010). doi:10.1103/PhysRevA.81.062348

    Article  ADS  Google Scholar 

  35. J. Barrett, Information processing in generalized probabilistic theories. Phys. Rev. A 75, 032304 (2007). doi:10.1103/PhysRevA.75.032304

    Article  ADS  Google Scholar 

  36. H. Barnum, J. Barrett, M. Leifer, A. Wilce, Generalized no-broadcasting theorem. Phys. Rev. Lett. 99(24), 240501 (2007). doi:10.1103/PhysRevLett.99.240501

    Article  ADS  Google Scholar 

  37. H. Barnum, J. Barrett, M. Leifer, A. Wilce, Teleportation in general probabilistic theories, ArXiv e-prints arXiv:0805.3553

  38. L. Hardy, A formalism-local framework for general probabilistic theories, including quantum theory. Math. Struct. Comput. Sci. 23(02), 399–440 (2013). doi:10.1017/S0960129512000163

    Article  MathSciNet  MATH  Google Scholar 

  39. H. Barnum, A. Wilce, Information processing in convex operational theories. Electron. Notes Theor. Comput. Sci. 270(1), 3–15 (2011)

    Article  Google Scholar 

  40. S. Abramsky, B. Coecke, A categorical semantics of quantum protocols, in Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science (IEEE, 2004), pp. 415–425. doi:10.1109/LICS.2004.1319636

  41. S. Abramsky, B. Coecke, Categorical quantum mechanics, in Handbook Of Quantum Logic and Quantum Structures: Quantum Logic, ed. by K. Engesser, D.M. Gabbay, D. Lehmann (Elsevier, 2008), pp. 261–324. doi:10.1016/B978-0-444-52869-8.500141

  42. B. Coecke, A universe of processes and some of its guises, in Deep Beauty: Understanding the Quantum World Through Mathematical Innovation, ed. by H. Halvorson (Cambridge University Press, Cambridge, 2010), pp. 129–186

    Google Scholar 

  43. B. Coecke, É.O. Paquette, Categories for the practising physicist, in New Structures for Physics (Springer, Berlin, 2011), pp. 173–286

    Google Scholar 

  44. S. Mac Lane, Categories for the Working Mathematician, vol. 5 (Springer, Berlin, 1978)

    Book  MATH  Google Scholar 

  45. B. Coecke, Quantum picturalism. Contemp. Phys. 51(1), 59–83 (2010). doi:10.1080/00107510903257624

    Article  ADS  Google Scholar 

  46. P. Selinger, A survey of graphical languages for monoidal categories, in New Structures for Physics. Lecture Notes in Physics, vol. 813, ed. by B. Coecke (2011). doi:10.1007/978-3-642-12821-9_4

    Google Scholar 

  47. G. Chiribella, Dilation of states and processes in operational-probabilistic theories, in Proceedings 11th Workshop on Quantum Physics and Logic, Kyoto, Japan, 4–6th June 2014. Electronic Proceedings in Theoretical Computer Science, vol. 172, ed. by B. Coecke, I. Hasuo, P. Panangaden (Open Publishing Association, 2014), pp. 1–14. doi:10.4204/EPTCS.172.1

    Google Scholar 

  48. R.W. Spekkens, Evidence for the epistemic view of quantum states: a toy theory. Phys. Rev. A 75, 032110 (2007). doi:10.1103/PhysRevA.75.032110

    Article  ADS  Google Scholar 

  49. G. Chiribella, G.M. D’Ariano, P. Perinotti, Quantum theory, namely the pure and reversible theory of information. Entropy 14(10), 1877–1893 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  50. B. Coecke, R. Lal, Causal categories: relativistically interacting processes. Found. Phys. 43(4), 458–501 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  51. B. Coecke, Terminality implies non-signalling, arXiv preprint arXiv:1405.3681

  52. E.C. Stueckelberg, Quantum theory in real Hilbert space. Helv. Phys. Acta 33(727), 458 (1960)

    MathSciNet  MATH  Google Scholar 

  53. H. Araki, On a characterization of the state space of quantum mechanics. Commun. Math. Phys. 75(1), 1–24 (1980)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  54. W.K. Wootters, Local accessibility of quantum states. Complex. Entropy Phys. Inf. 8, 39–46 (1990)

    Google Scholar 

  55. L. Hardy, W.K. Wootters, Limited holism and real-vector-space quantum theory. Found. Phys. 42(3), 454–473 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  56. C. Shannon, A mathematical theory of communication. Bell Syst. Tech. J. 27(3), 379–423 (1948). doi:10.1002/j.1538-7305.1948.tb01338.x

    Article  MathSciNet  MATH  Google Scholar 

  57. B. Schumacher, Quantum coding. Phys. Rev. A 51(4), 2738 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  58. C.H. Bennett, More about entanglement and cryptography (2007) http://www.lancaster.ac.uk/users/esqn/windsor07/Lectures/Bennett2.pdf. Accessed: 2014-11-14

  59. I.M. Gelfand, M.A. Naimark, On the imbedding of normed rings into the ring of operators in Hilbert space. Mat. Sb. 54(2), 197–217 (1943)

    MathSciNet  MATH  Google Scholar 

  60. I.E. Segal, Irreducible representations of operator algebras. Bull. Am. Math. Soc. 53(2), 73–88 (1947). doi:10.1090/S0002-9904-1947-08742-5

    Article  MathSciNet  MATH  Google Scholar 

  61. H. Everett III, Relative state formulation of quantum mechanics. Rev. Mod. Phys. 29(3), 454 (1957)

    Article  ADS  MathSciNet  Google Scholar 

  62. H. Barnum, C.P. Gaebler, A. Wilce, Ensemble steering, weak self-duality, and the structure of probabilistic theories. Found. Phys. 43(12), 1411–1427 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  63. M.-D. Choi, Completely positive linear maps on complex matrices. Linear Algebra Appl. 10(3), 285–290 (1975)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The work is supported by the Templeton Foundation under the project ID# 43796 A Quantum-Digital Universe, by the Foundational Questions Institute through the large grant The fundamental principles of information dynamics (FQXi-RFP3-1325), by the 1000 Youth Fellowship Program of China, and by the National Natural Science Foundation of China through Grants 11450110096 and 11350110207. GC acknowledges the hospitality of the Simons Center for the Theory of Computation and of Perimeter Institute for Theoretical Physics. Research at Perimeter Institute for Theoretical Physics is supported in part by the Government of Canada through NSERC and by the Province of Ontario through MRI.

Author information

Authors and Affiliations

  1. Department of Computer Science, The University of Hong Kong, Pokfulam road, Hong Kong, People’s Republic of China

    Giulio Chiribella

  2. QUIT Group, Dipartimento di Fisica, Università di Pavia, via Bassi 6, 27100, Pavia, Italy

    Giacomo Mauro D’Ariano & Paolo Perinotti

  3. INFN Sezione di Pavia, via Bassi 6, 27100, Pavia, Italy

    Giacomo Mauro D’Ariano & Paolo Perinotti

Authors
  1. Giulio Chiribella
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Giacomo Mauro D’Ariano
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Paolo Perinotti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Giulio Chiribella .

Editor information

Editors and Affiliations

  1. Department of Computer Science, The University of Hong Kong, Hong Kong, China

    Giulio Chiribella

  2. Perimeter Inst Theoretical Physics , Waterloo, Ontario, Canada

    Robert W. Spekkens

Rights and permissions

Reprints and permissions

Copyright information

© 2016 Springer Science+Business Media Dordrecht

About this chapter

Cite this chapter

Chiribella, G., D’Ariano, G.M., Perinotti, P. (2016). Quantum from Principles. In: Chiribella, G., Spekkens, R. (eds) Quantum Theory: Informational Foundations and Foils. Fundamental Theories of Physics, vol 181. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-7303-4_6

Download citation

  • DOI: https://doi.org/10.1007/978-94-017-7303-4_6

  • Published:

  • Publisher Name: Springer, Dordrecht

  • Print ISBN: 978-94-017-7302-7

  • Online ISBN: 978-94-017-7303-4

  • eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)

Publish with us

Policies and ethics

Search

Navigation