Rigorous Simulation-Based Analysis of Linear Hybrid Systems

Abstract

Design analysis of Cyber-Physical Systems (CPS) with complex continuous and discrete behaviors, in-practice, relies heavily on numerical simulations. While useful for evaluation and debugging, such analysis is often incomplete owing to the nondeterminism in the discrete transitions and the uncountability of the continuous space. In this paper, we present a precise notion of simulations for CPS called simulation-equivalent reachability, which includes all the states that can be reached by any simulation. While this notion is weaker than traditional reachability, we present a technique that performs simulation-equivalent reachability in an efficient, scalable, and theoretically sound and complete manner. For achieving this, we describe two improvements, namely invariant constraint propagation for handling invariants and on-demand successor deaggregation for handling discrete transitions. We use our tool implementation of the approach, HyLAA (Hybrid Linear Automata Analyzer), to evaluate the improvements, and demonstrate computing the simulation-equivalent reachable set for a replicated helicopter systems with over 1000 dimensions in about 10 min.

DISTRIBUTION A. Approved for public release; Distribution unlimited. (Approval AFRL PA #88ABW-2016-5197, 18 OCT 2016).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Cyber-Physical Systems (CPS) that involve interaction between a system’s software and the physical world can be naturally modeled using the framework of hybrid automata [4, 29]. A common industrial practice to design and debug these systems is to use a model-based design framework such as Simulink or Modelica, which produces concrete traces of system behavior. An engineer uses a combination of his or her intuition about potential edge cases and sampled simulations to try and find behaviors that violate the safety specification. While performing large numbers of simulations can be extremely useful, the space of possible simulations is often infinite, and so simulations can miss critical error cases. For large and complex models, with high numbers of dimensions, the amount of coverage provided by simulations decreases further, increasing the chances of missing a simulation that violates safety.

In this work, we add rigor to such simulation-based analysis and compute what we call the simulation-equivalent reachable set. To do this, we build upon a recently proposed method [18] that exploits the superposition property of linear systems by combining the information from selected individual simulations to reason about an unbounded number of simulations. We extend this approach to analyze a general linear hybrid system, and provide an analysis method which is exact, with respect to a particular simulation algorithm. Upon termination, if our algorithm infers that the system is safe, then no simulation enters the unsafe set; if our algorithm infers that the system is unsafe, a counter-example trace is provided. One of the main reasons to present an alternative notion of reachability is fundamentally driven by the desire to generate counterexamples which are of high importance during the debugging phase of design analysis. Additionally, while simulation-equivalent reachability is a bit weaker than traditional reachability, the simplifications enable analysis which is more scalable, as well as sound and complete. The contributions of this paper are as follows.

• 1. We formally state the simulation-equivalent reachability problem and provide a sound and complete algorithm for its computation.

• 2. We present two new improvements, first, for reducing the number of constraints in handling invariants, and second, for aggregating and deaggregating sets after discrete transitions, without losing simulation-equivalence.

• 3. We present an accuracy-equivalent comparison with traditional reachability algorithms, and evaluate the proposed techniques in a new tool called HyLAA (Hybrid Linear Automata Analyzer).

Related Approaches: Verification techniques for hybrid automata can be classified into two main categories: flow-pipe construction [13] and deductive verification [24, 31]. Flow-pipe construction methods, which are more closely related to this paper, are typically classified by the complexity allowed by their continuous dynamics. Existing techniques can handle systems where continuous dynamics are restricted to be timers [5, 10], piecewise constants [21, 26], linear [23, 25], and general nonlinear expressions [2, 12]. In this context, our approach fits in with the class of tools used to analyze linear systems. The proposed method differs, however, in that our analysis is sound and complete for simulation-equivalent reachability, and can provide concrete counterexamples if the system violates the safety specification. Systems with complex dynamics are sometimes analyzed using hybridization [6, 14]. In hybridization, complex dynamics are simplified as a hybrid system with simpler dynamics and nondeterministic inputs, where the inputs account for the simplification errors.

Simulations have also been leveraged before to perform more formal analysis of hybrid systems. One approach studies the effects of perturbations of the initial state on the divergence of trajectories [15,16,17, 20]. These approaches are different from the way HyLAA uses simulations, in that they reason about tubes of states around individual simulations. Other falsification methods use a metric to determine how close a particular simulation is to violating a formal specification [19], and then apply a global optimization routine to generate new simulation inputs which try to optimize the metric, essentially trying to generate simulations that are closer to a violation [9, 30]. While often better than purely random Monte Carlo simulation, this class of approaches is incomplete and so may still miss error trajectories.

2 Preliminaries

States and vectors are elements in $\mathbb {R}^n$ are denoted as x and v. Given a sequence $seq = s_1, s_2, \ldots$, the $i^{th}$ element in the sequence is denoted as seq[i]. In this work, we use the following mathematical notation of a linear hybrid automata.

Definition 1

A linear hybrid automaton is defined to be a tuple $\langle {Loc, X, Flow, Inv, Trans, Guard}\rangle$ where:

• Loc is a finite set of locations (also called modes).

• $X \subseteq \mathbb {R}^n$ is the state space of the behaviors.

• Flow: $Loc \rightarrow \textit{AffineDeq}(X)$ assigns an affine differential equation $\dot{x} = A_l x + B_l$ for location l of the hybrid automaton.

• Inv: $Loc \rightarrow 2^{\mathbb {R}^n}$ assigns an invariant set for each location of the hybrid automaton.

• Trans $\subseteq Loc \times Loc$ is the set of discrete transitions.

• Guard: $Trans \rightarrow 2^{\mathbb {R}^n}$ defines the set of states where a discrete transition is enabled. For a linear hybrid automaton, the invariants and guards are given as a conjunction of linear constraints.

The initial set of states $\varTheta$ is a subset of $Loc \times 2^{\mathbb {R}^n}$, where second element in the pair is a conjunction of linear constraints. An initial state $q_0$ is a pair $(Loc_0, x_0)$, such that $x_0 \in X$, and $(Loc_0, x_0) \in \varTheta$. Unsafe states are indicated by having a set of error modes, $U \subseteq Loc$.

Definition 2

Given a hybrid automaton and an initial set of states $\varTheta$, an execution of the hybrid automaton is a sequence of trajectories and actions $\tau _0 a_1 \tau _1 a_2 \ldots$ such that (i) the first state of $\tau _0$ denoted as $q_0$ is in the initial set, i.e., $q_0 = (Loc_0, x_0)\in \varTheta$, (ii) each $\tau _i$ is the solution of the differential equation of the corresponding location $Loc_i$, (iii) all the states in the trajectory $\tau _i$ respect the invariant of the location $Loc_i$, and (iv) the state of the trajectory before each action $a_i$ satisfies $Guard(a_i)$.

The set of states encountered by all executions that conform to the above semantics is called the reachable set. For linear systems, the closed form expression for the trajectories is given as $\tau _i(t) = e^{A_l t}\tau (0) + \int _{0}^{t}e^{A_l (t-\mu )}B_l d\mu$ where $A_l$ and $B_l$ define the affine dynamics of the mode. Instead of computing the reachable set of states, we compute the set of states which can be reached by a fixed simulation algorithm. We now precisely define the semantics for a simulation of hybrid automata that we will use in this paper.

Definition 3

A sequence $\rho _{H}(q_0,h) = q_0, q_1, q_2, \ldots$, where each $q_i = (Loc_i, x_i)$, is a $(q_0, h)$-simulation of the hybrid automaton H with initial set $\varTheta$ if and only if $q_0 \in \varTheta$ and each pair $(q_i, q_{i+1})$ corresponds to either: (i) a continuous trajectory in location $Loc_i$ with $Loc_i=Loc_{i+1}$ such that a trajectory starting from $x_i$ would reach $x_{i+1}$ after exactly h time units with $x_i \in Inv(Loc_i)$, or (ii) a discrete transition from $Loc_i$ to $Loc_{i+1}$ (with $Loc_{i-1} = Loc_i$) where $\exists a \in Trans$ such that $x_i = x_{i+1}$, $x_i \in Guard(a)$ and $x_{i+1} \in Inv(Loc_{i+1})$. Bounded-time variants of these simulations, with time bound T, are called $(q_0, h, T)$-simulations.

For simulations, h is called the step size and T is called time bound. While talking about the continuous or discrete behaviors of simulations, we abuse notation and use $x_i$, the continuous component of the state instead of $q_i$. Notice that the simulation engine given in Definition 3 does not check if the invariant is violated for the entire time interval, but only at a given time instance. Also, the discrete transitions are only enabled at time instances that are multiples of h. To avoid Zeno behaviors, the simulation engine forces that the system should spend at least h time units in each mode. Hence, if two consecutive states $x_i$ and $x_{i+1}$ corresponds to a continuous trajectory of the hybrid automaton, it is not necessary that $x_{i+1} \in Inv(Loc_i)$. If a guard is enabled and the invariant is still true, or if multiple guards are enabled, the simulation engine can make a nondeterministic choice. We call the set of states encountered by all simulations which conform to this definition the simulation-equivalent reachable set.

Condition (ii) in the semantics of simulations permits a discrete transition to be taken even if the invariant condition of the predecessor mode is false. This is necessary to handle the common case where a guard is the complement of an invariant, and a sampled simulation jumps over the guard boundary during a single step. If these types of behaviors are not desired, the guard can be explicitly strengthened with the invariant of the originating mode. For readers familiar with the simulation engines in standard tools like Simulink or Modelica, the defined simulation sequences do not perform special algorithms to isolate zero crossings, and the transitions are not necessarily urgent.

Definition 4

A given simulation $\rho _{H}(q_0,h)$ is said to be safe with respect to an unsafe set of locations U if and only if  $\forall q_i = (Loc_i, x_i) \in \rho _{H}(q_0,h)$, $Loc_i \notin U$. Safety for bounded time simulations are defined similarly.

Definition 5

A hybrid automaton H with initial set $\varTheta$, time bound T, and unsafe set of locations U is said to be safe with respect to its simulations if all simulations starting from $\varTheta$ for bounded time T are safe.

Fig. 1.

Observe that the state reached at time t from $x_0+v_1+v_2$ is identical to $\tau _i(x_0,t)+(\tau _i(x_0+v_1,t)-\tau _i(x_0,t)) +(\tau _i(x_0+v_2,t)-\tau _i(x_0,t))$.

Definition 6

Given any initial state $x_0$, vectors $v_1, \ldots , v_m$ where $v_i \in \mathbb {R}^n$, scalars $\alpha _1, \ldots , \alpha _m$, the trajectories of linear differential equations in a given location $\tau$ always satisfy

$$\tau (x_0 + \Sigma _{i=1}^m \alpha _i v_i, t) = \tau (x_0,t) + \Sigma _{i=1}^m \alpha _i (\tau (x_0 + v_i,t) - \tau (x_0,t)).$$

We exploit the superposition property of linear systems in order to compute the simulation-equivalent reachable set of states for a linear hybrid system. An illustration of the superposition principle for two vectors is shown in Fig. 1. Before describing the algorithm for computing the reachable set, we finally introduce the data structure called a generalized star that is used to represent the reachable set of states.

Definition 7

A generalized star (or simply star) $\varTheta$ is a tuple $\langle {c,V,P}\rangle$ where $c \in \mathbb {R}^n$ is called the center, $V = \{v_1,v_2,\ldots , v_m\}$ is a set of m ($\le n$) vectors in $\mathbb {R}^n$ called the basis vectors, and $P: \mathbb {R}^n \rightarrow \{\top , \bot \}$ is a predicate.

A generalized star $\varTheta$ defines a subset of $\mathbb {R}^n$ as follows.

$$\begin{aligned} \![\![{\varTheta \,}\!]\!]= \{ x\, |\, \exists \bar{\alpha } = [\alpha _1, \ldots , \alpha _m]^T \text{ such } \text{ that } x = c + \Sigma _{i=1}^n \alpha _i v_i \text{ and } P(\bar{\alpha }) = \top \} \end{aligned}$$

Sometimes we will refer to both $\varTheta$ and $[\![{\varTheta \,}\!]\!]$ as $\varTheta$.

In this paper, we consider predicates P which are conjunctions of linear constraints, in order to be able to use linear programming for several key operations on stars such as checking if a point is in a star.

Example 1

Consider a set $\varTheta \subset \mathbb {R}^2$ given as $\varTheta \, \mathop {=}\limits ^{\varDelta }\, \{ (x,y)\,|\, x \in [2,3], y \in [2,3] \}$. The given set $\varTheta$ can be represented as a generalized star in multiple ways. One way of representing the set is given as $\langle {c,V,P}\rangle$ where $c = (2.5, 2.5)$, $V = \{[0,1]^T, [0,1]^T\}$ and $P \,\mathop {=}\limits ^{\varDelta }\, -0.5 \le \alpha _1 \le 0.5 \wedge -0.5 \le \alpha _2 \le 0.5$. That is, the set $\varTheta$ is represented as a star with center (2.5, 2.5) with vectors as the orthonormal vectors in the Cartesian plane and predicate where the components along the basis vectors are restricted by the set $[-0.5, 0.5] \times [-0.5, 0.5]$.

Operations on Generalized Stars: In this paper we restrict our attention to stars with predicates that are conjunctions of linear inequalities. As generalized stars are used to represent the reachable set of states, one has to perform operations such as basis transformation, intersection, and union. For stars with linear predicates, one can perform basis and center transformation by changing the center to another center, the basis vectors to a new basis vector set (with same rank), and perform matrix multiplication.

Given two stars $S_1 \,\mathop {=}\limits ^{\varDelta }\, \langle {c,V,P_1}\rangle$ and $S_2 \,\mathop {=}\limits ^{\varDelta }\, \langle {c,V,P_2}\rangle$ the set intersection of two stars is obtained as $S_{\cap } \,\mathop {=}\limits ^{\varDelta }\, \langle {c,V,P_1 \wedge P_2}\rangle$ and their aggregation as $S_{agg} = \langle {c,V,P_{agg}}\rangle$ where $P_1 \vee P_2 \Rightarrow P_{agg}$. For computing $P_{agg}$ one can choose several template directions, compute the maximum and minimum values along each direction using linear programming.

2.1 Reachable Set Computation for Linear Dynamical Systems Using Simulations

We now outline the algorithm that computes the reachable set of states for continuous dynamics on which we base our approach. Owing to space limitations, we briefly describe the algorithm here, and note that a longer explanation and proof of correctness is available in prior work [18]. At its crux, the algorithm exploits the superposition principle of linear systems and computes the reachable states using a generalized star representation. For an n-dimensional system, this algorithm requires at most $n+1$ simulations.

Given an initial set $\varTheta \,\mathop {=}\limits ^{\varDelta }\, \langle {c, V, P}\rangle$ with $V = \{v_1, v_2, \ldots , v_m\} (m \le n)$, the algorithm performs a simulation starting from c (denoted as $\rho (c, h, k)$), and $\forall 1\le j \le n$, performs a simulation from $c+v_j$ (denoted as $\rho (c+v_j, h, k)$). For a given time instance $i\cdot h$, the reachable set denoted as $Reach_i(\varTheta )$ is defined as $\langle {c_i, V_i, P}\rangle$ where $c_i = \rho (c, h, k)[i]$ and $V_i = \langle {v_1', v_2', \ldots , v_m'}\rangle$ where $\forall 1\le j \le m, v_j' = \rho (c+v_j, h, k)[i] - \rho (c, h, k)[i]$. Notice that the predicate does not change for the reachable set, but only the center and the basis vectors are changed.

Fig. 2.

Illustration of the reachable set using sample simulations and generalized star representation. Notice that in the star representation, the predicate that defines the reachable set is same as that of the initial set.

An illustration of this reachable set computation is shown in Fig. 2. Here, as the system is 2-dimensional, a total number of three simulations are performed, one from center c and one from $c+v_1$ and one from $c+v_2$. The reachable set after time $i\cdot h$ is given as the star with center $c' = \rho (c, h, k)[i]$, basis vectors $v_1' = \rho (c+v_1, h, k)[i] - \rho (c, h, k)[i]$, and $v_2' = \rho (c+v_2, h, k)[i] - \rho (c, h, k)[i]$ and the same predicate P as the given in the initial set.

Remark 1

Observe that the reachable set computation described in Algorithm 1 is not dependent on the predicate of the initial set. Therefore, if the given initial set $\varTheta \,\mathop {=}\limits ^{\varDelta }\, \langle {c, V, P}\rangle$ is changed to $\langle {c, V, P'}\rangle$, the reachable set computed in line 7 changes from $\langle {c_i, V_i, P}\rangle$ to $\langle {c_i, V_i, P'}\rangle$. This key observation helps us in proposing new techniques for handling invariants and discrete transitions.

Assumptions: Since our method for reasoning about states reachable in the continuous space uses numerical simulations and superposition, we make a few key assumptions. First, the numerical computations performed by our algorithm are exact (we do not track floating-point errors through the computations). Second, the underlying ODE simulation engine provides an exact result. We believe that these assumptions are reasonable, because in practice, most of the system designers accept that numerical simulations are a very close approximation to a model’s true behavior, and using numerical simulations requires the same assumptions. A user concerned about the inaccuracy of numerical simulation can either use validated simulations [1] or compute the linear ODE solution as a matrix exponential to an arbitrary degree of precision.

3 Constraint Propagation for Invariants

The goal of this paper is to perform simulation-equivalent reachability for hybrid automata. While Algorithm 1 computes reachable set for a dynamical system, it does not take into account the invariant and the discrete transitions. An earlier extension of Algorithm 1 for hybrid systems propose handling the invariants by performing $Reach_i \,\cap \, Inv(l)$ where Inv(l) is the invariant of the current mode [18].

Fig. 3.

Figure depicting the overapproximation of the reachable set computed by performing $Reach_i \cap Inv(l)$ without invariant propagation.

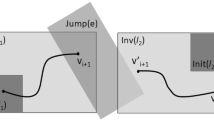
Although sound, such procedure would result in an overapproximation, but not a simulation-equivalent reachable set. Consider the illustration in Fig. 3 depicting reachable sets $Reach_i$ and $Reach_{i+1}$ and their overlap with the invariant of the current mode. If one considers the executions that visit $Reach_i\, \cap \, Inv(l)$, one can only reach the states labeled as $ActualReach_{i+1}(\varTheta )$. To avoid such overapproximations, we present an algorithm that performs constraint propagation for computing the reachable set while respecting the invariant.

We exploit the observation made in Remark 1 for performing constraint propagation. Consider the scenario where $Reach_i$ contains states that satisfy the invariant and states that violate the invariant. For accurately computing the reachable set for all the future iterations, one must only consider the states originating from $Reach_i \,\cap \, Inv(l)$. Given $Reach_i = \langle {c_i, V_i, P}\rangle$, we perform center and basis transformation on Inv(l) to represent it as a star with center $c_i$ and basis $V_i$ such that $Inv(l) = \langle {c_i, V_i, Q_i}\rangle$. Hence, $Reach_i \cap Inv(l) = \langle {c_i, V_i,P \wedge Q_i}\rangle$. From the correctness of Algorithm 1, it follows that the simulations reaching $\langle {c_i, V_i, P \wedge Q_i}\rangle$ should originate from $\varTheta '\subseteq \varTheta$ where $\varTheta ' = \langle {c, V, P \wedge Q_i}\rangle$.

For the time instances $j > i$, since the simulations should visit $\langle {c_i, V_i, P \wedge Q_i}\rangle$, they should originate from $\varTheta ' = \langle {c, V, P \wedge Q_i}\rangle$. This implies that the constraints $Q_i$ should be added to the predicate in $Reach_j$. Therefore, for every instance i, we propagate the constraints $Q_i$ for all future time instances. The reachable set at time instance j accumulates the constraints from time instances $0, 1, \ldots , j-1$ and updates the predicate with the conjunction of these constraints. We call this technique as invariant constraint propagation. This procedure is formally presented in Algorithm 2 and its correctness is given in Theorems 2 and 1.

Theorem 1 (Soundness)

Consider initial set $\varTheta \,\mathop {=}\limits ^{\varDelta }\, \langle {c,V,P}\rangle$, time bound $k\cdot h$, invariant Inv, and reachable set computed by Algorithm 2 as $Reach(\varTheta ) = R_0, R_1, \ldots , R_k$. Consider a simulation $x_0, x_1, \ldots , x_j$ where $j \le k$ such that $x_0 \in \varTheta$, and $\forall 0\le i \le j, x_i \in Inv$, then we have $\forall 0 \le i \le j, x_i \in R_i$.

Proof

Consider the initial state $x_0 \in \varTheta \cap Inv$, it automatically follows that $x_0 \in \langle {c_0, V_0, P \wedge Q_0}\rangle$, where $Q_0$ is computed in line 6 in the first iteration of the loop (lines 4–11). Hence, it follows that $\forall i > 0, x_i \in \langle {c_i, V_i, P\wedge Q_0}\rangle$.

Consider $x_i, 0< i \le k$, the $i^{th}$ state in the simulation that respects invariant. Therefore, we have that $\forall m < i, x_m \in Inv$. Consider $Q_0, Q_1, \ldots , Q_{i-1}$ be the clauses computed in line 6 for the iterations $0,1,\ldots , i-1$ of the loop respectively. Since $\forall m \le i, x_m \in Inv$, if follows that $x_m \in \langle {c_m, V_m, P \wedge Q_m}\rangle$. Therefore, the simulation should originate in $\langle {c, V, P \wedge Q_0 \wedge Q_1 \wedge \ldots \wedge Q_i}\rangle$. Hence, $x_i \in \langle {c_i, V_i, P \wedge Q_0\wedge Q_1 \wedge \ldots \wedge Q_i}\rangle$. Therefore, $x_i \in R_i$.

Theorem 2 (Completeness)

Given an initial set $\varTheta \,\mathop {=}\limits ^{\varDelta }\, \langle {c, V, P}\rangle$, dynamics A, B, time bound $k\cdot h$, invariant Inv, and the reachable set computed as $Reach(\varTheta ) = R_0, R_1, \ldots , R_k$ by Algorithm 2, we have $\forall 0 \le j \le k$, given any $x_j \in R_j$, the simulation $x_0, x_1, \ldots , x_j$ that reaches $x_j$ is such that $x_0 \in \varTheta$ and $\forall 0\le i \le j, x_i \in Inv$.

Proof

Consider the reachable set $Reach(\varTheta ) = R_0, R_1, \ldots , R_k$ computed by Algorithm 2 and an element $x_j \in R_j$. Consider the simulation $x_0, x_1, \ldots , x_j$ be a simulation that reaches $x_j$. Let $Q_0, Q_1, \ldots , Q_j$ represents the constraints computed in line 6 for the iterations $0, 1, \ldots , j$ of the loop from lines 4–11 respectively. Since $x_j \in R_j \,\mathop {=}\limits ^{\varDelta }\, \langle {c_j, V_j, P \wedge Q_0 \wedge Q_1 \wedge \ldots \wedge Q_j}\rangle$, it follows that the simulation should origin from $\varTheta ' = \langle {c, V, P \wedge Q_0 \wedge Q_1 \wedge \ldots \wedge Q_j}\rangle$. This simulation therefore respects the invariant at time instances $m \le j$ as $\varTheta ' \subseteq \langle {c, V, P \wedge Q_m}\rangle$. Therefore the simulation $x_0, x_1, \ldots , x_j$ is indeed a valid simulation.

Discussion: Theorems 2 and 1 establish that the reachable set returned by Algorithm 2 only contains all the states that are reachable by a simulation that respects the invariant. One potential drawback of the constraint propagation is that the number of clauses can increase linearly with the number of steps in the simulation. We mitigate this by performing three optimizations. First, we do not add any constraints if $Reach_i \subseteq Inv(l)$ because in such instances $P \Rightarrow Q_i$. Second, a constraint $Q_i$ is added to the list of constraints only if it is strictly stronger than the existing constraints. Formally, $Q_i$ is added if and only if $\lnot (P \wedge Q_0 \wedge Q_1 \wedge \ldots \wedge Q_{i-1} \Rightarrow Q_i)$. Third, we remove the redundant constraints, i.e., a constraint $Q_j$ is dropped from the list if $(P \bigwedge _{i=1 \ldots k}^{i \ne j}Q_i) \Rightarrow Q_j$. In practice, we observe that these optimizations drastically reduce the number of constraints to an almost constant.

4 Discrete Transitions and Reachable Set Computation

In this section, we discuss computing the simulation-equivalent reachable set for a given hybrid automaton across discrete transitions.

4.1 Guards

Algorithm 3, which computes the set of states obtained after a discrete transition takes an input the set of reachable states computed by Algorithm 1 (which does not take into account the invariant), and the list of constraints that needed to be added to predicates for respecting the invariants ${ ConstraintsList}$ computed by Algorithm 2. The algorithm for checking discrete transition does not consider the first element $R_0$ in the sequence $R_0, R_1, \ldots , R_k$. This is because the simulations generated enforce that at least a minimum time h is spent in each mode of the hybrid automaton. Given $1 \le i \le k$, the set of state in $R_i$ that can be reached by simulations that respect the invariants for time instances $0, 1, \ldots , i-1$ is computed by adding the constraints $Q_0, Q_1, \ldots , Q_{i-1}$ to the predicate. This new set is assigned as $R_i'$ in line 5. Notice that the number of constraints added for $R_i$ does not include $Q_i$. This is because the discrete transition can be taken even when the state does not satisfy the invariant of the current location. The correctness of Algorithm 3 is given in Theorem 3

Theorem 3 (Correctness)

Given a reachable set $R = R_0, R_1, \ldots , R_k$ from initial set $\varTheta$ computed by Algorithm 1, and the list of constraints $Q_0, Q_1, \ldots , Q_k$ computed by Algorithm 2, the following statements about ${ NextReach}$ returned by Algorithm 3 are true.

• 1. $\forall S\in { NextReach}, \forall x \in S$, $\exists \rho = x_0, x_1, \ldots , x_m, x$ such that $x_0 \in \varTheta$ and $\rho$ is a valid simulation.

• 2. For any valid simulation $\rho = x_0, x_1, \ldots , x_{m}, x_{m+1}$ starting from $\varTheta$, such that $\forall 0 \le i \le m, x_i \in Inv$, and $x_{m+1} \in G_a$, $\exists R \in { NextReach}$ such that $x_{m+1} \in R$.

Proof

Consider $S \in { NextReach}$ and $x \in S$, we have that $\exists R_0, R_1, \ldots , R_m, R_{m+1}$ and constraints $Q_0, Q_1, \ldots , Q_{m+1}$ such that $S = \langle c_{m+1}, V_{m+1}, P \wedge Q_0 \wedge \ldots \wedge Q_{m}\rangle$. Therefore, it follows that $x \in \langle {c_{m+1}, V_{m+1}, P \wedge Q_0 \wedge \ldots \wedge Q_{m}}\rangle$, therefore, there exists a simulation $x_0, \ldots , x_m, x$ such that $0\le i \le m, x_i \in Inv$. and $x_0 \in \varTheta$.

Next, consider a simulation $\rho = x_0, x_1, \ldots , x_m, x_{m+1}$, where $\forall 0\le i \le m, x_i \in Inv$, $x_{m+1}\in G_a$ for some a, it follows that $x_i \in \langle {c_i, V_i, P \wedge Q_0 \wedge \ldots \wedge Q_i }\rangle$. Hence $x_{m+1} \in \langle {c_{m+1}, V_{m+1}, P \wedge Q_0 \wedge \ldots \wedge Q_m }\rangle$. From Algorithm 3, it follows that $\langle {c_{m+1}, V_{m+1}, P \wedge Q_0 \wedge \ldots \wedge Q_m }\rangle \in { NextReach}$. Therefore $\exists R \in { NextReach}$ such that $x_{m+1} \in R$.

4.2 Algorithm for Computing Simulation-Equivalent Reachable Set

Algorithm 4 that computes the simulation-equivalent reachable set for hybrid automata uses Algorithms 2 and 3 as sub-routines for handling invariants and discrete transitions respectively. The set of initial states for each mode are stored in the queue called ${ queueStars}$. The algorithm first computes the reachable set using $n+1$ simulations by calling $\mathsf{SimulationsReachableSet}$ (Algorithm 1). Next, calling the $\mathsf{InvariantTrimming}$ procedure (Algorithm 2) uses the invariant of the mode to return the set of states that respect the invariant ($R'$) and the corresponding list of constraints for each set in the sequence (${ ConstraintsList}$). The call to $\mathsf{discreteTrans}$ then produces the initial states for the next mode, which get added to ${ queueStars}$. The correctness of Algorithm 4 follows from the correctness of Algorithms 2 and 3.

4.3 Aggregation and Deaggregation

A component of many flow-pipe construction methods is the aggregation of states that result from a discrete transition. This is often necessary because multiple regions in the reachable set have the guard enabled resulting in several regions being added to the ${ nextRegions}$ queue. Over multiple discrete transitions, this can cause an exponential blowup in the number of states in ${ queueStars}$.

The drawback of aggregation is that it introduces conservativeness in the reachability analysis. In general, a single convex set cannot exactly capture the union of two or more convex sets, so an overapproximation of the union is the only sound option. If the reachable set from an aggregated star reaches an unsafe mode, the user cannot discern whether this is because of overapproximation due to aggregation or if it corresponds to an unsafe simulation of the system.

For this reason, we propose a new aggregation and deaggregation approach. By default, we aggregate all the stars that make a discrete transition into to the same mode as $S_{agg}$ and compute the reachable set of $S_{agg}$. If $S_{agg}$ reaches a state when a guard is enabled, we deaggregate the star by splitting it into two stars. If $S_{agg}$ is an aggregation of $S_1, S_2, \ldots S_w$, then the two new stars are aggregations of $S_1, \ldots , S_{w/2}$ and of $S_{w/2 +1}, \ldots , S_w$ respectively. This process can repeat recursively if the new stars intersect the guard.

If $m\cdot h$ time units have elapsed before $S_{agg}$ reaches a guard, the component stars skip the first m steps in the reachable set computation and checking for discrete transitions. This is because if $S_{agg}$ did not reach any guard until m steps, then its component stars also did not reach any guard. However, one has to propagate the constraints from the invariants for all the deaggregated stars. This approach ensures that whenever a discrete transition is taken, there exists an unaggregated star for which the discrete transition is enabled. Therefore, if an unsafe mode is reached, there exists a simulation trace of the system that starts from initial set and reaches the unsafe mode, thus maintaining simulation-equivalence.

5 Implementation and Evaluation

The proposed simulation-equivalent algorithm has been implemented in a tool named HyLAA that is mostly written in Python, although computational libraries are used which may be written in other languages. Simulations are performed using scipy’s odeint function, which can handle stiff and non-stiff differential equations using the FORTRAN library odepack’s lsoda solver. Linear programming is performed using the GLPK library, and matrix operations are performed using numpy. HyLAA can produce static visualizations of the reachable set and live animations during the reachable set computation (that can be exported as videos) using matplotlib. The following experiments were performed using the model generation capability within the Hyst [7] tool, and hypy [8] was used to script together the the model generation with the tool execution. The measurements were performed using a 2.30 GHz Intel i5-5300U CPU with 16 GB RAM.

5.1 Scalability

We performed scalability measurement on a replicated version of the helicopter benchmark available on SpaceEx website¹. This model consists of a 28 dimensional helicopter plus controller system, along with a time dimension. We used the x8_over_time_large variant of the benchmark, considering the same initial states, step size, and time bound.

Fig. 4.

Plots of $x_8$ over time for the helicopter system show the selected accuracy settings result in similar plots. This remained true for replicated variants.

Fig. 5.

The runtime for the $n+1$ simulation continuous-post operation in HyLAA is generally faster than SpaceEx’s supp and stc methods.

We emphasize that we tried to explicitly control for the accuracy of the result in the comparison, which is not straightforward as different approaches use different parameters. From a preliminary analysis, we observed the $x_8$ variable always stays below 0.45, so we used this as a metric for accuracy. By adding a transition to unsafe mode if $x_8 \ge 0.45$, we tuned tool parameters until the condition was on the verge of being violated. For SpaceEx [23], we found that a flowpipe-tolerance of 0.0304 was safe for the stc scenario [22], whereas 0.5222 was safe for the supp scenario [28]. Furthermore, increasing these parameters by 0.0001 would cause forbidden error states to be reached. We also attempted to use Flow*’s [12] linear ODE mode, although failed to find a set of parameters for which the accuracy condition was satisfied. For HyLAA, we used the default simulation parameters used by odeint, absolute tolerance and relative tolerance of $1.49 \cdot 10^{-8}$, and no error states were reached. Then, for the actual runtime measurements, we removed the error states while keeping each tool’s accuracy parameters. This results in a plot of the reachable set of states that is qualitatively similar, as shown in Fig. 4.

We replicated the 28-dimensional helicopter multiple times within the same model, and measured the runtime of the reachability computation. The results are shown in Fig. 5. The simulation-equivalent approach outperforms the two SpaceEx scenarios on this model, and is capable of analyzing a 449 dimensional system (16 replicated helicopters plus time) in under a minute, and a system with 1009 dimensions (36 helicopters) in about 10 min. It is important to be aware that SpaceEx’s analysis is a guaranteed overapproximation (subject to floating-point error), whereas HyLAA’s correctness is subject to the accuracy of the underlying simulations, and only reasons about states at exact multiples of the time step.

5.2 Invariant Constraint Propagation

We next provide a simple evaluation of the importance of invariant constraint propagation as well as our proposed optimization. Consider a 2-D harmonic oscillator, a single-mode system with $\dot{x} = y$ and $\dot{y} = -x$. Trajectories of this system rotate clockwise around the origin. The initial set of states are $x \in [-6, -5]$ and $y \in [0, 0.1]$, and the invariant is $0 \le y \le 5.1$.

This system is designed so that most of the trajectories actually get trimmed away because of the invariant. Reachability analysis of this system was performed using SpaceEx’s stc scenario, Flow*, and HyLAA, and is shown in Fig. 6. Here, SpaceEx removes states which violate the invariant after computing states reachable by the continuous dynamics, which is sound, but results in an overapproximation. Flow* uses domain contraction of Taylor models [12] to trim invariant-violating states, and its result appears correct. HyLAA performs invariant constraint propagation, and also produces a correct result. The table shows the number of constraints in the final star when using HyLAA, with and without the invariant constraint trimming optimization.

Fig. 6.

The harmonic oscillator system with invariant $0 \le y \le 5.1$ demonstrates the benefit of invariant constraint propagation.

5.3 Successor Deaggregation

We next consider a benchmark which models the effects of backlash on an automotive drivetrain system [3, 27]. This a 7-dimensional linear system, which can be scaled as large as desired by adding additional rotating masses, each of which adds two dimensions to the system. The model has a PID controller and the reference input is changed from $-5$ to 5 at time 0.2. We add a time dimension to generate the reference input, bringing the number of dimensions to $8 + 2 \theta$ where $\theta$ is the number of additional masses. This model was specifically designed to stress guard intersection, and SpaceEx was noted as not being able to finish on smallest version of the benchmark, without shrinking the initial set to $5\%$ of its original size.

Fig. 7.

Projections of $x_3$ versus $x_1$ for the 10-dimensional drivetrain system. While complete aggregation fails to complete for this model, using deaggregation produces a similar plot to the unaggregated method in less time. (Color figure online)

Plots of the reachable set of states are shown in Fig. 7 for $\theta =1$. The system starts in the NegAngle mode (green). After 0.2 s, the reference trajectory changes from $-5$ to 5 (cyan). Then, the system’s trajectories reach the DeadZone mode (orange), and finally end in the PosAngle mode (magenta). Similar to SpaceEx, HyLAA did not complete reachable set computation with full aggregation (without deaggregation). The reason is that aggregation introduces overapproximation error which leads the approach to examine states that are not actually reachable. In this system, the aggregated star introduces new spurious discrete transitions from the DeadZone mode back to the NegAngle mode, leading to additional error when further discrete transitions are taken. Essentially, the computation explores spurious sequences of discrete transitions. The deaggregation method, however, splits aggregated states upon reaching a discrete transition, ensuring that every sequence of modes explored corresponds to a true simulation of the system. The result is closer to the exact unaggregated case, although using less computation time. A video of HyLAA’s visualization of this computation is available online².

To evaluate the effect of the deaggregatation approach, Table 1 shows the runtime as we increased the number of rotating masses. Notice that times can actually go down for some higher-dimensional versions of the benchmark, as the extra rotating masses can cause the generalized star to cross the guard boundary at a more orthogonal angle, reducing the number of stars in the successor mode. For example, in the unaggregated 10-d case, there are 24 successor stars after the second guard, compared with 13 successor stars in the 12-d case. Generally, deaggregation provides improvement over no aggregation, although the benefits are reduced in higher dimensions. This is because in these cases even a small amount of aggregation often causes enough error to reach new locations, resulting in immediate splitting of the aggregated star, which shows the importance of finding good template directions for aggregation [11].

Table 1. Drivetrain benchmark runtimes.

6 Conclusion

In this paper, we introduced the notion of simulation-equivalent reachability analysis, and provided a sound and complete algorithm for its computation. We do not believe this type of approach is at odds with traditional hybrid automata reachability computation, as the goal for both methods is to improve the state of practice of system design from an incomplete analysis based on simulations towards more rigorous approaches. Furthermore, the proposed enhancements, the elimination of accumulated invariant constraints and on-demand successor deaggregation, may be applied to both methods.

The advantage of the simulation-equivalent approach is increased scalability, which makes it applicable to larger CPS models. Furthermore, the approach and tool implementation generate concrete traces whenever a simulation can violate the system specification, making it useful to system engineers who may not have a formal methods background.