Abstract
For most high level languages, two procedures are equivalent if they transform a pair of isomorphic stores to isomorphic stores. However, tools for modular checking of such equivalence impose a stronger check where isomorphism is strengthened to equality of stores. This results in the inability to prove many interesting program pairs with recursion and dynamic memory allocation.
In this work, we present RIE, a methodology to modularly establish equivalence of procedures in the presence of memory allocation, cyclic data structures and recursion. Our technique addresses the need for finding witnesses to isomorphism with angelic allocation, supports reasoning about equivalent procedures calls when the stores are only locally isomorphic, and reasoning about changes in the order of procedure calls. We have implemented RIE by encoding it in the Boogie program verifier. We describe the encoding and prove its soundness.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Program maintenance dominates the program lifecycle. A study of application bugs that took more than one attempt to fix [35] found that 22–33% of fixes required a supplementary fix, and found a diverse range of errors including incomplete refactorings. A study of refactorings [8] found that across 12,922 refactorings from three software projects, 15% of refactorings induced a bug. Automatic program equivalence verification [19, 21, 29, 36] offers the potential to reduce problems by allowing a programmer to automatically (without programmer annotations) verify that the new version is behaviourally equivalent to the old.
The goal of these verification tools is to make the benefits of program equivalence verification available to programmers who are not verification experts. An automatic equivalence verification tool takes a pair of programs as input and then outputs whether the programs are equivalent or not (or perhaps times-out). Program equivalence is undecidable in the general case, however, some success has been achieved on programs with substantially similar structure. Since software is frequently modified in small incremental steps, versions tend to be structurally similar.
We know of two tools designed for fully-automatic program equivalence verification of programs with heaps: Symdiff [29] and RVT [21]. Symdiff [22, 26, 29, 30] is built on top of the Boogie [3] intermediate verification language which, in turn, uses the Z3 [16] satisfiability modulo theories (SMT) solver to discharge proof obligations. RVT uses a designed-for-purpose verification algorithm, which passes program fragments to the CBMC [14] bounded model checker.
Symdiff relates heaps using equality (of arrays modelling the heaps), which we will call e-equivalence, so programs that differ in the order or amount of dynamic memory allocation or garbage cannot be verified as equivalent by Symdiff. RVT does support differences in allocation, but assumes that all heap data structures are tree-like.Footnote 1
E-equivalence is too restrictive for programmers, who expect to be able to replace one procedure with another if the two have identical observable behaviour. A more intuitive notion of procedure equivalence for programs with dynamic memory allocation can be constructed using isomorphism between memory locations. Definitions of program equivalence based on a notion of isomorphism have been used in several formal systems [11, 37]. Our definition of equivalence is:
Two procedures are equivalent, if they terminate for the same set of initial stores, and if both procedures run to completion from isomorphic initial stores, they result in isomorphic final stores.
Our definition of equivalence matches intuition: it allows for differences in the order or amount of memory allocation and garbage and is not restricted to tree-like structures. Achieving automatic and modular verification presents several challenges:
-
Challenge 1 What kind of input do we need to give to an SMT solver so that it can even do the verification? We need to establish an isomorphism between unbounded heaps of arbitrary shape, which is computationally infeasible in general. Furthermore, a direct axiomatisation of isomorphism involves existentially quantifying the mapping between memory locations that characterises the isomorphism. SMT based verification systems are not very good at producing witnesses to such existentials and so a direct axiomatisation of isomorphism is ineffective.
Sometimes calls to equivalent procedures occur from stores that are not fully isomorphic, rather the stores are isomorphic in the footprint of the called procedures. This leads to the next two challenges:
-
Challenge 2 How can our tool determine when stores correspond in the footprint of a called procedure?
-
Challenge 3 What should we do about equivalent calls from non-isomorphic stores since they do not necessarily result in isomorphic stores?
-
Challenge 4 How do we decide which calls are equivalent when there may be many possible candidates? Equivalent calls may occur in different orders in each procedure, and moreover the procedure calls which correspond may differ from execution to execution depending on the initial state (i.e. program inputs).
1.1 Example
Consider the pair of equivalent procedures in Fig. 1 that differ in the order of memory allocation.
Both procedures are intended to copy the passed structure t. The procedures are equivalent on any input, whether the input is tree shaped or not. Our methodology RIE (Replace Isomorphism with Equality) and tool APE (Automatic Program Equivalence tool) can verify that. The procedures differ in two ways: Firstly, the allocation of the copied node has been moved from before the recursive calls on line 5 to after the recursive calls on line 22. Secondly, the order of the recursive calls on lines 7 and 8 has been reversed on lines 19 and 20. The procedures are written in a simple language we call \(\mathcal {L}\), formalised in Sect. 3.
The procedures are equivalent. An intuition as to why is: when t or r are null both procedures leave the heap unchanged. Otherwise, both procedures recursively copy all the nodes to the left, and all the nodes to the right, and return a newly allocated root node via the parameter r. The only pre-existing object modified by the procedures is the one pointed to by r. It is possible that r aliases a node reachable from t, but even so only the v field of r is written to, and only after the nodes have been copied. The objects allocated to rl and rr do not alias anything, so the recursive calls cannot modify the tree, and hence swapping the order of the recursive calls does not affect the result. The postcondition modifies {r} asserts that no existing object, other than r, is modified. For this example, our tool APE requires this framing assertion. Our approach can take advantage of any contracts that are available.
The procedures are not e-equivalent (so would fail to match in Symdiff) when the stores are related with equality. With non-deterministic allocation a procedure is not even equivalent to itself! It is straightforward to resolve with a deterministic allocator, e.g. one that starts at 0 and allocates the next address. Under this deterministic approach [29] a procedure is e-equivalent with itself, but lcopy and rcopy are still not e-equivalent as the allocations on Line 5 and Line 22 are allocated different addresses.
The example illustrates the challenges in the following ways. Challenge 1: equivalence requires that the final stores are isomorphic, but the recursive calls are unbounded so a tool has to check isomorphism of a graph of arbitrary shape and unbounded size. Challenge 2: the stores are not equivalent prior to the recursive calls. For instance, in lcopy three allocations (Lines 3 to 5) have occurred before the recursive calls, but in rcopy only two allocations have occurred (Lines 16 to 17). Challenge 3: the stores after the related calls on Line 7 and Line 20 are not generally isomorphic, since the store after Line 20 contains the effects of two recursive calls but the store after Line 7 contains the effect of only one recursive call. Challenge 4: we do not know in advance which recursive call in lcopy (Lines 7 and 8) corresponds to which recursive call in rcopy (Lines 19 and 20).
1.2 Contributions
We propose a sound methodology, RIE, for establishing isomorphic procedure equivalence which is effective in an SMT solver. RIE enables our tool APE to tackle challenge 1 by automatically establishing isomorphism using under-approximation and heap equality! RIE works by proving equivalence under the angelic allocation assumption; the memory locations are, as far as possible, assumed to be allocated in such a way as to make isomorphic heaps also equal.
We describe a simple language \(\mathcal {L}\) for which isomorphism implies equivalence of observable behaviours, and give a formal definition of what it means for \(\mathcal {L}\) to be closed under isomorphism.
RIE also simplifies challenges two, three and four. RIE allows us to use equality in place of isomorphism, so challenge 2 is addressed by extending the notion of heap equality to support partial heap equality, which we then apply to an overapproximation of the footprint of the procedures. Furthermore RIE rescues us from the need to produce a witness (from challenge 1) to the correspondence between procedure behaviour, instead we address challenge 3 by equating the write effects of equivalent procedures (soundly ignoring unobservable behavioural differences). We combine our technique with mutual summaries to address challenge 4.
In Sect. 2 we describe how RIE can be implemented to verify program equivalence. In Sect. 3 we formalise equivalence and isomorphism and outline RIE’s soundness proof. In Sect. 4 we discuss the effectiveness and limitations of RIE. Finally in Sect. 5 we discuss some related work and conclude.
2 Encoding in a Verifier
Our tool APE takes as input an L program and produces as output ‘success’, ‘failure’, or times out. It does this by translating the input program into Boogie code, which is fed into the Z3 SMT solver. The source code is available at https://github.com/lexicalscope/ape.
In this section we illustrate RIE by showing how APE encodes the example from Sect. 1.1 and how that encoding helps overcome the challenges detailed in the introduction. In particular, we show how verification under the assumption of “angelic allocation” proceeds. Previous work typically takes the approach of abstracting or overapproximating programs with dynamic allocation [11, 27, 40, 43], storeless semantics [13] go as far as abstracting away the observable store entirely. We make the surprising observation that under-approximating memory allocation is also a useful approach, and our formal system proves it sound. RIE establishes procedure equivalence by checking equivalence for only one pair of execution traces for each initial store. Specifically:
All pairs of executions from isomorphic initial stores result in isomorphic final stores if at least one pair of executions from each initial store results in equal final stores.
In particular, it is not necessary to consider all pairs of isomorphic initial stores. We prove this in Sect. 3.
RIE combines our ideas about establishing isomorphism using SMT technology with the prior work on product programs and mutual summaries to produce an automatic program equivalence tool that can verify our example. Standard single program verification tools can be applied to the problem of procedure equivalence using product programs [5, 7, 21, 29, 41], which encode the bodies of a pair of procedures into a single procedure such that verifying a safety property of the product procedure is equivalent to verifying a relational property of the procedure pair [5]. Furthermore, a technique called mutual summaries [22] can be applied to induce an SMT solver to search for interesting relations between procedure calls.
2.1 Angelic Allocation
APE checks equivalence for one pair of executions for each initial store. It does so by searching amongst the possible pairs of executions for a pair that result in equal stores (modulo garbage). Of interest, then, are pairs of executions where particular allocation sites (new) in each procedure are allocated the same addresses. In Fig. 1 there are three allocation sites in each procedure. This gives six possible correspondences between allocation sites (the variables on the left of the equality are from lcopy, and the variables on the right are from rcopy):
We do not know in advance which correspondence will be useful for verificationFootnote 2. In our example, it happens that correspondence (a) is the useful one. Pairs of (terminating) executions from the same initial store that have allocations in this correspondence will result in equal final stores. Hence, no direct checks for isomorphism are required. We will detail how procedure calls are handled shortly.
We induce the solver to search for the useful correspondence by constructing a pair of executions for each correspondence and using a disjunction to assert that at least one of them results in equivalent final stores. The Boogie-like pseudo code in Fig. 2 shows how APE encodes lcopy and rcopy into a single (Symdiff-style) product procedure. The inline commands (e.g. line 33) are not actual Boogie syntax but should be taken to mean that the statements from the body of the relevant procedure are copied into the product procedure at that point. When the procedures are inlined, they are rewritten to work on their own private copy of the heap with fresh variable names. After each inlined pair a different correspondence between allocation sites is assumed (lines 35 and 40). Finally a disjunction is asserted to challenge the verifier to prove that the final heaps are equal for at least one of the inlined pairs (line 44).
Thus, RIE allows us to establish isomorphism using only heap equality!
2.2 Heap Equality
Here we described how APE establishes heap equality, and discuss why our approach is powerful. Tools can relate programs in an intensional or extensional way [10]. Intensionally equal heaps are defined in the same way, whereas extensionally equal heaps have the same observable properties. For example, the heapsFootnote 3 \(h_1=h_0[(5,\mathtt {f}) \mapsto 7][(5,\mathtt {g}) \mapsto 8]\) and \(h_2=h_0[(5,\mathtt {g}) \mapsto 8][(5,\mathtt {f}) \mapsto 7]\) are not intensionally equal, but they are extensionally equal. Extensional relationships provide a powerful means to reason about reordering of store updates.
APE uses the extensional axiomatisation of heap equality shown in Fig. 3. The axiomatisation allows procedures to create different garbage by only requiring equality of the reachable heap. The parameter $roots is a set of references, and it overapproximates the references that are on the stack. The predicate $Reachable is an axiomatisation of heap reachability (something is unreachable when in a disjoint part of the heap) and is discussed in Sect. 4.3.
We define equality between heaps using a pair of implications that say that if an object is reachable in either heap, its fields must be equal in both heaps. An alternative, and perhaps more obvious, definition would be that the reachable sets are equal, and that each object in the reachable set has equal fields in both the heaps. The definitions are equivalent—since heaps that are equal in their reachable parts have the same reachability relation. On several examples the solver was unable to prove that the reachable sets are equal, but it is able to prove our definition.
2.3 Procedure Call
Challenges two, three and four in the introduction relate to the need to reason modularly about the behaviour of nested procedure calls, such as the recursive calls in the example Fig. 1. In this section we describe how our encoding in Fig. 4 leverages RIE to address these challenges.
Equivalent procedure calls do not always occur from isomorphic stores (challenge 2). This is overcome by considering only the region of the heap reachable from the procedure parameters when trying to establish equivalence of procedure calls. This corresponds to the predicate $Heap#EqualFromParams on line 79, detailed in Sect. 3.6.
Equivalent procedure calls do not necessarily result in isomorphic stores (challenge 3). This is overcome through our choice of procedure summary (line 80) and a frame axiom. The write effects of a pair of equivalent procedure calls are related by the predicate $SameDiff (line 81). The frame axiom appears as a free postconditionFootnote 4 of every procedure (lines 63 and 69). Both are described below.
Equivalent procedure calls are summarised by the predicate $SameDiff that relates the pre and post stores of both calls. $SameDiff approximates the actual behaviour of the procedures a surprising way, although equivalent procedures can vary in the amount and shape of garbage, $SameDiff states that equivalent procedure calls will always have equal effects, we justify this in Sect. 3.
The framing axioms (lines 63 and 69) restrict the write effects of the procedures to the part of the heap that was reachable from the procedure parameters. The axiom follows from the semantics of \(\mathcal {L}\). It is not known in advance which procedure calls might be equivalent (challenge 4). This is overcome by how the summary of the behaviour of equivalent procedures is encoded. Specifically, the encoding of mutual summaries presented by Hawblitzel et al. [22] is used to induce the SMT solver to search for related pairs of procedure calls. We detailed this encoding below.
Figure 4 shows how APE encodes the mutual summary for the procedures lcopy and rcopy. The encoding consists of several parts. Encountered calls to the procedures are abstracted by a pair of uninterpreted predicates (lines 57 and 58) which we call abstraction predicates. The predicates are uninterpreted so we precisely control their instantiation. They are given as free postconditions of the procedures lcopy (line 61) and rcopy (line 67). Encountering calls to these procedures causes the abstraction predicates to be instantiated in the solver’s E-graph. We set triggers (lines 75 and 76) so that the solver will instantiate the mutual summary axiom’s quantifiers (line 74) for each pair of instantiations of the abstraction predicates. Non-vacuous instantiations of the axiom occur when the solver is able to establish that the heaps reachable from the call parameters are equal, and hence the antecedent is satisfied.
During a Simplify [17] style SMT solver proof search the quantifiers that appear in an axiom are instantiated with ground terms from the solver’s E-graph that match triggers associated with the quantifier. In-turn, the axiom is applied to those instantiations to introduce new terms into the E-graph and so on. Thus, APE controls the proof search by a combination of the logical meaning of the axioms and the quantifier triggers.
The synthetic parameter $strat of lcopy (line 60) and rcopy (line 66) is introduced to prevent the proof search from trying to establish equivalence between procedure calls occurring under different allocation correspondences. For example, in Fig. 2, the inlining of lcopy on line 33 and line 39 will contain recursive calls to lcopy and rcopy respectively—but it is not useful to find relations between these calls as they pertain to different allocations correspondences. Specifically, the disjunction on line 44 asserts nothing about the relationship between those heaps. The parameter $strat represents the allocation correspondence in effect for that call, and the mutual summary trigger (lines 75 and 76 of Fig. 4) restricts instantiation of the quantifiers to calls which occurred under the same allocation correspondence.
We have completed our illustration of how the RIE methodology is implemented in a modular program equivalence tool. Discussion about the effectiveness and limitations of our approach is in Sect. 4.
3 Soundness of RIE
We now give a model of RIE and summarise a proof of its soundness. The semantics of \(\mathcal {L}\) come in two flavours: the \(\mathcal {V}\) semantics is the ordinary semantics of \(\mathcal {L}\). The \(\mathcal {A}\) semantics models our Boogie encoding, which includes the various approximations detailed in Sect. 2. We establish soundness of RIE by showing that equivalence under \(\mathcal {A}\) implies equivalence under \(\mathcal {V}\).
We expect a mapping between procedures names, \(\mathcal {E}\), which pairs procedures that are suspected to be equivalent. RIE takes the program and \(\mathcal {E}\) as input and tries to prove that indeed all pairs in \(\mathcal {E}\) are equivalent.
We start with an overview of the semantics of \(\mathcal {L}\), then define isomorphism and procedure equivalence. Then we detail how the various approximations are modelled in the \(\mathcal {A}\) semantics. Finally we give RIE’s soundness theoremFootnote 5.
3.1 Semantics of \(\mathcal {L}\)
\(\mathcal {L}\) is a simple imperative language. Figure 5 describes the standard aspects of \(\mathcal {L}\), while Fig. 6 describes the non-standard aspects. The following points are interesting about our semantics:
-
We distinguish between execution under \(\mathcal {V}\) and \(\mathcal {A}\) with a subscript, writing
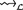 where \(\mathcal {L}\in \{\mathcal {V},\mathcal {A}\}\).
where \(\mathcal {L}\in \{\mathcal {V},\mathcal {A}\}\). -
We split procedure call into two: a “call” rule and a “body” rule, similar to Godlin and Strichman [21], to treat procedure call concretely in \(\mathcal {V}\) but abstractly in \(\mathcal {A}\). The latter is a first ingredient in reflecting mutual summaries.
-
Execution of pairs of procedures is included in the operational semantics, modelled by the rules COMV and COMA:
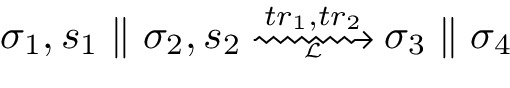
meaning statement \(s_1\) executed on store \(\sigma _1\) results in store \(\sigma _3\) producing trace \(tr_1\), and similarly for statement \(s_2\). These rules reflect product programs [1, 5, 29].
-
We require the program adhere to a specification given by \( Con \)Footnote 6.
-
The semantics are instrumented to produce a trace of the states reached during execution which we use to distinguish particular executions.
-
although our semantics is a big step semantics, we keep the whole calling context as part of the runtime configuration to allow us to give useful meaning to isomorphism of stores.
-
We assume loops have been encoded as recursive procedures.
We only discuss some of the rules of the operational semantics. NEW allocates a new object.Footnote 7 The address of the object must be fresh, and the object has all fields set to null. ASSIGN updates a stack variable x with the result of evaluating an expression e in the store \(\sigma \).
BOD executes the body of a procedure p by looking up and executing p’s statements. Our assumption that procedure contracts have already been verified, is modelled by the requirement \((\sigma _1,\sigma _3) \in Con (\texttt {p})\). Note that BOD pops the top of the final stack, while CALLA and CALLV push new frames (using the function \( mkframe \)).
CALLA models abstraction of procedure calls. The behaviour of the abstracted call is restricted by the procedure’s contract \( Con (\texttt {p})\), and the call may not free any allocated address (All that RIE actually requires is that the language not have concrete addresses so any language with garbage collection which does not support pointer arithmetic can be handled).
Angelic allocation in the rule COMA is modelled by the predicate over trace pairs \(\mathcal {I}\). The behaviour of called procedures in the \(\mathcal {A}\) semantics is modelled by the predicate over trace pairs \(\mathcal {M}\). We define \(\mathcal {I}\) and \(\mathcal {M}\), as the paper progresses.
3.2 Isomorphism
Stores are isomorphic if they differ only in the actual values of heap addresses or in garbage. An isomorphism is characterised by a bijection between values, \(\pi \). Definition 1 says that \(\sigma _1\) is isomorphic to \(\sigma _2\) with relation \(\pi \) iff the stacks of \(\sigma _1\) and \(\sigma _2\) are the same height; for each corresponding stack frame the same variables are defined; and \(\pi \) is an injection. Where \(\pi \) is the uniquely defined relation that maps the stack variables of \(\sigma _1\) to \(\sigma _2\), commutes with field dereference, and preserves the meaning of \(\texttt {null}\), \(\texttt {true}\), and \(\texttt {false}\).
Definition 1
(Isomorphism).

-
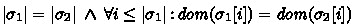
-
\(\pi \) is an injectionFootnote 8, written \( in {\left( \pi \right) }\)
Where \(\pi \) is the smallest relation that satisfies:

And 
In our notation: The number of stack frames in store \(\sigma \) is \(\left| {\sigma }\right| \). The value of variable x in the \(i^{\textit{th}}\) stack frame is \(\sigma [i](x)\). The domain of the mapping \(\pi \) is \( dom (\pi )\), and \( dom (\sigma [i])\) is the set of variables defined in the \(i^{\textit{th}}\) stack frame.
We also require that any contracts in the program are not sensitive to address values or garbage. We write \(\sigma _{i \ldots j}\) to mean \(\sigma _i,\ldots ,\sigma _j\).
Definition 2
(Contracts in \(\mathcal {L}\)). The contracts \( Con : Pid \rightarrow \mathcal {P}( Store \times Store )\), are sets of pairs of \( Store \) representing the set of acceptable pre and post stores of each procedure. We require that:
Lemma 1
(Isomorphism is an equivalence relation). The relation \(\approx \) is an equivalence relation (reflexive, symmetric, transitive).
The crucial property of \(\approx \) is that it is closed under execution. Namely, executing a statement from isomorphic stores results in isomorphic executions. Executions are isomorphic iff the elements of their traces are pairwise isomorphic (written \(tr_1 \approx tr_2\)), and have isomorphic write effects.
Lemma 2
( \(\mathcal {L}\) closed under isomorphism).
For every execution  , store \(\sigma _2\), and injection \(\pi _1\) if \(\sigma _1 \approx _{\pi _1} \sigma _2\) then
, store \(\sigma _2\), and injection \(\pi _1\) if \(\sigma _1 \approx _{\pi _1} \sigma _2\) then
-
there exists an execution
-
if \(\mathcal {L}{}=\mathcal {V}{}\), every execution
 is isomorphic to
is isomorphic to 
Executions  and
and  are isomorphic iff \(\exists \pi _{1,2} {{\mathrm{:}}}\)
are isomorphic iff \(\exists \pi _{1,2} {{\mathrm{:}}}\)

Where trace isomorphism is:

And where 
Proof
By induction on the derivation of  . Most cases are straightforward since no instruction is sensitive to the actual value of addresses. Note that every instruction makes the set of reachable addresses smaller, apart from \(\texttt {new}\) which expands it by exactly one fresh address—this corresponds to the fact that addresses are never synthesised and garbage is never resurrected. \(\square \)
. Most cases are straightforward since no instruction is sensitive to the actual value of addresses. Note that every instruction makes the set of reachable addresses smaller, apart from \(\texttt {new}\) which expands it by exactly one fresh address—this corresponds to the fact that addresses are never synthesised and garbage is never resurrected. \(\square \)
A way to think of closure under isomorphism is that \(\mathcal {L}\) is not sensitive to the actual values of addresses nor garbage. Many industrial languages (such as C, Java, Python, C\(^\sharp \), etc.) contain features that are sensitive to the actual values of heap addresses or order of allocation. Such sensitivity is typically not central to the language and it is often not necessary to use such features.
3.3 Regional Isomorphism
As discussed in Sect. 2, APE works by establishing isomorphisms between the heap regions reachable from procedure parameters (Line 79 of Fig. 4), so we introduce a notion of isomorphism between heap regions. The heap regions reachable from two sequences of parameter names W and X are isomorphic iff the sequences have the same length, and the relation (\(\pi \)) constructed by following all paths from the parameters is an injection:
Definition 3
(Regional Isomorphism).

Where \(\pi \) is the smallest relation which satisfies:

3.4 Procedure Equivalence
Procedures are equivalent if executing their bodies from isomorphic stores results in isomorphic stores. Executing \(\mathtt {body}~\texttt {p}\) means looking up and executing the statements that form the body of procedure \(\texttt {p}\). Note that rule BOD pops the top stack frame before completing, so stores \(\sigma _3,\sigma _4\) in Definition 4 are as observed by a caller. This means that equivalence relates to the observable behaviour of the procedure body, and that differences in local variables, etc., are ignored. The same definition of procedure equivalence applies to both the \(\mathcal {A}\) and the \(\mathcal {V}\) semantics.
Definition 4
(Procedure equivalence).

3.5 Angelic Allocation
We describe how angelic allocation is modelled by the predicate \(\mathcal {I}\) in the \(\mathcal {A}\) semantics rule COMA. The predicate selects the pairs of execution traces that exhibit desirable allocation patterns.
Predicate \(\mathcal {I}\) (Definition 6) retains only traces with heap regions that are equal at particular isomorphic points (Definition 5) in the traces. In APE, these points correspond to procedure entry, equivalent procedure calls and allocation sites. APE only verifies procedures from equal (rather than isomorphic) initial stores, discards execution pairs which don’t have interesting correspondences between allocations, and assumes procedures have equal effects. Because we are only trying to prove soundness of RIE, it is not necessary to fully specify how APE chooses which stores to equate. Rather, we prove that any assumption of store equality that the tool makes is sound, subject to the caveats in Definition 5.
Definition 5
(Isomorphic Points).
Any tool using RIE must define a function
with the following properties:
-
1.
The same set of points is produced for isomorphic traces:
$$ \forall tr_{3,4} {{\mathrm{:}}}tr_1\approx tr_3 {{\mathrm{\varvec{\;\wedge \;}}}}tr_2\approx tr_4 \implies pts (tr_1,tr_2) = pts (tr_3,tr_4) $$ -
2.
The traces are isomorphic at each of the points:

-
3.
If the initial stores of \(tr_1,tr_2\) are isomorphic, then the isomorphism is injective with all the other isomorphisms. Otherwise the isomorphisms are empty.
-
\( in {\left( \pi \cup \varPi (tr_1,tr_2)\right) }\)
-
\(\not \exists \pi {{\mathrm{:}}} fst (tr_1) \approx _{\pi } fst (tr_2) \implies \varPi (tr_1,tr_2) = \emptyset \)
-
Where

Definition 6
(Angelic Allocation).

Definition 5 requires that the points are selected symmetrically for isomorphic traces. This symmetry is critical for the soundness of RIE, which must verify at least one pair of execution traces for each initial state. Furthermore, the definition requires that the union of the isomorphisms between the selected heap regions is an injection. This corresponds to the fact that RIE is implemented by equating allocation sites, and will be discussed further in later sections, particularly Sect. 4.
3.6 Mutual Summaries of Equivalent Procedures
APE uses mutual summaries, lines 73 and 80 in Fig. 4, to allow the verifier to use facts about the behaviour of equivalent procedure calls in its proofs. It is needed in order for procedure equivalence to be a transitive relation.
APE’s use of mutual summaries is modelled by the rule CALLA, which overapproximates the behaviour of concrete procedure call. And the predicate \(\mathcal {M}\) in the rule COMA, which restricts the traces to those where the procedure pairs in \(\mathcal {E}\) behave equivalently.
The antecedent  expresses that the regions reachable from the parameters are isomorphic (as needed for challenge 2), while the conclusion
expresses that the regions reachable from the parameters are isomorphic (as needed for challenge 2), while the conclusion  expresses that the procedures have isomorphic write effects (as needed for challenge 3). In our example, the encoding of the antecedent is $Heap#EqualFromParams on line 79 of Fig. 4, while the encoding of the conclusion is $SameDiff on line 80 of Fig. 4.
expresses that the procedures have isomorphic write effects (as needed for challenge 3). In our example, the encoding of the antecedent is $Heap#EqualFromParams on line 79 of Fig. 4, while the encoding of the conclusion is $SameDiff on line 80 of Fig. 4.
Definition 7
(Mutual Summaries of Equivalent Procedures).

3.7 Soundness of RIE
We now give the theorem which guarantees soundness of RIE, and describe some keys points in its proof. Theorem 1 states that if all pairs in \(\mathcal {E}\) are mutually terminating and equivalent under the \(\mathcal {A}\) semantics, then they are also equivalent under the \(\mathcal {V}\) semantics. Mutual termination (\( mt \)) means that both procedures terminate for the same set of initial storesFootnote 9.
Theorem 1
(RIE is sound).

Where 

Proof
The proof proceeds by showing that for any pair of executions (\(tr_1,tr_2\)) from isomorphic initial stores in the \(\mathcal {V}\) semantics there exist an isomorphic execution (\(tr_5\) with \(tr_1\approx tr_5\)) such that that \(\mathcal {I}\) and \(\mathcal {M}\) hold for \((tr_1,tr_5)\) and thus the \(tr_5\) and \(tr_2\) executions compose by \(\parallel \) in the \(\mathcal {A}\) semantics. Then by the assumptions and transitivity of \(\approx \) we know that \(tr_1,tr_2\) end in isomorphic stores. The proof goes by an inner induction nested within an outer induction. We now write the proof in some more detail:
Assume  .
.
To show:

First Part: From Definition 5 we see that there is a \(\pi _2=\varPi (tr_1,tr_2)\) (1). By Lemma 3 (below) there exists a third execution  such that \(tr_1\) is isomorphic to \(tr_3\) with \(\pi _2\), i.e. \(tr_1\approx _{\pi _2}tr_3\), which means by Lemma 1 (symmetry) we get
such that \(tr_1\) is isomorphic to \(tr_3\) with \(\pi _2\), i.e. \(tr_1\approx _{\pi _2}tr_3\), which means by Lemma 1 (symmetry) we get  (2). Take any point \((i,j,X,Y) \in pts (tr_1, tr_2)\). To show:
(2). Take any point \((i,j,X,Y) \in pts (tr_1, tr_2)\). To show:  . By (1) exists \(\pi _4\) such that
. By (1) exists \(\pi _4\) such that  and \(\pi _4 \subseteq \pi _2\) (4). By (2) there exists \(\pi _3\) such that
and \(\pi _4 \subseteq \pi _2\) (4). By (2) there exists \(\pi _3\) such that  and
and  (3). Hence, by Lemma 1 (transitivity), we have that
(3). Hence, by Lemma 1 (transitivity), we have that  , we know \(\pi _3\) composed with \(\pi _4\) is large enough because X is a subset of the stack variables defined in \(tr_1[i]\), and \( dom (\pi _3)\) includes the values of all stack variables. By (3), (4), we know that \(\pi _3\) composed with \(\pi _4\) is a subset of the identity relation. So
, we know \(\pi _3\) composed with \(\pi _4\) is large enough because X is a subset of the stack variables defined in \(tr_1[i]\), and \( dom (\pi _3)\) includes the values of all stack variables. By (3), (4), we know that \(\pi _3\) composed with \(\pi _4\) is a subset of the identity relation. So  . Because
. Because  we have by definition
we have by definition  . Then we get
. Then we get  . And thus we have
. And thus we have  , which in turn gives us
, which in turn gives us  (5).
(5).
Second Part: We now proceed by induction on the size of the derivation of  .
.
It remains to show that, \(tr_2\) is also a trace under \(\mathcal {A}\) and that there is an \(\mathcal {A}\) trace \(tr_5\) isomorphic to \(tr_3\) such that \(\mathcal {M}(tr_5,tr_2)\) holds. Note that it is trivial to prove that apart from \(\parallel \) all the rules of \(\mathcal {A}\) semantics overapproximate the \(\mathcal {V}\) semantics (l1). By (l1) and induction on the derivation of  we get
we get  .
.
Base Case: there are no procedure calls in  . By Lemma 2 then
. By Lemma 2 then  also has no procedure calls. By (l1) and induction on the derivation of
also has no procedure calls. By (l1) and induction on the derivation of  we get
we get  . Since there are no procedure calls, trivially \(\mathcal {M}(tr_3,tr_2)\) and
. Since there are no procedure calls, trivially \(\mathcal {M}(tr_3,tr_2)\) and  . From the antecedent we know that \( lst (tr_3)\approx lst (tr_2)\), and since \(tr_1\approx tr_3\) then by transitivity of \(\approx \) we have
. From the antecedent we know that \( lst (tr_3)\approx lst (tr_2)\), and since \(tr_1\approx tr_3\) then by transitivity of \(\approx \) we have  . And since
. And since  and
and  base case is done.
base case is done.
Inductive Step: there are procedure calls in  .
.
-
To show: there exists an execution
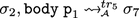 such that \(\mathcal {M}(tr_5,tr_2)\) and \(tr_5\approx _ id tr_3\) (6). Proceed by an inner induction over the derivation of
such that \(\mathcal {M}(tr_5,tr_2)\) and \(tr_5\approx _ id tr_3\) (6). Proceed by an inner induction over the derivation of 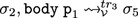 . Most cases are trivial. The interesting cases are CALLV where the called procedure is in \(\mathcal {E}\), and the inductive case TRANS. Inner Case: CALLV where the called procedure is in \(\mathcal {E}\). By case there is
. Most cases are trivial. The interesting cases are CALLV where the called procedure is in \(\mathcal {E}\), and the inductive case TRANS. Inner Case: CALLV where the called procedure is in \(\mathcal {E}\). By case there is  and \((\texttt {p}_3,\texttt {p}_4) \in \mathcal {E}\). Rule CALLV can only be applied if a shallower tree is derivable for the body of the called procedure. Therefore we apply the outer induction hypothesis, the antecedent \({ mt }_{\mathcal {V}}(\texttt {p}_3,\texttt {p}_4)\), and Lemma 3, to deduce that there exists \(\sigma _7\) such that
and \((\texttt {p}_3,\texttt {p}_4) \in \mathcal {E}\). Rule CALLV can only be applied if a shallower tree is derivable for the body of the called procedure. Therefore we apply the outer induction hypothesis, the antecedent \({ mt }_{\mathcal {V}}(\texttt {p}_3,\texttt {p}_4)\), and Lemma 3, to deduce that there exists \(\sigma _7\) such that  and \(\sigma _5\approx _{ id }\sigma _7\). From CALLA we see that
and \(\sigma _5\approx _{ id }\sigma _7\). From CALLA we see that  (intuition: we swap the behaviour of \(\texttt {p}_3\) for the behaviour of \(\texttt {p}_4\)). Take \(tr_5=(\mathtt {call}~\texttt {p}_3(x_1 \ldots x_n),\sigma _2,\sigma _7)\) and we have \(tr_3\approx _{ id }tr_5\). To show: \(\mathcal {M}(tr_5,tr_2)\). Take arbitrary \((\mathtt {call}~\texttt {p}_4(y_1 \ldots y_n),\sigma _8,\sigma _{10}) \in tr_2\) such that
(intuition: we swap the behaviour of \(\texttt {p}_3\) for the behaviour of \(\texttt {p}_4\)). Take \(tr_5=(\mathtt {call}~\texttt {p}_3(x_1 \ldots x_n),\sigma _2,\sigma _7)\) and we have \(tr_3\approx _{ id }tr_5\). To show: \(\mathcal {M}(tr_5,tr_2)\). Take arbitrary \((\mathtt {call}~\texttt {p}_4(y_1 \ldots y_n),\sigma _8,\sigma _{10}) \in tr_2\) such that  . To show: \(\exists \pi _6 {{\mathrm{:}}} in {\left( \pi _5 \cup \pi _6\right) } {{\mathrm{\varvec{\;\wedge \;}}}} effect (\sigma _2,\sigma _5) \approx _{\pi _6} effect (\sigma _8,\sigma _{10})\). This follows straightforwardly from Lemma 2 and the fact that the same procedure \(\texttt {p}_4\) was executed to obtain \(\sigma _5\) as to obtain \(\sigma _{10}\). Inner case done.
. To show: \(\exists \pi _6 {{\mathrm{:}}} in {\left( \pi _5 \cup \pi _6\right) } {{\mathrm{\varvec{\;\wedge \;}}}} effect (\sigma _2,\sigma _5) \approx _{\pi _6} effect (\sigma _8,\sigma _{10})\). This follows straightforwardly from Lemma 2 and the fact that the same procedure \(\texttt {p}_4\) was executed to obtain \(\sigma _5\) as to obtain \(\sigma _{10}\). Inner case done.Inner Case: TRANS By case there is
 and hence exists \(\sigma _9,tr_{7,9}\) such that
and hence exists \(\sigma _9,tr_{7,9}\) such that  . The proof goes as expected, by applying the inner induction hypothesis twice with one slight complexity. The first application constructs another execution of \(s_1\) with the desired properties; but that execution’s final store is not \(\sigma _9\)! Rather it is some other store (say \(\sigma _{11}\)) that is isomorphic to \(\sigma _9\). Before we apply the inner induction hypothesis a second time, we use Lemma 3 to construct an execution isomorphic to
. The proof goes as expected, by applying the inner induction hypothesis twice with one slight complexity. The first application constructs another execution of \(s_1\) with the desired properties; but that execution’s final store is not \(\sigma _9\)! Rather it is some other store (say \(\sigma _{11}\)) that is isomorphic to \(\sigma _9\). Before we apply the inner induction hypothesis a second time, we use Lemma 3 to construct an execution isomorphic to  but with initial store \(\sigma _{11}\). \(\mathcal {M}\) holds for the resultant traces by the same argument as the CALLV case. Inner case done. Hence \(\mathcal {M}(tr_5,tr_2)\). From (5) and (6) we also have \(\mathcal {I}(tr_5,tr_2)\). So we get that
but with initial store \(\sigma _{11}\). \(\mathcal {M}\) holds for the resultant traces by the same argument as the CALLV case. Inner case done. Hence \(\mathcal {M}(tr_5,tr_2)\). From (5) and (6) we also have \(\mathcal {I}(tr_5,tr_2)\). So we get that  is an execution under the \(\mathcal {A}\) semantics. Finally, from the antecedent we know that \( lst (tr_3)\approx lst (tr_4)\), and since \(tr_1\approx tr_3\approx tr_5\) and \(tr_2\approx tr_4\) then by transitivity of \(\approx \) we have \( lst (tr_1)\approx lst (tr_2)\). And since
is an execution under the \(\mathcal {A}\) semantics. Finally, from the antecedent we know that \( lst (tr_3)\approx lst (tr_4)\), and since \(tr_1\approx tr_3\approx tr_5\) and \(tr_2\approx tr_4\) then by transitivity of \(\approx \) we have \( lst (tr_1)\approx lst (tr_2)\). And since 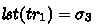 and \( lst (tr_2)=\sigma _4\) we are done.
and \( lst (tr_2)=\sigma _4\) we are done.
\(\square \)
The soundness proof of Theorem 1 relies on constructing alternative executions that are isomorphic using the identity bijection, Lemma 3 states that all such alternative executions are derivable in \(\mathcal {L}\).
Lemma 3
(Sufficent non-determinism). Given statement s, stores \(\sigma _{1 \ldots 3}\), mapping \(\pi _1\), and alternative allocation strategy \(\pi _{2}\), such that:
-
\(\sigma _1\) and \(\sigma _2\) are isomorphic with mapping \(\pi _1\): \(\sigma _1 \approx _{\pi _1} \sigma _2\)
-
s can execute to completion from \(\sigma _1\):

-
\(\pi _1\) and \(\pi _2\) map common addresses in the same way \( in {\left( \pi _1 \cup \pi _2\right) }\)
-
\(\forall (a_1,a_2) \in \pi _2 {{\mathrm{:}}}(a_1 \in {\sigma _1}^{\mathtt {heap}} \iff a_2 \in {\sigma _2}^{\mathtt {heap}})\)
Then there exists an isomorphic execution  such that:
such that:
Proof
By induction on the derivation of  the alternative execution is constructed. In particular note that because \(\pi _2\) does not map between allocated and unallocated addresses, the appropriate alternative address is always unallocated when an allocation statement is reached. And that, since \( in {\left( \pi _1 \cup \pi _2\right) }\) then all addresses that were already allocated at the start of the execution do not need to be allocated alternatives. The proof goes through for both \(\mathcal {V}\) and \(\mathcal {A}\). \(\square \)
the alternative execution is constructed. In particular note that because \(\pi _2\) does not map between allocated and unallocated addresses, the appropriate alternative address is always unallocated when an allocation statement is reached. And that, since \( in {\left( \pi _1 \cup \pi _2\right) }\) then all addresses that were already allocated at the start of the execution do not need to be allocated alternatives. The proof goes through for both \(\mathcal {V}\) and \(\mathcal {A}\). \(\square \)
4 Discussion
The number of correspondences between allocations (Sect. 2) is factorial in the maximum number of allocation sites in either procedure. Hence RIE is only practical for relatively small numbers of allocation sites. However, this is not as restrictive as it may seem because our approach is modular. In practice, when loops are encoded as procedure calls, then many interesting procedures contain only small numbers of allocations. In some cases it is also possible to split a procedure into chunks or abstract common parts. It is also likely that the applicability of this technique can be significantly extended by using additional static analysis to eliminate some of the permutations in advance. For example, the types of the objects being allocated could be used to eliminate permutations that aligned objects of different types.
Framing of procedure calls is important in verifying equivalence for many examples. APE has a fairly naive approach to framing and disjointness of heap regions, which restricts the class of examples it can currently deal with. However, our techniques, and choice of Dafny [32] style heap encoding, should be amenable to a more powerful framing methodology. Improving APE’s framing support is likely to significantly improve its completeness.
We considered many alternative approaches to establishing isomorphism. The natural approach using existentials does not work very well. We investigated several approaches using universal quantification. We tried defining heaps to be isomorphic if all pairs of paths that lead to related addresses in one heap also lead to related addresses in the other. We tried several approaches for limiting which, and what depth of paths should be considered by the solver. But the underlying doubly exponential complexity of comparing all pairs of paths impedes the applicability of that approach. The requirement that disjoint heap effects of procedure calls commute was an important design force: many alternative approaches required extensive additional axioms to handle the various cases, whereas our current approach of enumerating allocators seems to handle many cases naturally.
4.1 Examples
There are a collection of programs available from https://github.com/lexicalscope/ape#automatic-procedure-equivalence-tool that show the capabilities of APE. Several of them have been listed in Fig. 7 with timings performed on an Intel Core i5-3210M@2.5 GHz processor with 8 GB memory.
We surmise that the amount of time APE takes to verify an example is related to the number of allocations, the number of paths through the procedure, the number of procedure calls, the complexity of any framing reachability that needs to be solved, and the order that Z3 happens to apply the axioms (i.e. how far into the search space the solution lies—for example, reordering procedure calls usually slows the verification down).
RIE’s approach of using equality to establish isomorphism does prevent APE from establishing isomorphism in some cases where it would be helpful to do so. The example in Fig. 8 is from a refactoring of some code which manipulates a doubly linked list. Both procedures add an element to a list, but first remove it if it is already present. The left procedure has a redundant check that the item is in the list, in the right procedure this redundancy is removed.
The isomorphism between lines 88 and 105 relates the addresses in rf0 and rf. The isomorphism between lines 91 and 105 relates the addresses in rf1 and rf. If we were to assume equality for both of these isomorphisms then we would have \(\texttt {rf} = \texttt {rf0} = \texttt {rf1}\). However, rf0 is allocated by the new statement on line 87 whereas rf1 is allocated by the subsequent new statement on line 90. The semantics of new require that each allocation gives an address which was not previously allocated—i.e. that \(\texttt {rf0} \ne \texttt {rf1}\).
RIE, therefore, restricts the selected points in Definition 6 to prevent contradictory isomorphisms being selected. Due to this restriction a verifier using RIE alone may fail to produce a proof for some procedures that are in fact equivalent according to our definitions. Any tool using RIE in practice may choose to equate one pair of calls to find, but it must find some other way to deal with the other pair of calls (such as manually adding an additional specification of find).
4.2 Definitions of Isomorphism and Procedure Equivalence
Our definition of procedure equivalence is useful because it is a contextual equivalence [34] for \(\mathcal {L}\). This means that given equivalent procedures \(\texttt {p}_1,\texttt {p}_2\) and a program that calls \(\texttt {p}_1\), one can always change the program to call \(\texttt {p}_2\) instead without affecting the observable behaviour of the program. Of particular interest to programmers is Corollary 1: the relation \(\approx \) preserves the meaning of all assertions.
Corollary 1
(Isomorphism is assertion preserving).
Proof
Follows from Lemma 2 \(\square \)
Interestingly, it is possible to define isomorphism almost equivalently as the least-fixed-point interpretation of the relation:

where \(\sigma _\emptyset \) is the empty store. That is, it could be defined as a smallest relation closed under the atomic operations of the semantics. However, even though the semantics is naturally closed under \(\approx '\), the definition is not as helpful when trying to decide if a particular pair of stores are isomorphic. Regardless, a definition in this least-fixed-point style would allow us to construct a notion of isomorphism even for a semantics where we did not know an appropriate direct definition. Perhaps it is interesting to consider what assertion language would be preserved for any particular semantics given such a definition.
4.3 Reachability
Establishing reachability enables APE to prove interesting examples, but is ancillary to the focus of this paper RIE and angelic allocation. Still, our definition of equivalence allows differences in garbage (which is unreachable memory), and APE use reachability to reason about read and write effect framing as described in Sect. 2.3—so an useful axiomatisation of reachability is needed.
The partial axiomatisation of reachability used by APE, written in Boogie. The triggers are elided {...}. The function $Read(h,a,f) is the value of field f of object a in heap h, the predicate $Allocated($h,$a) holds if object $a is allocated in heap $h. The predicate $Edge($h, $a, $f, $c) holds if the field $f of object $a has the value $c in heap $h.
Figure 9 shows our Boogie encoding of reachability. We give several axioms for the predicate $Reach, which the tool instantiates in different circumstances controlled by various triggers (controlled programatically, users cannot write them). Rather than precisely deciding the reachability set, often it is necessary to prove disjointness of certain heap regions. For example, garbage objects are disjoint from the reachable region, and a property of a region is preserved over a procedure call if the region is disjoint from the call effects. Our choice of axioms enable the tool to establish a lack of reachability by showing either that there are no outgoing (line 130) or no incoming (line 127) edges to a particular heap region. Although the axioms line 127 and line 130 are logically equivalent, we use triggers to unroll them in different situations.
5 Related Work and Conclusions
The study of program equivalence arguably pre-dates the study of functional correctness. In his 1969 paper [23], Hoare identified that “Many [previous] axiomatic treatments of computer programming [2, 24, 46] tackle the problem of proving the equivalence, rather than the correctness, of algorithms”. To date, practical approaches to program equivalence rely on structural similarity of the programs. Many works focus on methods to account for some structural differences. The importance of program structure in proving program equivalence was observed by Dijkstra in 1972 [15], where he also observes that programmers are often called upon to modify existing programs.
Key developments in program equivalence have come from research into non-interference in secure information flow and compiler translation validation. Non-interference is the property that the values of secret inputs do not influence public outputs. Translation validation provides assurances that the program output by a compiler is correct with respect to the input program. Translation validation concerns itself with correctness of particular compiler runs, and does prove the compiler implementation correct. Non-interference can be formalised in terms of program equivalence [25], or more generally as a safety property over pairs of program traces [7, 41]. Methods for reducing safety properties over trace pairs to safety properties over single traces have been explored [9, 33] and generalised, particularly via product programs [4, 6] and similar [38, 42, 47]. Product programs combine a pair of programs into one, such that useful invariants can be formulated at interesting points in the product, and can generalise to relations between programs [5]. Compiler translation validation [28, 31, 38, 42, 47] is inherently a program equivalence question. Many techniques have been applied, several variations of product programs [47], constructing bisimulations between control flow graphs [28], iteratively applying equality axioms [38], or normalising [42] graph representations of the programs.
Relational Hoare Logic [5, 10,11,12, 45] (RHL) was proposed by Benton, in 2004 [10], in the course of proving the correctness of various compiler optimisations. The Hoare triple \(\{P\} S \{Q\}\) is extended to a Hoare quadruple by inclusion of two statements, rather than one, \(\{P\} C_1 \sim C_2 \{Q\}\). The pre and post conditions are lifted to relations over stores. RHL has been extended by various rules to account for differences in structure between the programs [5, 10]. Barthe, Crespo, and Kunz [5] pointed out that RHL is closely related to the idea of product programs. Several formal works tackle the problem of proving program equivalence in the presence of dynamic memory allocation. Pitts uses a simulation between memory locations when defining a semantic approach to program equivalence [37], the memory model is flat not a heap. Benton et al. uses isomorphism between heap regions when proposing an RHL that supports dynamic allocation [11]. Yang constructs a relational separation logic with support for dynamic allocation [45]. Sumner and Zhang propose a different approach, canonical memory addresses are constructed based on program control flow and syntactic elements. Banerjee, Schmidt, and Nikouei [1] propose a logic for weaving programs with structural differences so that relational properties of programs can be expressed. They extend this with a region logic to support reasoning about encapsulation in dynamically allocating programs; catering for equivalence between programs which vary the representation of objects.
5.1 Fully Automatic Equivalence Verification Tools
To our knowledge there are four other tools with the objective of fully automated verification of procedure equivalence for imperative programs: Symdiff [29], RVT [21], SCORE [36], and Rêve [19]. Symdiff [29] uses program verification to prove or provide counter examples of equivalence. It uses mutual summaries, and can infer intermediate summaries to establish equivalence. Conditional equivalence [22] can show partial equivalence over a subset of procedure inputs and construct summaries of interprocedural behavioural differences. Symdiff is built on Boogie [3]. Symdiff has no built-in support for procedures that differ in memory allocation. RVT [21] proves equivalence of some C programs. RVT generates loop and recursion free program fragments, which are verified by the CBMC [14] bounded model checker. Loops are encoded as recursive functions. Recursive calls are replaced by uninterpreted functions. Recently support for unbalanced recursive functions has been added [39]. RVT is extended to dynamic data structures involving pointers by generating (symbolic) bounded tree-like data structures as inputs for procedures. These initial tree-like structures are isomorphic up to some bound. RVT then verifies (up to the same bound) that those data structures remain isomorphic, at procedure calls and procedure return. The bound is determined by a syntactic overapproximation of the maximum depth of modification. No rigorous proof is presented for this extension to pointers. Rêve [19] and SCORE [36] support numerical programs without heaps. Rêve uses Horn constraints to verify equivalence of deterministic imperative programs with unbounded integer variables. Rêve infers inductive coupling predicates and as such can deal with loops and recursion where, for example, the number and meaning of procedure parameters has changed. The authors of Rêve propose in the future to extend their tool with an RVT-like approach to the heap. SCORE uses abstract interpretation over an interleaving of the programs. A good interleaving is found by searching. SCORE deals with numerical programs. For non-equivalent programs SCORE can compute an overapproximation of the semantic difference. The precision of this overapproximation is related to the size of the syntactic difference.
5.2 Conclusion
We defined procedure equivalence, and a sound methodology RIE, for automatically proving equivalence of programs which vary in dynamic memory allocation. We described our RIE encoding APE for equivalence verification (available at https://github.com/lexicalscope/ape). Our approach is fully automatic, and applicable to programs which manipulate heap data structures of any shape.
Notes
- 1.
For details, see Definition 2 (and the paragraph following) on page 5 of the 2009 paper by Godlin and Strichman [21].
- 2.
It is interesting to note that in this example the variable names suggest which correspondence is important, perhaps indicating that there may be useful heuristics that could improve performance—such as trying correspondence (a) first.
- 3.
\(h_0[(5,\mathtt {f})\mapsto 7]\) is the heap made by copying \(h_0\) and setting field f of object 5 to 7.
- 4.
A free postcondition may be assumed after a call, but is not checked.
- 5.
Full details of the proof can be found in the first author’s PhD thesis [44].
- 6.
We expect single program contracts to have been verified; programs with no contracts are also acceptable.
- 7.
In a concrete implementation we do not require that there is no garbage collection, just that the programmer cannot manipulate addresses.
- 8.
 .
. - 9.
We could produce a total definition of procedure equivalence by including a notion of mutual termination [18, 22] in Definition 4. However, APE does not yet reason about the termination behaviour of the procedures. A total notion of procedure equivalence is important, particularly where a transitive procedure equivalence relation is needed. Since our tool takes the same basic approach as Symdiff, it should be straightforward to incorporate existing mutual termination checking techniques [18, 20, 22].
References
Banerjee, A., Schmidt, D.A., Nikouei, M.: Relational logic with framing and hypotheses. In: FSTTCS (2016)
de Barker, J.W.: Axiomatics of simple assignment statements. In: MR 94 (1968)
Barnett, M., Chang, B.-Y.E., DeLine, R., Jacobs, B., Leino, K.R.M.: Boogie: a modular reusable verifier for object-oriented programs. In: Boer, F.S., Bonsangue, M.M., Graf, S., Roever, W.-P. (eds.) FMCO 2005. LNCS, vol. 4111, pp. 364–387. Springer, Heidelberg (2006). doi:10.1007/11804192_17
Barthe, G., Crespo, J.M., Kunz, C.: Beyond 2-safety: asymmetric product programs for relational program verification. In: Artemov, S., Nerode, A. (eds.) LFCS 2013. LNCS, vol. 7734, pp. 29–43. Springer, Heidelberg (2013). doi:10.1007/978-3-642-35722-0_3
Barthe, G., Crespo, J.M., Kunz, C.: Product programs and relational program logics. J. Logical Algebraic Methods Program. 85(5), 847–859 (2016)
Barthe, G., Crespo, J.M., Kunz, C.: Relational verification using product programs. In: Butler, M., Schulte, W. (eds.) FM 2011. LNCS, vol. 6664, pp. 200–214. Springer, Heidelberg (2011). doi:10.1007/978-3-642-21437-0_17
Barthe, G., D’Argenio, P.R., Rezk, T.: Secure information flow by self-composition. In: Proceedings of the 17th IEEE Workshop on Computer Security Foundations. IEEE Computer Society (2004)
Bavota, G., et al.: When does a refactoring induce bugs? An empirical study. In: 2012 IEEE 12th International Working Conference on Source Code Analysis and Manipulation (SCAM). IEEE (2012)
Benton, N.: Abstracting allocation. In: Ésik, Z. (ed.) CSL 2006. LNCS, vol. 4207, pp. 182–196. Springer, Heidelberg (2006). doi:10.1007/11874683_12
Benton, N.: Simple relational correctness proofs for static analyses and program transformations. In: Proceedings of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. ACM (2004)
Benton, N., et al.: Relational semantics for effect-based program transformations with dynamic allocation. In: Proceedings of the 9th ACM SIGPLAN International Conference on Principles and Practice of Declarative Programming. ACM (2007)
Beringer, L.: Relational decomposition. In: Eekelen, M., Geuvers, H., Schmaltz, J., Wiedijk, F. (eds.) ITP 2011. LNCS, vol. 6898, pp. 39–54. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22863-6_6
Bozga, M., Iosif, R., Laknech, Y.: Storeless semantics and alias logic. In: Proceedings of the 2003 ACM SIGPLAN Workshop on Partial Evaluation and Semantics-based Program Manipulation, PEPM 2003, San Diego, California, USA. ACM (2003)
Clarke, E., Kroening, D., Yorav, K.: Behavioral consistency of C and verilog programs using bounded model checking. In: 2003 Proceedings of the Design Automation Conference. IEEE (2003)
Dahl, O.J., Dijkstra, E.W., Hoare, C.A.R.: Structured Programming. Academic Press Ltd., Cambridge (1972)
Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78800-3_24
Detlefs, D., Nelson, G., Saxe, J.B.: Simplify: a theorem prover for program checking. J. ACM 52(3), 365–473 (2005)
Elenbogen, D., Katz, S., Strichman, O.: Proving mutual termination. Form. Methods Syst. Des. 47(2), 204–229 (2015)
Felsing, D., et al.: Automating regression verification. In: Proceedings of the 29th ACM/IEEE International Conference on Automated Software Engineering, ASE 2014. ACM (2014)
Godlin, B., Strichman, O.: Inference rules for proving the equivalence of recursive procedures. Acta Informatica 45(6), 403–439 (2008)
Godlin, B., Strichman, O.: Regression verification. In: Proceedings of the 46th Annual Design Automation Conference. ACM (2009)
Hawblitzel, C., Kawaguchi, M., Lahiri, S.K., Rebêlo, H.: Towards modularly comparing programs using automated theorem provers. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 282–299. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38574-2_20
Hoare, C.A.R.: An axiomatic basis for computer programming. Commun. ACM 12(10), 576–580 (1969)
Igarishi, S.: An axiomatic approach to equivalence problems of algorithms with applications. Ph.D. thesis (1964)
Joshi, R., Leino, K.R.M.: A semantic approach to secure information flow. Sci. Comput. Program. 37, 1–3 (2000)
Kawaguchi, M., Lahiri, S.K., Rebêlo, H.: Conditional equivalence. Technical report MSR-TR-2010-119. Microsoft, October 2010
Koutavas, V., Wand, M.: Small bisimulations for reasoning about higher-order imperative programs. In: Conference Record of the 33rd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. ACM (2006)
Kundu, S., Tatlock, Z., Lerner, S.: Proving optimizations correct using parameterized program equivalence. In: Proceedings of the 30th ACM SIGPLAN Conference on Programming Language Design and Implementation. ACM (2009)
Lahiri, S.K., Hawblitzel, C., Kawaguchi, M., Rebêlo, H.: SYMDIFF: a language-agnostic semantic diff tool for imperative programs. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 712–717. Springer, Heidelberg (2012). doi:10.1007/978-3-642-31424-7_54
Lahiri, S., et al.: Differential assertion checking. In: Foundations of Software Engineering. ACM (2013)
Le, V., Afshari, M., Su, Z.: Compiler validation via equivalence modulo inputs’. In: Proceedings of the 35th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2014. ACM (2014)
Leino, K.R.M.: Dafny: an automatic program verifier for functional correctness. In: Clarke, E.M., Voronkov, A. (eds.) LPAR 2010. LNCS (LNAI), vol. 6355, pp. 348–370. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17511-4_20
Leino, K.R.M., Müller, P.: Verification of equivalent-results methods. In: Drossopoulou, S. (ed.) ESOP 2008. LNCS, vol. 4960, pp. 307–321. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78739-6_24
Milner, R.: Fully abstract models of typed \(\lambda \)-calculi. Theor. Comput. Sci. 4(1), 1–22 (1977)
Park, J., et al.: An empirical study of supplementary bug fixes. In: 2012 9th IEEE Working Conference on Mining Software Repositories (MSR) (2012)
Partush, N., Yahav, E.: Abstract semantic differencing via speculative correlation. In: Proceedings of the 2014 ACM International Conference on Object Oriented Programming Systems Languages & Applications. ACM (2014)
Pitts, A.M.: Operational semantics and program equivalence. In: Barthe, G., Dybjer, P., Pinto, L., Saraiva, J. (eds.) APPSEM 2000. LNCS, vol. 2395, pp. 378–412. Springer, Heidelberg (2002). doi:10.1007/3-540-45699-6_8
Stepp, M., Tate, R., Lerner, S.: Equality-based translation validator for LLVM. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 737–742. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22110-1_59
Strichman, O., Veitsman, M.: Regression verification for unbalanced recursive functions. In: Fitzgerald, J., Heitmeyer, C., Gnesi, S., Philippou, A. (eds.) FM 2016. LNCS, vol. 9995, pp. 645–658. Springer, Heidelberg (2016). doi:10.1007/978-3-319-48989-6_39
Tennent, R.D., Ghica, D.R.: Abstract models of storage. High.-Order Symbolic Comput. 13(1), 119–129 (2000)
Terauchi, T., Aiken, A.: Secure information flow as a safety problem. In: Hankin, C., Siveroni, I. (eds.) SAS 2005. LNCS, vol. 3672, pp. 352–367. Springer, Heidelberg (2005). doi:10.1007/11547662_24
Tristan, J.-B., Govereau, P., Morrisett, G.: Evaluating value-graph translation validation for LLVM. In: Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation. ACM (2011)
Tzevelekos, N.: Program equivalence in a simple language with state. Comput. Lang. Syst. Struct. 38(2), 181–198 (2012)
Wood, T.: Equivalence verification for memory allocating procedures. Ph.D. thesis, Imperial College London, Under Submission
Yang, H.: Relational separation logic. Theor. Comput. Sci. 375, 1–3 (2007)
Yanov, Y.: Logical operator schemes. In: Kybernetilca I (1958)
Zaks, A., Pnueli, A.: CoVaC: compiler validation by program analysis of the cross-product. In: Cuellar, J., Maibaum, T., Sere, K. (eds.) FM 2008. LNCS, vol. 5014, pp. 35–51. Springer, Heidelberg (2008). doi:10.1007/978-3-540-68237-0_5
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Wood, T., Drossopolou, S., Lahiri, S.K., Eisenbach, S. (2017). Modular Verification of Procedure Equivalence in the Presence of Memory Allocation. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_35
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_35
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)









 where
where 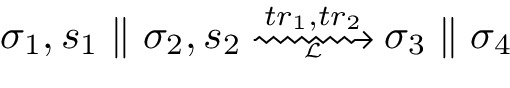


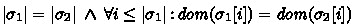
 is isomorphic to
is isomorphic to 

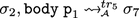 such that
such that 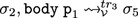 . Most cases are trivial. The interesting cases are CALLV where the called procedure is in
. Most cases are trivial. The interesting cases are CALLV where the called procedure is in  and
and  and
and  (intuition: we swap the behaviour of
(intuition: we swap the behaviour of  . To show:
. To show:  and hence exists
and hence exists  . The proof goes as expected, by applying the inner induction hypothesis twice with one slight complexity. The first application constructs another execution of
. The proof goes as expected, by applying the inner induction hypothesis twice with one slight complexity. The first application constructs another execution of  but with initial store
but with initial store  is an execution under the
is an execution under the 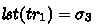 and
and 



 .
.