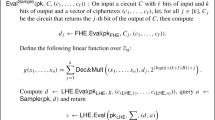Universal Constructions and Robust Combiners for Indistinguishability Obfuscation and Witness Encryption

Abstract

Over the last few years a new breed of cryptographic primitives has arisen: on one hand they have previously unimagined utility and on the other hand they are not based on simple to state and tried out assumptions. With the on-going study of these primitives, we are left with several different candidate constructions each based on a different, not easy to express, mathematical assumptions, where some even turn out to be insecure.

A combiner for a cryptographic primitive takes several candidate constructions of the primitive and outputs one construction that is as good as any of the input constructions. Furthermore, this combiner must be efficient: the resulting construction should remain polynomial-time even when combining polynomially many candidate. Combiners are especially important for a primitive where there are several competing constructions whose security is hard to evaluate, as is the case for indistinguishability obfuscation (IO) and witness encryption (WE).

One place where the need for combiners appears is in design of a universal construction, where one wishes to find “one construction to rule them all”: an explicit construction that is secure if any construction of the primitive exists.

In a recent paper, Goldwasser and Kalai posed as a challenge finding universal constructions for indistinguishability obfuscation and witness encryption. In this work we resolve this issue: we construct universal schemes for IO, and for witness encryption, and also resolve the existence of combiners for these primitives along the way. For IO, our universal construction and combiners can be built based on either assuming DDH, or assuming LWE, with security against subexponential adversaries. For witness encryption, we need only one-way functions secure against polynomial time adversaries.

P. Ananth—Partially supported by grant #360584 from the Simons Foundation. Partially supported by grants under Amit Sahai.

A. Jain—Supported by grants under Amit Sahai.

M. Naor—Research supported in part by grants from the Israel Science Foundation grant no. 1255/12, BSF and from the I-CORE Program of the Planning and Budgeting Committee and the Israel Science Foundation (grant no. 4/11). Moni Naor is the incumbent of the Judith Kleeman Professorial Chair.

A. Sahai—University of California Los Angeles and Center for Encrypted Functionalities. Research supported in part from a DARPA/ARL SAFEWARE award, NSF Frontier Award 1413955, NSF grants 1228984, 1136174, 1118096, and 1065276, a Xerox Faculty Research Award, a Google Faculty Research Award, an equipment grant from Intel, and an Okawa Foundation Research Grant. This material is based upon work supported by the Defense Advanced Research Projects Agency through the ARL under Contract W911NF-15-C-0205. The views expressed are those of the author and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

We live in a golden, but dangerous, age for cryptography. New primitives are proposed along with candidate constructions that achieve things that were previously in the realm of science fiction. Two such notable examples are indistinguishability obfuscation ¹ (IO), and witness encryption ² (WE). However, at the same time, we are seeing a steady stream of new attacks on assumptions that are underlie, or at least are closely related to, these new candidates. With this proliferation of constructions and assumptions comes the question: how do we evaluate these various assumptions, which constructions do we choose and how do we actually use them?

What is better: one candidate construction of indistinguishability obfuscation (IO) or two such candidate constructions? What about a polynomial-sized family of candidates? The usual approach should be “the more the merrier”, but how do we use these several candidates to actually obfuscate? The relevant notion is that of a combiner: it takes several candidates for a primitive and produces one instance of the primitive so that if any of the original ones is a secure construction then the result is a secure primitive. Furthermore, this combiner must be efficient: the resulting construction should remain polynomial-time. Another issue is what do we assume about the insecure constructions. Are they at least correct, i.e. do they maintain the functionality, or can they be arbitrarily faulty? We are interested in a combiner that adds very little complexity to the basic underlying schemes and assumes as little as possible regarding the insecure schemes, i.e. they may be completely dysfunctional. Furthermore, we would like the assumptions underlying our combiner to be as minimal and standard as possible.

One Candidate to Rule Them All (Theoretically Speaking). In fact, we can even go further: A closely related issue to the existence of combiners is that of a universal construction of a primitive: a concrete construction of the primitive that is secure if any secure construction exists. In the context of candidate constructions, a universal IO candidate would change the game considerably between attacker and defender: Currently, each IO candidate is based on specific mathematical techniques, and a cryptanalysis of each candidate can be done by finding specific weaknesses in the underlying mathematics. With a universal IO candidate, the only way to give a cryptanalysis of this candidate would be to prove that no secure IO scheme exists. To the best of our knowledge, no plausible approaches have been proposed for obtaining such a proof. Thus, a universal IO scheme would vastly raise the bar on what an attacker must do.

Furthermore, intriguingly, we note that IO exists if P=NP. In contrast to other objects in cryptography, IO by itself does not imply hardness. This raises the possibility of a future non-constructive existence proof for IO, even without needing to resolve P vs NP. If we have a universal IO scheme, then any such non-constructive proof would be made explicit: the universal IO scheme would be guaranteed to be secure.

Indeed, in a recent opinion paper regarding assumptions Goldwasser and Kalai [19] wrote:

We pose the open problem of finding a universal instantiations for other generic assumptions, in particular for IO obfuscation, witness encryption, or 2-message delegation for NP.

In this work we resolve two out of those three primitives, namely IO and witness encryption, for security against subexponential adversaries for IO, and polynomial adversaries for witness encryption. Our universal constructions also resolve the existence of combiners for these primitives along the way. For IO, our universal construction and combiners can be built based on either assuming DDH, or assuming LWE, with security against subexponential adversaries. For witness encryption, we need only one-way functions secure against polynomial adversaries.

Robust IO Combiners. We construct both (standard) combiners and robust combiners. A (standard) combiner handles only security: the promise is that all given candidates are correct, but only one is promised to be secure. These combiners are useful when different schemes are based on different hardness assumptions, but they all have a proof of correctness. The resulting combined scheme will be correct and as secure as all the underlying assumptions.

A robust combiner handles the case where security and correctness are both promised only for a single candidate. We only know of constructing universal schemes from robust combiners and in particular, (standard) combiners does not suffice.

The Status of IO Schemes or – Are We Dead Yet? The state of the art of IO is in flux. There is a steady stream of proposals for constructions and a similar stream of attacks on various aspects of the constructions. In order to clarify the state of the art in the full version [2] we provide a detailed explanation of the constructions, the attacks and what implications they have (a summary is provided in Fig. 13 of the full version). As of now (June 2016) there is no argument or attack known that implies that all iO schemes or primitives used by them are broken.

Brief History of Combiners and Universal Cryptographic Primitives. The notion of a combiner and its connection to universal construction were formalized by Harnik [21] (see also Herzberg [22, 23]). An early instance of a combiner for encryption is that of Asmuth and Blakely [8]. A famous example of a universal construction (and the source of the name) is that of one-functions due to Levin [27] (for details see Goldreich [17, Sect. 2.4.1]).

Related Work. Concurrent to our work, Fischlin et al. [13], building upon [24], also studied the notion of robust obfuscation combiners. The security notions considered in their work also deal with virtual black box obfuscation and virtual gray box obfuscation, that are not dealt with in our work. However, they achieve a much weaker result: they can only combine a constant number of candidates and furthermore, they assume that a majority of the candidates are correct. Thus, their combiners are not useful to obtaining any implication to universal indistinguishability obfuscation.

1.1 Our Results

Our first result is a construction of an IO combiner. We give two separate constructions, one using LWE, and other using DDH. Thus, we can build IO combiners from two quite different assumptions.

Theorem 1

(Informal). Under the hardness of Learning with Errors (LWE) and IO secure against sub-exponential adversaries, there exist an IO combiner.

Theorem 2

(Informal). Under the hardness of Decisional Diffie-Hellman (DDH) and IO secure against sub-exponential adversaries, there exist an IO combiner.

We show how to adapt the LWE-based IO combiner to obtain a universal IO scheme.

Theorem 3

(Informal). Under the hardness of Learning with Errors (LWE) against sub-exponential adversaries and the existence of IO secure against sub-exponential adversaries, there exists a universal IO scheme.

For witness encryption, we have similar results, under assumptions widely believed to be weaker. We prove the following theorem.

Theorem 4

(Informal). If one-way functions exist, then there exist a secure witness encryption combiner.

Again, we extend this and get a universal witness encryption scheme.

Theorem 5

(Informal). If one-way functions and witness encryption exist, then there is a universal witness encryption scheme.

Theorem 5 assumes the existence of one-way functions. Notice that if ${\mathsf {P}}={\mathsf {NP}}$ then WE exist, however, one-way functions do not. Thus, in most cryptographic application one-way functions are used as an additional assumption. Nevertheless, we can make a stronger statement: If there exist any hard-on-average language in ${\mathsf {NP}}$ then there is a universal WE scheme. In [25] it was shown that the existence of witness encryption and a hard-on-average language in ${\mathsf {NP}}$ implies the existence of one-way functions. By combing this with Levin’s universal one-way function [27] we obtain our result.

In full version, we present the constructions of universal secret sharing for NP and universal witness PRFs. Both these constructions assume only one-way functions.

2 Techniques

We present the technical challenges and describe how we overcome them.

2.1 Universal Obfuscation

A natural starting point is to revisit the construction of universal one-way functions [27] – constructions of other known universal cryptographic primitives [21] have the same flavor. An explicit function f is said to be a universal one-way function if the mere existence of any one-way function implies that f is one-way.

The universal one-way function $f_{\mathsf {univ}}$ on input $x= y_1 || \ldots || y_{\ell }$, where $|x|=\ell ^2$, executes as follows³:

• 1. Interpret the integer $i \in \{1,\ldots ,\ell \}$ as a Turing machine $M_i$. This interpretation is quite standard in the computational complexity literature⁴.

• 2. Output $M_1(y_1)||\cdots ||M_{\ell }(y_{\ell })$.

To argue security, we exploit the fact that there exists a secure one-way function represented by Turing machine $M_{\mathsf {owf}}$. Let $\ell _0$ be an integer that can be interpreted as $M_{\mathsf {owf}}$. We argue that it is hard to invert $M_{\mathsf {owf}}(x)$, where x has length at least $\ell _0^2$ and is drawn uniformly at random. To see why, notice that in Step 1, $M_{\mathsf {owf}}$ will be included in the enumeration. From the security of $M_{\mathsf {owf}}$ it follows that it is hard to invert $M_{\mathsf {owf}}(y_{\ell _0})$, where $y_{\ell _0}$ is the $\ell _0^{th}$ block of x. This translates to the un-invertibility of $f_{\mathsf {univ}}(x)$. This proves that $f_{\mathsf {univ}}$ is one-way⁵.

Let us try to emulate the same approach to obtain universal indistinguishability obfuscation. On input circuit C, first enumerate the Turing machines $M_1,\ldots ,M_{\ell }$, where $\ell$ here is the size of the circuit C. We interpret $M_i$’s as indistinguishability obfuscators. It is not clear how to implement the second step in the context of obfuscation – unlike one-way functions we cannot naïvely break the circuit into blocks and individually obfuscate each block. We need a mechanism to jointly obfuscate a circuit using multiple obfuscators $M_1,\ldots ,M_{\ell }$ such that the security of the joint obfuscation is guaranteed as long as one of the obfuscators is secure. This is where indistinguishability obfuscation combiners come in. Designing combiners for indistinguishability obfuscation involves a whole new set of challenges and we deal with them in a separate section (Sect. 2.2). For now, we assume we have such combiners at our disposal.

Warmup Attempt. Using combiners for IO, we propose the following approach to achieve universal obfuscation. The universal obfuscator $IO_{\mathsf {univ}}$ on input circuit C executes the following steps:

• 1. Interpret the integer $i \in \{1,\ldots ,\ell \}$ as a Turing machine $M_i$.

• 2. Obfuscate C by applying the IO combiner on the machines $M_1,\ldots ,M_{\ell }$. Output the result $\overline{C}$ of the IO combiner.

Unlike the case of one-way functions, in addition to security we need to argue correctness of the above scheme. An obfuscator $M_i$ is said to be correct if the obfuscated circuit $M_i(C)$ is equivalent to C (or agrees on most inputs) and this should be true for every circuit C. This in turn depends on the correctness of obfuscators $M_1,\ldots ,M_{\ell }$. But we don’t have any guarantee on the correctness of $M_1,\ldots ,M_{\ell }$.

Test-and-Discard. We handle this by first checking for every i whether the obfuscator $M_i$ is correct. This is infeasible in general. However, we test the correctness of $M_i$ only on the particular circuit obfuscated by $M_i$ during the execution of the universal obfuscation. In more detail, suppose we execute $IO_{\mathsf {univ}}$ on circuit C and during the execution of the IO combiner, let $\mathbf {[C]}_i$ (derived from C) be the circuit that we obfuscate using machine $M_i$. Then we test whether $M_i(\mathbf {[C]}_i)$ agrees with $M_i$ on significant fraction of inputs. This can be done by picking inputs at random and testing whether both circuits (obfuscated and un-obfuscated) agree on these inputs. If $M_i$ fails the test, it is discarded. If it passes the test, then $M_i$ cannot be used directly since $M_i(\mathbf {[C]}_i)$ could agree with $\mathbf {[C]}_i$ on $(1-1/\mathrm {poly})$-fraction of inputs and yet it could pass the test with non-negligible probability. So we need to reduce the error probability of $M_i(\mathbf {[C]}_i)$ to negligible before it is ready to be used.

Correctness Amplification. A first thought would be to use the recent work that shows an elegant correctness amplification for IO by Bitansky and Vaikuntanathan [6]. In particular, they show how to transform an obfuscator that is correct on at least $(1/2+1/\mathrm {poly})$-fraction of inputs into one that is correct on all inputs. At first glance this seems to be “just what the doctor ordered”, there is, however, one catch here: their transformation is guaranteed to work if the obfuscator is correct for every circuit C on at least $(1/2+1/\mathrm {poly})$-fraction of inputs. However, we are only ensured that it is approximately correct on only one circuit! Nonetheless we show how to realize correctness amplification with respect to a single circuit and ensure that $M_i(\mathbf {[C]}_i)$ does not agree with $\mathbf {[C]}_i$ on only negligible fraction of inputs. Once we perform the error amplification, the obfuscator $M_i$ will be used in the IO combiner. In the end, the result of the IO combiner will be an obfuscated circuit $\overline{C}$; the correctness guarantees of $M_i(\mathbf {[C]}_i)$, for every i, translate to the corresponding correctness guarantee of $\overline{C}$.

Handling Selective Abort Obfuscators. We now move on to security. For two equivalent circuits $C_0,C_1$, we need to argue that their obfuscations are computationally indistinguishable. To do this, we need to rely on the security of IO combiner. The security of IO combiner requires that as long as one of the machines $M_i$ is a secure obfuscator⁶ then the joint obfuscation of $C_0$ using $M_1,\ldots ,M_{\ell }$ is indistinguishable from the joint obfuscation of $C_1$ using the same candidates. The fact that same candidates are used is crucial here since the final obfuscated circuit could potentially reveal the description of the obfuscators combined.

However, there is no such guarantee offered in our case! Recall that we have a ‘test-and-discard’ phase where we potentially throw out some obfuscators. It might be the case that a particular candidate $M_{mal}$ is correct only on circuits derived from $C_0$ but fails on circuits derived from $C_1$. We call such obfuscators selective abort obfuscators. Clearly, selective abort obfuscators can lead to a complete break of security. In fact, if there are $\ell$ obfuscators used then potentially $\ell -1$ of them could be of selective abort type. To protect against these adversarial obfuscators we ensure that the distribution of the $\ell$ derived circuits is computationally independent from the circuit to obfuscate.

Issue of Runtime. While the above ideas ensure correctness and security, we haven’t yet shown that our scheme is efficient. In fact it could potentially be the case our scheme never halts on some inputs⁷. This could happen since we have no a priori knowledge on the runtime of the obfuscators considered. We propose a na$\mathrm {\ddot{i}}$ve solution to this problem: we assume the knowledge of an upper bound on the runtime of the actually secure obfuscator. In some sense, the assumption of time bound might be inherent – without this we are required to predict a bound on the runtime of a Turing machine and we know in general this is an undecidable problem.

2.2 Combiners for Indistinguishability Obfuscation

We now focus our attention on constructing an IO combiner. Recall, in the setting of IO combiner we are given multiple IO candidates⁸ with all of them satisfying correctness but with only one of them being secure. We then need to combine all of them to produce a joint obfuscator that is secure.

This scenario is reminiscent of a concept we are quite familiar with: Secure Multi-Party Computation (MPC). In the secure multi-party computation setting, there are multiple parties with individual inputs and the goal of all these parties is to jointly compute a functionality. The privacy requirement states that the inputs of the honest parties are hidden other than what can be leaked by the output.

Indeed, MPC provides a natural template to solve the problem of building an IO combiner: Let $\varPi _1,\ldots ,\varPi _n$ be the IO candidates and let C be the circuit to be obfuscated.

• Secret share the circuit C into n shares $s_1,\ldots ,s_n$.

• Take any n-party MPC protocol for the functionality $\mathcal {F}$ that can tolerate all-but-one malicious adversaries [18]. The n-input functionality $\mathcal {F}$ takes as input $( (s_1,x_1),(s_2,x_2),\ldots ,(s_n,x_n) )$; reconstructs C from the shares and outputs C(x) only if $x=x_1=\cdots =x_n$.

• Obfuscate the “code” (or algorithmic description) of the $i^{th}$ party using $\varPi _i$.

• The joint obfuscation of all the parties is the final obfuscated circuit!

To evaluate on an input x, perform the MPC protocol on the obfuscated parties with $(s_i,x)$ being the input of the $i^{th}$ party.

Could the above approach lead to a secure IO combiner? The hope is that the security of MPC can be used to argue that one of the shares (corresponding to the honest party) is hidden which then translates to the hiding of C.

However, we face some fundamental challenges in our attempt to realize the above template, and in particular we will not be able to just invoke general solutions like [18], and we will need to leverage more specialized cryptographic objects.

Challenge #1: Single-Input versus Multi-Inputs Security. Recall that in the context of MPC, we argue the security only for a particular set of inputs (one for every party) in one session. In particular, a fresh session needs to be executed to compute the functionality on a different set of inputs. However, obfuscation is re-usable – it enables multiple evaluations of the obfuscated circuit. The obfuscated circuit should hide the original circuit independent of the number of times the obfuscated circuit is evaluated. On the other hand, take the classical Yao’s garbled circuits [32], used in two party secure computation, for example. Suppose we are provided with the ability to evaluate the garbled circuit on two different inputs then the security completely breaks down.

Challenge #2: Power of the Adversary. Suppose we start with an arbitrary multi-round MPC protocol. In the world of IO combiners, this corresponds to executing a candidate multiple times during the evaluation of a single input. While the party in the MPC protocol can maintain state in between executions, a candidate does not have the same luxury since it is stateless. This enables the adversarial evaluator to launch so called resetting attacks: during the evaluation of the IO combiner on a single input x, a secure candidate could first be executed on transcripts consistent with x and later executed on transcripts consistent with a different input $x'$. Since, the secure candidate cannot maintain state, it is possible that it cannot recognize such a malicious execution. We need to devise additional mechanisms to prevent such attacks.

Challenge #3: Virtual Black Box Obfuscation versus IO. The above two challenges exist even if we had started off with virtual black box (VBB) obfuscation. Dealing with indistinguishability obfuscation as opposed to VBB presents us with fresh challenges. Indeed, in MPC, we take for granted that an honest party hides its input from the adversary. However, if we obfuscate the parties using IO, it is not clear whether the relevant input – the share of C – is hidden at all. Arguing this requires importing IO-friendly tools (for instance, [31]) studied in the recent literature and making it compatible with the tools of MPC that we want to use.

We will see next how to address the above challenges.

Our Approach. We present two different approaches to construct IO combiners. The first solution, in addition to existence of IO, assumes the hardness of Decisional Diffie Hellman. The second solution assumes additionally the hardness of learning with errors. Common to both these solutions is a technique of [9] that we’ll call the partition-programming technique. We give a brief overview of this technique below.

Partition-Programming Technique: Consider a randomized algorithm $P(\cdot ,\cdot )$ that takes as input secret sk, public instance $x \in \{0,1\}^{\lambda }$ and produces a distribution $\mathcal {D}_x$. Suppose there exists a simulator $\mathsf {Sim}$ that on input x outputs a distribution $\mathcal {D}^*_x$ such that the distributions $\mathcal {D}_x$ and $\mathcal {D}_x^*$ are statistically close.

Let us say we are given obfuscation of $P(sk,\cdot )$ (sk is hardwired in the program), we show how to use the partition-programming technique to remove the secret sk. We proceed in $2^{\lambda }$ hybrids: In the $i^{th}$ hybrid, we have a hybrid obfuscated program that on input x, executes P(sk, x) if $x \le i$ but otherwise it executes $\mathsf {Sim}(x)$. Now, the indistinguishability of $i^{th}$ hybrid and $(i+1)^{th}$ hybrid can be argued directly from the security of IO: here we are using the fact that the simulated distribution and the real distribution are statistically close. In the $(2^{\lambda +1})^{th}$ hybrid, we have a program that only uses $\mathsf {Sim}$, on every input, to generate the output distribution. Thus, we have removed the secret sk from the program.

This technique will come in handy when we address Challenge #1. We will see below how this technique will be used in both the solutions.

DDH-Based Solution. We begin by tackling Challenge #2. We noted that using interactive MPC solutions are bound to result in resetting attacks. Hence, we restrict our attention to non-interactive solutions. We need to determine our communication pattern between the candidates. In particular, we consider the “line” communication pattern: Suppose there are n candidates $\varPi _1,\ldots ,\varPi _n$ and let C be the circuit to be obfuscated. For this discussion, we use the same notation $\varPi _i$ to also refer to the circuit obfuscated by the candidate $\varPi _i$. The first obfuscated circuit $\varPi _1$ produces an output that will be input to $\varPi _2$ and so on. In the end, $\varPi _n$ will receive the input from $\varPi _{n-1}$ and the output of $\varPi _n$ will determine the final output.

Lets examine how to achieve a solution in the above communication model, by first considering a naïve approach: $\varPi _1$ has hardwired into it an encryption $\mathsf {Enc}(pk,C)$ of circuit C to be obfuscated. It receives an input x, it performs a part of the computation and sends the result to the next candidate $\varPi _2$ who performs another part of the computation, sends it to $\varPi _3$ and so on. In the end, the last candidate $\varPi _n$ has the secret key sk to decrypt the output. This is clearly insecure because if both $\varPi _1$ and $\varPi _n$ are broken then using sk and $\mathsf {Enc}(pk,C)$ we can recover the circuit C. This suggests the use of a re-encryption scheme. A re-encryption scheme is associated with public keys $pk_1,\ldots ,pk_{n+1}$ and corresponding re-encryption keys $rk_{1 \rightarrow 2},\ldots ,rk_{n \rightarrow (n+1)}$. The first candidate $\varPi _1$ will have hardwired into it $\mathsf {Enc}(pk_1,C)$ and the $i^{th}$ candidate has hardwired into it the re-encryption key $rk_{i \rightarrow i+1}$. Thus, the $i^{th}$ candidate performs part of the computation, re-encrypts with respect to $pk_{i+1}$ using its re-encryption key $rk_{i \rightarrow i+1}$. We provide the secret key $sk_{n+1}$, corresponding to public key $pk_{n+1}$, as part of the obfuscated circuit. Using this, the evaluator can decrypt the output and produce the answer. Intuitively, as long as one candidate hides one secret key, the circuit C should be safe.

The natural next step is to figure out how to implement the “computation” itself: one direction would be to consider re-encryption schemes that are homomorphic with respect to arbitrary computations. However, we currently do not know of the existence of such schemes based on DDH (for LWE-based solutions, see below). We note that [1] faced similar hurdles while designing DDH-based multi-server delegation schemes. They employed the use of re-randomizable garbled circuits to implement the “computation” aspect of the above approach. A re-randomizable garbling scheme is a garbling scheme which is accompanied by a re-randomization algorithm that takes as input garbled circuit-input wire keys pair $(\mathsf {GC},w_x)$ and outputs $(\mathsf {GC}^r,w_x^r)$.

Following along the lines of the approach of [1], we propose the following solution template:

• 1. First we compute the garbled circuit-wire keys pair $(\mathsf {GC}^1,w^1)$ of circuit C corresponding to the re-randomizable garbled circuits scheme. Here, $w^1$ comprises of keys associated to bits 0 and 1 with respect to every position. $\varPi _1$ has hardwired into it, $\mathsf {Enc}(pk_1,(\mathsf {GC}^1,w^1))$.

• 2. $\varPi _1$ takes as input x and produces $\mathsf {Enc}(pk_2,(\mathsf {GC}^2,w_x^2))$, where $(\mathsf {GC}^2,w_x^2)$ is obtained by first re-randomizing $(\mathsf {GC}^1,w^1)$ and then choosing the wire keys corresponding to x. This process is enabled using the re-encryption key $rk_{1 \rightarrow 2}$. In addition, we require that the re-encryption process allows for homomorphic operations – in particular, it should allow for homomorphism of re-randomization operation of the garbling schemes.

• 3. The $i^{th}$ candidate takes as input $\mathsf {Enc}(pk_{i},(\mathsf {GC}^i,w_x^i))$; homomorphically re-randomizes the garbled circuit while simultaneously re-encrypting the ciphertext to obtain $\mathsf {Enc}(pk_{i+1},(\mathsf {GC}^{i+1},w_x^{i+1}))$.

• 4. In the end, the $n^{th}$ candidate $\varPi _n$ outputs $\mathsf {Enc}(pk_{n+1},(\mathsf {GC}^{n+1},w_x^{n+1}))$. Using the secret key $sk_n$, we can decrypt the output $(\mathsf {GC}^{n+1},w_x^{n+1})$. We then evaluate the garbled circuit $\mathsf {GC}^{n+1}$ using the wire keys $w_x^{n+1}$ to recover the output.

We employ a specific re-randomizable garbled circuits by [15] and homomorphic re-encryption scheme by [7], where both these primitives can be based on DDH. The above template does not immediately work since an adversarial evaluator could feed in incorrect inputs to the secure candidate. While [1] used non-interactive zero knowledge proofs (NIZKs) to resolve this issue, we need to employ “IO-friendly” proofs such as statistically-sound NIZKs [5, 31]. Refer to full version [2] for the formal construction.

Security: To argue security, we need to rely on the security of re-encryption schemes in addition to the security guarantees of the other schemes. The security property of a re-encryption scheme states that given re-encryption keys $\{rk_{i \rightarrow i+1}\}_{i \in [n]} \backslash \{ rk_{\mathbf {i}\rightarrow \mathbf {i}+1}\}$ and a secret key $sk_{n+1}$, it is computationally hard to distinguish $\mathsf {Enc}(pk_1,m_0)$ from $\mathsf {Enc}(pk_1,m_1)$.

To argue the security of universal obfuscator, we have to get rid of the re-encryption key corresponding to the secure candidate – indeed, in the case of [1] the re-encryption key corresponding to the honest party is removed in the security proof. In our scenario, however, this can only be implemented if we hardwire all possible outputs inside the code of the secure candidate. Clearly, this is not possible since there are exponentially many outputs. This is where we will use the partition-programming technique to remove the re-encryption key. To apply the technique, we argue that the re-encrypted ciphertexts are statistically close to freshly generated ciphertexts (which will be our simulated distribution) and this property holds for the particular instantiation of [7] we are considering.

LWE-Based Solution. We give an alternate construction based on the learning with errors (LWE) assumption. One potential approach is to take the above solution and replace the DDH-based primitives with LWE-based primitives. Namely, we replace re-randomizable garbled circuits and re-encryption schemes with fully homomorphic encryption schemes. While we believe this is a viable approach, it turns out we can give an arguably more elegant solution by using the notion of multi-key fully homomorphic encryption [10, 28, 29]. A multi-key FHE allows for generating individual public key-secret key pairs $\{pk_i,sk_i\}$ such that they can be later combined to obtain a joint public key $\mathbf {pk}$. To be more precise, given a ciphertext with respect to $pk_i$, there is an “Expand” operation that transforms it into a ciphertext with respect to a joint public key $\mathbf {pk}$. Once this done, the resulting ciphertext can be homomorphically evaluated just like any FHE scheme. The resulting ciphertexts can then be individually decrypted using $sk_i$’s to obtain partial decryptions. Finally, there is a mechanism to combine the partial decryptions to obtain the final output.

Before we outline the solution below, we first fix the communication model. We consider a “star” interaction network: suppose there are n candidates $\varPi _1,\ldots ,\varPi _n$. Each candidate $\varPi _i$ is executed on the same input x. The joint outputs of all these candidates are then combined to obtain the final output. We propose the solution template based on multi-key FHE below.

• 1. We first secret share C into different shares $s_1,\ldots ,s_n$.

• 2. Generate public key-secret key pairs $\{pk_i,sk_i\}$ for all $i \in [n]$. Encrypt $s_i$ with respect to $pk_i$ to obtain the ciphertext $\mathsf {CT}_i$.

• 3. “Expand” every ciphertext $\mathsf {CT}_i$ into another ciphertext $\widehat{\mathsf {CT}_i}$ with respect to the joint public key $\mathbf {pk}$ which is a function of $(pk_1,\ldots ,pk_n)$.

• 4. Every candidate $\varPi _i$ has hardwired into it the secret key $sk_i$ and ciphertext $\widehat{\mathsf {CT}_i}$. It takes as input x and first homomorphically evaluates the universal circuit $U_x$ on $\widehat{\mathsf {CT}_i}$ to obtain an encryption of C(x), namely $\widehat{\mathsf {CT}_i^{C(x)}}$, with respect to $\mathbf {pk}$. Finally, using $sk_i$ it outputs the partial decryption of $\widehat{\mathsf {CT}_i^{C(x)}}$.

• 5. The different partial decryptions output by the candidates are later combined to obtain the final output.

Security: We rely on the semantic security of the MFHE scheme to argue the security of the obfuscator. The security notion of multi-key FHE intuitively guarantees that the semantic security on ciphertext $\mathsf {CT}_i$ can be argued as long as the adversary never gets the secret key $sk_i$ for some $i \in [n]$. A naïve approach is to remove the secret key $sk_{\mathbf {i}}$ from the secure candidate $\varPi _{\mathbf {i}}$. A similar issue that we encountered in the case of DDH-based solution arises here as well – we need to hardwire exponentially many outputs. Here comes partition-programming technique to the rescue! We show how to use this technique to remove $sk_{\mathbf {i}}$ after which we can argue the semantic security of MFHE, and thus the security of the obfuscator. To apply this technique, we need an alternate simulated distribution that simulates the partial decryption keys. We use the scheme of [29] who define such a simulatability property where the simulated distribution is statistically close to the real distribution. Refer to Sect. 4 for the formal construction.

The above LWE-based construction, unlike the DDH-based construction, satisfies some additional properties that are used to design a special type of IO combiner (we call this decomposable IO combiner in Sect. 3.1) which will then be used to construct universal indistinguishability obfuscation.

Robust IO Combiners. The description above details how to construct a (standard) IO combiner, that is, one that assumes all candidates are correct. The construction on a robust combiner is similar to the construction of the universal IO scheme. We discard candidates that are not approximately correct and boost the correctness of those that are. The difference between a universal scheme and a robust combiner is that in a robust combiner we are given n arbitrary candidates whereas in a universal scheme we construct the candidates by enumerating over TMs in a lexicographic order.

2.3 Universal Witness Encryption

We have discussed the construction of an IO combiner, and how to use the combiner to achieve a universal construction of IO. We describe our construction of a universal witness encryption (WE) scheme. We show that a universal WE scheme exists on the sole assumption of the existence of a one-way function. First, we construct a WE combiner. This is achieved similarly to combiners for public-key encryption [21], using secret sharing. To encrypt a message m one secret shares the message to n shares such that all of them are needed to recover the message. Then, he encrypts each share using a different candidate. If at least one of the candidate schemes is secure then at least one share is unrecoverable and the message remains hidden.

The main challenge constructing a universal WE scheme is handling correctness. In the universal IO construction we had two main steps. The first was to test whether a candidate is approximately correct. This step was accomplished easily by sampling the obfuscated circuit on random inputs and verifying its correctness. Notice that although we cannot verify that the candidate is approximately correct for all circuits, we can verify that it is correct for the circuit in hand. The second step was to boost the correctness to achieve (almost) perfect security. This was obtained by suitably adapting the transformation described by Bitansky and Vaikuntanathan [6] to work in our setting where we only have a correctness guarantee for a single circuit.

The techniques used for the universal IO scheme seem not to apply for WE. Consider a language L with a relation R and a candidate scheme $\varPi$. To test correctness on an input x and a message m, one needs to encrypt the message and decrypt the resulting ciphertext. However, decryption requires a valid witness for x, where it might be ${\mathsf {NP}}$-hard to find one! Testing, therefore, is limited to instances where it is easy to find a witness, a regime where witness encryption is trivial. Moreover, even given an approximate candidate, the boosting techniques used for the universal IO scheme do not apply for witness encryption.

Witness Injection. We describe a transformation that modifies any WE candidate scheme to be “testable” and also show how to boost the correctness of such testable schemes. Our first technique is to inject a “fake” witness for any x such that it will be easy to find this witness, for a party which has a trapdoor and computationally hard without the trapdoor (this is as in Feige and Shamir [12]). Moreover, this transformation will be indistinguishable for the (computationally bounded) candidate scheme.

Denote $(x,w) \in R$ for an instance x with a valid witness w. Let $\mathsf {PRG}$ be a length doubling pseudorandom generator. For any string z, we augment the language L and define $L_z$ with the relation $R_z$ such that

$$\begin{aligned} (x,w) \in R_z \iff (x,w) \in R \vee \mathsf {PRG}(w)=z. \end{aligned}$$

Notice that if we choose $z=\mathsf {PRG}(s)$ for a random seed s, then $L_z$ is the trivial language of all strings. Whereas, if z is chosen uniformly at random then with high probability $L_z$ is equivalent to L, and these two cases are indistinguishable for anyone not holding the seed. This step enables us to test a candidate for some specific instance x: We choose $z \leftarrow \mathsf {PRG}(s)$, encrypt relatively to $L_z$, decrypt using the “fake” witness s and verify the output. After testing, we replace z with a random string (outside the range of the $\mathsf {PRG}$) to get back the original language L. The problem is that this guarantees correctness only on our specific witness. The decryption algorithm, however, might refuse to cooperate for any other witness the user chooses to use.

Witness Protection Program. The next step is to apply what we call a witness-worst-case transformation. That is, a scheme that works on all witnesses with the same probability. Our main tool is a non-interactive zero knowledge (NIZK) proof system with statistical soundness. Suppose (P, V) is such a NIZK scheme with a common random string $\sigma$. Then we further augment the language $L_z$ to $L_{z,\sigma }$ with relation $R_{z,\sigma }$ such that:

$$\begin{aligned} (x,\pi ) \in R_{z,\sigma } \iff V(\sigma , x, \pi )=1. \end{aligned}$$

If $(x,w) \in R$ is a valid instance witness pair for L, then the corresponding witness for $L_{z,\sigma }$ will be $\pi \leftarrow P(\sigma ,x,w)$. That is, executing the transformed scheme on x, w relative to the language L translate to executing the original scheme on $x,\pi$ relative to the language $L_{z,\sigma }$ for a randomly chosen z. Finally, to boost the success probability we apply a standard “BPP amplification”; encrypt many times and take the majority.

The result is roughly the following algorithm. We take any scheme and apply our witness-worst-case transformation for $z \leftarrow \mathsf {PRG}(s)$. Afterwards, we can test it on a fake witness while we are assured that it will work the same for any other witness. Then, if the scheme passes all tests, we replace z with a random string, and boost the correctness such that it will work for any witness with all but negligible probability. Finally, we apply the WE combiner to get a universal scheme. For the exact details see Sect. 2.3.

Relying on One-Way Functions. The description above of a universal witness encryption scheme used NIZK proof system as a building block, where we promised using only one-way functions. These proofs are not known to be implied by one-way functions and moreover no universal NIZK scheme is known (and this is an interesting open problem!). However, standard interactive zero knowledge can be constructed for any language in ${\mathsf {NP}}$ for one-way functions and moreover there exist a universal one-way function [27]. Of course, we cannot use an interactive protocol, but, taking a closer look we observe that we can simulate a protocol between a verifier and a prover before the actual witness is given. That is, we can simulate a zero-knowledge protocol that might have many rounds, however, only the final round depends on the witness itself. Such protocols are known as pre-process non-interactive zero-knowledge protocols and where studied in [11, 26] where they proved how to construct them based on way-one functions.

For the final scheme, we will run the pre-process protocol to get two private states $\sigma _V$ and $\sigma _P$ for the verifier and the prover respectively, just before the final round. The modified language will be $L_{z,\sigma _V}$ with relation $R_{z,\sigma _V}$, where

$$\begin{aligned} (x,\pi ) \in R_{z,\sigma _V} \iff V(\sigma _V,x,\pi )=1. \end{aligned}$$

We will publish $\sigma _P$ as part of the encryption so that a user, given witness w can produce the corresponding final round of the proof $\pi \leftarrow P(\sigma _P,x,w)$. Notice that the given the state of the prover, $\sigma _P$, the proof $\pi$ is not zero-knowledge. However, since the decryption algorithm of the scheme does not get the state of the prover (only the state of the verifier) then from his perspective it is zero-knowledge.

3 Indistinguishability Obfuscation (IO) Combiners

Suppose we have many indistinguishability obfuscation (IO) schemes, also referred to as IO candidates). We are additionally guaranteed that one of the candidates is secure. No guarantee is placed on the rest of the candidates and they could all be potentially broken. Indistinguishability obfuscation combiners provides a mechanism of combining all these candidates into a single monolithic IO scheme that is secure. We emphasize that the only guarantee we are provided is that one of the candidates is secure and in particular, it is unknown exactly which of the candidates is secure.

We give a thorough formal treatment of the concept of IO combiners next. We start by providing the syntax of an obfuscation scheme and then present the definitions of a (secure) IO candidate. Then, in Sect. 3.1 we finally present the definition of IO combiner.

Syntax of Obfuscation Scheme. An obfuscation scheme associated to a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ consists of two PPT algorithms $(\mathsf {Obf},\mathsf {Eval})$ defined below.

• Obfuscate, $\overline{C} \leftarrow {\mathsf {Obf}}(1^{\lambda },C)$: It takes as input security parameter $\lambda$, a circuit $C \in \mathcal {C}_{\lambda }$ and outputs an obfuscation of C, $\overline{C}$.

• Evaluation, $y \leftarrow {\mathsf {Eval}}\left( \overline{C},x \right)$: This is a deterministic algorithm. It takes as input an obfuscation $\overline{C}$, input $x \in \{0,1\}^{\lambda }$ and outputs y.

Throughout this work, we will only be concerned with uniform $\mathsf {Obf}$ algorithms. That is, $\mathsf {Obf}$ and $\mathsf {Eval}$ are represented as Turing machines (or equivalently uniform circuits).

We define the notion of an IO candidate below. The following definition of obfuscation scheme incorporates only the correctness and polynomial slowdown properties of an indistinguishability obfuscation scheme [4, 14, 20].

Definition 1

( $\mu$ -Correct IO Candidate). An obfuscation scheme $\varPi =(\mathsf {Obf},\mathsf {Eval})$ is an $\mu$ -correct IO candidate for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$, with every $C \in \mathcal {C}_{\lambda }$ has size $\mathrm {poly}(\lambda )$, if it satisfies the following properties:

• Correctness: For every $C:\{0,1\}^{\lambda } \rightarrow \{0,1\} \in \mathcal {C}_{\lambda }, x \in \{0,1\}^{\lambda }$ it holds that:

  $$ \mathsf {Pr}\left[ \mathsf {Eval}\left( \mathsf {Obf}(1^{\lambda },C),x \right) =C(x) \right] \ge \mu (\lambda ), $$

  over the random coins of $\mathsf {Obf}$.

• Polynomial Slowdown: For every $C:\{0,1\}^{\lambda } \rightarrow \{0,1\} \in \mathcal {C}_{\lambda },$ we have the running time of $\mathsf {Obf}$ on input $(1^{\lambda },C)$ to be $\mathrm {poly}(|C|,\lambda )$. Similarly, we have the running time of $\mathsf {Eval}$ on input $(\overline{C},x)$ is $\mathrm {poly}(|\overline{C}|,\lambda )$.

Note that an identity function I is a valid IO candidate. We make use of this fact later on.

Remark 1

We say that $\varPi$ is an IO candidate if it is a $\mu$-correct IO candidate with $\mu =1$.

If any IO candidate additionally satisfies the following (informal) security property then we define it to be a secure IO candidate: for every pair of circuits $C_0$ and $C_1$ that are equivalent we have obfuscations of $C_0$ and $C_1$ to be indistinguishable by any PPT adversary.

Definition 2

( $\mu$ -Correct $\epsilon$ -Secure IO Candidate). An obfuscation scheme $\varPi =(\mathsf {Obf},\mathsf {Eval})$ for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ is a $\mu$ -correct $\epsilon$ -secure IO candidate if it satisfies the following conditions:

• $\varPi$ is a $\mu$-correct IO candidate with respect to $\mathcal {C}$,

• Security. For every PPT adversary $\mathcal {A}$, for every sufficiently large $\lambda \in \mathbb {N}$, for every $C_0,C_1 \in \mathcal {C}_{\lambda }$ with $C_0(x)=C_1(x)$ for every $x \in \{0,1\}^{\lambda }$ and $|C_0|=|C_1|$, we have:

  $$ \Big | \mathsf {Pr}\Big [0 \leftarrow {\mathcal {A}}\Big ( \mathsf {Obf}(1^{\lambda },C_0),C_0,C_1 \Big ) \Big ] - \mathsf {Pr}\Big [0 \leftarrow {\mathcal {A}}\Big ( \mathsf {Obf}(1^{\lambda },C_1),C_0,C_1 \Big ) \Big ] \Big | \le \epsilon (\lambda ) $$

We remarked earlier that identity function is an IO candidate. However, note that the identity function is not a secure IO candidate.

Remark 2

We say that $\varPi$ is a secure IO candidate if it is a $\mu$-correct $\epsilon$-secure IO candidate with $\mu =1$ and $\epsilon (\lambda ) = \mathsf {negl}(\lambda )$, for some negligible function $\mathsf {negl}$.

In the literature [14, 31], a secure IO candidate is simply referred to as an indistinguishability obfuscation scheme.

We have the necessary ingredients to define an IO combiner.

3.1 Definition of IO Combiner

We present the formal definition of IO combiner below. First, we provide the syntax of the IO combiner. Later we present the properties associated with an IO combiner.

There are two PPT algorithms associated with an IO combiner, namely, $\mathsf {CombObf}$ and $\mathsf {CombEval}$. Procedure $\mathsf {CombObf}$ takes as input circuit C along with the description of multiple IO candidates⁹ and outputs an obfuscation of C. Procedure $\mathsf {CombEval}$ takes as input the obfuscated circuit, input x, the description of the candidates and outputs the evaluation of the obfuscated circuit on input x.

Syntax of IO Combiner. We define an IO combiner $\varPi _{\mathsf {comb}}=(\mathsf {CombObf},\mathsf {CombEval})$ for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$.

• Combiner of Obfuscate algorithms, $\overline{C} \leftarrow {\mathsf {CombObf}}(1^{\lambda },C,\varPi _1,\ldots ,\varPi _n)$: It takes as input security parameter $\lambda$, a circuit $C \in \mathcal {C}$, description of IO candidates $\{\varPi _i\}_{i \in [n]}$ and outputs an obfuscated circuit $\overline{C}$.

• Combiner of Evaluation algorithms, $y \leftarrow {\mathsf {CombEval}}(\overline{C},x,\varPi _1,\ldots ,\varPi _n)$: It takes as input obfuscated circuit $\overline{C}$, input x, descriptions of IO candidates $\{\varPi _i\}_{i \in [n]}$ and outputs y.

We define the properties associated to any IO combiner. There are three main properties – correctness, polynomial slowdown, and security. The correctness and the polynomial slowdown properties are defined on the same lines as the corresponding properties of the IO candidates.

The intuitive security notion of IO combiner says the following: suppose one of the candidates is a secure IO candidate then the output of obfuscator ($\mathsf {CombObf}$) of the IO combiner on $C_0$ is computationally indistinguishable from the output of the obfuscator on $C_1$, where $C_0$ and $C_1$ are equivalent circuits.

Definition 3

( $(\mu ',\mu )$ -Correct $(\epsilon ',\epsilon )$ -Secure IO Combiner). Consider a circuit class $\mathcal {C}=\{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$. We say that $\varPi _{\mathsf {comb}}=(\mathsf {CombObf},\mathsf {CombEval})$ is a $(\mu ',\mu )$ -correct $(\epsilon ',\epsilon )$ -secure IO combiner if the following conditions are satisfied: Let $\varPi _1,\ldots ,\varPi _n$ be n $\mu$-correct IO candidates for P/poly, where $\mu$ is a function of $\mu '$ and $\epsilon$ is a function of $\epsilon '$.

• Correctness. Let $C \in \mathcal {C}_{\lambda \in \mathbb {N}}$ and $x \in \{0,1\}^{\lambda }$. Consider the following process: (a) $\overline{C} \leftarrow {\mathsf {CombObf}}(1^{\lambda },C,\varPi _1,\ldots ,\varPi _n)$, (b) $y \leftarrow {\mathsf {CombEval}}(\overline{C},x,\varPi _1,\ldots ,\varPi _n)$. Then, $\mathsf {Pr}[y=C(x)] \ge \mu '(\lambda )$ over the randomness of $\mathsf {CombObf}$.

• Polynomial Slowdown. For every $C:\{0,1\}^{\lambda } \rightarrow \{0,1\} \in \mathcal {C}_{\lambda },$ we have the running time of $\mathsf {CombObf}$ on input $(1^{\lambda },C,\varPi _1,\ldots ,\varPi _n)$ to be at most $\mathsf {poly}(|C|+n + \lambda )$. Similarly, we have the running time of $\mathsf {CombEval}$ on input $(\overline{C},x,\varPi _1,\ldots ,\varPi _n)$ to be at most $\mathsf {poly}(|\overline{C}|+ n +\lambda )$.

• Security. Let $\varPi _i$ be $\epsilon$-secure for some $i \in [n]$. For every PPT adversary $\mathcal {A}$, for every sufficiently large $\lambda \in \mathbb {N}$, for every $C_0,C_1 \in \mathcal {C}_{\lambda }$ with $C_0(x)=C_1(x)$ for every $x \in \{0,1\}^{\lambda }$ and $|C_0|=|C_1|$, we have:

  $$\begin{aligned}&\Big | \mathsf {Pr}\Big [0 \leftarrow {\mathcal {A}}\Big ( \overline{C_0},C_0,C_1,\varPi _1,\ldots ,\varPi _n \Big ) \Big ] - \mathsf {Pr}\Big [0 \leftarrow {\mathcal {A}}\Big ( \overline{C_1},C_0,C_1,\varPi _1,\ldots ,\varPi _n \Big ) \Big ] \Big | \\&\le \epsilon '(\lambda ), \end{aligned}$$

  where $\overline{C_b} \leftarrow {\mathsf {CombObf}}(1^{\lambda },C_b,\varPi _1,\ldots ,\varPi _n)$ for $b \in \{0,1\}$.

Some remarks are in order.

Remark 3

We say that $\varPi _{\mathsf {comb}}$ is an IO combiner if it is a $(\mu ',\mu )$-correct $(\epsilon ',\epsilon )$-secure IO combiner, where (a) $\mu '=1$, (b) $\mu =1$, (c) $\epsilon '=\mathsf {negl}'$ and, (d) $\epsilon =\mathsf {negl}$ with $\mathsf {negl}$ and $\mathsf {negl}'$ being negligible functions.

4 Constructions of IO Combiners

We propose constructions of combiners for indistinguishability obfuscation. Here we present a construction based on the learning with errors assumption. In full version [2], we also present a construction based on the decisional Diffie Hellman assumption. We present the formal construction below. For an informal explanation of the construction, we refer the reader to Introduction.

Construction. Consider a circuit class $\mathcal {C}$. We use a threshold multi-key FHE scheme $\mathsf {TMFHE}=(\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Expand},\mathsf {FHEEval},\mathsf {Dec},\mathsf {PartDec},\mathsf {FinDec})$. We additionally use a puncturable PRF family $\mathcal {F}$.

We construct an IO combiner $\varPi _{\mathsf {comb}}=\varPi _{\mathsf {comb}}[\varPi _1,\ldots ,\varPi _n]$ for $\mathcal {C}$ below.

It takes as input security parameter $\lambda$, circuit $C \in \mathcal {C}_{\lambda }$, description of candidates $\{\varPi _i=(\varPi _i.\mathsf {Obf},\varPi _i,\mathsf {Eval})\}_{i \in [n]}$ and does the following.

• 1. Initialization of TMFHE Parameters:

  • Execute the setup of the threshold multi-key FHE scheme, $\mathsf {params}\leftarrow {\mathsf {Setup}}(1^{\lambda },1^d)$, where $d=\mathrm {poly}(\lambda ,|C|)$ ¹⁰. Execute $\{ (sk_i,pk_i) \leftarrow {\mathsf {KeyGen}}(\mathsf {params})\}_{i\in [n]}$.

  • Sample n random strings $\{ S_i \}_{i\in [n]}$ of size $\mid C \mid$ such that $\bigoplus _{i \in [n]} S_i=C$.

  • For all $i\in [n]$, encrypt the string $S_i$ using $pk_i$, $\mathsf {CT}_i \leftarrow {\mathsf {Enc}}(pk_i,S_i)$.

  • For every $i \in [n]$, generate the expanded ciphertext under $pk_i$ by executing $\widehat{\mathsf {CT}_i} \leftarrow {\mathsf {Expand}}((pk_1,\ldots ,pk_n),i,\mathsf {CT}_i)$.

• 2. Obfuscating Circuits using IO Candidates:

  • For every $i \in [n]$, sample puncturable PRF keys $K^i \xleftarrow {\$} \{0,1\}^{\lambda }$.

  • For every $i \in [n]$, construct circuit $G_i=G_i\left[ K^i,sk_i,\{pk_i\}_{i \in [n]},\{\widehat{\mathsf {CT}_i}\}_{i \in [n]} \right] \in \mathcal {C}^i$ as described in Fig. 1.

  • Generate $\overline{G_i} \leftarrow {\varPi }_i.\mathsf {Obf}(1^{\lambda },G_i)$.

Output the obfuscation $\overline{C}=\left( \ \overline{G_1},\ldots ,\overline{G_n} \ \right)$.

On input an obfuscation $\overline{C}$, an input x, descriptions of candidates $\{\varPi _i\}_{i \in [n]}$ evaluate the obfuscations on input x to obtain $p_i \leftarrow {\varPi }_i.\mathsf {Eval}(\overline{G_i},x)$ for all $i \in [n]$. Execute the final decryption algorithm, $y \leftarrow {\mathsf {FinDec}}(p_1,\ldots ,p_n)$. Output y.

Fig. 1.

Circuit $G_i$

5 Universal Obfuscation

We introduce the notion of universal obfuscation. We define a pair of Turing machines $\varPi _{\mathsf {univ}}.\mathsf {Obf}$ and $\varPi _{\mathsf {univ}}.\mathsf {Eval}$ to be a universal obfuscation if the existence of a secure IO candidate implies that $(\varPi _{\mathsf {univ}}.\mathsf {Obf},\varPi _{\mathsf {univ}}.\mathsf {Eval})$ is also a secure IO candidate. Constructing a universal obfuscation scheme means that we can turn the mere existence of a secure IO candidate into an explicit construction. Formally, we have the following definition:

Definition 4

( $(T,\epsilon )$ -Universal Obfuscation). We say that a pair of Turing machines $\varPi _{\mathsf {univ}}=(\varPi _{\mathsf {univ}}.\mathsf {Obf},\varPi _{\mathsf {univ}}.\mathsf {Eval})$ is a universal obfuscation, parameterized by T and $\epsilon$, if there exists an $\epsilon$-secure indistinguishability obfuscator for P/poly with time function T then $\varPi _{\mathsf {univ}}$ is an indistinguishability obfuscator for P/poly with time function $\mathrm {poly}(T)$.

5.1 Construction of $(T,\epsilon )$-Universal Obfuscation

We proceed to construct a $(T,\epsilon )$-universal obfuscation. The core building block in our construction is a decomposable IO combiner – this is a specific type of IO combiner that satisfies additional properties (explained below).

Main Ingredient: Decomposable IO Combiner. A decomposable IO combiner is a type of IO combiner, where the obfuscate algorithm has a specific structure. In particular, the obfuscate algorithm takes as input circuit C to be obfuscated, the description of the candidates $\varPi _1,\ldots ,\varPi _{n}$ and executes in two main steps. In the first step, circuit C is preprocessed into n circuits $\mathbf {[C]}_1,\ldots ,\mathbf {[C]}_n$. In the second step, each individual circuit $\mathbf {[C]}_i$ is obfuscated using the candidate $\varPi _i$. The concatenation of the resulting obfuscated circuits is the final output.

In addition to the standard properties of IO combiner, we require that the decomposable IO combiner satisfies two more properties: Circuit-Specific Correctness and Decomposable Security. The formal description is given below.

Definition 5

(Decomposable IO Combiner). A $(\epsilon ',\epsilon )$-secure IO combiner $\varPi _{\mathsf {comb}}=(\varPi _{\mathsf {comb}}.\mathsf {Obf},\varPi _{\mathsf {comb}}.\mathsf {Eval})$ of $(\varPi _1,\ldots ,\varPi _n)$ for a class of circuits $\mathcal {C}=\{\mathcal {C}_{\lambda }\}$ is said to be $(\epsilon ',\epsilon )$ -secure $(\eta ',\eta )$ -decomposable IO combiner if there exists a PPT algorithm $\mathsf {Preproc}$ such that the following holds: $\varPi _{\mathsf {comb}}.\mathsf {Obf}$ on input $(1^{\lambda },C \in \mathcal {C}_{\lambda },\varPi _1,\ldots ,\varPi _{n})$ executes the steps:

• (a) (Preprocessing step) $\overline{C}=\left( \mathbf {[C]}_1,\ldots ,\mathbf {[C]}_{n},aux \right) \leftarrow {\mathsf {Preproc}}(1^{\lambda },1^{n},C)$,

• (b) (Candidate Obfuscation step) for all $i \in [n]$, $\overline{\mathbf {[C]}_i} \leftarrow {\varPi }_i.\mathsf {Obf}(1^{\lambda },\mathbf {[C]}_i)$,

• (c) Outputs $\overline{C}=\left( \overline{\mathbf {[C]}_1},\ldots ,\overline{\mathbf {[C]}_{n}},aux \right)$.

Additionally, we require the following properties to hold:

• $(\eta ',\eta )$ -Circuit-Specific Correctness. Consider a circuit $C \in \mathcal {C}_{\lambda }$. Let $( \mathbf {[C]}_1,\ldots ,\mathbf {[C]}_{n},aux ) \leftarrow {\mathsf {Preproc}}(1^{\lambda },1^{n},C)$. Let for all $i \in [n]$, $\overline{\mathbf {[C]}_i} \leftarrow {\varPi }_i.\mathsf {Obf}(1^{\lambda },\mathbf {[C]}_i)$. Denote $\overline{C}=(\overline{\mathbf {[C]}_1},\ldots ,\overline{\mathbf {[C]}_{n}})$.

  If for all $i \in [n]$, $\mathop {\mathsf {Pr}}\limits _{x \xleftarrow {\$} \{0,1\}^{\lambda }} \left[ \ \overline{\mathbf {[C]}_i}(x) = \mathbf {[C]}_i(x)\ \right] \ge \eta (\lambda )$ then

  $\mathop {\mathsf {Pr}}\limits _{x \xleftarrow {\$} \{0,1\}^{\lambda }}\left[ \ \overline{C}(x) = C(x)\ \right] \ge \eta '(\lambda )$.

• Decomposable Security: For every $C_0,C_1 \in \mathcal {C}_{\lambda }$ such that $|C_0|=|C_1|$, for every $\mathbf {i}\in [n]$, we have:

  $$ \left\{ \left\{ \mathbf {[C]}_i^0 \right\} _{\begin{array}{c} i \ne \mathbf {i},\\ i \in [n] \end{array}} \right\} \approx _c \left\{ \left\{ \mathbf {[C]}_i^1 \right\} _{\begin{array}{c} i \ne \mathbf {i},\\ i \in [n] \end{array}} \right\} , $$

where $\mathbf {[C]}_{i}^b \leftarrow {\mathsf {Preproc}}(1^{\lambda },1^n,C_b \in \mathcal {C}_{\lambda })$ for $b \in \{0,1\}$.

We claim that the construction of IO Combiner in Sect. 4 is already a decomposable IO combiner. To show this, we first note that the obfuscator $\varPi _{\mathsf {univ}}.\mathsf {Obf}$ in the construction in Sect. 4 can be decomposed in a preprocessing step and candidate obfuscation step: the preprocessing step comprises of all the steps till the generation of circuits $\{G_i\}_{i \in [n]}$ (Fig. 1). The output of the preprocessing step is $(G_1,\ldots ,G_n)$.

Furthermore, the circuit-specific correctness property was already proved in [2]. More specifically, we showed the aforementioned construction satisfies $(1-n \mu ,1-\mu )$-circuit specific correctness property. All is remaining is to show that the construction satisfies decomposable security. We prove the following theorem. The proof can be found in [2].

Theorem 6

The construction presented in Sect. 4 is a $(\mathsf {negl},\epsilon )$-secure $( 1-\frac{1}{\lambda },1-\frac{1}{\lambda ^2} )$-decomposable IO combiner, where the number of candidates is $\lambda$.

We construct a universal obfuscation scheme $\varPi _{\mathsf {univ}}=(\mathsf {Obf},\mathsf {Eval})$ for a class of circuits $\mathcal {C}$ below. Our scheme will be approximately correct. The main ingredient is a decomposable IO combiner (Definition 5) $\varPi _{\mathsf {comb}}=(\varPi _{\mathsf {comb}}.\mathsf {Obf},\varPi _{\mathsf {comb}}.\mathsf {Eval})$ for $\mathcal {C}$. But first, we establish some notation.

Notation. Let $\mathcal {S}$ be the class of all possible Turing machines. It is well known result [16] that there is a one-to-one correspondence between $\mathcal {S}^2$ and $\mathbb {N}$ given by $\phi : \mathbb {N} \rightarrow \mathcal {S}^2$. Furthermore, there is a fixed polynomial f such that the time to compute $\phi (j)$ is at most $\le f(j)$, for every $j \in \mathbb {N}$.

It takes as input security parameter $\lambda$, circuit $C \in \mathcal {C}_{\lambda }$ and executes the following steps:

• 1. Let $\phi (i)=(\varPi _i.\mathsf {Obf},\varPi _i.\mathsf {Eval})$, for $i \in \{1,\ldots ,\lambda \}$. Denote $\varPi _i=(\varPi _i.\mathsf {Obf},\varPi _i.\mathsf {Eval})$.

• 2. Preprocessing phase of Decomposable IO Combiner. First compute the preprocessing step, $( \mathbf {[C]}_1,\ldots ,\mathbf {[C]}_{n},aux )\leftarrow {\mathsf {Preproc}}(1^{\lambda },1^{n},C)$ ($n=\lambda$).

• 3. Eliminating Candidates with Large Runtimes. For all $i \in [\lambda ]$, execute $\varPi _i.\mathsf {Obf}( 1^{\lambda },\mathbf {[C]}_i )$ for at most $t=T \left( \lambda ,\big |\mathbf {[C]}_i \big | \right)$ number of steps. For every $i \in [\lambda ]$, if the computation of $\varPi _i.\mathsf {Obf}\left( 1^{\lambda },\mathbf {[C]}_i \right)$ does not abort within t number of time steps re-assign $\varPi _i.\mathsf {Obf}=I$ and $\varPi _i.\mathsf {Eval}=UTM$, where I is an identity TM¹¹ and UTM is a universal TM¹².

  At the end of this step, the execution of $\varPi _i.\mathsf {Obf}( 1^{\lambda },\mathbf {[C]}_i )$ takes time at most $T \left( \lambda ,\big |\mathbf {[C]}_i \big | \right)$.

• 4. Eliminates Candidates with Imperfect Correctness. For all $i \in [\lambda ]$, execute $\varPi _i.\mathsf {Obf}( 1^{\lambda },\mathbf {[C]}_i)$ for at most $t=T(\lambda ,\big |\mathbf {[C]}_i\big |)$ number of steps. Denote $\overline{\mathbf {[C]}_i}$ to be the result of computation. Denote $\ell$ to be the input length of $\mathbf {[C]}_i$. For every $i \in [n]$, sample $\lambda ^3$ points $x_{1,i},\ldots ,x_{\lambda ^3,i} \xleftarrow {\$} \{0,1\}^{\ell }$. Check if the following condition holds:

  $$\begin{aligned} \mathop {\bigwedge }\limits _{j=1}^{\lambda ^3} \left( \ \mathbf {[C]}_i(x_{j,i}) = \varPi _i.\mathsf {Eval}\left( \overline{\mathbf {[C]}_i},x_{j,i} \right) \ \right) = 1 \end{aligned}$$

  (1)

  If for any $i \in [\lambda ]$ the above condition does not hold, re-assign $\varPi _i.\mathsf {Obf}=I$ and $\varPi _i.\mathsf {Eval}=UTM$. At the end of this step, every candidate satisfies the above condition.

• 5. Candidate Obfuscation Phase of Decomposable IO Combiner. For all $i \in [\lambda ]$, execute $\varPi _i.\mathsf {Obf}\left( 1^{\lambda },\mathbf {[C]}_i \right)$ for at most $t=T(\lambda ,\big |\mathbf {[C]}_i\big |)$ number of steps. Denote $\overline{\mathbf {[C]}_i}$ to be the result of computation.

• 6. Output $\overline{C}=\left( (\varPi _1,\ldots ,\varPi _{\lambda }),\ (\overline{\mathbf {[C]}_1},\ldots ,\overline{\mathbf {[C]}_{\lambda }},aux) \right)$.

On input the obfuscated circuit $\overline{C}$ and input x, do the following. First parse $\overline{C}$ as $\left( (\varPi _1,\ldots ,\varPi _{\lambda }),\ \overline{C_{comb}}=(\overline{\mathbf {[C]}_1},\ldots ,\overline{\mathbf {[C]}_{\lambda }},aux) \right)$. Compute $y \leftarrow {\varPi _{\mathsf {comb}}}.\mathsf {Eval}\left( \overline{C_{comb}},x,\varPi _1,\ldots ,\varPi _{\lambda }\right)$. Output y.

Theorem 7

Assuming that $\varPi _{\mathsf {comb}}$ is a $(\mathsf {negl},\epsilon )$-secure $\left( 1-\frac{1}{\lambda },1-\frac{1}{\lambda ^2}\right)$-decomposable IO combiner, the above scheme $\varPi _{\mathsf {univ}}$ is a $(T,\epsilon )$-universal obfuscation that is $\left( 1-\frac{1}{\lambda } \right)$-correct.

Proof

We first remark about the running time of the obfuscator and the evaluator algorithms. First, we consider $\varPi _{\mathsf {univ}}.\mathsf {Obf}$. The running time of first step (Bullet 1) is $\lambda f(\lambda )=\mathrm {poly}(\lambda )$ (where f was defined earlier in the proof). The running time of each of the rest of the steps is $\mathrm {poly}(\lambda ,t,|C|)$. Plugging in the fact that $t=T\left( \lambda ,\mathrm {poly}(\lambda ,|C|) \right)$, we have that the total running time of all the steps to be $\mathrm {poly}(T(\lambda ,|C|))$ ¹³. We move on to $\varPi _{\mathsf {univ}}.\mathsf {Eval}$. Here, the running time is governed by the running time of the $\varPi _{\mathsf {comb}}.\mathsf {Eval}$ algorithm which is $\mathrm {poly}(T(\lambda ,|C|))$. And hence, the running time of $\varPi _{\mathsf {univ}}.\mathsf {Eval}$ is again $\mathrm {poly}(T(\lambda ,|C|))$.

Correctness. Consider the following lemma.

Lemma 1

$\varPi _{\mathsf {univ}}$ is a $\left( 1 -\frac{1}{\lambda } \right)$-correct IO candidate.

Proof

Consider a circuit $C \in \mathcal {C}_{\lambda }$. We prove the following claim. For all $i \in [n]$, let $( \mathbf {[C]}_1,\ldots ,\mathbf {[C]}_n,aux )\leftarrow {\mathsf {Preproc}}(1^{\lambda },1^n,C)$ with $n=\lambda$. Also, let $\{\varPi _i\}_{i \in [n]}$ be the description of the candidates at the end of Bullet 3. Note that some of the candidates could be re-assigned in Bullets 2 and 3. Let $\overline{\mathbf {[C]}_i} \leftarrow {\varPi }_i.\mathsf {Obf}(1^{\lambda },\mathbf {[C]}_i)$. We prove the following claim in full version [2].

Claim 8

Let $i \in [n]$ be such that

$$\mathop {\mathsf {Pr}}\limits _{x \xleftarrow {\$} \{0,1\}^{\lambda }} \left[ \ \mathbf {[C]}_i(x) = \varPi _i.\mathsf {Eval}( \overline{\mathbf {[C]}_i},x ) \right] \le 1 - \frac{1}{\lambda ^2}$$

Then, the $i^{th}$ candidate $\varPi _i$ satisfies Condition (1) (Bullet 4) with negligible probability (over the random coins of $x_{j,i}$).

The above claim proves that at the end of Bullet 4, with overwhelming probability the following holds for every $i \in [n]$:

$$ \mathop {\mathsf {Pr}}\limits _{x \xleftarrow {\$} \{0,1\}^{\lambda }} \left[ \ \mathbf {[C]}_i(x) = \varPi _i.\mathsf {Eval}( \overline{\mathbf {[C]}_i},x ) \right] \ge 1 - \frac{1}{\lambda ^2} $$

We now apply the circuit-specific completeness property of the $(1-\frac{1}{\lambda },1-\frac{1}{\lambda ^2})$-decomposable IO combiner $\varPi _{\mathsf {comb}}$ which ensures that the following holds:

$$ \mathop {\mathsf {Pr}}\limits _{x \xleftarrow {\$} \{0,1\}^{\lambda }} \left[ \ C(x) = \varPi _{\mathsf {comb}}.\mathsf {Eval}( \overline{C},x )\ \right] \ge 1 - \frac{1}{\lambda } $$

where $\overline{C}=(\overline{\mathbf {[C]}_1},\ldots ,\overline{\mathbf {[C]}_n},aux)$. Note that $\overline{C}$ is the output of $\varPi _{\mathsf {univ}}.\mathsf {Obf}$. Also, the output of $\varPi _{\mathsf {univ}}.\mathsf {Eval}$ on input $(\overline{C},x)$ is dictated by the result of $\varPi _{\mathsf {comb}}.\mathsf {Eval}(\overline{C},x)$.

Thus, we have

$$ \mathop {\mathsf {Pr}}\limits _{x \xleftarrow {\$} \{0,1\}^{\lambda }} \left[ \ C(x) = \varPi _{\mathsf {univ}}.\mathsf {Eval}( \overline{C},x )\ \right] \ge 1 - \frac{1}{\lambda }, $$

where $\overline{C} \leftarrow {\varPi _{\mathsf {univ}}}.\mathsf {Obf}(1^{\lambda },C)$.

Security. We prove the following lemma.

Lemma 2

$\varPi _{\mathsf {univ}}$ is a $(\mathsf {negl})$-secure IO candidate.

Proof

Recall that the universal obfuscator proceeds in two phases. In the first phase, it chooses the “correct" candidates and then in the second phase, it combines all these candidates to produce the obfuscated circuit. At first glance, it should seem that as long as we ensure that one of the “correct"candidates is secure then the security of IO combiner should hold, and thus the security of universal obfuscator will follow. To make this more precise, lets say $C_0$ and $C_1$ are two equivalent circuits. Let $\overrightarrow{\varPi _0}=\varPi _1^0,\ldots ,\varPi _{n_0}^0$ and $\overrightarrow{\varPi _1}=\varPi _1^1,\ldots ,\varPi _{n_1}^1$ be the “correct" candidates chosen with respect to $C_0$ and $C_1$ respectively. Now, assuming that $\overrightarrow{\varPi _0}$ and $\overrightarrow{\varPi _1}$ have at least one secure candidate; the hope is that we can then invoke the security of IO combiner to argue computational indistinguishability of obfuscation of $C_0$ and $C_1$. This does not work because the security of IO combiner dictates that $\overrightarrow{\varPi _0}=\overrightarrow{\varPi _1}$. Indeed obfuscation of $C_0$ (resp., $C_1$) could potentially reveal $\overrightarrow{\varPi _0}$ (resp., $\overrightarrow{\varPi _1}$) at which point no security holds. While we cannot argue that $\overrightarrow{\varPi _0}=\overrightarrow{\varPi _1}$, because of the selective abort obfuscators described in Introduction, we can still show that $\overrightarrow{\varPi _0} \approx _c \overrightarrow{\varPi _1}$. Arguing the indistinguishability of the candidates then helps us invoke the security of IO combiner and then the proof of the theorem follows. Arguing the indistinguishability of candidates is performed by invoking the decomposable security property of the underlying IO combiner. We present the key lemmas here. Completed proof can be found in the full version [2].

Formal Details. We first introduce some notation. Consider a circuit $C \in \mathcal {C}_{\lambda }$. Let $( (\varPi _1,\ldots ,\varPi _{\lambda }),(\overline{\mathbf {[C]}_1},\ldots ,\overline{\mathbf {[C]}_{\lambda }}),aux )$ be the output of $\varPi _{\mathsf {univ}}.\mathsf {Obf}(1^{\lambda },C)$. Note that many of the candidates $(\varPi _1,\ldots ,\varPi _{\lambda })$ could potentially be re-assigned during the execution of $\varPi _{\mathsf {univ}}.\mathsf {Obf}$. This re-assignment is a function of the circuit C that is obfuscated and the random coins of the algorithm. Hence, we can define a distribution $\mathsf {Dist}_{C,\lambda ,\mathbf {i}}$, parameterized by C, $\lambda$, $\mathbf {i}\in [n]$, on $\{0,1\}^{\lambda }$ such that $x \xleftarrow {\$} \mathsf {Dist}_{C,\lambda ,\mathbf {i}}$ defines which of the candidates gets re-assigned. That is, the $i^{th}$ bit $x_i=1$ indicates that $\varPi _i$ will remain unchanged and $x_i=0$ indicates that $\varPi _i$ is re-assigned. Furthermore, $x_{\mathbf {i}}$ is always 1.

In more detail, we define the sampling algorithm of distribution $\mathsf {Dist}_{\lambda ,C,\mathbf {i}}$ as follows: denote by $\varPi '_1,\ldots ,\varPi '_{\lambda }$ the set of candidates enumerated in Bullet 1 and let $\varPi _{\mathbf {i}}$ be an IO candidate that is always correct. Note that the description of these candidates are independent of the circuit C and they only depend on the security parameter $\lambda$. At the end of Bullet 4, denote the candidates to be $(\varPi _1,\ldots ,\varPi _{\lambda })$. We then assign x to be such that the $i^{th}$ bit of x, namely, $x_i=1$ if $\varPi '_i = \varPi _i$ else $x_i=0$ if $\varPi '_i \ne \varPi _i$. Output x. Note that $x_{\mathbf {i}}=1$ since $\varPi _{\mathbf {i}}$ is always correct.

The formal description of the sampling algorithm of $\mathsf {Dist}_{\lambda ,C,\mathbf {i}}$ is given next.

• Let $\phi (i)=(\varPi _i.\mathsf {Obf},\varPi _i.\mathsf {Eval})$, for $i \in \{1,\ldots ,\lambda \}$. Denote $\varPi _i=(\varPi _i.\mathsf {Obf},\varPi _i.\mathsf {Eval})$.

• First compute the preprocessing step, $(\mathbf {[C]}_1,\ldots ,\mathbf {[C]}_{n},aux)\leftarrow {\mathsf {Preproc}}(1^{\lambda },1^{n},C)$. Here, $n=\lambda$. Maintain another copy of the set of candidates - for every $i \in [\lambda ]$, set $\varPi '_i=\varPi _i$.

• For all $i \in [\lambda ]$, execute $\varPi _i.\mathsf {Obf}( 1^{\lambda },\mathbf {[C]}_i )$ for at most $t=T \left( \lambda ,\big |\mathbf {[C]}_i \big | \right)$ number of steps. For every $i \in [\lambda ]$, if the computation of $\varPi _i.\mathsf {Obf}\left( 1^{\lambda },\mathbf {[C]}_i \right)$ does not abort within t number of time steps re-assign $\varPi _i.\mathsf {Obf}=I$ and $\varPi _i.\mathsf {Eval}=UTM$, where I is an identity TM and UTM is a universal TM.

• For all $i \in [\lambda ]$, execute $\varPi _i.\mathsf {Obf}( 1^{\lambda },\mathbf {[C]}_i)$ for at most $t=T(\lambda ,\big |\mathbf {[C]}_i\big |)$ number of steps. Denote $\overline{\mathbf {[C]}_i}$ to be the result of computation. Denote $\ell$ to be the input length of $\mathbf {[C]}_i$. For every $i \in [n]$, sample $\lambda ^3$ points $x_{1,i},\ldots ,x_{\lambda ^3,i} \xleftarrow {\$} \{0,1\}^{\ell }$. Check if the following condition holds:

  $$\begin{aligned} \mathop {\bigwedge }\limits _{j=1}^{\lambda ^3} \left( \ \mathbf {[C]}_i(x_{j,i}) = \varPi _i.\mathsf {Eval}\left( \overline{\mathbf {[C]}_i},x_{j,i} \right) \ \right) = 1 \end{aligned}$$

  (2)

  If for any $i \in [\lambda ]$ the above condition does not hold, re-assign $\varPi _i.\mathsf {Obf}=I$ and $\varPi _i.\mathsf {Eval}=UTM$.

• Construct a string $x \in \{0,1\}^{\lambda }$ such that the $i^{th}$ bit $x_i$ is generated as:

  $$ x_i = \left\{ \begin{array}{rcl} 1, &{} \text{ if } &{} \varPi _i=\varPi '_{i} \\ 0, &{} \text{ otherwise } &{} \ \end{array}\right. $$

• Output x.

Remark 4

For every x in the support of $\mathsf {Dist}_{\lambda ,C,\mathbf {i}}$ we have $x_{\mathbf {i}}=1$ ($\mathbf {i}^{th}$ bit of x) since the $\mathbf {i}^{th}$ candidate is always correct.

We prove the following useful sub-lemma. For every two circuits $C_0,C_1$ we claim that the outputs of the corresponding distributions $\mathsf {Dist}_{\lambda ,C_0,\mathbf {i}}$ and $\mathsf {Dist}_{\lambda ,C_1,\mathbf {i}}$ are computationally indistinguishable. Here, $\mathbf {i}$ corresponds to the candidate that is always correct. The proof can be found in [2].

SubLemma 1

(Candidate Indistinguishability Lemma). For large enough security parameter $\lambda$, any two circuits $C_0,C_1 \in \mathcal {C}_{\lambda }$, $\mathbf {i}\in [n]$ we have $\{x \xleftarrow {\$} \mathsf {Dist}_{\lambda ,C_0,\mathbf {i}}\} \approx _c \{x \xleftarrow {\$} \mathsf {Dist}_{\lambda ,C_1,\mathbf {i}}\}$, where $\mathbf {i}^{th}$ candidate (respresented by $\phi (\mathbf {i})$) is always correct, assuming that $\varPi _{\mathsf {comb}}$ satisfies decomposable security property.

We now proceed to prove the main lemma. Recall that we are assured the existence of a secure IO candidate that is always correct. Let $\mathbf {i}\in \mathbb {Z}_{>0}$ be such that $\phi (\mathbf {i})$ represents the secure candidate. Let $\lambda \ge \mathbf {i}$. Consider two equivalent circuits $C_0,C_1 \in \mathcal {C}_{\lambda }$. That is, $|C_0|=|C_1|$ and for every $x \in \{0,1\}^{\lambda }$ we have $C_0(x)=C_1(x)$. Our goal is to show that $\varPi _{\mathsf {univ}}.\mathsf {Obf}(1^{\lambda },C_0) \approx _c \varPi _{\mathsf {univ}}.\mathsf {Obf}(1^{\lambda },C_1)$.

We define the following experiment. The following experiment, parameterized by $(C_0,C_1)$, is same as $\varPi _{\mathsf {univ}}.\mathsf {Obf}(1^{\lambda },C_0)$ except that the decision to choose which of the candidates to obfuscate the derived circuits $\{\mathbf {[C]}_i\}$ is made solely based on the circuit $C_1$.

• Let $\phi (i)=(\varPi _i.\mathsf {Obf},\varPi _i.\mathsf {Eval})$, for $i \in \{1,\ldots ,\lambda \}$. Denote $\varPi _i=(\varPi _i.\mathsf {Obf},\varPi _i.\mathsf {Eval})$.

• Compute the preprocessing step, $( \mathbf {[C]}_1,\ldots ,\mathbf {[C]}_{n},aux )\leftarrow {\mathsf {Preproc}}(1^{\lambda },1^{n},C_0)$ with $n=\lambda$.

• Sample x from $\mathsf {Dist}_{\lambda ,C_1,\mathbf {i}}$, where $\mathbf {i}\in [\lambda ]$. That is, x is sampled from the distribution $\mathsf {Dist}$ parameterized by $(\lambda ,C_1,\mathbf {i})$.

• For every $i \in [\lambda ]$ and $x_i=0$, re-assign $\varPi _i.\mathsf {Obf}=I$ and $\varPi _i.\mathsf {Eval}=UTM$.

• Execute $\overline{\mathbf {[C]}_i} \leftarrow {\varPi }_i.\mathsf {Obf}(1^{\lambda },\mathbf {[C]}_i)$ for at most $T(\lambda ,|\mathbf {[C]}_i|)$ number of steps.

• Output $\overline{C}=(\overline{\mathbf {[C]}_1},\ldots ,\overline{\mathbf {[C]}_{\lambda }})$.

Consider the following claims.

Claim 9

The distributions $D_0=\left\{ \mathsf {ExptObf}\left( 1^{\lambda },C_b,C_b,\mathbf {i}\right) \right\}$ and $D_1=\{\varPi _{\mathsf {univ}}.\mathsf {Obf}\left( 1^{\lambda },C_b \right) \}$ are identical, for $b \in \{0,1\}$.

The proof of the above claim follows directly from the description of $\mathsf {Dist}_{\lambda ,C,\mathbf {i}}$.

Claim 10

The distributions $D_0=\left\{ \mathsf {ExptObf}\left( 1^{\lambda },C_b,C_0,\mathbf {i}\right) \right\}$ and $D_1=\big \{ \mathsf {ExptObf}( 1^{\lambda } ,C_b,C_1,\mathbf {i}) \big \}$ are computationally indistinguishable for $b \in \{0,1\}$.

The proof of the above claim follows from the Candidate Indistinguishability Lemma (Lemma 1).

Claim 11

The distributions $D_0=\left\{ \mathsf {ExptObf}\left( 1^{\lambda },C_0,C_b,\mathbf {i}\right) \right\}$ and $D_1= \left\{ \mathsf {ExptObf}( 1^{\lambda } ,C_1,C_b,\mathbf {i}) \right\}$ are computationally indistinguishable for $b \in \{0,1\}$.

We rely on the security (third bullet in Definition 3) of decomposable IO combiner to prove this claim. That is, the output of the IO combiner on two equivalent circuits are computationally indistinguishable. The proof can be found in the full version [2].

From Claims 9, 10 and 11, it follows that $\varPi _{\mathsf {univ}}.\mathsf {Obf}(1^{\lambda },C_0) \approx _c \varPi _{\mathsf {univ}}.\mathsf {Obf}(1^{\lambda },C_1)$. In more detail,

$$\begin{aligned} \varPi _{\mathsf {univ}}(1^{\lambda },C_0)&\equiv \mathsf {ExptObf}\left( 1^{\lambda },C_0,C_0,\mathbf {i}\right) \ (\text { from Claim}~9) \\&\approx _c \mathsf {ExptObf}\left( 1^{\lambda },C_0,C_1,\mathbf {i}\right) (\text { from Claim}~10) \\&\approx _c \mathsf {ExptObf}\left( 1^{\lambda },C_1,C_1,\mathbf {i}\right) (\text { from Claim}~11) \\&\equiv \varPi _{\mathsf {univ}}(1^{\lambda },C_1) (\text { from Claim}~9) \end{aligned}$$

We have demonstrated that $\varPi _{\mathsf {univ}}$ satisfies both the correctness and security properties. This proves the theorem.

. In Step I, we showed how to construct a universal obfuscator that is $\left( 1-\frac{1}{\lambda } \right)$ correct. That is, for sufficiently large security parameter $\lambda \in \mathbb {N}$, every circuit $C \in \mathcal {C}_{\lambda }$, it holds that:

$$ \mathop {\mathsf {Pr}}\limits _{x \xleftarrow {\$} \{0,1\}^{\lambda } } \left[ \varPi _{\mathsf {univ}}.C(x)=\mathsf {Eval}(\overline{C},x)\ :\ \overline{C} \leftarrow {\varPi _{\mathsf {univ}}}.\mathsf {Obf}(1^{\lambda },C)\ \right] \ge 1 - \frac{1}{\lambda } $$

We now apply the transformation of BV [6] to obtain a universal obfuscator that is exact (with overwhelming probability). In particular, we apply their transformation that is based on sub-exponential LWE assumption.

That is, for every $C \in \mathcal {C}_{\lambda }, x \in \{0,1\}^{\lambda }$, with high probability it holds that:

$$ \mathsf {Pr}\left[ \varPi _{\mathsf {univ}}.C(x)=\mathsf {Eval}(\overline{C},x)\ :\ \overline{C} \leftarrow {\varPi _{\mathsf {univ}}}.\mathsf {Obf}(1^{\lambda },C)\ \right] = 1 $$

We state the formal theorem below.

Theorem 12

Assuming learning with errors secure against adversaries running in time $2^{n^{\epsilon '}}$ and $(1-1/{\lambda })$-correct $(T,\epsilon )$-universal obfuscation, we have a $(T,\epsilon )$ -universal obfuscation that is exact (with overwhelming probability).

Combining both the above steps and instantiating the decomposable IO combiner (Theorem 6) we get the following result:

Theorem 13

Assuming LWE secure against adversaries running in time $2^{n^{\epsilon '}}$, there exists a $(T,\epsilon )$-Universal Obfuscation with $\epsilon '$ being a function of $\epsilon$.

6 Witness Encryption Combiners

6.1 Definition of WE Combiner

We present the formal definition of a WE combiner below. The definition is similar to the definition of IO combiners. The task of the WE combiner is to take n candidates that are correct (in terms of encryption and decryption), and yield a scheme which is as secure as any one of the candidate schemes.

For a scheme $\varPi$ we say that it is a correct WE candidate if it satisfies that correctness requirement and we say that a candidate is secure if it satisfies the security requirement (definitions found in the full version). We say that it is correct and secure if it satisfies both the requirements.

There are two PPT algorithms associated with an WE combiner, namely, $\mathsf {CombEnc}$ and $\mathsf {CombDec}$. Procedure $\mathsf {CombEnc}$ takes as input an instance x, a message m along with the description of multiple WE candidates and outputs a ciphertext. Procedure $\mathsf {CombDec}$ takes as input the ciphertext, a witness w, the description of the candidates and outputs the original message. Since the execution times of the candidates could potentially differ, we require the algorithms $\mathsf {CombEnc}$ and $\mathsf {CombDec}$ in addition to their usual inputs also take a time function T as input. T dictates an upper bound on the time required to execute all the candidates.

Syntax of WE Combiner. We define an WE combiner $\varPi _{\mathsf {comb}}=(\mathsf {CombEnc},\mathsf {CombDec})$ for a language L.

• Combiner of encryption algorithms, $\mathsf {CT}\leftarrow {\mathsf {CombEnc}}(1^{\lambda },x,m,\varPi _1,\ldots ,\varPi _n,T)$: It takes as input security parameter $\lambda$, an instance x, a message m, description of WE candidates $\{\varPi _i\}_{i \in [n]}$, time function T and outputs a ciphertext.

• Combiner of decryption algorithms, $y \leftarrow {\mathsf {CombDec}}(\mathsf {CT},w,\varPi _1,\ldots ,\varPi _n,T)$: It takes as input a ciphertext $\mathsf {CT}$, a witness for the instance x, descriptions of WE candidates $\{\varPi _i\}_{i \in [n]}$, time function T and outputs y.

We define the properties associated with a WE combiner scheme. There are two properties – correctness and security. We only consider the scenario where all the candidate WE schemes are (almost) perfectly correct but only one of them is secure.

Definition 6

(Secure WE Combiner). Let $\varPi _1,\ldots ,\varPi _n$ be n (almost) perfectly correct WE candidates for ${\mathsf {NP}}$ (that is all the schemes are correct, however all of them need not be secure). We say that $\varPi _{\mathsf {comb}}=(\mathsf {CombEnc},\mathsf {CombDec})$ is a secure WE combiner if the following conditions are satisfied:

• Correctness. Consider the following process: (a) $\mathsf {CT}\leftarrow {\mathsf {CombEnc}}(1^{\lambda },x,m,\varPi _1,\ldots ,\varPi _n,T)$, (b) $y \leftarrow {\mathsf {CombDec}}(\mathsf {CT},w,\varPi _1,\ldots ,\varPi _n,T)$. Then, $\mathsf {Pr}[y=m] \ge 1-\mathsf {negl}(\lambda )$ over the randomness of $\mathsf {CombEnc}$.

• Security: If for some $i\in [n]$ candidate $\varPi _i$ is secure then, for any PPT adversary A and any polynomial $p(\cdot )$, there exists a negligible function $\mathsf {negl}(\cdot )$, such that for any $\lambda \in \mathbb N$, any $x\notin L$ and any two equal-length messages $m_1$ and $m_2$ such that $|x|,|m_1| \le p(\lambda )$, we have that

  $$\begin{aligned}&|\Pr [A(\mathsf {CombEnc}(1^{\lambda },x,m_1,\varPi _1,\ldots ,\varPi _n,T)=1] - \\&\Pr [A(\mathsf {CombEnc}(1^{\lambda },x,m_2,\varPi _1,\ldots ,\varPi _n,T))=1]| \le \mathsf {negl}(\lambda ). \end{aligned}$$

Henceforth, we set the time function to be an a priori fixed polynomial. In our constructions presented next, we drop the parameter T which is input to the above algorithms.

6.2 Construction of WE Combiner

We give a construction of a WE combiner. Formally, we prove the following theorem.

Theorem 14

If one-way functions exist, then there exists a secure WE combiner.

The construction is given below. As described in Sect. 2.3, the main ingredient of the construction is a (perfectly) secure secret sharing scheme.

It takes as input security parameter $\lambda$, instance x, message m, description of candidates $\{\varPi _i=(\varPi _i.\mathsf {Enc},\varPi _i.\mathsf {Dec})\}_{i \in [n]}$ and does the following.

• 1. Secret share the message. Choose n random strings $r_1,\ldots ,r_n \in \{ 0,1 \}^{|m|}$ such that $r_1 \oplus \ldots \oplus r_n=m$.

• 2. Encrypt shares using candidates. For $i \in [n]$, encrypt $r_i$ using candidate $\varPi _i$: $y_i \leftarrow \varPi _i.\mathsf {Enc}(x,r_i)$.

• 3. Output $(y_1,\ldots ,y_n)$.

: On input $\mathbf {y}=(y_1,\ldots ,y_n)$, an input x with witness w, descriptions of candidates $\{\varPi _i\}_{i \in [n]}$ run the decryption candidates to obtain $r_i \leftarrow {\varPi }_i.\mathsf {Dec}(1^\lambda ,y_i,w)$ for all $i \in [n]$. Compute $m \leftarrow r_1 \oplus \ldots \oplus r_n$ and output m.

Correctness: The correctness follows immediately from the scheme. For any $x \in L$ using the witness w we will get all $r_i$ for $i \in [n]$ and from them we compute the correct message $m = r_1 \oplus \ldots \oplus r_n$.

Security: To prove security, assume that $x \notin L$ and let $i^* \in [n]$ be such that candidate $\varPi _{i^*}$ is secure. Let $m_0,m_1$ be any two messages. Consider the following sequence of hybrids. Let $\mathsf {H}_0$, parameterized by $(r_1,\ldots ,r_n)$, be a distribution on the encryptions of $m_0$. That is, $\mathsf {H}_0$ is a distribution over $(y_1,\ldots ,y_n)$ where $y_i \leftarrow \varPi _i.\mathsf {Enc}(x,r_i)$ where $r_i$ are random strings such that $r_1 \oplus \ldots \oplus r_n=m_0$. Then we define $\mathsf {H}_1$, again parameterized by $(r_1,\ldots ,r_n)$, to be a distribution on encryptions of the message $m_0 \oplus m_1 \oplus r_i$. That is, $\mathsf {H}_0$ is a distribution over $y_{i^*} \leftarrow \varPi _{i^*}.\mathsf {Enc}(1^\lambda ,x,r')$ where $r'=m_0 \oplus m_1 \oplus r_i$. From the security of $\varPi _{i^*}$ we have that $\mathsf {H}_0 \approx \mathsf {H}_1$. Notice that

$$ r_1 \oplus \ldots \oplus r_{i^*-1} \oplus r' \oplus r_{i^*+1} \ldots \oplus r_n=m_0 \oplus m_1 \oplus m_0 = m_1. $$

Moreover, the distribution of $r_1,\ldots ,r_{i^*-1},r',r_{i^*+1},\ldots ,r_n$ and the distribution $r_1,\ldots ,r_n$ such that $r_1 \oplus \ldots \oplus r_n=m_1$ are identical. Therefore, if we define $\mathsf {H}_2$ to be the distribution on the honest encryptions of the message $m_1$ (i.e., performed according to the scheme), we get that $\mathsf {H}_1 \equiv \mathsf {H}_2$. Thus we have that $\mathsf {H}_0 \approx \mathsf {H}_2$ which proves the security of the above scheme.