Synthesizing Piece-Wise Functions by Learning Classifiers

Abstract

We present a novel general technique that uses classifier learning to synthesize piece-wise functions (functions that split the domain into regions and apply simpler functions to each region) against logical synthesis specifications. Our framework works by combining a synthesizer of functions for fixed concrete inputs and a synthesizer of predicates that can be used to define regions. We develop a theory of single-point refutable specifications that facilitate generating concrete counterexamples using constraint solvers. We implement the framework for synthesizing piece-wise functions in linear integer arithmetic, combining leaf expression synthesis using constraint-solving and predicate synthesis using enumeration, and tie them together using a decision tree classifier. We demonstrate that this approach is competitive compared to existing synthesis engines on a set of synthesis specifications.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The field of synthesis is an evolving discipline in formal methods that is seeing a renaissance, mainly due to a variety of new techniques [1] to automatically synthesize small expressions or programs that are useful in niche application domains, including end-user programming [14], filling holes in program sketches [32], program transformations [7, 18], automatic grading of assignments [2, 30], synthesizing network configurations and migrations [21, 29], as well as synthesizing annotations such as invariants or pre/post conditions for programs [12, 13].

The field of machine learning [22] is close to program synthesis, especially when the specification is a set of input-output examples. The subfield of inductive programming has a long tradition in solving this problem using inductive methods that generalize from the sample to obtain programs [19]. Machine learning, which is the field of learning algorithms that can predict data from training data, is a rich field that encompasses algorithms for several problems, including classification, regression, and clustering [22].

The idea of using inductive synthesis for more general specifications than input-output examples has been explored extensively in program synthesis research. The counterexample guided inductive synthesis (CEGIS) approach to program synthesis advocates pairing inductive learning algorithms with a verification oracle: in each round, the learner learns inductively from a set of (counter-)examples and proposes an expression which the verification oracle checks against the specification, and augments the set of samples with a new counterexample [32]. A majority of the current synthesis approaches rely on counter-example guided inductive synthesis [12, 13, 16, 32].

In this paper, we consider logical specifications for synthesis, where the goal of synthesis is to find some expression e for a function f, in a particular syntax, that satisfies a specification $\forall \vec {x}.~ \psi (\vec {x})$.¹ We will assume that $\psi$ is quantifier-free, that the satisfiability of the quantifier-free theory of the underlying logic is decidable, and that there is an effective algorithm that can produce models. The goal of this paper is to develop a framework for expression synthesis that can learn piece-wise functions using a learning algorithm for classifiers with the help of two other synthesis engines, one for synthesizing expressions for single inputs and another for synthesizing predicates that separate concrete inputs from each other. The framework is general in the sense that it is independent of the logic used to write specifications and the logic used to express the synthesized expressions.

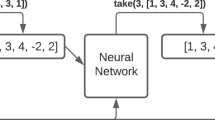
A piece-wise function is a function that partitions the input domain into a finite set of regions, and then maps each region using a simpler class of functions. The framework that we build for expression synthesis is also counterexample-guided, and proceeds in the following fashion (see Fig. 1 on p. 195 and the figure on the right):

• In every round, the learner proposes a piece-wise function H for f, and the verification oracle checks whether it satisfies the specification. If not, it returns one input $\vec {p}$ on which H is incorrect. (Returning such a counterexample is nontrivial; we will discuss this issue below.)

• We show that we can now use an expression synthesizer for the single input $\vec {p}$ which synthesizes an expression that maps $\vec {p}$ to a correct value. This expression synthesizer will depend on the underlying theory of basic expressions, and we can use any synthesis algorithm that performs this task.

• Once we have the new expression, we compute for every counterexample input obtained thus far the set of basic expressions synthesized so far that work correctly for these inputs. This results in a set of samples, where each sample is of the form $(\vec {p}, Z)$, where $\vec {p}$ is a concrete input and Z is the set of basic expressions that are correct for $\vec {p}$ (see points with sets of labels in figure above). The problem we need to solve now can be seen as a multi-label classification problem— that of finding a mapping from every input to an expression that is consistent with the set of samples.

• Since we want a classification that is a piece-wise function that divides the input domains into regions, and since the predicates needed to define regions can be arbitrarily complex and depend on the semantics of the underlying logical theory, we require a predicate synthesizer that synthesizes predicates that can separate concrete inputs with disjoint sets of labels. Once we have such a set of predicates, we are equipped with an adequate number of regions to find a piece-wise function.

• The final phase uses classification learning, to generalize the samples to a function from all inputs to basic expressions (see figure above). The learning should be biased towards finding simple functions, finding few regions, or minimizing the Boolean expression that describes the piece-wise function.

The framework above requires many components, in addition to the expression synthesizer and predicate synthesizer. First, given a hypothesis function H and a specification $\forall \vec {x}.~ \psi (f,\vec {x})$, we need to find a concrete counterexample input on which H is wrong. It turns out that there may be no such input point for some specifications and even if there was, finding one may be hard. We develop a theory of single-point definable specifications whose definition ensures such counterexample inputs always exist, and a subclass of single-point refutable specifications that reduce finding such counterexample inputs to satisfiability problems over the underlying logical domain (which is decidable). Our framework works robustly for the class of singe-point refutable specifications, and we show how to extract concrete counterexamples, how to automatically synthesize a new specification tailored for any input $\vec {p}$ to be given to the expression synthesizer, and how to evaluate whether particular expressions work for particular inputs.

In current standard CEGIS approaches [1, 32], when H and $\forall \vec {x}.~ \psi (f,\vec {x})$ are presented, the teacher simply returns a concrete value of $\vec {x}$ for which $\lnot \psi (H/f,\vec {x})$ is satisfied. We emphasize that such valuations for the universally quantified variables cannot be interpreted as inputs on which H is incorrect, and hence cannot be used in our framework. The framework of single-point refutable specifications and the counterexample input generation procedures we build for them is crucial in order to be able to use classifiers to synthesize expressions.

The classifier learning algorithm can be any learning algorithm for multi-label classification (preferably with the learning bias as described above) but must ensure that the learned classifier is consistent with the given samples. Machine-learning algorithms more often than not make mistakes and are not consistent with the sample, often because they want to generalize assuming that the sample is noisy. In Sect. 4, we describe the second contribution of this paper— an adaptation of decision-tree learning to multi-label learning that produces classifiers that are consistent with the sample. We also explore a variety of statistical measures used within the decision-tree learning algorithm to bias the learning towards smaller trees in the presence of multi-labeled samples. The resulting decision-tree learning algorithms form one class of classifier learning algorithms that can be used to synthesize piece-wise functions over any theory that works using our framework.

The third contribution of the paper is an instantiation of our framework to build an efficient synthesizer of piece-wise linear integer arithmetic functions for specifications given in the theory of linear integer arithmetic. We implement the components of the framework for single-point refutable functions: to synthesize input counterexamples, to reformulate the synthesis problem for a single input, and to evaluate whether an expression works correctly for any input. These problems are reduced to the satisfiability of the underlying quantifier-free theory of linear integer arithmetic, which is decidable using SMT solvers. The expression-synthesizer for single inputs is performed using an inner CEGIS-based engine using a constraint solver. The predicate synthesizer is instantiated using an enumerative synthesis algorithm. The resulting solver works extremely well on a large class of benchmarks drawn from the SyGuS 2015 synthesis competition [3] (linear integer arithmetic track) where a version of our solver fared significantly better than all the traditional SyGuS solvers (enumerative, stochastic, and symbolic constraint-based solvers). In our experience, finding an expression that satisfies a single input is a much easier problem for current synthesis engines (where constraint solvers that compute the coefficients defining such an expression are effective) than finding one that satisfies all inputs. The decision-tree based classification, on the other hand, solves the problem of generalizing this labeling to the entire input domain effectively.

Related Work. Our learning task is closely related to the syntax-guided synthesis framework (SyGuS) [1], which provides a language, similar to SMTLib [5], to describe synthesis problems. Several solvers following the counterexample-guided inductive synthesis approach (CEGIS) [32] for SyGuS have been developed [1], including an enumerative solver, a solver based on constraint solving, one based on stochastic search, and one based on the program synthesizer Sketch [31]. Recently, a solver based on CVC4 [26] has also been presented.

There has been several works on synthesizing piece-wise affine models of hybrid dynamical systems from input-output examples [4, 6, 11, 34] (we refer the reader to [24] for a comprehensive survey). The setting there is to learn an affine model passively (i.e., without feedback whether the synthesized model satisfies some specification) and, consequently, only approximates the actual system. A tool for learning guarded affine functions, which uses a CEGIS approach, is Alchemist [28]. In contrast to our setting, it requires that the function to synthesize is unique.

The learning framework we develop in this paper, as well as the synthesis algorithms we use for linear-arithimetic (the outer learner, the expression synthesizer and the predicate synthesizer) can be seen as abstract learning frameworks [20] (see [23] for details).

2 The Synthesis Problem and Single-Point Refutable Specifications

The synthesis problem we tackle in this paper is that of finding a function f that satisfies a logical specification of the form $\forall \vec {x}.~ \psi (f, \vec {x})$, where $\psi$ is a quantifier-free first-order formula over a logic with fixed interpretations of constants, functions, and relations (except for f). Further, we will assume that the quantifier-free fragment of this logic admits a decidable satisfiability problem and furthermore, effective procedures for producing a model that maps the variables to the domain of the logic are available. These effective procedures are required in order to generate counterexamples while performing synthesis.

For the rest of the paper, let f be a function symbol with arity n representing the target function that is to be synthesized. The specification logic is a formula in first-order logic, over an arbitrary set of function symbols $\mathcal{F}$, (including a special symbol f), constants $\mathcal{C}$, and relations/predicates $\mathcal{P}$, all of which with fixed interpretations, except for f. We will assume that the logic is interpreted over a countable universe D and, further, and that there is a constant symbol for every element in D. For technical reasons, we assume that negation is pushed into atomic predicates.

The specification for synthesis is a formula of the form $\forall \vec {x}.\psi (f,\vec {x})$ where $\psi$ is a formula expressed in the following grammar (where $g \in \mathcal{F}$, $c \in \mathcal{C}$, $P \in \mathcal {P}$):

$$\begin{aligned} Term\,\,t :\,\!:\!\!-~&x \mid c \mid f(t_1, \ldots , t_n) \mid g(\vec {\,t\,}) \\ Formula\,\,\varphi :\,\!:\!\!-~&P(\vec {\,t\,}) \mid \lnot P(\vec {\,t\,}) \mid \varphi \vee \varphi \mid \varphi \wedge \varphi \end{aligned}$$

We will assume that equality is a relation in the logic, with the standard model-theoretic interpretation.

The synthesis problem is to find, given a specification $\forall \vec {x}. ~\psi (f,\vec {x})$, a definition for the function f in a particular syntax that satisfies the specification. More formally, given a subset of function symbols $\widehat{\mathcal{F}} \subseteq \mathcal{F}$ (excluding f) and a subset of constants $\widehat{\mathcal{C}}$ and a subset of relation/predicate symbols $\widehat{\mathcal{P}} \subseteq \mathcal{P}$, the task is to find an expression e for f that is a term with free variables $y_1, \ldots , y_n$ adhering to the following syntax (where $\widehat{g} \in \widehat{\mathcal{F}}$, $\widehat{c} \in \widehat{\mathcal{C}}$, $\widehat{P} \in \widehat{\mathcal{P}}$)

$$\begin{aligned} Expr\,\,t :\,\!:\!\!-~ \widehat{c} \mid y_i \mid \widehat{g}(\vec {\,t\,}) \mid \textit{ite}(\widehat{P}(\vec {\,t\,}), ~t, ~t), \end{aligned}$$

such that e satisfies the specification, i.e., $\forall \vec {x}. ~\psi (e/f,\vec {~x~}\!)$ is valid.

Single-Point Definable Specifications. In order to be able to define a general CEGIS algorithm for synthesizing expressions for f based on learning classifiers, as described in Sect. 1, we need to be able to refute any hypothesis H that does not satisfy the specification with a concrete input on which H is wrong. We will now define sufficient conditions that guarantee this property. The first is a semantic property, called single-point definable specifications, that guarantees the existence of such concrete input counterexamples and the second is a syntactic fragment of the former, called single-point refutable specifications, that allows such concrete counterexamples to be found effectively using a constraint solver.

A single-point definable specification is, intuitively, a specification that restricts how each input is mapped to the output, independent of how other inputs are mapped to outputs. More precisely, a single-point definable specification restricts each input $\vec {p}\in D^n$ to a set of outputs $X_{\vec {p}} \subseteq D$ and allows any function that respects this restriction for each input. It cannot, however, restrict the output on $\vec {p}$  based on how the function behaves on other inputs. Many synthesis problems fall into this category (see Sect. 6 for several examples taken from a recent synthesis competition).

Formally, we define this concept as follows. Let $I = D^n$ be the set of inputs and $O=D$ be the set of outputs of the function being synthesized.

Definition 1

(Single-point Definable (SPD) Specifications). A specification $\alpha$ is said to be single-point definable if the following holds. Let $\mathcal {F}$ be the class of all functions that satisfy the specification $\alpha$. Let $g: I \rightarrow O$ be a function such that for every $\vec {p} \in I$, there exists some $h \in \mathcal {F}$ such that $g(\vec {p})=h(\vec {p})$. Then, $g \in \mathcal {F}$ (i.e., g satisfies the specification $\alpha )$.

Intuitively, a specification is single-point definable if whenever we construct a function that maps each input independently according to some arbitrary function that satisfies the specification, the resulting function satisfies the specification as well. For each input $\vec {p}$, if $X_{\vec {p}}$ is the set of all outputs that functions that meet the specification map $\vec {p}$ to, then any function g that maps every input $\vec {p}$ to some element in $X_{\vec {p}}$ will also satisfy the specification. This captures the requirement, semantically, that the specification constrains the outputs of each input independent of other inputs.

For example, the following specifications are all single-point definable specifications over the first-order theory of arithmetic:

• $f(15,23)=19 \wedge f(90,20)=91 \wedge \ldots \wedge f(28,24)=35$.

  More generally, any set of input-output samples can be written as a conjunction of constraints that forms a single-point definable specification.

• Any specification that is not realizable (has no function that satisfies it).

• $\forall x.~ ( f(0)=0 \wedge f(x\!+\!1)=f(x)+1 )$.

  The identity function is the only function that satisfies this specification. Any specification that has a unique solution is clearly single-point definable.

While single-point definable specifications are quite common, there are prominent specifications that are not single-point definable. For example, inductive loop invariant synthesis specifications for programs are not single-point definable, as counterexamples to the inductiveness constraint involve two counterexample inputs (the ICE learning model [12] formalizes this). Similarly, ranking function synthesis is also not single-point definable.

Note that for any SPD specification, if H is some expression conjectured for f that does not satisfy the specification, there will always be one input $\vec {p} \in D^n$ on which H is definitely wrong in that no correct solution agrees with H on $\vec {p}$. More precisely, we obtain the following directly from the definition.

Proposition 1

Let $\forall \vec {x}.~ \psi (f,\vec {x})$ be a single-point definable specification and let $h:D^n \rightarrow D$ be an interpretation for f such that $\forall \vec {x}.~ \psi (f,\vec {x})$ does not hold. Then there is an input $\vec {p} \in D^n$ such that for every function $h':D^n \rightarrow D$ that satisfies the specification, $h(\vec {p}) \not = h'(\vec {p})$.

Single-Point Refutable Specifications. While the above proposition ensures that there is a counterexample input for any hypothesized function that does not satisfy a single-point definable function, it does not ensure that finding such an input is tractable. We now define single-point refutable specifications, which we show to be a subclass of single-point definable specifications, and for which we can reduce the problem of finding counterexample inputs to logical satisfiability of the underlying quantifier-free logic.

Intuitively, a specification $\forall \vec {x}.~\psi (f,\vec {x})$ is single-point refutable if for any given hypothetical interpretation H to the function f that does not satisfy the specification, we can find a particular input $\vec {p} \in D^n$ such that the formula $\exists \vec {x}.~\lnot \psi (f,\vec {x})$ evaluates to true, and where the truthhood is caused solely by the interpretation of H on $\vec {p}~$. The definition of single-point refutable specifications is involved as we have to define what it means for H on $\vec {p}$ to solely contribute to falsifying the specification.

We first define an alternate semantics for a formula $\psi (f,\vec {~x~}\!)$ that is parameterized by a set of n variables $\vec {u}$ denoting an input, a variable v denoting an output, and a Boolean variable b. The idea is that this alternate semantics evaluates the function by interpreting f on $\vec {u}$ to be v, but “ignores” the interpretation of f on all other inputs, and reports whether the formula would evaluate to b. We do this by expanding the domain to $D\cup \{\bot \}$, where $\bot$ is a new element, and have f map all inputs other than $\vec {u}$ to $\bot$. Furthermore, when evaluating formulas, we let them evaluate to b only when we are sure that the evaluation of the formula to b depended only on the definition of f on $\vec {u}$. We now define this alternate semantics by transforming a formula $\psi (f,\vec {~x~}\!)$ to a formula with the usual semantics, but over the domain $D \cup \{\bot \}$. In this transformation, we will use if-then-else ($\textit{ite})$ terms for simplicity.

Definition 2

(The Isolate Transformer) . Let $\vec {u}$ be a vector of n first-order variables (where n is the arity of the function to be synthesized), v a first-order variable (different from ones in $\vec {u})$, and $b \in \{T, F\}$. Moreover, let $D^+ = D \cup \{\bot \}$, where $\bot \not \in D$, be the extended domain, and let the functions and predicates be extended to this domain (the precise extension does not matter).

For a formula $\psi (f,\vec {~x~}\!)$, we define the formula $\textit{Isolate}_{\vec {u},v,b}(\psi (f,\vec {~x~}\!))$ over the extended domain by

$$\begin{aligned} Isolate_{\vec {u},v,b}(\psi (f,\vec {~x~}\!)) :=ite \biggl ( \bigvee _{x_i} x_i = \bot , \lnot b, Isol_{\vec {u},v,b}( \psi (f,\vec {~x~}\!)) \biggr ), \end{aligned}$$

where $\textit{Isol}_{\vec {u},v,b}$ is defined recursively as follows:

• $Isol_{\vec {u},v,b}(x) = x$

• $Isol_{\vec {u},v,b}(c) = c$

• $Isol_{\vec {u},v,b} ( g(t_1,\ldots ,t_k) ) = ite ( \bigvee _{i=1}^k Isol_{\vec {u},v,b}(t_i) = \bot , \bot , g(\textit{Isol}_{\vec {u},v,b}(t_1),\ldots ,Isol_{\vec {u},v,b}(t_k)) )$

• $Isol_{\vec {u},v,b} ( f(t_1,\ldots ,t_n) ) = ite ( \bigwedge _{i=1}^n Isol_{\vec {u},v,b}(t_i) = u[i], v, \bot )$

• $Isol_{\vec {u},v,b} ( P(t_1,\ldots ,t_k) ) = ite ( \bigvee _{i=1}^k Isol_{\vec {u},v,b} (t_i) = \bot , \lnot b, P(Isol_{\vec {u},v,b}(t_1),\ldots ,Isol_{\vec {u},v,b}(t_k) ))$

• $Isol_{\vec {u},v,b} ( \lnot P(t_1,\ldots ,t_k) ) = ite ( \bigvee _{i=1}^k Isol_{\vec {u},v,b} (t_i) = \bot , \lnot b, \lnot P(Isol_{\vec {u},v,b}(t_1),\ldots ,Isol_{\vec {u},v,b}(t_k) ))$

• $Isol_{\vec {u},v,b} ( \varphi _1 \vee \varphi _2 ) = Isol_{\vec {u},v,b} (\varphi _1) \vee Isol_{\vec {u},v,b} (\varphi _2)$

• $Isol_{\vec {u},v,b} ( \varphi _1 \wedge \varphi _2 ) = Isol_{\vec {u},v,b} (\varphi _1) \wedge Isol_{\vec {u},v,b} (\varphi _2)$

Intuitively, the function $Isolate_{\vec {u},v,b}(\psi )$ captures whether $\psi$ will evaluate to b if f maps $\vec {u}$ to v and independent of how f is interpreted on other inputs. A function of the form $f(t_1, \ldots t_n)$ is interpreted to be v if the input matches $\vec {u}$ and otherwise evaluated to $\bot$. Functions on terms that involve $\bot$ are sent to $\bot$ as well. Predicates are evaluated to b only if the predicate is evaluated on terms none of which is $\bot$— otherwise, they get mapped to $\lnot b$, to reflect that it will not help to make the final formula $\psi$ evaluate to b. Note that when $Isolate_{\vec {u},v,b}(\psi )$ evaluates to $\lnot b$, there is no property of $\psi$ that we claim. Also, note that $\textit{Isolate}_{\vec {u},v,b}(\psi (f,\vec {x}))$ has no occurrence of f in it, but has free variables $\vec {x}$, $\vec {u}$ and v.

We can show (using a induction over the structure of the specification) that the isolation of a specification to a particular input with $b=F$, when instantiated according to a function that satisfies a specification, cannot evaluate to false (see the full paper [23] for a proof).

Lemma 1

Let $\forall \vec {x}.~ \psi (f,\vec {~x~}\!)$ be a specification and $h :D^n \rightarrow D$ a function satisfying the specification. Then, there is no interpretation of the variables in $\vec {u}$ and $\vec {x}$ (over D) such that if v is interpreted as $h(\vec {u})$, the formula $\textit{Isolate}_{\vec {u},v,F}(\psi (f,\vec {~x~}\!))$ evaluates to false.

We can also show (again using structural induction) that when the isolation of the specification with respect to $b=F$ evaluates to false, then v is definitely not a correct output on $\vec {u}$ (see the full paper [23] for a proof).

Lemma 2

Let $\forall \vec {x}.~ \psi (f,\vec {~x~}\!)$ be a specification, $\vec {p} \in D^n$ an interpretation for $\vec {u}$, and $q \in D$ an interpretation for v such that there is some interpretation for $\vec {x}$ that makes the formula $\textit{Isolate}_{\vec {u},v,F}(\psi (f,\vec {~x~}\!))$ evaluate to false. Then, there exists no function h satisfying the specification that maps $\vec {p}$ to q.

We can now define single-point refutable specifications.

Definition 3

(Single-point Refutable Specifications (SPR)). A specification $\forall \vec {x}.~ \psi (f,\vec {~x~}\!)$ is said to be single-point refutable if the following holds. Let $H: D^n \rightarrow D$ be any interpretation for the function f that does not satisfy the specification (i.e., the specification does not hold under this interpretation for f). Then, there exists some input $\vec {p}$ that is an interpretation for $\vec {u}$ and an interpretation for $\vec {x}$ such that when v is interpreted to be $H(\vec {u})$, the isolated formula $\textit{Isolate}_{\vec {u},v,F}( \psi (f,\vec {~x~}))$ evaluates to false.

Intuitively, the above says that a specification is single-point refutable if whenever a hypothesis function H does not find a specification, there is a single input $\vec {p}$ such that the specification evaluates to false independent of how the function maps inputs other than $\vec {p}$. More precisely, $\psi$ evaluates to false for some interpretation of $\vec {x}$ only assuming that $f(\vec {p})=H(\vec {p})$.

We can show that single-point refutable specifications are single-point definable, which we formalize below (a proof can be found in [23]).

Lemma 3

If a specification $\forall \vec {x}.~ \psi (f,\vec {~x~}\!)$ is single-point refutable, then it is single-point definable.

In the following, we list some examples and non-examples of single-point refutable specifications in the first-order theory of arithmetic:

• $f(15,23)=19 \wedge f(90,20)=91 \wedge \ldots \wedge f(28,24)=35$.

  More generally, any set of input-output samples can be written as a conjunction of constraints that forms a single-point refutable specification.

• $\forall x. ( f(0)=0 \wedge f(x\!+\!1)=f(x)+1$ is not a single-point refutable specification thought it is single-point definable. Given a hypothesis function (e.g., $H(i)=0$, for all i), the formula $f(x\!+\!1)=f(x)$ evaluates to false, but this involves the definition of f on two inputs, and hence we cannot isolate a single input on which the function H is incorrect. (In evaluating the isolated transformation of the specification parameterized with $b=F$, at least one of $f(x\!+\!1)$ and f(x) will evaluate to $\bot$ and hence the whole formula never evaluate to false.)

When a specification $\forall \vec {x}. ~\psi (f,\vec {x})$ is single-point refutable, given an expression H for f that does not satisfy the specification, we can check satisfiability of the formula $\exists \vec {u}\, \exists v \exists \vec {x}.~ \left( v\!=\!H(\vec {u}) \wedge \lnot \textit{Isolate}_{\vec {u},v,F} (\psi (H/f, \vec {x}))\,\right)$. Assuming the underlying quantifier-free theory has a decidable satisfiability problem and can also come up with a model, the valuation of $\vec {u}$ gives a concrete input $\vec {p}$, and Lemma 2 shows that H is definitely wrong on this input. This will form the basis of generating counterexample inputs in the synthesis framework that we outline next.

3 A General Synthesis Framework by Learning Classifiers

We now present our general framework for synthesizing functions over a first-order theory that uses machine-learning of classifiers. Our technique, as outlined in the introduction, is a counterexample-guided inductive synthesis approach (CEGIS), and works most robustly for single-point refutable specifications.

Given a single-point refutable specification $\forall \vec {x}.~\psi (f,\vec {x})$, the framework combines several simpler synthesizers and calls to SMT solvers to synthesize a function, as depicted in Fig. 1. The solver globally maintains a finite set of expressions E, a finite set of predicates A (also called attributes), and a finite set S of multi-labeled samples, where each sample is of the form $(\vec {p}, Z)$ consisting of an input $\vec {p} \in D^n$ and a set $Z\subseteq E$ of expressions that are correct for $\vec {p}$ (such a sample means that the specification allows mapping $\vec {p}$ to $e(\vec {p})$, for any $e \in Z$, but not to $e'(\vec {p})$, for any $e' \in E \setminus Z$).

Fig. 1.

A general synthesis framework based on learning classifiers

Phase 1: In every round, the classifier produces a hypothesis expression H for f. The process starts with a simple expression H, such as one that maps all inputs to a constant. We feed H in every round to a counterexample input finder module, which essentially is a call to an SMT solver to check whether the formula

$$\begin{aligned} \exists \vec {u} ~\exists v ~\exists \vec {x}. ~(v=H(\vec {u}) \wedge \lnot \textit{Isolate}_{\vec {u},v,F}(\psi (f,\vec {x}))) \end{aligned}$$

is satisfiable. Note that from the definition of the single-point refutable functions (see Definition 3), whenever H does not satisfy the specification, we are guaranteed that this formula is satisfiable, and the valuation of $\vec {u}$ in the satisfying model gives us an input $\vec {p}$ on which H is definitely wrong (see Lemma 2). If H satisfies the specification, the formula would be unsatisfiable (by Lemma 1) and we can terminate, reporting H as the synthesized expression.

Phase 2: The counterexample input $\vec {p}~$ is then fed to an expression synthesizer whose goal is to find some correct expression that works for $\vec {p}$. We facilitate this by generating a new specification for synthesis that tailors the original specification to the particular input $\vec {p}$. This new specification is the formula

$$\begin{aligned} \psi \!\!\downarrow _{\vec {p}}(\widehat{f},\vec {x}) :=\textit{Isolate}_{\vec {u},v,T}(\psi (f,\vec {x}))[\vec {p}/\vec {u}, \widehat{f}(\vec {p})/v]. \end{aligned}$$

Intuitively, the above specification asks for a function $\widehat{f}$ that “works” for the input $\vec {p}$. We do this by first finding the formula that isolates the specification to $\vec {u}$ with output v and demand that the specification evaluates to true; then, we substitute $\vec {p}~$ for $\vec {u}$ and a new function symbol $\widehat{f}$ evaluated on $\vec {p}$ for v. Any expression synthesized for $\widehat{f}$ in this synthesis problem maps $\vec {p}$ to a value that is consistent with the original specification. We emphasize that we can use any expression synthesizer for this new specification.

Phase 3: Once we synthesize an expression e that works for $\vec {p}$, we feed it to the next phase, which adds e to the set of all expressions E (if e is new) and adds $\vec {p}$ to the set of samples. It then proceeds to find the set of all expressions in E that work for all the inputs in the samples, and computes the new set of samples. In order to do this, we take every input $\vec {r}$ that previously existed, and ask whether e works for $\vec {r}$, and if it does, add e to the set of labels for $\vec {r}$. Also, we take the new input $\vec {p}$ and every expression $e' \in E$, and check whether $e'$ works for $\vec {p}$.

To compute this labeling information, we need to be able to check, in general, whether an expression $e'$ works for an input $\vec {r}$. We can do this using a call to an SMT solver that checks whether the formula $\forall \vec {x}. ~\psi \!\!\downarrow _{\vec {r}}(e'(\vec {r})/\widehat{f}(\vec {r}), \,\vec {x})$ is valid.

Phase 4: We now have a set of samples, where each sample consists of an input and a set of expressions that work for that input. This is when we look upon the synthesis problem as a classification problem— that of mapping every input in the domain to an expression that generalizes the sample (i.e., that maps every input in the sample to some expression that it is associated with it). In order to do this, we need to split the input domain into regions defined by a set of predicates A. We hence need an adequate set of predicates that can define enough regions that can separate the inputs that need to be separated.

Let S be a set of samples and let A be a set of predicates. Two samples $(\vec {j}, E_1)$ and $(\vec {j'}, E_2)$ are said to be inseparable if for every predicate $p\in A$, $p(\vec {j}) \equiv p(\vec {j'})$. The set of predicates A is said to be adequate for a sample S if any set of inseparable inputs in the sample has a common label as a classification. In other words, if every subset $T \subseteq S$, say $T= \{ (\vec {i_1}, E_1), (\vec {i_2}, E_2), \ldots (\vec {i_t}, E_t) \}$, where every pair of inputs in T is inseparable, then $\bigcap _{i=1}^t E_i \not = \emptyset$. We require the attribute synthesizer to synthesize an adequate set of predicates A, given the set of samples.

Intuitively, if T is a set of pairwise inseparable points with respect to a set of predicates P, then no classifier based on these predicates can separate them, and hence they all need to be classified using the same label; this is possible only if the set of points have a common expression label.

Phase 5: Finally, we give the samples and the predicates to a classification learner, which divides the set of inputs into regions, and maps each region to a single expression such that the mapping is consistent with the sample. A region is a conjunction of predicates and the set of points in the region is the set of all inputs that satisfy all these predicates. The classification is consistent with the set of samples if for every sample $(\vec {r},Z) \in S$, the classifier maps $\vec {r}$ to a label in Z. (In Sect. 4, we present a general learning algorithm based on decision trees that learns such a classifier from a set of multi-labeled samples, and which biases the classifier towards small trees.)

The classification synthesized is then converted to an expression in the logic (this will involve nested ite expressions using predicates to define the regions and expressions at leaves to define the function). The synthesized function is fed back to the counterexample input finder, as in Phase 1, and the process continues until we manage to synthesize a function that meets the specification.

4 Multi-Label Decision Tree Classifiers

In this section, we sketch a decision tree learning algorithm for a special case of the so-called multi-label learning problem, which is the problem of learning a predictive model (i.e., a classifier) from samples that are associated with multiple labels. For the purpose of learning the classifier, we assume samples to be vectors of the Boolean values $\mathbb B = \{F, T\}$ (these encode the values of the various attributes on the counterexample input returned). The more general case that datapoints also contain rational numbers can be handled in a straightforward manner as in Quinlan’s C5.0 algorithm [25, 27].

To make the learning problem precise, let us fix a finite set $L = \{\lambda _1, \ldots , \lambda _k\}$ of labels with $k \ge 2$, and let $\vec {x}_1, \ldots , \vec {x}_m$ denote m individual inputs (in the following also called datapoints). The task we are going to solve, which we call disjoint multi-label learning problem (cf. Jin and Ghahramani [17]), is

“Given a finite training set $S = \{ (\vec {x}_1, Y_1), \ldots , (\vec {x}_m, Y_m) \}$ where $Y_i \subseteq L$ and $Y_i \ne \emptyset$ for every $i \in \{1, \ldots , m\}$, find a decision tree classifier $h :\mathbb B^m \rightarrow L$ such that $h(\vec {x}) \in Y$ for all $(\vec {x}, Y) \in S$.”

Note that this learning problem is a special case of the multi-label learning problem studied in machine learning literature, which asks for a classifier that predicts all labels that are associated with a datapoint. Moreover, it is important to emphasize that we require our decision tree classifier to be consistent with the training set (i.e., it is not allowed to misclassify datapoints in the training set), in contrast to classical machine learning settings where classifier are allowed to make (small) errors.

We use a straightforward modification of Quinlan’s C 5.0 algorithm [25, 27] to solve the disjoint multi-label learning problem. (We refer to standard text on machine learning [22] for more information on decision tree learning.) This modification, sketched in pseudo code as Algorithm alg:decisionspstree, is a recursive algorithm that constructs a decision tree top-down. More precisely, given a training set S, the algorithm heuristically selects an attribute $i \in \{1, \ldots , m \}$ and splits the set into two disjoint, nonempty subsets $S_i = \{ (\vec {x}, Y) \in S \mid x_i = T \}$ and $S_{\lnot i} = \{ (\vec {x}, Y) \in S \mid x_i = F \}$ (we explain shortly how the attribute i is chosen). Then the algorithm recurses on the two subsets, whereby it no longer considers the attribute i. Once the algorithm arrives at a set $S'$ in which all datapoints share at least one common label (i.e., there exists a $\lambda \in L$ such that $\lambda \in Y$ for all $(\vec {x}, Y) \in S'$), it selects a common label $\lambda$ (arbitrarily), constructs a single-node tree that is labeled with $\lambda$, and returns from the recursion. However, it might happen during construction that a set of datapoints does not have a common label and cannot be split by any (available) attribute. In this case, it returns an error, as the set of attributes is not adequate (which we make sure does not happen in our framework).

The selection of a “good” attribute to split a set of datapoints lies at the heart of the decision tree learner as it determines the size of the resulting tree and, hence, how well the tree generalizes the training data. The quality of a split can be formalized by the notion of a measure, which, roughly, is a measure $\mu$ mapping pairs of sets of datapoints to a set R that is equipped with a total order $\preceq$ over elements of R (usually, $R = \mathbb R_{\ge 0}$ and $\preceq$ is the natural order over $\mathbb R$). Given a set S to split, the learning algorithm first constructs subsets $S_i$ and $S_{\lnot i}$ for each available attribute i and evaluates each such candidate split by computing $\mu (S_i, S_{\lnot i})$. It then chooses a split that has the least value.

In the single-label setting, information theoretic measures, such as information gain (based on Shannon entropy) and Gini, have proven to produce successful classifiers [15]. In the case of multi-label classifiers, however, finding a good measure is still a matter of ongoing research (e.g., see Tsoumakas and Katakis [33] for an overview). Both the classical entropy and Gini measures can be adapted to the multi-label case in a straightforward way by treating datapoints with multiple labels as multiple identical datapoints with a single label (we describe these in the full paper [23]). Another modification of entropy has been proposed by Clare and King [9]. However, these approaches share a disadvantage, namely that the association of datapoints to sets of labels is lost and all measures can be high, even if all datapoints share a common label; for instance, such a situation occurs for $S = \{ (\vec {x}_1, Y_1), \ldots , (\vec {x}_n, Y_n) \}$ with $\{ \lambda _1, \ldots , \lambda _\ell \} \subseteq Y_i$ for every $i \in \{1, \ldots , n \}$.

Ideally, one would like to have a measure that maps to 0 if all datapoints in a set share a common label and to a value strictly greater than 0 if this is not the case. We now present a measure, based on the combinatorial problem of finding minimal hitting sets, that has this property. To the best of our knowledge, this measure is a novel contribution and has not been studied in the literature.

For a set S of datapoints, a set $H \subseteq L$ is a hitting set if $H \cap Y \ne \emptyset$ for each $(\vec {x}, Y) \in S$. Moreover, we define the measure $hs (S) = \min _{\text {hitting set H}} |H| - 1$, i.e., the cardinality of a smallest hitting set reduced by 1. As desired, we obtain $hs (S) = 0$ if all datapoints in S share a common label and $hs (S) > 0$ if this is not the case. When evaluating candidate splits, we would prefer to minimize the number of labels needed to label the datapoints in the subsets; however, if two splits agree on this number, we would like to minimize the total number of labels required. Consequently, we propose $R = \mathbb N \times \mathbb N$ with $(n, m) \preceq (n', m')$ if and only if $n < n'$ or $n = n' \wedge m \le m'$, and as measures $\mu _ hs (S_1, S_2) = (\max {\{ hs (S_1), hs (S_2) \}}, hs (S_1) + hs (S_2))$. As computing $hs (S)$ is computationally hard, we implemented a standard approximate greedy algorithm (the dual of the standard greedy set cover algorithm [8]), which runs in time polynomial in the size of the sample and whose solution is at most a logarithmic factor of the optimal solution.

5 A Synthesis Engine for Linear Integer Arithmetic

We now describe an instantiation of our framework (described in Sect. 3) for synthesizing functions expressible in linear integer arithmetic against quantified linear integer arithmetic specifications.

The counterexample input finder (Phase 1) and the computing of labels for counterexample inputs (Phase 3) are implemented straightforwardly using an SMT solver (note that the respective formulas will be in quantifier-free linear integer arithmetic). The $\textit{Isolate}()$ function works over a domain $D \cup \{\bot \}$; we can implement this by choosing a particular element $\widehat{c}$ in the domain and modeling every term using a pair of elements, one that denotes the original term and the second that denotes whether the term is $\bot$ or not, depending on whether it is equal to $\widehat{c}$. It is easy to transform the formula now to one that is on the original domain D (which in our case integers) itself.

Expression Synthesizer. Given an input $\vec {p}$, the expression synthesizer has to find an expression that works for $\vec {p}$. Our implementation deviates slightly from the general framework.

In the first phase, it checks whether one of the existing expressions in the global set E already works for $\vec {p}$. This is done by calling the label finder (as in Phase 3). If none of the expressions in E work for $\vec {p}$, the expression synthesizer proceeds to the second phase, where it generates a new synthesis problem with specification $\forall \vec {x}.~ \psi {\downarrow }_{\vec {p}} (\hat{f}, \vec {x})$ according to Phase 2 of Sect. 3, whose solutions are expressions that work for $\vec {p}$. It solves this synthesis problem using a simple CEGIS-style algorithm, which we sketch next.

Let $\forall \vec {x}.~ \psi (f, \vec {x})$ be a specification with a function symbol $f :\mathbb Z^n \rightarrow Z$, which is to be synthesized, and universally quantified variables $\vec {x} = (x_1, \ldots , x_m)$. Our algorithm synthesizes affine expressions of the form $\left( \sum _{i = 1}^n a_i \cdot y_i\right) + b$ where $y_1, \ldots , y_n$ are integer variables, $a_i \in \mathbb Z$ for $i \in \{1, \ldots , n\}$, and $b \in \mathbb Z$. The algorithm consists of two components, a synthesizer and a verifier, which implement the CEGIS principle in a similar but simpler manner as our general framework. Roughly speaking, the synthesizer maintains an (initially empty) set $V \subseteq \mathbb Z^m$ of valuations of the variables $\vec {x}$ and constructs an expression H for the function f that satisfies $\psi$ at least for each valuation in V (as opposed to all possible valuations). Then, it hands this expression over to the verifier. The task of the verifier is to check whether H satisfies the specification. If this is the case, the algorithm has identified a correct expression, returns it, and terminates. If this not the case, the verifier extracts a particular valuation of the variables $\vec {x}$ for which the specification is violated and hands it over to the synthesizer. The synthesizer adds this valuation to V, and the algorithm iterates.

Predicate Synthesizer. Since the decision tree learning algorithm (which is our classifier) copes extremely well with a large number of attributes, we do not spend time in generating a small set of predicates. We build an enumerative predicate synthesizer that simply enumerates and adds predicates until it obtains an adequate set.

More precisely, the predicate synthesizer constructs a set $A_q$ of attributes for increasing values of $q \in \mathbb N$. The set $A_q$ contains all predicates of the form $\sum _{i = 1}^n a_i \cdot y_i \le b$, where $y_i$ are variables corresponding to the function arguments of the function f that is to be synthesized, $a_i \in \mathbb Z$ such that each $\Sigma _{i=1}^n |a_i| \le q$, and $|b| \le q^2$. If $A_q$ is already adequate for S (which can be checked by recursively splitting the sample with respect to each predicate in $A_q$ and checking if all samples at each leaf has a common label), we stop, else we increase the parameter q by one and iterate. Note that the predicate synthesizer is guaranteed to find an adequate set for any sample. The reason for this is that one can separate each input $\vec {p}$ into its own subsample (assuming each individual variable is also an attribute) provided q is large enough.

Fig. 2.

Experimental results

6 Evaluation

We implemented the framework described in Sect. 5 for specifications written in the SyGuS format [1]. The implementation is about 5 K lines in C++ with API calls to the Z3 SMT solver [10].

The implementations of the LIA counter-example finder and the expression synthesizer use several heuristics. The counter-example finder prioritizes data-points that have a single classification, and returns multiple counterexamples in each round. The expression synthesizer uses a combination of enumeration (for small degree expressions) and constraint-solving (for larger ones), and prioritizes returning expressions that work for multiple neighboring inputs. More details are in the extended version [23].

We evaluated our tool parameterized using the different measures in Sect. 4 against 43 benchmarks, and report here a representative 24 of them. These benchmarks are predominantly from the 2014 and 2015 SyGuS competition [1, 3]. Additionally, there is an example from [16] for deobfuscating C code using bitwise operations on integers (we query this code 30 times on random inputs, record its output and create an input-output specification, Jha_Obs, from it). The synthesis specification max2Univ reformulates the specification for max2 using universal quantification, as

$$\begin{aligned} \forall x,r,y_1,y_2. ~(r<0) \Rightarrow (( y_1\!\! = \!\!x \wedge y_2 \!\!=\!\! x\!+\!r) \vee (y_1\!\! =\!\! x\!+\!r \wedge y_2 \!\!=\!\!x)) \Rightarrow max(y_1,y_2) = x. \end{aligned}$$

All experiments were performed on a system with an Intel Core i7-4770HQ 2.20 GHz CPU and 4 GB RAM running 64-bit Ubuntu 14.04 with a 200 seconds timeout. The results of the 24 representative benchmarks are depicted in Fig. 2.

Figure 2 compares three measures: e-gini, pq-entropy and hitting set (pq-entropy refers to the measure proposed by Clare and King [9]). All solvers time-out on two benchmarks each. None of the algorithms dominates. The hitting-set measure is the only one to solve LinExpr_eq2. E-gini and pq-entropy can solve the same set of benchmarks but their performance differs on the example* specs, where e-gini performs better, and max* where pq-entropy performs better.

The CVC4 SMT-solver based synthesis tool [26] (which won the linear integer arithmetic track in the SyGuS 2015 competition [3]) worked very fast on these benchmarks, in general, but does not generalize from underspecifications. On specifications that list a set of input-output examples (marked with * in Fig. 2), CVC4 simply returns the precise map that the specification contains, without generalizing it. CVC4 allows restricting the syntax of target functions, but using this feature to force generalization (by disallowing large constants) renders them unsolvable. CVC4 was also not able to solve, surprisingly, the fairly simple specification max2Univ (although it has the single-invocation property [26]).

The general track SyGuS solvers (enumerative, stochastic, constraint-solver, and Sketch) [1] do not work well for these benchmarks (and did not fare well in the competition either); for example, the enumerative solver, which was the winner in 2014 can solve only 15 of the 43 benchmarks.

The above results show that the synthesis framework developed in this paper that uses theory-specific solvers for basic expressions and predicates, and combines them using a classification learner yields a competitive solver for the linear integer arithmetic domain. We believe more extensive benchmarks are needed to choose the right statistical measures for decision-tree learning.