Towards a Formal Theory of Graded Monads

Abstract

We initiate a formal theory of graded monads whose purpose is to adapt and to extend the formal theory of monads developed by Street in the early 1970’s. We establish in particular that every graded monad can be factored in two different ways as a strict action transported along a left adjoint functor. We also explain in what sense the first construction generalizes the Eilenberg-Moore construction while the second construction generalizes the Kleisli construction. Finally, we illustrate the Eilenberg-Moore construction on the graded state monad induced by any object V in a symmetric monoidal closed category $\mathscr {C}$.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

An important principle in categorical semantics is that lax algebraic structures are transported along left adjoint functors. This principle is a bit abstract and not so well known, so let us explain what it means. Suppose that we pick a 2-monad T on the 2-category Cat of categories and a category $\mathscr {B}$ equipped with a lax algebra structure of the 2-monad T, provided by the functor

$$*_\mathscr {B}\quad : \quad T\mathscr {B}\longrightarrow \mathscr {B}$$

Suppose moreover that the category $\mathscr {B}$ is related to a category $\mathscr {A}$ by adjunction where the functor $L:\mathscr {A}\rightarrow \mathscr {B}$ is left adjoint to the functor $R:\mathscr {B}\rightarrow \mathscr {A}$, in the following way:

In that case, the composite functor

$$*_{\mathscr {A}} \quad :=\quad R \circ *_{\mathscr {B}} \circ TL \quad : \quad T\mathscr {A}\longrightarrow \mathscr {A}$$

provides a lax algebra structure on the category $\mathscr {A}$ inherited from the lax algebra structure of the category $\mathscr {B}$. This basic observation was inspired by homotopy theory and played a central rôle in the early development by Melliès of tensorial logic [9, 10, 15]. A particularly important instance is the following one. Every monoidal category $(\mathscr {M},\otimes ,I)$ induces a 2-monad

$$T \quad = \quad \mathscr {A}\quad \mapsto \quad \mathscr {M}\times \mathscr {A}\quad : \quad Cat \longrightarrow Cat$$

on the category Cat. An algebra (in the strict sense) of the 2-monad T is a functor

$$\begin{aligned} *\quad : \quad \mathscr {M}\times \mathscr {C}\quad \longrightarrow \quad \mathscr {C}\end{aligned}$$

(1)

which satisfies the equations:

$$\begin{aligned} m*(n*A) = (m\otimes n)*A \quad \quad A = I*A \end{aligned}$$

(2)

for all objects m, n of the category $\mathscr {M}$ and every object A of the category $\mathscr {C}$. As such, a strict T-algebra is the same thing as an action of the monoidal category $(\mathscr {M},\otimes ,I)$ over the category $\mathscr {C}$. By way of comparison, a lax T-algebra structure on a category $\mathscr {C}$ is a functor (1) where the equalities (2) are replaced by a family of morphisms

$$ \mu _{m,n,A}: m*(n*A) \rightarrow (m\otimes n)*A \quad \quad \eta _{A} : A \rightarrow I*A $$

natural in objects m, n of the category $\mathscr {M}$ and in the object A of the category $\mathscr {C}$, and making the three coherence diagrams commute for all objects m, n, p of the category $\mathscr {M}$ and all objects A of the category $\mathscr {C}$:

So, a lax T-algebra defines what is traditionally called a lax action of the monoidal category $\mathscr {M}$ on the category $\mathscr {C}$. Now, suppose that the category $\mathscr {B}$ is equipped with an action

$$ \circledast \quad : \quad \mathscr {M}\times \mathscr {B}\quad \longrightarrow \quad \mathscr {B}. $$

In that case, the category $\mathscr {A}$ inherits a lax action

$$ *\quad : \quad \mathscr {M}\times \mathscr {A}\quad \longrightarrow \quad \mathscr {A}$$

along the left adjoint functor L, defined as the composite

$$ m*A \quad :=\quad R(m\circledast LA). $$

Since adjunctions $L\dashv R$ and actions $\circledast :\mathscr {M}\times \mathscr {B}\rightarrow \mathscr {B}$ are ubiquitous in programming language semantics, this inheritance property implies that the notion of lax action is just as central in the theory.

Note that in the particular case when the monoidal category $\mathscr {M}$ coincides with the terminal category 1, a lax action of $\mathscr {M}$ on a category $\mathscr {C}$ is the same thing as a monad S on the category $\mathscr {C}$, with $(S,\mu ^\prime ,\eta ^\prime )$ defined as

$$ SA :=I *A \quad \quad \quad \mu ^\prime _A :=\mu _{I,I,A}:SSA\rightarrow SA\quad \quad \quad \eta ^\prime _A :=\eta _{A}:A\rightarrow SA $$

For that reason, Melliès found convenient to introduce the terminology of parametric monad in his work on tensorial logic [10, 13]. One additional reason for choosing that terminology was that the dual notion of parametric comonad appeared at about the same time in his work with Grellois on higher-order model-checking [6]. The idea of developing a general theory of parametric monads for effect systems and of parametric comonads for resource systems emerged at this point and was announced in [12] as an algebraic counterpart to the works on implicit complexity [4] and on linear dependent types [5]. At about the same time, Petricek, Orchard and Mycroft designed the syntax and semantics of a calculus which can explicitly manage resource usage based on the structure of graded comonads  [17]. The concept and terminology of parametric monad was then taken up and popularised by Katsumata [8] with a series of new applications to the semantics of effect systems. Milius, Pattinson and Schröder applied graded monads to extend the trace semantics of coalgebras with the concept of trace length [16].

The combination of these works raised a lot of interest in the community and established the notion of parametric monad as an important concept of the discipline. We thus feel useful and timely to join forces and to develop a formal theory of parametric monads inspired by the seminal work by Street [21] on formal monads in 2-categories. However, before doing that, we will explain in Sect. 2 why we decided to revise the original terminology and to call graded monad what we used to call parametric monad. As we will see, the change of terminology is justified mathematically, and the terminology seems to be convenient in itself¹.

Using the new terminology, one of the main contributions of the paper will be to establish that given a monoidal category $(\mathscr {M},\otimes ,I)$, every graded monad

$$ *\quad : \quad \mathscr {M}\times \mathscr {A}\quad \longrightarrow \quad \mathscr {A}$$

is the graded monad

$$\begin{aligned} m*A \quad :=\quad R(m\circledast LA) \end{aligned}$$

(3)

associated to an adjunction

and to a strict action

$$ \circledast \quad : \quad \mathscr {M}\times \mathscr {B}\quad \longrightarrow \quad \mathscr {B}. $$

of the monoidal category $(\mathscr {M},\otimes ,I)$ on the category $\mathscr {B}$. Following an original idea by Street [20], we will establish that the factorisation (3) can be performed in two different ways. One recovers in the particular case $\mathscr {M}=1$ the factorisation of a monad $S=R\circ L$ as an adjunction $L\dashv R$ using either the category $\mathscr {B}$ of Eilenberg-Moore algebras, or the Kleisli category $\mathscr {B}$ associated to the monad S. As we will see in Sects. 3.1 and 3.2, the constructions of the Eilenberg-Moore category and of the Kleisli category are more involved in the case of a graded monad. In particular, in order to recover the expected universal characterizations of Eilenberg-Moore and Kleisli objects in the more general case of graded monads, the category $\mathscr {B}$ has to be considered as an object of the 2-category of $\mathscr {M}$-categories, where by $\mathscr {M}$-category, we mean a category $\mathscr {C}$ equipped with a strict action of $\mathscr {M}$.

Since the Eilenberg-Moore and Kleisli constructions are a bit formal, we find it instructive to illustrate them with a specific example. Besides the original example of the continuation monad treated in [15], an original motivation for the notion of graded monad emerged in the study of the local state monad [14, 18]. As we will see in Sect. 3.1, an interesting aspect of the theory is that an Eilenberg-Moore algebra of a graded monad $*:\mathscr {M}\times \mathscr {A}\rightarrow \mathscr {A}$, which we call a graded algebra, is defined as a functor $A:\mathscr {M}\rightarrow \mathscr {A}$ equipped with a family of morphisms

$$ h_{m,n} \quad : \quad m*A_n \rightarrow A_{m\otimes n} $$

natural in $m,n\in \mathscr {M}$ and making the diagrams below commute

for all objects m, n, p of the monoidal category $(\mathscr {M},\otimes ,I)$. In particular, in the case $\mathscr {A}=Set$, the category $\mathscr {B}$ of Eilenberg-Moore algebras of the graded monad $*$ can be seen as a category of covariant presheaves over $\mathscr {M}$ with an extra structure provided by the family of morphisms $h_{m,n}$.

We will illustrate the construction with an example: suppose given a symmetric monoidal closed category $(\mathscr {C},\otimes ,\multimap \!\,,I)$ equipped with an object V, where V stands for values. The category $\mathscr {C}$ is then equipped with a parametric monad

$$ *\quad : \quad Inj \times \mathscr {C}\quad \longrightarrow \quad \mathscr {C}$$

where $(Inj,+,0)$ denotes the monoidal category with natural numbers

$$[m] \quad = \quad \{0,\dots ,m-1\}$$

seen as finite sets as objects, and injections $f:[m]\rightarrow [n]$ as morphisms. We will often write m for the object [m]. The lax action of the monoidal category $(Inj,+,0)$ over the category $\mathscr {C}$ is defined as

$$ n*A \quad :=\quad V^{\otimes n} \multimap \!\, (V^{\otimes n} \otimes A) $$

where we write $V^{\otimes n}$ for the object V to the tensorial power n:

$$ V^{\otimes n} \quad :=\quad V \otimes \cdots \otimes V. $$

We show that, in the particular case when $\mathscr {C}=Set$, the category $\mathscr {B}$ of algebras of the graded monad $*:Inj\times Set\rightarrow Set$ coincides with the category of S-algebras for a monad S on the presheaf category [Inj, Set]. The monad S is moreover described by a Lawvere theory with arities $\mathscr {L}$ in the sense of [14] which is presented by generators and relations in the Appendix.

We believe that these constructions are interesting in themselves. They also contribute to the general theory of graded monads, and more generally, of parametric notions of effects and resources.

Plan of the Paper. We start by explaining in Sect. 2 why it makes sense to call graded monads what we used to call parametric monads. Then, we describe in Sect. 3 the Eilenberg-Moore construction (see Sect. 3.1) and the Kleisli construction (see Sect. 3.2) for graded monads. After that, in Sect. 4 we provide a 2-categorical perspective on our construction, by proving that we indeed defined the Eilenberg-Moore and Kleisli objects in the sense of Street. We illustrate the construction by applying it in Sect. 5 to the Inj-graded state monad $\mathbf {S}$ on the category Set. In particular, we present by generators and relations the Lawvere theory characterizing the graded $\mathbf {S}$-algebras of the graded state monad $\mathbf {S}$ as covariant presheaves over Inj with an extra structure.

2 Parametric Monads Are Graded Monads

Quite obviously, the terminology “graded” comes from the ring-theoretic concept of “graded ring”. Let $(R,+,0,\times ,1)$ be a ring and $\mathbf{N}$ be the additive monoid on natural numbers. An $\mathbf{N}$ -grading on R is an $\mathbf{N}$-indexed family $(A_m)_{m\in \mathbf{N}}$ of abelian groups such that $R=\bigoplus _{m\in \mathbf N}A_m$ and such that the following holds for all $m,n\in \mathbf{N}$:

$$\begin{aligned} \{x\times y~|~x\in A_m,y\in A_n\}\subseteq A_{m+n}. \end{aligned}$$

(4)

From these conditions, it follows that $1\in A_0$ and $A_0$ is a subring of R. An $\mathbf{N}$ -graded ring is a pair of a ring R and an $\mathbf{N}$-grading $(A_m)_{m\in \mathbf{N}}$ on it.

An $\mathbf{N}$-grading $(A_m)_{m\in \mathbf{N}}$ on R, which is the primary data of the $\mathbf{N}$-graded ring, depicts a monoid-like structure in $\mathbf{Ab}$. It consists of (1) multiple carrier objects $A_m$ given for each grade $m\in \mathbf{N}$, (2) a unit group homomorphism $r_0:\mathbf{Z}\rightarrow A_0$ at grade 0, which corresponds to $1\in A_0$, and (3) a family of grade-respecting multiplications $r_{m,n}:A_m\otimes A_n\rightarrow A_{m+n}$, which are restrictions of the multiplication $(\times ):R\otimes R\rightarrow R$ by the condition (4). These morphisms satisfy the usual unit and associativity laws. We thus call such a structure an $\mathbf{N}$ -graded monoid in $\mathbf{Ab}$ [19], and identify it with a lax monoidal functor of type $(\mathbf{N},+,0)\rightarrow (\mathbf{Ab},\otimes ,\mathbf{Z})$, because both structures carry exactly the same data. More generally, for $\mathscr {M}$ a monoidal category, we define an $\mathscr {M}$ -graded monoid in a monoidal category $\mathscr {C}$ to be a lax monoidal functor of type $\mathscr {M}\rightarrow \mathscr {C}$. Of course, ordinary monoids coincide with 1-graded monoids.

A $\mathscr {M}$ -graded monad on $\mathscr {A}$ may be then defined as an $\mathscr {M}$-graded monoid in the strict monoidal category $([\mathscr {A},\mathscr {A}],\circ ,Id)$ of endofunctors on $\mathscr {A}$, in the style of [19, Sect. 1.1]. An easy calculation shows that $\mathscr {M}$-graded monads on $\mathscr {A}$ bijectively correspond to lax $\mathscr {M}$-actions on $\mathscr {A}$ in the previous section, and to $\mathscr {M}$-parametric monads on $\mathscr {A}$ as they are called in [8, 10, 13]. Following this correspondence, in the rest of the paper we use the terminology “graded monad” instead of “parametric monad”. The main reason for this change is that it makes it easy to relate categorical concepts around graded monads and algebraic concepts around graded rings. For instance, one easily sees that the concept of graded algebra of a graded monad, introduced in the previous section, is a categorical analogue of the concept of graded module over a graded ring.

3 Adjunction Pairs Induced from Graded Monads

Throughout this section we fix a monoidal category $(\mathscr {M},\otimes ,I)$, which we will consider strict for convenience, together with an $\mathscr {M}$-graded monad $\mathbf {T}=(*,\mu ,\eta )$ on a given category $\mathscr {A}$. We have explained in the introduction that every adjunction $L\dashv R:\mathscr {B}\rightarrow \mathscr {A}$ combined with a strict $\mathscr {M}$-action $\circledast$ on the category $\mathscr {B}$ induces an $\mathscr {M}$-graded monad $m*a=R(m\circledast La)$ on the category $\mathscr {A}$. Especially, when $\mathscr {M}=1$, this reduces to the well-known fact that the adjunction $L\dashv R$ induces a monad $R\circ L$. Conversely, a natural question is whether one can derive any $\mathscr {M}$-graded monad $\mathbf {T}=(*,\mu ,\eta )$ on a category $\mathscr {A}$ as the result of “deforming” a strict $\mathscr {M}$-action $\circledast$ on a category $\mathscr {B}$ along a suitable adjunction $L\dashv R$ with $L:\mathscr {A}\rightarrow \mathscr {B}$. Just as in the case of monads, we provide two answers, each of them corresponding to a different construction of the category $\mathscr {B}$ as the category $\mathscr {A}^{\mathbf {T}}$ of Eilenberg-Moore algebras, or as the Kleisli category $\mathscr {A}_{\mathbf {T}}$ associated to the graded monad $\mathbf {T}$. The constructions require that the category $\mathscr {M}$ is small, and we thus make this hypothesis from now on. A pair of very similar constructions have been studied by Street in a nice but not sufficiently known paper [20] where two ordinary functors $\hat{F},\tilde{F}:\mathscr {M}\rightarrow Cat$ are associated to a given lax functor $F:\mathscr {M}\rightarrow Cat$ starting from a category $\mathscr {M}$. As we will see, the two constructions adapt Street’s original constructions and mildly extend it to allow $\mathscr {M}$ to be any monoidal category (seen as a one-object 2-category).

3.1 The Eilenberg-Moore Construction

Given an $\mathscr {M}$-graded monad $\mathbf {T}=(*,\mu ,\eta )$ over a category $\mathscr {A}$, the category $\mathscr {A}^{\mathbf {T}}$ of its Eilenberg-Moore algebras is defined in the following way.

Definition 1

(graded $\mathbf {T}$ -algebras). A graded $\mathbf {T}$-algebra is a pair (A, h) that consists of a functor $A:\mathscr {M}\rightarrow \mathscr {A}$ and of a family h of morphisms

$$ h_{m,n}: m*A_n\rightarrow A_{m\otimes n} $$

natural in m, n and making the diagrams below commute for all objects m, n, p of $\mathscr {M}$:

(5)

Definition 2

(homomorphisms). Given two graded ${\mathbf {T}}$-algebras (A, h) and $(A',h')$, a homomorphism

$$ \varphi \quad : \quad (A,h) \quad \longrightarrow \quad (A^\prime ,h^\prime ) $$

is defined as a natural transformation $\varphi : A\Rightarrow A^\prime$ making the diagram below commute for all objects m, n of $\mathscr {M}$:

(6)

Definition 3

(Eilenberg-Moore construction). The category $\mathscr {A}^{\mathbf {T}}$ has graded $\mathbf {T}$-algebras as objects and homomorphisms between them as morphisms.

One important observation is that the category $\mathscr {A}^{\mathbf {T}}$ admits the following strict $\mathscr {M}$-action.

Definition 4

(strict action). The strict $\mathscr {M}$-action

$$\circledast \quad : \quad \mathscr {M}\times \mathscr {A}^{\mathbf {T}}\quad \longrightarrow \quad \mathscr {A}^{\mathbf {T}}$$

of an object $p\in \mathscr {M}$ is defined as follows: it transports a graded $\mathbf {T}$-algebra (A, h) to the graded $\mathbf {T}$-algebra defined by right translation:

$$ p\circledast (A,h) \quad :=\quad \big ((A_{m\otimes p})_{m\in \mathscr {M}},(h_{m,n\otimes p})_{m,n\in \mathscr {M}}\big ) $$

and it transports a homomorphism $\varphi :(A,h)\rightarrow (A',h')$ into the homomorphism

$$ p\circledast \varphi \,\, : \,\, p\circledast (A,h) \,\, \longrightarrow \,\, p\circledast (A',h') $$

defined by the natural transformation:

$$(p\circledast \varphi )_n \,\, :=\,\, \varphi _{n\otimes p} \,\, : \,\, A_{n\otimes p}\rightarrow A^\prime _{n\otimes p}$$

It is worth observing that the definition of the action of p and of q on a graded $\mathbf {T}$-algebra (A, h) ensures that the equality below (expected by the definition of an $\mathscr {M}$-action) is satisfied:

$$ p\circledast (q \circledast (A,h)) \quad = \quad (p\otimes q)\circledast (A,h) $$

for all objects p, q of the monoidal category $\mathscr {M}$.

Theorem 5

The functor $u^{\mathbf {T}}:\mathscr {A}^{\mathbf {T}}\rightarrow \mathscr {A}$ defined by $(A,h)\mapsto A_I$ has a left adjoint $f^{\mathbf {T}}$ such that the graded monad $\mathbf {T}=(*,\mu ,\eta )$ coincides with the graded monad

$$(m,a)\quad \mapsto \quad u^{\mathbf {T}}(m\circledast (f^{\mathbf {T}}(a))) \quad : \quad \mathscr {M}\times \mathscr {A}\quad \longrightarrow \quad \mathscr {A}$$

derived from the adjunction $f^{\mathbf {T}}\dashv u^{\mathbf {T}}$ and from the $\mathscr {M}$-action $\circledast$ on $\mathscr {A}^\mathbf {T}$.

The functor $f^{\mathbf {T}}$ is constructed in the following way: to any object a of the category $\mathscr {A}$, it associates the graded $\mathbf {T}$-algebra $f^{\mathbf {T}} (a)$ defined by the functor

$$ f^{\mathbf {T}} (a) \quad :=\quad m \quad \mapsto \quad m*a \quad : \quad \mathscr {M}\quad \longrightarrow \quad \mathscr {A}$$

together with the family of morphisms

$$ h_{m,n}\quad :=\quad \mu _{m,n,a} \quad : \quad m*(n*a) \quad \longrightarrow \quad (m\otimes n)*a. $$

3.2 The Kleisli Construction

Given an $\mathscr {M}$-graded monad $\mathbf {T}=(*,\mu ,\eta )$ over a category $\mathscr {A}$, the Kleisli category $\mathscr {A}_{\mathbf {T}}$ is defined in the following way.

Definition 6

(Kleisli construction). The category $\mathscr {A}_\mathbf {T}$ has objects the pairs (m, a) where m is an object of $\mathscr {M}$ and a is an object of $\mathscr {A}$, and each hom-set is defined by the coend formula

$$ \mathscr {A}_\mathbf {T}\big ((m,a),(m^\prime ,a^\prime )\big )\quad :=\quad \int ^{n\in \mathscr {M}} \mathscr {A}(a,n*a^\prime )\times \mathscr {M}(m\otimes n,m^\prime ). $$

In other words, a morphism is an equivalence class of triples of the form

$$[\,n,a\xrightarrow {f} n*a^\prime ,m\otimes n\xrightarrow {w} m^\prime \,]$$

modulo the equivalence relation defined by the coend formula. The identity morphism on (m, a) is defined as

$$[I,a\xrightarrow {\eta } I*a, m\otimes I\xrightarrow {\mathrm {id}_{}} m]$$

and the composition of morphisms is defined as

$$\begin{aligned}{}[n^\prime ,a^\prime&\xrightarrow {f^\prime } n^\prime *a^{\prime \prime },m^\prime \otimes n^\prime \xrightarrow {w^\prime } m^{\prime \prime }]\circ n,a\xrightarrow {f} n*a^\prime ,m\otimes n\xrightarrow {w} m^\prime ]\\&:=\quad [n\otimes n^\prime , a\xrightarrow {f} n*a^\prime \xrightarrow {n*f^\prime }n*n^\prime *a^{\prime \prime }\xrightarrow {\mu _{n,n^\prime } } (n\otimes n^\prime )*a^{\prime \prime },\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad m\otimes n\otimes n^\prime \xrightarrow {w\otimes n'}m^\prime \otimes n^\prime \xrightarrow {w^\prime }m^{\prime \prime }]. \end{aligned}$$

Definition 7

We define a strict $\mathscr {M}$-action $\circledast$ on $\mathscr {A}_\mathbf {T}$ by

$$\begin{aligned} l\circledast (m,a):= & {} (l\otimes m,a) \\ v\circledast [n,f,w]:= & {} [n,f,v\otimes w] \quad (v: l\rightarrow l^\prime ,[n,f,w]:(m,a)\rightarrow (m',a')) \end{aligned}$$

Theorem 8

The functor $v_{\mathbf {T}}:\mathscr {A}\rightarrow \mathscr {A}_{\mathbf {T}}$ defined by $a\mapsto (I,a)$ has a right adjoint $g_{\mathbf {T}}$ such that the graded monad $\mathbf {T}=(*,\mu ,\eta )$ coincides with the graded monad

$$(m,a)\quad \mapsto \quad g_{\mathbf {T}}(m\circledast (v_{\mathbf {T}}(a))) \quad : \quad \mathscr {M}\times \mathscr {A}\quad \longrightarrow \quad \mathscr {A}$$

derived from the adjunction $v_{\mathbf {T}}\dashv g_{\mathbf {T}}$ and from the $\mathscr {M}$-action $\circledast$ on $\mathscr {A}_\mathbf {T}$.

The right adjoint functor $g_{\mathbf {T}}:\mathscr {A}_{\mathbf {T}} \rightarrow \mathscr {A}$ is defined as $g_{\mathbf {T}} (m,a) :=m*a$ on objects and

$$\begin{aligned} g_{\mathbf {T}}([\,n,a\xrightarrow {f} n*a^\prime ,&m\otimes n\xrightarrow {w} m^\prime \,])\\&:=\quad m*a \xrightarrow {m*f} m*n*a^\prime \xrightarrow {\mu _{m,n}} (m\otimes n)*a^\prime \xrightarrow {w*a^\prime } n^\prime *a^\prime \end{aligned}$$

on morphisms $[\,n,a\xrightarrow {f} n*a^\prime ,m\otimes n\xrightarrow {w} m^\prime \,]:(m,a)\rightarrow (m^\prime ,a^\prime )$.

3.3 Resolutions of Graded Monads

What are special about the Eilenberg-Moore and Kleisli resolutions of a graded monad? To answer this question, we introduce a suitable category consisting of resolutions of a graded monad, and show that Eilenberg-Moore and Kleisli resolutions are terminal and initial objects in this category. This is an extension of the theory of resolutions of monads to graded monads.

The key ingredient of a resolution of an $\mathscr {M}$-graded monad is a category with strict $\mathscr {M}$-actions. For the categorical treatment of such categories, we introduce the 2-category $\mathscr {M}\hbox {-} Cat$ of categories with strict $\mathscr {M}$-actions. It is the Eilenberg-Moore 2-category of the 2-monad $\mathscr {M}\times (-)$ on Cat. We associate to it the 2-adjunction $F^{\mathscr {M}}\dashv U^{\mathscr {M}}:\mathscr {M}\hbox {-} Cat\rightarrow Cat$ that behaves as follows on 0-cells:

$$\begin{aligned} {F^\mathscr {M}}(\mathscr {A}):=(\mathscr {M}\times \mathscr {A}, (\otimes )\times \mathscr {A}:\mathscr {M}\times \mathscr {M}\times \mathscr {A}\rightarrow \mathscr {M}\times \mathscr {A}) ,\quad {U^\mathscr {M}}(\mathscr {A},\circledast ):=\mathscr {A}. \end{aligned}$$

Definition 9

Let $\mathbf {T}=(*,\mu ,\eta )$ be an $\mathscr {M}$-graded monad on $\mathscr {A}$.

• A resolution of $\mathbf {T}$ is a tuple of a 0-cell $(\mathscr {B},\circledast )$ in $\mathscr {M}\hbox {-} Cat$ and an adjunction $l\dashv r:\mathscr {B}\rightarrow \mathscr {A}$ in Cat such that $\mathbf {T}$ coincides with the graded monad $r(-\circledast (l-))$ derived from the adjunction $l\dashv r$ and the strict $\mathscr {M}$-action $\circledast$.

• Given two resolutions $((\mathscr {B},\circledast ),l\dashv r)$ and $((\mathscr {B}',\circledast '),l'\dashv r')$ of $\mathbf {T}$, a morphism from the former to the latter is a 1-cell $h:(\mathscr {B},\circledast )\rightarrow (\mathscr {B}',\circledast ')$ in $\mathscr {M}\hbox {-} Cat$ such that $h\circ l=l'$ and $r=r'\circ h$ (here $U^\mathscr {M}$ is implicitly applied to h).

• We define the category $Res(\mathbf {T})$ of resolutions of $\mathbf {T}$ by the above data.

4 Towards a Formal Theory of Graded Monads

We explain how Street’s formal theory of monads can be adapted in order to characterize the two constructions of $\mathscr {A}^{\mathbf {T}}$ and of $\mathscr {A}_{\mathbf {T}}$ described in Sect. 3 as universal constructions. In his seminal paper [21], Street developed a general theory of monads relative to an arbitrary 2-category K, so that the usual theory of monads is regained by instantiating K by Cat, the 2-category of categories, functors, and natural transformations.

Definition 10

A monad $\mathbf {T}$ in K is given by a 0-cell k, a 1-cell $T:k\rightarrow k$, and 2-cells $\mu :T\circ T\Rightarrow T$ of K and $\eta :\mathrm {id}_{k}\Rightarrow T$, satisfying the usual axioms $\mu \circ \eta T=\mathrm {id}_{T}=\mu \circ T\eta$ and $\mu \circ T\mu =\mu \circ \mu T$.

Among his various abstract developments of the theory, the notions of Eilenberg-Moore object and Kleisli object for a monad in a 2-category will be the most important ones to our current work. We adopt the following definition, which appears for instance in [20]:

Definition 11

The Eilenberg-Moore object of $\mathbf {T}$ is a 0-cell $k^\mathbf {T}$ such that there is a family of isomorphisms of categories

$$ K(x,k^\mathbf {T})\quad \cong \quad K(x,k)^{K(x,\mathbf {T})} $$

2-natural in $x\in K$. Here the category on the right hand side is the (usual) Eilenberg-Moore category of the monad $K(x,\mathbf {T})$ on the category K(x, k).

Definition 12

The Kleisli object of $\mathbf {T}$ is a 0-cell $k_\mathbf {T}$ such that there is a family of isomorphisms of categories

$$ K(k_\mathbf {T},x)\quad \cong \quad K(k,x)^{K(\mathbf {T},x)} $$

2-natural in $x\in K$. Here the category on the right hand side is the (usual) Eilenberg-Moore category of the monad $K(\mathbf {T},x)$ on the category K(k, x).

Now a remarkable point is that from this simple and abstract definition, one can reconstruct a fair amount of the well-known properties of Eilenberg-Moore or Kleisli categories, including the existence of adjunctions which generate the monads, and the existence and uniqueness of comparison 1-cells. The interested reader should consult [21] for an ingenious 2-categorical manipulation achieving this reconstruction. In what follows, however, we choose to describe the adjunctions explicitly, for the sake of concreteness. As we did in Sect. 3, we suppose here that the category $\mathscr {M}$ is small, a necessary condition in order to perform the constructions of the Eilenberg-Moore and Kleisli objects.

4.1 A 2-Category for Eilenberg-Moore Objects

We introduce the 2-category $E^{++}$ where the category $\mathscr {A}^{\mathbf {T}}$ of graded algebras (Definition 1) arises as an Eilenberg-Moore object in it. This 2-category is obtained by a suitable lax comma construction for the 3-category $2\hbox {-} Cat$ of 2-categories, 2-functors, 2-natural transformations and modifications. We denote the terminal 2-category by 1.

Definition 13

We define the 2-category $E^{++}$ by the following data.

• A 0-cell of $E^{++}$ is a 2-functor $a: 1\rightarrow A$ where A is a 2-category; equivalently, it is a pair (A, a) where a is a 0-cell of A.

• A 1-cell of $E^{++}$ from (A, a) to $(A^\prime ,a^\prime )$ is a diagram in $2\hbox {-} Cat$

  

  filled with a 2-natural transformation f; equivalently, it is a pair (F, f) where $f: Fa\rightarrow a^\prime$ is a 1-cell of $A^\prime$.

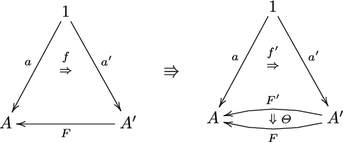
• A 2-cell of $E^{++}$ from (F, f) to $(F^\prime ,f^\prime )$ is a pair $(\varTheta ,\alpha )$ where $\varTheta :F\rightarrow F'$ is a 2-natural transformation and $\alpha$ is a modification of the following type:

  

  Equivalently, $\alpha$ is a 2-cell of $A^\prime$ of the following type:

  

The first projection of the data defines a 2-functor $p^{++}:E^{++}\rightarrow 2\hbox {-} Cat_2$, where $2\hbox {-} Cat_2$ is the 2-category of 2-categories, 2-functors, and 2-natural transformations. We take a fibrational viewpoint [1, 7] and say a notion X is above I if $p^{++}(X)=I$. A first key observation is the following:

Proposition 14

Let $(\mathscr {M},\otimes ,I)$ be a strict monoidal category and $\mathscr {A}$ a category. Then, an $\mathscr {M}$-graded monad on $\mathscr {A}$ is the same thing as a monad in $E^{++}$ on $(Cat,\mathscr {A})$, above the 2-monad $\mathscr {M}\times (-)$ on Cat.

Thanks to this proposition, it makes sense to speculate on the Eilenberg-Moore objects (in the sense of Street) of graded monads in this 2-category $E^{++}$. Indeed, $E^{++}$ turns out to admit Eilenberg-Moore objects of graded monads, and moreover the Eilenberg-Moore adjunction for an $\mathscr {M}$-graded monad lies above that for the 2-monad $\mathscr {M}\times (-)$.

Proposition 15

The following is an adjunction in the 2-category $E^{++}$:

Proof

In general, for an adjunction $L\dashv R$ in $2\hbox {-} Cat_2$ and a morphism $(R,r):(D,d)\rightarrow (C,c)$ in $E^{++}$, a left adjoint to (R, r) above L in $E^{++}$ bijectively corresponds to a left adjoint to $r:c\rightarrow Rd$ in C. By letting (R, r) be $(U^\mathscr {M},u^{\mathbf {T}})$, where $u^{\mathbf {T}}$ is a right adjoint, we obtain the above left adjoint, lying above $F^\mathscr {M}$.

A long, but straightforward calculation establishes the announced result:

Theorem 16

There is a family of isomorphisms of categories

$$ E^{++}(({X},x),(\mathscr {M}\hbox {-} Cat,\mathscr {A}^\mathbf {T}))\quad \cong \quad E^{++}(({X},x),(Cat,\mathscr {A}))^{E^{++}(({X},x),\mathbf {T})} $$

2-natural in $({X},x)\in E^{++}$.

Corollary 17

Let $\mathbf {T}$ be a graded monad. Then $((\mathscr {A}^{\mathbf {T}},\circledast ),f^{\mathbf {T}}\dashv u^{\mathbf {T}})$ is terminal in the category $Res(\mathbf {T})$ of resolutions of $\mathbf {T}$.

Proof

The idea is similar to that of Proposition 15.

4.2 A 2-Category for Kleisli Objects

We next introduce the 2-category $E^{--}$ where the category $\mathscr {A}_\mathbf {T}$ (Definition 6) arises as a Kleisli object in it. It turns out to be a certain dual of the 2-category $E^{++}$:

Definition 18

Define the 2-category $E^{--}$ as follows.

• A 0-cell of $E^{--}$ is a 2-functor $a: 1\rightarrow A$ where A is a 2-category; equivalently, it is a pair (A, a) where a is a 0-cell of A.

• A 1-cell of $E^{--}$ from (A, a) to $(A^\prime ,a^\prime )$ is a diagram in $2\hbox {-} Cat$

  

  filled with a 2-natural transformation f; equivalently, it is a pair (F, f) where $f: a\rightarrow Fa^\prime$ is a 1-cell of A.

• A 2-cell of $E^{--}$ from (F, f) to $(F^\prime ,f^\prime )$ is a pair $(\varTheta ,\alpha )$ where $\varTheta :F'\rightarrow F$ is a 2-natural transformation and $\alpha$ is a modification of the following type:

  

  Equivalently, $\alpha$ is a 2-cell of A of the following type:

  

Again the first projection of the data defines a 2-functor $p^{--}:E^{--}\rightarrow 2\hbox {-} Cat_2^{op(1,2)}$, where $2\hbox {-} Cat_2^{op(1,2)}$ is the 2-category obtained by reversing both 1-cells and 2-cells of $2\hbox {-} Cat_2$.

Proposition 19

Let $(\mathscr {M},\otimes ,I)$ be a strict monoidal category and $\mathscr {A}$ a category. Then, an $\mathscr {M}$-graded monad on $\mathscr {A}$ is the same thing as a monad in $E^{--}$ on $(Cat,\mathscr {A})$, above the 2-comonad $[\mathscr {M},-]$ on Cat.

The 2-category $E^{--}$ admits Kleisli objects of graded monads, and the Kleisli adjunction for an $\mathscr {M}$-graded monad lies above the co-Eilenberg-Moore adjunction for the 2-comonad $[\mathscr {M},-]$. Observe that the 2-comonad $[\mathscr {M},-]$, being right adjoint to the 2-monad $\mathscr {M}\times (-)$, has as its co-Eilenberg-Moore 2-category again the 2-category $\mathscr {M}\hbox {-} Cat$. Let us denote $V_\mathscr {M}\dashv G_\mathscr {M}$ for the associated 2-adjunction. Their behaviour on 0-cells are given as follows:

$$\begin{aligned} {G_\mathscr {M}}(\mathscr {C}):=([\mathscr {M},\mathscr {C}], \otimes ^{\wedge }:\mathscr {M}\times [\mathscr {M},\mathscr {C}]\rightarrow [\mathscr {M},\mathscr {C}]),\quad {V_\mathscr {M}}(\mathscr {C},\circledast ):=\mathscr {C}, \end{aligned}$$

where $\otimes ^{\wedge } (m,C)=C(-\otimes m)$.

Proposition 20

The following is an adjunction in the 2-category $E^{--}$:

Proof

We give a proof similar to Proposition 15. This time we use the following fact: for an adjunction $L\dashv R$ in $2\hbox {-} Cat_2$ and a 1-cell $(L,l):(C,c)\rightarrow (D,d)$ in $E^{--}$, a right adjoint to (L, l) above R in $E^{--}$ bijectively corresponds to a right adjoint to $l:c\rightarrow Ld$ in C.

Theorem 21

There is a family of isomorphisms of categories

$$ E^{--}((\mathscr {M}\hbox {-} Cat,\mathscr {A}_\mathbf {T}),({X},{x}))\quad \cong \quad E^{--}((Cat,\mathscr {A}),({X},x))^{E^{--}(\mathbf {T},({X},x))} $$

2-natural in $({X},x)\in E^{--}$.

A key to the proof of this theorem is the observation that every 1-cell $[n,a\xrightarrow {f} n*a^\prime ,m\otimes n\xrightarrow {w} m^\prime ]$ of $\mathscr {A}_\mathbf {T}$ can be decomposed as

$$\begin{aligned}&[n,a\xrightarrow {f} n*a^\prime ,m\otimes n\xrightarrow {w} m^\prime ]\\&\quad =\quad (w\circledast v_\mathbf {T}(a^\prime ))\circ (m\circledast [n,n*a^\prime \xrightarrow {\mathrm {id}_{}}n*a^\prime ,I\otimes n \xrightarrow {\mathrm {id}_{}} n]) \circ (m\circledast v_\mathbf {T}(f)). \end{aligned}$$

Corollary 22

Let $\mathbf {T}$ be an $\mathscr {M}$-graded monad. Then $((\mathscr {A}_{\mathbf {T}},\circledast ),v_{\mathbf {T}}\dashv g_{\mathbf {T}})$ is initial in the category $Res(\mathbf {T})$ of resolutions of $\mathbf {T}$.

5 Illustration: The Graded State Monad

Suppose given an object V in a symmetric monoidal closed category $\mathscr {C}$. We start by describing the graded state monad

$$ \mathbf {S}=(*,\mu ,\eta ) \quad : \quad Inj\times \mathscr {C}\quad \longrightarrow \quad \mathscr {C}$$

mentioned at the end of the introduction, and defined as

$$ n*A \quad :=\quad V^{\otimes n} \multimap \!(V^{\otimes n}\otimes A). $$

One simple way to define the graded monad $\mathbf {S}$ is to start from the observation that the formula $A\mapsto n*A$ defines an Inj-indexed monad, defined as a functor

$$ \begin{array}{ccccc} *&\quad : \quad&Inj&\quad \longrightarrow \quad&\mathbf {Mnd}(\mathscr {C}) \end{array} $$

from the category Inj to the category $\mathbf {Mnd}(\mathscr {C})$ of monads over the category $\mathscr {C}$, and monad homomorphisms between them. We write

$$\mu _{m,A} : m*(m*A) \longrightarrow m*A \quad \quad \quad \quad \quad \eta _{m,A} : A \longrightarrow m*A$$

for the multiplication and unit of the monad $A\mapsto m*A$. The multiplication $\mu _{m,n,A}$ of the graded state monad $\mathbf {S}$ may be then defined as the composite

where the lefthand side morphism is defined by the injection morphisms $\mathbf {inl}:m\rightarrow m+n$ and $\mathbf {inr}:n\rightarrow m+n$ and where $\mu _{m+n,A}$ is the multiplication of the monad $A\mapsto (m+n)*A$. Similarly, the unit $\eta _A:A\rightarrow 0*A$ of the graded monad $\mathbf {S}$ is defined as $\eta _{\,0,A}$ which is an isomorphism. This defines the graded monad $\mathbf {S}=(*,\mu ,\eta )$. More generally, one observes that every $\mathscr {M}$-indexed monad induces an $\mathscr {M}$-graded monad in this way, when the unit I of the monoidal category $(\mathscr {M},\otimes ,I)$ is initial, as in the case of the category Inj.

We find instructive to explicate the notion of graded $\mathbf {S}$-algebra introduced in Sect. 3.1 in the particular case when $\mathscr {C}=Set$ and where V is a finite set. As in the case of any such cartesian closed category $\mathscr {C}$, the action can be rewritten as

$$ n*A\quad =\quad (V^n\Rightarrow V^n)\times (V^n\Rightarrow A). $$

Now, a graded $\mathbf {S}$-algebra (A, h) is given by a functor $A:Inj\rightarrow Set$, together with a family h of functions

$$ h_{m,n}\quad :\quad (V^m\Rightarrow V^m)\times (V^m\Rightarrow A_n)\quad \longrightarrow \quad A_{m+n} $$

subject to the axioms (5) of graded algebras. Since

$$ (V^m\Rightarrow V^m)\times (V^m\Rightarrow A_n) \quad =\quad \coprod _{f\in (V^m\Rightarrow V^m)}(V^m\Rightarrow A_n), $$

one can see the family h as a family of operations

$$ \langle f,n \rangle \quad :\quad V^m \Rightarrow A_n\quad \longrightarrow \quad A_{m+n}. $$

indexed by the functions $f:V^m\rightarrow V^m$ and the natural numbers n. Note that each such operation $\langle f,n \rangle$ transports $V^m$ elements of grade n into an element of grade $m+n$. As such, a graded $\mathbf {S}$-algebra (A, h) can be seen in terms of multisorted universal algebra as a family $(A_m)_{m\in \mathbf{N}}$ of sets with sorts provided by natural numbers $m\in \mathbb {N}$. Following [3, 11, 14], the algebraic theory can be presented by extending with the operations $\langle f,n \rangle$ the trivial Lawvere theory with arities

$$\varSigma (Inj)^{\,op} \longrightarrow [Inj,Set]$$

whose models are the covariant presheaves over [Inj, Set] with the generators $\langle f,n \rangle$ together with a number of equations expressing that

• the family $h_{m,n}: m*A_n\rightarrow A_{m\otimes n}$ is natural in m and n,

• h satisfies the Eq. (5) of a graded $\mathbf {S}$-algebra.

The equations are given in the Appendix. The resulting algebraic presentation of graded $\mathbf {S}$-algebras by operations and equations enables one to establish that

Theorem 23

The canonical forgetful functor $U:Set^\mathbf {S}\rightarrow [Inj,Set]$ given by $(A,h)\mapsto A$ is monadic.

One main reason for studying the Inj-graded monad $\mathbf {S}$ is that it induces in this way a monad on [Inj, Set] with arities $\varTheta :\varSigma Inj^{\,op}\rightarrow [Inj,Set]$ whose Lawvere theory with arities $\varTheta$ is a sub-theory of the Lawvere theory  (with same arities) of the local state monad L presented by generators and relations in [14].

Interestingly, the resulting algebraic theory captures only a restricted part of the original algebraic theory  since the multiplication $\mu _{m,n,A}$ does not enable the graded algebra $(A_m)_{m\in Inj}$ to pass states from one layer of application $(m*-)$ of the graded state monad to the next layer $(n*-)$. This limitation should not be seen as a defect but rather as a feature of the graded state monad $\mathbf {S}$ since it enables us to delineate a natural fragment of the local state monad L.

Appendix: An Algebraic Presentation of Graded \(\mathbf {S}\)-Algebras

Formulated in the language of multisorted universal algebra, a graded $\mathbf {S}$-algebra (A, h) is completely determined by a family $(A_m)_{m\in \mathbf{N}}$ of sets equipped with an operation $A_v:A_m\rightarrow A_n$ for each injection $v:m\rightarrow n$ and with an operation $\langle f,n \rangle : A_n^{V^m}\rightarrow A_{m+n}$ for each pair of natural numbers m, n and each function $f:V^m\rightarrow V^m$. These operations should moreover satisfy the equations below. First of all, the two functoriality equations below:

$$ A_{\mathrm {id}_{m}} = \mathrm {id}_{A_m} \qquad \qquad \qquad A_{w\circ v}= A_w\circ A_v. $$

Then, the naturality equation, for all injections $v:m\rightarrow m^\prime$ and $w:n\rightarrow n^\prime$,

$$ A_{v+w}(\langle f,n \rangle (a_i)_{i\in V^m})\quad =\quad \langle v\bullet f,n^\prime \rangle (A_w(a_{i^\prime \circ v}))_{i^\prime \in V^{m^\prime }}, $$

where the function $v\bullet f:V^{m^\prime }\rightarrow V^{m^\prime }$ is defined as

$$ \big ((v\bullet f) (val_{k^\prime })_{k^\prime \in m^\prime }\big )_{l^\prime } \quad =\quad {\left\{ \begin{array}{ll} \big (f(val_{v(k)})_{k\in m}\big )_l &{}\text{ if } l^\prime = v(l) \text{ for } \text{ some } l\in m;\\ val_{l^\prime } &{} \text{ otherwise. }\end{array}\right. } $$

Then, the unit equation

$$ \langle \mathrm {id}_{V^0},m \rangle \quad =\quad \mathrm {id}_{A_m}, $$

for a function $f:V^m\rightarrow V^m$ and an injection $v:m\rightarrow m^\prime$ ; and finally the associativity equation

$$ \langle f \rangle _{n+p}(\langle g_i,p \rangle (a_{i,j})_{j\in V^n})_{i\in V^m} \quad = \quad \langle f\star (g_i)_{i\in V^m}, p \rangle (a_{i,j})_{i,j\in V^{m+n}}, $$

where the function

$$f\star (g_i)_{i\in V^m} \quad : \quad V^{m+n} \quad \longrightarrow \quad V^{m+n}$$

is defined as follows, for a function $f:V^m\rightarrow V^m$ and for a family of functions $(g_i:V^n\rightarrow V^n)_{i\in V^m}$:

$$ \big ((f\star (g_i)_{i\in V^m}) (val_{k},wal_{k^\prime })_{k\in m,k^\prime \in n}\big )_{l} ={\left\{ \begin{array}{ll} \big (f(val_k)_{k\in m}\big )_l &{}\text{ if } l\in m,\\ \big (g_{(val_k)_{k\in m}}(wal_{k^\prime })_{k^\prime \in n}\big )_l &{} \text{ if } l\in n. \end{array}\right. } $$

Homomorphisms of graded $\mathbf {S}$-algebras are just families of maps $\varphi _m:A_m\rightarrow A^\prime _m$ commuting with the operations introduced above.