Abstract
We describe an approach to the verified implementation of transformations on functional programs that exploits the higher-order representation of syntax. In this approach, transformations are specified using the logic of hereditary Harrop formulas. On the one hand, these specifications serve directly as implementations, being programs in the language \(\lambda \)Prolog. On the other hand, they can be used as input to the Abella system which allows us to prove properties about them and thereby about the implementations. We argue that this approach is especially effective in realizing transformations that analyze binding structure. We do this by describing concise encodings in \(\lambda \)Prolog for transformations like typed closure conversion and code hoisting that are sensitive to such structure and by showing how to prove their correctness using Abella.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
This paper concerns the verification of compilers for functional (programming) languages. The interest in this topic is easily explained. Functional languages support an abstract view of computation that makes it easier to construct programs and the resulting code also has a flexible structure. Moreover, these languages have a strong mathematical basis that simplifies the process of proving programs to be correct. However, there is a proviso to this observation: to derive the mentioned benefit, the reasoning must be done relative to the abstract model underlying the language, whereas programs are typically executed only in their compiled form. To close the gap, it is important also to ensure that the compiler that carries out the translation preserves the meanings of programs.
The key role that compiler verification plays in overall program correctness has been long recognized; e.g. see [22, 27] for early work on this topic. With the availability of sophisticated systems such as Coq [8], Isabelle [33] and HOL [15] for mechanizing reasoning, impressive strides have been taken in recent years towards actually verifying compilers for real languages, as seen, for instance, in the CompCert project [21]. Much of this work has focused on compiling imperative languages like C. Features such as higher-order and nested functions that are present in functional languages bring an additional complexity to their implementation. A common approach to treating such features is to apply transformations to programs that render them into a form to which more traditional compilation methods can be applied. These transformations must manipulate binding structure in complex ways, an aspect that requires special consideration at both the implementation and the verification level [3].
Applications such as those above have motivated research towards developing good methods for representing and manipulating binding structure. Two particular approaches that have emerged from this work are those that use the nameless representation of bound variables due to De Bruijn [9] and the nominal logic framework of Pitts [35]. These approaches provide an elegant treatment of aspects such as \(\alpha \)-convertibility but do not directly support the analysis of binding structure or the realization of binding-sensitive operations such as substitution. A third approach, commonly known as the higher-order abstract syntax or HOAS approach, uses the abstraction operator in a typed \(\lambda \)-calculus to represent binding structure in object-language syntax. When such representations are embedded within a suitable logic, they lead to a succinct and flexible treatment of many binding related operations through \(\beta \)-conversion and unification.
The main thesis of this paper, shared with other work such as [7, 16], is that the HOAS approach is in fact well-adapted to the task of implementing and verifying compiler transformations on functional languages. Our specific objective is to demonstrate the usefulness of a particular framework in this task. This framework comprises two parts: the \(\lambda \)Prolog language [30] that is implemented, for example, in the Teyjus system [36], and the Abella proof assistant [4]. The \(\lambda \)Prolog language is a realization of the hereditary Harrop formulas or HOHH logic [25]. We show that this logic, which uses the simply typed \(\lambda \)-calculus as a means for representing objects, is a suitable vehicle for specifying transformations on functional programs. Moreover, HOHH specifications have a computational interpretation that makes them implementations of compiler transformations. The Abella system is also based on a logic that supports the HOAS approach. This logic, which is called \(\mathcal {G}\), incorporates a treatment of fixed-point definitions that can also be interpreted inductively or co-inductively. The Abella system uses these definitions to embed HOHH within \(\mathcal {G}\) and thereby to reason directly about the specifications written in HOHH. As we show in this paper, this yields a convenient means for verifying implementations of compiler transformations.
An important property of the framework that we consider, as also of systems like LF [17] and Beluga [34], is that it uses a weak \(\lambda \)-calculus for representing objects. There have been attempts to derive similar benefits from using functional languages or the language underlying systems such as Coq. Some benefits, such as the correct implementation of substitution, can be obtained even in these contexts. However, the equality relation embodied in these systems is very strong and the analysis of \(\lambda \)-terms in them is therefore not limited to examining just their syntactic structure. This is a significant drawback, given that such examination plays a key role in the benefits we describe in this paper. In light of this distinction, we shall use the term \(\lambda \) -tree syntax [24] for the more restricted version of HOAS whose use is the focus of our discussions.
The rest of this paper is organized as follows. In Sect. 2 we introduce the reader to the framework mentioned above. We then show in succeeding sections how this framework can be used to implement and to verify transformations on functional programs. We conclude the paper by discussing the relationship of the ideas we describe here to other existing work.Footnote 1
2 The Framework
We describe, in turn, the specification logic and \(\lambda \)Prolog, the reasoning logic, and the manner in which the Abella system embeds the specification logic.
2.1 The Specification Logic and \(\lambda \)Prolog
The HOHH logic is an intuitionistic and predicative fragment of Church’s Simple Theory of Types [12]. Its types are formed using the function type constructor  over user defined primitive types and the distinguished type
over user defined primitive types and the distinguished type  for formulas. Expressions are formed from a user-defined signature of typed constants whose argument types do not contain
for formulas. Expressions are formed from a user-defined signature of typed constants whose argument types do not contain  and the logical constants
and the logical constants
 and
and  of type
of type  and \(\varPi _\tau \) of type
and \(\varPi _\tau \) of type  for each type \(\tau \) not containing
for each type \(\tau \) not containing  . We write
. We write  and
and  , which denote implication and conjunction respectively, in infix form. Further, we write
, which denote implication and conjunction respectively, in infix form. Further, we write  , which represents the universal quantification of x over M, as
, which represents the universal quantification of x over M, as  .
.
The logic is oriented around two sets of formulas called goal formulas and program clauses that are given by the following syntax rules:


Here, A represents atomic formulas that have the form  where p is a (user defined) predicate constant, i.e. a constant with target type
where p is a (user defined) predicate constant, i.e. a constant with target type  . Goal formulas of the last two kinds are referred to as hypothetical and universal goals. Using the notation \(\varPi _{\bar{\tau }}\bar{x}\) to denote a sequence of quantifications, we see that a program clause has the form
. Goal formulas of the last two kinds are referred to as hypothetical and universal goals. Using the notation \(\varPi _{\bar{\tau }}\bar{x}\) to denote a sequence of quantifications, we see that a program clause has the form  or
or  . We refer to A as the head of such a clause and G as the body; in the first case the body is empty.
. We refer to A as the head of such a clause and G as the body; in the first case the body is empty.
A collection of program clauses constitutes a program. A program and a signature represent a specification of all the goal formulas that can be derived from them. The derivability of a goal formula G is expressed formally by the judgment  in which \(\varSigma \) is a signature, \(\varTheta \) is a collection of program clauses defined by the user and \(\varGamma \) is a collection of dynamically added program clauses. The validity of such a judgment—also called a sequent—is determined by provability in intuitionistic logic but can equivalently be characterized in a goal-directed fashion as follows. If G is conjunctive, it yields sequents for “solving” each of its conjuncts in the obvious way. If it is a hypothetical or a universal goal, then one of the following rules is used:
in which \(\varSigma \) is a signature, \(\varTheta \) is a collection of program clauses defined by the user and \(\varGamma \) is a collection of dynamically added program clauses. The validity of such a judgment—also called a sequent—is determined by provability in intuitionistic logic but can equivalently be characterized in a goal-directed fashion as follows. If G is conjunctive, it yields sequents for “solving” each of its conjuncts in the obvious way. If it is a hypothetical or a universal goal, then one of the following rules is used:


In the \(\varPi \)R rule, c must be a constant not already in \(\varSigma \); thus, these rules respectively cause the program and the signature to grow while searching for a derivation. Once G has been simplified to an atomic formula, the sequent is derived by generating an instance of a clause from \(\varTheta \) or \(\varGamma \) whose head is identical to G and by constructing a derivation of the corresponding body of the clause if it is non-empty. This operation is referred to as backchaining on a clause.
In presenting HOHH specifications in this paper we will show programs as a sequence of clauses each terminated by a period. We will leave the outermost universal quantification in these clauses implicit, indicating the variables they bind by using tokens that begin with uppercase letters. We will write program clauses of the form  as A
as A
 G. We will show goals of the form
G. We will show goals of the form  and
and  as \(G_1\)
,
\(G_2\) and
as \(G_1\)
,
\(G_2\) and  , respectively, dropping the type annotation in the latter if it can be filled in uniquely based on the context. Finally, we will write abstractions as
, respectively, dropping the type annotation in the latter if it can be filled in uniquely based on the context. Finally, we will write abstractions as  instead of
instead of  .
.
Program clauses provide a natural means for encoding rule based specifications. Each rule translates into a clause whose head corresponds to the conclusion and whose body represents the premises of the rule. These clauses embody additional mechanisms that simplify the treatment of binding structure in object languages. They provide \(\lambda \)-terms as a means for representing objects, thereby allowing binding to be reflected into an explicit meta-language abstraction. Moreover, recursion over such structure, that is typically treated via side conditions on rules expressing requirements such as freshness for variables, can be captured precisely through universal and hypothetical goals. This kind of encoding is concise and has logical properties that we can use in reasoning.
We illustrate the above ideas by considering the specification of the typing relation for the simply typed \(\lambda \)-calculus (STLC). Let N be the only atomic type. We use the HOHH type  for representations of object language types that we build using the constants
for representations of object language types that we build using the constants  and
and  . Similarly, we use the HOHH type
. Similarly, we use the HOHH type  for encodings of object language terms that we build using the constants
for encodings of object language terms that we build using the constants  and
and  . The type of the latter constructor follows our chosen approach to encoding binding: for example, we represent the STLC expression
. The type of the latter constructor follows our chosen approach to encoding binding: for example, we represent the STLC expression  by the HOHH term
by the HOHH term  . Typing for the STLC is a judgment written as \(\varGamma \vdash T :\) Ty that expresses a relationship between a context \(\varGamma \) that assigns types to variables, a term T and a type Ty. Such judgments are derived using the following rules:
. Typing for the STLC is a judgment written as \(\varGamma \vdash T :\) Ty that expresses a relationship between a context \(\varGamma \) that assigns types to variables, a term T and a type Ty. Such judgments are derived using the following rules:


The second rule has a proviso: y must be fresh to \(\varGamma \). In the \(\lambda \)-tree syntax approach, we encode typing as a binary relation between a term and a type, treating the typing context implicitly via dynamically added clauses. Using the predicate  to represent this relation, we define it through the following clauses:
to represent this relation, we define it through the following clauses:


The second clause effectively says that  has the type
has the type  if
if  has type
has type  in an extended context that assigns
in an extended context that assigns  the type
the type  . Note that the universal goal ensures that
. Note that the universal goal ensures that  is new and, given our encoding of terms,
is new and, given our encoding of terms,  represents the body of the object language abstraction in which the bound variable has been replaced by this new name.
represents the body of the object language abstraction in which the bound variable has been replaced by this new name.
The rules for deriving goal formulas give HOHH specifications a computational interpretation. We may also leave particular parts of a goal unspecified, representing them by “meta-variables,” with the intention that values be found for them that make the overall goal derivable. This idea underlies the language \(\lambda \)Prolog that is implemented, for example, in the Teyjus system [36].
2.2 The Reasoning Logic and Abella
The inference rules that describe a relation are usually meant to be understood in an “if and only if” manner. Only the “if” interpretation is relevant to using rules to effect computations and their encoding in the HOHH logic captures this part adequately. To reason about the properties of the resulting computations, however, we must formalize the “only if” interpretation as well. This functionality is realized by the logic \(\mathcal {G}\) that is implemented in the Abella system.
The logic \(\mathcal {G}\) is also based on an intuitionistic and predicative version of Church’s Simple Theory of Types. Its types are like those in HOHH except that the type  replaces
replaces  . Terms are formed from user-defined constants whose argument types do not include
. Terms are formed from user-defined constants whose argument types do not include  and the following logical constants:
and the following logical constants:  and
and  of type
of type  ;
;  , \({\vee }\) and
, \({\vee }\) and  of type
of type  for conjunction, disjunction and implication; and, for every type \(\tau \) not containing
for conjunction, disjunction and implication; and, for every type \(\tau \) not containing  , the quantifiers
, the quantifiers  and \(\exists _\tau \) of type
and \(\exists _\tau \) of type  and the equality symbol
and the equality symbol  of type
of type  . The formula \(B =_\tau B'\) holds if and only if B and \(B'\) are of type \(\tau \) and equal under \(\alpha \beta \eta \) conversion. We will omit the type \(\tau \) in logical constants when its identity is clear from the context.
. The formula \(B =_\tau B'\) holds if and only if B and \(B'\) are of type \(\tau \) and equal under \(\alpha \beta \eta \) conversion. We will omit the type \(\tau \) in logical constants when its identity is clear from the context.
A novelty of \(\mathcal {G}\) is that it is parameterized by fixed-point definitions. Such definitions consist of a collection of definitional clauses each of which has the form  where A is an atomic formula all of whose free variables are bound by \(\bar{x}\) and B is a formula whose free variables must occur in A; A is called the head of such a clause and B is called its body.Footnote 2 To illustrate definitions, let
where A is an atomic formula all of whose free variables are bound by \(\bar{x}\) and B is a formula whose free variables must occur in A; A is called the head of such a clause and B is called its body.Footnote 2 To illustrate definitions, let  represent the type of lists of HOHH formulas and let
represent the type of lists of HOHH formulas and let  and
and  , written in infix form, be constants for building such lists. Then the append relation at the
, written in infix form, be constants for building such lists. Then the append relation at the  type is defined in \(\mathcal {G}\) by the following clauses:
type is defined in \(\mathcal {G}\) by the following clauses:


This presentation also illustrates several conventions used in writing definitions: clauses of the form  are abbreviated to \(\forall {\bar{x}}, A\), the outermost universal quantifiers in a clause are made implicit by representing the variables they bind by tokens that start with an uppercase letter, and a sequence of clauses is written using semicolon as a separator and period as a terminator.
are abbreviated to \(\forall {\bar{x}}, A\), the outermost universal quantifiers in a clause are made implicit by representing the variables they bind by tokens that start with an uppercase letter, and a sequence of clauses is written using semicolon as a separator and period as a terminator.
The proof system underlying \(\mathcal {G}\) interprets atomic formulas via the fixed-point definitions. Concretely, this means that definitional clauses can be used in two ways. First, they may be used in a backchaining mode to derive atomic formulas: the formula is matched with the head of a clause and the task is reduced to deriving the corresponding body. Second, they can also be used to do case analysis on an assumption. Here the reasoning structure is that if an atomic formula holds, then it must be because the body of one of the clauses defining it holds. It therefore suffices to show that the conclusion follows from each such possibility.
The clauses defining a particular predicate can further be interpreted inductively or coinductively, leading to corresponding reasoning principles relative to that predicate. As an example of how this works, consider proving


assuming that we have designated  as an inductive predicate. An induction on the first occurrence of
as an inductive predicate. An induction on the first occurrence of  then allows us to assume that the entire formula holds any time the leftmost atomic formula is replaced by a formula that is obtained by unfolding its definition and that has
then allows us to assume that the entire formula holds any time the leftmost atomic formula is replaced by a formula that is obtained by unfolding its definition and that has  as its predicate head.
as its predicate head.
Many arguments concerning binding require the capability of reasoning over structures with free variables where each such variable is treated as being distinct and not further analyzable. To provide this capability, \(\mathcal {G}\) includes the special generic quantifier \(\nabla _\tau \), pronounced as “nabla”, for each type \(\tau \) not containing  [26]. In writing this quantifier, we, once again, elide the type \(\tau \). The rules for treating \(\nabla \) in an assumed formula and a formula in the conclusion are similar: a “goal” with
[26]. In writing this quantifier, we, once again, elide the type \(\tau \). The rules for treating \(\nabla \) in an assumed formula and a formula in the conclusion are similar: a “goal” with  in it reduces to one in which this formula has been replaced by
in it reduces to one in which this formula has been replaced by  where
where  is a fresh, unanalyzable constant called a nominal constant. Note that
is a fresh, unanalyzable constant called a nominal constant. Note that  has a meaning that is different from that of
has a meaning that is different from that of  : for example,
: for example,  is provable but
is provable but  is not.
is not.
\(\mathcal {G}\) allows the  quantifier to be used also in the heads of definitions. The full form for a definitional clause is in fact \(\forall {\bar{x}} \nabla {\bar{z}}, A \triangleq B\), where the
quantifier to be used also in the heads of definitions. The full form for a definitional clause is in fact \(\forall {\bar{x}} \nabla {\bar{z}}, A \triangleq B\), where the  quantifiers scope only over A. In generating an instance of such a clause, the variables in \(\bar{z}\) must be replaced with nominal constants. The quantification order then means that the instantiations of the variables in \(\bar{x}\) cannot contain the constants used for \(\bar{z}\). This extension makes it possible to encode structural properties of terms in definitions. For example, the clause
quantifiers scope only over A. In generating an instance of such a clause, the variables in \(\bar{z}\) must be replaced with nominal constants. The quantification order then means that the instantiations of the variables in \(\bar{x}\) cannot contain the constants used for \(\bar{z}\). This extension makes it possible to encode structural properties of terms in definitions. For example, the clause  defines
defines  to be a recognizer of nominal constants. Similarly, the clause
to be a recognizer of nominal constants. Similarly, the clause  defines
defines  such that
such that  holds just in the case that
holds just in the case that  is a nominal constant and
is a nominal constant and  is a term that does not contain
is a term that does not contain  . As a final example, consider the following clauses in which
. As a final example, consider the following clauses in which  is the typing predicate from the previous subsection.
is the typing predicate from the previous subsection.


These clauses define  such that
such that  holds exactly when
holds exactly when  is a list of type assignments to distinct variables.
is a list of type assignments to distinct variables.
2.3 The Two-Level Logic Approach
Our framework allows us to write specifications in HOHH and reason about them using \(\mathcal {G}\). Abella supports this two-level logic approach by encoding HOHH derivability in a definition and providing a convenient interface to it. The user program and signature for these derivations are obtained from a \(\lambda \)Prolog program file. The state in a derivation is represented by a judgment of the form  . where \(\varGamma \) is the list of dynamically added clauses; additions to the signature are treated implicitly via nominal constants. If \(\varGamma \) is empty, the judgment is abbreviated to
. where \(\varGamma \) is the list of dynamically added clauses; additions to the signature are treated implicitly via nominal constants. If \(\varGamma \) is empty, the judgment is abbreviated to  . The theorems that are to be proved mix such judgments with other ones defined directly in Abella. For example, the uniqueness of typing for the STLC based on its encoding in HOHH can be stated as follows:
. The theorems that are to be proved mix such judgments with other ones defined directly in Abella. For example, the uniqueness of typing for the STLC based on its encoding in HOHH can be stated as follows:


This formula talks about the typing of open terms relative to a dynamic collection of clauses that assign unique types to (potentially) free variables.
The ability to mix specifications in HOHH and definitions in Abella provides considerable expressivity to the reasoning process. This expressivity is further enhanced by the fact that both HOHH and \(\mathcal {G}\) support the \(\lambda \)-tree syntax approach. We illustrate these observations by considering the explicit treatment of substitutions. We use the type  and the constant
and the constant  to represent mappings for individual variables (encoded as nominal constants) and a list of such mappings to represent a substitution; for simplicity, we overload the constructors
to represent mappings for individual variables (encoded as nominal constants) and a list of such mappings to represent a substitution; for simplicity, we overload the constructors  and
and  at this type. Then the predicate
at this type. Then the predicate  such that
such that  holds exactly when M’ is the result of applying the substitution ML to M can be defined by the following clauses:
holds exactly when M’ is the result of applying the substitution ML to M can be defined by the following clauses:


Observe how quantifier ordering is used in this definition to create a “hole” where a free variable appears in a term and application is then used to plug the hole with the substitution. This definition makes it extremely easy to prove structural properties of substitutions. For example, the fact that substitution distributes over applications and abstractions can be stated as follows:


An easy induction over the definition of substitution proves these properties.
As another example, we may want to characterize relationships between closed terms and substitutions. For this, we can first define well-formed terms through the following HOHH clauses:


Then we characterize the context used in  derivations in Abella as follows:
derivations in Abella as follows:


Intuitively, if  and
and  hold, then M is a well-formed term whose free variables are given by
hold, then M is a well-formed term whose free variables are given by  . Clearly, if
. Clearly, if  holds, then M is closed. Now we can state the fact that a closed term is unaffected by a substitution:
holds, then M is closed. Now we can state the fact that a closed term is unaffected by a substitution:


Again, an easy induction on the definition of substitutions proves this property.
3 Implementing Transformations on Functional Programs
We now turn to the main theme of the paper, that of showing the benefits of our framework in the verified implementation of compilation-oriented program transformations for functional languages. The case we make has the following broad structure. Program transformations are often conveniently described in a syntax-directed and rule-based fashion. Such descriptions can be encoded naturally using the program clauses of the HOHH logic. In transforming functional programs, special attention must be paid to binding structure. The \(\lambda \)-tree syntax approach, which is supported by the HOHH logic, provides a succinct and logically precise means for treating this aspect. The executability of HOHH specifications renders them immediately into implementations. Moreover, the logical character of the specifications is useful in the process of reasoning about their correctness.
This section is devoted to substantiating our claim concerning implementation. We do this by showing how to specify transformations that are used in the compilation of functional languages. An example we consider in detail is that of closure conversion. Our interest in this transformation is twofold. First, it is an important step in the compilation of functional programs: it is, in fact, an enabler for other transformations such as code hoisting. Second, it is a transformation that involves a complex manipulation of binding structure. Thus, the consideration of this transformation helps shine a light on the special features of our framework. The observations we make in the context of closure conversion are actually applicable quite generally to the compilation process. We close the section by highlighting this fact relative to other transformations that are of interest.
3.1 The Closure Conversion Transformation
The closure conversion transformation is designed to replace (possibly nested) functions in a program by closures that each consist of a function and an environment. The function part is obtained from the original function by replacing its free variables by projections from a new environment parameter. Complementing this, the environment component encodes the construction of a value for the new parameter in the enclosing context. For example, when this transformation is applied to the following pseudo OCaml code segment


it will yield


We write  here to represent a closure whose function part is
here to represent a closure whose function part is  and environment part is
and environment part is  , and
, and  to represent the i-th projection applied to an “environment parameter”
to represent the i-th projection applied to an “environment parameter”  . This transformation makes the function part independent of the context in which it appears, thereby allowing it to be extracted out to the top-level of the program.
. This transformation makes the function part independent of the context in which it appears, thereby allowing it to be extracted out to the top-level of the program.
The Source and Target Languages. Figures 1 and 2 present the syntax of the source and target languages that we shall use in this illustration. In these figures, T, M and V stand respectively for the categories of types, terms and the terms recognized as values. \(\mathbb {N}\) is the type for natural numbers and n corresponds to constants of this type. Our languages include some arithmetic operators, the conditional and the tuple constructor and destructors; note that  represents the predecessor function on numbers, the behavior of the conditional is based on whether or not the “condition” is zero and
represents the predecessor function on numbers, the behavior of the conditional is based on whether or not the “condition” is zero and  and
and  are the projection operators on pairs. The source language includes the recursion operator
are the projection operators on pairs. The source language includes the recursion operator  which abstracts simultaneously over the function and the parameter; the usual abstraction is a degenerate case in which the function parameter does not appear in the body. The target language includes the expressions
which abstracts simultaneously over the function and the parameter; the usual abstraction is a degenerate case in which the function parameter does not appear in the body. The target language includes the expressions  and
and  representing the formation and application of closures. The target language does not have an explicit fixed point constructor. Instead, recursion is realized by parameterizing the function part of a closure with a function component; this treatment should become clear from the rules for typing closures and for evaluating the application of closures that we present below. The usual forms of abstraction and application are included in the target language to simplify the presentation of the transformation. The usual function type is reserved for closures; abstractions are given the type
representing the formation and application of closures. The target language does not have an explicit fixed point constructor. Instead, recursion is realized by parameterizing the function part of a closure with a function component; this treatment should become clear from the rules for typing closures and for evaluating the application of closures that we present below. The usual forms of abstraction and application are included in the target language to simplify the presentation of the transformation. The usual function type is reserved for closures; abstractions are given the type  in the target language. We abbreviate
in the target language. We abbreviate  by \((M_1,\ldots ,M_n)\) and
by \((M_1,\ldots ,M_n)\) and  where \(\mathbf {snd}\) is applied \(i-1\) times for \(i \ge 1\) by \(\pi _i(M)\).
where \(\mathbf {snd}\) is applied \(i-1\) times for \(i \ge 1\) by \(\pi _i(M)\).
Typing judgments for both the source and target languages are written as \(\varGamma \vdash M : T\), where \(\varGamma \) is a list of type assignments for variables. The rules for deriving typing judgments are routine, with the exception of those for introducing and eliminating closures in the target language that are shown below:


In  , the function part of a closure must be typable in an empty context. In
, the function part of a closure must be typable in an empty context. In  , \(x_f\), \(x_e\) must be names that are new to \(\varGamma \). This rule also uses a “type” l whose meaning must be explained. This symbol represents a new type constant, different from \(\mathbb {N}\) and \(()\) and any other type constant used in the typing derivation. This constraint in effect captures the requirement that the environment of a closure should be opaque to its user.
, \(x_f\), \(x_e\) must be names that are new to \(\varGamma \). This rule also uses a “type” l whose meaning must be explained. This symbol represents a new type constant, different from \(\mathbb {N}\) and \(()\) and any other type constant used in the typing derivation. This constraint in effect captures the requirement that the environment of a closure should be opaque to its user.
The operational semantics for both the source and the target language is based on a left to right, call-by-value evaluation strategy. We assume that this is given in small-step form and, overloading notation again, we write  to denote that M evaluates to \(M'\) in one step in whichever language is under consideration. The only evaluation rules that may be non-obvious are the ones for applications. For the source language, they are the following:
to denote that M evaluates to \(M'\) in one step in whichever language is under consideration. The only evaluation rules that may be non-obvious are the ones for applications. For the source language, they are the following:


For the target language, they are the following:


One-step evaluation generalizes in the obvious way to n-step evaluation that we denote by  . Finally, we write \(M \hookrightarrow V\) to denote the evaluation of M to the value V through 0 or more steps.
. Finally, we write \(M \hookrightarrow V\) to denote the evaluation of M to the value V through 0 or more steps.
The Transformation. In the general case, we must transform terms under mappings for their free variables: for a function term, this mapping represents the replacement of the free variables by projections from the environment variable for which a new abstraction will be introduced into the term. Accordingly, we specify the transformation as a 3-place relation written as  , where M and \(M'\) are source and target language terms and \(\rho \) is a mapping from (distinct) source language variables to target language terms. We write \((\rho , x \mapsto M)\) to denote the extension of \(\rho \) with a mapping for x and \((x \mapsto M) \in \rho \) to mean that \(\rho \) contains a mapping of x to M. Figure 3 defines the
, where M and \(M'\) are source and target language terms and \(\rho \) is a mapping from (distinct) source language variables to target language terms. We write \((\rho , x \mapsto M)\) to denote the extension of \(\rho \) with a mapping for x and \((x \mapsto M) \in \rho \) to mean that \(\rho \) contains a mapping of x to M. Figure 3 defines the  relation in a rule-based fashion; these rules use the auxiliary relation
relation in a rule-based fashion; these rules use the auxiliary relation  that determines an environment corresponding to a tuple of variables. The \({\text {cc-let}}\) and \({\text {cc-fix}}\) rules have a proviso: the bound variables, x and f, x respectively, should have been renamed to avoid clashes with the domain of \(\rho \). Most of the rules have an obvious structure. We comment only on the ones for transforming fixed point expressions and applications. The former translates into a closure. The function part of the closure is obtained by transforming the body of the abstraction, but under a new mapping for its free variables; the expression
that determines an environment corresponding to a tuple of variables. The \({\text {cc-let}}\) and \({\text {cc-fix}}\) rules have a proviso: the bound variables, x and f, x respectively, should have been renamed to avoid clashes with the domain of \(\rho \). Most of the rules have an obvious structure. We comment only on the ones for transforming fixed point expressions and applications. The former translates into a closure. The function part of the closure is obtained by transforming the body of the abstraction, but under a new mapping for its free variables; the expression  means that all the free variables of
means that all the free variables of  appear in the tuple. The environment part of the closure correspondingly contains mappings for the variables in the tuple that are determined by the enclosing context. Note also that the parameter for the function part of the closure is expected to be a triple, the first item of which corresponds to the function being defined recursively in the source language expression. The transformation of a source language application makes clear how this structure is used to realize recursion: the constructed closure application has the effect of feeding the closure to its function part as the first component of its argument.
appear in the tuple. The environment part of the closure correspondingly contains mappings for the variables in the tuple that are determined by the enclosing context. Note also that the parameter for the function part of the closure is expected to be a triple, the first item of which corresponds to the function being defined recursively in the source language expression. The transformation of a source language application makes clear how this structure is used to realize recursion: the constructed closure application has the effect of feeding the closure to its function part as the first component of its argument.
3.2 A \(\lambda \)Prolog Rendition of Closure Conversion
Our presentation of the implementation of closure conversion has two parts: we first show how to encode the source and target languages and we then present a \(\lambda \)Prolog specification of the transformation. In the first part, we discuss also the formalization of the evaluation and typing relations; these will be used in the correctness proofs that we develop later.
Encoding the Languages. We first consider the encoding of types. We will use  as the \(\lambda \)Prolog type for this encoding for both languages. The constructors
as the \(\lambda \)Prolog type for this encoding for both languages. The constructors  and
and  will encode, respectively, the natural number, unit and pair types. There are two arrow types to be treated. We will represent \(\rightarrow \) by
will encode, respectively, the natural number, unit and pair types. There are two arrow types to be treated. We will represent \(\rightarrow \) by  and
and  by
by  . The following signature summarizes these decisions.
. The following signature summarizes these decisions.


We will use the \(\lambda \)Prolog type  for encodings of source language terms. The particular constructors that we will use for representing the terms themselves are the following, assuming that
for encodings of source language terms. The particular constructors that we will use for representing the terms themselves are the following, assuming that  is a type for representations of natural numbers:
is a type for representations of natural numbers:


The only constructors that need further explanation here are  and
and  . These encode binding constructs in the source language and, as expected, we use \(\lambda \)Prolog abstraction to capture their binding structure. Thus,
. These encode binding constructs in the source language and, as expected, we use \(\lambda \)Prolog abstraction to capture their binding structure. Thus,  is encoded as
is encoded as  . Similarly, the \(\lambda \)Prolog term
. Similarly, the \(\lambda \)Prolog term  represents the source language expression
represents the source language expression  .
.
We will use the \(\lambda \)Prolog type  for encodings of target language terms. To represent the constructs the target language shares with the source language, we will use “primed” versions of the \(\lambda \)Prolog constants seen earlier; e.g.,
for encodings of target language terms. To represent the constructs the target language shares with the source language, we will use “primed” versions of the \(\lambda \)Prolog constants seen earlier; e.g.,  of type
of type  will represent the null tuple. Of course, there will be no constructor corresponding to
will represent the null tuple. Of course, there will be no constructor corresponding to  . We will also need the following additional constructors:
. We will also need the following additional constructors:


Here,  encodes \(\lambda \)-abstraction and
encodes \(\lambda \)-abstraction and  and
and  encode closures and their application. Note again the \(\lambda \)-tree syntax representation for binding constructs.
encode closures and their application. Note again the \(\lambda \)-tree syntax representation for binding constructs.
Following Sect. 2, we represent typing judgments as relations between terms and types, treating contexts implicitly via dynamically added clauses that assign types to free variables. We use the predicates  and
and  to encode typing in the source and target language respectively. The clauses defining these predicates are routine and we show only a few pertaining to the binding constructs. The rule for typing fixed points in the source language translates into the following.
to encode typing in the source and target language respectively. The clauses defining these predicates are routine and we show only a few pertaining to the binding constructs. The rule for typing fixed points in the source language translates into the following.


Note how the required freshness constraint is realized in this clause: the universal quantifiers over  and
and  introduce new names and the application
introduce new names and the application  replaces the bound variables with these names to generate the new typing judgment that must be derived. For the target language, the main interesting rule is for typing the application of closures. The following clause encodes this rule.
replaces the bound variables with these names to generate the new typing judgment that must be derived. For the target language, the main interesting rule is for typing the application of closures. The following clause encodes this rule.


Here again we use universal quantifiers in goals to encode the freshness constraint. Note also how the universal quantifier over the variable  captures the opaqueness quality of the type of the environment of the closure involved in the construct.
captures the opaqueness quality of the type of the environment of the closure involved in the construct.
We encode the one step evaluation rules for the source and target languages using the predicates  and
and  . We again consider only a few interesting cases in their definition. Assuming that
. We again consider only a few interesting cases in their definition. Assuming that  and
and  recognize values in the source and target languages, the clauses for evaluating the application of a fixed point and a closure are the following.
recognize values in the source and target languages, the clauses for evaluating the application of a fixed point and a closure are the following.


Note here how application in the meta-language realizes substitution.
We use the predicates nstep (which relates a natural number and two terms) and  to represent the n-step and full evaluation relations for the source language, respectively. These predicates have obvious definitions. The predicates
to represent the n-step and full evaluation relations for the source language, respectively. These predicates have obvious definitions. The predicates  and
and  play a similar role for the target language.
play a similar role for the target language.
Specifying Closure Conversion. To define closure conversion in \(\lambda \)Prolog, we need a representation of mappings for source language variables. We use the type  and the constant
and the constant  to represent the mapping for a single variable.Footnote 3 We use the type
to represent the mapping for a single variable.Footnote 3 We use the type  for lists of such mappings, the constructors
for lists of such mappings, the constructors  and
and  for constructing such lists and the predicate
for constructing such lists and the predicate  for checking membership in them. We also need to represent lists of source and target language terms. We will use the types
for checking membership in them. We also need to represent lists of source and target language terms. We will use the types  and
and  for these and for simplicity of discussion, we will overload the list constructors and predicates at these types. Polymorphic typing in \(\lambda \)Prolog supports such overloading but this feature has not yet been implemented in Abella; we overcome this difficulty in the actual development by using different type and constant names for each case.
for these and for simplicity of discussion, we will overload the list constructors and predicates at these types. Polymorphic typing in \(\lambda \)Prolog supports such overloading but this feature has not yet been implemented in Abella; we overcome this difficulty in the actual development by using different type and constant names for each case.
The crux in formalizing the definition of closure conversion is capturing the content of the  rule. A key part of this rule is identifying the free variables in a given source language term. We realize the requirement by defining a predicate
rule. A key part of this rule is identifying the free variables in a given source language term. We realize the requirement by defining a predicate  that is such that if
that is such that if  holds then
holds then  is a list that includes all the free variables of M and
is a list that includes all the free variables of M and  is another list that contains only the free variables of M. We show a few critical clauses in the definition of this predicate, omitting ones whose structure is easy predict.
is another list that contains only the free variables of M. We show a few critical clauses in the definition of this predicate, omitting ones whose structure is easy predict.


The predicate combine used in these clauses is one that holds between three lists when the last is a combination of the elements of the first two. The essence of the definition of fvars is in the treatment of binding constructs. Viewed operationally, the body of such a construct is descended into after instantiating the binder with a new variable marked notfree. Thus, the variables that are marked in this way correspond to exactly those that are explicitly bound in the term and only those that are not so marked are collected through the second clause. It is important also to note that the specification of fvars has a completely logical structure; this fact can be exploited during verification.
The  rule requires us to construct an environment representing the mappings for the variables found by fvars. The predicate mapenv specified by the following clauses provides this functionality.
rule requires us to construct an environment representing the mappings for the variables found by fvars. The predicate mapenv specified by the following clauses provides this functionality.


The  rule also requires us to create a new mapping from the variable list to projections from an environment variable. Representing the list of projection mappings as a function from the environment variable, this relation is given by the predicate mapvar that is defined by the following clauses.
rule also requires us to create a new mapping from the variable list to projections from an environment variable. Representing the list of projection mappings as a function from the environment variable, this relation is given by the predicate mapvar that is defined by the following clauses.


We can now specify the closure conversion transformation. We provide clauses below that define the predicate cc such that  holds if M’ is a transformed version of M under the mapping Map for the variables in Vs; we assume that Vs contains all the free variables of M.
holds if M’ is a transformed version of M under the mapping Map for the variables in Vs; we assume that Vs contains all the free variables of M.


These clauses correspond very closely to the rules in Fig. 3. Note especially the clause for transforming an expression of the form  that encodes the content of the \({\text {cc-fix}}\) rule. In the body of this clause, fvars is used to identify the free variables of the expression, and mapenv and mapvar are used to create the reified environment and the new mapping. In both this clause and in the one for transforming a let expression, the \(\lambda \)-tree representation, universal goals and (meta-language) applications are used to encode freshness and renaming requirements related to bound variables in a concise and logically precise way.
that encodes the content of the \({\text {cc-fix}}\) rule. In the body of this clause, fvars is used to identify the free variables of the expression, and mapenv and mapvar are used to create the reified environment and the new mapping. In both this clause and in the one for transforming a let expression, the \(\lambda \)-tree representation, universal goals and (meta-language) applications are used to encode freshness and renaming requirements related to bound variables in a concise and logically precise way.
3.3 Implementing Other Transformations
We have used the ideas discussed in the preceding subsections in realizing other transformations such as code hoisting and conversion to continuation-passing style (CPS). These transformations are part of a tool-kit used by compilers for functional languages to convert programs into a form from which compilation may proceed in a manner similar to that for conventional languages like C.
Our implementation of the CPS transformation is based on the one-pass version described by Danvy and Filinski [13] that identifies and eliminates the so-called administrative redexes on-the-fly. This transformation can be encoded concisely and elegantly in \(\lambda \)Prolog by using meta-level redexes for administrative redexes. The implementation is straightforward and similar ones that use the HOAS approach have already been described in the literature; e.g. see [37].
Our implementation of code hoisting is more interesting: it benefits in an essential way once again from the ability to analyze binding structure. The code hoisting transformation lifts nested functions that are closed out into a flat space at the top level in the program. This transformation can be realized as a recursive procedure: given a function  , the procedure is applied to the subterms of M and the extracted functions are then moved out of
, the procedure is applied to the subterms of M and the extracted functions are then moved out of  . Of course, for this movement to be possible, it must be the case that the variable x does not appear in the functions that are candidates for extraction. This “dependency checking” is easy to encode in a logical way within our framework.
. Of course, for this movement to be possible, it must be the case that the variable x does not appear in the functions that are candidates for extraction. This “dependency checking” is easy to encode in a logical way within our framework.
To provide more insight into our implementation of code-hoisting, let us assume that it is applied after closure conversion and that its source and target languages are both the language shown in Fig. 2. Applying code hoisting to any term will result in a term of the form


where, for \(1 \le i \le n\), \(M_i\) corresponds to an extracted function. We will write this term below as  where
where  and, correspondingly,
and, correspondingly,  .
.
We write the judgment of code hoisting as  where \(\rho \) has the form \((x_1,\ldots ,x_n)\). This judgment asserts that \(M'\) is the result of extracting all functions in M to the top level, assuming that \(\rho \) contains all the bound variables in the context in which M appears. The relation is defined by recursion on the structure of M. The main rule that deserves discussion is that for transforming functions. This rule is the following:
where \(\rho \) has the form \((x_1,\ldots ,x_n)\). This judgment asserts that \(M'\) is the result of extracting all functions in M to the top level, assuming that \(\rho \) contains all the bound variables in the context in which M appears. The relation is defined by recursion on the structure of M. The main rule that deserves discussion is that for transforming functions. This rule is the following:


We assume here that  and, by an abuse of notation, we let
and, by an abuse of notation, we let  denote \((g~(f_1,\ldots ,f_n))\). This rule has a side condition: x must not occur in
denote \((g~(f_1,\ldots ,f_n))\). This rule has a side condition: x must not occur in  . Intuitively, the term
. Intuitively, the term  is transformed by extracting the functions from within M and then moving them further out of the scope of x. Note that this transformation succeeds only if none of the extracted functions depend on x. The resulting function is then itself extracted. In order to do this, it must be made independent of the (previously) extracted functions, something that is achieved by a suitable abstraction; the expression itself becomes an application to a tuple of functions in an appropriate let environment.
is transformed by extracting the functions from within M and then moving them further out of the scope of x. Note that this transformation succeeds only if none of the extracted functions depend on x. The resulting function is then itself extracted. In order to do this, it must be made independent of the (previously) extracted functions, something that is achieved by a suitable abstraction; the expression itself becomes an application to a tuple of functions in an appropriate let environment.
It is convenient to use a special representation for the result of code hoisting in specifying it in \(\lambda \)Prolog. Towards this end, we introduce the following constants:


Using these constants, the term  that results from code hoisting will be represented by
that results from code hoisting will be represented by


We use the predicate  to represent the code hoisting judgment. The context \(\rho \) in the judgment will be encoded implicitly through dynamically added program clauses that specify the translation of each variable
to represent the code hoisting judgment. The context \(\rho \) in the judgment will be encoded implicitly through dynamically added program clauses that specify the translation of each variable  . In this context, the rule for transforming functions, the main rule of interest, is encoded in the following clause:
. In this context, the rule for transforming functions, the main rule of interest, is encoded in the following clause:


As in previous specifications, a universal and a hypothetical goal are used in this clause to realize recursion over binding structure. Note also the completely logical encoding of the requirement that the function argument must not occur in the nested functions extracted from its body: quantifier ordering ensures that FE cannot be instantiated by a term that contains x free in it. We have used the predicate extract to build the final result of the transformation from the transformed form of the function body and the nested functions extracted from it; the definition of this predicate is easy to construct and is not provided here.
4 Verifying Transformations on Functional Programs
We now consider the verification of \(\lambda \)Prolog implementations of transformations on functional programs. We exploit the two-level logic approach in this process, treating \(\lambda \)Prolog programs as HOHH specifications and reasoning about them using Abella. Our discussions below will show how we can use the \(\lambda \)-tree syntax approach and the logical nature of our specifications to benefit in the reasoning process. Another aspect that they will bring out is the virtues of the close correspondence between rule based presentations and HOHH specifications: this correspondence allows the structure of informal proofs over inference rule style descriptions to be mimicked in a formalization within our framework.
We use the closure conversion transformation as our main example in this exposition. The first two subsections below present, respectively, an informal proof of its correctness and its rendition in Abella. We then discuss the application of these ideas to other transformations. Our proofs are based on logical relation style definitions of program equivalence. Other forms of semantics preservation have also been considered in the literature. Our framework can be used to advantage in formalizing these approaches as well, an aspect we discuss in the last subsection.
4.1 Informal Verification of Closure Conversion
To prove the correctness of closure conversion, we need a notion of equivalence between the source and target programs. Following [28], we use a logical relation style definition for this purpose. A complication is that our source language includes recursion. To overcome this problem, we use the idea of step indexing [1, 2]. Specifically, we define the following mutually recursive simulation relation \(\sim \) between closed source and target terms and equivalence relation \(\approx \) between closed source and target values, each indexed by a type and a step measure.


Note that the definition of \(\approx \) in the fixed point/closure case uses \(\approx \) negatively at the same type. However, it is still a well-defined notion because the index decreases. The cumulative notion of equivalence, written  , corresponds to two expressions being equivalent under any index.
, corresponds to two expressions being equivalent under any index.
Analyzing the simulation relation and using the evaluation rules, we can show the following “compatibility” lemma for various constructs in the source language.
Lemma 1
-
1.
If
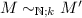 then
then  . If also
. If also  then
then 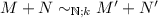 .
.
-
2.
If
 then
then 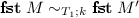 and
and  .
. -
3.
If
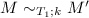 and
and 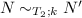 then
then 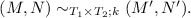
-
4.
If
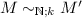 ,
, 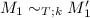 and
and  , then
, then  .
. -
5.
If
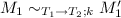 and
and 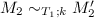 then
then 
The proof of the last of these properties requires us to consider the evaluation of the application of a fixed point expression which involves “feeding” the expression to its own body. In working out the details, we use the easily observed property that the simulation and equivalence relations are closed under decreasing indices.
Our notion of equivalence only relates closed terms. However, our transformation typically operates on open terms, albeit under mappings for the free variables. To handle this situation, we consider semantics preservation for possibly open terms under closed substitutions. We will take substitutions in both the source and target settings to be simultaneous mappings of closed values for a finite collection of variables, written as \((V_1/x_1,\ldots ,V_n/x_n)\). In defining a correspondence between source and target language substitutions, we need to consider the possibility that a collection of free variables in the first may be reified into an environment variable in the second. This motivates the following definition in which \(\gamma \) represents a source language substitution:


Writing  for the concatenation of two substitutions viewed as lists, equivalence between substitutions is then defined as follows:
for the concatenation of two substitutions viewed as lists, equivalence between substitutions is then defined as follows:


Note that both relations are indexed by a source language typing context and a step measure. The second relation allows the substitutions to be for different variables in the source and target languages. A relevant mapping will determine a correspondence between these variables when we use the relation.
We write the application of a substitution \(\gamma \) to a term M as \(M[\gamma ]\). The first part of the following lemma, proved by an easy use of the definitions of \(\approx \) and evaluation, provides the basis for justifying the treatment of free variables via their transformation into projections over environment variables introduced at function boundaries in the closure conversion transformation. The second part of the lemma is a corollary of the first part that relates a source substitution and an environment computed during the closure conversion of fixed points.
Lemma 2
Let  and \(\delta ' = (V_1'/y_1,\ldots ,\)
\(V_n'/y_n,V_e/x_e)\) be source and target language substitutions and let \(\varGamma = (x_m':T_m',\ldots ,x_1':T_1',x_n:T_n,\ldots ,x_1:T_1)\) be a source language typing context such that
and \(\delta ' = (V_1'/y_1,\ldots ,\)
\(V_n'/y_n,V_e/x_e)\) be source and target language substitutions and let \(\varGamma = (x_m':T_m',\ldots ,x_1':T_1',x_n:T_n,\ldots ,x_1:T_1)\) be a source language typing context such that  . Further, let \(\rho = (x_1 \mapsto y_1,\ldots ,x_n \mapsto y_n, x_1' \mapsto \pi _1(x_e), \ldots , x_m' \mapsto \pi _m(x_e))\).
. Further, let \(\rho = (x_1 \mapsto y_1,\ldots ,x_n \mapsto y_n, x_1' \mapsto \pi _1(x_e), \ldots , x_m' \mapsto \pi _m(x_e))\).
-
1.
If \(x : T \in \varGamma \) then there exists a value \(V'\) such that \((\rho (x))[\delta '] \hookrightarrow V'\) and
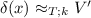 .
. -
2.
If \(\varGamma ' = (z_1:T_{z_1},\ldots ,z_j:T_{z_j})\) for \(\varGamma ' \subseteq \varGamma \) and
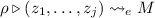 , then there exists \(V_e'\) such that \(M[\delta '] \hookrightarrow V_e'\) and
, then there exists \(V_e'\) such that \(M[\delta '] \hookrightarrow V_e'\) and 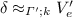 .
.
The proof of semantics preservation also requires a result about the preservation of typing. It takes a little effort to ensure that this property holds at the point in the transformation where we cross a function boundary. That effort is encapsulated in the following strengthening lemma in the present setting.
Lemma 3
If \(\varGamma \vdash M:T\), \(\{x_1,\ldots ,x_n\} \supseteq \mathbf {fvars}(M)\) and \(x_i:T_i \in \varGamma \) for \(1 \le i \le n\), then \(x_n:T_n ,\ldots ,x_1:T_1 \vdash M :T\).
The correctness theorem can now be stated as follows:
Theorem 4
Let  and \(\delta ' = (V_1'/y_1,\ldots ,\)
\(V_n'/y_n,V_e/x_e)\) be source and target language substitutions and let \(\varGamma = (x_m':T_m',\ldots ,x_1':T_1',x_n:T_n,\ldots ,x_1:T_1)\) be a source language typing context such that
and \(\delta ' = (V_1'/y_1,\ldots ,\)
\(V_n'/y_n,V_e/x_e)\) be source and target language substitutions and let \(\varGamma = (x_m':T_m',\ldots ,x_1':T_1',x_n:T_n,\ldots ,x_1:T_1)\) be a source language typing context such that  . Further, let \(\rho = (x_1 \mapsto y_1,\ldots ,x_n \mapsto y_n, x_1' \mapsto \pi _1(x_e), \ldots , x_m' \mapsto \pi _m(x_e))\). If \(\varGamma \vdash M:T\) and
. Further, let \(\rho = (x_1 \mapsto y_1,\ldots ,x_n \mapsto y_n, x_1' \mapsto \pi _1(x_e), \ldots , x_m' \mapsto \pi _m(x_e))\). If \(\varGamma \vdash M:T\) and  , then
, then  .
.
We outline the main steps in the argument for this theorem: these will guide the development of a formal proof in Sect. 4.2. We proceed by induction on the derivation of  , analyzing the last step in it. This obviously depends on the structure of M. The case for a number is obvious and for a variable we use Lemma 2.1. In the remaining cases, other than when M is of the form
, analyzing the last step in it. This obviously depends on the structure of M. The case for a number is obvious and for a variable we use Lemma 2.1. In the remaining cases, other than when M is of the form  or
or  , the argument follows a set pattern: we observe that substitutions distribute to the sub-components of expressions, we invoke the induction hypothesis over the sub-components and then we use Lemma 1 to conclude. If M is of the form
, the argument follows a set pattern: we observe that substitutions distribute to the sub-components of expressions, we invoke the induction hypothesis over the sub-components and then we use Lemma 1 to conclude. If M is of the form  , then \(M'\) must be of the form
, then \(M'\) must be of the form  . Here again the substitutions distribute to \(M_1\) and \(M_2\) and to \(M_1'\) and \(M_2'\), respectively. We then apply the induction hypothesis first to \(M_1\) and \(M_1'\) and then to \(M_2\) and \(M_2'\); in the latter case, we need to consider extended substitutions but these obviously remain equivalent. Finally, if M is of the form
. Here again the substitutions distribute to \(M_1\) and \(M_2\) and to \(M_1'\) and \(M_2'\), respectively. We then apply the induction hypothesis first to \(M_1\) and \(M_1'\) and then to \(M_2\) and \(M_2'\); in the latter case, we need to consider extended substitutions but these obviously remain equivalent. Finally, if M is of the form  , then \(M'\) must have the form
, then \(M'\) must have the form  . We can prove that the abstraction \(M_1'\) is closed and therefore that
. We can prove that the abstraction \(M_1'\) is closed and therefore that  . We then apply the induction hypothesis. In order to do so, we generate the appropriate typing judgment using Lemma 3 and a new pair of equivalent substitutions (under a suitable step index) using Lemma 2.2.
. We then apply the induction hypothesis. In order to do so, we generate the appropriate typing judgment using Lemma 3 and a new pair of equivalent substitutions (under a suitable step index) using Lemma 2.2.
4.2 Formal Verification of the Closure Conversion Implementation
In the subsections below, we present a sequence of preparatory steps, leading eventually to a formal version of the correctness theorem.
Auxiliary Predicates Used in the Formalization. We use the techniques of Sect. 2 to define some predicates related to the encodings of source and target language types and terms that are needed in the main development; unless explicitly mentioned, these definitions are in \(\mathcal {G}\). First, we define the predicates ctx and ctx’ to identify typing contexts for the source and target languages. Next, we define in HOHH the recognizers tm and tm’ of well-formed source and target language terms. A source (target) term M is closed if {tm M} ({tm’ M}) is derivable. The predicate  recognizes source types. Finally,
recognizes source types. Finally,  is a predicate such that
is a predicate such that  holds if L is a source language typing context and Vs is the list of variables it pertains to.
holds if L is a source language typing context and Vs is the list of variables it pertains to.
Step indexing uses ordering on natural numbers. We represent natural numbers using z for 0 and s for the successor constructor. The predicate is_nat recognizes natural numbers. The predicates lt and le, whose definitions are routine, represent the “less than” and the “less than or equal to” relations.
The Simulation and Equivalence Relations. The following clauses define the simulation and equivalence relations.


The formula (sim T K M M’) is intended to mean that M simulates M’ at type T in K steps;  has a similar interpretation. Note the exploitation of \(\lambda \)-tree syntax, specifically the use of application, to realize substitution in the definition of equiv. It is easily shown that sim holds only between closed source and target terms and similarly equiv holds only between closed source and target values.Footnote 4
has a similar interpretation. Note the exploitation of \(\lambda \)-tree syntax, specifically the use of application, to realize substitution in the definition of equiv. It is easily shown that sim holds only between closed source and target terms and similarly equiv holds only between closed source and target values.Footnote 4
Compatibility lemmas in the style of Lemma 1 are easily stated for sim. For example, the one for pairs is the following.


These lemmas have straightforward proofs.
Representing Substitutions. We treat substitutions as discussed in Sect. 2. For example, source substitutions satisfy the following definition.


By definition, these substitutions map variables to closed values. To accord with the way closure conversion is formalized, we allow multiple mappings for a given variable, but we require all of them to be to the same value. The application of a source substitution is also defined as discussed in Sect. 2.


As before, we can easily prove properties about substitution application based on this definition such as that such an application distributes over term structure and that closed terms are not affected by substitution.
The predicates subst’ and app_subst’ encode target substitutions and their application. Their formalization is similar to that above.
The Equivalence Relation on Substitutions. We first define the relation subst_env_equiv between source substitutions and target environments:


Using subst_env_equiv, the needed relation between source and target substitutions is defined as follows.


Lemmas about
 ,
,  and
and
 . Lemma 3 translates into a lemma about
. Lemma 3 translates into a lemma about  in the implementation. To state it, we define a strengthening relation between source typing contexts:
in the implementation. To state it, we define a strengthening relation between source typing contexts:


(prune_ctx Vs L L’) holds if L’ is a typing context that “strengthens” L to contain type assignments only for the variables in Vs. The lemma about fvars is then the following.


To prove this theorem, we generalize it so that the HOHH derivation of  is relativized to a context that marks some variables as not free. The resulting generalization is proved by induction on the fvars derivation.
is relativized to a context that marks some variables as not free. The resulting generalization is proved by induction on the fvars derivation.
A formalization of Lemma 2 is also needed for the main theorem. We start with a lemma about mapvar.


In words, this lemma states the following. If L is a source typing context for the variables \((x_1,\ldots ,x_n)\), ML is a source substitution and VE is an environment equivalent to ML at L, then mapvar determines a mapping for \((x_1,\ldots ,x_n)\) that are projections over an environment with the following character: if the environment is taken to be VE, then, for \(1 \le i \le n\), \(x_i\) is mapped to a projection that must evaluate to a value equivalent to the substitution for \(x_i\) in ML. The lemma is proved by induction on the derivation of {mapvar Vs Map}.
Lemma 2 is now formalized as follows.


Two new predicates are used here. The judgment (vars_of_subst’ ML’ Vs’) “collects” the variables in the target substitution ML’ into Vs’. Given source variables  and target variables
and target variables  , the predicate to_mapping creates in
, the predicate to_mapping creates in  the mapping
the mapping


The conclusion of the lemma is a conjunction representing the two parts of Lemma 2. The first part is proved by induction on  , using the lemma for mapvar when X is some \(x_i' (1 \le i \le m)\). The second part is proved by induction on
, using the lemma for mapvar when X is some \(x_i' (1 \le i \le m)\). The second part is proved by induction on  using the first part.
using the first part.
The Main Theorem. The semantics preservation theorem is stated as follows:


We use an induction on {cc Map Vs M M’}, the closure conversion derivation, to prove this theorem. As should be evident from the preceding development, the proof in fact closely follows the structure we outlined in Sect. 4.1.
4.3 Verifying the Implementations of Other Transformations
We have used the ideas presented in this section to develop semantics preservation proofs for other transformations such as code hoisting and the CPS transformation. We discuss the case for code hoisting below.
The first step is to define the step-indexed logical relations \(\sim '\) and \(\approx '\) that respectively represent the simulation and equivalence relation between the input and output terms and values for code hoisting:


We can show that \(\sim '\) satisfies a set of compatibility properties similar to Lemma 1.
We next define a step-indexed relation of equivalence between two substitutions \(\delta = {(V_1/x_1,\ldots ,V_m/x_m)}\) and \(\delta ' = {(V_1'/x_1,\ldots ,V_m'/x_m)}\) relative to a typing context \(\varGamma = ({x_m:T_m,\ldots , x_1:T_1})\):


The semantics preservation theorem for code hoisting is stated as follows:
Theorem 5
Let \(\delta = {(V_1/x_1,\ldots ,V_m/x_m)}\) and \(\delta ' = {(V_1'/x_1,\ldots ,V_m'/x_m)}\) be substitutions for the language described in Fig. 2. Let \(\varGamma = (x_m:T_m,\ldots ,x_1:T_1)\) be a typing context such that  . Further, let \(\rho = (x_1,\ldots ,x_m)\). If
. Further, let \(\rho = (x_1,\ldots ,x_m)\). If  and
and  hold, then
hold, then  holds.
holds.
The theorem is proved by induction on the derivation for  . The base cases follow easily, possibly using the fact that
. The base cases follow easily, possibly using the fact that  . For the inductive cases, we observe that substitutions distribute to the sub-components of expressions, we invoke the induction hypothesis over the sub-components and we use the compatibility property of \(\sim '\). In the case of an abstraction, \(\delta \) and \(\delta '\) must be extended to include a substitution for the bound variable. For this case to work out, we must show that the additional substitution for the bound variable has no impact on the functions extracted by code hoisting. From the side condition for the rule deriving
. For the inductive cases, we observe that substitutions distribute to the sub-components of expressions, we invoke the induction hypothesis over the sub-components and we use the compatibility property of \(\sim '\). In the case of an abstraction, \(\delta \) and \(\delta '\) must be extended to include a substitution for the bound variable. For this case to work out, we must show that the additional substitution for the bound variable has no impact on the functions extracted by code hoisting. From the side condition for the rule deriving  in this case, the extracted functions cannot depend on the bound variable and hence the desired observation follows.
in this case, the extracted functions cannot depend on the bound variable and hence the desired observation follows.
In the formalization of this proof, we use the predicate constants  and
and  to respectively represent \(\sim '\) and \(\approx '\). The Abella definitions of these predicates have by now a familiar structure. We also define a constant subst_equiv’ to represent the equivalence of substitutions as follows:
to respectively represent \(\sim '\) and \(\approx '\). The Abella definitions of these predicates have by now a familiar structure. We also define a constant subst_equiv’ to represent the equivalence of substitutions as follows:


The representation of contexts in the code hoisting judgment in the HOHH specification is captured by the predicate ch_ctx that is defined as follows:


The semantics preservation theorem is stated as follows, where vars_of_ctx’ is a predicate for collecting variables in the typing contexts for the target language, vars_of_ch_ctx is a predicate such that (vars_of_ch_ctx L Vs) holds if L is a context for code hoisting and Vs is the list of variables it pertains to:


The proof is by induction on  and its structure follows that of the informal one very closely. The fact that the extracted functions do not depend on the bound variable of an abstraction is actually explicit in the logical formulation and this leads to an exceedingly simple argument for this case.
and its structure follows that of the informal one very closely. The fact that the extracted functions do not depend on the bound variable of an abstraction is actually explicit in the logical formulation and this leads to an exceedingly simple argument for this case.
4.4 Relevance to Other Styles of Correctness Proofs
Many compiler verification projects, such as CompCert [21] and CakeML [20], have focused primarily on verifying whole programs that produce values of atomic types. In this setting, the main requirement is to show that the source and target programs evaluate to the same atomic values. Structuring a proof around program equivalence base on a logical relation is one way to do this. Another, sometimes simpler, approach is to show that the compiler transformations permute over evaluation; this method works because transformations typically preserve values at atomic types. Although we do not present this here, we have examined proofs of this kind and have observed many of the same kinds of benefits to the \(\lambda \)-tree syntax approach in their context as well.
Programs are often built by composing separately compiled modules of code. In this context it is desirable that the composition of correctly compiled modules preserve correctness; this property applied to compiler verification has been called modularity. Logical relations pay attention to equivalence at function types and hence proofs based on them possess the modularity property. Another property that is desirable for correctness proofs is transitivity: we should be able to infer the correctness of a multi-stage compiler from the correctness of each of its stages. This property holds when we use logical relations if we restrict attention to programs that produce atomic values but cannot be guaranteed if equivalence at function types is also important; it is not always possible to decompose the natural logical relation between a source and target language into ones between several intermediate languages. Recent work has attempted to generalize the logical relations based approach to obtain the benefits of both transitivity and modularity [32]. Many of the same issues relating to the treatment of binding and substitution appear in this context as well and the work in this paper therefore seems to be relevant also to the formalization of proofs that use these ideas.
Finally, we note that the above comments relate only to the formalization of proofs. The underlying transformations remain unchanged and so does the significance of our framework to their implementation.
5 Related Work and Conclusion
Compiler verification has been an active area for investigation. We focus here on the work in this area that has been devoted to compiling functional languages. There have been several projects with ambitious scope even in this setting. To take some examples, the CakeML project has implemented a compiler from a subset of ML to the X86 assembly language and verified it using HOL4 [20]; Dargaye has used Coq to verify a compiler from a subset of ML into the intermediate language used by CompCert [14]; Hur and Dreyer have used Coq to develop a verified single-pass compiler from a subset of ML to assembly code based on a logical relations style definition of program equivalence [19]; and Neis et al. have used Coq to develop a verified multi-pass compiler called Pilsner, basing their proof on a notion of semantics preservation called Parametric Inter-Languages Simulation (PILS) [32]. All these projects have used essentially first-order treatments of binding, such as those based on a De Bruijn style representation.
A direct comparison of our work with the projects mentioned above is neither feasible nor sensible because of differences in scope and focus. Some comparison is possible with a part of the Lambda Tamer project of Chlipala in which he describes the verified implementation in Coq of a compiler for the STLC using a logical relation based definition of program equivalence [11]. This work uses a higher-order representation of syntax that does not derive all the benefits of \(\lambda \)-tree syntax. Chlipala’s implementation of closure conversion comprises about 400 lines of Coq code, in contrast to about 70 lines of \(\lambda \)Prolog code that are needed in our implementation. Chlipala’s proof of correctness comprises about 270 lines but it benefits significantly from the automation framework that was the focus of the Lambda Tamer project; that framework is built on top of the already existing Coq libraries and consists of about 1900 lines of code. The Abella proof script runs about 1600 lines. We note that Abella has virtually no automation and the current absence of polymorphism leads to some redundancy in the proof. We also note that, in contrast to Chlipala’s work, our development treats a version of the STLC that includes recursion. This necessitates the use of a step-indexed logical relation which makes the overall proof more complex.
Other frameworks have been proposed in the literature that facilitate the use of HOAS in implementing and verifying compiler transformations. Hickey and Nogin describe a framework for effecting compiler transformations via rewrite rules that operate on a higher-order representation of programs [18]. However, their framework is embedded within a functional language. As a result, they are not able to support an analysis of binding structure, an ability that brings considerable benefit as we have highlighted in this paper. Moreover, this framework offers no capabilities for verification. Hannan and Pfenning have discussed using a system called Twelf that is based on LF in specifying and verifying compilers; see, for example, [16] and [29] for some applications of this framework. The way in which logical properties can be expressed in Twelf is restricted; in particular, it is not easy to encode a logical relation-style definition within it. The Beluga system [34], which implements a functional programming language based on contextual modal type theory [31], overcomes some of the shortcomings of Twelf. Rich properties of programs can be embedded in types in Beluga, and Belanger et al. show how this feature can be exploited to ensure type preservation for closure conversion [7]. Properties based on logical relations can also be described in Beluga [10]. It remains to be seen if semantics preservation proofs of the kind discussed in this paper can be carried out in the Beluga system.
While the framework comprising \(\lambda \)Prolog and Abella has significant benefits in the verified implementation of compiler transformations for functional languages, its current realization has some practical limitations that lead to a larger proof development effort than seems necessary. One such limitation is the absence of polymorphism in the Abella implementation. A consequence of this is that the same proofs have sometimes to be repeated at different types. This situation appears to be one that can be alleviated by allowing the user to parameterize proofs by types and we are currently investigating this matter. A second limitation arises from the emphasis on explicit proofs in the theorem-proving setup. The effect of this requirement is especially felt with respect to lemmas about contexts that arise routinely in the \(\lambda \)-tree syntax approach: such lemmas have fairly obvious proofs but, currently, the user must provide them to complete the overall verification task. In the Twelf and Beluga systems, such lemmas are obviated by absorbing them into the meta-theoretic framework. There are reasons related to the validation of verification that lead us to prefer explicit proofs. However, as shown in [6], it is often possible to generate these proofs automatically, thereby allowing the user to focus on the less obvious aspects. In ongoing work, we are exploring the impact of using such ideas on reducing the overall proof effort.
Notes
- 1.
The actual development of several of the proofs discussed in this paper can be found at the URL http://www-users.cs.umn.edu/~gopalan/papers/compilation/.
- 2.
To be acceptable, definitions must cumulatively satisfy certain stratification conditions [23] that we adhere to in the paper but do not explicitly discuss.
- 3.
This mapping is different from the one considered in Sect. 2.3 in that it is from a source language variable to a target language term.
- 4.
The definition of equiv uses itself negatively in the last clause and thereby violates the original stratification condition of \(\mathcal {G}\). However, Abella permits this definition under a weaker stratification condition that ensures consistency provided the definition is used in restricted ways [5, 38], a requirement that is adhered to in this paper.
References
Ahmed, A.: Step-indexed syntactic logical relations for recursive and quantified types. In: Sestoft, P. (ed.) ESOP 2006. LNCS, vol. 3924, pp. 69–83. Springer, Heidelberg (2006)
Appel, A.W., McAllester, D.: An indexed model of recursive types for foundational proof-carrying code. ACM Trans. Program. Lang. Syst. 23(5), 657–683 (2001)
Aydemir, B.E., et al.: Mechanized metatheory for the masses: the PoplMark challenge. In: Hurd, J., Melham, T. (eds.) TPHOLs 2005. LNCS, vol. 3603, pp. 50–65. Springer, Heidelberg (2005)
Baelde, D., Chaudhuri, K., Gacek, A., Miller, D., Nadathur, G., Tiu, A., Wang, Y.: Abella: a system for reasoning about relational specifications. J. Formalized Reasoning 7(2), 1–89 (2014)
Baelde, D., Nadathur, G.: Combining deduction modulo and logics of fixed-point definitions. In: Proceedings of the 2012 27th Annual IEEE/ACM Symposium on Logic in Computer Science, pp. 105–114. IEEE Computer Society (2012)
Bélanger, O.S., Chaudhuri, K.: Automatically deriving schematic theorems for dynamic contexts. In: Proceedings of the 2014 International Workshop on Logical Frameworks and Meta-languages: Theory and Practice. ACM Press (2014)
Savary-Belanger, O., Monnier, S., Pientka, B.: Programming type-safe transformations using higher-order abstract syntax. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 243–258. Springer, Heidelberg (2013)
Bertot, Y., Castéran, P.: Interactive Theorem Proving and Program Development: Coq’Art: The Calculus of Inductive Constructions. Texts in Theoretical Computer Science. Springer, Heidelberg (2004)
de Bruijn, N.G.: Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with application to the Church-Rosser Theorem. Indagationes Mathematicae 34(5), 381–392 (1972)
Cave, A., Pientka, B.: A case study on logical relations using contextual types. In: Proceedings of the Tenth International Workshop on Logical Frameworks and Meta Languages: Theory and Practice, EPTCS, vol. 185, pp. 33–45 (2015)
Chlipala, A.: A certified type-preserving compiler from lambda calculus to assembly language. In: Proceedings of the 2007 ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 54–65. ACM Press (2007)
Church, A.: A formulation of the simple theory of types. J. Symb. Logic 5, 56–68 (1940)
Danvy, O., Filinski, A.: Representing control: a study of the CPS transformation. Math. Struct. Comput. Sci. 2, 361–391 (1992)
Dargaye, Z.: Vérification formelle d’un compilateur optimisant pour langages fonctionnels. Ph.D. thesis, l’Université Paris 7-Denis Diderot, France (2009)
Gordon, M.J.C.: Introduction to the HOL system. In: Archer, M., Joyce, J.J., Levitt, K.N., Windley, P.J. (eds.) Proceedings of the International Workshop on the HOL Theorem Proving System and its Applications, pp. 2–3. IEEE Computer Society (1991)
Hannan, J., Pfenning, F.: Compiler verification in LF. In: 7th Symposium on Logic in Computer Science. IEEE Computer Society Press (1992)
Harper, R., Honsell, F., Plotkin, G.: A framework for defining logics. J. ACM 40(1), 143–184 (1993)
Hickey, J., Nogin, A.: Formal compiler construction in a logical framework. Higher-Order Symb. Comput. 19(2–3), 197–230 (2006)
Hur, C.K., Dreyer, D.: A Kripke logical relation between ML and assembly. In: Proceedings of the 38th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 133–146. ACM Press (2011)
Kumar, R., Myreen, M.O., Norrish, M., Owens, S.: CakeML: a verified implementation of ML. In: Proceedings of the 41st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 179–191. ACM Press (2014)
Leroy, X.: Formal certification of a compiler back-end or: programming a compiler with a proof assistant. In: Conference Record of the 33rd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 42–54. ACM Press (2006)
McCarthy, J., Painter, J.: Correctness of a compiler for arithmetic expressions. In: Proceedings of Symposia in Applied Mathematics. Mathematical Aspects of Computer Science, vol. 19, pp. 33–41. American Mathematical Society (1967)
McDowell, R., Miller, D.: Cut-elimination for a logic with definitions and induction. Theoret. Comput. Sci. 232, 91–119 (2000)
Miller, D.: Abstract syntax for variable binders: an overview. In: Palamidessi, C., Moniz Pereira, L., Lloyd, J.W., Dahl, V., Furbach, U., Kerber, M., Lau, K.-K., Sagiv, Y., Stuckey, P.J. (eds.) CL 2000. LNCS (LNAI), vol. 1861, pp. 239–253. Springer, Heidelberg (2000)
Miller, D., Nadathur, G.: Programming with Higher-Order Logic. Cambridge University Press, Cambridge (2012)
Miller, D., Tiu, A.: A proof theory for generic judgments. ACM Trans. Comput. Logic 6(4), 749–783 (2005)
Milner, R., Weyrauch, R.: Proving compiler correctness in a mechanized logic. In: Meltzer, B., Michie, D. (eds.) Machine Intelligence, vol. 7, pp. 51–72. Edinburgh University Press, Edinburgh (1972)
Minamide, Y., Morrisett, G., Harper, R.: Typed closure conversion. Technical report CMU-CS-95-171, School of Computer Science, Carnegie Mellon University (1995)
Murphy VII, T.: Modal types for mobile code. Ph.D. thesis, Carnegie Mellon University (2008)
Nadathur, G., Miller, D.: An overview of \(\lambda \)Prolog. In: Fifth International Logic Programming Conference, pp. 810–827. MIT Press (1988)
Nanevski, A., Pfenning, F., Pientka, B.: Contextual model type theory. ACM Trans. Comput. Logic 9(3), 1–49 (2008)
Neis, G., Hur, C.K., Kaiser, J.O., McLaughlin, C., Dreyer, D., Vafeiadis, V.: Pilsner: a compositionally verified compiler for a higher-order imperative language. In: Proceedings of the 20th ACM SIGPLAN International Conference on Functional Programming, pp. 166–178. ACM Press (2015)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. Springer, Heidelberg (2002)
Pientka, B., Dunfield, J.: Beluga: a framework for programming and reasoning with deductive systems (system description). In: Giesl, J., Hähnle, R. (eds.) IJCAR 2010. LNCS, vol. 6173, pp. 15–21. Springer, Heidelberg (2010)
Pitts, A.M.: Nominal logic, a first order theory of names and binding. Inf. Comput. 186(2), 165–193 (2003)
Qi, X., Gacek, A., Holte, S., Nadathur, G., Snow, Z.: The Teyjus system - Version 2. http://teyjus.cs.umn.edu/
Tian, Y.H.: Mechanically verifying correctness of CPS compilation. In: Twelfth Computing: The Australasian Theory Symposium. CRPIT, vol. 51, pp. 41–51. ACS (2006)
Tiu, A.: Stratification in logics of definitions. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS, vol. 7364, pp. 544–558. Springer, Heidelberg (2012)
Acknowledgements
We are grateful to David Baelde for his help in phrasing the definition of the logical relation in Sect. 4.2. The paper has benefited from many suggestions from its reviewers. This work has been supported by the National Science Foundation grant CCF-0917140 and by the University of Minnesota through a Doctoral Dissertation Fellowship and a Grant-in-Aid of Research. Opinions, findings and conclusions or recommendations that are manifest in this material are those of the participants and do not necessarily reflect the views of the NSF.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wang, Y., Nadathur, G. (2016). A Higher-Order Abstract Syntax Approach to Verified Transformations on Functional Programs. In: Thiemann, P. (eds) Programming Languages and Systems. ESOP 2016. Lecture Notes in Computer Science(), vol 9632. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49498-1_29
Download citation
DOI: https://doi.org/10.1007/978-3-662-49498-1_29
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49497-4
Online ISBN: 978-3-662-49498-1
eBook Packages: Computer ScienceComputer Science (R0)











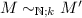 then
then  . If also
. If also  then
then 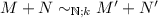 .
. then
then 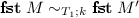 and
and  .
.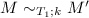 and
and 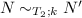 then
then 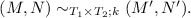
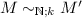 ,
, 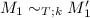 and
and  , then
, then  .
.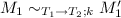 and
and 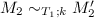 then
then 
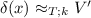 .
.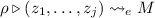 , then there exists
, then there exists 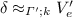 .
.