On the Impact of Known-Key Attacks on Hash Functions

Abstract

Hash functions are often constructed based on permutations or blockciphers, and security proofs are typically done in the ideal permutation or cipher model. However, once these random primitives are instantiated, vulnerabilities of these instantiations may nullify the security. At ASIACRYPT 2007, Knudsen and Rijmen introduced known-key security of blockciphers, which gave rise to many distinguishing attacks on existing blockcipher constructions. In this work, we analyze the impact of such attacks on primitive-based hash functions. We present and formalize the weak cipher model, which captures the case a blockcipher has a certain weakness but is perfectly random otherwise. A specific instance of this model, considering the existence of sets of B queries whose XOR equals 0 at bit-positions C, where C is an index set, covers a wide range of known-key attacks in literature. We apply this instance to the PGV compression functions, as well as to the Grøstl (based on two permutations) and Shrimpton-Stam (based on three permutations) compression functions, and show that these designs do not seriously succumb to any differential known-key attack known to date.

1 Introduction

Cryptographic hash functions are conventionally built on top of compression functions, and in turn on one or more blockciphers. Since the first appearance of such compression function $\mathsf {F}(h,m)=\mathrm {DES}_m(h)$ by Rabin [49] in the late 70s, many blockcipher-based functions appeared in the literature [23, 25, 29, 30, 40, 43, 48, 58]. These all enjoy security proofs in the ideal model, where the underlying ciphers are assum ed to behave ideally. Characteristic to these designs is that the key input to the cipher depends on the input to the compression function, and that the key scheduling needs to be sufficiently strong. For instance, Biryukov et al. [6] derived a related-key attack on AES and claimed that it invalidates the security of the Davies-Meyer compression function when the underlying primitive is instantiated with AES. A more recent approach to compression function design is to base them on a limited number of permutations [8, 41, 42, 51, 57]. These permutations could be designed from scratch, or obtained by fixing a small set of keys and using a blockcipher for these keys only. Related- or chosen-key attacks on blockciphers do not help the adversary here, as the keys are fixed.

Known-Key Security of Blockciphers. While in the classical security models for blockciphers the key is secret and randomly drawn and the adversary’s target is to distinguish the instantiation of the cipher from a random permutation (also known as (strong) pseudorandom permutation security), this notion does not apply if the key is known to the adversary. At ASIACRYPT 2007, Knudsen and Rijmen [27] introduced known-key security of blockciphers. Here, the key is presumed known, and the adversary succeeds in distinguishing if it identifies a structural property of the cipher. Andreeva et al. [1] proposed a way to formalize the known-key security of blockciphers based on the underlying primitives. The model is derived from the indifferentiability framework [37] and hence all composition results carry over. Intuitively: suppose some cryptosystem $\mathsf {F}$ is proven to achieve a certain level of security in the ideal permutation model, and consider $\mathsf {F}'$ to be $\mathsf {F}$ with the permutations replaced by independent blockcipher instantiations. Then, $\mathsf {F}'$ achieves the same level of security as $\mathsf {F}$, up to the known-key indifferentiability bound of the underlying blockciphers.

In [1], several blockcipher constructions are proven to be known-key indifferentiable, such as the multiple Even-Mansour cipher and 14 rounds of balanced Feistel with random functions (using a result of Holenstein et al. [24]). For such ciphers, the above approach works well, although for Even-Mansour the composition is trivial (one essentially replaces an ideal permutation by an ideal permutation) and for Feistel with 14 rounds security is only guaranteed up to $2^{n/32}$ queries, where n is the state size of the cipher.

Known-Key Attacks on Blockciphers. Knudsen and Rijmen also demonstrated that the Feistel network on n bits with 7 rounds (called “Feistel$_7$”) is not known-key indifferentiable [1, 27]: an adversary can generically find $2^{n/2}$ plaintext/ciphertext tuples (m, c) and $(m',c')$ satisfying $\mathsf {Ri}_{n/2}(m\oplus c\oplus m'\oplus c') = 0$ (where $\mathsf {Ri}_{r}(x)$ outputs the $r$ rightmost bits of x). This result has lead to a wave of other known-key attacks on practical constructions, including generalized/extended variants of Feistel [1, 27, 47, 53, 56], reduced versions of AES or Rijndael [22, 27, 38, 44, 52], reduced variants of the blockciphers underlying SHA-2 and SHA-3 finalists BLAKE and Skein [2, 7, 31, 34, 60], and many more [3, 11, 12, 14, 17, 18, 28, 33, 46, 47, 54, 55]. This paper will mostly be concerned with differential known-key attacks, including rebound- and boomerang-based attacks (the majority of above-mentioned attacks). We highlight two results that are among the best-known ones and that exemplify the idea of the other attacks. Gilbert and Peyrin [22] used the rebound technique [39] to derive a known-key attack on 8 rounds of AES (called “AES$_8$”). It starts from the middle, and results in a differential trail with four active words in the beginning, and four at the end. These active words are overlapping at two positions, hence one could consider this result as two tuples (m, c) and $(m',c')$ satisfying $m\oplus c\oplus m'\oplus c'=0$ at 10n / 16 bit-positions. The adversary has $2^{15}\le 2^{n/8}$ degrees of freedom in the attack, and for any choice it results in such a tuple with a certain probability. (The bound of $2^{n/8}$ is used for simplicity later on.) The second attack we highlight is by Yu et al. [60], who employ the boomerang technique [59] to attack 36 rounds of the blockcipher Threefish-512 (called “Threefish$_{36}$”) used in Skein. This attack results in four tuples $(m^{1},c^{1}), \ldots , (m^{4},c^{4})$ satisfying $m^{1}\oplus \cdots \oplus c^{4}=0$. The adversary has $2^n$ degrees of freedom, but any trial succeeds with probability approximately $2^{-454}$. Therefore, the expected number of solutions is about $2^{n-454}\le 2^{n/8}$. This attack is in fact a known-related-key attack, where a fixed difference in the key exists. For simplicity, we condone this, observing that an attack with no key difference must logically be harder.

In any of these cases, the traditional and commonly employed ideal cipher/permutation model falls short: results achieved in this model do not necessarily hold if the primitives are instantiated with Feistel$_7$, AES$_8$, Threefish$_{36}$, or any other known-key distinguishable cipher.

1.1 Our Contributions

In their seminal work, Knudsen and Rijmen state: “In some cases blockciphers are used with a key that is known to the adversary, and at least to a certain extent, the key is under the adversary’s control. Our attacks are quite relevant to this case.” We investigate this fundamental question whether known-key attacks invalidate the security of primitive-based hash functions, but we do so in a much more general way. At a high level, we present a model that goes beyond the traditional ideal cipher model as well as the principle of known-key attacks and that allows to generically analyze the impact of various weaknesses of blockciphers on various blockcipher- and permutation-based cryptosystems.

Model. A naive approach to analyzing the impact of known-key attacks would be to simply plug a certain blockcipher construction into a hash function and to analyze its security, but this would be a devious and complex combinatorial task: for a function based on r permutations, plugging Feistel$_7$ into it would lead to 7r underlying primitive calls. Note that proving security of the Feistel construction itself is already extraordinarily hard [16, 24, 32]. Instead, we model the blockciphers in such a way that they behave randomly, except that an adversary can exploit the particular relation. More formally, we pose a certain predicate $\varPhi$, and we draw blockciphers randomly from the set of all ciphers that comply with predicate $\varPhi$. Throughout, we refer to this model as the “weak cipher model (WCM).” It corresponds to the ideal cipher model if $\varPhi$ is trivial.

We present an explicit description of a random weak cipher for the case where $\varPhi$ implies for each key k the existence of A sets of B queries $\{(k,m^{1},c^{1}),\ldots ,(k,m^{B},c^{B})\}$ that comply with a certain condition $\varphi$. These ciphers are modeled to have three interfaces: forward queries, inverse queries, and predicate queries. Forward and inverse queries are as usual; on a predicate query, an adversary is given a set of B queries satisfying $\varphi$. Multiple technicalities are involved in this formalization. Most importantly, predicate $\varPhi$ applies to tuples of queries, rather than single queries only, and some query responses may have a reduced entropy.

Above-mentioned known-key attacks are covered by our model if the condition $\varphi$ states for some $C\subseteq \{1,\ldots ,n\}$ that

$$\begin{aligned} \mathsf {Bits}_{C}\left( m^{1}\oplus c^{1}\oplus \cdots \oplus m^{B}\oplus c^{B}\right) =0\,, \end{aligned}$$

(1)

where $\mathsf {Bits}_{C}(x)$ outputs a string consisting of all bits of x whose index is in C. (In fact, our model is much more general: above-mentioned attacks aim to generate only one relation, while we allow an adversary to see multiple relations.) The value A usually depends on n and C is regularly a large subset. We consider B being a relatively small number (independent of n). For the above-mentioned attack on Feistel$_7$, $A=2^{n/2}$, $B=2$, and C corresponds to the rightmost n / 2 bits. Similarly, the attacks on AES$_8$ (for $A=2^{n/8}$, $B=2$, and C a certain set of size 10n / 16) and Threefish$_{36}$ (for $A=2^{n/8}$, $B=4$, and $C=\{1,\ldots ,n\}$) are covered, and so are almost all known differential (rebound- or boomerang-based) known-key attacks. We remark that, on the other hand, the predicate is not well-suited for integral-based known-key attacks: upon a predicate query an attacker would receive $B\approx 2^n$ queries.

The weak cipher model is similar to an approach followed by Bresson et al. [15] for the indifferentiability analysis of the SHA-3 candidate Shabal if the underlying blockcipher shows some non-random behavior, and by Bouillaguet et al. [13] to analyze the indifferentiability security of SIMD when the underlying compression function is distinguishable from a random function. However, in both approaches, the underlying biased primitives were relatively easy to model. For instance in [15] (using our terminology), predicate $\varPhi$ is a relation that holds for single queries only, and not for combinations of queries. This considerably simplifies the analysis: one can derive a bias $\beta$ to measure the distance between primitive responses and fully random responses, and consider oracle responses to be drawn from a set of size at least $2^{n-\beta }$, and the original indifferentiability analysis carries over with minor modifications. The predicate used in the analysis in [13], on the other hand, does apply to tuples of queries, but the model can simply be described using two sampling algorithms, and an adversary cannot hit a weak pair by accident (which is possible in our analysis). Liskov [35] used a similar approach to prove indifferentiability security of the zipper hash if the underlying compression function is invertible up to a certain degree. However, the analysis is significantly simpler, as this primitive can be perfectly modeled. We finally remark that Katz et al. [26] analyze the impact of related-key attacks on blockciphers to hash functions. However, in their model, the differences $\varDelta k,\varDelta x,\varDelta y$ are fixed, an ideal cipher is generated for half of the key space, and for the other half the cipher is adjusted as $\mathsf {E}_k(x,y)=\mathsf {E}_{k\oplus \varDelta k}(x\oplus \varDelta x) \oplus \varDelta _y$. This primitive can be easily modeled, but is also too generous to the attacker.

To our knowledge, this is the first attempt to formally analyze the effect of a wide class of blockcipher attacks on higher level cryptographic functions. Nonetheless, the weak cipher model is in essence still a model: we use an abstraction of the cryptanalytic known-key attacks in such a way that the ideal cipher model can be relaxed to cope them. A further discussion on the accuracy of the model is given in Sect. 7.

Table 1. Security results for the PGV, Grøstl, and Shrimpton-Stam compression functions in the weak cipher model. Ideal cipher/permutation model bounds match the ones of $B\ge 3$. All results are tight except for the case $(B=1,|C|>n/2)$ for Shrimpton-Stam.

Application to Blockcipher-Based Hash Functions. Preneel, Govaerts, and Vandewalle (PGV) [48] classified the 64 most basic ways of constructing a 2n-to-n-bit compression function from a blockcipher with n-bit key and n-bit state, and claimed security of 12 of them. A formal security analysis of these functions in the ICM has been performed by Black et al. [9], and later by Duo and Li [19], Stam [58], and Black et al. [10]. In more detail, in the ICM these constructions achieve tight collision security up to about $2^{n/2}$ queries and preimage security up to about $2^n$ queries. Baecher et al. [4] recently showed that the 12 secure PGV functions can be divided into two classes, in such a way that if a primitive makes one function secure it makes the entire class secure.

As first application of our model, we consider the PGV compression functions in the WCM and derive collision and preimage bounds for general (A, B, C). A schematic summary of the results for various B and C is given in Table 1 (we remark that A is merely a technical parameter that has no influence on the results). We also show that the bounds are optimal, by providing matching attacks. Some of these attacks are similar to methods used in [27, 53, 56] to detect (near-)collisions in certain PGV modes of operations using known-key attacks.

Application to Permutation-Based Hash Functions. We also apply the WCM to permutation-based compression functions. This is particularly interesting for two reasons: (i) it allows us to understand the impact of distinguishers on permutations that are used in hash functions, and (ii) a blockcipher with a fixed and known key is a permutation and can be used as such. In more detail, we consider the Grøstl compression function [21] and the permutation-based equivalent of the Shrimpton-Stam compression function [57] (see also Fig. 4). In the IPM, the former is proven to achieve collision security up to $2^{n/4}$ queries, where n is the state size, and preimage security up to $2^{n/2}$ [20]. Rogaway and Steinberger [51] showed via an automated analysis that the latter function is collision and preimage resistant up to $2^{n/2}$ queries (asymptotically). This has been confirmed in the generalized work of Mennink and Preneel [41].

A summary of our findings for the Grøstl and Shrimpton-Stam compression functions in the WCM is given in Table 1. All results are tight, except for the case $(B=1,|C|>n/2)$ for Shrimpton-Stam, for which we leave proving tightness as an open problem. We remark that the analysis for these schemes is much more demanding as multiple primitives are involved.

Impact. An application of our formalization to the PGV functions and various permutation-based functions shows that these achieve a comparable level of security in the ideal and weak cipher model for a spectrum of choices for (A, B, C). This result particularly implies that most relevant rebound-based (including [12, 22, 28, 38, 52, 53, 56]) and boomerang-based (including [2, 7, 31, 54, 60]) known-key attacks known to date do not invalidate the security of such functions, or only have a little effect. For instance, the above-discussed attack on Feistel$_7$ satisfies $B=2$ and $|C|=n/2$ and it does not affect the security; similarly for Threefish$_{36}$ for which $B=4$. The attack on AES$_8$ is covered for $B=2$ and $|C|=10n/16$, which demonstrates a slight security degradation to $2^{6n/16}$ for the PGV functions, but this may in part be due to our over-generosity to the adversary. We remark that, even though we focused on collision and preimage resistance, the techniques can be generalized to other security notions, such as near-collisions. This may entail differences in the security results.

We stress that these results do not mean that the analyzed functions are secure when the underlying permutations are instantiated with, say, Feistel$_7$ or Threefish$_{36}$: it only means that existing known-key attacks, or more general weaknesses such as relation (1), alone are not sufficient to invalidate the collision and preimage security of the construction. Indeed, more sophisticated attacks which are not yet covered by our application of the WCM may still invalidate the security of certain modes [6]. It remains a challenging open research problem to generalize the findings to underlying primitives that have multiple or different weaknesses.

1.2 Outline

In Sect. 2, we formally present the “weak cipher model,” and in Sect. 3 we show how it relates to known-key attacks. We apply the model to the PGV functions in Sect. 4, to the Grøstl compression function in Sect. 5, and to Shrimpton-Stam in Sect. 6. We conclude this work in Sect. 7.

2 Weak Cipher Model

If X is a set, by $x\xleftarrow {{\scriptscriptstyle \$}}X$ we denote the uniformly random sampling of an element from X. By $X\xleftarrow {{\scriptscriptstyle \cup }}x$, we denote $X\leftarrow X\cup \{x\}$. For a bit string x, its bits are numbered $x=x_{|x|}\cdots x_2x_1$. If $C\subseteq \{1,\ldots ,|x|\}$, the function $\mathsf {Bits}_{C}(x)$ outputs a string consisting of all bits of x whose index is in C. Abusing notation, $\mathsf {Bits}_{\overline{C}}(x)$ always denotes the remaining bits (technically, $\overline{C}=\{1,\ldots ,|x|\}\backslash C$). For $0\le r\le |x|$, we consider $\mathsf {Ri}_{r}(x)$ that outputs the $r$ rightmost bits of x. In other words, $\mathsf {Ri}_{r}(x)=\mathsf {Bits}_{\{1,\ldots ,r\}}(x)$. For a function f, by $\mathsf {dom}(f)$ and $\mathsf {rng}(f)$ we denote its domain and range, respectively.

2.1 Security Model

For $\kappa \ge 0$ and $n\ge 1$, by $\mathrm {BC}(\kappa ,n)$ we denote the set of all blockciphers with $\kappa$-bit key operating on n bits. If $\kappa =0$, $\mathrm {BC}(n):=\mathrm {BC}(0,n)$ denotes the set of all n-bit permutations. If $\varPhi$ is a predicate, by $\mathrm {BC}[\varPhi ](\kappa ,n)$ we denote the subset of ciphers of $\mathrm {BC}(\kappa ,n)$ that satisfy predicate $\varPhi$. For $\pi \in \mathrm {BC}[\varPhi ](\kappa ,n)$, the input-output tuples are denoted (k, x, z), where $\pi (k,x)=\pi _k(x)=z$ and $\pi ^{-1}(k,z)=\pi _k^{-1}(z)=x$. The key k is omitted in case $\kappa =0$.

Let $\mathsf {F}:\{0,1\}^{s}\rightarrow \{0,1\}^{n}$ be a compressing function instantiated with $\ell \ge 1$ primitives from $\mathrm {BC}[\varPhi ](\kappa ,n)$, for some predicate $\varPhi$. Throughout, we consider security of $\mathsf {F}$ in an idealized model: we consider an adversary $\mathcal {A}$ that is a probabilistic algorithm with oracle access to a randomly sampled primitive $\varvec{\pi }=(\pi _1,\ldots ,\pi _\ell )\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi ](\kappa ,n)^\ell$. $\mathcal {A}$ is information-theoretic and its complexity is only measured by the number of queries made to its oracles. The adversary can make forward and inverse queries to its oracles, and these queries are stored in a query history $\mathcal {Q}$.

A collision-finding adversary $\mathcal {A}$ for $\mathsf {F}$ aims at finding two distinct inputs to $\mathsf {F}$ that compress to the same range value. In more detail, we say that $\mathcal {A}$ succeeds if it finds two distinct inputs $X,X'$ such that $\mathsf {F}(X)=\mathsf {F}(X')$ and $\mathcal {Q}$ contains all queries required for these evaluations of $\mathsf {F}$. We define by

$$\begin{aligned} \mathbf {Adv}_{\mathsf {F}}^{\mathrm {col}}(\mathcal {A}) = \mathbf {Pr}\left( \varvec{\pi }\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi ](\kappa ,n)^\ell ,\,X,X'\leftarrow \mathcal {A}^{\varvec{\pi }} \,:\, X\ne X' \,\wedge \, \mathsf {F}(X)=\mathsf {F}(X') \right) \end{aligned}$$

the probability that $\mathcal {A}$ succeeds in this. By $\mathbf {Adv}_{\mathsf {F}}^{\mathrm {col}}(q)$ we define the maximum collision advantage taken over all adversaries making q queries.

For preimage resistance, we focus on everywhere preimage resistance [50], which captures preimage security for every point of $\{0,1\}^{n}$. Let $Z\in \{0,1\}^{n}$ be any range value. Then, we say that $\mathcal {A}$ succeeds in finding a preimage if it obtains an input X such that $\mathsf {F}(X)=Z$ and $\mathcal {Q}$ contains all queries required for this evaluation of $\mathsf {F}$. We define by

$$\begin{aligned} \mathbf {Adv}_{\mathsf {F}}^{\mathrm {epre}}(\mathcal {A}) = \max _{Z\,\in \,\{0,1\}^{n}} \mathbf {Pr}\left( \varvec{\pi }\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi ](\kappa ,n)^\ell ,\,X\leftarrow \mathcal {A}^{\varvec{\pi }}(Z) \ :\, \mathsf {F}(X)=Z \right) \end{aligned}$$

the probability that $\mathcal {A}$ succeeds, maximized over all possible choices for Z. By $\mathbf {Adv}_{\mathsf {F}}^{\mathrm {epre}}(q)$ we define the maximum (everywhere) preimage advantage taken over all adversaries making q queries.

If $\varPhi$ is a trivial relation, we have $\mathrm {BC}[\varPhi ](\kappa ,n)=\mathrm {BC}(\kappa ,n)$, and the above definitions boil down to security in the ideal cipher model (ICM) if $\kappa >0$ or the ideal permutation model (IPM) if $\kappa =0$. On the other hand, if $\varPhi$ is a non-trivial predicate, it strictly reduces the set $\mathrm {BC}(\kappa ,n)$. In this case, we will refer to the model as the “weak cipher model (WCM),” for both $\kappa >0$ and $\kappa =0$. Very informally, this model still involves random ciphers/permutations, with the difference that an adversary may exploit a certain additional property. The modeling of a randomly drawn weak ciphers is much more delicate.

2.2 Random Weak Cipher

For a certain class of predicates, we discuss how to model a randomly drawn weak cipher $\pi$ from $\mathrm {BC}[\varPhi ](\kappa ,n)$. Let $A,B\in \mathbb {N}$. We will consider predicates that imply, for every $k\in \{0,1\}^{\kappa }$, the existence of A sets of B distinct queries $\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}$ that satisfy $\varphi _k\big (\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}\big )$ for some condition $\varphi$ depending on key k. The predicate is denoted $\varPhi (A,B,\varphi )$. A is merely a technical parameter, and throughout we assume it is larger than q, the number of oracle calls an adversary can make. This definition of $\varPhi (A,B,\varphi )$ is fairly general. Particularly, predicate B-sets may overlap and the condition $\varphi$ can represent any function on the inputs. We note that $\varPhi$ can be easily generalized to tuples of different length and/or to multiple types of conditions at the same time.

Traditionally, an adversary has only forward $\pi _k(x)$ and inverse $\pi _k^{-1}(z)$ query access. In order for the adversary to be able to exploit the weakness present in $\pi$, we give it additional access to $\pi$ via a “predicate query” $\pi ^\varPhi _k(y)$: on input of $y\in \{1,\ldots ,A\}$, the adversary obtains a B-set $\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}$ that satisfies $\varphi _k\big (\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}\big )$.

A formal description of how to model $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi )](\kappa ,n)$ is given in Fig. 1. Here, for every $k\in \{0,1\}^{\kappa }$, $P_k$ is an initially empty list of $\pi _k$-evaluations, where a regular forward/inverse query adds one element (x, z) to $P_k$ and a $\pi ^\varPhi _k$-query may add up to B elements. Additionally, $P^\varPhi _k$ is an initially empty list of queries to $\pi ^\varPhi _k$. We denote by $\varSigma _k(P_k,P^\varPhi _k)\subseteq \left( \{0,1\}^{n}\times \{0,1\}^{n}\right) ^B$ the set of all tuples $\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}$ such that

• (i) $x^{1},\ldots ,x^{B}$ are pairwise distinct and $z^{1},\ldots ,z^{B}$ are pairwise distinct;

• (ii) $\forall _{\ell =1}^B:\;$ $x^{\ell }\in \mathsf {dom}(P_k) \Longrightarrow z^{\ell }=P_k(x^{\ell })$ and $z^{\ell }\in \mathsf {rng}(P_k) \Longrightarrow x^{\ell }=P_k^{-1}(z^{\ell })$;

• (iii) $\varphi _k\big (\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}\big )$ holds;

• (iv) $\{(x^{p(1)},z^{p(1)}),\ldots ,(x^{p(B)},z^{p(B)})\}\not \in \mathsf {rng}(P^\varPhi _k)$ for any permutation p on $\{1,\ldots ,B\}$.

For a new query $\pi ^\varPhi _k(y)$, the response is then randomly drawn from $\varSigma _k(P_k,P^\varPhi _k)$. Conditions (i–iii) are fairly self-evident; note particularly that an existing $(x,z)\in P_k$ may appear in multiple predicate queries. Condition (iv) assures that the drawing from $\varSigma _k(P_k,P^\varPhi _k)$ is not just an old predicate query or a reordering thereof. The usage of this set $\varSigma _k(P_k,P^\varPhi _k)$ allows for a uniform behavior of $\pi ^\varPhi _k$ for every k, and in general of $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi )](\kappa ,n)$, modulo the known existence of condition $\varphi$. This step is fundamental to our model and new compared with previous approaches of [13, 15, 35]. We remark that the model allows adversaries to make their queries at their own discretion, e.g., duplicate queries and regular queries after predicate queries are allowed.

Fig. 1.

Random weak cipher $\pi$. An adversary has access to $\pi ,\pi ^{-1}$, and $\pi ^\varPhi$.

2.3 Random Abortable Weak Cipher

Security analyses in the WCM are significantly more complex than in the ICM or IPM, which is in part because predicate queries may consist of older queries. This will particularly be an issue once collisions among queries are investigated. To suit the analysis for this case, we transform the WCM to an abortable weak cipher model (AWCM), which we denote as $\overline{\mathrm {BC}}[\varPhi (A,B,\varphi )](\kappa ,n)$. At a high-level, an abortable weak cipher responds to predicate queries with new query tuples only, and aborts once it turns out that an older query appears in a newer predicate query.

For any $k\in \{0,1\}^{\kappa }$ and partial $P_k$ and $P^\varPhi _k$, define by $\bar{\varSigma }_k(P^\varPhi _k)\subseteq \left( \{0,1\}^{n}\times \{0,1\}^{n}\right) ^B$ the set of all tuples $\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}$ such that

• (iii) $\varphi _k\big (\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}\big )$ holds;

• (iv) $\{(x^{p(1)},z^{p(1)}),\ldots ,(x^{p(B)},z^{p(B)})\}\not \in \mathsf {rng}(P^\varPhi _k)$ for any permutation p on $\{1,\ldots ,B\}$.

$\bar{\varSigma }_k(P^\varPhi _k)$ differs from $\varSigma (P_k,P^\varPhi _k)$ in that conditions (i) and (ii) are omitted, and particularly: it is independent of $P_k$. A formal description of a random cipher $\bar{\pi }\xleftarrow {{\scriptscriptstyle \$}}\overline{\mathrm {BC}}[\varPhi (A,B,\varphi )](\kappa ,n)$ is given in Fig. 2. It deviates from Fig. 1 as follows: for every key k, $\bar{\pi }^\varPhi _k$ responds randomly from $\bar{\varSigma }_k(P^\varPhi _k)$, and it aborts if the response violates one of the two skipped conditions of $\varSigma _k(P_k,P^\varPhi _k)$.

Fig. 2.

Random abortable weak cipher $\bar{\pi }$. An adversary has access to $\bar{\pi },\bar{\pi }^{-1}$, and $\bar{\pi }^\varPhi$.

The next lemma shows that the WCM and AWCM are indistinguishable as long as the abortable weak r cipher does not abort, approximately up to the birthday bound. Here, we assume that $\bar{\varSigma }_k(P^\varPhi _k)$ is always large enough.

Lemma 1

Let $\bar{\pi }\xleftarrow {{\scriptscriptstyle \$}}\overline{\mathrm {BC}}[\varPhi (A,B,\varphi ^C)](\kappa ,n)$. Consider an adversary that makes q queries to $\bar{\pi }$. Then,

$$\begin{aligned} \mathbf {Pr}\left( \bar{\pi }\textit{ sets }\mathsf {abort}\right) \le \frac{B^2q(q+1)}{2^n - \frac{B!q2^n}{|\bar{\varSigma }_k(\varnothing )|}}\,. \end{aligned}$$

Proof

Consider the $i^\mathrm{th}$ query, for $i\in \{1,\ldots ,q\}$, and assume it is a predicate query $\bar{\pi }^\varPhi _k(y)$. We will consider the probability that this query makes $\bar{\pi }$ abort, provided it has not aborted so far. Prior to this $i^\mathrm{th}$ query, $|P_k|\le B(i-1)$ and $|P^\varPhi _k|\le i$. Basic combinatorics shows that

$$\begin{aligned} |\bar{\varSigma }_k(P^\varPhi _k)| = |\bar{\varSigma }_k(\varnothing )| - B!\cdot |P^\varPhi _k|\,, \end{aligned}$$

where we use that $\bar{\pi }$ has not aborted so far. This $i^\mathrm{th}$ query aborts only if for some $\ell \in \{1,\ldots ,B\}$, the value $x^{\ell }$ equals an element in $\mathsf {dom}(P_k)\cup \{x^{1},\ldots ,x^{\ell -1}\}$ or the value $z^{\ell }$ equals an element in $\mathsf {rng}(P_k)\cup \{z^{1},\ldots ,z^{\ell -1}\}$.

Define by $\bar{\varSigma }_k^{\mathsf {abort}}(P^\varPhi _k)$ the set of all elements of $\bar{\varSigma }_k(P^\varPhi _k)$ that would lead to $\mathsf {abort}$. We have 2B possible values to cause the abort (namely, $x^{1},\ldots ,z^{B}$), and it causes the abort if it equals an element in a set of size at most $|P_k|+B$. For any of these $2B(|P_k|+B)$ choices, the number of tuples in $\bar{\varSigma }_k(P^\varPhi _k)$ complying with this choice is at most $\frac{|\bar{\varSigma }_k(\varnothing )|}{2^n}$. Thus,

$$\begin{aligned} \mathbf {Pr}\left( \bar{\pi }^\varPhi (y) \text { sets }\mathsf {abort}\right)&= \frac{|\bar{\varSigma }_k^{\mathsf {abort}}(P^\varPhi _k)|}{|\bar{\varSigma }_k(P^\varPhi _k)|} \le \frac{2B(|P_k|+B)\cdot \frac{|\bar{\varSigma }_k(\varnothing )|}{2^n}}{|\bar{\varSigma }_k(\varnothing )| - B!\cdot |P^\varPhi _k|} \le \frac{2B^2i}{2^n - \frac{B!q2^n}{|\bar{\varSigma }_k(\varnothing )|}}\,. \end{aligned}$$

The proof is completed by summation over $i=1,\ldots ,q$.$\quad \square$

3 Modeling Known-Key Attacks

We next apply the WCM to known-key attacks. For the sake of explanation, we first reconsider the Knudsen-Rijmen attack on Feistel$_7$ [27]. (A detailed description of the attack is also given in the full version of this paper.) Let $n\in \mathbb {N}$, and let $\pi :=\pi _k$ be an instance of Feistel$_7$ with fixed key k. Knudsen and Rijmen revealed four functions $f,f',g,g':\{0,1\}^{n/2}\rightarrow \{0,1\}^{n}$ such that for all $y\in \{0,1\}^{n/2}$:

$$\begin{aligned}&g(y)=\pi (f(y)) \text { and } g'(y)=\pi (f'(y))\,, \nonumber \\&\mathsf {Ri}_{n/2}\left( f(y)\oplus g(y)\right) = \mathsf {Ri}_{n/2}\left( f'(y)\oplus g'(y)\right) . \end{aligned}$$

(2)

These four functions depend on the cryptographic primitive underlying Feistel$_7$ in a complicated way. Therefore, we can safely assume that these functions behave sufficiently random, besides this particular relation (2), and that they are unknown to the adversary. $f,f',g,g'$ are all injective and satisfy $f(y)\ne f'(y)$ and $g(y)\ne g'(y)$ for all y. On the other hand, collisions of the form $f(y)=f'(y')$ and $g(y)=g'(y')$ may occur.

Generically, the attack demonstrates that for key k there exist $2^{n/2}$ possibly overlapping sets of distinct queries $\{(x^{1},z^{1}),(x^{2},z^{2})\}$ that satisfy $\mathsf {Ri}_{n/2}\big (x^{1}\oplus z^{1}\oplus x^{2}\oplus z^{2}\big )=0$. In other words, Feistel$_7$ meets predicate $\varPhi (2^{n/2},2,\varphi ^{\mathrm {Feistel}_7})$, where

$$\begin{aligned} \varphi ^{\mathrm {Feistel}_7}_k\big (\{(x^{1},z^{1}),(x^{2},z^{2})\}\big )\;:\; \mathsf {Ri}_{n/2}\left( x^{1}\oplus z^{1}\oplus x^{2}\oplus z^{2}\right) =0\,. \end{aligned}$$

Here, we remark that the Knudsen-Rijmen attack works for any fixed but known key k, and that condition $\varphi ^{\mathrm {Feistel}_7}_k$ is in fact independent of the key. In this work, we will consider a more general predicate $\varPhi (A,B,\varphi ^C)$ for $A,B\in \mathbb {N}$ and $C\subseteq \{1,\ldots ,n\}$, where

$$\begin{aligned} \varphi ^C_k\big (\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}\big )\;:\; \mathsf {Bits}_{C}\left( x^{1}\oplus z^{1}\oplus \cdots \oplus x^{B}\oplus z^{B}\right) =0\,. \end{aligned}$$

(3)

This generalized predicate considers the case of arbitrary but fixed and known keys, where the adversary can even choose the key every time it makes a predicate query. Note that also the attacks on AES$_8$ and Threefish$_{36}$ (see Sect. 1) are covered, as they satisfy $\varPhi (2^{n/8},2,\varphi ^C)$ for certain C of size 10n / 16 and $\varPhi (2^{n/8},4,\varphi ^{\{1,\ldots ,n\}})$, respectively. In general, all rebound- or boomerang-based known-key attack in literature are covered by predicate $\varPhi (A,B,\varphi ^C)$ for some A, B, C. Here, B is always a value independent of n (usually 2 or 4) and C is regularly a large subset (of size at least n / 4). Throughout, we consider A to be sufficiently large.

3.1 Basic Computations for AWCM

For the specific condition $\varphi ^C$ of (3), we derive a simpler bound on the probability that a primitive $\bar{\pi }\xleftarrow {{\scriptscriptstyle \$}}\overline{\mathrm {BC}}[\varPhi (A,B,\varphi ^C)](\kappa ,n)$ aborts, along with some other elementary observations for $\bar{\pi }$. To this end, we define the notation “[X],” which equals 1 if X holds and 0 otherwise. For conciseness, we introduce the function $\delta _{B,C}[b]$ defined as

$$\begin{aligned} \delta _{B,C}[b]=2^{|C|}[B=b]+[B>b]\,. \end{aligned}$$

(4)

Lemma 2

Let $\bar{\pi }\xleftarrow {{\scriptscriptstyle \$}}\overline{\mathrm {BC}}[\varPhi (A,B,\varphi ^C)](\kappa ,n)$. Consider an adversary that makes $q\le 2^{n-1}/B$ queries to $\bar{\pi }$. Then,

$$\begin{aligned} \mathbf {Pr}\left( \bar{\pi }\textit{ sets }\mathsf {abort}\right) \le \frac{B^2q(q+1)}{2^n - Bq}\,. \end{aligned}$$

(5)

Let $k\in \{0,1\}^{\kappa }$ and let $Z,Z',Z''\in \{0,1\}^{n}$. Consider any new query $\bar{\pi }^\varPhi _k(y)$ and assume it does not abort. Write the response as $\{(x^{1},z^{1}),\ldots ,(x^{B},z^{B})\}$. Then,

• (i) $\forall \;a\in \{1,\ldots ,B\}:\; \mathbf {Pr}\left( x^{a}=Z\right)$, $\mathbf {Pr}\left( z^{a}=Z\right) \le \frac{1}{2^n-Bq}$;

• (ii) $\forall \;a\in \{1,\ldots ,B\}:\; \mathbf {Pr}\left( x^{a}\oplus z^{a}=Z\right) \le \frac{\delta _{B,C}}{2^n-Bq}$;

• (iii) $\forall \;\{a,b\}\subseteq \{1,\ldots ,B\}:\; \mathbf {Pr}\left( x^{a}\oplus z^{a}=Z \wedge x^{b}\oplus z^{b}=Z'\right) \le \frac{\delta _{B,C}[2]}{2^{2n}-Bq}$;

• (iv) .

Proof

Recall from the proof of Lemma 1 that

$$\begin{aligned} |\bar{\varSigma }_k(P^\varPhi _k)| = |\bar{\varSigma }_k(\varnothing )| - B!|P^\varPhi _k|\,, \end{aligned}$$

where $|P^\varPhi _k|\le q$. For the specific predicate analyzed in this lemma, $|\bar{\varSigma }_k(\varnothing )| = (2^n)^{2B-1}2^{n-|C|}$. In the remainder, we regularly bound $B!\le B\cdot (2^n)^{2B-2}$ for $B\ge 1$ or $B!\le B\cdot (2^n)^{2B-4}$ for $B\ge 2$.

Probability of Abortion. The bound of (5) directly follows from Lemma 1, the above-mentioned size of $\bar{\varSigma }_k(\varnothing )$, and the bound on B!.

Part (i). Define by $\bar{\varSigma }_k^{\mathrm {(i)}}(P^\varPhi _k)$ the set of all elements of $\bar{\varSigma }_k(P^\varPhi _k)$ that satisfy $x^{a}=Z$. Then, $|\bar{\varSigma }_k^{\mathrm {(i)}}(P^\varPhi _k)| \le (2^n)^{2B-2}2^{n-|C|}$, and

$$\begin{aligned} \mathbf {Pr}\left( x^{a}=Z\right) = \frac{|\bar{\varSigma }_k^{\mathrm {(i)}}(P^\varPhi _k)|}{|\bar{\varSigma }_k(P^\varPhi _k)|} \le \frac{1}{2^n-Bq}\,. \end{aligned}$$

A similar analysis applies to the case $z^{a}=Z$.

Part (ii). Define by $\bar{\varSigma }_k^{\mathrm {(ii)}}(P^\varPhi _k)$ the set of all elements of $\bar{\varSigma }_k(P^\varPhi _k)$ that satisfy $x^{a}\oplus z^{a}=Z$. We make a distinction between $B=1$ and $B>1$. In case $B>1$, a similar reasoning as in (i) applies, and we have $|\bar{\varSigma }_k^{\mathrm {(ii)}}(P^\varPhi _k)| \le (2^n)^{2B-2}2^{n-|C|}$. On the other hand, if $B=1$, we have $|\bar{\varSigma }_k^{\mathrm {(ii)}}(P^\varPhi _k)| = 0$ if $\mathsf {Bits}_{C}(Z)\ne 0$ and $|\bar{\varSigma }_k^{\mathrm {(ii)}}(P^\varPhi _k)|\le 2^n$ if $\mathsf {Bits}_{C}(Z)=0$. In any case,

$$\begin{aligned} |\bar{\varSigma }_k^{\mathrm {(ii)}}(P^\varPhi _k)| \le (2^n)^{2B-2}2^{n-|C|}\delta _{B,C}[1]\,, \end{aligned}$$

and

$$\begin{aligned} \mathbf {Pr}\left( x^{a}\oplus z^{a}=Z\right) = \frac{|\bar{\varSigma }_k^{\mathrm {(ii)}}(P^\varPhi _k)|}{|\bar{\varSigma }_k(P^\varPhi _k)|} \le \frac{\delta _{B,C}[1]}{2^n-Bq}\,. \end{aligned}$$

Part (iii). This part only applies to $B>1$; if $B=1$ the probability equals 0 by construction. Define by $\bar{\varSigma }_k^{\mathrm {(iii)}}(P^\varPhi _k)$ the set of all elements of $\bar{\varSigma }_k(P^\varPhi _k)$ that satisfy $x^{a}\oplus z^{a}=Z$ and $x^{b}\oplus z^{b}=Z'$. We make a distinction between $B=2$ and $B>2$. In case $B>2$, a similar reasoning as in (i) and (ii) applies, and we have $|\bar{\varSigma }_k^{\mathrm {(iii)}}(P^\varPhi _k)| \le (2^n)^{2B-3}2^{n-|C|}$. On the other hand, if $B=2$, we have $|\bar{\varSigma }_k^{\mathrm {(iii)}}(P^\varPhi _k)| = 0$ if $\mathsf {Bits}_{C}(Z\oplus Z')\ne 0$ and $|\bar{\varSigma }_k^{\mathrm {(iii)}}(P^\varPhi _k)|\le (2^n)^2$ if $\mathsf {Bits}_{C}(Z\oplus Z')=0$. In any case,

$$\begin{aligned} |\bar{\varSigma }_k^{\mathrm {(iii)}}(P^\varPhi _k)| \le (2^n)^{2B-3}2^{n-|C|}\delta _{B,C}[2]\,, \end{aligned}$$

and

$$\begin{aligned} \mathbf {Pr}\left( x^{a}\oplus z^{a}=Z \wedge x^{b}\oplus z^{b}=Z'\right) = \frac{|\bar{\varSigma }_k^{\mathrm {(iii)}}(P^\varPhi _k)|}{|\bar{\varSigma }_k(P^\varPhi _k)|} \le \frac{\delta _{B,C}[2]}{2^{2n}-Bq}\,. \end{aligned}$$

Part (iv). The approach is fairly similar to case (iii). If $B=1$ the probability is 0 by construction. Define by $\bar{\varSigma }_k^{\mathrm {(iv)}}(P^\varPhi _k)$ the set of all elements of $\bar{\varSigma }_k(P^\varPhi _k)$ that satisfy $x^{a}=Z$, $x^{b}=Z'$, and $x^{a}\oplus z^{a}\oplus x^{b}\oplus z^{b}=Z''$. In case $B>2$, we have $|\bar{\varSigma }_k^{\mathrm {(iv)}}(P^\varPhi _k)| \le (2^n)^{2B-4}2^{n-|C|}$. On the other hand, if $B=2$, we have $|\bar{\varSigma }_k^{\mathrm {(iv)}}(P^\varPhi _k)| = 0$ if $\mathsf {Bits}_{C}(Z'')\ne 0$ and $|\bar{\varSigma }_k^{\mathrm {(iv)}}(P^\varPhi _k)|\le 2^n$ if $\mathsf {Bits}_{C}(Z'')=0$. In any case,

$$\begin{aligned} |\bar{\varSigma }_k^{\mathrm {(iv)}}(P^\varPhi _k)| \le (2^n)^{2B-4}2^{n-|C|}\delta _{B,C}[2]\,, \end{aligned}$$

and

$$\begin{aligned} \mathbf {Pr}\left( x^{a}=Z \wedge x^{b}=Z' \wedge x^{a}\oplus z^{a}\oplus x^{b}\oplus z^{b}=Z''\right) = \frac{|\bar{\varSigma }_k^{\mathrm {(iv)}}(P^\varPhi _k)|}{|\bar{\varSigma }_k(P^\varPhi _k)|} \le \frac{\delta _{B,C}[2]}{2^{3n}-Bq}\,. \end{aligned}$$

   $\square$

4 Application to PGV Compression Functions

We consider the 12 blockcipher-based compression functions from Preneel, Govaerts, and Vandewalle (PGV) [48]. In the ICM these constructions achieve tight collision security up to about $2^{n/2}$ queries and preimage security up to about $2^n$ queries [9, 10, 19, 58]. The 12 constructions are depicted in Fig. 3. Here, we follow the ordering of [10], where $\mathrm {PGV}1$, $\mathrm {PGV}2$, and $\mathrm {PGV}5$ are better known as the Matyas-Meyer-Oseas [36], Miyaguchi-Preneel, and Davies-Meyer [45] compression functions.

Fig. 3.

The 12 PGV compression functions. When in iteration mode, the message comes in at the top. The groups $G_1$ and $G_2$ refer to Lemma 3.

Baecher et al. [4] analyzed the 12 PGV constructions under ideal cipher reducibility, which at a high level covers the idea of two constructions being equally secure for the same underlying idealized blockcipher. They divide the PGV functions into two classes, in such a way that if some blockcipher makes one of the constructions secure, it makes all functions in the corresponding class secure. Applied to our WCM, the results of Baecher et al. imply the following:

Lemma 3

(Ideal Cipher Reducibility of PGV [4], informal). Let $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi ](n,n)$ for some predicate $\varPhi$. Let

$$\begin{aligned} G_1 = \{1,4,5,8,9,12\}\,,\textit{ and } G_2 = \{2,3,6,7,10,11\}\,. \end{aligned}$$

For any $\alpha \in \{1,2\}$ and $i,j\in G_{\alpha }$, $\mathrm {PGV}i$ and $\mathrm {PGV}j$ achieve the same level of collision and preimage security once instantiated with $\pi$.

Baecher et al. also derive a reduction between the two classes, but this reduction requires a non-direct transformation on the ideal cipher $\pi$ ¹, making it unsuitable for our purposes. Thanks to Lemma 3, it suffices to only analyze $\mathrm {PGV}1$ and $\mathrm {PGV}2$ in the WCM: the bounds carry over to the other 10 PGV constructions. In Sect. 4.1 we analyze the collision security of these functions in the WCM. The preimage security is considered in Sect. 4.2.

4.1 Collision Security

Theorem 1

Let $n\in \mathbb {N}$. Let $\alpha \in \{1,2\}$ and consider $\mathrm {PGV}\alpha$. Suppose $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n,n)$. Then, for $q\le 2^{n-1}/B$,

$$\begin{aligned} \mathbf {Adv}_{\mathrm {PGV}\alpha }^{\mathrm {col}}(q) \le \frac{B^2\delta _{B,C}[1]q^2}{2^n} + {B\atopwithdelims ()2}\frac{2\delta _{B,C}[2]q}{2^n} + \frac{4B^2q^2}{2^n}\,. \end{aligned}$$

Proof

We focus on $\mathrm {PGV}2$. The analysis for $\mathrm {PGV}1$ is a simplification due to the absence of the feed-forward of the key. We consider any adversary that has query access to $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n,n)$ and makes q queries. As a first step, we move from $\pi$ to $\bar{\pi }\xleftarrow {{\scriptscriptstyle \$}}\overline{\mathrm {BC}}[\varPhi (A,B,\varphi ^C)](n,n)$. By Lemma 2, this costs us an additional term $\frac{B^2q(q+1)}{2^n-Bq}$.

A collision for $\mathrm {PGV}2$ would imply the existence of two distinct query pairs $(k_{},x_{},z_{}),(k_{}',x_{}',z_{}')$ such that $k\oplus x\oplus z = k'\oplus x'\oplus z'$. We consider the $i^{\mathrm{th}}$ query ($i\in \{1,\ldots ,q\}$) to be the first query to make this condition satisfied, and sum over $i=1,\ldots ,q$ at the end. For regular (forward or inverse) queries, the analysis of [9, 10, 58] mostly carries over. The analysis of predicate queries is a bit more technical.

Query $\varvec{\bar{\pi }_k(x)}$ or $\varvec{\bar{\pi }_k^{-1}(z)}$ . The cases are the same by symmetry, and we consider $\bar{\pi }_k(x)$ only. Denote the response by z. There are at most $B(i-1)$ possible $(k_{}',x_{}',z_{}')$. As z is randomly drawn from a set of size at least $2^n-Bq$, it satisfies $z=k\oplus x\oplus k'\oplus x'\oplus z'$ with probability at most $\frac{B(i-1)}{2^n-Bq}$.

Query $\varvec{\bar{\pi }^\varPhi _k(y)}$ . Denote the query response by $\{(k,x^{1},z^{1}),\ldots ,(k,x^{B},z^{B})\}$. In case the B-set contributes only to $(k_{},x_{},z_{})$, the same reasoning as for regular queries applies with the difference that any query of the B-set may be successful and that the bound of Lemma 2 part (ii) applies: $\frac{B^2\delta _{B,C}[1](i-1)}{2^n-Bq}$.

Now, consider the case the predicate query contributes to both $(k_{},x_{},z_{})$ and $(k_{},x_{}',z_{}')$. There are ${B\atopwithdelims ()2}$ ways for the predicate query to contribute (or 0 if $B=1$). By Lemma 2 part (iii), which considers the success probability for any such combination, the predicate query results in a collision with probability at most ${B\atopwithdelims ()2}\frac{\delta _{B,C}[2]2^n}{2^{2n}-Bq}$.

Conclusion. Taking the maximum of all success probabilities, the $i^{\mathrm{th}}$ query is successful with probability at most $\frac{B^2\delta _{B,C}[1](i-1)}{2^n-Bq} + {B\atopwithdelims ()2}\frac{\delta _{B,C}[2]2^n}{2^{2n}-Bq}$. Summation over $i=1,\ldots ,q$ gives

$$\begin{aligned} \mathbf {Adv}_{\mathrm {PGV}2}^{\mathrm {col}}(q) \le \frac{B^2\delta _{B,C}[1]q^2}{2(2^n-Bq)} + {B\atopwithdelims ()2}\frac{\delta _{B,C}[2]q}{2^n-Bq} + \frac{B^2q(q+1)}{2^n-Bq}\,, \end{aligned}$$

where the last part of the bound comes from the transition from WCM to AWCM. The proof is completed by using the fact that $2^n-Bq\ge 2^{n-1}$ for $Bq\le 2^{n-1}$, and that $q+1\le 2q$ for $q\ge 1$. $\quad \square$

We note that the bound gets worse for increasing values of B. This has a technical cause: predicate queries are counted equally expensive as regular queries, but result in up to B new query tuples. This leads to several factors of B in the bound. As this work is mainly concerned with differential known-key attacks for which B is regularly small, these factors are of no major influence.

The implications of the bound of Theorem 1 become more visible when considering particular choices of B and C.

• (i) If $B=1$, then $\mathbf {Adv}_{\mathrm {PGV}\alpha }^{\mathrm {col}}(q) \le \frac{2^{|C|}q^2}{2^n} + \frac{4q^2}{2^n}$;

• (ii) If $B=2$, then $\mathbf {Adv}_{\mathrm {PGV}\alpha }^{\mathrm {col}}(q) \le \frac{20q^2}{2^n} + \frac{4\cdot 2^{|C|}q}{2^n}$;

• (iii) If $B\ge 3$ (independent of n), then $\mathbf {Adv}_{\mathrm {PGV}\alpha }^{\mathrm {col}}(q) \le \frac{5B^2q^2}{2^n} + \frac{B^2q}{2^n}$.

In other words, for $B=2$ and C with $|C|\le n/2$, or for $B\ge 3$ constant and C arbitrary, the PGV functions achieve the same $2^{n/2}$ collision security level as in the ICM. On the other hand, if $B=1$, collisions can be found in about $2^{(n-|C|)/2}$ queries, and if $B=2$ with $|C|>n/2$, in about $2^{n-|C|}<2^{n/2}$ queries. See also Table 1.

4.2 Tightness

For the cases $B=1$ and C arbitrary, and $B=2$ and C arbitrary such that $|C|>n/2$, we derive generic attacks that demonstrate tightness of the bound of Theorem 1. Knudsen and Rijmen [27] and Sasaki et al. [53, 56] already considered how to exploit a known-key pair for the underlying blockcipher to find a collision for the Matyas-Meyer-Oseas ($\mathrm {PGV}1$) and/or Miyaguchi-Preneel ($\mathrm {PGV}2$) compression functions. Their attacks correspond to our $B=2$ case.

Proposition 1

( $\varvec{B=1}$ ). Let $n\in \mathbb {N}$. Let $\alpha \in \{1,2\}$ and consider $\mathrm {PGV}\alpha$. Suppose $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,1,\varphi ^C)](n,n)$. Then, $\mathbf {Adv}_{\mathrm {PGV}\alpha }^{\mathrm {col}}(q)\ge \frac{q^2}{2^{n-|C|}}$.

Proof

We construct a collision-finding adversary $\mathcal {A}$ for $\mathrm {PGV}2$. It fixes key $k=0$, and makes predicate queries to $\pi ^\varPhi _k$ on input of distinct values y to obtain q queries $(k,x_y,z_y)$ satisfying $\mathsf {Bits}_{C}(x_y\oplus z_y)=0$. Any two such queries collide on the entire state, $k\oplus x_y\oplus z_y = k\oplus x_{y'}\oplus z_{y'}$, with probability at least $\frac{q^2}{2^{n-|C|}}$. The attack for $\mathrm {PGV}1$ is the same as we have taken $k=0$. $\quad \square$

Proposition 2

( $\varvec{B=2\,}$ and $\varvec{|C|>n/2}$ ). Let $n\in \mathbb {N}$. Let $\alpha \in \{1,2\}$ and consider $\mathrm {PGV}\alpha$. Suppose $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,2,\varphi ^C)](n,n)$. Then, $\mathbf {Adv}_{\mathrm {PGV}\alpha }^{\mathrm {col}}(q)\ge \frac{q}{2^{n-|C|}}$.

Proof

We construct a collision-finding adversary $\mathcal {A}$ for $\mathrm {PGV}2$. It fixes key $k=0$, and makes predicate queries to $\pi ^\varPhi _k$ on input of distinct values y to obtain q 2-sets $\{(k,x_y^{1},z_y^{1}),(k,x_y^{2},z_y^{2})\}$ satisfying $\mathsf {Bits}_{C}\left( x_y^{1}\oplus z_y^{1}\right) =\mathsf {Bits}_{C}\left( x_y^{2}\oplus z_y^{2}\right)$. These two queries collide on the entire state, $k\oplus x_y^{1}\oplus z_y^{1} = k\oplus x_y^{2}\oplus z_y^{2}$, with probability at least $\frac{1}{2^{n-|C|}}$. If the adversary makes q predicate queries, we directly obtain our bound. The attack for $\mathrm {PGV}1$ is the same as we have taken $k=0$. $\quad \square$

4.3 Preimage Security

Theorem 2

Let $n\in \mathbb {N}$. Let $\alpha \in \{1,2\}$ and consider $\mathrm {PGV}\alpha$. Suppose $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n,n)$. Then, for $q\le 2^{n-2}/B$,

$$\begin{aligned} \mathbf {Adv}_{\mathrm {PGV}\alpha }^{\mathrm {epre}}(q) \le \left( \frac{2Bq}{2^n}\right) ^B + \frac{2B^2\delta _{B,C}[1]q}{2^n}\,. \end{aligned}$$

The proof is given in Appendix A. It is much more involved than the one of Theorem 1, particularly as we cannot make use of abortable ciphers. Entering various choices of B and C shows that in the PGV functions remain mostly unaffected in the WCM if $B\ge 2$, and the same security level as in the ICM is achieved [9, 10, 58]. A slight security degradation appears for $B=1$ as preimages can be found in about $2^{n-|C|}$. In the full version, we present a matching attack in the WCM.

5 Application to Grøstl Compression Function

We consider the provable security of the compression function mode of operation of Grøstl [21] (see also Fig. 4):

$$\begin{aligned} \mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}(x_1,x_2) = x_2\oplus \pi _1(x_1)\oplus \pi _2(x_1\oplus x_2)\,. \end{aligned}$$

(6)

The Grøstl compression function is in fact designed to operate in a wide-pipe mode, and in the IPM, the function is proven collision secure up to about $2^{n/4}$ queries and preimage secure up to $2^{n/2}$ queries [20]. We consider the security of $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}$ in the WCM, where $(\pi _1,\pi _2)\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n)^2$. We remark that in this section we consider keyless primitives, hence $\kappa =0$ and the k-input is dropped throughout. We furthermore note that finding collisions and preimages for $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}$ is equivalent to finding them for

$$\begin{aligned} \mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}'(x_1,x_2) = x_1\oplus x_2\oplus \pi _1(x_1)\oplus \pi _2(x_2)\,, \end{aligned}$$

(7)

as $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}(x_1,x_2)=\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}'(x_1,x_1\oplus x_2)$, and we will consider $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}'$ throughout.

Fig. 4.

Grøstl compression function (left) and Shrimpton-Stam (right).

5.1 Collision Security

Theorem 3

Let $n\in \mathbb {N}$. Suppose $(\pi _1,\pi _2)\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n)^2$. Then, for $q\le 2^{n-1}/B$,

$$\begin{aligned} \mathbf {Adv}_{\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}'}^{\mathrm {col}}(q) \le \frac{B^4\delta _{B,C}[1]q^4}{2^n} + {B\atopwithdelims ()2}\frac{2\delta _{B,C}[2](q^2+2^{n/2-|C|}q)}{2^n} + \frac{B^2q^2}{2\cdot 2^{n/2}} + \frac{4B^2q^2}{2^n}\,. \end{aligned}$$

The proof is given in the full version of the paper. If we enter particular choices of B and C into the bound, we find results comparable to the case of Sect. 4.1. In more detail, for $B=2$ and C with $|C|\le n/2$, or for $B\ge 3$ constant and C arbitrary, $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}$ achieves the same $2^{n/4}$ collision security level as in the ICM [20]. If $B=1$, the bound guarantees security up to about $2^{(n-|C|)/4}$, and if $B=2$ with $|C|>n/2$, collisions can be found in about $2^{(n-|C|)/2}$ queries. See also Table 1. In the full version, we also show that the bound is optimal, by presenting tight attacks on $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}'$ in the WCM.

5.2 Preimage Security

Theorem 4

Let $n\in \mathbb {N}$. Suppose $(\pi _1,\pi _2)\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n)^2$. Then, for $q\le 2^{n-1}/B$,

$$\begin{aligned} \mathbf {Adv}_{\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}'}^{\mathrm {epre}}(q) \le \frac{2B^2\delta _{B,C}[1](q^2+2^{n/2-|C|}q)}{2^n} + \frac{Bq}{2^{n/2}} + \frac{4B^2q^2}{2^n}\,. \end{aligned}$$

The proof is given in the full version of the paper. As before, we find that $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}$ remains unaffected in the WCM for most cases, the sole exception being $B=1$ for which preimages can be found in about $2^{(n-|C|)/2}$. In the full version, we also show that the bound is optimal, by presenting a tight attack on $\mathsf {F}_\mathrm {Gr{\scriptscriptstyle \varnothing }stl}'$ for $B=1$ in the WCM.

6 Application to Shrimpton-Stam Compression Function

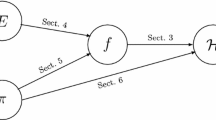
In this section, we consider the provable security of the Shrimpton-Stam compression function [57] (see also Fig. 4):

$$\begin{aligned} \mathsf {F}_\mathrm {SS}(x_1,x_2) = x_1\oplus \pi _1(x_1)\oplus \pi _3(x_1\oplus \pi _1(x_1)\oplus x_2\oplus \pi _2(x_2))\,. \end{aligned}$$

(8)

This function is proven asymptotically optimally collision and preimage secure up to $2^{n/2}$ queries in the IPM [41, 51, 57]. We consider the security of $\mathsf {F}_\mathrm {SS}$ in the WCM, where $(\pi _1,\pi _2,\pi _3)\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n)^3$. (As in Sect. 5 we consider keyless functions, hence $\kappa =0$ and the key inputs are dropped throughout.) Our findings readily apply to the generalization of $\mathsf {F}_\mathrm {SS}$ of [41]. The analysis of this construction is significantly more complex than the ones of Sects. 4 and 5.

6.1 Collision Security

Theorem 5

Let $n\in \mathbb {N}$. Suppose $(\pi _1,\pi _2,\pi _3)\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n)^3$. Then,

• (i) If $B=1$ and C arbitrary, $\mathbf {Adv}_{\mathsf {F}_\mathrm {SS}}^{\mathrm {col}}(2^{(n-|C|)/2-n\varepsilon })\rightarrow 0$ for $n\rightarrow \infty$;

• (ii) If $B=2$ and C with $|C|\le n/2$, $\mathbf {Adv}_{\mathsf {F}_\mathrm {SS}}^{\mathrm {col}}(2^{n/2-n\varepsilon })\rightarrow 0$ for $n\rightarrow \infty$;

• (iii) If $B=2$ and C with $|C|>n/2$, $\mathbf {Adv}_{\mathsf {F}_\mathrm {SS}}^{\mathrm {col}}(2^{n-|C|-n\varepsilon })\rightarrow 0$ for $n\rightarrow \infty$;

• (iv) If $B\ge 3$ (independent of n) and C arbitrary, $\mathbf {Adv}_{\mathsf {F}_\mathrm {SS}}^{\mathrm {col}}(2^{n/2-n\varepsilon })\rightarrow 0$ for $n\rightarrow \infty$.

Due to the technicality of the proof, the results are expressed in asymptotic terms. The proof is given in the full version of the paper. For $B=2$ and C with $|C|\le n/2$, or for $B\ge 3$ constant and C arbitrary, $\mathsf {F}_\mathrm {SS}$ achieves the same security level as in the IPM. On the other hand, if $B=1$, or if $B=2$ but $|C|>n/2$, Theorem 5 results in a worse bound. See also Table 1. In the full version, we also show that the bound is optimal, by presenting tight attacks on $\mathsf {F}_\mathrm {SS}$ in the WCM.

6.2 Preimage Security

Theorem 6

Let $n\in \mathbb {N}$. Suppose $(\pi _1,\pi _2,\pi _3)\xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n)^3$. Then,

• (i) If $B=1$ and C with $|C|\le n/2$, $\mathbf {Adv}_{\mathsf {F}_\mathrm {SS}}^{\mathrm {epre}}(2^{n/2-n\varepsilon })\rightarrow 0$ for $n\rightarrow \infty$;

• (ii) If $B=1$ and C with $|C|>n/2$, $\mathbf {Adv}_{\mathsf {F}_\mathrm {SS}}^{\mathrm {epre}}(2^{n-|C|-n\varepsilon })\rightarrow 0$ for $n\rightarrow \infty$;

• (iii) If $B\ge 2$ (independent of n) and C arbitrary, $\mathbf {Adv}_{\mathsf {F}_\mathrm {SS}}^{\mathrm {epre}}(2^{n/2-n\varepsilon })\rightarrow 0$ for $n\rightarrow \infty$.

As for collision resistance, the results are expressed in asymptotic terms. The proof is given in the full version of the paper. The bounds match the ones in the IPM, except for the case of $B=1$ and $|C|>n/2$. We leave it as an open problem to prove tightness of Theorem 6 part (ii).

7 Conclusions

Since their formal introduction by Knudsen and Rijmen at ASIACRYPT 2007 [27], numerous known-key attacks on blockciphers have appeared in literature. These attacks are often considered delicate, as it is not always clear to what extent they influence the security of cryptographic functions based on these known-key blockciphers. We presented the weak cipher model in order to investigate this impact. For a specific instance of this model, considering the existence of A sets of B queries that satisfy condition $\varphi ^C$ of (3), we proved that the PGV compression functions [48], the Grøstl compression function [21], and the Shrimpton-Stam compression function [57] remain mostly unaffected by the generalized weakness. Additionally, preimage security of the functions turned out to be significantly less susceptible to these types of weaknesses than collision security. The results can be readily generalized to other primitive-based functions, such as the double block length compression functions Tandem-DM, Abreast-DM, and Hirose’s compression functions [23, 30], and to the permutation-based sponge mode [5].

Our model is general enough to cover practically all differential known-key attacks in literature, such as latest results based on the rebound attack [12, 22, 28, 38, 52, 53, 56] and on the boomerang attack [2, 7, 31, 54, 60]. To our knowledge, our work provides the first attempt to formally analyze the effect of a wide class of cryptanalytic attacks from a modular and provable security point of view. It is a step in the direction of security beyond the ideal model, connecting practical attacks from cryptanalysis with ideal model provable security. There is still a long way to go: in order to make the connection between the two fields, we abstracted known-key attacks to a certain degree. It remains a highly challenging open research problem to generalize our findings to multiple or different weaknesses, and to different permutation-based cryptographic functions. These generalizations include the analysis of known-key based constructions for more advanced conditions $\varphi$ (such as arbitrary polynomials).

A Proof of Theorem 2

We focus on $\mathrm {PGV}2$. The analysis for $\mathrm {PGV}1$ is a simplification due to the absence of the feed-forward of the key. We consider any adversary that has query access to $\pi \xleftarrow {{\scriptscriptstyle \$}}\mathrm {BC}[\varPhi (A,B,\varphi ^C)](n,n)$ and makes q queries. Let $Z\in \{0,1\}^{n}$. A preimage for Z would imply the existence of a query $(k_{},x_{},z_{})$ such that $x\oplus z = k\oplus Z$. We consider the $i^{\mathrm{th}}$ query ($i\in \{1,\ldots ,q\}$) to be the first query to make this condition satisfied, and sum over $i=1,\ldots ,q$ at the end. For regular (forward or inverse) queries, the analysis of [9, 10, 58] mostly carries over. The analysis of predicate queries is a more technical, particularly as we cannot make use of abortable ciphers.

Query $\varvec{\pi _k(x)}$ or $\varvec{\pi _k^{-1}(z)}$ . The cases are the same by symmetry, and we consider $\pi _k(x)$ only. Denote the response by z. As z is randomly drawn from a set of size at least $2^n-Bq$, it satisfies $z=x\oplus k\oplus Z$ with probability at most $\frac{1}{2^n-Bq}$.

Query $\varvec{\pi ^\varPhi _k(y)}$ . Denote the query response by $\{(k,x^{1},z^{1}),\ldots ,(k,x^{B},z^{B})\}$. If all tuples are old, the query cannot be successful as no earlier query was successful, and so we assume it contains at least one new tuple. The response is drawn uniformly at random from the set $\varSigma _k(P_k,P^\varPhi _k)$. For $\ell =0,\ldots ,B$, denote by $\varSigma _k^{\ell }(P_k,P^\varPhi _k)$ the subset of all responses that have $\ell$ new query tuples and $B-\ell$ old query tuples (which already appear in $P_k$). By construction,

$$\begin{aligned} \varSigma _k(P_k,P^\varPhi _k) = \bigcup _{\ell =0}^B \varSigma _k^{\ell }(P_k,P^\varPhi _k)\,. \end{aligned}$$

(9)

Define furthermore for $\ell =1,\ldots ,B$ by $\varSigma _k^{\ell ,\mathrm {pre}}(P_k,P^\varPhi _k)$ the subset of elements of $\varSigma _k^{\ell }(P_k,P^\varPhi _k)$ for which one of the new query tuples satisfies $x\oplus z=k\oplus Z$ (recall that we have excluded the case of $\ell =0$). The predicate query is successful with probability

$$\begin{aligned} \mathbf {Pr}\left( \pi ^\varPhi _k(y) \text { sets } \mathsf {pre}_{}(\mathcal {Q}_{i})\right) = \sum _{\ell =1}^B \frac{|\varSigma _k^{\ell ,\mathrm {pre}}(\mathsf {P_k},P^\varPhi _k)|}{|\varSigma _k(P_k,P^\varPhi _k)|}\,. \end{aligned}$$

(10)

Using (9), we bound (10) as

$$\begin{aligned} \mathbf {Pr}\left( \pi ^\varPhi _k(y) \text { sets } \mathsf {pre}_{}(\mathcal {Q}_{i})\right) \le \frac{|\varSigma _k^{1,\mathrm {pre}}(P_k,P^\varPhi _k)|}{|\varSigma _k^{B}(P_k,P^\varPhi _k)|} + \sum _{\ell =2}^B \frac{|\varSigma _k^{\ell ,\mathrm {pre}}(P_k,P^\varPhi _k)|}{|\varSigma _k^{\ell }(P_k,P^\varPhi _k)|}\,. \end{aligned}$$

(11)

The reason why $\ell =1$ is treated differently, will become clear shortly.

We next bound all relevant sets. Here, for integers $a\ge b\ge 1$, we denote by ${a}^{\underline{b}}=\frac{a!}{(a-b)!}$ the falling factorial power. Starting with the numerators, for $\ell =1$ we have

$$\begin{aligned} |\varSigma _k^{1,\mathrm {pre}}(P_k,P^\varPhi _k)| \le B\cdot {|P_k|}^{\underline{B-1}}\cdot (2^n-|P_k|)\,. \end{aligned}$$

Indeed, we have B positions for the sole new query to appear and ${|P_k|}^{\underline{B-1}}$ choices for the old queries. For the new query, without loss of generality $(k,x^{B},z^{B})$, it needs to satisfy $\mathsf {Bits}_{C}(x^{B}\oplus z^{B})=\mathsf {Bits}_{C}(x^{1}\oplus \cdots \oplus z^{B-1})$ and $x^{B}\oplus z^{B}=k\oplus Z$. We have $2^n-|P_k|$ possible choices for $x^{B}$, and any choice gives at most one possible $z^{B}$. We remark that $|\varSigma _k^{1,\mathrm {pre}}(P_k,P^\varPhi _k)|$ will probably be about a factor $2^{-|C|}$ less, as we should only count all possible solutions for the $B-1$ old queries that satisfy $\mathsf {Bits}_{C}(x^{1}\oplus \cdots \oplus z^{B-1})=\mathsf {Bits}_{C}(k\oplus Z)$. Deriving a tighter bound would be a cumbersome exercise, but fortunately there is no need to do so: the fraction of elements in $\varSigma _k(P_k,P^\varPhi _k)$ consisting of $B-1$ old tuples is already small enough for the case $B>1$. This is the reason why we use a special treatment for the case of $\ell =1$ in (11).

For $\ell \in \{2,\ldots ,B\}$ we have

$$\begin{aligned} |\varSigma _k^{\ell ,\mathrm {pre}}(P_k,P^\varPhi _k)| \le {B\atopwithdelims ()\ell }\cdot {|P_k|}^{\underline{B-\ell }}\cdot {(2^n-|P_k|)}^{\underline{\ell }}\cdot \ell \cdot {(2^n-|P_k|)}^{\underline{\ell -2}}\cdot 2^{n-|C|}\,. \end{aligned}$$

Again, the first term comes from identifying at which positions the new queries appear and the second term comes from the selection of old queries. Next, we have ${(2^n-|P_k|)}^{\underline{\ell }}$ choices for the x-values and $\ell$ positions for the “winning query” to occur. For this particular winning query, the corresponding z-value is fixed by the equation $x\oplus z=k\oplus Z$. For the remaining $\ell -1$ z-values, there are ${(2^n-|P_k|)}^{\underline{\ell -2}}$ possibilities to freely fix the first $\ell -2$ of them, and the last one will be adapted to the predicate condition, and can take at most $2^{n-|C|}$ values.

Regarding the denominators, for $\ell \in \{1,\ldots ,B\}$ we have

$$\begin{aligned} |\varSigma _k^{\ell }(P_k,P^\varPhi _k)|&\ge {B\atopwithdelims ()\ell }\cdot {|P_k|}^{\underline{B-\ell }}\cdot \left( \begin{array}{l} {(2^n-|P_k|)}^{\underline{\ell }}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}\cdot 2^{n-|C|}\,\,-\\ \; Bq\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}\cdot 2^{n-|C|} \end{array} \right) \!, \end{aligned}$$

which can be seen as follows. As before, we have ${B\atopwithdelims ()\ell }$ positions for the new queries to appear and ${|P_k|}^{\underline{B-\ell }}$ possible lists of old queries. Regarding the $\ell$ new queries, without loss of generality $(k,x^{1},z^{1}),\ldots ,(k,x^{\ell },z^{\ell })$, these need to satisfy $\mathsf {Bits}_{C}(x^{1}\oplus \cdots \oplus z^{\ell })=\mathsf {Bits}_{C}(x^{\ell +1}\oplus \cdots \oplus z^{B})$. We first compute the number of choices for these new queries where $z^{\ell }$ is only used to adapt to this condition and does not need to satisfy that it is fresh. For this case, we have precisely ${(2^n-|P_k|)}^{\underline{\ell }}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}$ choices for $x^{1},\ldots ,z^{\ell -1},x^{\ell }$, and $2^{n-|C|}$ possibilities for the adaption value $z^{\ell }$.

Now, we subtract the cases where this adapted value happens to collide, either with an older value in $\mathsf {rng}(P_k)$ or with any of the new $z^{1},\ldots ,z^{\ell -1}$. Any of these choices would fix $z^{\ell }$ (in total at most $(|P_k|+\ell -1)$ possibilities). Similarly to the analysis for $|\varSigma _k^{\ell ,\mathrm {pre}}(P_k,P^\varPhi _k)|$, where now $x^{\ell }$ will be used to be adapted to the predicate condition, there are at most

$$\begin{aligned} (|P_k|+\ell -1)\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}\cdot 2^{n-|C|} \end{aligned}$$

choices for the fresh values. As $\ell \le B$, and additionally $|P_k|\le B(i-1)\le B(q-1)$ for the current query, we obtain our bound for $|\varSigma _k^{\ell }(P_k,P^\varPhi _k)|$. The bound can be simplified to

$$\begin{aligned} |\varSigma _k^{\ell }(P_k,P^\varPhi _k)| \ge {B\atopwithdelims ()\ell }\cdot {|P_k|}^{\underline{B-\ell }}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}\cdot 2^{n-|C|}\cdot \left( 2^n-2Bq\right) , \end{aligned}$$

using that $\frac{{(2^n-|P_k|)}^{\underline{\ell }}}{{(2^n-|P_k|)}^{\underline{\ell -1}}}=2^n-|P_k|-(\ell -1)\ge 2^n-Bq$.

Plugging these bounds into (11), we find for the case $B=1$:

$$\begin{aligned} \mathbf {Pr}\left( \pi ^\varPhi _k(y) \text { sets } \mathsf {pre}_{}(\mathcal {Q}_{i})\right) \le \frac{2^n-|P_k|}{2^{n-|C|}\cdot \left( 2^n-2q\right) } \le \frac{2^{|C|}}{2^n-2q}\,. \end{aligned}$$

For the case $B>1$ the computation is a bit more elaborate:

$$\begin{aligned} \mathbf {Pr}\left( \pi ^\varPhi _k(y) \text { sets } \mathsf {pre}_{}(\mathcal {Q}_{i})\right) \le&\;\frac{B\cdot (2^n-|P_k|)}{{(2^n-|P_k|)}^{\underline{B-1}}\cdot 2^{n-|C|}\cdot \left( 2^n-2Bq\right) }\cdot \frac{{|P_k|}^{\underline{B-1}}}{{(2^n-|P_k|)}^{\underline{B-1}}}\,+\\&\;\sum _{\ell =2}^B \frac{{(2^n-|P_k|)}^{\underline{\ell }}\cdot {(2^n-|P_k|)}^{\underline{\ell -2}}}{{(2^n-|P_k|)}^{\underline{\ell -1}}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}}\cdot \frac{\ell }{2^n-2Bq}\,. \end{aligned}$$

For the first fraction we use that $2^n-|P_k|\le {(2^n-|P_k|)}^{\underline{B-1}}$ as $B>1$, and additionally that $|C|\le n$. For the falling factorial powers of the second fraction, we use that ${|P_k|}^{\underline{B-1}}\le (Bq)^{B-1}$ and ${(2^n-|P_k|)}^{\underline{B-1}}\ge (2^n-|P_k|-(B-1))^{B-1}\ge (2^n-2Bq)^{B-1}$. For the fraction in the sum, we use that $\frac{{(2^n-|P_k|)}^{\underline{\ell }}\cdot {(2^n-|P_k|)}^{\underline{\ell -2}}}{{(2^n-|P_k|)}^{\underline{\ell -1}}\cdot {(2^n-|P_k|)}^{\underline{\ell -1}}}=\frac{2^n-|P_k|-(\ell -1)}{2^n-|P_k|-(\ell -2)}\le 1$. We obtain:

$$\begin{aligned} \mathbf {Pr}\left( \pi ^\varPhi _k(y) \text { sets } \mathsf {pre}_{}(\mathcal {Q}_{i})\right)&\le \frac{B}{2^n-2Bq}\cdot \frac{(Bq)^{B-1}}{(2^n-2Bq)^{B-1}} + \sum _{\ell =2}^B \frac{\ell }{2^n-2Bq}\\&\le \frac{B^Bq^{B-1}}{(2^n-2Bq)^B} + \frac{B^2}{2^n-2Bq}\,. \end{aligned}$$

Conclusion. Taking the maximum of all success probabilities, the $i^{\mathrm{th}}$ query is successful with probability at most $\frac{B^Bq^{B-1}}{(2^n-2Bq)^B} + \frac{B^2\delta _{B,C}[1]}{2^n-2Bq}$. Summation over $i=1,\ldots ,q$ gives

$$\begin{aligned} \mathbf {Adv}_{\mathrm {PGV}2}^{\mathrm {epre}}(q) \le \frac{B^Bq^B}{(2^n-2Bq)^B} + \frac{B^2\delta _{B,C}[1]q}{2^n-2Bq}\,. \end{aligned}$$

The proof is completed by using the fact that $2^n-2Bq\ge 2^{n-1}$ for $Bq\le 2^{n-2}$.