Improved Test Pattern Generation for Hardware Trojan Detection Using Genetic Algorithm and Boolean Satisfiability

Abstract

Test generation for Hardware Trojan Horses (HTH) detection is extremely challenging, as Trojans are designed to be triggered by very rare logic conditions at internal nodes of the circuit. In this paper, we propose a Genetic Algorithm (GA) based Automatic Test Pattern Generation (ATPG) technique, enhanced by automated solution to an associated Boolean Satisfiability problem. The main insight is that given a specific internal trigger condition, it is not possible to attack an arbitrary node (payload) of the circuit, as the effect of the induced logic malfunction by the HTH might not get propagated to the output. Based on this observation, a fault simulation based framework has been proposed, which enumerates the feasible payload nodes for a specific triggering condition. Subsequently, a compact set of test vectors is selected based on their ability to detect the logic malfunction at the feasible payload nodes, thus increasing their effectiveness. Test vectors generated by the proposed scheme were found to achieve higher detection coverage over large population of HTH in ISCAS benchmark circuits, compared to a previously proposed logic testing based Trojan detection technique.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Modern electronic design and manufacturing practices make a design vulnerable to malicious modifications. Malicious circuitry embedded as a result of such modifications, commonly referred to as Hardware Trojan Horses (HTHs), have been demonstrated to be potent threats [6]. The stealthy nature of HTHs help them to evade conventional post-manufacturing testing. Once deployed in-field, HTHs get activated under certain rare conditions (depending on internal or external stimulus), and can potentially cause disastrous functional failure or leakage of secret information.

Recent research on HTHs mainly focuses on the modelling and detection of HTHs [4, 13, 16, 17, 19, 21]. A vast majority of the detection mechanisms proposed till date utilizes the anomaly in the side-channel signatures (e.g. delay, transient and leakage power) in the presence of HTH in the circuit [2, 11, 19]. However, side-channel approaches are susceptible to experimental and process variation noise. Thus, detection of small Trojans, especially combinatorial ones, becomes challenging through these approaches. Another approach is to employ design modification techniques to either prevent Trojan insertion or to make inserted Trojans more easily detectable [3, 17, 20].

An adversary may use very rare internal logic conditions to trigger a HTH, so that it remains well hidden during testing. Usually, it is assumed that the attacker will generate the trigger signal form a combination of internal nets of the circuit whose transition probability is very low. She may try to activate them simultaneously to their rare values thus achieving an extremely low triggering probability. Based on this assumption, several Trojan detection techniques have been proposed till date [5, 17] which try to activate the Trojans either fully or partially by triggering the rare nodes, thus creating anomaly at the output logic values, or in some side channel signals viz. transient power. In [17, 21] the authors proposed a design-for-testability (DFT) technique which inserts dummy scan flip-flops to make the transition probability of low transition nets higher in a special “authentication mode”. However, it was found that careful attackers can evade this scheme easily [18]. Another powerful DFT technique is obfuscating or encrypting the design by inserting some extra gates in it [3, 7], so that the actual functionality of the circuit is hidden, consequently making it difficult for an adversary to estimate the actual transition probabilities at the internal nodes. However, such “logic encryption” schemes have been recently broken [14].

Fig. 1.

Motivational example: variation of trigger and Trojan coverage with rareness threshold ($\theta$) by the MERO [5] technique for c7552 (a) on sets of Trojans considered as in [5]; (b) on a set of rarely triggered Trojans (effective triggering probability below $10^{-6}$).

Observing the vulnerability of DFT techniques against intelligent attackers, in [5] a test pattern generation scheme called MERO was proposed. MERO uses the philosophy of N-detect test to activate individually a set of nodes in a circuit to their less-probable values whose transition probabilities are below a specific threshold (termed rareness threshold and usually denoted by $\theta$). The test generation is continued until each of the nodes gets activated to their rare values at least N-times. It was shown through simple theoretical analysis and experimental results that if N is sufficiently large, then a Trojan whose trigger condition is composed jointly of rare values at these rare nodes, is highly likely to be activated by the application of this test set.

Although MERO proposes a relatively simple heuristic for test generation it is found to have the following shortcomings:

• 1. When tested on a set of “hard-to-trigger” Trojans (with triggering probability in the range of $10^{-6}$ or less), the test vector set generated by MERO was found to have poor coverage both over triggering combinations and Trojans. Figure 1(b) presents the variation of trigger and Trojan coverage with the rareness threshold ($\theta$) value for the ISCAS–85 circuit c7552, where the Trojan trigger probability is the effective Trojan triggering probability considering all the nodes together, unlike in [5], which considered trigger probability at individual nodes (see Fig. 1(a)). It was found that best coverage was achieved for $\theta$ in the range $0.08-0.12$, and this trend was consistent for all the benchmark circuits considered. However, the best achievable coverage was still below 50%, for even circuits of moderate size like c7552.

• 2. Although individual activation of each individual rare nodes at least N-times increases the activation probability of rare node combinations on average, there is always a finite probability that combinations with extremely low activation probability will not be triggered for a given value of N. As a result, even for small ISCAS–85 circuits like c432, the MERO test generation method misses some rare node patterns even after several independent runs. This fact can be utilized by an intelligent adversary.

• 3. MERO explores a relatively small numbers of test vectors, as the heuristic perturbs only a single bit at a time of an obtained test vector to generate new test vectors.

• 4. Another problem with the MERO algorithm is that, while generating the test vectors, it only considers the activation of the triggering conditions, and ignores whether the triggered Trojan actually caused any logic malfunction at the primary output of the circuit under test.

1.1 Main Idea and Our Contribution

Motivated by the above mentioned shortcomings of [5], in this paper we propose an improved ATPG scheme to detect small combinational and sequential HTHs, which are otherwise often difficult to detect by side channel analysis, or can bypass design modification based detection schemes. We note that for higher effectiveness, a test generation algorithm for Trojan detection must simultaneously consider trigger coverage and Trojan coverage. Firstly, we introduce a combined Genetic Algorithm (GA) and Boolean satisfiability (SAT) based approach for test pattern generation. GA has been used in the past for fault simulation based test generation [15]. GA is attractive for getting reasonably good test coverage over the fault list very quickly, because of the inherent parallelism of GA which enables relatively rapid exploration of a search space. However, it does not guarantee the detection of all possible faults, specially for those which are hard to detect. On the other hand, SAT based test generation has been found to be remarkably useful for hard-to-detect faults. However, it targets the faults one by one, and thus incurs higher execution time for easy-to-detect faults which typically represent the majority of faults [8]. It has another interesting feature that it can declare whether a fault is untestable or not.

In case of HTH, the number of candidate trigger combinations has an exponential dependence on the number of rare nodes considered. Even if we limit the number of Trojan inputs to four (because of VLSI design and side–channel information leakage considerations), the count is quite large. Thus, we have a large candidate trigger list and it is not possible to handle each fault in that list sequentially. However, many of these trigger conditions are not actually satisfiable, and thus cannot constitute a feasible trigger. Hence, we combine the “best of both worlds” for GA and SAT based test generation. The rationale is that most of the easy-to-excite trigger conditions, as well as a significant number of hard-to-excite trigger conditions will be detected by the GA within reasonable execution time. The remaining unresolved trigger patterns are input to the SAT tool; if any of these trigger conditions is feasible, then SAT returns the corresponding test vector. Otherwise, the pattern will be declared unsolvable by the SAT tool itself. As we show later, this combined strategy is found to perform significantly better than MERO. In the second phase of the scheme, we refine the test set generated by GA and SAT, by judging its effectiveness from the perspective of potency of the triggered Trojans. For each feasible trigger combination found in the previous step, we find most of the possible payloads using a fault simulator. For this, we model the effect of each Trojan instance (defined by a combination of a feasible trigger condition and the payload node) as a stuck-at fault, and test whether the fault can be propagated to the output by the same test vector which triggered the Trojan. This step helps to find out a compact test set which remarkably improves the Trojan coverage. To sum up, the following are the main contributions of this paper:

• 1. An improved ATPG heuristic for small combinational and sequential HTH detection is presented which utilizes two well known computational tools, GA and SAT. The proposed heuristic is able to detect HTH instances triggered by extremely rare internal node conditions, while having acceptable execution time. Previous work has reported that partial activation of the Trojan with accompanying high sensitivity side channel analysis is quite effective in detecting large HTHs [17], but not so effective for ultra-small Trojans. Hence, our work fills an important gap in the current research.

• 2. The tuning of the test vector set considering the possible payloads for each trigger combination makes the test set more compact, and increases its effectiveness of exploring the Trojan space.

• 3. The relative efficacy of the proposed scheme with respect to the scheme proposed in [5] has been demonstrated through experimental results on a subset of ISCAS–85 and ISCAS–89 circuits.

• 4. Since the triggering condition, corresponding triggering test vectors, as well as the possible payload information for each of the feasible triggers are generated during the execution, a valuable Trojan database for each circuit is created, which may be utilized for diagnosis purposes too. This database is enhanced for multiple runs of the algorithm, because of the inherent randomized nature of the GA which enables newer portions of the Trojan design space to be explored.

The rest of the paper is organized as follows. Section 2 presents a brief introduction to GA and SAT, as relevant in the context of ATPG for Trojan detection. The complete ATPG scheme is described in Sect. 3. Experimental results are presented and analyzed in Sect. 4, along with discussions on the possible application of the proposed scheme for Trojan diagnosis and side channel analysis based Trojan detection. The paper is concluded in Sect. 5, with directions of future work.

Fig. 2.

Example of (a) combinational and (b) sequential (counter-like) Trojan. The combinational Trojan is triggered by the simultaneous occurrence of logic–1 at two internal nodes. The sequential (counter-like) Trojan is triggered by $2^k$ positive ($0 \rightarrow 1$) transitions at the input of the flip-flops.

2 GA and SAT in the Context of ATPG for Trojan Detection

2.1 Hardware Trojan Models

We consider simple combinational and sequential HTHs, where a HTH instance is triggered by the simultaneous occurrence of rare logic values at one or more internal nodes of the circuit. We find the rare nodes ($\mathcal {R}$) of the circuit with a probabilistic analysis. Details of this analysis can be found in [17, 21]. Once activated, the Trojan flips the logic value at an internal payload node. Figure 2 shows the type of Trojans considered by us.

Notice that it is usually infeasible to enumerate all HTHs in a given circuit. Hence, we are forced to restrict ourselves to analysis results obtained from a randomly selected subset of Trojans. The cardinality of the set of Trojans selected depends on the size of the circuit being analyzed. Since we are interested only in small Trojans, a random sample $\mathcal {S}$ of up to four rare node combinations is considered. Let us denote the set of rare nodes as $\mathcal {R}$, with $|\mathcal {R}| = r$ for a specific rareness threshold ($\theta$). The set of all possible rare node combinations is then the power set of $\mathcal {R}$, denoted by $2^\mathcal {R})$. Thus, the population of Trojans under consideration is the set $\mathcal {K}$, where $\mathcal {K} \subseteq 2^\mathcal {R}$ and $|\mathcal {K}|$ is ${r \atopwithdelims ()1} + {r \atopwithdelims ()2} + {r \atopwithdelims ()3} + {r \atopwithdelims ()4}$. Thus, $\mathcal {S} \subseteq \mathcal {K}$.

We intentionally chose $\theta =0.1$ for our experiments, which is lower than the value considered in [5] ($\theta =0.2$). The choice is based on the observed coverage trends of our experiments on “hard-to-trigger” Trojans in Sect. 1, where it was observed that the coverage is maximized for $\theta$ values in the range $0.08-0.12$ for most ISCAS benchmark circuits.

2.2 Genetic Algorithm (GA) for ATPG

Genetic algorithm (GA) is an well known bio-inspired, stochastic, evolutionary search algorithm based upon the principles of natural selection [10]. GA has been widely used in diverse fields to tackle difficult non-convex optimization problems, both in discrete and continuous domains. In GA, the quality of a feasible solution is improved iteratively, based on computations that mimic basic genetic operations in the biological world. The quality of the solution is estimated by evaluating the numerical value of an objective function, usually termed the “fitness function” in GA. In the domain of VLSI testing, it has been successfully used for difficult test generation and diagnosis problems [15]. In the proposed scheme, GA has been used as a tool to automatically generate quality test patterns for Trojan triggering. During test generation using GA, two points were emphasized:

• an effort to generate test vectors that would activate the most number of sampled trigger combinations, and,

• an effort to generate test vectors for hard-to-trigger combinations.

However, as mentioned in the previous section, the major effort for GA was dedicated to meet the first objective.

To meet both of the goals, we used a special data structure as well as a proper fitness function. The data structure is a hash table which contains the triggering combinations and their corresponding activating test vectors. Let $\mathcal {S}$ denote the sampled set of trigger conditions being considered. Each entry in the hash table ($\mathcal {D}$) is a tuple (s, $\{t_i\}$), where $s \in \mathcal {S}$ is a trigger combination from the sampled set ($\mathcal {S}$) and $\{t_i\}$ is the set of distinct test vectors activating the trigger combination s. Note that, a single test vector $t_i$ may trigger multiple trigger combinations and thus can be present multiple times in the data structure for different trigger combinations (s). The data structure is keyed with trigger combination s. Initially, $\mathcal {D}$ is empty; during the GA run, $\mathcal {D}$ is updated dynamically, whenever new triggering combinations from $\mathcal {S}$ are found to be satisfied. The fitness function is expressed as:

$$\begin{aligned} f(t)= R_{count}(t) + w* I(t) \end{aligned}$$

(1)

where f(t) is the fitness value of a test vector t; $R_{count}(t)$ counts the number of rare nodes triggered by the test vector t; w ($>1$) is a constant scaling factor, and I(t) is a function which returns the relative improvement of the database $\mathcal {D}$ due to the test vector t. The term “relative improvement of the database” (I(t)) can be explained as follows. Let us interpret the data structure $\mathcal {D}$ as a histogram where the bins are defined by unique trigger combinations $s \in \mathcal {S}$, and each bin contains its corresponding activating test vectors $\{t_i\}$. Before each update of the database, we calculate the number of test patterns in each bin which is to be updated. The relative improvement is defined as:

$$\begin{aligned} I(t) = \frac{n_2(s) - n_1(s)}{n_2(s)} \end{aligned}$$

(2)

where: $n_1(s)$ is the number of test patterns in bin s before update, and $n_2(s)$ is the number of test patterns in bin s after update.

Note that for each test pattern t that enters the database D, the numerator will be either 0 or 1 for an arbitrary trigger combination s. However, the denominator will have larger values with the minimum value being 1. Thus, for any bin s, when it gets its $1^{st}$ test vector, the above mentioned ratio achieves the maximum value 1, whereas when a bin gets its $n^{th}$ test vector, the fraction is $\frac{1}{n}$. The value gradually decreases as the number of test vectors in s increases. This implies that as a newer test vector is generated, its contribution is considered more important if it has been able to trigger an yet unactivated trigger condition s , than if it activates a trigger condition that has already been activated by other test vector(s). Note that, for bins s having zero test vectors before and after update (i.e. trigger conditions which could not be activated at the first try), we assign a very small value $10^{-7}$ for numerical consistency. The scaling factor w is proportional to the relative importance of the relative improvement term; in our implementation, w was set to have the value 10.

The rationale behind the two terms in the fitness function is as follows. The first term in the fitness function prefers test patterns that simultaneously activate as many trigger nodes as possible, thus recording test vectors each of which can potentially cover many trigger combinations. The inclusion of the second term has two effects. Firstly, the selection pressure of GA is set towards hard-to-activate patterns by giving higher fitness value to those test patterns that are capable of hard–to–trigger conditions. Secondly, it also helps the GA to explore the sampled trigger combination space evenly. To illustrate this, let us consider the following example.

Fig. 3.

Example of two–point crossover and mutation in Binary Genetic Algorithm.

Suppose, we have five rare nodes $r_1, r_2, r_3, r_4, r_5$. We represent the activation of these five nodes by a binary vector r of length five, where $r_i = 1$ denotes that the $i^{th}$ rare node has been activated to its rare value and $r_i = 0$ otherwise. Thus, a pattern 11110 implies the scenario where the first four rare nodes have been simultaneously activated. Now, the test vector t, which generates this rare node triggering pattern also triggers the patterns 10000, 01000, 00100, 00010, 11000, $\dots$, 11100, i.e. any subset of the triggered rare nodes. Mathematically, if there are in total r rare nodes and $r'$ rare nodes are simultaneously triggered in a pattern ( $r' < r$ ) by a test vector t , then the $2^{r'}$ subsets of the triggered rare nodes are also triggered by the same test vector. Hence, maximizing $r'$ increases the coverage over the trigger combination sample set.

The test generation problem is modelled as a maximization problem, and solved using a variation of GA termed Binary Genetic Algorithm (BGA) [10]. Each individual in the population is a bit pattern called a “chromosome”, which represents an individual test vector. Two operations generate new individuals by operating on these chromosomes: crossover and mutation. Crossover refers to the exchange of parts of two chromosomes to generate new chromosomes, while mutation refers to the random (probabilistic) flipping of bits of the chromosomes to give rise to new behaviour. Figure 3 shows examples of two–point crossover and mutation in BGA. We used a two–point crossover and binary mutation, with a crossover probability of 0.9 and mutation probability of 0.05, respectively. The collection of individuals at every iteration is termed a population. A population size of 200 was used for combinatorial circuits and 500 for sequential circuits. Two terminating conditions were used: (i) when the total number of distinct test vectors in the database crosses a certain threshold value $\#T$, or (ii) if 1000 generations had been reached. The initialization of the population is done by test vectors satisfying some rare node combinations from the sample set. These rare node combinations are randomly selected and the test vectors were found using SAT tools (details are given in the following subsection). Algorithm 1, shows the complete test generation scheme using GA. Notice that the initial test vector population is generated by solving a small number of triggering conditions using SAT.

Among the sampled trigger instances, many might not be satisfiable, as we do not have any prior information about them. Moreover, although GA traverses the given trigger combination sample space reasonably rapidly, it cannot guarantee to be able to generate test vectors that would activate all the hard-to-trigger patterns. Thus, even after the GA test generation step, we were left with some trigger combinations among which some are not satisfiable and others are extremely hard to detect. However, as the number of such remaining combinations are quite less (typically 5–10 % of the selected samples) we can apply SAT tools to solve them. We nest describe the application of SAT in our ATPG scheme.

Fig. 4.

Illustration: formulation of a SAT instance which activates 3 rare nodes simultaneously.

2.3 SAT for Hard–to–Activate Trigger Conditions

Boolean Satisfiability (SAT) tools are being used to solve ATPG problems since the last decade [8]. They are found to be robust, often succeeding to find test patterns in large and pathological ATPG problems, where traditional ATPG algorithms have been found wanting. Unlike classical ATPG algorithms, SAT solver based schemes do not work on the circuit representation (e.g. netlist of logic gates) directly. Instead, they formulate the test pattern generation problem as one or more SAT problems. A n-variable Boolean formula $f(x_1, x_2, \ldots , x_n)$ in Conjunctive Normal Form (CNF) is said to be satisfiable if there exists a value assignment for the n variables, such that $f = 1$. If no such assignment exists, f is said to be unsatisfiable. Boolean satisfiability is an NP-Complete problem. Sophisticated heuristics are used to solve SAT problems, and powerful SAT solver software tools have become available in recent times (many of them are free). The ATPG problem instance is first converted into a CNF and then input to a SAT solver. If the solver returns a satisfiable assignment within a specified time the problem instance is considered to be satisfiable and unsatisfiable, otherwise.

As mentioned previously, we apply the SAT tool only for those trigger combinations for which GA fails to generate any test vector. Let us denote the set of such trigger combinations as $\mathcal {S}' \subseteq \mathcal {S}$. We consider each trigger combination $s \in \mathcal {S}'$, and input it to the SAT tool. This SAT problem formulation is illustrated by an example in Fig. 4. Let us consider the three rare nodes shown in Fig. 4(a) with their rare values. To create a satisfiability formula which simultaneously activates these three nodes to their rare value, we construct the circuit shown in Fig. 4(b). The SAT instance is thus formed which tries to achieve a value 1 at wire(node) d.

After completion of this step, most trigger combinations in the set $\mathcal {S}'$ will be found to be satisfiable by the SAT tool, which will also return the corresponding test vectors. However, some of the trigger combinations will still remain unsolved, which would be lebelled as unsatisfiable. Thus the set $\mathcal {S}'$ is partitioned into two disjoint subsets $\mathcal {S}_{sat}$ and $\mathcal {S}_{unsat}$. The first subset is accepted and the data structure $\mathcal {D}$ is updated with the patterns in this subset, whereas the second subset is discarded. This part of the flow has been summarized in Algorithm 2.

Fig. 5.

Impact of Trojan payload selection: (a) golden circuit; (b) payload-1 which has no effect on output; (c) payload-2 which has effect on the output.

The basic ATPG mechanism now in place, we next describe the refinement of the scheme to take the impact of the payload into consideration, and also achieve test compaction in the process.

3 Improving the Proposed Scheme: Payload Aware Test Set Selection and Test Compaction

3.1 Payload Aware Test Vector Selection

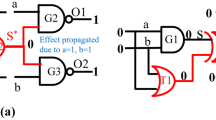
Finding out proper trigger-payload pairs to enumerate feasible HTH instances a is non-trivial computational problem. In combinational circuits, one necessary condition for a node to be a payload is that its topological rank must be higher than the topologically highest node of the trigger combination, otherwise there is a possibility of forming a “combinational loop”; however, this is not a sufficient condition. In general, a successful Trojan triggering event provides no guarantee regarding its propagation to the primary output to cause functional failure of the circuit. As an example, let us consider the circuit of Fig. 5(a). The Trojan is triggered by an input vector 1111. Figures 5(b) and 5(c) show two potential payload positions. It can be easily seen that independent of the applied test vector at in circuit input, for position-1 the Trojan effect gets masked and cannot be detected. On the other hand, the Trojan effect at position-2 can be detected.

Fig. 6.

PTV generation example: (a) triggering pattern; (b) corresponding set of test vectors; (c) generated PTV.

It is important to identify, for each trigger combination, the constrained primary input values. For this, we consider each Trigger combination and their corresponding set of trigger test vectors at a time. To be precise, we consider the entries (s, $\{t_i\}$) from the database $\mathcal {D}$, one at a time. Let us denote the set of test vectors corresponding to a specific s as $\{t^{s}_{i}\}$. Next, for each test vector $t \in \{t^{s}_{i}\}$, we find out which of the primary inputs, if any, remains static at a specific value (either logic–0 or logic–1). These input positions are the positions needed to be constrained to trigger the triggering combination. We fill the rest of the input positions with don’t-care (X) values, thus creating a single test-vector containing 0, 1 and X values. We call such 3-valued vectors Pseudo Test Vector (PTV). Figure 6 illustrates the process of PTV generation with a simple example, where the leftmost and the rightmost positions of the vectors are at logic-1.

At the next step, we perform a three-value logic simulation of the circuit with the PTV and note down values obtained at all the internal wires (nodes) which are at topologically higher positions from the nodes in the trigger combination. Then for each of these nodes we consider a stuck-at fault according to the following rule:

• 1. If the value at that node is 1, we consider a stuck-at-zero fault there.

• 2. If the value at that node is 0, we consider a stuck-at-one fault there.

• 3. If the value at that node is X, we consider a both stuck-at-one and stuck-at-zero fault at that location.

Fig. 7.

The complete test generation and evaluation flow.

At the next step, this fault list ($\mathcal {F}_{s}$) and the set of test vectors considered ($\{t^{s}_{i}\}$) is input to a fault simulator. We used the HOPE [12] fault simulator in diagnostic mode for this purpose. The output will be the set of faults that are detected ($\mathcal {F}^{s}_{detected} \subseteq \mathcal {F}_{s}$) as well as the corresponding test vectors which detect them. The detected faults constitutes the list of potential payload positions for the trigger combination. Thus, after detecting the feasible payloads, we greedily select a subset of the test vector set $\mathcal {T}_s \subseteq \{t^{s}_{i}\}$ which achieves complete coverage for the entire fault list. The test vectors belonging to the rest of $\{t^{s}_{i}\}$, i.e. $\{t^{s}_{i}\} - \mathcal {T}_s$, can be discarded to be redundant. Although a greedy selection, we found that this step reduces the overall test set size significantly. Further test compaction can be achieved, at the cost of additional computational overhead, using specialized test compaction schemes (Fig. 7).

One important point worth noting is that, it is not guaranteed by the proposed test generation scheme that all possible test vectors which trigger a particular trigger combination will get generated. As the fault list ($\mathcal {F}_{s}$) is calculated only based on the test vectors in $\{t^{s}_{i}\}$, it might not cover all possible payloads for a trigger combination s. However, for each test vector $t \in \{t^{s}_{i}\}$, it is guaranteed that all feasible payloads will be enumerated. Further, it can be deterministically decided if a test vector $t \in \{t^{s}_{i}\}$ will have any payload or not. In fact, for most of the trigger combinations, we got test vectors which are either redundant, or doesn’t have any payload. It is also observed that the number of test vectors for some hard-to-activate trigger combinations are really low (typically 1 to 5 vectors). For these cases, the fault coverage may be poor and many payloads for the trigger combination remains unexplored. To resolve this issue, we add some extra test vectors derived by filling the don’t care bits (if any) of the PTV. This is only done for those trigger combinations for which the number of triggering vectors are less than five. These newly generated vectors are needed to be checked by simulation so that they successfully trigger the corresponding triggering combination, before their inclusion to the test set $\{t^{s}_{i}\}$. This step is found to improve the test coverage. The compacted test vector selection scheme is described in Algorithm 3. At the end of this step, we obtain a compact set of test vectors with high trigger and Trojan coverage.

3.2 Evaluation of Effectiveness

It is reasonable to assume that an attacker will be only interested in Trojans with low effective triggering probability, irrespective of the individual rareness values of the constituent rare nodes. Thus, a natural approach for an attacker would be to rank the Trojans according to their triggering probability and select Trojans which are below some specific triggering threshold ($P_{tr}$). Intuitively, an attacker may choose the Trojan which is rarest among all, but it may lead to easy detection as very rare Trojans are often found to be significantly small in number and are expected to be well tracked by the tester. Thus, a judicious attacker would select a Trojan that will remain well-hidden in the pool of Trojans, but achieves extremely low Triggering probability at the same time. To simulate the above mentioned behaviour of the attacker, we first select new samples of candidate Trojans from the Trojan space with varying range of $\theta$ values. We denote each of such samples as $\mathcal {S}^{\theta }_{test}$ and ensure that $|\mathcal {S}^{\theta }_{test}| = |\mathcal {S}|$. Subsequently, each of these sets is refined by the SAT tool by selecting only feasible Trojans. By feasible Trojans we mean the Trojans which are triggerable and whose impacts are visible at the outputs. We denote the set of such feasible Trojan sets obtained for different $\theta$ values as $\{\mathcal {S}^{f}_{test}\}$. Next, we filter out Trojans from these sets which are below a specified triggering threshold $P_{tr}$. Finally, all these subsets are combined to form a set of Trojans $\mathcal {S}^{tr}_{test}$. This set contains Trojans whose triggering probabilities are below $P_{tr}$ and is used for the evaluation of the effectiveness of the proposed methodology. The value of $P_{tr}$ is set to $10^{-6}$ based on the observation that for most of the benchmark circuits considered, there are roughly 30% Trojans which have triggering probabilities below $10^{-6}$. Also, below the range ($10^{-7}-10^{-8}$) the number of Trojans are extremely low, which may leave the attacker only with a few options.

4 Experimental Results and Discussion

4.1 Experimental Setup

The test generation scheme, including the GA and the evaluation framework, were implemented using C++. We used the zchaff SAT solver [9] and HOPE fault simulator [12]. We restricted ourselves to a random sample of 100, 000 trigger combinations [5], each having up to four rare nodes as trigger nodes. We also implemented the MERO methodology side by side for comparison. We evaluated the effectiveness of the proposed scheme on a subset of ISCAS-85 and ISCAS-89 benchmark circuits, with all ISCAS-89 sequential circuits converted to full scan mode. The implementation was performed and executed on a Linux workstation with a 3 GHz processor and 8 GB of main memory.

Table 1. Comparison of the proposed scheme with MERO with respect to testset length.

Table 2. Trigger and Trojan coverage at various stages of the proposed scheme. at $\theta = 0.1$ for random sample of Trojans upto 4 rare node triggers (Sample size is 100, 000 for combinational circuits and 10, 000 for sequential circuits).

4.2 Test Set Evaluation Results

Table 1 presents a comparison of the testset lengths generated by the proposed scheme, with that generated by MERO. It also demonstrates the impact of Algo-3, by comparing the test vector count before Algo-3 ($TC_{GASAT}$) and after Algo-3 ($TC_f$). As would be evident, for similar number of test patterns the proposed scheme achieves significantly better trigger as well as Trojan coverage than MERO. The gate count of the circuits and the time required to generate the corresponding testsets is also presented to exhibit the scalability of the ATPG heuristic.

Table 2 presents the improvement in trigger and Trojan coverage at the end of each individual step of the proposed scheme, to establish the importance of each individual step. From the table, it is evident that the first two steps consistently increase the trigger and Trojan coverage. However, after the application of payload aware test set selection (Algo-3), the trigger coverage slightly decreases for some circuits, whereas the Trojan coverage slightly increases. The decrement in trigger coverage is explained by the fact that some of the trigger combinations do not have any corresponding payload – as a result of which they are removed. In contrary, the addition of some “extra test vectors” by Algo-3 helps to improve the Trojan coverage.

Table 3 presents the trigger and Trojan coverage for eight benchmark circuits, compared MERO test patterns with $N = 1000$ and $\theta$ $= 0.1$. In order to make a fair comparison, we first count the number of distinct test vectors generated by MERO ($TC_{MERO}$) with the above mentioned setup, and then set GA to run until the number of distinct test vectors in the database becomes higher than $TC_{MERO}$. We denote the number of distinct test vectors after GA run as $TC_{GA}$. Note that, the SAT step is performed after the GA run, and thus the total number of test vectors after the SAT step ($TC_{GASAT}$) is slightly higher than $TC_{MERO}$. The test vector count further reduces after the Algo-3 is run. We denote the final test vector count as $TC_f$.

Table 3. Comparison of trigger and Trojan Coverage among MERO patterns and patterns generated with the proposed scheme with $\theta = 0.1$; $N = 1000$ (for MERO) and for trigger combinations containing up to four rare nodes.

Fig. 8.

Comparison of trigger and Trojan coverage of the proposed scheme with MERO, with varying triggering threshold ($\theta$).

Fig. 9.

Trigger and Trojan coverage of the proposed scheme on a set of special Trojans, which combine some easily triggerable nodes with some extremely rare nodes.

Table 4. Coverage comparison between MERO and the proposed Scheme for sequential Trojans. The sequential Trojan model considered is same as  [5].

To further illustrate the effectiveness of the proposed scheme, in Fig. 8 we compare the trigger and Trojan coverage obtained from MERO with that of the proposed scheme, by varying the rareness threshold ($\theta$) for the c7552 benchmark circuit. It is observed that the proposed scheme outperforms MERO to a significant extent. Further, it is interesting to note that both MERO and the proposed scheme achieve the best coverage at $\theta = 0.09$. The coverage gradually decreases towards both higher and lower values of $\theta$. The reason is that for higher $\theta$ values (e.g. 0.2, 0.3), the initial candidate Trojan sample set ($\mathcal {S}$), over which the heuristic implementation is tuned, contains a large number of “easy-to-trigger” combinations. Hence, the generated test set remains biased towards “easy-to-trigger” Trojans and fails to achieve good coverage over the “hard-to-trigger” evaluation set used. On the other hand, at low $\theta$ values the cardinality of the test vector set created becomes very small as the number of potent Trojans at this range of $\theta$ is few, and they are sparsely dispersed in the candidate Trojan set $\mathcal {S}$. As a result, this small test set hardly achieves significant coverage over the Trojan space. The coverage for Trojans constructed by combining some easily triggerable nodes with some extremely rare nodes also follows a similar trend (shown in Fig. 9). It can be thus remarked that the tester should choose a $\theta$ value, so that the initial set $\mathcal {S}$ contains a good proportion of Trojans with low triggering probability, while also covering most of the moderately rare nodes.

Finally, we test our scheme with sequential Trojans. The counter based Trojan model as described in [5] was considered. We consider Trojans up to four states, as larger Trojans have been reported to be easily detectable by side channel analysis techniques [17]. It can be observed form Table 4 that as for the combinational circuits, the the proposed scheme outperforms MERO.

4.3 Application to Trojan Diagnosis

Diagnosis of a Trojan once it gets detected is important for system-level reliability enhancement. In [19], the authors proposed a gate-level-characterization (GLC) based Trojan diagnosis method. The scheme proposed in this paper can be leveraged for a test diagnosis methodology. The data structure $\mathcal {D}$ can be extended to a complete Trojan database, which will contain four-tuples (s, V, P, O), where s is a trigger combination, V is the set of corresponding triggering test vectors, P is the set of possible payloads, and O is the set of faulty outputs corresponding to the test patterns in V, due to the activation of some Trojan instance. Based on this information, one can design diagnosis schemes using simple cause-effect-analysis, or other more sophisticated techniques. The complete description of a diagnosis scheme is however out of the scope of this paper.

4.4 Application to Side Channel Analysis Based Trojan Detection

Most recent side-channel analysis techniques target the preferential activation of a specific region of the circuit, keeping the other regions dormant [1, 19], since side channel analysis is more effective if the Trojan is activated, at least partially [17]. Hence, the proposed technique, with its dual emphasis on test pattern generation directed towards triggering of Trojans, as well as propagation of the Trojan effect to the primary output, can be a valuable component of a side channel analysis based Trojan detection methodology.

5 Conclusions

Detection of ultra small Hardware Trojans has traditionally proved challenging by both logic testing and side channel analysis. We have developed an ATPG scheme for detection of HTHs dependent on rare input triggering conditions, based on the dual strengths of Genetic Algorithm and Boolean Satisfiability. The technique achieves good test coverage and compaction and also outperforms a previously proposed ATPG heuristic for detecting HTHs for benchmark circuits. Future research would be directed towards developing comprehensive Trojan diagnosis methodologies based on the database created by the current technique.