Keywords

1 Introduction

We are facing a fundamental change with respect to computing and information technologies. For a few years the computing world has begun to move towards the “many computers – one user” paradigm, in which the computing devices are often every day devices – a situation frequently referred to as the Internet of Things (IoT). At the same time, security has become an increasingly important issue for many IoT applications as more and more sensitive personal data is transferred in a wireless manner. This implies that the use of cryptography primitives in daily life plays an increasingly crucial role. Among the different primitives, block ciphers are arguably the most widely used ones.

Great progress has been made in designing and analyzing block ciphers, especially with the introduction of the AES, but also more recently with many block ciphers appearing in the area of lightweight cryptography. However, there is still research on fundamental aspects of these ciphers going on and important questions are still not understood. For instance we are not able to assess the security of a block cipher as such, but only its security against known attacks. The two main classes to be considered here are linear and differential attacks and their variants.

Differential Cryptanalysis. The first type of attacks that is applicable to a large set of block ciphers is the differential attack introduced by Biham and Shamir in [8]. Since its invention in the early nineties several variants, tweaks and generalizations have been discussed. In 1994, Knudsen introduced so-called truncated differentials attacks [25]. This relaxation of classical differential attacks has since then been applied to many (round-reduced) block ciphers. In the same paper, Knudsen furthermore introduced the concept of higher-order differentials, an attack vector based on initial consideration by Lai in [27]. Another variant of differential cryptanalysis (again by Knudsen) is impossible differentials cryptanalysis which uses differentials with probability zero. This concept, introduced in [26] has later been successfully applied numerously, e.g. to (almost) break the cipher Skipjack [3]Footnote 1. In 1999, Wagner introduced the boomerang attack, which allows to connect two differentials over parts of a cipher that do not coincide in the middle. This attack allowed, among others, to break the cipher COCONUT98 [39]. Later, the boomerang attack itself has been generalized to amplified boomerang attack [24] and rectangle attack [4].

Linear Cryptanalysis. The second general applicable attack on block ciphers is the Matsui’s linear attack [34]. Similarly to differential attacks, since its introduction many extensions and improvements have been made, and we mention a selection here. A more precise estimate for the success probability and the data complexity are given by Selçuk [38]. The effect of using more than one linear trail, referred to as linear hulls, has been introduced by Nyberg [37]; see also Daemen and Rijmen [21]. Multidimensional linear attacks have been studied by Hermelin, Cho, and Nyberg [23] as a way to further reduce the data complexity of the basic attack. These approaches have been used for example by Cho [20]. More recently, the zero-correlation attacks introduced by Bogdanov et al. in [15] have become popular. These attacks, which can be seen as the natural counterpart of the impossible differential attacks, are based on linear approximations with probability exactly \(1/2\). A further generalization of zero-correlation attacks, namely attacks based on key-invariant biases, was presented in [13].

Theoretical Links Between Linear and Differential Cryptanalysis. Most of the work has been done independently for linear and differential cryptanalysis and there are examples of ciphers that are more resistant against one type than against the other. However, the concepts are closely related. A first fundamental link between them was already given in 1994 by Chabaud and Vaudenay (see [19]), where it was shown that the probability of a differential can be expressed in terms of a sum of correlations of linear approximations. Interestingly, this link was for a long time not used in practice due to its large computational complexity. Only in 2013, Blondeau and Nyberg used the link in [11] to compute the probability of a differential given the correlations of many linear approximations. As a second result [12], Blondeau and Nyberg generalized the link to the case of multidimensional linear distinguishers and truncated differential distinguishers.

Differential-Linear Cryptanalysis. On the cryptanalytical side, differential and linear attacks have been used jointly for the first time by Langford and Hellman [30]. The basic idea of differential-linear cryptanalysis is to split the cipher under consideration into two parts. The split should be such that, for the first part of the cipher there exists a strong truncated differential and for the second part there exists a strongly biased linear approximation. In [30], the particular case where the differential over the first part holds with probability one has been introduced. Later on, Biham et al. [5, 29] generalized this attack using a probabilistic truncated differential on the first rounds of the distinguisher.

More recently in 2012 [33], Lu studied the validity of the model proposed by Biham et al. with the aim of minimizing the assumptions needed for the validity of the attack.

Wagner presented ideas towards a unified view of statistical block cipher cryptanalysis [40]. While concentrating on structural similarities between different attacks in a Markov setting he relied, albeit with some doubts, on the previously made heuristic assumptions under which the differential-linear attacks had been claimed to work.

It is very remarkable that in none of the previous work on differential-linear cryptanalysis, the theoretical link presented in [19] between linear and differential attacks is used to model –and understand better– the general behavior of differential-linear cryptanalysis.

Our Contribution. In this paper we take the natural step and apply the theoretical link between linear and differential cryptanalysis to differential-linear cryptanalysis. This, not surprisingly, has a couple of nice consequences.

To the best of our knowledge, we are, for the first time, able to exactly express the bias of a differential-linear approximation by a closed expression. The formula is exact under the sole assumption that the two parts of the cipher are independent. In particular it is exact when averaging over all round-keys.

While evaluating this exact expression is (for full-scale ciphers) computational unfeasible, the formulation given in Theorem 2 allows, under clear assumption, to approximate the bias efficiently. In this sense we hereby complement the work of Lu by stating minimal assumptions.

Moreover, given this exact expression and –along with this– a deeper understanding of differential-linear attacks allows us to substantially generalize the attack vector. In particular, we study the possibility to take into consideration the hull of a differential-linear approximation and introduce a multidimensional generalization of differential-linear cryptanalysis which is defined for multiple input differences and multidimensional linear output masks.

Note that, we do not propose new concrete attacks. But rather we provide a sound framework for previous and future work on differential-linear cryptanalysis.

Organization of the Paper. In Sect. 2, we fix our notations and state several general results on differential and linear cryptanalysis. The related work is resumed in Sect. 3. In Sect. 4, we develop the exact expression for the bias of the differential-linear distinguisher (cf. Theorem 2) and outline its meaning with an example using the block cipher Serpent. Furthermore, we elaborate more on the comparison with previous work. In Sect. 5, we derive conditions on how and if it is possible to obtain good and practical estimations of the exact expression. We back-up our assumption with experiments using small scale variants of the cipher PRESENT. Finally, in Sect. 6, we generalize the concept of differential-linear cryptanalysis to the case of multiple differentials and multiple linear approximations and derive expressions for the biases and the attack complexities for this generalization. Sect. 7 concludes the paper.

2 Basics of Linear and Differential Cryptanalysis

2.1 Linear Correlation and Differential Probability

In differential cryptanalysis [8], the attacker is interested in identifying and exploiting non-uniformity in occurrences of plaintext and ciphertext differences. Given a vectorial Boolean function \(F:\mathbb {F}_2^{n}\rightarrow \mathbb {F}_2^{n}\), a differential is given by a pair \((\delta ,\varDelta )\) of an input difference \(\delta \in \mathbb {F}_2^{n}\) and an output difference \(\varDelta \in \mathbb {F}_2^{n}\) and its probability is defined as

$$ \mathbf{P}[\delta \overset{F}{\rightarrow }\varDelta ] = 2^{-n}\#\{x\in \mathbb {F}_2^{n}\,|\, F(x)+ F(x +\delta ) = \varDelta \}. $$

Linear cryptanalysis [34] uses a linear relation between bits from plaintexts, corresponding ciphertexts and encryption key. A linear relation of bits of data \(x \in \mathbb {F}_2^{n}\) is determined by a mask \(a \in \mathbb {F}_2^{n}\) and is given as a Boolean function \(f(x) = a\cdot x\) where “\(\,\cdot \,\)” is the natural inner product of the vectors \(a\) and \(x\) in \(\mathbb {F}_2^{n}\). The strength of a linear relation is measured by its correlation.

The correlation of a Boolean function \(f:\mathbb {F}_2^{n}\rightarrow \mathbb {F}_2^{}\) is defined as

$$ \mathrm{\mathbf{cor}}(f) = \mathrm{\mathbf{cor}}(f(x))= 2^{-n}\Big [\#\left\{ x\in \mathbb {F}_2^{n}|f(x)=0\right\} -\#\left\{ x\in \mathbb {F}_2^{n}|f(x)= 1 \right\} \Big ], $$

where the quantity within brackets correspond to the Fourier coefficient of \(f\) at zero, and can be computed using the Walsh transform of \(f\), see e.g. [18].

In this paper, a block cipher or a part of it with a fixed key and block size \(n\) is considered as a bijective vector-valued Boolean function \(F:\mathbb {F}_2^{n}\rightarrow \mathbb {F}_2^{n}\). In the general model of differential-linear cryptanalysis to be built in this paper, we consider a set of input differences to the cipher which form a linear subspace of \(\mathbb {F}_2^{n}\). Given a subspace \(U\) of \(\mathbb {F}_2^{n}\), let us denote by \(U^{\perp }\) the orthogonal subspace of \(U\) with respect to the inner product of \(\mathbb {F}_2^{n}\). Then

$$\begin{aligned} U^{\perp } = \{v \in \mathbb {F}_2^{n}\,|\, u\cdot v = 0,\, \text{ for } \text{ all } u \in U \}. \end{aligned}$$

Let us denote by \(0_{\ell } \in \mathbb {F}_2^{\ell }\) the all-zero string of length \(\ell \). If \(U = \mathbb {F}_2^{s}\times \{0_t\}\), for some positive integers \(s\) and \(t\), where \(s+t =n\), then \(U^{\perp } = \{0_s\}\times \mathbb {F}_2^{t}\). In this manner we obtain a splitting of \(\mathbb {F}_2^{n}\) to two mutually orthogonal subspaces, whose intersection is \(\{0_n\}\). Another type of example of orthogonal subspaces is obtained for \(U = \{(0,0),(1,1)\}\times \{0_{n-2}\}\). Then \(U^{\perp } = \{(0,0),(1,1)\}\times \mathbb {F}_2^{n-2}\), in which case \(U\subset U^{\perp } \). In any case, the dimensions of \(U\) and \(U^{\perp }\) add up to \(n\).

A truncated differential [25] over a vectorial Boolean function \(F:\mathbb {F}_2^{n}\rightarrow \mathbb {F}_2^{n}\) is a set of ordinary differentials \((\delta ,\varDelta )\) where the input differences \(\delta \in U^{\perp }\) and the output differences \(\varDelta \in V^{\perp }\). In this paper we assume that \(U\) and \(V\) are linear subspaces of \(\mathbb {F}_2^{n}\). In this manner, the truncated differential is determined by a pair of linear spaces \(U\) and \(V\). The strength of a truncated differential is often measured by the number of solutions \((x,\delta ,\varDelta ) \in \mathbb {F}_2^{n}\times (U^{\perp }\setminus \{0\})\times V^{\perp }\) to the equation

$$\begin{aligned} F(x+\delta ) + F(x) = \varDelta . \end{aligned}$$
(1)

To facilitate the derivations in this paper we will use a different but closely related quantity, which allows the zero difference in the input. It is straightforward to show that, the number of solutions \((x,\delta ,\varDelta ) \in \mathbb {F}_2^{n}\times U^{\perp }\times V^{\perp }\) of (1) can be computed as

$$\begin{aligned} \sum _{\delta \in U^{\perp }, \varDelta \in V^{\perp }}\#\{x\in \mathbb {F}_2^{n}\,|\, F(x+\delta ) + F(x) = \varDelta \}. \end{aligned}$$

We denote by \(\mathbf{P}[U^{\perp }\overset{F}{\rightarrow }V^{\perp }]\) the probability that a pair of inputs \((x, x+\delta )\), where \(x\) is picked uniformly at random in \(\mathbb {F}_2^{n}\) and \(\delta \in U^{\perp }\), gives an output difference \(\varDelta \in V^{\perp }\).

Proposition 1

Let \(U\) and \(V\) be linear subspaces of \(\mathbb {F}_2^{n}\), we have

$$\begin{aligned} \mathbf{P}[U^{\perp }\overset{F}{\rightarrow }V^{\perp }]= & {} \frac{1}{2^{n}|U^{\perp }|}\# \{(x,\delta ,\varDelta ) \in \mathbb {F}_2^{n}\times U^{\perp }\times V^{\perp } \,|\, F(x+\delta ) + F(x)= \varDelta \}\nonumber \\= & {} \frac{1}{|U^{\perp }|} \sum _{\delta \in U^{\perp },\,\varDelta \in V^{\perp }} \mathbf{P} [\delta \overset{F}{\rightarrow }\varDelta ]. \end{aligned}$$
(2)

The probability \(\mathbf{P}[U^{\perp }\overset{F}{\rightarrow }V^{\perp }]\) which can be expressed in the two different ways shown in Proposition 1 will be called the truncated differential probability.

Let us denote by \(\mathbf{P}[U^{\perp }\setminus \{0\}\overset{F}{\rightarrow }V^{\perp }]\) the probability for the truncated differential derived analogically as above but without allowing the zero input difference. Then we have the following relation:

$$\begin{aligned} |U^{\perp }|\cdot \mathbf{P}[U^{\perp }\overset{F}{\rightarrow }V^{\perp }] = 1 +(|U^{\perp }|-1)\cdot \mathbf{P}[U^{\perp }\setminus \{0\}\overset{F}{\rightarrow }V^{\perp }]. \end{aligned}$$
(3)

In particular, for the ordinary differential probability, we have

$$\begin{aligned} \mathbf{P}[\delta \overset{F}{\rightarrow }\varDelta ] = 2\cdot \mathbf{P}[sp(\delta )\overset{F}{\rightarrow }\varDelta ]-1, \end{aligned}$$

for all \(\delta ,\,\varDelta \in \mathbb {F}_2^{n}\), \(\delta \ne 0\). Here, as well as later in the paper, we use the notation \(sp(a)\) to denote the vector subspace \(\{0,a\} \subset \mathbb {F}_2^{n}\) spanned by \(a\).

Recalling the symmetry of the probability of single differential for a bijective function \(F\)

$$\begin{aligned} \mathbf{P} [\delta \overset{F}{\rightarrow }\varDelta ] = \mathbf{P} [\varDelta \overset{F^{-1}}{\rightarrow }\delta ], \end{aligned}$$

let us note that the truncated differential probability is not symmetric, except in the case when \(|U| = |V|\). In general, we have

$$\begin{aligned} |U^{\perp }|\cdot \mathbf{P} [U^{\perp }\overset{F}{\rightarrow }V^{\perp }] = |V^{\perp }| \cdot \mathbf{P} [V^{\perp }\overset{F^{-1}}{\rightarrow }U^{\perp }]. \end{aligned}$$

Let us recall the link between the differential probabilities and the squared correlations of linear approximations of vectorial Boolean functions presented by Chabaud and Vaudenay [19]. In the context of this paper we write it as follows.

$$\begin{aligned} \mathbf{P}[\delta \overset{F}{\rightarrow }\varDelta ] = 2^{-n} \sum _{u\in \mathbb {F}_2^{n}} \sum _{v\in \mathbb {F}_2^{n}} (-1)^{u\cdot \delta + v\cdot \varDelta } \mathrm{\mathbf{cor}}^2\left( u\cdot x+ v\cdot F(x)\right) , \end{aligned}$$
(4)

where \(F:\mathbb {F}_2^{n}\rightarrow \mathbb {F}_2^{n}\) is a vectorial Boolean function, and \((\delta ,\,\varDelta ) \in \mathbb {F}_2^{n}\times \mathbb {F}_2^{n}\). By applying this link for all \(\delta \in U^{\perp }\) and \(\varDelta \in V^{\perp }\) in (2) we obtain the following result which is a generalization of [11, 12].

Theorem 1

The probability of a truncated differential with input differences in \(U^\perp \) and output differences in \(V^\perp \) can be computed as a sum of squared correlations with input masks in \(U\) and output masks in \(V\) as

$$\begin{aligned} \mathbf{P}[U^{\perp } \overset{F}{\rightarrow } V^{\perp }] = \frac{1}{|V|}\sum _{u\in U,v\in V } \mathrm{\mathbf{cor}}^2\left( u \cdot x+ v\cdot F(x)\right) . \end{aligned}$$

Proof

If for \(u\in \mathbb {F}_2^{n}\) we have \(u\cdot \delta = 1\) for some \(\delta \in U^{\perp }\) then the linear function \(\delta \mapsto u\cdot \delta \) is non-zero, and hence balanced on \(U^{\perp }\). Thus in this case \(\sum _{\delta \in U^{\perp }} (-1)^{u\cdot \delta } = 0\). This is not the case exactly if we have \(u\in U\), and then \(\sum _{\delta \in U^{\perp }} (-1)^{u\cdot \delta } = |U^{\perp }|\). Then, applying the same reasoning for all \(v\in \mathbb {F}_2^{n}\) gives the claim.    \(\square \)

Corollary 1

For all \(w\in \mathbb {F}_2^{n}\setminus \{0\}\) and \(\varDelta \in \mathbb {F}_2^{n}\setminus \{0\}\) we have

$$\begin{aligned} \mathbf{P}[\varDelta \overset{F}{\rightarrow } sp(w)^{\perp }] = \sum _{v\in sp(\varDelta )^{\perp }}\mathbf{cor}^2(v\cdot x + w\cdot F(x)). \end{aligned}$$

Proof

From (3) and Theorem 1, we have

$$\begin{aligned}&\mathbf{P}[\varDelta \overset{F}{\rightarrow } sp(w)^{\perp }] = 2\cdot \mathbf{P}[sp(\varDelta ) \overset{F}{\rightarrow } sp(w)^{\perp }] -1 \\&= 2\cdot \frac{1}{2} \cdot \sum _{v\in sp(\varDelta )^{\perp }, b\in sp(w)}\mathbf{cor}^2(v\cdot x + b\cdot F(x)) -1\\&= \sum _{v\in sp(\varDelta )^{\perp }}\mathbf{cor}^2(v\cdot x + w\cdot F(x)). \end{aligned}$$

   \(\square \)

2.2 Round Independence

Computation of differential probabilities or linear correlations over an iterated cipher is often done assuming that the rounds of the cipher behave independently.

Definition 1

Two parts \(E_0\) and \(E_1\) of an \(n\)-bit block cipher \(E = E_1\circ E_0\) are said to be differentially round independent if for all \((\delta ,\varOmega )\in \mathbb {F}_2^{n}\times \mathbb {F}_2^{n}\) the following holds

$$\begin{aligned} \mathbf{P}[\delta \overset{E}{\rightarrow }\varOmega ] = \sum _{\varDelta \in \mathbb {F}_2^{n}} \mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ] \mathbf{P}[\varDelta \overset{E_1}{\rightarrow }\varOmega ]. \end{aligned}$$

Analogically, the parts \(E_0\) and \(E_1\) are said to be linearly round independent if for all \((u, w) \in \mathbb {F}_2^{n}\times \mathbb {F}_2^{n}\) the following holds

$$\begin{aligned} \mathrm{\mathbf{cor}}^2(u\cdot x + w\cdot E(x))= \sum _{v\in \mathbb {F}_2^{n}}\mathrm{\mathbf{cor}}^2(u\cdot x + v\cdot E_0(x))\mathrm{\mathbf{cor}}^2(v\cdot y + w\cdot E_1(y)). \end{aligned}$$

It was proved in [2] that the rounds of a Markov cipher [28] are both differentially and linearly round independent. Next we show that differential and linear round independence are equivalent concepts for any cipher.

Proposition 2

Two parts \(E_0\) and \(E_1\) of an \(n\)-bit block cipher \(E = E_1\circ E_0\) are differentially round independent if and only if they are linearly round independent.

Proof

Let us start by stating (4) in the following equivalent form

$$\begin{aligned} \sum _{\delta \in \mathbb {F}_2^{n}}(-1)^{u\cdot \delta } \mathbf{P}[\delta \overset{F}{\rightarrow }\varDelta ] = \sum _{v\in \mathbb {F}_2^{n}} (-1)^{v\cdot \varDelta } \mathrm{\mathbf{cor}}^2\left( u\cdot x+ v\cdot F(x)\right) . \end{aligned}$$

This is obtained by applying the inverse Fourier transform to the input difference. By applying it to the output difference, another equivalent form can be given where the first summation is taken over \(\varDelta \) and the second summation over \(u\). We refer to these equations as partial inverses of (4). A further variant is obtained by applying the inverse Fourier transform on both differences. We call it the inverse of (4).

Let us now assume that the parts of the cipher are differentially round independent. Then using the inverse of (4) and the assumption of differential round independence, we get

$$\begin{aligned}&\mathrm{\mathbf{cor}}^2\left( u\cdot x+ w\cdot E(x)\right) = 2^{-n} \sum _{\delta \in \mathbb {F}_2^{n}} \sum _{\varOmega \in \mathbb {F}_2^{n}} (-1)^{u\cdot \delta + w\cdot \varOmega } \mathbf{P}[\delta \overset{E}{\rightarrow }\varOmega ]\\&= 2^{-n} \sum _{\varDelta \in \mathbb {F}_2^{n}} \sum _{\delta \in \mathbb {F}_2^{n}} (-1)^{u\cdot \delta } \mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ] \sum _{\varOmega \in \mathbb {F}_2^{n}} (-1)^{w\cdot \varOmega } \mathbf{P}[\varDelta \overset{E_1}{\rightarrow }\varOmega ]. \end{aligned}$$

Then using the both partial inverses of (4) we obtain

$$\begin{aligned}&\mathrm{\mathbf{cor}}^2\left( u\cdot x+ w\cdot E(x)\right) \\&= 2^{-n}\!\!\!\sum _{\varDelta \in \mathbb {F}_2^{n}}\! \sum _{v\in \mathbb {F}_2^{n}} (-1)^{v\cdot \varDelta }\mathrm{\mathbf{cor}}^2\!\left( u\cdot x\!+\! v\cdot E_0(x)\right) \!\! \sum _{v'\in \mathbb {F}_2^{n}}\! (-1)^{v'\cdot \varDelta }\mathrm{\mathbf{cor}}^2\left( v'\cdot y\!+\! w\cdot E_1(y)\right) \\&= 2^{-n}\!\!\sum _{v\in \mathbb {F}_2^{n}}\sum _{v'\in \mathbb {F}_2^{n}}\mathrm{\mathbf{cor}}^2\!\left( u\cdot x\!+\! v\cdot E_0(x)\right) \mathrm{\mathbf{cor}}^2\left( v'\cdot y\!+\! w\cdot E_1(y)\right) \!\!\sum _{\varDelta \in \mathbb {F}_2^{n}} (-1)^{(v+v')\cdot \varDelta } . \end{aligned}$$

The sum over \(\varDelta \) is non-zero if and only if \(v = v'\) and the value of this sum, \(2^{n}\), cancels with the factor \(2^{-n}\). We can then see that the condition of linear round independence is satisfied. The converse proof is analogous.    \(\square \)

Few ciphers satisfy round independence in the strict sense of Definition 1. On the other hand, \(n\)-bit ciphers of the form \(E_K(x) = E_1(E_0(x)+K)\) with \(n\)-bit key \(K\) are round independent on average over the key. For simplicity, the results given in this paper will be stated in terms of strict round independence, but can be reformulated using average round independence for such ciphers.

3 Previous Work

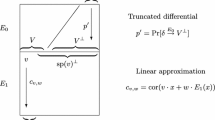
Let \(E:\mathbb {F}_2^{n}\rightarrow \mathbb {F}_2^{n}\) be a cipher. When applying the technique of differential-linear cryptanalysis the iterated block cipher is presented as a composition \(E=E_1\circ E_0\) of two parts. The first part \(E_0\) is chosen in such a way that there is some strong truncated differential over \(E_0\). Let \(U\) and \(V\) be the subspaces that define the truncated differential. Typically, the input difference space \(U\) is selected so that \(U^{\perp }\) is one-dimensional. The output difference space \(V^{\perp }\) is usually larger. It is then assumed that there is a strong linear approximation \((v,w)\) over \(E_1\), where \(v\in V\), which means that \(v \cdot \varDelta = 0\) for all \(\varDelta \in V^{\perp }\).

In this section, we assume that the input-difference space \(U^{\perp }\) is one-dimensional. Let \(\delta \) be the sole non-zero element in \(U^{\perp }\). Then the bias of the differential-linear approximation is defined as

$$ \mathcal E_{\delta ,w}:=\mathbf{P}[w\cdot \left( E(x+\delta )+E(x)\right) = 0] -\frac{1}{2}. $$

In the previous treatments [5, 30, 33], \(\mathcal E_{\delta ,w}\) is evaluated using the Piling-up lemma [34] by decomposing the Boolean variable \(w\cdot \left( E(x+\delta )+E(x)\right) \) as a sum of three variables

$$\begin{aligned} w\cdot \left( E(x+\delta )+E(x)\right)= & {} v\cdot E_0(x+\delta )+w\cdot E(x+\delta )\nonumber \\+ & {} v\cdot \left( E_0(x+\delta )+ E_0(x)\right) \\+ & {} v\cdot E_0(x)+w\cdot E(x),\nonumber \end{aligned}$$
(5)

which are assumed to be independent as \(x\) varies.

By using the following notation for the involved biases

$$\begin{aligned} \epsilon _{v,w}= & {} \mathbf{P}[v\cdot y + w\cdot E_1(y)=0] -\frac{1}{2}\nonumber \\ \varepsilon _{\delta ,v}= & {} \mathbf{P}[v\cdot \left( E_0(x+\delta )+ E_0(x)\right) =0]-\frac{1}{2} = \mathbf{P}[\delta \overset{E_0}{\rightarrow } sp(v)^{\perp }] -\frac{1}{2} , \end{aligned}$$
(6)

the Piling-up lemma gives

$$\begin{aligned} \mathcal E_{\delta ,w} = 4 \varepsilon _{\delta ,v} \epsilon _{v,w}^2. \end{aligned}$$
(7)

It remains to determine \(\varepsilon _{\delta ,v}\) given the truncated differential probability \(\mathbf{P}[\delta \overset{E_0}{\rightarrow } V^{\perp }]\). This is where the previous studies differ. In [30], \(\mathbf{P}[\delta \overset{E_0}{\rightarrow } V^{\perp }] = 1\), in which case \(\mathbf{P}[\delta \overset{E_0}{\rightarrow } sp(v)^{\perp }] = 1\), since \(v\in V\). According to Biham et al. [7] this was generalized first in [29] and later by Biham et al. [5] to the case where \(\mathbf{P}[\delta \overset{E_0}{\rightarrow } V^{\perp }] < 1\). In [5], Biham et al. denote this probability by \(p'\) and by assuming that when \(\varDelta \notin V^{\perp }\) the parities of \(v\cdot \varDelta \) are balanced they obtain the estimate

$$ \mathbf{P}[\delta \overset{E_0}{\rightarrow } sp(v)^{\perp }] \approx p' + (1-p')\frac{1}{2}. $$

This exact equality holds if \(p' = 1\). In general, it gives only an approximation, for the simple reason that if a linear function \(v \cdot y\) vanishes in \(V^{\perp }\), it cannot be balanced outside \(V^{\perp }\). The approximation is better, if \(V^{\perp }\) is small, which is the case studied in [5]. This approximation becomes worse, however, as \(V^{\perp }\) increases. The extreme case is \(sp(v) = V\). Then \(v\cdot y = 1\), for all \(y\notin V^{\perp }\).

This problem was observed by Lu and suggested to be solved in his study [33] by restricting to the case where the output difference space of the truncated differential is the hyperplane \(sp(v)^{\perp }\).

As in practice, \(V^{\perp }\) is often smaller than a zero space of a linear Boolean function, we have that \(\mathbf{P}[\delta \overset{E_0}{\rightarrow } V^{\perp }]\) is less than or equal to \(\mathbf{P}[\delta \overset{E_0}{\rightarrow } sp(v)^{\perp }]\). It can also be strictly less, in which case replacing the latter by the former in the estimation of the bias (6) may lead to a wrong result for \(\mathcal E_{\delta ,w}\). Biham et al. suggest that the other output differences \(\varDelta \in sp(v) \setminus V^{\perp }\) may occur with high probability and affect their approximation and stress the importance to do experimental verification.

Note that it would be possible to fix the assumption by Biham et al. by correcting the probability of zero parity outside \(V^{\perp }\) to \((2^{n-1}- |V^{\perp }|)/(2^{n} - |V^{\perp }|)\).

In [32], the authors mention the possibility of using multiple linear approximations in order to improve the complexity of a differential-linear distinguisher. Their study, which is based on the differential-linear model of Biham et al. [6] and on the multiple linear model of Biryukov et al. [9], assume that the distinguisher is built from the combination of only one truncated differential with independent linear approximations.

The goal of this paper is to analyze in more detail what is happening in the intermediate layer of the differential-linear approximation and take into account not only more high-probability output differences from \(E_0\) but also more, not necessarily independent, linear approximations over \(E_1\). Still, many differences and linear masks in the intermediate layer must be left out. To handle them in Theorem 3, we make an assumption analogical to the one of Biham et al. but corrected.

4 Differential-Linear Hull

The basic tool in examining the intermediate layer between \(E_0\) and \(E_1\) is the following theorem. We use the notation \(\mathcal E_{\delta ,w}\) and \(\varepsilon _{\delta ,v}\) introduced in the preceding section, and denote the correlation of the linear approximation \(v\cdot y+ w \cdot E_1(y)\) by \(c_{v,w}\). Then \(c_{v,w} = 2\epsilon _{v,w}\) in relation to the notation used in the preceding section.

Theorem 2

Assume that the parts \(E_0\) and \(E_1\) of the block cipher \(E= E_1\circ E_0\) are independent. Using the notation previously defined, for all \(\delta \in \mathbb {F}_2^{n}\setminus \{0\}\) and \(w\in \mathbb {F}_2^{n}\setminus \{0\}\), we have

$$\begin{aligned} \mathcal E_{\delta ,w}=\sum _{v\in \mathbb {F}_2^{n}} \varepsilon _{\delta ,v}c_{v,w}^2. \end{aligned}$$
(8)

Proof

First, we apply the assumption of independence to the probability \(\mathbf{P}[\delta \overset{E}{\rightarrow } sp(w)^{\perp }]\) and then, the link given by Corollary 1 to the differential probability over \(E_1\).

$$\begin{aligned}&\mathbf{P}[\delta \overset{E}{\rightarrow } sp(w)^{\perp }] = \sum _{\varDelta \in \mathbb {F}_2^{n}} \mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ] \mathbf{P}[\varDelta \overset{E_1}{\rightarrow }sp(w)^{\perp }] \\&=\sum _{\varDelta \in \mathbb {F}_2^{n}} \mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ] \sum _{v\in sp(\varDelta )^\perp } \mathrm{\mathbf{cor}}^2(v\cdot y + w\cdot E_1(y))\\&=\sum _{v\in \mathbb {F}_2^{n}} \sum _{\varDelta \in sp(v)^{\perp }} \mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ] \mathrm{\mathbf{cor}}^2(v\cdot y + w\cdot E_1(y))\\&=\sum _{v\in \mathbb {F}_2^{n}} \mathbf{P}[\delta \overset{E_0}{\rightarrow }sp(v)^{\perp }] \mathrm{\mathbf{cor}}^2(v\cdot y + w\cdot E_1(y)), \end{aligned}$$

where changing the order of summation is possible since

$$\begin{aligned} \{(v,\varDelta )\,|\,\varDelta \in \mathbb {F}_2^{n},\,v\in sp(\varDelta )^{\perp }\} = \{(v,\varDelta )\,|\,v \in \mathbb {F}_2^{n},\,\varDelta \in sp(v)^{\perp }\}. \end{aligned}$$

Now by subtracting \(\frac{1}{2}\) from both of the sides of the obtained equality and using Parseval’s theorem gives the result.    \(\square \)

We call the expression (8) the differential-linear hull of \(E = E_1\circ E_0.\) The differential-linear method has been previously applied in cases, where only one correlation \(c_{v,w}\) has been identified to have a large absolute value but the output differential space of the truncated differential is smaller than the zero space of \(v\). Consequently more than one trail must be taken into account when estimating the bias of the differential-linear approximation. We illustrate this in the context of an attack on the Serpent cipher [1].

Example on Serpent. Differential-linear cryptanalysis [6, 22] which has been applied to many ciphers, remains with the multidimensional linear cryptanalysis [35, 36] the most powerful attack on the Serpent cipher [1]. In this section, we summarize, in our notation, the distinguisher proposed in [6], on 9 rounds of Serpent.

To be useful in a key-recovery attack, the distinguisher was defined as starting from the second round of the cipher. First a truncated differential is defined on 3 rounds of Serpent. In this attack, only one input difference is taken into consideration meaning that \(U^{\perp }\) is one-dimensional. The output space of the truncated differential consists of all differences which have the bits number 1 and 117 equal to zero. Hence it is the orthogonal of the two-dimensional space \(V\) spanned by the bits (taken as basis vectors) number 1 and 117. The truncated differential probability \(\mathbf{P}[\delta \overset{E_0}{\rightarrow } V^\perp ]\) being large, it can, as typically in differential-linear cryptanalysis, be computed experimentally and was evaluated in [6] to \(2^{-1}+2^{-6}\). The strong linear approximation over the six following rounds has input mask \(\nu \in V\) where both bits number 1 and 117 are equal to 1. The output mask is denoted by \(w\). The correlation of this linear approximation is estimated to \(c_{\nu ,w}=2^{-26}\).

The resulting differential-linear relation spans over 9 rounds of Serpent. In [6], its bias was estimated to \( \varepsilon _{\delta ,\nu }c^2_{\nu ,w}\) with \(\varepsilon _{\delta ,\nu }=2^{-7}\) to obtain

$$\begin{aligned} \mathcal E_{\delta ,w}\approx \varepsilon _{\delta ,\nu }c_{\nu ,w}^2 =2^{-7}\cdot 2^{-52}. \end{aligned}$$
(9)

Later, in [22], another similar distinguisher on Serpent was provided. The only difference was that a new and stronger truncated differential over the three rounds of \(E_0\) was used.

Our aim is to analyze the conditions under which the approximation (9) is justified. From Theorem 2 we deduce that \(\mathcal E_{\delta ,w}\) can be computed as

$$\begin{aligned} \mathcal E_{\delta ,w}=\sum _{v\in V} \varepsilon _{\delta ,v}c_{v,w}^2 + \sum _{v\in \mathbb {F}_2^{n}\setminus V} \varepsilon _{\delta ,v}c_{v,w}^2. \end{aligned}$$
(10)

We observe that for the two masks \(v\in V\), for which only one bit, either number 1 or 117, is equal to 1, the correlations \(c_{v,w}\) are equal to zero. Then it follows that the first sum on the right side of (10) is, indeed, equal to \(\varepsilon _{\delta ,\nu }c^2_{\nu ,w}\). It remains to examine under which assumptions the sum (9) is an underestimate of the actual bias (10). This will be done in a more general setting in Sect. 5.1.

5 Intermediate Space

5.1 Estimation of the Bias

In this section, we aim to analyze whether we can obtain a good estimate of the bias of a differential-linear relation. For a better illustration, the analysis provided in this section is based on Theorem 2 where the differential-linear approximation is defined for one input difference \(\delta \) and one output mask \(w\). A generalization of this result for sets of input differences and output masks will be given in Sect. 6.

In the differential context, it is well known that the expected probability of a differential is underestimated if we are only able to collect a small number of differential characteristics relative to the differential.

As recalled in Sect. 3, in the few available analyses in the differential-linear context, the bias of the differential-linear approximation is estimated as the combination of one strong truncated differential with one strong linear approximation. In this section, we discuss the possibility of generalizing this result to obtain a better estimate of the bias \(\mathcal E_{\delta ,w}\) by using the hull of a differential-linear approximation more efficiently. From Theorem 2, we know that an accurate computation of the bias of a differential-linear approximation requires the knowledge of the correlations over \(E_1\) for all input masks \(v\in \mathbb {F}_2^{n}\), which is impossible in practice for many ciphers.

From Theorem 2 and as given in Eq. (10) the bias of a differential-linear approximation can be decomposed into two sums with respect to a set \(V\).

$$\begin{aligned} \mathcal E_{\delta ,w}=\sum _{v\in V, v\ne 0} \varepsilon _{\delta ,v}c_{v,w}^2+\sum _{v\notin V} \varepsilon _{\delta ,v}c_{v,w}^2. \end{aligned}$$

Notice that the bias of a different-linear equation can be, as in the linear context, positive or negative. As the complexity of the underlying attack is independent of the sign, we talk, as in the linear context, of absolute bias \(|\mathcal E_{\delta ,w}|\).

Assumption 1

Given a set \(V\) we assume that

$$\begin{aligned} |\sum _{v\in V, v\ne 0}\varepsilon _{\delta ,v}c_{v,w}^2|\le |\mathcal E_{\delta ,w}|, \end{aligned}$$

meaning that \(|\sum _{v\in V}\varepsilon _{\delta ,v}c_{v,w}^2|\) is an underestimate of the bias of the differential-linear approximation with input difference \(\delta \) and output mask \(w\).

The only way to check if we have an under or over estimate of the actual probability consists in experimentally computing the bias of a differential-linear approximation on a reduced number of round of the cipher. These experiments should be done in respect to the intermediate space \(V\). In [5, 6], experiments of this type where already conducted to check the validity of their results.

If the intermediate space \(V\) is large, it is infeasible to compute the biases \(\varepsilon _{\delta ,v}\) over \(E_0\) or the correlations \(c_{v,w}\) over \(E_1\) for all \(v\in V\). Next, based on the assumption that some probabilities over \(E_0\) are equal, we show that \(\sum _{v\in V}\varepsilon _{\delta ,v}c_{v,w}^2\) can be estimated from the product of one truncated differential probability with the capacity of one multidimensional-linear approximation.

Theorem 3

Let \(\varepsilon _{\delta ,V}=\mathbf{P}[\delta \overset{E_0}{\rightarrow } V^\perp ]-\dfrac{1}{|V^|}\) be the bias of a truncated differential with one non-zero input difference \(\delta \) and output differences in \(V^\perp \). Further, we denote by \(C_{V,w}= \sum _{v\in V, v\ne 0}c_{v,w}^2\) the capacity of the multidimensional linear approximation with all input masks \(v\) in \(V\) and one output mask \(w\ne 0\).

If then, for all \(\varDelta \notin V^\perp \), the probabilities \(\mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ]\) are equal, we have

$$\begin{aligned} \sum _{v\in V}\varepsilon _{\delta ,v}c^2_{v,w}= & {} \dfrac{1}{2}\dfrac{|V|}{|V|-1}\varepsilon _{\delta ,V} C_{V,w}. \end{aligned}$$
(11)

Proof

For a purpose of clarity, let us denote \(Q=\mathbf{P}[\delta \overset{E_0}{\rightarrow } V^\perp ]\). We denote by \(p\) the common value of the probabilities \(\mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ]\) for \(\varDelta \notin V^\perp \). Then by \(\sum _{\varDelta \in \mathbb {F}_2^{n}} \mathbf{P} [\delta \overset{E_0}{\rightarrow } \varDelta ]=1\) we deduce that \(p=\dfrac{1-Q}{2^n-|V^\perp |}\).

Since \(V^\perp \subset sp(v)^\perp \) holds for all \(v\in V\), we have

$$\begin{aligned} \mathbf{P}[\delta \overset{E_0}{\rightarrow } sp(v)^\perp ]= & {} \mathbf{P}[\delta \overset{E_0}{\rightarrow } V^\perp ]+\sum _{\small \varDelta \in sp(v)^\perp ,\; \varDelta \notin V^\perp } \mathbf{P}[\delta \overset{E_0}{\rightarrow } \varDelta ]\\= & {} Q+(2^{n-1}-|V^\perp |)\cdot \dfrac{1-Q}{2^n-|V^\perp |}. \end{aligned}$$

Therefore, for all \(v\in V\), we have

$$\begin{aligned} \varepsilon _{\delta ,v}= & {} \mathbf{P}[\delta \overset{E_0}{\rightarrow } sp(v)^\perp ]-\dfrac{1}{2}=Q+\left( 2^{n-1}-|V^\perp |\right) \dfrac{1-Q}{2^n-|V^\perp |}-\dfrac{1}{2}\\= & {} \dfrac{1}{2}\cdot \dfrac{2^nQ-|V^\perp |}{2^n-|V^\perp |}=\dfrac{1}{2}\cdot \dfrac{Q-|V|^{-1}}{1-|V|^{-1}}\\= & {} \dfrac{1}{2}\cdot \dfrac{|V|}{|V|-1}\left( Q-\dfrac{1}{|V|}\right) = \dfrac{1}{2}\cdot \dfrac{|V|}{|V|-1}\varepsilon _{\delta ,V}. \end{aligned}$$

And we deduce

$$\begin{aligned} \sum _{v\in V}\varepsilon _{\delta ,v}c_{v,w}= \dfrac{1}{2}\dfrac{|V|}{|V|-1}\varepsilon _{\delta ,V} \sum _{v\in V}c^2_{v,w}= \dfrac{1}{2}\dfrac{|V|}{|V|-1}\varepsilon _{\delta ,V} C_{V,w}. \end{aligned}$$

   \(\square \)

Let us note that if \(|V|=2\), we have \(\sum _{v\in V}\varepsilon _{\delta ,v}c^2_{v,w} = \varepsilon _{\delta ,V}C_{V,w}\). The larger the size of \(|V|\), the closer to \(\dfrac{1}{2}\varepsilon _{\delta ,V}C_{V,w}\) we are.

5.2 Experiments

The experiments of this section have been performed on a 32-bit scaled version of PRESENT [14, 31] called SmallPresent-[8]. The differential-linear approximations are defined for one input difference \(\delta \) and one output mask \(w\). To limit the number of assumptions, the bias \(\varepsilon _{\delta ,v}\) and the correlations \(c_{v,w}\) are computed experimentally using \(2^{30}\) plaintexts and averaged over \(200\) keys. When using Theorem 2, round independence is only required between \(E_0\) and \(E_1\).

The purpose of these experiments was to check the accuracy of Assumption 1. In each of the figures of this section, we plotted as a reference the experimental bias

$$\begin{aligned} \mathcal E_{\delta ,w}=\mathbf{P}[\delta \rightarrow sp(w)^\perp ]-2^{-1}, \end{aligned}$$
(12)

over 8 rounds of SmallPresent-[8] and given a space \(V\), compare it with

$$\begin{aligned} \sum _{v\in V}\varepsilon _{\delta ,v}c^2_{v,w}. \end{aligned}$$
(13)

While experiments have been performed for many differential-linear approximations on 8 rounds of SmallPresent-[8], we present results for the input difference \(\delta =\mathtt{0x1}\) and the output mask \(w=\mathtt{0x80000000}\). The bias of this differential-linear approximation is positive and we are expecting under Assumption 1 to find that (13) is an underestimate of the actual bias. In Fig. 1, resp. in Fig. 2, the differentials are taken over 3 rounds, resp. 4 rounds, and the correlations are taken over \(5\) rounds, resp. \(4\) rounds of SmallPresent-[8]. The space \(V\) is chosen to be linear.

As the accuracy of these approximations depends mostly on the size of the intermediate space, we study the evolution of (13) in regards to \(\log (|V|)\).

Fig. 1.
figure 1

Estimation of the bias a differential-linear approximation on 3+5 rounds of SmallPresent-[8] for two different chains of intermediate spaces.

Full size image

Result of the different experiments show that in the case of SmallPresent-[8], (13) gives as expected an underestimate of the actual bias \(\mathcal E_{\delta ,w}\). In most of the cases by increasing the size of the intermediate space \(V\), we have a better estimate of the bias (in this experiments, the initial spaces \(V\) are subset of the larger ones). Nevertheless as the second sum of (10) is not always positive we observe that this gain can be somewhat relative. When experiments are conducted for a fixed key instead of averaged over keys, we strictly observe that (13) is not an increasing function of \(|V|\).

In Theorem 3, based on the assumption that for all \(\varDelta \notin V^\perp \), the probabilities \(\mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ]\) are equal, we propose an estimate of (13). This one is relatively easier to compute since, independently of the size of \(V\), only one truncated differential probability and one capacity need to be computed. The blue curves in Figs. 1 and 2 correspond to the computation of the expression on the right side of (11). While this expression seems to be a correct estimate of (13) for \(V\) of small size, the assumption that for all \(\varDelta \notin V^\perp \), the probabilities \(\mathbf{P}[\delta \overset{E_0}{\rightarrow }\varDelta ]\) are equal, is getting less realistic when increasing the size of the space \(V\).

Fig. 2.
figure 2

Estimation of the bias of a differential-linear approximation on 4+4 rounds of SmallPresent-[8] for two different chains of intermediate spaces.

Full size image

This phenomenon also appears when multiplying truncated differential probabilities over rounds of the cipher to obtain the probability of a truncated distinguisher and has been experimentally tested for instance in [17].

6 Multidimensional Differential-Linear Distinguisher

6.1 The Model

The idea of taking advantage of multiple differentials or multiple linear approximations is widely spread out in the cryptographic community. To generalize the results of Sect. 4, let us now consider the case where the space \(U^{\perp }\) of possible input differences is an arbitrary subspace of \(\mathbb {F}_2^{n}\). The linear approximation over \(E_1\) is assumed to be multidimensional such that the output masks form a linear subspace \(W\) of \(\mathbb {F}_2^{n}\). We denote its orthogonal space by \(W^{\perp }\).

The conditions on which it would be possible to combine such a truncated differential and multidimensional linear approximation to a strong truncated differential over the full cipher are similar to the ones in the one-dimensional case expressed in Sect. 5.

We express here the generalization of Theorem 2 to compute the bias

$$\begin{aligned} \mathcal E_{U,W}=\mathbf{P}[U^\perp \setminus \{0\} \overset{E}{\rightarrow } W^\perp ]-\dfrac{1}{|W|}, \end{aligned}$$
(14)

of a multidimensional differential-linear approximation.

Theorem 4

Let \(\mathcal E_{U,W}\) as in (14). Assume that the parts \(E_0\) and \(E_1\) of the block cipher \(E = E_1 \circ E_0\) are independent. Then

$$\begin{aligned} \mathcal E_{U,W}= & {} \dfrac{2}{|W|}\sum _{v\in \mathbb {F}_2^{n},v\ne 0}\varepsilon _{U,v}C_{v,W}, \end{aligned}$$
(15)

where \(\varepsilon _{U,v}=\mathbf{P}[U^\perp \setminus \{0\} \overset{E_0}{\rightarrow } sp(v)^\perp ]-1/2\), and \(C_{v,W}=\sum _{w\in W, w\ne 0}\mathrm{\mathbf{cor}}^2(v\cdot y + w\cdot E_1(y)), \) is for \(v\ne 0\), the capacity of the multidimensional linear approximation with input mask \(v\) and all nonzero output masks \(w\) in \(W\).

Proof

First, let us state the following generalization of Corollary 1. Given a bijective function \(F:\mathbb {F}_2^{n}\rightarrow \mathbb {F}_2^{n}\), a subspace \(U\subset \mathbb {F}_2^{n}\) and a mask vector \(v\in \mathbb {F}_2^{n}\), we have

$$\begin{aligned} 2\mathbf{P}[U^{\perp }\overset{F}{\rightarrow } sp(v)^{\perp }] -1 = \sum _{u\in U}\mathbf{cor}^2(u\cdot x + v\cdot F(x)). \end{aligned}$$

Using Theorem 1 to write the truncated differential probability in terms of squared correlations, we apply this result together with Proposition 2 to obtain

$$\begin{aligned}&\mathbf{P}[U^{\perp }\overset{E}{\rightarrow } W^{\perp }] = \dfrac{1}{|W|}\sum _{u\in U,v\in \mathbb {F}_2^{n} ,w\in W} \mathbf{cor}^2(u\cdot x + v\cdot E_0(x)) \mathbf{cor}^2 (v\cdot y + w\cdot E_1(y)) \\&= \dfrac{1}{|W|}\sum _{v\in \mathbb {F}_2^{n}}\left( 2\mathbf{P}[U^{\perp }\overset{E_0}{\rightarrow }sp(v)^{\perp }] -1\right) \sum _{w\in W}\mathbf{cor}^2(v\cdot y + w\cdot E_1(y)). \end{aligned}$$

The next step consists at removing the zero from the possible input differences. To use relation (3) we multiply the probabilities on the first and second line by \(|U|\) and then subtract \(1=\dfrac{1}{|W|}\sum _{w\in W}\sum _{v\in \mathbb {F}_2^{n}} \mathbf{cor}^2(v\cdot y + w\cdot E_1(y))\) to get

$$\begin{aligned}&(|U|-1)\mathbf{P}[U^{\perp }\setminus \{0\}\overset{E}{\rightarrow } W^{\perp }] =\dfrac{1}{|W|}\sum _{v\in \mathbb {F}_2^{n}}\left( 2|U|\mathbf{P}[U^{\perp }\overset{E_0}{\rightarrow }sp(v)^{\perp }] -|U|-1\right) C_{v,W} \\&=\dfrac{1}{|W|}\sum _{v\in \mathbb {F}_2^{n}} \left( 2(|U|\mathbf{P}[U^{\perp }\overset{E_0}{\rightarrow }sp(v)^{\perp }] -1) -|U|+1\right) C_{v,W}\\&=\dfrac{1}{|W|}\sum _{v\in \mathbb {F}_2^{n}} \left( (|U|-1)(2\mathbf{P}[U^{\perp }\setminus \{0\}\overset{E_0}{\rightarrow }sp(v)^{\perp }] -1)\right) C_{v,W}. \end{aligned}$$

We obtain the claim by dividing the first and last expression in this chain of equalities by \(|U|-1\) and then observing that the term for \(v =0\) in the last expression is equal to \(1/|W|\).    \(\square \)

6.2 Complexity of a Distinguishing Attack

When the differential-linear approximation is characterized by only one output mask \(w\), as the data complexity is inverse proportional to the square of the bias \(\mathcal E_{\delta ,w}\), larger its absolute value is, less costly the underlined distinguishing attack is. When using multiple output masks, the differential-linear probability should be distinguishable from the uniform probability \(\dfrac{1}{|W|}\) and the data complexity of the differential-linear distinguisher depends of the number \(|W|\) of output masks. As classically done in the differential context, using multiple input differences allows the construction of structures and divides the data complexity of the distinguisher by \(|U^\perp |\).

Proposition 3

Using the framework of [10, 16, 38], the data complexity of a “multidimensional” differential-linear distinguisher with input differences in \(U^\perp \) and output masks in \(W\) is proportional to

$$\begin{aligned} \dfrac{2}{|U^\perp |}\dfrac{|W|^{-1}}{\mathcal E_{U,W}^2} =\dfrac{|W|}{2|U^\perp |}\dfrac{1}{(\sum _v \varepsilon _{U,v}C_{v,W})^2}. \end{aligned}$$
(16)

When increasing the number of output masks, for each \(v\in \mathbb {F}_2^{n}\) the capacity \(C_{v,W}\) increases. In general, the data complexity, as indicated by (16), depends on the balance between the factor \(|W|\) and the effect of the capacity \(C_{v,W}\) on the squared differential-linear bias.

6.3 Estimation of the Bias

As in the one-dimensional case, we discuss in this section some conditions on which we can compute the bias of a multidimensional differential-linear approximation. The approach is similar to the one of Sect. 5.

Given a set \(V\), the sum (15) can be decomposed into two sums:

$$\begin{aligned} \mathcal E_{U,W}= \dfrac{2}{|W|}\sum _{v\in V, v\ne 0}\varepsilon _{U,v}C_{v,W}+\dfrac{2}{|W|}\sum _{v\notin V}\varepsilon _{U,v}C_{v,W} \end{aligned}$$
(17)

Practical computation of the bias of a multidimensional differential-linear approximation relies on the fact that computing only the first partial sum gives us an underestimate of the absolute bias \(|\mathcal E_{U,W}|\).

Assumption 2

We assume that

$$\begin{aligned} |\mathcal E_{U,W}| \ge \left| \dfrac{2}{|W|}\sum _{v\in V,v\ne 0}\varepsilon _{U,v}C_{v,W}\right| . \end{aligned}$$

It is straightforward to generalize Theorem 3 to the multidimensional case.

Corollary 2

Let \(\mathcal E_{U,V}=\mathbf{P}[U^\perp \setminus \{0\}\overset{E_0}{\rightarrow } V^\perp ]-\dfrac{1}{|V^|}\) be the bias of a truncated differential with non-zero input differences in \(U^{\perp }\) and output differences in \(V^\perp \). Further, we denote by \(C_{V,W}= \sum _{w\in W, w\ne 0}\sum _{v\in V}c_{v,w}^2\) the capacity of the multidimensional linear approximation. If then, for all \(\varDelta \notin V^\perp \) the probabilities \(\mathbf{P}[U^\perp \setminus \{0\}\overset{E_0}{\rightarrow }\varDelta ]\) are equal, we have

$$\begin{aligned} \dfrac{2}{|W|}\sum _{v\in V}\varepsilon _{U,v}C_{v,W}= & {} \dfrac{1}{|W|}\dfrac{|V|}{|V|-1}\varepsilon _{U,V} C_{V,W}. \end{aligned}$$

To test the validity of the results presented in this section, similar experiments than the ones presented in Sect. 5.2 have been conducted on SmallPresent[8]. Conclusion of these experiments are similar to the ones in the one-dimensional case. In the case of the PRESENT cipher, these experiments show that

$$ \left| \dfrac{2}{|W|}\sum _{v\in V}\varepsilon _{U,v}C_{v,W}\right| , $$

is an underestimate of the absolute bias of the multidimensional differential-linear approximation. As in Sect. 5.2, we observe that the assumption about the equality of the probabilities \(\mathbf{P}[U^\perp \setminus \{0\}\overset{E_0}{\rightarrow }\varDelta ]\) made in Corollary 2, influences the computational result when \(|V|\) is large.

7 Conclusion

In this paper, we studied and generalized the differential-linear cryptanalysis. Starting from the observation that any differential-linear relation can be regarded as a truncated differential or a multidimensional linear approximation we derive a general expression of its bias based on the link between differential probabilities and linear correlations provided by Chabaud and Vaudenay.

We also revisit previous studies and applications of differential-linear cryptanalysis, where the bias of the differential-linear approximation has often been estimated under some heuristic assumptions, implicitly or explicitly present in the derivations. We derive our general formula of the bias under the sole assumption of round independence of the parts of the cipher, and identify new additional assumptions for computing efficient estimates of it. Extensive experiments have been performed to test the validity of these assumptions. Although no new applications of differential-linear cryptanalysis are presented in this paper, the potential and generality of our sound framework is demonstrated by its ability to explain existing examples of differential-linear cryptanalysis.