A Coalgebraic View of Characteristic Formulas in Equational Modal Fixed Point Logics

Abstract

The literature on process theory and structural operational semantics abounds with various notions of behavioural equivalence and, more generally, simulation preorders. An important problem in this area from the point of view of logic is to find formulas that characterize states in finite transition systems with respect to these various relations. Recent work by Aceto et al. shows how such characterizing formulas in equational modal fixed point logics can be obtained for a wide variety of behavioural preorders using a single method. In this paper, we apply this basic insight from the work by Aceto et al. to Baltag’s “logics for coalgebraic simulation” to obtain a general result that yields characteristic formulas for a wide range of relations, including strong bisimilarity, simulation, as well as bisimulation and simulation on Markov chains and more. Hence this paper both generalizes the work of Aceto et al. and makes explicit the coalgebraic aspects of their work.

Supported by The Netherlands Organisation for Scientific Research VIDI project 639.072.904.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The literature on process theory and structural operational semantics contains a multitude of various notions of behavioural equivalence and, more generally, simulation preorders. The most prominent example, perhaps, is the notion of strong bisimulation: given labelled transition systems $S$ and $T$, a relation $Z$ between states of $S$ and states of $T$ is said to be a strong bisimulation if the following conditions hold:

• Forth: If $u Z v$ and $u \mathop {\longrightarrow }\limits ^{a} u^\prime$ for some action $a$, then there is $v^\prime$ with $v \mathop {\longrightarrow }\limits ^{a} v^\prime$ and $u^\prime Z v^\prime$.

• Back: If $u Z v$ and $v \mathop {\longrightarrow }\limits ^{a} v^\prime$, then there is $u^\prime$ with $u \mathop {\longrightarrow }\limits ^{a} u^\prime$ and $u^\prime Z v^\prime$.

The weaker notion of simulation is like bisimulation except that the “Back” condition is dropped. Another way to weaken the notion of strong bisimulation is to “truncate” the silent $\tau$-transitions, according to the intuition that bisimulation should capture equivalence of observable behaviour. The resulting concept of behavioural equivalence is called weak bisimulation.

An important problem in this area from the point of view of logic is to find formulas that characterize states in finite transition systems with respect to these various relations. For example, in the case of strong bisimilarity, we want to find a formula $\varphi$ that characterizes a given state $u$ in a finite labelled transition system $S$ “up to bisimilarity”, in the sense that a state $v$ in a transition system $T$ satisfies $\varphi$ if and only if $(T,v)$ is bisimilar with $(S,u)$. Recent work by Aceto et al. shows how such characterizing formulas in equational modal fixed point logics can be obtained for a wide variety of behavioural preorders using a single method. In such equational fixed point logics, the semantics of formulas is parametric in a system of equations, which are to be read (in this context) as greatest fixed point definitions of variables. For example, in Hennessy-Milner logic, the equation

$$ p := \varphi \wedge [a] p$$

assigns to the variable $p$ the meaning: “the formula $\varphi$ is true throughout every $a$-path starting from the current state”. Generally, a fixed point language allows us to characterize infinite or looping behaviour of a model using finitary formulas.

In this paper, we apply the basic insight from the work by Aceto et al. to Baltag’s “logics for coalgebraic simulation”, which generalize the original coalgebraic languages introduced by Moss in the seminal paper [13], to obtain a general result that yields characteristic formulas for a wide range of relations. These include strong bisimilarity, simulation, as well as bisimulation and simulation on Markov chains and more. The key observations that will drive the result are:

• 1. The semantics for the modal operators and the various notions of simulation both arise from the same concept of relation lifting via a lax extension.

• 2. A finite coalgebra can itself be viewed as a system of equations.

These features of the logics make the construction of the characteristic formulas particularly direct and natural. However, the syntax of these languages directly involve the functor $T$, and can be somewhat difficult to grasp intuitively. Therefore, we also provide conditions that allow us to automatically derive characteristic formulas in the language of predicate liftings for a given (finitary) functor. These latter languages have become increasingly popular in the coalgebraic logic community, and they have the advantage of staying closer to the more conventional syntax of languages like Hennessy-Milner logic.

2 Basics

2.1 Set Coalgebras and Lax Extensions

In this section we introduce some basic concepts from coalgebra theory that will be used later on. We assume familiarity with basic category theoretic concepts. We fix a functor $T : \mathbf {Set} \rightarrow \mathbf {Set}$, where $\mathbf {Set}$ is the category of sets and mappings For simplicity, we assume that $T$ preserves set inclusions, so that a set inclusion $\iota : X \rightarrow Y$ is mapped to a set inclusion $T\iota : TX \rightarrow TY$. This assumption is actually more innocent than it may seem at first, since every set functor is naturally isomorphic “up-to-$\emptyset$” to one that preserves set inclusions. More precisely, for every set functor $T$ there is a functor $T^\prime$ such that the restrictions of these two functors to the full subcategory of non-empty sets are naturally isomorphic, see [1] for details.

We will make use of an approach to coalgebraic logic developed by Alexandru Baltag, based on certain methods of extending the signature functor $T$ to relations [3]. This approach is a generalization of the original formulation of coalgebraic logic due to Moss [13]. While Baltag uses “weak $T$-relators” (for more on relators and simulations [7, 9, 17]), we shall here use the slightly more general notion of “lax extension” [11], which works just as well. Besides that, our approach is the same as Baltag’s.

Definition 1

Given a function $f:X\rightarrow Y$, let $\widehat{f} = \{(x,f(x))\mid x\in X\}$ be the graph of $f$. Let $\varDelta _X = \widehat{ Id _X}$ be the graph of the identity map on $X$.

The concept of a lax extension is defined as follows:

Definition 2

A lax extension of a set functor $T$ is a relation lifting (i.e. a mapping that sends every relation $R \subseteq X \times Y$ to a relation $LR \subseteq TX \times TY$) subject to the constraints:

• L1: $R \subseteq S$ implies $LR \subseteq LS$,

• L2: $LR ; LS \subseteq L(R ; S)$,

• L3: $\widehat{Tf} \subseteq L\widehat{f}$ for any mapping $f$.

Thus lax extensions are lax endofunctors on the $2$-category of sets and relations with inclusions between relations as the $2$-cells. Note that condition L3 implies that

$$\begin{aligned} \varDelta _{TX} \subseteq L \varDelta _X \end{aligned}$$

(1)

for all sets $X$, since $\varDelta _{TX} = \widehat{ Id _{TX}} = \widehat{T ( Id _X)}$. A good example of a lax extension (that also happens to be a weak relator), which we will come back to several times, is the following:

Example 1

The finitary covariant powerset functor ($T = \mathcal {P}_\omega$) has a lax extension given by

$$ L_{ sim }R := \{(A,B) \in \mathcal {P}_\omega X \times \mathcal {P}_\omega Y \mid \forall a \in A \;\exists b \in B : a R b\}. $$

In other words, $L_{ sim }R$ consists of all pairs $(A,B)$, such that there is a function from $A$ to $B$ whose graph is a subset of $R$. It is easy to see that L1 and L2 hold. For L3, let $f:X\rightarrow Y$, and let $A\widehat{\mathcal {P}_\omega f}B$. This means that $B= f[A]$. As $f$ maps $A$ to $B$ and its graph is $\widehat{f}$, we have that $A L_{ sim }\widehat{f} B$.

Definition 3

${\varvec{(L}}$-simulation). An $L$ -simulation from a $T$-coalgebra $(X,\alpha )$ to $(Y,\beta )$ is a binary relation $Z \subseteq X \times Y$ such that $u Z v$ implies $\alpha (u) (LZ) \beta (v)$. Given pointed $T$-coalgebras $(\mathfrak {A},u)$ and $(\mathfrak {B},v)$, we write $(\mathfrak {A},u)\preceq _L (\mathfrak {B},v)$ to say that there is an $L$-simulation $Z$ from $\mathfrak {A}$ to $\mathfrak {B}$ with $u Z v$.

Note that $L_{ sim }$-simulation (with $L_{ sim }$ from Example 1) is simulation on Kripke frames.

2.2 Symmetric Lax Extensions and Bisimulation

We write the converse of a relation $R$ as $R^\circ$. Given a relation lifting $L$, let $L^{\circ }:R\mapsto (L(R^{\circ }))^\circ$. Call a relation lifting $L$ symmetric if $L = L^{\circ }$.

Example 2

(Barr extension). Given sets $X,Y$ and a binary relation $R \subseteq X \times Y$, the relation $\overline{T} R \subseteq TX \times TY$ is defined by

$$ a \overline{T}R b \; \Leftrightarrow \; \exists c \in T(R) : \, T\pi _X(c) = a \; \& \; T\pi _Y(c) = b. $$

Here, $\pi _X$ and $\pi _Y$ are the projections from the product $X\times Y$. Then $\overline{T}$ is a symmetric relation lifting, and in the case where $T$ preserves weak pullbacks, $\overline{T}$ is a symmetric lax extension of $T$ called the Barr extension of $T$ [4].

Definition 4

Given a set functor $T$, a $T$ -bisimulation is an $L$-simulation, where $L = \overline{T}$.

We could also call a $T$-bisimulation a $\overline{T}$-bisimulation, and we will more generally define what is meant by $L$-bisimulation for any lax extension $L$ (not necessarily symmetric) that extends $\overline{T}$ in that $\overline{T}R \subseteq LR$ for each relation $R$. We first observe the following.

Observation 1

If $L$ is a lax extension that extends $\overline{T}$, then $L^{\circ }$ is a lax extension.

Proof

We prove each case in turn.

• By L1 in Definition 2, we have

  $$ R \subseteq S \; \Rightarrow \; R^\circ \subseteq S^\circ \; \Rightarrow \; L(R^\circ ) \subseteq L(S^\circ )\; \Rightarrow \; L^{\circ }(R) \subseteq L^{\circ }(S). $$

• We reason as follows:

  $$\begin{aligned} L^{\circ }(R);L^{\circ }(S)&= (L(R^\circ ))^\circ ;(L(S^\circ )^\circ ) = (L(S^\circ );L(R^\circ ))^\circ \\&\subseteq (L(S^\circ ;R^\circ ))^\circ = (L((R;S)^\circ ))^\circ = L^{\circ }(R;S). \end{aligned}$$

• Let $f:X\rightarrow Y$. For $a\in TX$, we have

  $$\begin{aligned} a (\overline{T}\widehat{f})(Tf(a))&\Rightarrow (Tf(a))(\overline{T}(\widehat{f}^\circ ))a \qquad (\overline{T}~\mathrm{is~a~symmetric ~relation~lifting })\\&\Rightarrow (Tf(a))(L(\widehat{f}^\circ ))a \qquad (\overline{T}R\subseteq LR~\mathrm{for~all~relations~R })\\&\Rightarrow a (L\widehat{f})(Tf(a)). \end{aligned}$$

  Thus $\widehat{Tf}\subseteq L^\circ (\widehat{f})$.   $\square$

Definition 5

Given a lax extension $L$, let $B(L)$ be defined¹ by

$$\begin{aligned} B(L) = L \cap L^{\circ }. \end{aligned}$$

We call $B(L)$ the bisimulator of $L$.

The reader can easily check that the following holds:

Observation 2

If $L_1$ and $L_2$ are lax extensions, then $L_1\cap L_2$ is a lax extension.

Hence we get:

Observation 3

If $L$ is a lax extension, such that $\overline{T}R\subseteq LR$ for each relation $R$, then its bisimulator $B(L)$ is a symmetric lax extension.

Proof

First note that as $L$ extends $\overline{T}$, we have by Observation 1 that $L^{\circ }$ is a lax extension. Then by Observation 2, $B(L)$ is a lax extension. By definition $B(L)$ is symmetric.   $\square$

Remark 1

If $L_{ sim }$ is the lax extension for the finitary power set functor $\mathcal {P}_\omega$ that was given in Example 1, then $B(L_{ sim }) = \overline{\mathcal {P}_\omega }$.

Definition 6

If $L$ is a lax extension, such that $\overline{T}R\subseteq LR$ for every relation $R$, then an $L$ -bisimulation is a $B(L)$-simulation.

By the previous remark, $Z$ is an $L_{ sim }$-bisimulation if and only if $Z$ is a $\overline{\mathcal {P}_\omega }$-bisimulation.

3 Coalgebraic Logic with Fixed Point Equations

3.1 Basic Coalgebraic Modal Logic

Definition 7

Given a (finite) set of variables $V$, the syntax of the basic coalgebraic logic over $V$ is defined as the smallest set $\mathcal {L}$ such that

• $p \in \mathcal {L}$ for all $p \in V$,

• $\varphi ,\psi \in \mathcal {L}$ implies $\varphi \wedge \psi \in \mathcal {L}$ and $\varphi \vee \psi \in \mathcal {L}$,

• if $\varPhi$ is a finite subset of $\mathcal {L}$ then $\square a \in \mathcal {L}$ and $\Diamond a \in \mathcal {L}$ for each $a \in T\varPhi$.

The following observation is made in [18]:

Proposition 1

Let $T$ be a set functor that preserves inclusions. Then for any $a \in TX$ where $X$ is a finite set, there is a unique smallest set $Y\subseteq X$ with $a \in T Y$.

In particular, this guarantees that for any formula $\Box a$ or $\Diamond a$, there is a unique smallest set of formulas $\varPhi$ with $a \in T \varPhi$. We denote this set by $SPT (a)$, for “support of $a$”. When $X$ is understood by context, we write $SPT$ for $SPT _X$.

Given a fixed valuation, a function $\upsilon : V \rightarrow \mathcal {P}(X)$ (equivalently $\upsilon \in \mathcal {P}(X)^V$), we define the satisfaction relation $\vDash _\upsilon$ between pointed coalgebras $(\mathfrak {A},u)$ (where $\mathfrak {A}= (X,\alpha )$) and formulas in $\mathcal {L}(V)$, relative to the valuation $\upsilon$, with the following inductive clauses:

• $(\mathfrak {A},u)\vDash _\upsilon p$ iff $u \in \upsilon (p)$, for a propositional variable $p$,

• $(\mathfrak {A},u)\vDash _\upsilon \varphi \wedge \psi$ iff $(\mathfrak {A},u)\vDash _\upsilon \varphi$ and $(\mathfrak {A},u)\vDash _\upsilon \psi$,

• $(\mathfrak {A},u)\vDash _\upsilon \varphi \vee \psi$ iff $(\mathfrak {A},u)\vDash _\upsilon \varphi$ or $(\mathfrak {A},u)\vDash _\upsilon \psi$,

• $(\mathfrak {A},u) \vDash _{\upsilon } \Box a$ iff $\alpha (u) (L\vDash _\upsilon ) a$,

• $(\mathfrak {A},u) \vDash _{\upsilon } \Diamond a$ iff $\alpha (u) (L^{\circ }(\vDash _\upsilon )) a$.

Sometimes the definition of the semantics of $\Box a$ and $\Diamond a$ are given with $\vDash _\upsilon$ replaced with $\vDash _{\upsilon }\upharpoonright _{X\times SPT (a)} \;=\; \vDash _\upsilon \cap \; X\times SPT (a)$. We show that both definitions are equivalent.

Observation 4

If $L$ is a lax extension, then $\alpha (u) (L\vDash _{\upsilon }\upharpoonright _{X\times SPT (a)}) a$ if and only if $\alpha (u) (L\vDash _{\upsilon }) a$.

Proof

First note that ${\vDash _{\upsilon }\upharpoonright _{X\times SPT (a)}}\subseteq {\vDash _{\upsilon }}$ and hence by L1, $\alpha (u) (L\vDash _{\upsilon }\upharpoonright _{X\times SPT (a)}) a$ implies $\alpha (u) (L\vDash _{\upsilon }) a$. For the other direction, suppose that $\alpha (u) (L\vDash _{\upsilon }) a$. By definition of $SPT$, $a\in T SPT (a)$, and hence $(a,a)\in \varDelta _{T SPT (a)}$. By (1), $(a,a)\in L\varDelta _{ SPT (a)}$. Then $\alpha (u) (L\vDash _{\upsilon });L(\varDelta _{ SPT (a)})a$. The desired result follows from this, L2, and the fact that ${\vDash _{\upsilon }\upharpoonright _{X\times SPT (a)}} = (\vDash _{\upsilon });(\varDelta _{ SPT (a)})$.   $\square$

Remark 2

If $L$ is a symmetric lax extension, then the formulas $\Box a$ and $\Diamond a$ are equivalent. In this case, we might write $\nabla a$ instead of $\Box a$ to emphasize that $\Box$ and $\Diamond$ are the same. If $L = \overline{T}$, then these modalities are the same as the $\nabla$-modality from the (finitary version of) Moss’ presentation of coalgebraic logic [13].

3.2 Fixed Point Semantics

In this section we introduce the (greatest) fixed point semantics for the logic $\mathcal {L}(V)$, relative to a system of equations. First, we have to say more precisely what a system of equations is:

Definition 8

(System of equations). Given a set of variables $V$, a system of fixed-point equations is defined to be a mapping $s : V \rightarrow \mathcal {L}(V)$.

We shall construct a fixed point semantics using a system of equations as a parameter. First note that the set $\mathcal {P}(X)^V$ of $V$-indexed tuples of subsets of a set $X$, or “valuations in $X$”, forms a complete lattice under the relation $\sqsubseteq$ of point-wise set inclusion. That is, given $\upsilon , \upsilon ^\prime : V \rightarrow \mathcal {P}(X)$ we set

$$\upsilon \sqsubseteq \upsilon ^\prime \text { iff } \forall x \in V: \upsilon (x) \subseteq \upsilon ^\prime (x).$$

We denote the arbitrary (potentially infinite) join operation in this lattice by $\bigvee$. The reader can now easily check that a system of fixed point equations $s$ defines a monotone operation $\mathcal {O}_s$ on the lattice of valuations $\mathcal {P}(X)^V$, by letting (for $\upsilon : V \rightarrow \mathcal {P}(X)$ and $x \in V$):

$$\mathcal {O}_s(\upsilon )(x) = \{w \in X \mid (\mathfrak {A},w)\vDash _{\upsilon } s(x)\}.$$

By the Knaster-Tarski fixed point theorem, $\mathcal {O}_s$ is guaranteed a greatest fixed point, which we denote $GFP (s)$, so that

$$ GFP (s) := GFP (\mathcal {O}_s) = \bigvee \{\sigma : V \rightarrow \mathcal {P}(X) \mid \sigma \sqsubseteq \mathcal {O}_s(\sigma )\}.$$

For a pointed coalgebra $(\mathfrak {A},u)$ we write $(\mathfrak {A},u)\vDash _s \varphi$ as an abbreviation for $(\mathfrak {A},u)\vDash _{ GFP (s)} \varphi$, and say in this case that $(\mathfrak {A},u)$ satisfies the formula $\varphi$ relative to the system of equations $s$. We could, of course, introduce a least fixed point semantics relative to $s$ in the same way, but since we will not have any use for that here we refrain from doing so.

The following observation will be used for proving the correctness of the characteristic formula for mutual simulation in Example 7. It plays a somewhat similar role as [2, Lemma 4.6] toward this goal.

Observation 5

Let $s$ and $t$ be systems of equations, such that $s = t\upharpoonright V_0$ for some subset $V_0$ of the variables used in $t$. Given a $T$-coalgebra $(\mathfrak {A},u)$, and a variable $x\in V_0$,

$$ (\mathfrak {A},u)\models _s~x~\mathrm{iff }~(\mathfrak {A},u)\models _t x. $$

Proof

The proof of this is a straightforward induction. The key observation is that as $s = t\upharpoonright V_0$, for each $p \in V_0$, $t(p)$ is a formula over the variables in $V_0$, and hence all variables not in $V_0$ are “unreachable” in $t$ from variables in $V_0$.   $\square$

4 Characteristic Formulas

Definition 9

Given a lax extension $L$ and coalgebras $\mathfrak {A}= (X,\alpha )$ and $\mathfrak {B}=(Y,\beta )$, let $\mathcal {F}_L$ be the endofunction on $\mathcal {P}(X\times Y)$ defined by

$$ (x,y)\in \mathcal {F}_L(R) \Leftrightarrow \alpha (x) (LR) \beta (y). $$

Note that $\mathcal {F}_L$ is a monotone increasing function on the complete lattice of relations in $\mathcal {P}(X\times Y)$, and hence by the Knaster-Tarski fixed point theorem, $\mathcal {F}_L$ has a greatest fixed point. It is clear that a relation $R \subseteq X \times Y$ is a post-fixed point of $\mathcal {F}_L$ iff it is an $L$-simulation, and so the greatest fixed point of $\mathcal {F}_L$ is the relation $\preceq _L$, i.e. we have $(u,v) \in GFP(\mathcal {F}_L)$ iff there is an $L$-simulation relating $u$ to $v$.

We consider the language $\mathcal {L}(X)$ with $X$ being the set of variables. Let $\varPhi$ be a function from relations in $\mathcal {P}(X\times Y)$ to valuations in $\mathcal {P}(Y)^X$, such that $\varPhi (R)(x) = \{y\mid (x,y)\in R\}$. Let $\varPsi$ be the function from relations in $\mathcal {P}(Y\times X)$ to valuations in $\mathcal {P}(Y)^X$, such that $\varPsi (R)(x) = \varPhi (R^\circ )(x) = \{y\mid (y,x)\in R\}$.

Definition 10

Let $\mathfrak {A}= (X,\alpha )$ and $\mathfrak {B}=(Y,\beta )$ be $T$-coalgebras. We say that a system of equations $s:X\rightarrow \mathcal {L}(X)$ directly expresses the endofunction $\mathcal {F}_L$ if for $Z\subseteq Y\times X$

$$ (\mathfrak {B},y)\vDash _{\varPsi (Z)} s(x) \Leftrightarrow (y,x)\in \mathcal {F}_L(Z). $$

Similarly, we say that a system of equations $s:X\rightarrow \mathcal {L}(X)$ conversely expresses the endofunction $\mathcal {F}_L$ if for $Z\subseteq X\times Y$

$$ (\mathfrak {B},y)\vDash _{\varPhi (Z)} s(x) \Leftrightarrow (x,y)\in \mathcal {F}_L(Z). $$

Theorem 1

If $s$ directly expresses $\mathcal {F}_L$, then

$$ (\mathfrak {B},v)\vDash _s u \text { iff } (\mathfrak {B}, v) \preceq _{L} (\mathfrak {A}, u). $$

If $s$ conversely expresses $\mathcal {F}_L$, then

$$ (\mathfrak {B},v)\vDash _s u \text { iff } (\mathfrak {A}, u) \preceq _{L} (\mathfrak {B}, v). $$

The idea behind this theorem has been used for some time, and has been given in papers such as [2, 14, 15]. The presentation in this paper is most similar to a formulation given in [15], which addressed probabilistic simulations in a non-coalgebraic setting. The proofs given in those papers apply to this setting as well. However, we provide a sketch of the proof here to emphasize that it applies to our more general (coalgebraic) setting.

Proof

(sketch). Recall that $\mathcal {O}_s$ is a function from $\mathcal {P}(Y)^X$ to itself, such that $\mathcal {O}_s(\upsilon )(x) = \{y\mid (\mathfrak {B},y)\vDash _\upsilon s(x)\}$, and this function has the greatest fixed point $GFP (s)$. It follows directly from the definitions that $s$ directly expresses $\mathcal {F}_L$ if and only if the following diagram commutes:

Similarly, $s$ conversely expresses $\mathcal {F}_L$ if and only if the following commutes:

Hence, if $s$ directly expresses $\mathcal {F}_L$ then, since the function $\varPsi$ is an isomorphism between the lattices of relations in $\mathcal {P}(Y\times X)$ and variable interpretations in $\mathcal {P}(Y)^X$, by [2, Theorem 2.3] it maps the greatest fixed point of $\mathcal {F}_L$ to the greatest fixed point of $\mathcal {O}_s$, that is $GFP (s) = \varPsi ( GFP (\mathcal {F}_L)) = \varPsi (\preceq _L)$. So we get

$$\begin{aligned} (\mathfrak {B},v)\vDash _s u&\Leftrightarrow (\mathfrak {B},v)\vDash _{ GFP (s)} u \\&\Leftrightarrow v \in GFP(s)(u) \\&\Leftrightarrow v \in \varPsi (\preceq _L)(u) \\&\Leftrightarrow v \preceq _L u. \end{aligned}$$

Similarly, the function $\varPhi$ is an isomorphism between relations in $\mathcal {P}(X\times Y)$ and variable interpretations in $\mathcal {P}(Y)^X$, and hence if $s$ conversely expresses $\mathcal {F}_L$ it maps the greatest fixed point of $\mathcal {F}_L$ to the greatest fixed point of $\mathcal {O}_s$, that is $GFP (s) = \varPhi ( GFP (\mathcal {F}_L)) = \varPhi (\preceq _L)$. So we get

$$\begin{aligned} (\mathfrak {B},v)\vDash _s u&\Leftrightarrow (\mathfrak {B},v)\vDash _{ GFP (s)} u \\&\Leftrightarrow v \in GFP(s)(u) \\&\Leftrightarrow v\in \varPhi (\preceq _L)(u)\\&\Leftrightarrow u \preceq _L v \end{aligned}$$

as required.   $\square$

We are now left with the task to find systems of equations that express $\mathcal {F}_L$ (directly and conversely). The main observation here is that, with the semantics we are using here for the $\Box$- and $\Diamond$-operators, this is easy: a finite $T$-coalgebra almost is a system of equations!

To be precise, fix a finite $T$-coalgebra $\mathfrak {A}= (X,\alpha )$. We treat the set $X$ as a set of variables and consider the language $\mathcal {L}(X)$. We define two systems of equations $s_\square$ and $s_\Diamond$ by setting

$$s_\square (u) := \square \alpha (u)$$

and

$$ s_\Diamond (u) := \Diamond \alpha (u).$$

We then get the following result:

Lemma 1

For any lax extension $L$, where $L^\circ$ is also a lax extension, $s_\Box$ directly expresses $\mathcal {F}_L$, and $s_\Diamond$ conversely expresses $\mathcal {F}_L$.

Proof

Let $Z\subseteq Y\times X$. Given $x\in X$, note that

$$ \vDash _{\varPsi (Z)}\upharpoonright _{Y\times SPT (\alpha (x))}\subseteq Z \subseteq {\vDash _{\varPsi (Z)}}. $$

Then by L2 and Observation 4, $\beta (y) (L\vDash _{\psi (Z)}) \alpha (x)$ iff $\beta (y) (LZ) \alpha (x)$. Then

$$\begin{aligned} (\mathfrak {B},y)\vDash _{\varPsi (Z)} s_\Box (x)&\Leftrightarrow (\mathfrak {B},y)\vDash _{\varPsi (Z)} \Box \alpha (x)\\&\Leftrightarrow \beta (y) (L\vDash _{\varPsi (Z)}) \alpha (x)\\&\Leftrightarrow (\beta (y),\alpha (x))\in L(Z)\\&\Leftrightarrow (y,x)\in \mathcal {F}_L(Z). \end{aligned}$$

This proves that $s_\Box$ directly expresses $\mathcal {F}_L$.

To see that $s_\Diamond$ conversely expresses $\mathcal {F}_L$, let $Z\subseteq X\times Y$. Then, as $\varPhi (Z) = \varPsi (Z^\circ )$,

$$\begin{aligned} (\mathfrak {B},y)\vDash _{\varPhi (Z)} s_\Diamond (x)&\Leftrightarrow (\mathfrak {B},y)\vDash _{\varPsi (Z^\circ )} \Diamond \alpha (x)\\&\Leftrightarrow \beta (y) (L^\circ \vDash _{\varPsi (Z^\circ )}) \alpha (x)\\&\Leftrightarrow (\beta (y),\alpha (x))\in L^\circ (Z^\circ )\\&\Leftrightarrow (\alpha (x),\beta (y))\in L(Z)\\&\Leftrightarrow (x,y)\in \mathcal {F}_L(Z). \end{aligned}$$

   $\square$

From Lemma 1 together with Theorem 1, we immediately get our main result:

Theorem 2

Let $\mathfrak {B}= (Y,\beta )$ be any $T$-coalgebra. Then, for $u \in X$ and $v \in Y$, relative to the system of equations $s_\square$ we have

$$(1)\quad (\mathfrak {B},v)\vDash u \text { iff } (\mathfrak {B}, v) \preceq _{L} (\mathfrak {A}, u).$$

Conversely, relative to the system of equations $s_\Diamond$ we have

$$(2)\quad (\mathfrak {B},v)\vDash u \text { iff } (\mathfrak {A}, u) \preceq _{L} (\mathfrak {B}, v).$$

We also get characteristic formulas for various notions of bisimilarity as an easy corollary to this result. Given a lax extension $L$ that extends $\overline{T}$, we use $\sim _L$ as an abbreviation for the simulation relation $\preceq _{B(L)}$, where $B(L)$ is the bisimulator of $L$.

Corollary 1

Let $\mathfrak {A}= (X,\alpha )$ be a $T$-coalgebra and let $s_{\Box ,\Diamond }$ be the system of equations over $X$ defined by

$$v \mapsto \Box \alpha (v) \wedge \Diamond \alpha (v).$$

Then for $u\in X$ and any pointed $T$-coalgebra $(\mathfrak {B},w)$ we have

$$ (\mathfrak {B},w)\vDash _{s_{\Box ,\Diamond }} u \text { iff } (\mathfrak {B},w)\sim _L (\mathfrak {A},u).$$

Proof

Let $\nabla$ be the “box modality” corresponding to the lax extension $B(L)$. It is easy to see that $s_{\Box ,\Diamond }$ gives rise to the same operator on the lattice of evaluations in a coalgebra $\mathfrak {B}$ as the system $s_\nabla$ defined by

$$v \mapsto \nabla \alpha (v).$$

The corollary now follows from Theorem 2 applied to $s_\nabla$.   $\square$

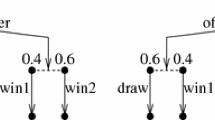
Example 3

Consider the $\mathcal {P}$-coalgebra $\mathfrak {A}$ depicted by

Then, given that $\Box$ is for example the box modality corresponding to $L_{ sim }$, the system of equations $s_\Box$ is given by

$$\begin{aligned} s_\Box (x)&= \Box \emptyset \\ s_\Box (y)&= \Box \{x,z\}\\ s_\Box (z)&= \Box \{z\} \end{aligned}$$

Remark 3

In the case where $L$ is the Barr extension of $T$ (where $T$ preserves weak pullbacks), the system of equations $s_\Box$ (equivalently $s_\Diamond$) can viewed as a very simple “$T$-automaton” in the sense of [18]. Hence [18, Proposition 4.9], which shows that any finite $T$-coalgebra can be characterized up to bisimilarity by a suitable $T$-automaton, can be seen as a special instance of Theorem 2.

4.1 Predicate Liftings

The $\Box$ and $\Diamond$ modalities used to obtained characteristic formulas above have the nice feature that the appropriate connection between the formulas and the lax extension $L$ is built directly into the semantics. On the other hand, these modalities are rather abstract. By contrast, modalities based on predicate liftings are relatively easy to grasp and are formally closer to the standard modalities used in Hennessy-Milner logic and other modal logics for specification of various kinds of transition systems. In this section we provide conditions on a lax extension $L$ that allow us to derive characteristic systems of equations for $L$-simulation in the language of predicate liftings. This is very closely related to a recent result by Marti and Venema, appearing first in [10] and later in [12]. The result builds on earlier work by A. Kurz and R. Leal [8], and provides a translation of nabla-style coalgebraic logic corresponding to a lax extension into the logic of predicate liftings. The one subtle difference is that, while Marti and Venema restrict attention to symmetric lax extensions, we are interested also in the non-symmetric case. The non-symmetric case allows us to characterize simulation preorders whereas the symmetric only allows us to characterize behavioral equivalences.

Definition 11

An $n$-ary predicate lifting for a set functor $T$ is a natural transformation

$$\lambda : Q^n \rightarrow QT$$

where $Q$ is the contravariant powerset functor².

Fix a finitary functor $T : \mathbf {Set} \rightarrow \mathbf {Set}$ and a lax extension $L$ that extends $\overline{T}$. Given a set $V$ of variables, the language of all predicate liftings $\Lambda$ for $T$ over the variables $V$ is given by the grammar:

$$\mathcal {L}_\Lambda (V) \ni \varphi {::}= x \mid \varphi \wedge \varphi \mid \varphi \vee \varphi \mid \lambda (\varphi ,\ldots ,\varphi ), $$

where $x$ ranges over $V$ and $\lambda$ ranges over predicate liftings. Given a coalgebra $\mathfrak {A}= (X,\alpha )$ and a valuation $\upsilon : V \rightarrow \mathcal {P}X$, the semantics is given by the usual clauses for variables and Booleans, with the evaluation clause for liftings:

$$(\mathfrak {A},u)\vDash _\upsilon \lambda (\varphi _1,\ldots ,\varphi _n) \Leftrightarrow \alpha (u) \in \lambda _X( tr _\mathfrak {A}^\upsilon (\varphi _1),\ldots , tr _\mathfrak {A}^\upsilon (\varphi _n)),$$

where, here and from now on, $tr _\mathfrak {A}^\upsilon : \mathcal {L}_\Lambda (V) \rightarrow Q X$ sends a formula $\varphi$ to its “truth set”:

$$ tr _\mathfrak {A}^\upsilon (\varphi ) = \{v\in X \mid (\mathfrak {A},v)\vDash _\upsilon \varphi \}.$$

A system of equations is a mapping $s : X \rightarrow \mathcal {L}_\Lambda (V)$. Any system of equations $s$ gives rise to an operator $\mathcal {O}_s$ on the lattice of evaluations in $\mathfrak {A}$ in the same way as before; if this operator is always monotone, then we say that the system $s$ is positive. In this case the operator always has a greatest fixed point, and we write $(\mathfrak {A},u)\vDash _s \varphi$ as shorthand for $(\mathfrak {A},u)\vDash _{ GFP (s)} \varphi$, where the evaluation $GFP (s)$ is the greatest fixed point for this operator.

We introduce some notation: given a set $X$, let $\in _X$ denote the membership relation from $X$ to $QX$. Consider the following conditions on $L$:

• A1 Given a mapping $f : Z \rightarrow X$ and a relation $R \subseteq X \times Y$, we have

  $$ \widehat{Tf};LR = L(\widehat{f};R).$$

• A2 Given a relation $R \subseteq X \times Y$ and a mapping $f : Z \rightarrow Y$, we have

  $$ L(R;(\widehat{f})^\circ ) = LR;(\widehat{Tf})^\circ .$$

It is shown in [10, Proposition 3.10] and [12, Proposition 5] that these conditions hold for all symmetric lax extensions.

Example 4

The reader can verify that these conditions hold for the lax extension $L_{ sim }$ from Example 1.

Observation 6

If A1 and A2 hold for $L$, then they hold for $L^\circ$ also.

An immediate consequence of the conditions A1 and A2 is the following:

Lemma 2

If $L$ satisfies A1 and A2, then the mappings $d_X : TQX \rightarrow QTX$ defined by

$$a \mapsto \{b \in TX \mid b (L\in _X) a\}$$

form a distributive law, i.e. they are the components of a natural transformation

$$d : TQ \rightarrow QT.$$

The case where $L$ is symmetric is shown is given in [12, Proposition 19]. Below we verify that the equations A1 and A2 suffice for the proof to go through.

Proof

Let $h : X \rightarrow Y$ be any mapping and let $a \in TQY$. First, note that

$$\begin{aligned} \in _X;(\widehat{Qh})^\circ = \widehat{h};\in _Y \end{aligned}$$

(2)

since, for $u \in X$ and $z \in QY$, we have $u \in Qh(z)$ iff $h(u) \in z$. We calculate:

$$\begin{aligned} d_X \circ TQh (a)&= \{b \in TX \mid b (L\in _X) TQh(a)\}&\\&= \{b \in TX \mid b (L\in _X); (\widehat{TQh})^\circ a\}&\\&= \{b \in TX \mid b (L(\in _X ; (\widehat{Qh})^\circ )) a\}&{\text {by}}~\mathbf{A2 }\\&= \{b \in TX \mid b (L(\widehat{h} ; \in _Y)) a\}&{\text {by}}~(2)\\&= \{b \in TX \mid b (\widehat{Th} ; (L\in _Y)) a\}&{\text {by}}~\mathbf{A1 }\\&= \{b \in TX \mid Th(b) (L\in _Y) a\} \\&= QTh \circ d_Y(a), \end{aligned}$$

and we have proven that $d_X \circ TQh = QTh \circ d_Y$, so that $d$ is a natural transformation.    $\square$

Lemma 3

Suppose $L$ satisfies A1 and A2, and let $d$ be the distributive law determined by $L$, according to Lemma 2. Let $\mathfrak {A}= (X,\alpha )$ be a coalgebra and $\upsilon : V \rightarrow \mathcal {P}X$ a valuation. Then for $a \in TX$ and $b \in T\mathcal {L}(V)$, we have

$$a (L \vDash _\upsilon ) b \text { iff } a \in d_X \circ T( tr ^\upsilon _\mathfrak {A})(b) .$$

From this point we can simply apply the same techniques that are used in [10, 12] to translate $\nabla$-formulas into the language of predicate liftings: since $T$ is finitary it has a presentation as a quotient of a polynomial functor:

$$p : \coprod _{n\in \omega }\varSigma _n \times (-)^n \rightarrow T,$$

where each $\varSigma _n$ is a constant set³ (see [1] for details). Given $n\in \omega$ and $\sigma _n \in \varSigma _n$, we get a natural transformation $p^{\sigma _n} : (-)^n \rightarrow T$ by

$$p^{\sigma _n}_X(u_1,\ldots ,u_n) = p_X(\sigma _n,u_1,\ldots ,u_n).$$

We will simply write $p^\sigma$ from now on, letting the index $n$ be made clear from context. We can exploit the presentation $p$ to derive a set of predicate liftings for $T$:

Definition 12

Given $\sigma \in \varSigma _n$, define the “Moss lifting” $\mu [\sigma ] : Q^n \rightarrow QT$ by

$$(X_1,\ldots ,X_n) \mapsto d_X \circ p^\sigma _{QX}(X_1,\ldots ,X_n) .$$

We now come to the main lemma of this section:

Lemma 4

Suppose that $L$ satisfies conditions A1 and A2. Let $\mathfrak {A}= (X,\alpha )$ be a finite $T$-coalgebra. Then there exist systems of equations

$$s_1,s_2 : X \rightarrow \mathcal {L}_\Lambda (X)$$

such that, relative to any coalgebra $\mathfrak {B}= (Y,\beta )$, $\mathcal {O}_{s_1}: \mathcal {P}(Y)^X \rightarrow \mathcal {P}(Y)^X$ is the same as $\mathcal {O}_{s_\Box }$, and also $\mathcal {O}_{s_2}=\mathcal {O}_{s_\Diamond }$.

Proof

For the first part of the lemma, fix $u \in X$. We have $\alpha (u) \in TX \subseteq T\mathcal {L}(V)$. Since the presentation $p$ is point-wise surjective, there are $x_1,\ldots ,x_n \in X$ and $\sigma \in \varSigma _n$ with

$$p^\sigma _X(x_1,\ldots ,x_n) = \alpha (u)$$

Since $p^ \sigma$ is natural and $T$ preserves inclusions we get

$$p^\sigma _{\mathcal {L}(V)}(x_1,\ldots ,x_n) = \alpha (u)$$

Let $\mu [\sigma ] : Q^n \rightarrow QT$ denote the $n$-ary Moss lifting determined by $\sigma$ using the distributive law $d$ induced by $L$, and set

$$s_1(u) = \mu [\sigma ](x_1,\ldots ,x_n).$$

Then, for $v \in Y, u \in X$ and a valuation $\upsilon$, we get

$$\begin{aligned}&(\mathfrak {B},v)\vDash _\upsilon s_\Box (u) \\ \text { iff }&(\mathfrak {B},v)\vDash _\upsilon \Box \alpha (u) \\ \text { iff }&\beta (v) L(\vDash _\upsilon ) \alpha (u) \\ \text { iff }&\beta (v) \in d_{Y} \circ T(tr^\upsilon _\mathfrak {B})(\alpha (u)) \qquad \qquad \qquad \qquad \ \ \ \ \ \!\!\!\!\!{\text {by Lemma 3}} \\ \text { iff }&\beta (v) \in d_{Y} \circ T(tr^\upsilon _\mathfrak {B})(p^\sigma _{\mathcal {L}(V)}(x_1,\ldots ,x_n)) \\ \text { iff }&\beta (v) \in d_{Y} \circ p^\sigma _{QY}(tr^\upsilon _\mathfrak {B}(x_1),\ldots , tr^\upsilon _\mathfrak {B}(x_n)) {\qquad \qquad }\mathrm{by~naturality~of~p^\sigma }\\ \text { iff }&\beta (v) \in \mu [\sigma ]_Y(tr^\upsilon _\mathfrak {B}(x_1),\ldots , tr^\upsilon _\mathfrak {B}(x_n))\\ \text { iff }&\beta (v) \in \mu [\sigma ]_Y(\upsilon (x_1),\ldots , \upsilon (x_n))\\ \text { iff }&(\mathfrak {B},v) \vDash _\upsilon \mu [\sigma ](x_1,\ldots ,x_n) \\ \text { iff }&(\mathfrak {B},v)\vDash _\upsilon s_1(u). \end{aligned}$$

It clearly follows that the systems of equations $s_\Box$ and $s_1$ give rise to the same operator on the lattice of valuations in $\mathfrak {B}$.

For the second part of the lemma, we make use of Observation 6 and reason exactly the same way using the distributive law determined by $L^\circ$.   $\square$

Note that if $s_1,s_2$ always give rise to the same operators on evaluations as $s_\Box ,s_\Diamond$, then these systems of equations must be positive! Hence, we get:

Theorem 3

Suppose that $L$ satisfies conditions A1 and A2. Given a finite $T$-coalgebra $\mathfrak {A}= (X,\alpha )$, there exist positive systems of equations

$$s_1,s_2 : X \rightarrow \mathcal {L}_\Lambda (X)$$

such that for any $u \in X$ and any pointed $T$-coalgebra $(\mathfrak {B},v)$, we have

$$ (\mathfrak {B},v)\vDash _{s_1} u \text { iff } (\mathfrak {B},v) \preceq _L (\mathfrak {A},u)$$

and

$$(\mathfrak {B},v)\vDash _{s_2} u \text { iff } (\mathfrak {A},u) \preceq _L (\mathfrak {B},v) .$$

Proof

Easy corollary from the previous lemma and Theorem 2.   $\square$

5 Applications

In this final section, we provide examples of lax extensions for various functors that give rise to simulations and bisimulations that have been used in the literature. All these examples are taken from the papers [2, 15].

Finitary Power Set Functor.

Example 5

(simulations). Consider the following lax extensions for the covariant powerset functor:

$$ \begin{aligned} L_{ sim }R&:= \{(A,B) \in \mathcal {P}_\omega X \times \mathcal {P}_\omega Y \mid \forall a \in A \;\exists b \in B : a R b\},\\ L_{ rs }R&:= \{(A,B) \in \mathcal {P}_\omega X \times \mathcal {P}_\omega Y \mid (\forall a \in A \;\exists b \in B : a R b)\, \& \, (A=\emptyset \Rightarrow B=\emptyset ) \},\\ L_{ cs }R&:= \{(A,B) \in \mathcal {P}_\omega X \times \mathcal {P}_\omega Y \mid A\ne \emptyset \Rightarrow (B\ne \emptyset \; \& \;\forall b \in B \;\exists a \in A : a R b)\}. \end{aligned}$$

Recall that $L_{ sim }$ was already given in Example 1 and $L_{ sim }$-simulations are ordinary simulations. Also, $L_{ rs }$-simulations are ready simulations and $L_{ cs }$-simulations are conformance simulations. Item (2) of Theorem 2 yields characteristic formulas for each of these simulations.

Example 6

(bisimulation). Let $L$ be one of $L_{ sim }$, $L_{ rs }$, or $L_{ cs }$ from Example 5. In each of these cases its bisimulator $B(L)$ is the same, and is given by

$$ \begin{aligned} B(L)R = \{(A,B) \in \mathcal {P}_\omega X \times \mathcal {P}_\omega Y \mid&\;\forall a \in A \;\exists b \in B : a R b, \;\; \& \;\;\\&\;\forall b\in B\; \exists a\in A:aRb\}. \end{aligned}$$

Hence by Remark 1, $B(L)$ is the Barr extension $\overline{\mathcal {P}_\omega }$ for the finitary power set functor, and the main theorem gives characteristic formulas for bisimulation.

Example 7

(mutual simulation). Given states $u \in X$ and $v \in Y$ in $\mathcal {P}_\omega$-coalgebras $\mathfrak {A}= (X,\alpha )$ and $\mathfrak {B}= (Y,\beta )$, we say that $u$ and $b$ are mutually simulated, written $(\mathfrak {A},u)\approx (\mathfrak {B},v)$, if there is a simulation $S$ from $\mathfrak {A}$ to $\mathfrak {B}$ with $u S v$ and a simulation $S^\prime$ from $\mathfrak {B}$ to $\mathfrak {A}$ with $v S^\prime u$. In other words, $(\mathfrak {A},u)\approx (\mathfrak {B}, v)$ iff $(\mathfrak {A},u)\preceq _{L_{ sim }} (\mathfrak {B},v)$ and $(\mathfrak {B},v)\preceq _{L_{ sim }} (\mathfrak {A}, u)$. Given a finite $\mathcal {P}_\omega$-coalgebra $\mathfrak {A}= (X,\alpha )$ and $u\in X$, we want to find a system of equations that allows us to characterize $(\mathfrak {A},u)$ up to mutual simulation. There is a simple way to obtain such a system of equations from the main theorem. Let $s_\square : u\mapsto \Box \alpha (u)$, and $s_\Diamond : u\mapsto \Diamond \alpha (u)$. Take the disjoint union of $X$ with itself, i.e. the coproduct

$$X + X = (X \times \{0\}) \cup (X \times \{1\})$$

as a new set of variables. Let $\iota _1$ and $\iota _2$ be the left and right insertions of $X$ into this coproduct, and define the system of equations $s$ by setting

• $s(w,0) = \square (\mathcal {P}_\omega \iota _1 (\alpha (w)))$ and

• $s(w,1) = \Diamond (\mathcal {P}_\omega \iota _2 (\alpha (w)))$.

Note that $\mathcal {P}_\omega \iota _1(\alpha (w)) \in \mathcal {P}_\omega (X\times \{0\})$, $\mathcal {P}_\omega \iota _1(\alpha (w)) \in \mathcal {P}_\omega (X + X)$, and similarly for $\mathcal {P}_\omega \iota _2(\alpha (w))$, and hence $s$ maps variables in $X+X$ to formulas in the language $\mathcal {L}(X+X)$. With respect to this system of equations, the formula $(u,0) \wedge (u,1)$ is a characteristic formula for the pointed coalgebra $(\mathfrak {A},u)$ w.r.t. mutual simulation. To see this, first let $t_i = s\upharpoonright _{X\times \{i\}}$ for $i=\{0,1\}$. As $s_\square$ and $t_0$ are isomorphic, and similarly $s_\Diamond$ and $t_1$, it is easy to see that for any pointed coalgebra $(\mathfrak {B},v)$, we have

• $(\mathfrak {B},v)\vDash _{s_\square } u$ iff $(\mathfrak {B},v)\vDash _{t_0} (u,0)$,

• $(\mathfrak {B},v)\vDash _{s_\Diamond } u$ iff $(\mathfrak {B},v)\vDash _{t_1} (u,1)$.

Using this and Observation 5, we have that for any pointed coalgebra $(\mathfrak {B},v)$, we have

• $(\mathfrak {B},v)\vDash _{s_\square } u$ iff $(\mathfrak {B},v)\vDash _{s} (u,0)$,

• $(\mathfrak {B},v)\vDash _{s_\Diamond } u$ iff $(\mathfrak {B},v)\vDash _{s} (u,1)$.

It is immediate from this and Theorem 2 (the main theorem) that

$$(\mathfrak {B},v)\vDash _s (u,0) \wedge (u,1)\text { iff } (\mathfrak {A},u) \approx (\mathfrak {B},v)$$

as required.

Finite Probability Functor. Given a partial function $\rho :X\rightarrow [0,1]$, and a subset $B\subseteq X$, let

$$\rho [B] = \sum _{b\in B \cap \mathrm {dom}(\rho )}\rho (b).$$

Let $\mathcal {D}$ be the finite probability functor as given in [13, Example 3.5]: $\mathcal {D}$ maps each set $X$ to the set of partial functions from $\rho :X\rightarrow [0,1]$, such that $\mathrm {dom}(\rho )$ is finite and $\rho [X] = 1$, and maps each function $f:X\rightarrow Y$ to $\mathcal {D}f:\mathcal {D}X \rightarrow \mathcal {D}Y$ given by

$$ ((\mathcal {D}f)\rho )(y) = \rho [f^{-1}[\{y\}]] = \sum \{\rho (x):x\in Supp \,{\rho }, f(x)=y\}. $$

for each $\rho \in \mathcal {D}X$ and $y\in f[\mathrm {dom}(\rho )]$. Then $\mathcal {D}$ preserves inclusions (this is the reason for $\rho$ being a partial rather than total function). A coalgebra $\alpha : A\rightarrow \mathcal {D}A$ corresponds to a Markov chain.

Given a relation $R\subseteq X\times Y$ and $A\subseteq X$, let $R[A] = \{b\mid \exists a\in A:aRb\}$.

Example 8

(Simulation and bisimulation on Markov chains). Let

$$ L_{ mc }R := \{(p,q) \in \mathcal {D}X \times \mathcal {D}Y \mid \forall C\subseteq X, p[C]\le q[R[C]]\}. $$

Then $L$ is a lax extension of the finite probability functor $\mathcal {D}$.

The lax extension $L$ corresponds to both simulation and bisimulation on Markov chains, and so the main theorem gives characteristic formulas for this relation (simulation and bisimulation are distinguished in variations of these Markov chains such as in [6] as well as with the probabilistic automata in Example 9 below). Furthermore, it is immediate from the equivalence of items 1 and 3 in [15, Lemma 1] that $L$ is in fact just the Barr extension of $\mathcal {D}$.

Finite Non-deterministic Probability Functor. We call the functor $\mathcal {P}_\omega \circ \mathcal {D}$ the finite nondeterministic probability functor. A coalgebra for $\mathcal {P}_\omega \circ \mathcal {D}$ corresponds to a probabilistic automaton (which is essentially a Markov chain with non-deterministic transitions to distributions).

Example 9

(Simulation on Probabilistic Automata). The finite non-deterministic probability functor has a lax extension

$$ L_{ pa }R := \{(A,B) \in \mathcal {P}_\omega \mathcal {D}X \times \mathcal {P}_\omega \mathcal {D}Y \mid \forall p\in A, \;\exists q\in B: \forall C\subseteq X, p[C]\le q[R[C]]\}. $$

Such a lax extension corresponds to simulation (on probabilistic automata), and so we find characteristic formulas for such simulations.

Example 10

(Probabilistic simulation on Probabilistic Automata). Given an element $\mu \in \mathcal {D}\mathcal {D}X$, let $\gamma (\mu ) = \nu \in \mathcal {D}(X)$, where $\nu (x) = \sum _{\nu '\in \mathrm {dom}(\mu )}\nu '(x)\mu (\nu ')$. Then probabilistic simulation (see [16]) is defined by the relation lifting:

$$\begin{aligned} L_{ psim }R:= \{(A,B) \in \mathcal {P}_\omega \mathcal {D}X \times \mathcal {P}_\omega \mathcal {D}Y \mid&\forall p\in A, \;\exists q\in \mathcal {D}B: \\&\forall C\subseteq X, p[C]\le \gamma (q)[R[C]]\}. \end{aligned}$$

It can be checked that this is a lax extension. It is easy to see that $L_{ psim }$ is monotone (L1 holds) and as $L_{ pa }\subseteq L_{ psim }$, L3 holds for $L_{ psim }$ as well. To see that L2 holds. Suppose that $A (L_{ psim }R) B$ and $B(L_{ psim }S) C$, and let $\mu \in A$. Then there exists a $\tilde{\nu }\in \mathcal {D}B$, such that for all $Z\subseteq A$, $\mu [Z]\le \gamma (\tilde{\nu })[R[Z]]$. Also, for each $\nu \in Supp \,\tilde{\nu }$, there exists $\tilde{\rho }_\nu \in \mathcal {D}C$, such that for all $Z\subseteq B$, $\nu [Z]\le \gamma (\tilde{\rho }_\nu )[S[Z]]$. Now let $\tilde{\sigma } = \sum _{\nu \in Supp \,\tilde{\nu }}\tilde{\nu }(\nu )\tilde{\rho }_\nu$. Then for any $Z\subseteq A$,

$$\begin{aligned} \mu [Z]&\le \gamma (\tilde{\nu })[R[Z]] \\&= \sum _{\nu \in Supp \,{\tilde{\nu }}} \tilde{\nu }(\nu ) \nu [R[Z]]\\&\le \sum _{\nu \in Supp \,{\tilde{\nu }}} \tilde{\nu }(\nu ) \gamma (\tilde{\rho }_\nu )[(R;S)[Z]]\\&= \sum _{\nu \in Supp \,{\tilde{\nu }}} \tilde{\nu }(\nu ) \sum _{\rho \in Supp \,{\tilde{\rho }_\nu }} \tilde{\rho }_\nu (\rho )\rho [(R;S)[Z]]\\&= \sum _{\nu \in Supp \,{\tilde{\nu }}} \sum _{\rho \in Supp \,{\tilde{\rho }_\nu }} ( \tilde{\nu }(\nu ) \tilde{\rho }_\nu (\rho ))\cdot \rho [(R;S)[Z]]\\&= \sum _{\rho \in Supp \,{\tilde{\sigma }}} \left( \sum _{\{\nu \mid \rho \in Supp \,\tilde{\rho }_\nu \}} \tilde{\nu }(\nu ) \tilde{\rho }_\nu (\rho )\right) \rho [(R;S)[Z]]\\&= \gamma (\tilde{\sigma })[(R;S)[Z]]. \end{aligned}$$

As $L_{ psim }$ is a lax extension, Theorem 2 yields characteristic formulas.

Labelled Powerset Functor. Let $A$ be a set of labels, and let $\mathcal {P}_A$ be the functor that maps each object $X$ to $(\mathcal {P}_\omega (X))^A$, and maps each morphism $f:X\rightarrow Y$ to $\mathcal {P}_Af: h \mapsto k$, where $k:a\mapsto f[h(a)]$. Such a functor corresponds to a multi-modal Kripke frame.

Example 11

(multi-modal simulation). Let

$$ L_{ msim }R := \{(h,k)\mid \forall a\in A \forall x\in h(a) \exists y\in k(a): xRy\} . $$

In other words $L_{ msim }R$ consists of all pairs $(h,k)$, such that for all $a\in A$, there is a function $f:h(a)\rightarrow k(a)$, whose graph is a subset of $R$. Since $L_{ msim }$ is a lax extension, the main theorem yields a characteristic formula.

Weak Simulation and Bisimulation. Let $A$ be a set of labels and designate $\tau \in A$ to be a “silent action”, not to be counted in a weak simulation. We aim to define a lax extension to capture weak simulation of transition systems. Here, we cannot simply work with the labelled powerset functor; the problem is that this functor only catches the “one-step” behaviours, while weak simulation crucially involves iterated behaviour. We will solve this problem by modelling transition systems as coalgebras for a suitable co-monad.

It is well known that the forgetful functor from the category of $\mathcal {P}_A$-coalgebras to the category $\mathbf {Set}$ of sets and mappings has a right adjoint [5], and this adjunction gives rise to a co-monad on $\mathbf {Set}$. Here, we shall describe essentially the same co-monad in more concrete terms: let a rooted tree $t$ over a set $X$ be a prefix closed set of strings in $\mathbb {N}^*$; being prefix closed, $t$ must include the empty string $\varepsilon$. An $A$-labelled rooted tree is a pair $(t,\lambda )$, where $t$ is a rooted tree and $\lambda :t\rightarrow A$ is a labelling function. Let $C_A : \mathbf {Set} \rightarrow \mathbf {Set}$ be defined by setting:

• For a set $X$, $C_A(X)$ is the set of $(X\times A)$-labelled and finitely branching rooted trees, with $\pi _2\lambda (\varepsilon ) = \tau$ (as an arbitrary convention).

• For a mapping $h : X \rightarrow Y$, $C_A h : C_A X \rightarrow C_A Y$ is defined by letting $C_A h$ map a tree $(t,\lambda )$ to the tree $(t,\lambda ^\prime )$ with labelling $\lambda ^\prime$ obtained by the assignment $x\mapsto (h(\pi _1\lambda (x)),\pi _2\lambda (x))$.

Intuitively, $C_A X$ is the set of possible behaviours for a $\mathcal {P}_A$-coalgebra with domain $X$.

The functor $C_A$ is a co-monad on $\mathbf {Set}$. The co-unit $\eta : C_A \rightarrow Id_\mathbf {Set}$ is defined by letting $\eta _X$ send a tree $(t,\lambda ) \in C_A X$ to $\pi _1(\lambda (\varepsilon )) \in X$. The co-multiplication $\mu : C_A \rightarrow C_A \circ C_A$ is defined by letting $\mu _X$ send a tree $(t,\lambda ) \in C_A X$ to the “tree of trees” $(t,\lambda ')$ in $C_A(C_A (X))$, such that $\lambda ':w\mapsto ((t_w,\lambda _w),\pi _2\lambda (w))$, where

• $t_w = \{v \in \mathbb {N}^*\mid w\cdot v\in t\}$ and

• $\lambda _w:t_w\rightarrow X\times A$, where $\lambda _w(v) = \left\{ \begin{array}{ll} \lambda (w\cdot v) &{} v\ne \varepsilon \\ (\pi _1\lambda (w), \tau )&{} v=\varepsilon \end{array}\right. .$

A labelled transition system can be represented as a coalgebra $\alpha : X \rightarrow C_A X$ for this co-monad, meaning that the following diagrams are required to commute:

Forgetting the co-monad structure of $C_A$ we can just view it as an ordinary set functor, and so it makes sense to speak of a lax extension of $C_A$. We want to define a lax extension that captures weak simulation between labelled transition systems. Given a set $X$, a labelled tree $(t,\lambda ) \in C_A X$ and a label $a$, define the relation

$$\mathop {\longrightarrow }\limits ^{t,\lambda ,a} \;\subseteq X \times X$$

by setting $x \mathop {\longrightarrow }\limits ^{t,\lambda ,a} y$ iff there is an $a$-labelled edge from $x$ to $y$ in the labelled tree $(t,\lambda )$, that is, there exists $w$ and $w\cdot n$ in $t$, such that $\pi _1(\lambda (w))=x$ and $\lambda (w\cdot n) = (y,a)$. Let $\mathop {\longrightarrow }\limits ^{t,\lambda ,a^\star }$ be the transitive reflexive closure of $\mathop {\longrightarrow }\limits ^{t,\lambda ,a}$. For a labelled tree $(t,\lambda )$, say that a node $v$ is $a$-reachable from $u$ in $(t,\lambda )$ if there are nodes $u^\prime$ and $v^\prime$ with

$$u \mathop {\longrightarrow }\limits ^{t,\lambda ,\tau ^\star } u^\prime \mathop {\longrightarrow }\limits ^{t,\lambda ,a} v^\prime \mathop {\longrightarrow }\limits ^{t,\lambda ,\tau ^\star } v$$

and denote by $re (t,\lambda ,a)$ the set of nodes $a$-reachable in $(t,\lambda )$ from the root $\pi _1(\lambda (\varepsilon ))$ of $t$. Then $C_A$ has a lax extension $L_{ weak }$ defined, for $R \subseteq X \times Y$, by setting $L_{ weak }R$ to be the set of pairs $((t,\lambda ),(t^\prime ,\lambda ')) \in C_A X \times C_A Y$ satisfying

$$ \forall a \in A\setminus \{\tau \}\; \forall x \in re (t,\lambda ,a)\; \exists y \in re (t^\prime ,\lambda ^\prime ,a) : x R y.$$

This lax extension gives $\Box$- and $\Diamond$-modalities evaluated on $C_A$-coalgebras as before, and we can derive characteristic formulas for $L_{ weak }$-simulation using Theorem 2. In particular, these formulas will characterize $L_{ weak }$-simulation among coalgebras for $C_A$ as a co-monad, and among these coalgebras $L_{ weak }$-simulation can be taken to model weak simulation in the usual sense. Weak bisimulation is handled by considering the bisimulator of $L_{ weak }$.