Keywords

1 Introduction

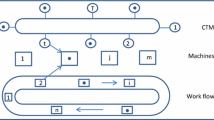
Flexible manufacturing system (FMS) is an automated manufacturing system that consists of numerical control machines and an automated material handling/storage system, which are controlled by a computer control system. Each machine has an automatic tool changer that can interchange cutting tools automatically, which allows consecutive operations to be performed with negligible setup times. Therefore, an FMS is capable of processing various part types simultaneously with higher utilization.

Part selection, alternatively called batching in the literature, is the problem of selecting the parts to be produced during the upcoming planning period. Most previous studies on FMS part selection propose single-period models that determine a set of parts to be produced simultaneously during an upcoming period. See Hwang and Shogan [1], Kim and Yano [2] and Bilge et al. [3] for examples. To obtain better solutions over the planning horizon with multiple periods, some articles extend the single-period models to multi-period ones. See Stecke and Toczylowski [4] and Lee and Kim [5] for examples.

This study focuses on a multi-period part selection problem with controllable processing times, which is the problem of determining a set of parts and their processing times in each period of a planning horizon. The controllable processing times imply that part processing times are not given, but can be changed to cope with system requirements such as energy consumption, scheduling performances, and so on. See Nowicki and Zdrzalka [6] for the detail of the controllable processing time concept.

To represent the problem mathematically, an integer programming model is developed. Then, due to the complexity of the problem, two-phase heuristics are proposed in which an initial solution is obtained by a greedy heuristic under initial processing times and then it is improved using local search methods while adjusting part processing times. Computational experiments were done, and the results are reported.

2 Problem Description

The FMS considered in this study consists of one or more numerical control machines, each of which has a tool magazine of a limited tool slot capacity. The machines can process different parts with negligible setup times if tooled differently in the tool magazines. To produce a part, several tools are required and each tool requires one or more slots in the tool magazine, where each tool has multiple copies with a limited life. Also, processing times of parts are controllable with different processing costs.

The problem is to determine the set of parts to be produced in each period of a planning horizon and their processing times while satisfying the constraints on processing time capacity, tool magazine capacity, tool copies and tool lives. The objective is to minimize the sum of part processing, earliness/tardiness, subcontracting and tool costs. The problem can be represented as the following integer programming model. The notations used are summarized below.

Parameters

\( d_{i} \) :

due-date of part \( i \)

\( cp_{i}^{j} \) :

processing cost of part \( i \) under the \( j \)th available processing time

\( cd_{ih} \) :

earliness or tardiness cost of part \( i \) incurred when it is assigned to period \( h \), i.e.

$$ cd_{ih} = \left\{ {\begin{array}{*{20}c} {\epsilon_{i} \cdot \left( {d_{i} - h} \right), if h \le d_{i} } \\ {\tau_{i} \cdot \left( {h - d_{i} } \right), if h \ge d_{i} ,} \\ \end{array} } \right. $$

where \( \epsilon_{i } \) and \( \tau_{i } \) are per-period earliness and tardiness cost of part \( i \), respectively

\( cs_{i} \) :

subcontracting cost of part \( i \)

\( ct_{t} \) :

cost of tool type \( t \)

\( p_{i}^{j} \) :

\( j \)th available processing time of part \( i \)

$$ \left( {p_{i}^{1} \le p_{i}^{2} \le \cdots \le p_{i}^{{J_{i} }} \,{\text{and}}\,cp_{i}^{1} \ge cp_{i}^{2} \ge \cdots \ge cp_{i}^{{J_{i} }} \,{\text{for}}\,{\text{all}}\,i.} \right) $$
\( TC_{t} \) :

number of available copies of tool type \( t \)

\( TL_{t} \) :

life of tool type \( t \)

\( s_{t} \) :

number of slots required by tool type \( t \)

\( \varPhi_{t} \) :

set of parts that require tool type \( t \)

\( L \) :

aggregated processing time capacity in period \( h \)

\( S \) :

aggregated tool magazine capacity in period \( h \)

Decision variables

\( x_{ih}^{j} \) :

= 1 if part \( i \) is assigned to period \( h \) with the \( j \)th available processing time, and 0 otherwise

\( y_{th} \) :

number of copies for tool type \( t \) used in period \( h \)

Now, the integer programming model is given below. The detailed explanation is skipped here due to the space limitation. The problem [P] is NP-hard because the problem with fixed part processing times can be reduced to the generalized assignment problem that is known to be NP-hard [7].

$$ \begin{aligned} & \left[ {\mathbf{P }} \right]{\text{Minimize}}\;\sum\nolimits_{i = 1}^{I} {\sum\nolimits_{j = 1}^{{J_{i} }} {\sum\nolimits_{h = 1}^{H} {cp_{i}^{j} \cdot x_{ih}^{j} + } } } \, \sum\nolimits_{i = 1}^{I} {\sum\nolimits_{j = 1}^{{J_{i} }} {\sum\nolimits_{h = 1}^{H} {cd_{ih} \cdot x_{ih}^{j} } } } \\ & \quad \quad \quad \quad \quad \quad \quad \quad + \sum\nolimits_{i = 1}^{I} {cs_{i} } \cdot \left( {1 - \sum\nolimits_{j = 1}^{{J_{i} }} {\sum\nolimits_{h = 1}^{H} {x_{ih}^{j} } } } \right) + \sum\nolimits_{t = 1}^{T} {\sum\nolimits_{h = 1}^{H} {ct_{th} \cdot y_{th} } } \\ \end{aligned} $$

subject to

$$ \sum\nolimits_{j = 1}^{{J_{i} }} {\sum\nolimits_{h = 1}^{H} {x_{ih }^{j} \le 1} } \quad \quad \quad \quad \quad \quad \text{for}{\kern 1pt} \text{all}\;i $$
(1)
$$ \sum\nolimits_{i = 1}^{I} {\sum\nolimits_{j = 1}^{{J_{i} }} {p_{i}^{j} \cdot x_{ih}^{j} \le L} } \quad \quad \quad \quad \;\text{for}{\kern 1pt} \text{all}\;h $$
(2)
$$ \sum\nolimits_{t = 1}^{T} {s_{t} \cdot y_{th} \le S} \quad \quad \quad \quad \quad \quad \quad \text{for}{\kern 1pt} \text{all}\;h $$
(3)
$$ \sum\nolimits_{h = 1}^{H} {y_{th} \le TC_{t} } \quad \quad \quad \quad \quad \quad \quad \text{for}{\kern 1pt} \text{all}\;t $$
(4)
$$ \sum\nolimits_{{i \in \varPhi_{t} }} {\sum\nolimits_{j = 1}^{{J_{i} }} {p_{i}^{j} \cdot x_{ih}^{j} \le TL_{t} \cdot y_{th} } } \quad \quad \text{for}{\kern 1pt} \text{all}\;t\,\text{and}\;h $$
(5)
$$ x_{ih}^{j} \in \left\{ {0,1} \right\}\quad \quad \quad \quad \quad \quad \quad \quad \text{for}{\kern 1pt} \text{all}\;i,j\,\text{and}\;h $$
(6)
$$ y_{th} \ge 0\,{\text{and integer}}\quad \quad \quad \quad \quad {\text{for all}}\,t\,{\text{and}}\,h $$
(7)

3 Solution Approach

3.1 Phase I: Obtaining an Initial Solution

An initial solution is obtained by sorting the parts in the non-increasing order of subcontracting costs and allocating each part in the sorted list to the period with the smallest earliness/tardiness cost while satisfying the constraints.

3.2 Phase II: Improvement

Before explaining the improvement methods, the processing time adjustment method when a part cannot be moved to a period due to the time capacity is explained.

Adjusting Part Processing Times.

If a part cannot be allocated to a period due to the processing time capacity, it is checked if the part can be allocated to the period after adjusting the processing times of the part as well as the parts allocated already to the period. Specifically, it is checked if a part to be moved can be allocated to a period while improving the current solution after its processing time is reduced. If it is not possible, the processing times of the parts allocated already to the period are changed one-by-one and check the possibility of moving the part to the period. For this purpose, the following rules to select the part to be moved are tested. In the following, \( j(i) \) denotes the index for the processing time selected for part \( i \).

  • CTR (cost/time ratio): select part \( i^{*} \) such that

    $$ i^{*} = {\text{argmin}}_{{i \in X_{h} }} \left\{ {{{\left( {cp_{i }^{j\left( i \right) - 1} - cp_{i}^{j\left( i \right)} } \right)} \mathord{\left/ {\vphantom {{\left( {cp_{i }^{j\left( i \right) - 1} - cp_{i}^{j\left( i \right)} } \right)} {\left( {p_{i}^{j\left( i \right)} {-} p_{i}^{j\left( i \right) - 1} } \right)}}} \right. \kern-0pt} {\left( {p_{i}^{j\left( i \right)} {-} p_{i}^{j\left( i \right) - 1} } \right)}}} \right\} $$

  • MCI (minimum cost increase): select part \( i^{*} \) such that \( i^{*} = {\text{argmin}}_{{i \in X_{h} }} \left\{ {cp_{i }^{j\left( i \right)} - cp_{i}^{j\left( i \right) - 1} } \right\} \)

  • MTD (maximum time decrease): select part \( i^{*} \) such that \( i^{*} = {\text{argmax}}_{{i \in X_{h} }} \left\{ {p_{i}^{j\left( i \right)} {-} p_{i}^{j\left( i \right) - 1} } \right\} \)

Improvement.

The improvement method consists of interchange, insertion, perturbation and reallocations of subcontracted parts in sequence. For the current solution, let \( P_{T} \) and \( P_{E} \) denote the set of tardy and early parts, respectively.

Interchange Method.

The parts in \( P_{T} \) (\( P_{E} \)) are sorted in the non-increasing order of the tardiness (earliness) costs. Then, according to the sorted list, each part is interchanged with the ones in the periods with less earliness (tardiness) costs than that of the part considered while adjusting the processing times of the parts to be interchanged and included in the periods that the parts are to be inserted and the best one is selected.

Insertion Method.

Each part in \( P_{T} \) and \( P_{E} \) is removed from its original period and then it is inserted to another feasible period that reduces the total cost. To reduce the search space, we consider the periods with less earliness or tardiness costs than that of the part to be moved for the parts in \( P_{T} \) and \( P_{E} \). The following two methods are tested.

  • BI (best improvement): The parts in \( P_{T} \) (\( P_{E} \)) are sorted in the non-increasing order of their tardiness (earliness) costs. Then, from the first part in the sorted list, it is removed from its original period and then allocated to the first feasible period that improves the current solution while adjusting the part processing times.

  • HI (hybrid improvement): From the first part, the first and the best periods that improve the current solution are found and then the better one is selected.

Perturbation Method.

Each of the parts allocated to its due-date period is moved to the period with the minimum increase in cost and then the part with the largest earliness or tardiness cost is moved from the original period to the due-date period.

Reallocation Method.

The subcontracted parts are sorted in the non-increasing order of subcontracting costs. Then, from the first to the last part in the sorted list, it is inserted to the first feasible period that improves the current solution while adjusting the processing times of relevant parts, where the insertions are done from the due-date to other periods in the non-decreasing order of earliness and tardiness cost.

4 Computational Results

Computational experiments were done to identify the best one among the 6 combinations of 3 processing time adjustment methods (CTR, MCI and MTD) and 2 variations of the improvement methods (BI and HI). The algorithms were coded in C++ and the tests were done on a PC with Intel Core i7 CPU at 3.40 GHz.

The first test was done for small-sized test instances and reports the percentage gaps from the optimal solution values, i.e. \( 100 \cdot {{\left( {C_{a} - C_{opt} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{a} - C_{opt} } \right)} {C_{opt} }}} \right. \kern-0pt} {C_{opt} }} \), where \( C_{a} \) is the objective value obtained from combination a and \( C_{opt} \) is the optimal values obtained from the CPLEX with a time limit of 3600 s. For this test, 60 instances with 5 periods were generated randomly, i.e. 10 instances for each of the 6 combinations of 3 levels for the number of parts (20, 30 and 50) and 2 levels of the number of tools (tight and loose). The detailed data generation method is skipped due to the space limitation.

Test results are summarized in Table 1 that shows the number of instances that the CPLEX gave optimal solutions within 3600 s and the average percentage gaps. Although no one dominates the others, CTR-HI works better than the others and its overall average gap was 1.80. Finally, the CPU seconds of the two-phase heuristics are not reported since all the test instances were solved within 3 s.

Table 1. Test results for small-sized test instances
Full size table

The second test was done on large-sized instances. Because the optimal solutions could not be obtained, we compared them using the relative performance ratio, i.e.

$$ 100 \cdot {{\left( {C_{a} - C_{best} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{a} - C_{best} } \right)} {C_{best} }}} \right. \kern-0pt} {C_{best} }}, $$

where \( C_{best} \) is the best objective value among those obtained by all combinations. Table 2 shows the test results that are similar to those for the small-sized instances.

Table 2. Test results for large-sized test instances
Full size table

5 Concluding Remarks

We considered multi-period part selection for FMSs with controllable processing times. The problem is to determine the set of parts and their processing times that satisfy the processing time and the tool magazine capacities in each period of a planning horizon for the objective of minimizing the sum of part processing, earliness/tardiness, subcontracting and tool costs. The number of available tool copies, tool life restrictions and tool sharing were also considered. An integer programming model was developed, and then two-phase heuristics were proposed in which an initial solution is obtained by a greedy algorithm under initial processing times and then it is improved using two local search methods. Computational experiments were done on a number of test instances, and the best ones were reported.

For further research, it is needed to develop meta-heuristics that can improve the solution quality especially for large-sized instances. Also, the problem can be integrated with other problems such as loading and scheduling.