Abstract
The aim of the present paper is to analyze the problem of assuring the feasibility of a mechanism (game form), implementing in Nash equilibrium a given social choice rule abbreviated as (SCR) when the mechanism is constrained as to the way in which it is permitted to depend on endowments. A social choice rule is a correspondence specifying outcomes considered to be desirable in a given economy (environment). A mechanism is defined by (a) an outcome function and (b) a strategy domain prescribed for each player. Our outcome functions are not permitted to depend at all on the initial endowments. As to strategy domains, the ith agent’s strategy domain S i is only permitted to depend on that agent’s endowment, but not on the endowments, other agents. (For earlier results concerning endoment manipulation, see Postlewaite (1979) and Sertel (1990).)
This paper is a revised, shortened version of a book contribution originally published together with the late Leonid Hurwicz in a festschrift for Stan Reiter.
Hurwicz L., Maskin E., Postlewaite A. (1995) Feasible Nash Implementation of Social Choice: Rules When the Designer Does not Know Endowments or Production Sets.
In: Ledyard J.O. (ed) The Economics of Informational Decentralization: Complexity, Efficiency, and Stability. Springer, Boston, MA © Springer Science+Business Media New York 1995.
The preface for this version was added by Eric Maskin.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Earlier models of tatonnement and of proposed mechanisms designed to implement social choice rules (e.g., Walras or Lindahl) were criticized for not guaranteeing the feasibility at disequilibrium points. Some, like the Walrasian auctioneer, were not balanced (1), others failed to assure individual feasibility. (See Wilson 1976.)
- 2.
From now on “implementation” is to be understood in the sense of Nash non-cooperative equilibria. Let n be the number of players, Z the outcome space (the space of allocations), S the joint strategy space, i.e., S = S 1 × … × S n, where S i is the strategy domain of the ith player, and let h: S → Z be the outcome function. An SCR, denoted by F, is a correspondence from the space E of environments into Z, specifying for each environment (economy) e in E a nonempty set in the outcome space Z. An environment (economy) is defined as an n-tuple of characteristics e i = (C i, ω i, R i), where, for the ith agent, C i is the admissible consumption set, w i the initial endowment, and R i the (weak) preference relation. I.e, e = (e 1, … , e n) and E is the class of a priori admissible environments. A possible interpretation is that the designer believes (correctly) that an environment (economy) outside of E will not occur.
We say that a mechanism (S, h) Nash implements an SCR F over a class of environments E if it is the case that, for every e in E, (1) the set of Nash equilibrium outcomes N S,h(e) generated by the mechanism (S, h) is nonempty, and (2) this set N S,h(e) is a subset of F(e). (The term sometimes used in the literature for this concept is “weakly implements.”) The mechanism (S, h) is said to fully implement F over E if, for every e in E, N S,h(e) = F(e). In most of the present paper we actually deal with a singleton-valued correspondence F, i.e., one equivalent to a function. In that case the two concepts of implementation coincide and we simply say that (S, h) implements the social choice function f, abbreviated SCF, the function equivalent to the singleton-valued correspondence F. (A method for extending our results to correspondences is illustrated in the Appendix to Sect. II.A.1, in Hurwicz et al. 1995.)
- 3.
Those formulating the rules are often collectively referred to as “the designer.” Hence the title of this paper.
- 4.
Of course, because of the non-exaggeration requirement, an agent’s claim as to his/her own endowment provides partial information as to the true endowment, namely that the true endowment is at least as high as that claimed.
- 5.
For example, maximin, Nash, etc.
- 6.
Preferences do not affect feasibility.
- 7.
Maskin’s construction is an algorithm in the sense that it is a ‘recipe’ for constructing implementing mechanisms for a class of SCR’s (by inserting the SCR F in an outcome function schema), rather than a single mechanism.
- 8.
On the other hand, the designer does not know which preference profile (from a known family of profiles) will prevail.
- 9.
When the goods are physical their existence (and ownership) might have to be shown. Similarly, proof might be required for claimed rights or entitlements, or ever claimed skills. See discussion in Hong and Page (1994).
- 10.
I.e., where the balance condition is in the form of a weak inequality rather than equality (called “weak balance”).
- 11.
The environments e ik has the endowment profile \( \overline{\omega} \) but may differ with respect to preferences.
- 12.
The amount received by i is a positive component z i.
- 13.
To simplify exposition, we confine ourselves in this section to single-valued social choice rules; subsequently, we shall extend our treatment to correspondences.
- 14.
The term “optimal” is always used in the sense of the given performance function f.
- 15.
We use, here and elsewhere, the somewhat imprecise notation which identifies (S i, S 1, … , S i−1, S i+1, … , S n) with (S 1, … , S i−1, S i, S i+1, … , S n).
- 16.
∏j ≠ i S j = S 1 × … × S i−1 × S i+1 × … × S n.
- 17.
It would be possible to relax our assumptions by replacing the requirement \( \overset{\circ }{\omega_i}\geqslant 0 \) by \( \overset{\circ }{\omega_i} \)⫺0 and, at the same time weaken \( {w}_i^i\geqslant 0 \) to: \( {w}_i^i\geqslant 0 \) if \( \overset{\circ }{\omega_i}\geqslant 0 \). But we cannot permit an agent to claim \( {w}_i^i=0 \) when \( \overset{\circ }{\omega_i}\geqslant 0 \). For let all agents claim zero endowments while in fact \( \underset{i\in N}{\Sigma}\overset{\circ }{\omega_i}\geqslant 0 \). Then, since the possibility of withholding means that \( {w}_i^i+{h}_i(s) \)⫺ 0 for all i ∈ N, the net Nash allocation would have to be 0 for everyone, and this might be non-optimal.
If the assumptions were relaxed along the indicated lines, a minor modification would have to be made in the outcome function.
- 18.
Here W- is mnemonic for withholding, as distinct from strategies to be labeled D-, in which an agent may not withhold but only destroy his endowment, and from those labeled WD-, where the agent may do both.
- 19.
Here 0 is a net trade (the l-dimensional null vector), strictly preferred by i to the net trade \( {f}_i\kern-0.05em \left(\overset{\circ }{\underrightarrow{\omega}}\kern-0.25em \right) \).
- 20.
With ‖ x ‖ denoting the norm of the vector x; any norm can be used.
- 21.
That is, \( {w}_i^i=-b \).
- 22.
When the requirement \( \overset{\circ }{\omega_i}\in {\mathrm{\mathbb{R}}}_{+0}^l\kern-0.2em \) is relaxed to
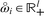 , the above definition is generalized as follows: f is non-confiscatory (NC) if \( \forall i\in N,\forall \overset{\circ }{\underrightarrow{\omega}}\in {\mathrm{\mathbb{R}}}_{+}^{ln},\overset{\circ }{\omega_i}\geqslant 0 \) implies \( \overset{\circ }{\omega_i}+{f}_i\kern0.15em \left(\overset{\circ }{\underrightarrow{\omega}}\kern-0.15em \right)\geqslant 0 \).
, the above definition is generalized as follows: f is non-confiscatory (NC) if \( \forall i\in N,\forall \overset{\circ }{\underrightarrow{\omega}}\in {\mathrm{\mathbb{R}}}_{+}^{ln},\overset{\circ }{\omega_i}\geqslant 0 \) implies \( \overset{\circ }{\omega_i}+{f}_i\kern0.15em \left(\overset{\circ }{\underrightarrow{\omega}}\kern-0.15em \right)\geqslant 0 \). - 23.
But not necessarily continuous.
- 24.
Note that the continuity of preferences is only needed for the necessity part of Theorm 1.2.
- 25.
Because \( w\sim ij={w}_i^j=\overset{\circ }{\omega_j} \) for all i ≠ j.
- 26.
By assumption, # N = n⫺3.
- 27.
These properties of h(·) can be verified directly.
- 28.
Proof: (omitting reference to s′):
h j⫺\( -{w}_j^j \) implies \( \sum \limits_{j\ne i}{h}_j \)⫺\( -\sum \limits_{j\ne i}{w}_j^j. \)
But balance implies Σj ≠ i h j = −h i. Hence, the previous inequality can be written as −h i⫺\( -{\Sigma}_{j\ne i}{w}_j^j \) which is equivalent to h i⫹\( {\Sigma}_{j\ne i}{w}_j^j \).
- 29.
Since i ≠ j.
- 30.
- 31.
The \( {w}_i^i \) component can be interpreted as the i-th agent’s claim concerning his own initial endowment.
- 32.
That is, \( A\left({w}_1^1,\dots, {w}_n^n\right) \) would be the set of feasible net allocations if \( \left({w}_1^1,\dots, {w}_n^n\right) \) were the true endowment profile.
- 33.
Note that the continuity of preference is only needed for the necessity part of this theorem.
- 34.
See also the theorem in Saijo (1988, p. 698), and theorem M 1 in Hurwicz (1986, p. 86); in the latter the assumptions of transitivity and completeness are dispensed with. The latter paper follows Maskin’s original schema, with Lemmas 1 (p. 88) and 2 (p. 90) corresponding to Maskin’s Theorems 4 and 5, respectively.
- 35.
This is so because, for n⫺3, in a pure exchange economy with strictly increasing preferences, the “no veto power” (NVP) requirement in Maskin’s Theorem 5 is necessarily satisfied.
- 36.
Since i ≠ j.
- 37.
It may be that this same modification would also work in Sect. 3.1.1.
- 38.
f is non-confiscatory (NC) if \( \forall i\in N,\forall \overset{\circ }{\underrightarrow{\omega}}\in {\mathrm{\mathbb{R}}}_{+0}^{ln},\overset{\circ }{\omega_i}+{f}_i\left(\overset{\circ }{\underrightarrow{\omega}}\right)\geqslant 0 \).
- 39.
NC is however, not a necessary condition for D-implementability.
- 40.
Note, however, that for purposes of this section\( {z}_i^{\prime}\kern0.36em {R}_i\kern0.36em {z}_i^{{\prime\prime} } \)should be interpreted as \( \left({w}_i^i+{z}_i^{\prime}\right)\ {R}_i\ \left({w}_i^i+{z}_i^{{\prime\prime}}\right). \)
- 41.
I.e., the formula of rule (b) for W-implementation applies.
- 42.
The paragraph starting with the words “Since f is IR …”
- 43.
Ending with “Hence s is an NE.”
- 44.
In fact k ∈ M(s) means that \( {w}_k^k\geqslant {w}_r^k \) for all r in N/{k}.
- 45.
For suppose that among agents other than i there are present at least two distinct profiles, say for agents j and k. If j and k disagree as to i’s endowment, so that \( {w}_j^i\ne {w}_k^i \), then i can choose \( {\tilde{w}}_i^i\geqslant 0 \), so that \( {\tilde{w}}_i^i \) is simultaneously different from \( {w}_j^i \) and \( {w}_k^i \) and not higher than ω i. On the other hand if j and k agree about i’s endowment, then they must disagree about the endowment of some agent r other than i (since, by hypothesis, they are in disagreement). In that case agent i can choose \( {\tilde{w}}_i^r \) that is different both from \( {w}_j^r \) and \( {w}_k^r \) (without removing any existing disagreements). In either case, the result is that \( \left(\tilde{s}\right)>2 \), contrary to the hypothesis of 1.B”.
- 46.
\( {\beta}_r\left(\tilde{s}\right)={\beta}_r(s) \) because β r (·) does not depend on r’s statements concerning the others’ endowments.
- 47.
The superscript refers to the game (W or D).
References
Groves, T., & Ledyard, J. (1977). Optimal allocation of public goods a solution to the ‘free rider’ problem. Econometrica, 45, 783–811.
Hong, L., & Page, S. (1994). Reducing informational costs in endowment mechanisms. Economic Design, 1(1), 103–117.
Hurwicz, L. (1972). On informationally decentralized systems. In C. B. McGuire & R. Radner (Eds.), Decision and organization. Amsterdam: North-Holland.
Hurwicz, L. (1986). On the implementation of social choice rules in irrational societies. In W. P. Heller, R. M. Starr, & D. A. Starrett (Eds.), Essays in Honor of Kenneth J. Arrow (Vol. 1). Cambridge: Cambridge University Press.
Hurwicz, L., Maskin, E., & Postlewaite, A. (1995). Feasible Nash implementation of social choice: Rules when the designer does not know endowments or production sets. In J. O. Ledyard (Ed.), The economics of informational decentralization: Complexity, efficiency, and stability. Boston, MA: Springer.
Maskin, E. (1977). Nash equilibrium and welfare optimality. Published in Review of Economic Studies 66: 1999, 23–38.
Nakamura, S. (1989). Efficient feasible Nash mechanisms with production and externalities. Doctoral dissertation, University of Minnesota.
Nakamura, S. (1990). A feasible Nash implementation of Walrasian equilibria in the two-agent economy. Economics Letters, 34, 5–9.
Page, S. (1989). Reducing the dimension of the message space in HMP. Unpublished note, dated July 1989.
Postlewaite, A. (1979). Manipulation via endowments. Review of Economic Studies, 46, 255–262.
Saijo, T. (1988). Strategy space reduction in Maskin’s theorem: Sufficient conditions for Nash implementation. Econometrica, 56(3), 693–700.
Sertel, M. (1994). Manipulating Lindahl equilibrium via endowments. Economics Letters, 34, 5–9.
Wilson, R. (1976). Competitive processes of price formation: A survey of several models. Mimeo: Stanford University (IMSSS).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Hurwicz, L., Maskin, E., Postlewaite, A. (2019). Feasible Nash Implementation of Social Choice Rules When the Designer Does Not Know Endowments. In: Trockel, W. (eds) Social Design. Studies in Economic Design. Springer, Cham. https://doi.org/10.1007/978-3-319-93809-7_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-93809-7_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93808-0
Online ISBN: 978-3-319-93809-7
eBook Packages: Economics and FinanceEconomics and Finance (R0)


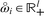 , the above definition is generalized as follows: f is non-confiscatory (NC) if
, the above definition is generalized as follows: f is non-confiscatory (NC) if